All Solutions
Page 65: Practice Problems
textbf{underline{textit{Solution}}}
$$
{parvspace{abovedisplayskip}noindent
begin{tabular}{>{$}l{${}}c<{{}$} @{} l}}
{end{tabular}parvspace{belowdisplayskip}}
textbf{underline{textit{Knowns:}}} The final velocity of the golf ball knowing its initial and the acceleration constant and the duration of the acceleration, can be calculated using the following equation
[ v_f = v_i + a t tag{1}]
Where,
begin{conditions}
v_f &: & The final speed of the ball.\
v_i &: & The initial speed of the ball.\
a &: &The acceleration constant.\
t &: &Duration of the acceleration.
end{conditions}
And since the ball is slowing as it moves toward the golf hole “as the hill is inclined toward the direction of the motion of the ball'', thus the ball is acceleration is negative, hence we substitute by the given value of the acceleration constant in equation (1) with a negative sign.\
It is given that the initial speed is 2 m/s, and the deceleration constant is 0.5 m/s$^2$ and the duration of the deceleration is 2 s, thus we can use equation (1) to find the final velocity.\
enumerate[bfseries (a)]
item Substituting the knowns in equation (1), we find the final velocity of the ball after 2 seconds of constant deceleration.
begin{align*}
v_f &= 2 – 0.5 left( 2right)\
&= fbox{$1 ~ rm{m/s}$}\
intertext{Thus, the final speed of the ball after 2 seconds, is 1 m/s.}
end{align*}
item Knowing that the velocity of the ball after 2 seconds is 1 m/s, we can calculate the final velocity of the ball if it kept decelerating for more 6 seconds “i.e. the total time of deceleration is 8 seconds” with the same constant of deceleration
begin{align*}
v_f &= 1 – 0.5 left( 6 right)\
&= -2 ~ rm{m/s}\
end{align*}
item The golf player hit the ball giving it an initial speed of 2 m/s, up toward the golf-hole on an inclined hill which works on decelerating the ball.\
Thus the ball gets slower as the time goes by till after 4 seconds the ball is velocity come to rest due to deceleration of the inclined hill, where the final velocity is calculated using equation (1).\
And then the ball starts to be accelerated in the negative direction “toward the player once again” and after 4 more seconds the ball is final velocity is 2 m/s toward the player.
item 1 m/s.
item -2 m/s.
item The ball rolls up toward the golf-hole on the inclined hill till it gets to rest after 4 seconds, and then rolls back toward the player once again.
textbf{underline{textit{Solution}}}
$$
{parvspace{abovedisplayskip}noindent
begin{tabular}{>{$}l{${}}c<{{}$} @{} l}}
{end{tabular}parvspace{belowdisplayskip}}
textbf{underline{textit{Knowns:}}} The final velocity of the bus knowing its initial and the acceleration constant and the duration of the acceleration, can be calculated using the following equation
[ v_f = v_i + a t tag{1}]
Where,
begin{conditions}
v_f &: & The final speed of the bus.\
v_i &: & The initial speed of the bus.\
a &: &The acceleration constant.\
t &: &Duration of the acceleration.
end{conditions}
And since the bus is speeding then the acceleration constant is positive, hence we substitute by the given value of the acceleration constant in equation (1) with a positive sign.\
It is given that the initial speed of the bus is 30 km/hr, and the acceleration constant is 3.5 m/s$^2$ and the duration of the acceleration is 6.8 s, thus we can use equation (1) to find the final velocity but first we need to convert the unit of the initial speed of bus from km/hr to m/s.\
And since 1 km = 1000 m and 1 hr = 3600 second, thus we convert the initial speed of the bus as follows
[ 30 ~ dfrac{rm{km}}{rm{hr}} ~ dfrac{1000 ~ rm{m}}{1 ~ rm{km}} ~ dfrac{1 ~ rm{hr}}{3600 ~ rm{s}} = 30 ~ dfrac{1000}{3600} ~ dfrac{rm{m}}{rm{s}} approx 8.3 ~ rm{m/s}]
begin{align*}
v_f &= 8.3 + 3.5 left( 6.8right)\
&= fbox{$32.1 ~ rm{m/s}$}\
intertext{Thus, the final speed of the bus is 32.1 m/s.}
end{align*}
v_{f} = v_{i} + aDelta t
$$
v_{f} = 8.3m/s +3.5m/s^2(6.8s)
$$
v_{f} =32.1m/s
$$
v_{f} =32.1m/s
$$
textbf{underline{textit{Solution}}}
$$
noindent
begin{tabular}{>{$}l{${}}c<{{}$} @{} l}}
{end{tabular}parvspace{belowdisplayskip}}
textbf{underline{textit{Knowns:}}} The duration of acceleration required for a car to reach the a final velocity of 28 m/s can be calculated knowing the initial speed and the constant of acceleration using the following equation
[ t = dfrac{v_f-v_i}{a} tag{1}]
Where,
begin{conditions}
t &: &Duration of the acceleration.\
v_f &: & The final speed of the bus.\
v_i &: & The initial speed of the bus.\
a &: &The acceleration constant.
end{conditions}
And since the car is speeding then the acceleration constant is positive, hence we substitute by the given value of the acceleration constant in equation (1) with a positive sign.\
It is given that the initial speed of the car is zero, and the acceleration constant is 5.5 m/s$^2$ and the final speed of the car is 28 m/s, thus we can use equation (1) to find the duration of acceleration.\
begin{align*}
t &=dfrac{28 – 0}{5.5}\
&= fbox{$5.1 ~ rm{m/s}$}\
intertext{Thus, the duration of the acceleration for the car to reach a final speed of 28 m/s accelerating from rest with a constant of acceleration of 5.5 m/s$^2$ is 5.1 seconds.}
end{align*}
v_{f} = v_{i} + aDelta t
$$
28m/s = 0 +5.5m/s^2(t)
$$
t =5.1s
$$
$upsilon_{i}=22 dfrac{text{m}}{text{s}}$ $upsilon_{f}=3 dfrac{text{m}}{text{s}}$
$a=-2.1 dfrac{text{m}}{text{s}^2}$
Note, since the car is slowing acceleration is negative.
Use the kinematic equation of motion for uniform acceleration from the Table 3-3.
$$
begin{align*}
upsilon_{f} &=upsilon_{i}+a Delta t tag{Equation 1.}\
end{align*}
$$
To find time before car travelling $3.0 text{m}/text{s}$ , we must rearrange equation 1
$$
begin{align*}
upsilon_{f} -upsilon_{i} &= a Delta t tag{Divide both sides by $a$.}\
dfrac{upsilon_{f} -upsilon_{i}}{a} &=dfrac{ a Delta t}{a} \
Delta t &=dfrac{upsilon_{f} -upsilon_{i}}{a}tag{Equation 2.}\
end{align*}
$$
Substitute values into equation 2 and solve for time,
$$
begin{align*}
Delta t &=dfrac{ bigg(3 dfrac{text{m}}{text{s}} bigg)- bigg(22 dfrac{text{m}}{text{s}} bigg)}{-2.1 dfrac{text{m}}{text{s}^2} }tag{Plug in values.}\
Delta t &=dfrac{ bigg(-19 dfrac{text{m}}{text{s}} bigg)}{-2.1 dfrac{text{m}}{text{s}^2} } \
Delta t &=9.047 text{s} \\
end{align*}
$$
v_{f} = v_{i} + aDelta t
$$
3.0m/s = 22m/s +(-2.1m/s^2)(t)
$$
t =9.0s
$$
textbf{underline{textit{Solution}}}
$$
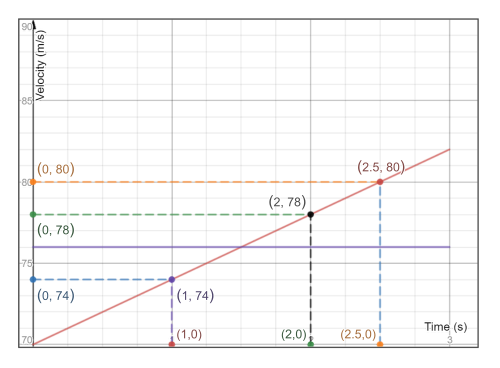
And since it is asking for the velocities for the speeding airplane therefor it is asking for the velocities for the airplane which is represented by the inclined line “the straight line whose slope is non-zero”.\
In order to find the velocities of the airplane at the stated times, we draw a vertical line from the times “at $x$-axis” at which it is required to find the velocity of the airplane.\
As the velocities is represented on the $y$-axis, then we try to find the $y$-component of the coordinates of the point of intersection with the straight line, as shown in the textbf{graph} where the speeding airplane is represented with red line.\
We find that the velocities are respectively:
newcounter{inlineenum}
renewcommand{theinlineenum}{bfseriesalph{inlineenum}}
newenvironment{inlineenum}
{unskipignorespacessetcounter{inlineenum}{0}%
renewcommand{item}{refstepcounter{inlineenum}{{theinlineenum})~}}}
{ignorespacesafterend}
center
inlineenum
item 74 m/s quad quad
item 78 m/s quad quad
item 80 m/s
renewcommand{theinlineenum}{bfseriesalph{inlineenum}}
newenvironment{inlineenum}
{unskipignorespacessetcounter{inlineenum}{0}%
renewcommand{item}{refstepcounter{inlineenum}{{theinlineenum})~}}}
{ignorespacesafterend}
center
inlineenum
item 74 m/s quad quad
item 78 m/s quad quad
item 80 m/s
dfrac{1,000m}{1km} ; dfrac{3600s}{1h}
$$
dfrac{75m}{1s}cdotdfrac{3600s}{hour}cdotdfrac{1km}{1000m}
$$
dfrac{mcdot scdot km}{scdot hcdot m}
$$
$$
1text{ km} = 1000text{ m}
tag{1}
$$
so rearranging that we get:
$$
1text{ m} = frac{1text{ km}}{1000}
tag{2}
$$
$$
1text{ h} = 3600text{ s}
tag{3}
$$
so rearranging that we get:
$$
1text{ s} = frac{1text{ h}}{3600}
tag{4}
$$
$$
begin{align*}
v &= 75 , frac{text{m}}{text{s}}\
&= 75 cdot frac{ left(dfrac{1text{ km}}{1000} right)}{ left(dfrac{1text{ h}}{3600} right)}\
&= 75 cdot left(frac{3600}{1000} right) cdot left(frac{1text{ km}}{1text{ h}} right)\
&= 75 cdot 3.6 , frac{text{km}}{text{h}}\
&= boxed{270 , frac{text{km}}{text{h}}}
end{align*}
$$
textbf{underline{textit{Solution}}}
$$
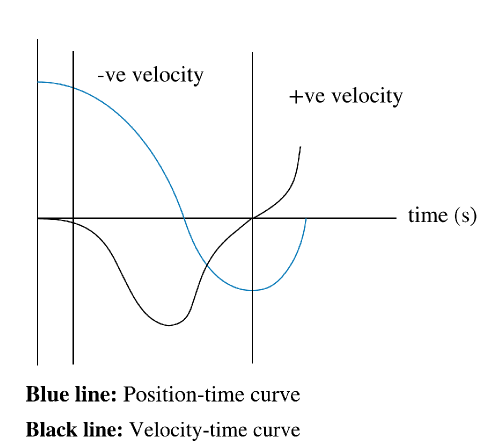
Since in a position-time graph, the slope of the line representing the motion of the object yields the velocity, and since the given curve in the graph is not a straight line, therefor the velocity of the object is not uniform it is changing continuously.
At a given point on a curve “i.e. at a given time and position” the slope of the tangent of this point represent the slope of the curve at this point, which is the velocity of the object at this particular instant.
From the look of the tangent, the object kept some uniform velocity passing the origin and then until the point of inflection in the position-time graph, where the tangent started to have a positive slope, which means that the object changed direction and kept moving with some speed toward the positive direction.
And, eventually it stopped at the origin and thus we have some picturing of how would our velocity-time graph look like.
$$
y=f(x)
$$
Since, we know that the slope of the curve represent, the velocity of the object thus, by simply differentiating the function that representing the position-time graph with respect of time, we would obtain a function that would perfectly fit the curve, such that
$$
y’=f'(x)
$$
Is the function that would represent the velocity-time graph, giving a closer look we found that the behavior of the curve is very close to cosine function $cos(x)$ “though not exactly periodic or symmetric” however as the behavior is very similar to the cosine function, we will assume that the position is given by some function
$$
y=cos(x) tag{1}
$$
By-differentiating equation (1) of position-time graph with respect to time “as time is plotted on $x$-axis thus we differentiate with respect to $x$” we would have the function that represent the motion of the pony in a velocity-time graph, such that
$$
dfrac{dy}{dx} = y’ = – sin(x)
$$
Thus, the function representing the curve would be very similar to the given curve except it would start from the origin, and it would have the same behavior as $-sin(x)$ “of course not a perfect periodic sine function but it would give us an idea how would the curve behaves”.
$textbf{underline{textit{note:}}}$ Again, the given position-time curve is not perfectly expressed by cosine function, however this approach is to help visualize the behavior of the velocity-time graph function.
textbf{underline{textit{Solution}}}
$$
{parvspace{abovedisplayskip}
noindent
begin{tabular}{>{$}l{${}}c<{{}$} @{} l}}
{end{tabular}parvspace{belowdisplayskip}}
begin{enumerate}[bfseries (a)]
item ~
end{enumerate}In the velocity-time graph, the slope of the line that represents the motion of the body yields its acceleration, where the velocity is represented on the $y$-axis and the time on $x$-axis.\
Where, the line representing the motion in the velocity-time graph in a given time interval, would be the line connecting between the 2 points $(v_f,t_f)$ and $(v_i,t_i)$.\
Where,
begin{conditions}
v_i& :& The initial velocity of the driver in the given time interval.\
v_f&: & The final velocity of the driver in the given time interval.\
t_i &: & The initial time of the driver at which the velocity is $v_i$.\
t_f &: & The final time of the driver at which the velocity is $v_f$.\
end{conditions}
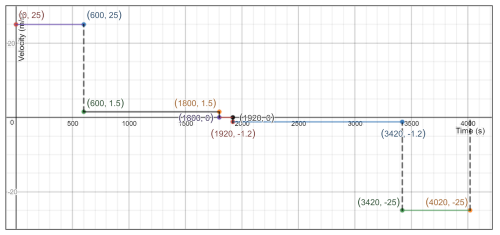
And since the velocity is constant at 25 m/s for 10 minutes, hence there is no acceleration therefor the line representing such motion would be a horizontal line “slope zero'' and drawn from the point on $y$-axis (0,25).\
And then it was given, that the car was stopped and the drivers walk in the same direction “thus the line representing the motion of the driver would have a the same velocity sign'' but with a reduced value of 1.5 m/s.\
And since it is given that he is walking with a constant pace for 20 minutes, therefor the line representing his motion would be the straight horizontal line connecting between the points (600,1.5) and (1800,1.5).\
{parvspace{abovedisplayskip}
noindent
begin{tabular}{>{$}l{${}}c<{{}$} @{} l}}
{end{tabular}parvspace{belowdisplayskip}}
enumerate[bfseries ]
item ~\
And after reaching the gas station the driver was stationary filling the gasoline can for 2 minutes, thus the line representing the motion of the driver during this time interval is a straight horizontal line connecting between the points $left( 1800,0right)$ and $left(1920,0right)$.\
And then the driver walked back to the car with a speed of 1.2 m/s, and we don't know for how long, but since the it was given that the driver walked with a speed of 1.5 m/s with a constant pace, for 20 minute then we can calculate how far was the gasoline station from the car, from the following equation
begin{align*}
d &= v t tag{1}\
intertext{Where,
begin{conditions}
d&: & Distance between the car and the gas station.\
v & :& The speed of the driver.\
t&: & The time took for the driver to reach the gas station.
end{conditions}
Thus, the distance between the car and the gas station is}
d &= 1.5 times 1200\
&= fbox{$1800 ~ rm{m}$}
intertext{And by knowing the distance between the car and gas station and knowing the speed of the driver when returning back to the car we can find the time he took to reach back to the car using equation (1)}
t&= dfrac{d}{v}\
&= dfrac{1800}{1.2}\
&= fbox{$1500 ~ rm{s}$}
end{align*}
Therefor, the line representing his motion would be a horizontal straight line connecting between (-1.2,1920) and (-1.2,3420).
At last the driver, decides to drive the car back home with a speed of 25 m/s and since the car at the beginning took 10 minutes to reach its position, thus it would take also 10 minutes to return back home.
Hence, the line representing this motion would be a horizontal line connecting between points (-25,3420) and (-25, 4020).
Thus, the motion of the whole journey is represented in a velocity-time graph, as in the following $textbf{graph}$
{parvspace{abovedisplayskip}
indent
begin{tabular}{>{$}l{${}}c<{{}$} @{} l}}
{end{tabular}parvspace{belowdisplayskip}}
begin{enumerate}[bfseries (b)]
item
end{enumerate}
From equation (1), the area under the line the velocity-time graph represents, the total distance traveled.\
And from knowing the time interval of motion in the velocity-time graph, and knowing the speed and the distance traveled by the car at each interval, we can draw our position-time graph.\
Where the line representing the motion in position-time graph would be the line between the two points $(x_f,t_t)$ and $(x_i,t_i)$ .\
Where,
begin{conditions}
x_i& :& The initial position of the driver in the given time interval.\
x_f&: & The final position of the driver in the given time interval.\
t_i &: & The initial time of the driver at which his position was at $x_i$.\
t_f &: & The final time of the driver at which his position was at $x_f$.\
end{conditions}
Therefor, the total distance traveled and the line representing the motion of the driver in the position-time graph in each of the following time interval:
begin{flalign*}
& textbf{underline{textit{[0,600]s:}}} & &&~ intertext{The car traveled a distance equal to the area under the line which is a rectangular whose sides are 25 and 600, thus the area is}&& d = 25 times 600= 15,000 ~ rm{m}&& && intertext{And since the speed is 25 m/s therefor the slope of the line is 25, thus the line representing the motion at this time interval would be a line joining the 2 points (0,0) and (600,15000)}&&\
end{flalign*}
& textbf{underline{textit{[600,1800] s:}}} & &&~ intertext{Therefor, from the area the total distance traveled is}&& d = 1.5 times 1200 = 1800 ~ rm{m}&& && intertext{And since the speed is 1.5 m/s and in the positive direction, therefor the slope of the line is 1.5, and hence the line which represents the motion at this time interval would be a line joining the 2 points (600,15000) and (1800,16800)}&&\
& textbf{underline{textit{[1800,3300]s:}}} & &&~ intertext{Therefor, from the area the total distance traveled is}&& d = 1.2 times 1500 = 1800 ~ rm{m}&& && intertext{And since the speed is 1.2 m/s and in the negative direction of that the previous time interval, therefor the slope of the line is -1.5, and hence the line representing the motion at this time interval would be a line joining the 2 points (1800,16800) and (3300,15000)}&&\
& textbf{underline{textit{[3300,3900]s:}}} & &&~ intertext{Therefor, from the area the total distance traveled is}&& d = 600 times 25 = 15,000 ~ rm{m}&& && intertext{And since the speed is 25 m/s and in the negative direction, therefor the slope of the line is -25 m/s, and hence the line representing the motion at this time interval would be a line joining the 2 points (3300,15000) and (3900,0)}&&\
end{flalign*}
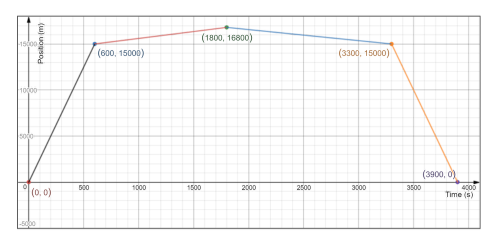
item See graph, 1800 m and 1500 s.
item See graph.
v_{f} = v_{i} + aDelta t
$$
0m/s =1.75m/s +(-.20m/s^2)(t)
$$
t =8.8s
$$
– The initial speed of the skateboarder $v_{text{i}}=1.75 , frac{text{m}}{text{s}}$
– The final speed of the skateboarder $v_{text{f}}=0$ (the moment when she begins to move back happens right after the moment that her velocity falls to zero)
– The acceleration over the given time interval $a=-0.20 , frac{text{m}}{text{s}^2}$
**Required:**
– The time interval of the deceleration.
We know that the average acceleration of a moving object can be expressed via the initial and final velocities and the elapsed time interval as:
$$
a = frac{v_{text{f}} – v_{text{i}}}{Delta t}
tag{1}
$$
Rearranging the previous expression for the time interval we get:
$$
Delta t = frac{v_{text{f}} – v_{text{i}}}{a}
tag{2}
$$
$$
begin{align*}
Delta t &= frac{0 – 1.75 , frac{text{m}}{text{s}}}{-0.20 , frac{text{m}}{text{s}^2}}\
&= 8.75text{ s}\
&= boxed{8.8text{ s}}
end{align*}
$$
Where we rounded the final expression to $2$ significant digits since that reflects the precision of the least precise piece of the given data.
textbf{underline{textit{Solution}}}
$$
{parvspace{abovedisplayskip}
indent
begin{tabular}{>{$}l{${}}c<{{}$} @{} l}}
{end{tabular}parvspace{belowdisplayskip}}
textbf{underline{textit{Knowns:}}} Knowing the final and initial speed of the race car and the duration of the deceleration we can find the deceleration constant from the following equation
[ Delta v = attag{1}]
Where,
begin{conditions}
Delta v&: & Is the difference between the final and initial velocity.\
~ a&: & The deceleration constant.\
~ t&: & The duration of the deceleration.
end{conditions}
By calculating the deceleration constant from equation (1), we can find the total distance traveled by the car using the following equation
[ Delta d = dfrac{v_f^2-v_i^2}{2a} tag{2}]
Where,
begin{conditions}
Delta d&: & Is the distance traveled by the car.\
~ a&: & The deceleration constant.\
~ v_f&: & The final velocity of the car.\
~ v_i&: & The initial velocity of the car.
end{conditions}
And it is given that the final velocity of the car is 22 m/s and the initial velocity of the car is 44 m/s, and the duration of the deceleration is 11 s.
$$
begin{align*}
a&=dfrac{v_f-v_i}{t}\
&=dfrac{22-44}{11}\
&= -2 ~ rm{m/s}^2
end{align*}
$$
Knowing the deceleration constant we now can use equation (2), to find the total distance traveled by the car during this period.
$$
begin{align*}
Delta d &= dfrac{22^2 – 44^2}{2timesleft( -2right)}\
&= fbox{$363 ~ rm{m}$}
end{align*}
$$
begin{align*}
Delta d &= dfrac{left( v_f^2 -v_i^2right) t}{2 left( v_f – v_iright)}\
intertext{And, $left(v_f^2-v_i^2 right)= left( v_f – v_iright)left(v_f+v_i right)$, which is the difference between two squares thus}
Delta d&= dfrac{1}{2} left( v_f + v_iright) t
end{align*}
Which is easier to use, as the equation of the distance traveled is in terms of knowns given in the problem.
$$d= dfrac{1}{2}left(v_i+v_f right)t tag{1}$$
Rearranging in terms of the duration of motion, we get
$$t=dfrac{2d}{left(v_i+v_f right)}tag{2}$$
Where,
– $d$: The distance the car moved while accelerating.
– $v_i$: The initial velocity by which the car was going
– $v_f$: The final velocity the car reached after the acceleration.
– $t$: The duration of acceleration.
Thus, knowing all the parameters in equation (2) we can calculate the duration of acceleration the car accelerated to reach its final velocity.
It is given that the initial velocity of the car is 15 m/s and its final velocity is 25 m/s and the distance the car moved while accelerating is 125 m.
$$begin{align*}
t &= dfrac{2.0 times 125}{left(15+25 right)}\
&= fbox{$6.25 ~ mathrm{s}$}
end{align*}$$
Since the least number of significant figures in the multiplication and division process is 2 significant figures, therefore the final result must have only 2 significant figures therefore the final result must be 6.3 s.
textbf{underline{textit{Solution}}}
$$
$$
d= dfrac{1}{2}left(v_i+v_f right)t tag{1}
$$
Rearranging in terms of the initial velocity, we get
$$
v_i=dfrac{2d}{t}-v_f tag{2}
$$
Thus, knowing all the parameters in equation (2) we can calculate the initial velocity from which the bike rider started accelerating.
$$
begin{align*}
v_i &= dfrac{2.0 times 19.0}{4.5}-7.5\
&= fbox{$0.944 ~ rm{m/s}$}
end{align*}
$$
Since the least number of digits after the decimal is 1, therefor the final result must have only 1 significant figure after the digit “according to the rules of addition for significant figures”, therefor the final result is 0.9 m/s.
textbf{underline{textit{Solution}}}
$$
As, the runner ran for 15 minutes with a uniform velocity of 4.5 m/s, thus we can calculate the distance the runner traveled during the 15 minutes using the following equation
$$
d_1= vt tag{1}
$$
And, while the runner is climbing the hill his velocity decelerates with a constant of acceleration given to be 0.05 m/s$^2$, and came to stop after 90 seconds, thus knowing that his initial velocity was 4.5 m/s the moment he started running the hill, and knowing the constant of deceleration and the duration of motion we can use the following equation
$$
d_2 = v_i t + dfrac{1}{2} a t^2 tag{2}
$$
And, thus the total distance the runner traveled is the sum of both distance, which is
$$
d_{tot} = d_1 + d_2 tag{3}
$$
First, we calculate the distance the runner moved before reaching the hill using equation (1), and substituting the knowns and since the duration of motion is 15 minutes we convert into units of seconds as the speed is in the units of m/s, thus we multiply by 60 and hence the distance is
begin{align*}
d_1 &= 4.50 times 15.0 times 60.0 \
&= 4050 ~ rm{m}
intertext{And, after reaching the hill and as the runner is initial speed is 4.5 m/s and the deceleration constant is 0.05 m/s$^2$ “we assign a negative sign as it is decelerating” and the duration of motion is 90 seconds, we use equation (2), and the runner distance over the hill is }
d_2 &= 4.5 times 90 – dfrac{1}{2} times 0.05 times 90^2\
&= 4.5 times 90 – 0.50 times 0.05 times 90^2\
&= 405 – 202.5 \
&= 202.5 ~ rm{m}
intertext{And, thus the total distance the runner covered using equation (2) is}
d_{tot} &= 4050 + 202.5 \
&= fbox{$4252.5 ~ rm{m}$}
end{align*}
textbf{underline{textit{note:}}} Since, the least number of significant figures in the operation of $d_1$ is 3, therefor the final answer should have also 3 significant figures, thus the answer is 4050.\
And since the least number of digits in left side multiplication is 2 therefor the product should be 410 m, and the product at the right term in $d_2$ should have only 2 significant figure therefor the answer should be 200 m, and since both terms have zero decimals then the final answer in the subtraction should also have no decimals, therefor $d_2$ is final answer is 210.\
And since the terms in $d_{tot}$ is 4050 and 210 both having no decimals, therefor the result of adding both numbers should have no decimals as well, therefor the final result should be 4260.\
$v_{f}=v_{i}+overline{a}t$
$d_{f}-d_{i}=v_{i}t+displaystyle frac{1}{2}overline{a}t^{2}$
$v_{f}^{2}=v_{i}^{2}+ 2 overline{a}(d_{f}-d_{i})$
Since the initial velocity was 0, the first formula gives
$d_{f1}=displaystyle frac{1}{2}cdot(frac{1}{2} m/s^{2})cdot(6s)^{2}=9m$
The second part of motion is with constant acceleration.
$d_{f2}=vt_{2}=(3.00m/s)(6s)=18m.$
In total,
**We know that:**
– His acceleration is $a=0.5 , frac{text{m}}{text{s}^2}$
– The first time interval is $Delta t_1=6.0text{ s}$
– His velocity after the acceleration $v=3.0 , frac{text{m}}{text{s}}$
– The second time interval is also $Delta t_2=6.0text{ s}$
Since the acceleration is constant, the movement describing the first interval will be an inclined line of constant positive slope.
After that, the bike moves with uniform velocity, so that will correspond to a horizontal line on the velocity-time graph.
Both time intervals are of equal length.

As instructed, now that we have constructed the graph, we will find the total displacement of the bike by calculating the area under the line.
We see that this area can be broken into two sub-areas, one for each time interval.
$$
A_1 = frac{1}{2} cdot v cdot Delta t_1
$$
Plugging in the numbers we get:
$$
begin{align*}
A_1 &= frac{1}{2} cdot left(3.0 , frac{text{m}}{cancel{text{s}}} cdot 6.0cancel{text{ s}} right)\
&= boxed{9text{ m}}
end{align*}
$$
$$
A_2 = v cdot Delta t_2
$$
Plugging in the numbers we get:
$$
begin{align*}
A_2 &= 3.0 , frac{text{m}}{cancel{text{s}}} cdot 6.0cancel{text{ s}}\
&= boxed{18text{ m}}
end{align*}
$$
$$
begin{align*}
d &= d_1 + d_2\
&= A_1 + A_2\
&= 9text{ m} + 18text{ m}\
&= boxed{27text{ m}}
end{align*}
$$
This is the sought-after displacement!
$v_{f}=v_{i}+overline{a}t$
$d_{f}-d_{i}=v_{i}t+displaystyle frac{1}{2}overline{a}t^{2}$
$v_{f}^{2}=v_{i}^{2}+ 2 overline{a}(d_{f}-d_{i})$
For part 1 ( Constant acceleration):
so
$d_{mathrm{f}}=displaystyle frac{v_{f}^{2}-v_{i}^{2}}{2mathrm{a}}$
and, since $v_{mathrm{i}}=0.00mathrm{m}/mathrm{s}$
$d_{mathrm{f}}=displaystyle frac{v_{f}^{2}}{2mathrm{a}}=frac{(18.0mathrm{m}/mathrm{s})^{2}}{(2)(2.00mathrm{m}lmathrm{s}^{2})}=81.0mathrm{m}$
$d_{2}=vt=(18.0mathrm{m}lmathrm{s})(60.0mathrm{s})=1.08times 10^{3}mathrm{m}$
In total,
$d=d_{1}+d_{2}$
$$
=81.0mathrm{m}+1.08times 10^{3}mathrm{m}
$$
$$
=1.16times 10^{3}mathrm{m}
$$
1.16times 10^{3}mathrm{m}
$$
– The acceleration is $a=2.0 , frac{text{m}}{text{s}^2}$
– The velocity after the acceleration $v_{text{f}}=18.0 , frac{text{m}}{text{s}}$
– The time interval of uniform motion is $Delta t=60.0text{ s}$
We need to calculate the total displacement.
$$
v_{text{f}}^2 = v_{text{i}}^2 + 2 cdot a cdot d_1
tag{1}
$$
Where we denoted the displacement with the index $1$ to differentiate it from the second displacement we will calculate next.
$$
d_1 = frac{v_{text{f}}^2 – v_{text{i}}^2}{2a}
tag{2}
$$
Now inserting the fact that the initial velocity is zero we get:
$$
d_1 = frac{v_{text{f}}^2}{2a}
tag{3}
$$
$$
begin{align*}
d_1 &= frac{ left(18.0 , frac{text{m}}{text{s}} right)^2}{2 cdot left(2.0 , frac{text{m}}{text{s}^2} right)}\
&= boxed{81text{ m}}
end{align*}
$$
Here the bike moves uniformly, so the displacement here is easily found:
$$
d_2 = v_{text{f}} cdot Delta t
tag{4}
$$
$$
begin{align*}
d_2 &= 18.0 , frac{text{m}}{cancel{text{ s}}} cdot 60.0cancel{text{ s}}\
&= boxed{1,080text{ m}}
end{align*}
$$
$$
begin{align*}
d &= d_1 + d_2\
&= 1,080text{ m} + 81text{ m}\
&= 1,161text{ m}\
&= boxed{1.16text{ km}}
end{align*}
$$
textbf{underline{textit{Solution}}}
$$
[d=vt tag{1} ]
And, Sunee is running for a 5 km race, thus the remaining distance to the finish line is 98 m, and since we know that Sunee accelerated till it reached the finish line for a duration of 19.4 seconds, and knowing the initial velocity by which Sunee was running, thus we can use the following equation to find the acceleration
[d= v_i t + dfrac{1}{2} a t^2 ]
Where, only the acceleration $a$ is unknown, rearranging the equation in terms of acceleration
[a = dfrac{2left(d-v_it right)}{t^2} tag{2} ]
Where,
newenvironment{conditions}
{parvspace{abovedisplayskip}
noindent
begin{tabular}{>{$}c{${}}c<{{}$} @{} p{9.1 cm}}}
{end{tabular}parvspace{belowdisplayskip}}
begin{conditions}
a &: & The constant of acceleration.\
v_i &: & The initial velocity by which Sunee was running.\
d & :& The distance Sunee moved while accelerating.\
t & :& Duration of acceleration .\
end{conditions}
$$
begin{align*}
a &= dfrac{2(98- left(4.3 times 19.4 right) )}{19.4^2}\
&= fbox{$0.07748 rm{m/s}^2$}
end{align*}
$$
And since the least number of significant figures in the multiplication is 2, therefor the final answer should have 2 significant figures only, hence the final result is 0.078 m/s$^2$.

