Home Page Textbooks Physics: Principles and Problems Page 52: Assessment

Physics: Principles and Problems

9th Edition

Elliott, Haase, Harper, Herzog, Margaret Zorn, Nelson, Schuler, Zitzewitz

ISBN: 9780078458132

Textbook solutions

All Solutions

Page 52: Assessment

Exercise 34

Step 1

1 of 1

Information can be represented in various forms in physics. These forms are with words, a data table, a position time graph, and a motion diagram. Therefore equivalent representations goes in the big circle and the other words go in the small circles.

Exercise 35

Solution 1

Solution 2

Step 1

1 of 4

$$
textbf{underline{textit{Solution}}}
$$

Step 2

2 of 4

The motion-diagram is used to represent the motion of the object, where it is represented using dots which indicates the position of the object at giving instant.\

Moreover, the time interval between two consecutive dots are made to have some specific value of choice, where we can make the time interval between two consecutive dots to be 1 second for example, and also we can draw the distance between the dots using any scale of choice so we can represent the distance moved by the object in a given time interval.\

For example if we draw the dots such that 1 cm on paper scales to 10 m, thus drawing two consecutive dots separated by 1 cm and whose time interval is 1 second means that the object moved 10 m in 1 second, thus we can define the position of a given object during a given instant of time using a motion diagram.\

Moreover, as we know the distance between the dots represent the distance and knowing the time interval between the dots, we can calculate the velocity of the object at a given instant, where
[ v= dfrac{d}{t}]
Where,
newenvironment{conditions}
{parvspace{abovedisplayskip}
noindent
begin{tabular}{>{$}c{${}}c<{{}$} @{} p{10 cm}}}
{end{tabular}parvspace{belowdisplayskip}}
begin{conditions}
v& :& The velocity of the object. at a given dot “instant of time''.\
d &: & The distance separated between the dots “the distance the object moved''.\
t& :& The time duration of the motion “the time interval between the dots''.\end{conditions}

Step 3

3 of 4

And since, we know the velocity of the object at each given instant of time “dots” and knowing the time interval between each two consecutive dots, we can also find the acceleration where
[ a = dfrac{v_f – v_i}{t}]
Where,
newenvironment{conditions}
{parvspace{abovedisplayskip}
noindent
begin{tabular}{>{$}c{${}}c<{{}$} @{} p{10 cm}}}
{end{tabular}parvspace{belowdisplayskip}}
begin{conditions}
a&: & The acceleration of the object at a given time interval.\
v_f & :& The final velocity of the object.\
v_i &: & The initial velocity of the object.\
t & :& the duration during which the velocity of the object changed.\
end{conditions}

Thus, basically representing the motion of some object using the motion diagram actually helps solving some problems concerns the motion of the object, such as finding the velocity and acceleration, but mainly it is one way to represent a given physical problem to help visualize and solve the given problem.

Result

4 of 4

It can be used to find the acceleration and the velocity of the object if proper information concerning the distance and the time interval between the consecutive dots, but mainly it is used to represent and visualize a given physical problem.

Step 1

1 of 2

A motion diagram provides a visual aid to a problem. This visual aid makes it easier for the student to understand and picture the actual situation presented in the problem. It also makes it very simple to compare two situations at the same time in a simple picture.

Result

2 of 2

See explanation

Exercise 36

Step 1

1 of 2

An object will be a point particle only if the object is relatively small when compared to how far it moves and if the object’s internal motions are irrelevant.

Result

2 of 2

if the object is relatively small and if internal motions are irrelevant.

Exercise 37

Solution 1

Solution 2

Step 1

1 of 2

Position and displacement are different from distance as position and displacement rely on information about which direction the object will move. Distance does not take into account the direction.

Step 2

2 of 2

Distance and displacement are different from position as both of these describe how an object’s location changes during a period of time. Position tells us exactly where the object is at a specific time.

Step 1

1 of 4

In this problem, we are asked to explain the difference between position, distance, and displacement.

Step 2

2 of 4

**Position**

The position is a vector pointing from the origin to the object it describes.

Though it changes as time passes if the object moves, it in no way needs movement to be defined. It is defined for a stationary object as well.

Step 3

3 of 4

**Distance**

Distance is a scalar quantity describing the length of a line joining two points in space.

Though it changes as time passes if the relevant objects move, it in no way needs movement to be defined. It is defined for stationary objects as well.

Step 4

4 of 4

**Displacement**

Displacement is a vector pointing from the initial position, to the final position of an object it describes.

Since it describes how an object changes its position as time passes, it needs movement to be defined.
It is actually zero for stationary objects.

Exercise 38

Step 1

1 of 1

If you read a clock’s time in the beginning and end of an interval and then subtract the beginning time from the ending time, then you can find the time interval taken place.

Exercise 39

Solution 1

Solution 2

Result

1 of 1

Record the positions of each skater at every time interval. Then, find the velocity. The one with the greater velocity will pass the other one. The lines will intersect if they pass one another on a graph.

Step 1

1 of 3

In this problem, we are asked to explain how a position-time graph can be used to determine if and when one skater will pass by another skater if we know that they are moving along the same line.

Step 2

2 of 3

We know that lines on a position-time graph represent the position coordinate as a function of the time coordinate.

If two lines intersect, that means that the bodies they describe have both coordinates the same. That is, they are located at the same point in the same moment of time.

This means that if two lines intersect, that corresponds to one skater passing by the other one.

Step 3

3 of 3

We just want to add that if there is no intersection point on the graph visible, that doesn’t necessarily mean that no such point will occur in the future.

If two lines appear to converge, an intersection will happen at some point, and it will correspond to one skater passing by the other.

Exercise 40

Step 1

1 of 1

The walker and runner will have straight lines on their position-time graphs. They both start at the same position; however, the runner will have a steeper slope (higher velocity) than the walker because the runner is traveling at a faster pace than the walker.

Exercise 41

Step 1

1 of 2

The slope of a position time graph is the objects velocity. Slope is defined as $Delta y / Delta x$ and the y variable is displacement and the x variable is time. the change in displacement over time is the definition of the velocity formula

Result

2 of 2

see explanation

Exercise 42

Step 1

1 of 1

You can calculate the average velocity from the given information; however, you can’t find the instantaneous velocity because it is essentially the derivative of the object’s average velocity equation.

Exercise 43

Step 1

1 of 4

$Delta t + Delta d$ will increase when either constant increase.

Step 2

2 of 4

The sign of $Delta d – Delta t$ will depend on how big $Delta d$ and $Delta t$ is.

Step 3

3 of 4

$Delta t times Delta d$ will increase when either constant increases.

Step 4

4 of 4

$dfrac{Delta t}{Delta d}$ decreases when there is an increasing displacement. It will also increase when there is an increase in the time period.

Exercise 44

Step 1

1 of 1

Footballs can be a point particle if the football’s rotations aren’t taken into account. Also if the football is small (compared to the distance it is thrown. Usually if you throw a football more than 1 or 2 yards), then it can be a point particle as well.

Exercise 45

Step 1

1 of 1

Football players are point particles if their motions aren’t important and is they are small in comparison to how far they run.

Exercise 46

Step 1

1 of 3

a. According to the graph, relative to runner B who starts at the y-intercept, runner A got a head start of 4 units.

Step 2

2 of 3

b. Runner B has a steeper slope (which means a higher velocity) when compared to runner A; therefore, runner B runs faster.

Step 3

3 of 3

c. Runner B surpasses runner A at point P since that’s where they intersect.

Exercise 47

Step 1

1 of 5

Moolinda has the flattest slope; therefore, she must be the slowest.

Step 2

2 of 5

Dolly has a flat slope; however, her slope is slightly steeper than Moolinda, but not as steep as either Elsie or Bessie.

Step 3

3 of 5

Bessie’s slope is steeper than Dolly’s but not as steep as Elsie’s; therefore, Bessie is next.

Step 4

4 of 5

Elsie has the steepest slope when compared to all of them; therefore, she is the fastest.

Result

5 of 5

Moolinda, Dolly, Bessie, Elsie

Exercise 48

Solution 1

Solution 2

Step 1

1 of 3

$$
textbf{underline{textit{Solution}}}
$$

Step 2

2 of 3

enumerate[bfseries (a)]
item If we examine the given graph, we find that the position is represented on the $y$-axis and the time is represented on the $x$-axis.\

And since the slope is given by
[ m=dfrac{y_2-y_1}{x_1-x_2}]

Thus, the slope of the line “representing the motion of the rabbit” is the speed of the rabbit, and if the speed of the rabbit is doubled then the slope will be doubled, thus the straight line representing the rabbit is motion will be steeper.\

item If the rabbit ran in the opposite direction with the same speed, then the line representing the motion of the rabbit would have a slope with the same magnitude and a negative sign, and the position would be represented on the negative $y$-axis, as follows

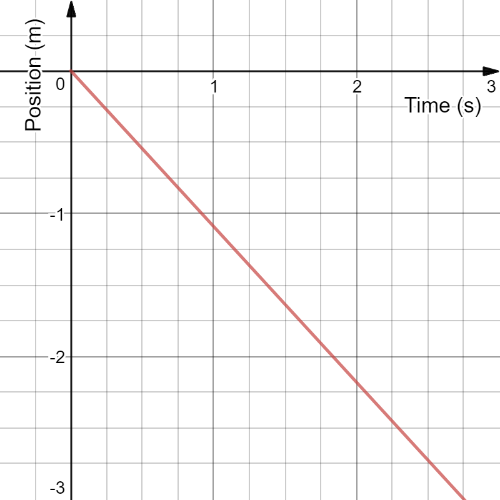
Exercise scan

Result

3 of 3

enumerate[bfseries (a)]
item As the speed is doubled, the slope of the straight line in position-time graph is doubled.
item The graph would have a slope with the same magnitude and negative sign, and the position would be represented on the -ve $y$-axis

Step 1

1 of 3

a) If the rabbit was twice as fast, then the slope of the graph would be twice as steep as they are covering more distance over a short amount of time.

Step 2

2 of 3

If the rabbit runs in the opposite direction, then the magnitude of the slope would be the same; however, the value would be negative since it’s traveling in the opposite direction.

Result

3 of 3

a) the slope would be twice as steep, b) the magnitude of the slope is the same; however, it would be negative

Exercise 49

Solution 1

Solution 2

Step 1

1 of 3

d = vt

Distance is speed times time.

Step 2

2 of 3

d = (4.0 m/s)(5s) = 20m

Plug in the values for speed (4.0 m/s) and time (5.0 s) and compute.

Result

3 of 3

d = 20m

Step 1

1 of 5

**Given:**
– The speed of the bike $v=4.0 , frac{text{m}}{text{s}}$
– The time interval of movement $Delta t=5.0text{ s}$

**Required:**
– The total distance traveled.

Step 2

2 of 5

**Approach**

We know that the speed of a moving object can be expressed via the distance traveled and the elapsed time interval as:
$$
v = frac{d}{Delta t}
tag{1}
$$

Step 3

3 of 5

Rearranging for the total distance we get:
$$
d = v cdot Delta t
tag{2}
$$

Step 4

4 of 5

Plugging in the values we get:
$$
begin{align*}
d &= 4.0 , frac{text{m}}{cancel{text{s}}} cdot 5cancel{text{ s}}\
&= boxed{20text{ m}}
end{align*}
$$

Result

5 of 5

$d = 20text{ m}$

Exercise 50

Solution 1

Solution 2

Step 1

1 of 3

$$
d = vt
$$

Distance is velocity times time.

Step 2

2 of 3

$$
d = left( 3.00 times 10^{8} m/sright)left( 8.3 minright)left( dfrac{60 s}{1 min}right) = 1.5 times 10^{11} m
$$

Plug in the velocity and time into the equation. Then use dimensional analysis to convert the units to SI units using the conversion 1 min = 60s.

Result

3 of 3

$d = 1.5 times 10^{11}$ m

Step 1

1 of 6

**Given:**
– The speed of light $c=3.0 times 10^{8} , frac{text{m}}{text{s}}$
– The time interval of movement $Delta t=8.3text{ min}$

**Required:**
– The total distance traveled.

Step 2

2 of 6

**Approach**

We know that the speed of a moving object can be expressed via the distance traveled and the elapsed time interval as:
$$
v = frac{d}{Delta t}
tag{1}
$$
The same is true for light $(v=c)$.

Step 3

3 of 6

Rearranging for the total distance we get:
$$
d = c cdot Delta t
tag{2}
$$

Step 4

4 of 6

First we will convert the time interval from minutes to seconds:
$$
begin{align*}
Delta t &= 8.3text{ min}\
&= 8.3cancel{text{ min}} cdot 60 , frac{text{s}}{cancel{text{min}}}\
&= boxed{490text{ s}}
end{align*}
$$

Step 5

5 of 6

Now plugging the values into the expression $(2)$ we get:
$$
begin{align*}
d &= left(3.0 times 10^{8} , frac{text{m}}{cancel{text{s}}} right) cdot left(490cancel{text{ s}} right)\
&= boxed{1.5 times 10^{11}text{ m}}
end{align*}
$$

Result

6 of 6

$d = 1.5 times 10^{11}text{ m}$

Exercise 51

Solution 1

Solution 2

Step 1

1 of 3

$$
d = vt
$$

Distance is velocity times time.

Step 2

2 of 3

$$
d = left( 55 km/hright)left(0.75 s right)left(dfrac{1000 m}{1 km} right)left( dfrac{1 h}{3600 s}right) = 11 m
$$

Plug in the velocity and time into the equation. Then use dimensional analysis to convert the units to SI units using the conversion 1 km = 1000 m; 1 h = 3600 s.

Result

3 of 3

$d = 11$ m

Step 1

1 of 6

**Given:**
– The speed of the car $v=55 , frac{text{km}}{text{h}}$
– The time interval of movement $Delta t=0.75text{ s}$

**Required:**
– The total distance traveled.

Step 2

2 of 6

**Approach**

We know that the speed of a moving object can be expressed via the distance traveled and the elapsed time interval as:
$$
v = frac{d}{Delta t}
tag{1}
$$

Step 3

3 of 6

Rearranging for the total distance we get:
$$
d = v cdot Delta t
tag{2}
$$

Step 4

4 of 6

First we will convert the speed of the car from kilometers per hour $(text{km/h})$ to meters per second $(text{m/s})$:
$$
begin{align*}
v &= 55 , frac{text{km}}{text{h}}\
&= 55 cdot left(frac{1000text{ m}}{3600text{ s}} right)\
&= boxed{15.28 , frac{text{m}}{text{s}}}
end{align*}
$$

Where we used the fact that $1text{ km}=1000text{ m}$ and $1text{ h}=3600text{ s}$.

Step 5

5 of 6

Now plugging the values into the expression $(2)$ we get:
$$
begin{align*}
d &= 15.28 , frac{text{m}}{cancel{text{s}}} cdot 0.75cancel{text{ s}}\
&= boxed{11.5text{ m}}
end{align*}
$$

Result

6 of 6

$d =11.5text{ m}$

Exercise 52

Step 1

1 of 2

We should use $d=vt$ equation;

From above equation $t=dfrac{d}{v}$

$t=dfrac{(4.3km)(dfrac{1000m}{1km})}{4.0m/s}$

$t=1075s simeq18min$

Result

2 of 2

$$
textit{color{#c34632} $ 18 $ $min $}
$$

Exercise 53

Step 1

1 of 4

$$
textbf{underline{textit{Solution}}}
$$

Step 2

2 of 4

$textbf{underline{textit{Knowns:}}}$

Knowing the speed by which each driver travels and the distance traveled we can find how long did it take for each driver to reach its final destination.

Where the total distance traveled by each car is given to be 50 km, and the speed of each car is 95 and 90 km/hr.

And the time of the journey can be calculated using the following equation

$$
t= v/d tag{1}
$$

Thus, we can find the time of the journey of each car using equation (1) and by subtracting we can find how long did the first driver to reach the final destination would have to wait for the other driver.

Step 3

3 of 4

textbf{underline{textit{Calculations:}}}\

Thus the time of journey for each car using equation (1) and knowing the speed of each car and the traveled distance is as follows
begin{align*}
intertext{The time of journey of the car going with speed of 95 km/hr}
t_{95} &= 50/95 \
&=0.526 ~ rm{hr}\
&= 31.579 ~ rm{min}
intertext{And, the time of the journey of the car going with speed of 90 km/hr is}
t_{90}&= 50/90\
&= 0.556 ~ rm{hr}\
&= 33.33 ~ rm{min}\
end{align*}

And knowing the time took by each car to reach its final destination we can find the time difference by which the first car have to wait, where the time difference is

begin{align*}
Delta t &= t_{90} – t_{95}\
&= 33.33 – 31.58 \
&= fbox{$1.75 ~ rm{min}$}\
end{align*}

Thus, the first car to arrive have to wait for 1.75 minutes or for 105 seconds before the second car arrives.\

Result

4 of 4

105 seconds

Exercise 54

Step 1

1 of 3

(a) The x axis should read 0.0, 10.0, 20.0, etc, as the text requires. Exercise scan

Step 2

2 of 3

(b) 550 m

Result

3 of 3

click for graph/answers

Exercise 55

Step 1

1 of 5

$$
textbf{underline{textit{Solution}}}
$$

Step 2

2 of 5

The given particle model diagram, shows the motion of the chicken from one side of the street to the other side, where the diagram models the position of the chicken in a time intervals of 0.1 s.\

And checking the given diagram carefully we notice that the points are equidistant which means that the chicken is moving with a constant pace having a uniform speed.\

And we would take the beginning side of the road is the point of origin and moving a distance $Delta x$ every 0.1 seconds such that the following textbf{table} describes the particle diagram
begin{flushleft}
begin{tabular}{|| c ||c | c | c | c | c | c | c | c |}
hline hline
Position $Delta x$ & 0 &1 $Delta x$ & 2 $Delta x$ & 3 $Delta x$ & 4 $Delta x$ & 5 $Delta x$ & 6 $Delta x$ & 7 $Delta x$ \
hline
Time (s)& 0&0.1 & 0.2 &0.3&0.4&0.5&0.6&0.7\
hline hline
end{tabular}
newline
vspace*{1 cm}
newline
begin{tabular}{||c||c| c | c| c| c| c|c|}
hline hline
Position $Delta x$ & 8 $Delta x$ & 9 $Delta x$ & 10 $Delta x$ & 11 $Delta x$ & 12 $Delta x$ & 13 $Delta x$ & 14 $Delta x$ \
hline
Time (s)&0.8& 0.9 & 1.0 &1.1&1.2&1.3&1.4 \
hline hline
end{tabular}
newline
vspace*{1 cm}
newline
begin{tabular}{||c|| c| c| c| c|c|}
hline hline
Position $Delta x$ & 15 $Delta x$ &16$Delta$ & 17$Delta x$ & 18$Delta x$ & 19$Delta x$\
hline
Time (s) &1.5 &1.6& 1.7& 1.8&1.9\
hline hline
end{tabular}
end{flushleft}

Step 3

3 of 5

From the previous table, we can plot the $textbf{graph}$ as follows where we chose the step of the $y$-axis in units of $Delta x$

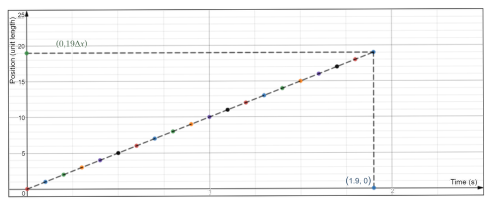
Exercise scan

Step 4

4 of 5

Where the general equation of straight lines is given by

$$
y=mx+c
$$

And since the straight line passing through the origin thus the $y$-intercept is $c=0$, and the slope of this line using any 2 points on the given line is given by

$$
m = dfrac{y_2 – y_1}{x_2 -x_1}=dfrac{Delta x}{0.1} = 10 Delta x
$$

Therefor the equation of this straight line is

$$
y = left(10Delta x right) x
$$

$textbf{underline{textit{note:}}}$ we used $Delta x$ as a unit length “the distance between the two consecutive points in the particle diagram”, as the distance between the two points is not given.

Result

5 of 5

See graph, The equation is $y=left(10Delta x right) x$

Exercise 56

Step 1

1 of 3

a) to determine when Joszi and Heike are in the same place, determine the points of intersections:
the graphs intersect in the interval [1h,1.12h]

Step 2

2 of 3

b) Joszi passes Heike after 1.12 h

Step 3

3 of 3

c) there is a swift current where there is a slope change, so it’s between 6 km and 9km,

Exercise 57

Step 1

1 of 3

**Known values:**
$$begin{align*}
v_A&=75 mathrm{km/h}\
v_B&=85 mathrm{km/h} \
t&=2 mathrm{h} \
x&=120 mathrm{km}
end{align*}$$
**Unkonwn values:**
$$begin{align*}
x_{A (2 mathrm{h})}&=? \
x_{B (2 mathrm{h})}&=? \
t_{A (x=120 mathrm{km})}&=? \
t_{B (x=120 mathrm{km})}&=?
end{align*}$$

Step 2

2 of 3

We have one and that is the origin of the coordinate system for the other we have to calculate the position of both cars after two hours. To be able to draw a $x-t$ graph, we need two points.

$$begin{align*}
v&=dfrac{x}{t} rightarrow x=vcdot t\
x_{A (t=2 mathrm{h})}&=v_A cdot t \
&=75 mathrm{km/h} cdot 2mathrm{h} \
&=150 mathrm{km}\
\
x_{B (t=2 mathrm{h})}&=v_A cdot t \
&=85 mathrm{km/h} cdot 2mathrm{h} \
&=170 mathrm{km}
end{align*}$$

Calculating the time it takes an individual car to pass a gas station is simply calculating the time it takes to travel $120 mathrm{km}$:
$$begin{align*}
t&=dfrac{x}{v} \
t_{A (x=120 mathrm{km})}&=dfrac{x}{v_A} \
&=dfrac{120 mathrm{km}}{75 mathrm{km/h}} \
&=1.6 mathrm{h}=1 mathrm{h} 36 mathrm{min} \
\
t_{B (x=120 mathrm{km})}&=dfrac{x}{v_A} \
&=dfrac{120 mathrm{km}}{85 mathrm{km/h}} \
&=1.4 mathrm{h}=1 mathrm{h} 24 mathrm{min}
end{align*}$$

Step 3

3 of 3

Now let’s sketch a $x-t$ graph.
![‘slader’](https://d2nchlq0f2u6vy.cloudfront.net/21/03/20/b87a89c4722e6af9c174c1efe4e86efc/3ada761c6a7549691b46ed4faed5166e/image_scan.png)

It is important to note that cars drive at a constant speed which means that the $x-t$ graph will be linear.

**Conclusion.**

$$begin{align*}
x_{A (t=2 mathrm{h})}&=150 mathrm{km} \
x_{B(t=2 mathrm{h})}&=170 mathrm{km} \
t_{A (x=120 mathrm{km})}&=1.6 mathrm{h} \
t_{B (x=120 mathrm{km})}&=1.4 mathrm{h}
end{align*}$$

Exercise 58

Step 1

1 of 3

Known:

$$
begin{align*}
s_1&= 50 mathrm {km} tag{school to beach} \
s_2&= s_1 – 10 mathrm{km} = 40 mathrm{km} tag{store to beach} \
t_A&= 12:00 mathrm{P.M.} tag{departure time of A} \
t_B&= 12:30 mathrm{P.M.} tag{departure time of B} \
v_A&=40 mathrm{km/h} \
v_B&= 100 mathrm{km/h}
end{align*}
$$

Unknown:

$$
begin{align*}
t’_A&=? tag{time of arrival of A} \
t’_B&=? tag{time of arrival of B} \
Delta t&=? tag{travel time}
end{align*}
$$

Step 2

2 of 3

Time is calculated by adding the travel time to the departure time:

$$
begin{align*}
Delta t&=t+t’
end{align*}
$$

Travel time is thus obtained by dividing the path by the speed:

$$
begin{align*}
Delta t&=dfrac{s}{v} \
Delta t_A&=dfrac{s_2}{v_A} \
&=dfrac{40 mathrm{km}}{40 mathrm{km/h}} \
&=1 mathrm{h} \
\
Delta t_B&=dfrac{s_a}{v_B} \
&=dfrac{50 mathrm{km}}{100 mathrm{km/h}} \
&=0.5 mathrm{h}=30 mathrm{min} \
\
t’_A&=t_A+Delta t_A \
&=12:00 mathrm{P.M} + 1 mathrm{h} \
&=13:00 mathrm{P.M.} \
\
t’_B&=t_B+Delta t_B \
&=12:30 mathrm{P.M} + 30 mathrm{min} \
&=13:00 mathrm{P.M.} \
end{align*}
$$

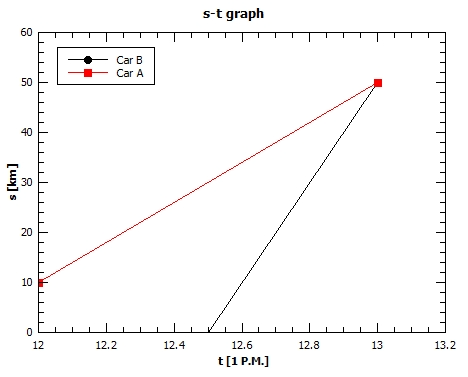
Exercise scan

Result

3 of 3

Both cars arrive at the beach at $13 mathrm{P.M.}$

Exercise 59

Step 1

1 of 6

$$
textbf{underline{textit{Solution}}}
$$

Step 2

2 of 6

$textbf{underline{textit{First graphically:}}}$ We start by finding the answer graphically, we start by plotting a line for each of the cars.

As we are to plot a position-time graph where we are the position is plotted on $y$-axis and the time on $x$-axis thus the slope is given $m=dfrac{Delta y}{Delta x}=dfrac{text{Distance traveled}}{text{Time interval}}$

Which represents the speed of the car thus the slope of the line is equal to the speed of car.

Hence for car a A a line is drawn to represent the motion of the car, Since it is given that the car starts at position 48 km from the origin and with a speed of 36 km/s, therefor we draw a line where it starts from point 48 on the $y$-axis and the slope of the drawn line will be 36 km/s.

For Car B since it is given that car starts it is journey after 0.5 hr and with a speed of 48 km/s, hence a line would be drawn to start from point 0.5 on the $x$-axis and the slope of the drawn line will be 48 km/s.

The following $textbf{graph}$ represents the motion of car A and B.

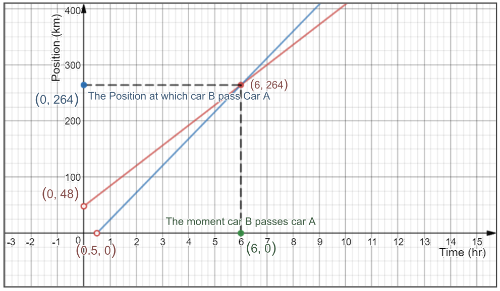
Exercise scan

Step 3

3 of 6

From the above figure, we find that the two lines intersects at some point which simply means that car B outrun car A.\

The point of intersection is co-ordination is $left( 6,264right)$ which means the car B will out run car A after 6 hrs and at a position 264 km, at this point the car A would have traveled a distance 216 km from the beginning of its journey “reference point 48 km”. \

Thus, the answer for the questions from the graph will be:
begin{enumerate}[bfseries (a)]
item 6 hours.
item 264 km.
item 216 km.
end{enumerate}

textbf{underline{textit{note:}}} All the points are obtained from the given graph.

Step 4

4 of 6

$textbf{underline{textit{Second algebraically:}}}$ We find the solution to the answer this time algebraically, to do so we need to find the equation of motion for each line that represents the motion of the car in the position-time graph.

The general equation for any straight line is given by
$y = mx+c$
Where, $m$ represents the slope “speed” of the car and $c$ is the $y$-intercept of the line.

For car A, the line have a slope of 36 km/s and starts from point $left( 0,48right)$ on the $y$-axis, therefor the equation for the straight line that represents the motion of car A is

$$
y_A = 36 x_A + 48
$$

It is more tricky to find the equation of straight line for car B, if we written the equation in terms of car B is position and time then we would get something like this,

$$
y_B = 48 x_Btag{2}
$$

This equation simply means that we have different $x$-axis origins for both cars, and we can’t have 2 different co-ordinates thus we need to express the equation of car B in terms of $x_A$ and as car A had a head start of 0.5 hr thus the equation of car B is

$$
y_b = 48 left(x_A -0.5 right) tag{3}
$$

Step 5

5 of 6

Now we know the equation of both lines representing the cars motion, we can find the moment and the position at which car B passes car A.\

For car B to pass car A it means that although car A had a head start of 48 km, but as the car B is faster than car A then there is a moment where car B would pass car, at this specific point “textbf{underline{Both car are at the same position}}” which means that both $y_A$ and $y_B$ are equal.\

Thus, we have
begin{align*}
y_A &= y_B \
intertext{Substituting by equation (1) and equation (3), solving we for $x_A$ we get}
36 x_A + 48 &= 48left(x_A-0.5 right) \
36 x_A + 48 &= 48 x_A -24\
12 x_A &= 72\
x_A &= 6 hrs.
end{align*}
Thus car B passes car A when the time was 6 hrs, substituting by the value of $x_A$ in equation (1) or (5) we can find the position at which the car was after 6 hrs, substituting gives 264 km, thus we have the same answers obtained graphically as before.

Result

6 of 6

enumerate[bfseries (a)]
item 6 hrs.
item 264 km
item 216 km.

Exercise 60

Step 1

1 of 5

$$
textbf{underline{textit{Solution}}}
$$

Step 2

2 of 5

enumerate[bfseries (a)]
item ~\ From the position-time graph:

textbf{underline{textit{Section I and II:}}} for time interval of nearly 7.5 seconds, Jim moved forward in the aisle cutting a distance of 6 meters, and he stopped for time interval approximately 17.5 seconds.\

textbf{underline{textit{Section III and IV:}}} after then he kept moving for more 12.5 seconds cutting a further distance of 6 m more in the aisle, and then he stopped again for nearly a 5 seconds.\

textbf{underline{textit{Section V and VI:}}} and then he moved back toward the initial position getting back to 3 m from the initial position in time interval of 9 seconds and stopped for 5 seconds.\

textbf{underline{textit{Section VII and VIII:}}} and then he moved into the aisle again to a position 6 m in time interval of 2 seconds stopped for 3 seconds.\

textbf{underline{textit{Section IX:}}} and then he went to the initial position at the beginning of the aisle in 5 seconds.

Step 3

3 of 5

flushleft
enumerate[bfseries (b)]
item ~From the graph:\
noindent
{color{white} rule{linewidth}{0.5mm} }
Jim had a position of 6 m at:
itemize
item time interval [7.5,25] seconds.
item time 43 seconds
item time interval [52.5, 56] seconds

Step 4

4 of 5

enumerate[bfseries (c)]
item ~ From the graph:\
noindent
{color{white} rule{linewidth}{0.5mm} }
The first moment Jim reached the position of 12 m inside the aisle is 32.5 seconds after the beginning of his journey thus it took him 32.5 seconds.\

Between 37 seconds and 46 seconds “a 9 seconds interval” he cut a distance of 9 m, thus his average velocity is
[ dfrac{text{Change in position}}{text{Time interval}} = dfrac{-1}{1}=-1 ~ rm{m/s}]
Thus his average velocity during this time interval is -1 m/s or 1 m/s in the direction toward the beginning of the aisle.

Result

5 of 5

enumerate[bfseries (a)]
item See description.
item at time interval [7.5,25] , 43 and time interval [52.5,56] seconds.
item -1 m/s or 1 m/s toward the beginning of the aisle.

Exercise 61

Step 1

1 of 3

$$
textbf{underline{textit{Solution}}}
$$

Step 2

2 of 3

From the given data in the table we, plot a position-time graph as in the following $textbf{graph}$, the red line represent the least square fitting line“best fit line”.

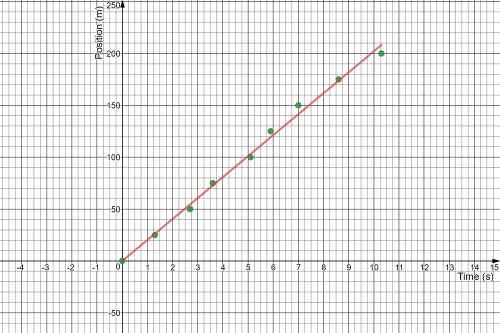
As we plot the position on $y$-axis and the time on $x$-axis we find that the slope of this line represents the speed of the car, where the slope of this line is given by the ratio between the change in the position “rise” and the change in the time “run” as follows
$m= dfrac{y_2 – y_1}{x_2 – x_1}tag{1}$ where $left(x_1,y_1 right)$ and $left(x_2,y_2 right)$ are points on the best fit line, by taking any 2 points on the best fit line and using equation (1) “if drawn by hand” or using graph calculator we find that the slope of this line is 20.20, thus the equation of this line is
$y=20.2 x$
Thus the speed of the car is $fbox{20.2 m/s}$.

Exercise scan

Result

3 of 3

20.2 m/s

Exercise 62

Step 1

1 of 4

$$
textbf{underline{textit{Solution}}}
$$

Step 2

2 of 4

$textbf{underline{textit{Knowns:}}}$

It is given that the car traveled an average of 48 km/hr in the first half of the total journey distance, and it is required to know what should the car speed in the second half of the journey distance in order to achieve an average speed of 90 km/hr.

The situation is described using the following $textbf{diagram}$, where $x_1=x_2$ and $t_1$ is the time interval the car took to cut the first half of the journey distance $x_1$ and $t_2$ is the time interval the car took to cut the second half of the journey distance $x_2$, where the total distance is $x_{tot} = x_1 + x_2$ and the total time interval is $t_{tot} = t_1 + t_2$

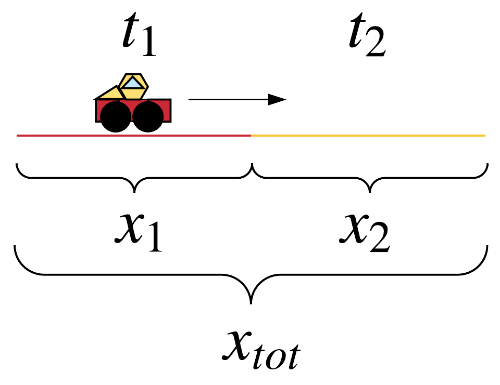
Exercise scan

Step 3

3 of 4

$textbf{underline{textit{Calculations:}}}$

Since it is given that the car has an average speed of 48 during the first half of the journey, which means

$$
dfrac{x_1}{t_1}= 48 ~ rm{km/hr} tag{1}
$$

And it is required to find the speed by which the car should go in the second half of the journey, i.e.

$$
dfrac{x_2}{t_2} = ~ ??
$$

In order to maintain a total trip average speed of 90 km/hr,i.e.

$$
dfrac{x_{tot}}{t_{tot}}= dfrac{x_1+x_2}{t_1+t_2} =90 ~ rm{km/hr}tag{2}
$$

And since $x_1 = x_2$ thus equation (2) becomes

$$
dfrac{2x_1}{left( t_{1}+t_2right)} = 90 tag{3}
$$

And from equation (1), we get that
$x_1 = 48 t_1 tag{4}$
Substituting equation (4) in equation (3), we get

$$
begin{align*}
dfrac{96 t_1}{t_1 + t_2} &= 90\
96 t_1 &= 90t_1 + 90t_2\
t_2 &= dfrac{1}{15} ~ t_1
end{align*}
$$

Which basically means that the car should cut the remaining distance 15 times faster than what it took to cut through the first half, i.e.

$$
begin{align*}
dfrac{x_2}{t_2}&= dfrac{x_1}{t_2}\
&=15 ~ dfrac{x_1}{t_1}\
&= 15times 48\
&= fbox{$720 ~ rm{km/hr}$} \
end{align*}
$$

For a car this speed is not reasonable !!

Result

4 of 4

720 km/hr

Exercise 63

Step 1

1 of 1

Get several people together and give everyone a watch. Synchronize the watches and stand along the street separated by a consistent distance, maybe 10 m or so. When the motorcycle passes, have each person record the time (at least to an accuracy of seconds) that the motorcycle crossed in front of them. Plot a position time graph, and compute the slope of the best-fit line. If the slope is greater than 25 mph, the motorcycle is speeding.

Exercise 64

Step 1

1 of 3

$$
textbf{underline{textit{solution}}}
$$

Step 2

2 of 3

A horizontal line in a position-time graph, implies that the object have the same position at a different times, such object motion “stationary” represented on a graph would have a slope which can be calculated using the following

$$
m = dfrac{y_2-y_1}{x_2-x_1} tag{1}
$$

Using equation (1) to find the slope of the horizontal line, we will find that the slope of such lines is zero which means that the speed of such objects is zero, thus it is normal to find such lines on a position-time graph.

For a Vertical line in a position-time graph, it would means that the object would have a different position at the same moment. which would be very unreasonable to our daily life observation.

In terms of slope calculation using the limit as x approaches zero from the right in equation (1), where

$$
m =lim_{Delta x to 0^{+}} dfrac{Delta y}{Delta x} = infty
$$

Which means, such objects that would have a vertical line is an object having an infinite speed which is not possible, as the maximum universal speed is the speed of the light.

$textbf{underline{textit{note:}}}$ We took the limit of the slope as $Delta x$ approaches zero is because we can’t simply say that $1/0$ is infinity it is undefined in the sense that there is no unique value of $x$ that would give such result, i.e. we wouldn’t be able to differentiate between the followings

$$
dfrac{1}{1-1} = dfrac{1}{2-2} =… =dfrac{1}{x-x}=dfrac{1}{0}
$$

Moreover, we have to define whether $Delta x$ approaches zero from the right or the left, i.e. whether “it is a negative and approaching zero” or whether “it a positive and approaching a zero”, as the first is $-infty$ and the later is $+infty$.

Result

3 of 3

It is possible to have a horizontal line on a position-time graph, but we couldn’t have a vertical line such graphs.

Exercise 65

Step 1

1 of 2

By the late 1600s, the prevailing view was that the speed of light was infinite. 1667. Galileo measured the speed of light by sending a light signal using lamps between two hills. Although they did not determine the speed, they did noticed that it was finite. 1676. Olaf Romer arrives at the results $c = 2.1 times 10 ^ 8 mathrm {m / s}$ by studying the eclipses of Jupiter’s moons. 1728. Bradley approaches the exact value by studying stellar aberration and arrives at the result $c = 301 000 mathrm {km /s}$. 1875. Leon Foucault introduces the method of measurement using a rotating mirror. 1878. A.A. Michelson perfected it and came up with the result $c = 299,792 mathrm {km / s}$ which lasted for the next 40 years. Later with the development of teoretical physics when it was concluded that light is an electromagnetic wave, scientists began to study electromagnetic standing waves, more precisely their interference. Finally, in 1983, the interferometer and measurement method were perfected, and using the speed of light as a constant $c = 299 792 458 mathrm {km / s}$, a unit for length was defined, a meter as the distance that light travels by $1 / {299 792 458} mathrm {s}$.

Result

2 of 2

Determining the speed of light has been a long process involving a variety of innovative ideas and technological advances.

Exercise 66

Step 1

1 of 2

Probably the most famous battle of sprint and endurance in the animal world is the one between the cheetah and the antelope. A cheetah can reach a speed of about $108 mathrm {km/h}( = 30) mathrm {m/s}$ but can maintain that speed for approximately $30 mathrm {s}$. On the other hand, an antelope, although slower with $54 mathrm {km/h}( = 15 mathrm {m/s})$, can maintain that speed much longer. For a cheetah, that means it can catch an antelope even if antelope got about $400 mathrm {m}$ head start. For the antelope on the other hand, this means that if she manages to escape the cheetah in just 30 seconds, her life is safe. For this reason, both species have developed other adaptations to take full advantage of them. For example, an antelope has a much wider field of view but does not have the ability to estimate distance like a cheetah. Another example of an animal that uses high speed in a short time interval is the gray falcon that reaches speeds of 390 km/h by diving into free fall. On the other hand many migratory birds travel much more slowly but can cover huge distances,
of thousands of miles

Result

2 of 2

Examples of animals that can reach high speeds in a short period of time are the cheetah and the gray falcon, while the animals with high endurance are antelopes and migratory birds.

Exercise 67

Solution 1

Solution 2

Step 1

1 of 3

A.)58 nanoseconds = 5.8 E-8 seconds
B.) 9270 milliseconds = 9.27 seconds

Step 2

2 of 3

C.) 0.046 Gs = 46,000,000 Seconds
D.) 12.3 ks= 12,300 Seconds

Result

3 of 3

a.) 5.8 E-8 b.) 46,000,000 c.) 9.27 d.) 12,300

Step 1

1 of 6

In this problem, we need to convert the given time measurements to seconds.
– $t_{text{a}}=58text{ ns}$
– $t_{text{b}}=0.046text{ Gs}$
– $t_{text{c}}=9270text{ ms}$
– $t_{text{d}}=12.3text{ ks}$

Step 2

2 of 6

**Part a)**

Using $1text{ ns}=1 times 10^{-9}text{ s}$ we get:
$$
begin{align*}
t_{text{a}} &= 58text{ ns}\
&= 58 times 10^{-9}text{ s}\
&= boxed{5.8 times 10^{-8}text{ s}}
end{align*}
$$

Step 3

3 of 6

**Part b)**

Using $1text{ Gs}=1 times 10^{9}text{ s}$ we get:
$$
begin{align*}
t_{text{b}} &= 0.046text{ Gs}\
&= 0.046 times 10^{9}text{ s}\
&= boxed{46 times 10^{6}text{ s}}
end{align*}
$$

Step 4

4 of 6

**Part c)**

Using $1text{ ms}=1 times 10^{-3}text{ s}$ we get:
$$
begin{align*}
t_{text{c}} &= 9270text{ ms}\
&= 9270 times 10^{-3}text{ s}\
&= boxed{9.27text{ s}}
end{align*}
$$

Step 5

5 of 6

**Part d)**

Using $1text{ ks}=1 times 10^{3}text{ s}$ we get:
$$
begin{align*}
t_{text{d}} &= 12.3text{ ks}\
&= 12.3 times 10^{3}text{ s}\
&= boxed{12,300text{ s}}
end{align*}
$$

Result

6 of 6

$t_{text{a}}=5.8 times 10^{-8}text{ s}$

$t_{text{b}}=46 times 10^{6}text{ s}$

$t_{text{c}}=9.27text{ s}$

$t_{text{d}}=12,300text{ s}$

Exercise 68

Step 1

1 of 5

a. 3218 kg

Each number is significant; therefore, there are 4 significant digits.

Step 2

2 of 5

b. 60.080 kg

Each number is significant; the zeros between the 6 and 8 are significant and the end 0 is measured for more accuracy and is significant. Therefore, there are 5 significant digits.

Step 3

3 of 5

c. 801 kg

Each number is significant; therefore, there are 3 significant digits.

Step 4

4 of 5

d. 0.000534 kg

The leading zeroes are not significant; only the number 5, 3, and 4 are significant. Therefore, there are 3 significant digits.

Result

5 of 5

a) 4, b) 5, c) 3, d) 3

Exercise 69

Step 1

1 of 3

(a)

To add or subtract measurements, first perform the operation, then
round off the result to correspond to the least-precise value involved.

Here, it is one tenth (second value, 2.1)

Answer: 7.4 mm

Step 2

2 of 3

(b) and (c)

To multiply or divide measurements, perform the calculation and then round to the same number of significant digits as the least-precise measurement.

(b)

3.65 has three significant digits, so

$49.6 m^2$

(c)

83.2 has three significant digits, so

70.4 kg

Result

3 of 3

7.4 mm
$49.6 m^2$
70.4 kg

unlock

All Solutions

Page 52: Assessment

Haven't found what you were looking for?

Search for samples, answers to your questions and flashcards