All Solutions
Page 80: Assessment
We need to fulfill the following map with the terms we are given:
| Position| | |
|–|–|–|
| | |a |
| |m/s | |
Each column stands for a quantity of motion. In this problem, there are three quantities: Position, velocity and acceleration.
*First row*: Indicates the name of a quantity of motion.
*Second row*: Indicates the symbol of a quantity named above.
*Thrid row*: Indicates the unit in which a quantity is measured.
We already have the first element in the row (Position), so we need to put the name of the second two quantities (Velocity and Acceleration) in the second two elements of the row.
Since we see that the unit for the second column is $dfrac{m}{s}$, which is the unit of velocity, we know that the second element of the first row is “Velocity”. This leaves the third element of the row only to be “Acceleration”. So we have:
| Position|Velocity |Acceleration |
|–|–|–|
| | |a |
| |m/s | |
Since we now know which column represents which quantity of motion and we know that the second row indicates the symbol of a quantity, we can easily fulfill the second row.
The symbol for displacement is “$d$”, the symbol for velocity is “$v$” and the symbol for acceleration is already fulfilled “$a$”. So we have:
| Position|Velocity |Acceleration |
|–|–|–|
|d |v |a |
| |m/s | |
The third row indicates the unit in which the quantity is measured. We are left with only two terms two fulfill: $mathrm{m}$ and $mathrm{dfrac{m}{s^2}}$. The first corresponds to the position and the second corresponds to the acceleration. So we have:
| Position|Velocity |Acceleration |
|–|–|–|
|d |v |a |
|m |m/s | m/s^2|
textbf{underline{textit{Solution}}}
$$
[a=dfrac{v_f-v_i}{t} =dfrac{dv}{dt} ]
newenvironment{conditions}
{parvspace{abovedisplayskip}
noindent
begin{tabular}{>{$}c{${}}c<{{}$} @{} p{9.1 cm}}}
{end{tabular}parvspace{belowdisplayskip}}
Where,
begin{conditions}
a &: & The acceleration of the object under study.\
v_i &: & The initial velocity of the object.\
v_f &: & The final velocity of the object.\
t &: & The duration of motion.
end{conditions}
$$
a=dfrac{v_f-v_i}{t}
$$
textbf{underline{textit{Solution}}}
$$
enumerate[bfseries (a)]
item An object slowing down must have an acceleration in an opposite direction of its motion and since its acceleration is positive therefor the object is moving in a negative direction.\
Therefor, an example of an object which is slowing down and having a positive acceleration, is an object moving in the negative direction with some speed and decelerating “having a positive acceleration”.\
item An object speeding must have an acceleration in the same direction as of its motion and since its acceleration is negative therefor the object is moving in a negative direction.\
Therefor, an example of an object which is going faster and having a negative acceleration, is an object moving in the negative direction with some speed and accelerating “having a negative acceleration”.\
item An object moving in a negative direction, and having an acceleration in a direction opposite to its motion.
item An object moving in a negative direction, and having an acceleration in the same direction as that of its motion.
textbf{underline{textit{Solution}}}
$$
And in a velocity-time graph, the slope of the curve in general represents the acceleration of the moving object represented on the graph.
And since the slope of the tangent is the slope of the specific point on the curve from which the tangent is drawn, therefor it represents the acceleration at this given instant of time which is the definition of the “$textbf{instantaneous acceleration}$”.
Let’s say that car moves in the positve direction. If some constant force is acting opposite to the car’s direction (let’s say some strong wind), depending on how strong is the force, car can either decelerate a little, or decelerate to the point that the force takes over and car moves in the opposite direction to the initial one.
parallel to the t-axis, the acceleration is equal to 0.
textit{color{#c34632} $ See$ $Explanation $}
$$
Since the acceleration $a$ is defined as the change in velocity $varDelta v$ in time interval $varDelta t$:
$$begin{align}
a=dfrac{varDelta v}{varDelta t}
end{align}$$
and the velocity doesn’t change with time, we have that $varDelta v=0$, and thus we conclude that for this case $mathrm{underline{acceleration~is~zero}}$.
textbf{underline{textit{Solution}}}
$$
$$
v=dfrac{d}{t} tag{1}
$$
Therefor, the distance from equation (1) can be calculated using the following equation
$$
d=vttag{2}
$$
And, in velocity-time graph the area under a given curve is calculated by
$$
A = int y ~ dx
$$
Which is the product of the velocity $y$-component and time$x$-component which is from equation (2) the distance, therefor the area under a curve represents the displacement “distance” the object under observation moved during a given time interval.
$textbf{underline{textit{note:}}}$ instead of using the integration one can simply calculate the area under the given curve by using the simple geometrical rules for the area of a rectangle, triangle and trapezoid “the usual cases confronted through this chapter”, the main point is that the area under the given curve is the product of the $y$-component and the $x$-component which carries the same physical dimension of a distance in a velocity-time graph.
textbf{underline{textit{Solution}}}
$$
{parvspace{abovedisplayskip}
noindent
begin{tabular}{>{$}c{${}}c<{{}$} @{} p{0.743linewidth}}}
{end{tabular}parvspace{belowdisplayskip}}
The summary for the equations used to calculate each of the position , velocity and time are as follows, keeping in mind that this equations is only valid for objects moving with a uniform acceleration.\
textbf{underline{textit{Position:}}}
Keeping in mind that the distance is given by $d=x_f – x_i$, where $x_f$ is the final position and the $x_i$ is the initial position, knowing the distance and either one of the position we can find the other position.
begin{conditions}
d= dfrac{1}{2} left(v_i + v_g right)t&: & this equation is used to calculate the distance the object moved knowing the initial and final velocity and the duration of motion.\
d= v_i t+dfrac{1}{2}at^2 &: & This equation is used to calculate the distance the object moved knowing the initial velocity and the constant of acceleration and the duration of motion.\
d=dfrac{v_f^2-v_i^2}{2a} &: & This equation is used to calculate the distance the object moved knowing the initial and final velocity of the object and knowing the constant of acceleration.\
end{conditions}
{parvspace{abovedisplayskip}
noindent
begin{tabular}{>{$}c{${}}c<{{}$} @{} p{9.1 cm}}}
{end{tabular}parvspace{belowdisplayskip}}
textbf{underline{textit{Velocity:}}}
There are 3 velocities that are usually asked in the problems, which are the average velocity, and either the initial and final velocity and maybe both, we list the equation for each as follows
begin{conditions}
v_{av} = dfrac{1}{2}left(v_i + v_f right)&: & this equation is used to calculate the average velocity knowing the initial and final velocity.\
&&\
v_f = v_i + at &: & This equation is used to calculate the final velocity of the object knowing the initial velocity and the constant of acceleration and the duration of motion.\
&&\
v_i = v_f – at &: & This equation is used to calculate the initial velocity of the object knowing the final velocity and the constant of acceleration and the duration of motion.\
&&\
v_i = dfrac{2d}{t}-v_f &: & This equation is used to calculate the initial velocity of the object knowing the final velocity of the object, knowing the distance the object moved and the duration of motion.\
&&\
v_f = dfrac{2d}{t}-v_i &: & This equation is used to calculate the final velocity of the object knowing the initial velocity of the object, knowing the distance the object moved and the duration of motion.\
&&\
v_i = dfrac{d- left(1/2right)at^2}{t}&: & This equation is used to calculate the initial velocity of the object knowing the distance the object moved, the constant of acceleration and the duration of object motion.\
&&\
v_f^2 = v_i^2 + 2ad&: & This equation is used to calculate the final velocity of the moving object knowing the initial velocity, the constant of acceleration and the distance the object moved.\
&&\
v_i^2 = v_f^2 – 2ad&: & This equation is used to calculate the initial velocity of the moving object knowing the final velocity, the constant of acceleration and the distance the object moved.
end{conditions}
{parvspace{abovedisplayskip}
noindent
begin{tabular}{>{$}c{${}}c<{{}$} @{} p{9.1 cm}}}
{end{tabular}parvspace{belowdisplayskip}}
textbf{underline{textit{Time:}}}
begin{conditions}
t= dfrac{v_f – v_i}{a} &: & this equation is used to calculate the duration of motion for the object knowing the initial and final velocity and the constant of acceleration.\
t= dfrac{2d}{v_f + v_i} &: & this equation is used to calculate the duration of motion for the object knowing the initial and final velocity of the object and the distance the object moved.\
dfrac{1}{2}at^2 + v_it-d= 0 &: & this equation is used to calculate the duration of motion for the object knowing the initial, the distance the object moved and knowing the constant of acceleration.\ && textbf{underline{textit{note:}}} this equation is quadratic which means that there is two solution that satisfies this equation depending on the given scenario in which the equation is used maybe one of the solution or both are accepted.\
end{conditions}
It is easier to memorize the four main equations and selecting the equation which is in terms of all the givens in the problem and then manipulate them “rearrange them in terms of the unknowns required to calculate” in order to calculate the required, we list the following four equations as follows
* $v_f=v_i+at$
* $d=dfrac{1}{2} left(v_i+v_f right)t$
* $d=v_it+dfrac{1}{2}at^2$
* $v_f^2 = v_i^2 + 2 a d$
And of course, the equation for the average acceleration is $v_{av}=dfrac{1}{2}left(v_i+v_fright)$, and keeping in mind that the distance is in terms of initial and final position is $d=x_f-x_i$.
textbf{underline{textit{Solution}}}
$$
Such observation violates our daily life observation such as the hammer and feather being dropped from the same height we find that the hammer reaches the ground first.
But in fact this is totally normal for the steel and aluminium ball to reach at the same time, where in the hammer-feather scenario, the difference in the time was due to the air resistance.
Where the air shows a much greater resistance to the motion of the feather, thus we observe that it took a greater period of time to reach the ground.
But in the case of two object of the same size and shape, the air resistance shows the same magnitude of resistance to both sphere’s motion.
Among which are the following factors:
* Shape, where different shapes have a different drag coefficient i.e. shows a greater or reduced tendency to be slowed by the air.
* Size, as the greater the size of the ball or the object the greater the surface are that is being dragged “or resisted by the air” therefor the greater the size the greater the drag force.
* Velocity, where we don’t have a concise formula to calculate the drag force, in fact the formula used differs with the range of the velocity by which the object is moving.
It was found that for relatively slow object the drag force is proportional to the speed of the object, while for the relatively fast moving objects, the drag force is found to be proportional to the cube of the velocity.
That is why the car-fuel consumption increases a lot when driving at high speed, due to the greater increase in the drag force in order to counteract the increase in drag force and moving the car faster.
$textbf{underline{textit{In Short:}}}$ Two sphere having the same size and shape, would be resisted by the air-equally.
Now, the total sum of the force acting on the sphere is the sum of the drag force and the gravitational force, we know that the drag force is equal for the spheres which means that both spheres have an upward acceleration of the same magnitude, due to the fact that they both have the same shape and size.
But in order for both spheres to reach the ground at the same time, they both must have the same magnitude of the gravitational force, but do they have the same amount of gravitational force ?
$textbf{underline{textit{Or}}}$ more precisely do the two spheres are accelerated downward by the same magnitude?
$$
F= ma tag{1}
$$
And since both spheres have a different mass, they both have a different gravitational force $F$from equation (1), where in fact the steel ball being heavier would have a greater gravitational force.
But, if we examined equation (1) more carefully in terms of acceleration, for simplicity we rearrange equation (1) as follows
$$
a = dfrac{F}{m} tag{2}
$$
From equation (2), we find that the in case of the steel as the mass is heavier the gravitational force is greater, and in case of Aluminium ball as it have a reduced mass the gravitational force is smaller.
i.e. in the general the ratio between the gravitational force and the mass of the object is always constant, which is equal downward acceleration and that in our case is equal to the acceleration constant of gravity 9.81 m/s$^2$
Which means that both spheres are accelerated downward with same magnitude.
And since both spheres have the same upward acceleration due to drag force, and they both have the same downward acceleration due to gravitational force.
Then they both have the same net downward acceleration “we assumed the net direction is downward as it is given that they are falling”, therefor they both reach the ground at the same time.
And also due to the matter of fact that they both are accelerated downward due to the gravitational force by the same magnitude.
Thus both have the same net magnitude of acceleration downward, and hence when dropped from the same level they will always reach the ground at the same time.
textbf{underline{textit{Solution}}}
$$
Where the drag force is an upward force “opposite to the direction of motion of free fall object”, which is a result of the air resistance.
Drag force depends on many factors, including the shape, size and the velocity of the falling object.
$textbf{underline{textit{Shape:}}}$ where the smoother the shape of the object “more aerodynamic like object” the less resistance it faces from the air, and hence it would have a smaller drag coefficient, which means a smaller drag force and thus the object would fall faster.
So basically different shapes would have different drag coefficient “it is a measure of how efficient would the air or fluid in general would resist the motion of the object” and the smaller it gets the less effective “or have no effect on the motion of the object” is the fluid in resisting the object is motion.
$textbf{underline{textit{Size:}}}$ as size differs the drag force would also differs usually a bigger sized object would have a greater surface area thus would result in a greater resistance from as more air is impinging the object during the motion.
$textbf{underline{textit{Velocity:}}}$ it was found that as the object moves with a very high speed it would face an increased drag force as the value of drag force varies with speed.
Thus, an object where we can not neglect the air resistance, is an object which would have a big size “and surface area” and which doesn’t have an aerodynamic shape “shapes with very high drag coefficient” and dropped from relatively high altitudes since objects that are dropped from a higher altitude would have a greater velocities thus would face a greater drag force.
textbf{underline{textit{Solution}}}
$$
Where the drag force is an upward force “opposite to the direction of motion of free fall object”, which is a result of the air resistance.
Drag force depends on many factors, including the shape, size and the velocity of the falling object.
$textbf{underline{textit{Shape:}}}$ where the smoother the shape of the object “more aerodynamic like object” the less resistance it faces from the air, and hence it would have a smaller drag coefficient, which means a smaller drag force and thus the object would fall faster.
So basically different shapes would have different drag coefficient “it is a measure of how efficient would the air or fluid in general would resist the motion of the object” and the smaller it gets the less effective “or have no effect on the motion of the object” is the fluid in resisting the object is motion.
$textbf{underline{textit{Size:}}}$ as size differs the drag force would also differs usually a bigger sized object would have a greater surface area thus would result in a greater resistance from as more air is impinging the object during the motion.
$textbf{underline{textit{Velocity:}}}$ it was found that as the object moves with a very high speed it would face an increased drag force as the value of drag force varies with speed.
Thus, an object where we can safely neglect the air resistance, is an object which would have a reduced size and an aerodynamic shape “shapes with very small drag coefficient” and dropped from relatively small heights since objects that are dropped from a higher altitude would have a greater velocities thus would face a greater drag force.
textbf{underline{textit{Solution}}}
$$
In this case, the acceleration in an opposite direction of the car motion would be positive, therefor the acceleration would be positive.
And the car would be slowing down, in terms of magnitude of its velocity.
Despite the fact that the acceleration is not negative, yet in this case it is slowing down.
textbf{underline{textit{Solution}}}
$$
Since it is slowing down, then there must be some kind of acceleration “for example the resistance of air, pull of the gravity” which acts on the croquet to slow it down.
And in order for this acceleration to slow down the croquet ball, it must act on the croquet ball in a direction opposite to the direction of movement.
And since it is assumed that the croquet ball is moving in a positive direction, then the acceleration must be in a negative direction.
Therefor, the velocity and the acceleration doesn’t not have the same sign.
textbf{underline{textit{Solution}}}
$$
$$
a = dfrac{Delta v}{Delta t}
$$
And if the final speed is the same as the initial speed “which is the case for a body moving at constant speed” the acceleration using the above formula would be zero.
textbf{underline{textit{Solution}}}
$$
And in order to be able to judge whether the acceleration is zero, increasing or decreasing we must observe the velocity at different time intervals in order to be able to find the acceleration.
An example, a ball tossed vertically upward with some initial speed would be always acted upon with an acceleration to the negative direction “toward the center of the eart”.
The acceleration of gravity works on decreasing the speed of the ball till it reaches zero and then start to gain speed again in the opposite direction of the motion at the beginning.
At the moment the ball reaches the maximum height “the point at which the ball came at rest”, the acceleration of gravity is still acting on the ball, it doesn’t simply vanish it is always there and with a constant in magnitude “the variation in the magnitude of the acceleration is negiligble at relatively small heights” eventhough the velocity is zero.
Mathematically by calculating the acceleration of the ball, by observing an initial speed zero at the maximum height at some instant of time and the final speed of a negative value as it goes back downward at another instant of time.
We find using the following formula for the acceleration by definition
$$
a=dfrac{Delta v}{Delta t}
$$
[ v_f = v_i + a Delta t]
Where,
newenvironment{conditions}
{parvspace{abovedisplayskip}
noindent
begin{tabular}{>{$}c{${}}c<{{}$} @{} l}}
{end{tabular}parvspace{belowdisplayskip}}
begin{conditions}
Delta v&: & The change between final and initial speed .\
Delta t &: & The duration of acceleration/deceleration.\
end{conditions}
That the acceleration on the ball has actually a value, which is equal to the constant of acceleration due to gravity 9.81 m/s$^2$.\
And if we used this formula everywhere during the motion of the ball we would always find that the ball is acted upon by the acceleration of gravity with a constant magnitude.\
Where, as the change of the time gets smaller the change in the velocity gets also smaller, such that the value of the acceleration is existent and the same.\
If we take the limit as $Delta t rightarrow 0$, i.e. we are calculating the acceleration of the gravity at 2 points very near to each other that in fact they are almost at the same point at maximum height “where the velocity is zero''.\
We would find that from the above formula of the acceleration the ball is still acted upon with the acceleration of gravity with a constant magnitude.\
textbf{underline{textit{Solution}}}
$$
As, the problem is asking for the changes in the first gear this means, that it is asking for the changes for the curve representing the motion from the origin to the first black dot.
And from the axes label, we know that this is velocity-time graph, where the velocity is represented on the $y$-axis and the time on $x$-axis.
$textbf{Changes in the velocity:}$ And during this time interval [0,2.5] seconds, the car speed is always increasing where by looking at the values of the $y$-component for the line representing the car motion, we find that it was at rest initially and then its final speed was nearly 7 m/s.
And since this is a velocity-time graph then the slope of the line representing the motion of the car, represents the acceleration of the car.
But since the line representing the motion is not a straight line, therefor the slope of the line representing the motion “the acceleration of the car” is not constant and varies constantly.
To find the slope of a curve other than a straight line we have to find for every point, where the slope varies for every point on the line representing the motion.
In order to calculate the slope at a point on the curve, we draw the tangent to this point and then find the slope of the tangent line.
Thus, the acceleration is always positive and greatest at the beginning of the car journey, and the smallest just before the gear change.
After the gear change, by drawing a tangent line at a point just after the gear change and a tangent line at a point just before the gear change.
We find that the tangent line after the gear change is much steeper than it was before the gear change, which means that it have a greater “numerical” slope value, which means that it has a greater acceleration after the gear change.
Therefor, the acceleration is greater after the gear change than it was before the gear change.
* $textbf{The changes in velocity:}$ The velocity is always positive and increasing with different rates, where the acceleration is not constant, and the initial speed of the car was at rest and the final speed of the car is about 7 m/s.
* $textbf{The changes in acceleration:}$ The acceleration is always positive, with a changing value where it was the greatest initially and then gradually decreasing till the gear change.
* The acceleration is greater after the gear change.
textbf{underline{textit{Solution}}}
$$
And since the slope in the displacement-time graph represents the velocity of the object/person under observation, therefor the motion represented by the straight line is the motion of a person moving with a constant velocity in one direction.
$textbf{For the given graph on the right:}$ examining the graph carefully, as before the slope of the line represents the velocity of the person moving under observation, the steeper the slope “high numerical value slope” the greater the magnitude of the velocity “Or simply the greater the speed”.
And the sign accompanied the slope represents the direction of the velocity, i.e. a straight line whose slope is -ve means that the body is moving in a -ve direction.
Observing the slope of the each segment in the graph “Comparing which segment is steeper or shallower” we can know at which time interval, the person under observation was walking the fastest or the slowest and whether the object was going faster or slower compared to other time intervals.
Moreover, we find that the slope of segment $BC$ is the greatest and the slope of the segment $FG$ is the smallest.
Between Segment $AB$ the person was moving with a certain pace and then increased it speed during $2/5$ this time interval.
Then the person walked faster in the time interval of the segment $BC$ and then slowed down in the time interval between $CD$ and then came at rest in the time interval $DE$.
Till then he walked back in the opposite direction with some speed in $EF$ time interval, and then with increased speed in the time interval $FG$ and then slowed down again in the time interval $GH$, till he walked back to the same place from where he started his journey.
$textbf{Right graph:}$ The person is moving with ever increasing speed till the end of the time interval between $CD$ and in a positive direction.
And then he came at rest during the time interval $DE$ and then walked back to the initial position where the person kept increasing his speed till time interval $GH$ where he walked with a reduced pace and at the time interval $GH$ then he reached at the starting position once again.
textbf{underline{textit{Solution}}}
$$
Since the slope of the curve in the position-time graph represent the velocity of the object, thus by finding the slope one can find the velocity-time graph that would represent the given motion in those given graphs.
By observing the graph, one may find that the curve in this graph is represented by a parabolic function where
[ y=cx^2]
Where,
newenvironment{conditions}
{parvspace{abovedisplayskip}
noindent
begin{tabular}{>{$}c{${}}c<{{}$} @{} p{9.1 cm}}}
{end{tabular}parvspace{belowdisplayskip}}
begin{conditions}
y &: & The $y$-axis on which the displacement is represented.\
x &: & The $x$-axis on which the time is represented.\
c & :& Is a constant.\
end{conditions}
And, since the displacement-time graph can be represented by the given equation of parabola, we can differentiate this function to find the velocity-time graph, where differentiating this equation with respect to $x$ “time'' yields the equation of velocity
[ y'=dfrac{dy}{dx}= 2cx]
This is equation of straight line whose slope is $2c$ and passes through the origin, and thus the velocity-time graph is as follows
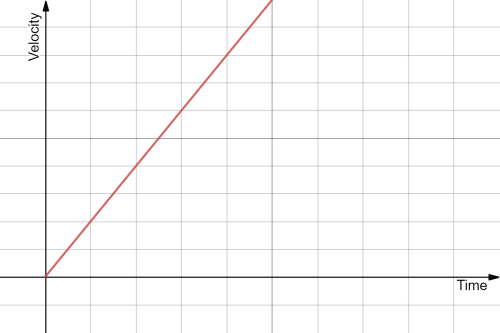
The slope of the straight line on the left yields a negative value and the straight line on the right yields a positive value, thus at first the object had some value of speed in the negative direction and then it changed the direction of its motion toward the positive direction with some speed.
And as the slope is constant everywhere therefor the object is moving with a uniform speed therefor it has a zero acceleration, and hence it would be represented on a velocity-time graph using a horizontal lines where the slope of the horizontal lines is zero, and the slope of the curve in velocity-time graph represents the acceleration.
Therefor the velocity-time graph that would represent such displacement-time graph is as follows

The slope of the straight line on the left yields a positive value, while the slope of the straight line on the right yields a positive value with a reduced numerical value “magnitude”, which represent the motion of an object which is moving toward a positive direction with some speed, and then it decreased it speed and kept going in the same direction.
Also, since the slope is constant along the given straight line, therefor the object was moving uniformly thus as before it would be represented by a horizontal line in the velocity-time graph.
Therefor, the velocity-time graph representing the given motion in this graph is as follows

textbf{underline{textit{Solutions}}}
$$
And knowing that the object is under the influence of the acceleration of gravity, and knowing that the final velocity is zero and that the duration of deceleration is 7 seconds, thus we can find the distance traveled using the following equation
$$
{v_f}^2 = {v_i}^2 +2ad tag{1}
$$
But first we need to find the initial velocity, which can be calculated from the following equation
$$
v_f = v_i + at tag{2}
$$
Rearranging in terms of initial velocity, we get
$$
v_i = v_f – at tag{3}
$$
Substituting equation (3) in (1), and knowing that the final velocity is zero, we get
$$
0 = (-at)^2 + 2 ad tag{4}
$$
And since, the acceleration is acting on the object is in a direction opposite to the direction of motion therefor we assign a -ve sign to the acceleration, thus equation (4) becomes
$$
d = dfrac{a^2t^2}{2a}= dfrac{at^2}{2}tag{5}
$$
Thus, we can use equation (5) to find the maximum height the object reached “i.e. the displacement the object moved during this time interval”.
For an object $textbf{free falling}$, since it start falling at rest hence we know that its initial velocity is zero, we can find its final velocity using equation (2), and then by knowing the final velocity we can use equation (1) to find the distance the falling object made during this time duration.
Where he only difference is that the upward shot object have a final velocity of zero, while for the free falling one it has an initial velocity of zero “i.e. the final and initial velocity is interchanged for each case”, therefor equation (4) for the free falling object is
[(at)^2= 0 -2ad ]
And, thus the distance the free falling object moved is
[d = – dfrac{at^2}{2} tag{6}]
textbf{underline{textit{note:}}} for the free falling object, the acceleration and velocity both have the same sign “direction” where as the in the upward shot object they both have a different sign, where in the later case the acceleration of gravity works on slowing down the object.\
textbf{underline{textit{note:}}} We notice that the distance for the upward shot using equation (5) is +ve, which means that the object moved beyond the starting point, and for the free falling object using equation (6) is -ve which means that it moved below the starting point.\
The definition of the parameters used in each equation,
newenvironment{conditions}
{parvspace{abovedisplayskip}
noindent
begin{tabular}{>{$}c{${}}c<{{}$} @{} p{9.1 cm}}}
{end{tabular}parvspace{belowdisplayskip}}
begin{conditions}
v_i &:& The initial speed of the object.\
v_f &:& The final speed of the object.\
a &:& The constant of acceleration.\
d &:& The displacement the object moved.\
t &:& Duration of the movement.
end{conditions}
$$
begin{align*}
d&= 0.50 times left(at^2 right)\
&= 0.50 times (9.81 times 7.0^2)\
&= fbox{$240.345 rm{m}$}
end{align*}
$$
And using equation (6) to find the distance the object moved for the free falling object, we get
$$
begin{align*}
d&= -0.50 times left(at^2 right)\
&= -0.50 times (9.81 times 7.0^2)\
&= fbox{$-240.345 rm{m}$}
end{align*}
$$
$textbf{underline{textit{note:}}}$ Since the least number of significant figure in the multiplication is 2, therefor the final answer must be rounded to 2 significant figure, therefor the final answer is 240 m.
$textbf{underline{textit{note:}}}$ The sign of the distance moved indicates the direction at which the object moved, whether it is beyond or below the starting point.
textbf{underline{textit{Solution}}}
$$
To answer our question, we need first to find the relation between the maximum height and the constant of acceleration at the same velocity, and as we know that the final velocity is zero, we use the following equation
$$
{v_f}^2 = {v_i}^2 – 2 a d
$$
Substituting the final velocity to be zero, and rearranging in terms of constant of acceleration we get
$$
a = dfrac{{v_i}^2}{2d} tag{1}
$$
item From equation (1) as it is given that the initial velocity by which the ball was thrown is the same, and since it is given that the constant of acceleration is three times its value on Earth.\
Therefor from equation (1) it is clear that the maximum height the ball would reach is 1/3 rd the value of the maximum height if its value on Earth if it was throwing with the same initial velocity.\
To clarify more, the maximum height the ball would reach at Earth is
[ d_{E}= dfrac{{v_i}^2}{2a_{E}} tag{a}]
And, the maximum height it will reach on Jupiter is
[ d_{J}= dfrac{{v_i}^2}{2a_{J} tag{b} }]
and since it is given that $a_{M}=dfrac{1}{3}a_{E}$, thus substituting in equation (b), we get
[ d_{J}= dfrac{{v_i}^2}{2left( 3 a_{E} right)} = dfrac{1}{3} left( dfrac{{v_i}^2}{2a_{E}}right) tag{c}]
And, from equation (a) we substitute in equation (c), we get
[ d_{J} = dfrac{1}{3} d_{E}]
Thus, the maximum height the ball would reach on Jupiter is one-third the maximum height the ball would reach on Earth.\
item If the ball is thrown on Jupiter with an initial speed 3 times that on Earth, and an acceleration which is 3 times that of Earth, then using equation (1) we have
The maximum height reached on Jupiter is
[ d_{J} = dfrac{{v_{J}}^2}{2a_{J}}]
The maximum height reached on Earth is
[ d_{E} = dfrac{{v_{E}}^2}{2a_{E}}]
And since, the initial velocity by which the ball on Jupiter was thrown is three time that of the initial speed of the ball on earth, thus $v_{J}= 3 v_{E}$.\
And as the constant of acceleration on Jupiter is three times that of earth $a_{J}=3a_{E}$, therefor substituting in the above equations and equating we have
[ d_{J} = dfrac{9{v_{E}}^2}{2 times 3a_{E}}= dfrac{9}{3} left( dfrac{{v_{E}}^2}{2a_{E}} right)= 3 d_{E}]
Thus, in case of the ball was thrown on Jupiter with 3 times the initial speed by which the ball would be thrown on Earth, the maximum height would be 3 time the maximum height on Earth.\
item The maximum height on Jupiter the ball would reach if thrown with the same initial velocity on Earth, would be one-third the maximum height the ball would reach on Earth.
item The maximum height the ball would reach on Jupiter in this case would be 3 times the maximum height the ball would reach on earth with one third the initial speed.\
textbf{underline{textit{Solution:}}}
$$
$textbf{underline{textit{Average velocity:}}}$ it is the total distance traveled during a total time interval “duration of time”.
And knowing that the car drived for 2 hours at constant speed of 40 km/hr and drived for more 2 hours at a constant speed of 60 km/hr both having the same direction.
Where we can find the distance traveled by the car moving with a constant speed using the following equation
$$
d = vt
$$
Thus we can find the total distance and the total duration of the journey and from which we can find the average velocity of the car.
enumerate[bfseries (a)]
item Knowing the speed of the car and the duration during which the car was moving, thus using equation (1) we can find the distance the car moved during the first 2 hours
begin{align*}
d &= 40 times 2\
&= 80 ~ rm{km}
intertext{And during the second 2 hours the car moved a distance of}
d &= 60 times 2\
&= 120 ~ rm{km}
intertext{Therefor, the total distance is 200 km and the total duration is 4 hours, therefor the average velocity by definition is}
v_{av} &= dfrac{200}{4}\
&= fbox{$50 ~ rm{km/hr}$}
end{align*}
item As the car is moving with a constant speed, and knowing the speed of the car and knowing the distance through which car moved we can find the time took the car to cut this distance using equation (1), where
[t = dfrac{d}{v} ]
Thus, as it is given that the car moved a distance of 100 km with 2 speeds once with a speed of 40 km/hr and once with 60 km/hr, we can find the time took by the car to move the 100 km by each speed.\
The time took for the car to cut a distance of 100 km by a speed of 40 km/hr is
begin{align*}
t_{40} &= dfrac{100}{40}\
&= 2.5 ~ rm{hr}
intertext{And the time took for the car to cut a distance of 100 km by a speed of 60 km/hr is}
t_{60} &= dfrac{100}{60}\
&= 1.7 ~ rm{hr}
intertext{Thus the total duration of the car journey is 4.2 hours and the total distance moved by the car is 200 km, therefor by definition the average velocity of the car is}
v_{av} &= dfrac{200}{4.2}\
&= fbox{$47.62 ~ rm{km/hr}$}
end{align*}
item 50 km
item 48 km
a = dfrac{v_{f}-v_{i}}{t}
$$
a = dfrac{96m/s-32m/s}{8s}
$$
8m/s^2
$$
8m/s^2
$$
a = dfrac{v_{f}-v_{i}}{t}
$$
1.6m/s^2 = dfrac{v_{f}-22m/s}{6.8s}
$$
33m/s
$$
– Initial velocity: $v_0=22 mathrm{~dfrac{m}{s}}$
– Acceleration: $a=1.6mathrm{~dfrac{m}{s^2}}$
– Time interval: $varDelta t=6.8mathrm{~sec}$
**Objective**
– Find final velocity $v_f$
In order to solve this problem, we can use the definition of acceleration $a$ as the change in velocity $varDelta v$ in time interval $varDelta t$:
$$begin{align}
a=dfrac{varDelta v}{varDelta t}
end{align}$$
We can apply this to our case, where velocity changes from $v_0$ to final velocity $v_f$ (So, $varDelta v=v_f-v_0$) in time interval $varDelta t$.
We can now apply this to equation $(1)$ and get the answer for $v_f$.
$$begin{aligned}
a&=dfrac{varDelta v}{varDelta t} nonumber
\&=dfrac{ v_f – v_0}{varDelta t} rightarrow v_f=v_0+acdotvarDelta t
end{aligned}$$
We can now put in the given information and calculate the final velocity $v_f$.
$$begin{aligned}
v_f&=v_0+acdotvarDelta t
\&=22+1.6cdot 6.8
\&=boxed{32.88 mathrm{~dfrac{m}{s}}}
end{aligned}$$
a) 6 m/s^2 ; b)0m/s^2 ; c) -2m/s^2; d) -4m/s^2
$$
textbf{underline{textit{Solution}}}
$$
* In a velocity-time graph, the slope of the curve representing the motion yields the acceleration of the object under.
And if the curve is not a straight line, then the slope “and therefor the acceleration” is not constant along the curve but instead it is varying continuously, in order to find the acceleration of the given object at some instant of time, we find the slope of the tangent line to this specific point, which will yield the acceleration at this given instant of time “instantaneous acceleration” .
Thus, if we find that the slope of the line is positive this would simply means that the object is accelerating, and if it is negative then it is decelerating, thus we can tell whether the object is speeding up or down by simply checking the sign of the slope at different time intervals.
* Moreover, as long as the object is having a velocity of a positive value, then it is moving in the positive direction only if it have a negative velocity then it is moving in the negative direction, and hence we can check the $y$-component at different instant times to know the exact moment at which the object reversed its direction.
* Average acceleration, simply means the change in the velocity in a given period of time, which can be calculated using the following equation
$$
a=dfrac{Delta v}{Delta t}=dfrac{v_f – v_i}{t_f – t_i}tag{1}
$$
Thus using equation (1), we can find the average acceleration at different time intervals.
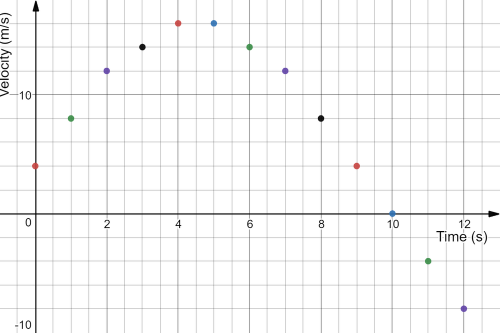
item From the above plotted graph, we can check whether the object is speeding up or slowing down by checking the sign of the slope.\
During the time interval [0,4] seconds the curve is having a positive sign all along this time interval, and thus the object is speeding up during this time interval.\
During the time interval [4,5] seconds the initial and final velocity is the same therefor the average acceleration during this time is zero, thus the object is neither accelerating nor decelerating.\
During the time interval [5,10] seconds, the curve starts to have a negative sign which indicates that the object is speeding down “decelerates”.\
In the time interval [10,12] seconds, the slope is still having a negative sign but the velocity becomes negative as well, therefor the object is speeding up but in the negative direction.\
item The object reverse it is direction at the moment the object starts having a negative velocity, from the graph we find that the object starts having a negative velocity just exactly after 10 seconds, thus the object reverse its direction after 10 seconds.\
item From equation (1), we can calculate the average acceleration during time interval [0,2] seconds, and during the time interval [7,12] seconds.
During the time interval [0,2] from the table the initial velocity is 4 m/s and the final velocity is 12 m/s and the duration of time is 2 seconds, therefor using equation (1) the average acceleration is
begin{align*}
a_{av} &= dfrac{12-4}{2}\
&= 4~ rm{m/s}^2
end{align*}
During the time interval [7,12] from the table the object have an initial velocity of 12 m/s and a final velocity of -8 m/s and the duration of motion is 5 seconds, therefor the average acceleration is
begin{align*}
a_{av} &= dfrac{-8-12}{5}\
&= -4 ~ rm{m/s}^2
end{align*}
Therefor during the time interval [0,2] seconds and [7,12] seconds both time intervals have the same magnitude of acceleration but toward opposite direction where the first is having a magnitude of acceleration of 4 m/s$^2$ in the positive direction and the later have the same magnitude but in the negative direction.
item The object during the following time interval:
begin{itemize} item textbf{underline{[0,4] rm{s}:}} the object was speeding up.\
item textbf{underline{[4,5] rm{s}:}} the object was neither accelerating nor decelerating.\
item textbf{underline{[5,10] rm{s}:}} the object was speeding down.\
item textbf{underline{[10,12] rm{s}:}} the object was speeding up in the negative direction.
end{itemize}
item The object reverse its direction after 10 seconds.
item Both have the same magnitude and different directions.
$v_{f} = v_{i} + at$
$V_{f}=2.35X10^{5}-1.1×10^{12}x1.5×10^{-7}$
=7×10$^{4}$m/s
$v_{i}=2.35×10^{5}m/s$
t=1.5x$10^{-7}$sec
a=-1.1×10$^{12}m/s^2$
$v_{f}$=?
– Initial velocity: $v_0=2.35times 10^5 mathrm{~dfrac{m}{s}}$
– Acceleration: $a=-1.10times10^{12}mathrm{~dfrac{m}{s^2}}$
– Time interval: $varDelta t=1.5times10^{-7}mathrm{~sec}$
**Objective**
– Find final velocity $v_f$
In order to solve this problem, we can use the definition of acceleration $a$ as the change in velocity $varDelta v$ in time interval $varDelta t$:
$$begin{align}
a=dfrac{varDelta v}{varDelta t}
end{align}$$
We can apply this to our case, where velocity changes from $v_0$ to final velocity $v_f$ (So, $varDelta v=v_f-v_0$) in time interval $varDelta t$.
We can now apply this to equation $(1)$ and get the answer for $v_f$.
$$begin{aligned}
a&=dfrac{varDelta v}{varDelta t} nonumber
\&=dfrac{ v_f – v_0}{varDelta t} rightarrow v_f=v_0+acdotvarDelta t
end{aligned}$$
We can now put in the given information and calculate the final velocity $v_f$.
$$begin{aligned}
v_f&=v_0+acdotvarDelta t
\&=2.35times 10^5+(-1.10times10^{12}cdot 1.5times10^{-7})
\&=2.35times 10^5+(-1.10cdot 1.5)times 10^5
\&=(2.35-1.10cdot1.5)times10^5
\&=boxed{0.7times10^5 mathrm{~dfrac{m}{s}}}
end{aligned}$$
$$
begin{align*}
Delta v_A &=17.9 mathrm{m/s} \
Delta v_B &=22.4 mathrm{m/s} \
Delta v_C &=26.8 mathrm{m/s} \
Delta t_A &=4 mathrm{s} \
Delta t_B &=3.5 mathrm{s} \
Delta t_C &=6.0 mathrm{s}
end{align*}
$$
Unknown:
$$
begin{align*}
a_A&=? \
a_B&=? \
a_C&=?
end{align*}
$$
$$
begin{align*}
a&=dfrac{Delta v}{Delta t} \
\
a_A&=dfrac{Delta v_A}{Delta t_A}\
&= dfrac{17.9 mathrm{m/s}}{4 mathrm{s}}\
&= 4.475 mathrm{m/s^2} \
\
a_B&=dfrac{Delta v_B}{Delta t_B}\
&= dfrac{22.4 mathrm{m/s}}{3.5 mathrm{s}}\
&= 6.4 mathrm{m/s^2}\
\
a_C&=dfrac{Delta v_C}{Delta t_C}\
&= dfrac{26.8 mathrm{m/s}}{6.0 mathrm{s}}\
&= 4.467 mathrm{m/s^2} \
\
a_B&<a_A<a_C
end{align*}
$$
a_B<a_A<a_C Rightarrow car B rightarrow car A rightarrow car C
$$
$$
begin{align*}
v_i&=145 mathrm{m/s}\
t&=20 mathrm{s}\
a&=23.1 mathrm{m/s^2} \
v_s&=331 mathrm{m/s} tag{speed of sound}
end{align*}
$$
Unknown:
$$
begin{align*}
v_f&=? \
v_f/v_s&=?
end{align*}
$$
$$
a=dfrac{v_f-v_i}{t} rightarrow v_f=at+v_i
$$
$$
begin{align*}
v_f&=at+v_i\
&=23.1 mathrm{m/s^2}20 mathrm{s}+145 mathrm{m/s} \
&=boxed{ 607 mathrm{m/s} }\
\
v_f&=v_f/v_s \
&=dfrac{v_f}{v_s} \
&=dfrac{607 mathrm{m/s}}{331 mathrm{m/s}} \
&=boxed{ 1.834 v_s }
end{align*}
$$
This ratio is also known as Mach number so we can write $mathrm{Ma}=1.834$.
begin{align*}
a) & v_f=607 mathrm{m/s} \
b) & v_f/v_s=1.834
end{align*}
$$
textbf{underline{textit{Solution}}}
$$
Referring to the given figure, we find that it is a velocity-time graph and since the product of velocity and time is the distance moved, and since the velocity is represented on the $y$-axis and the time is represented on the $x$-axis thus the area under the curve represents the distance moved by the object.\
Thus in order to find the distance the object moved during a given time interval, all we need is to find the area bounded between the curve and the $x$-axis.\
And knowing that the area of the triangle is given by
[ Area= dfrac{1}{2} times b times h]
And that of the rectangle is
[ Area = w times h]
Where,
newenvironment{conditions}
{parvspace{abovedisplayskip}
noindent
begin{tabular}{>{$}c{${}}c<{{}$} @{} p{9.1 cm}}}
{end{tabular}parvspace{belowdisplayskip}}
begin{conditions}
b &: & The base of the triangle .\
h &: & The height of the traingle .\
w &: & width of the rectangle .\
l &: & The length of the rectangle.\
end{conditions}
item textbf{underline{textit{During time interval [0,5] s:}}}
The area the curve makes with the $x$-axis is a triangle whose height is 30 m/s and the base of the triangle is 5 seconds, thus the area is [ Area = dfrac{1}{2} times 5 times 30 = 75 ~ rm{m}]
item textbf{underline{textit{During time interval [5,10] s:}}}
The area the curve makes with the $x$-axis is a rectangle whose height is 30 m/s and the base of the rectangle is 5 seconds, thus the area is [ Area = 5 times 30 = 150 ~ rm{m}]
item textbf{underline{textit{During time interval [10,15] s:}}}
The area the curve makes with the $x$-axis is the sum of the area of the triangle whose height is 10 m/s and the base of the triangle is 5 seconds and the area of the rectangle whose base is 5 seconds and the height is 20 m/s, thus the area is [ Area = 20 times 5 + dfrac{1}{2} times 5 times 10= 125 ~ rm{m}]
item textbf{underline{textit{During time interval [0,25] s:}}}
During the time interval [15, 25] seconds: The area under the curve is the sum of the area of the rectangle during the time interval [15,20] seconds, whose base is 5 second and height is 20 m/s.\
And during the time interval [20,25] seconds: The area the curve makes with the $x$-axis is the area of a triangle whose height is 20 m/s and the base of the triangle is 5 seconds.\
Thus the area during time interval [15,25] seconds is [ Area = 5times 20 +dfrac{1}{2} times 5 times 20 = 150 ~ rm{m}]
And the total area during the time interval [0,15] seconds is the sum of the following areas
[ Area = 75 + 150 + 125 =350 ~ rm{m}]
And therefor the total area during the time interval [0.25] seconds is $Area = 350 + 150 = 500 ~ rm{m}$
item 75 ~ rm{m}
item 150 ~ rm{m}
item 125 ~ rm{m}
item 500 ~ rm{m}
textbf{underline{textit{Solution}}}
$$
[{v_f}^2 = {v_i}^2 +2ad tag{1} ]
Where,\
newenvironment{conditions}
{parvspace{abovedisplayskip}
noindent
begin{tabular}{>{$}c{${}}c<{{}$} @{} l}}
{end{tabular}parvspace{belowdisplayskip}}
begin{conditions}
v_i&: & The initial speed of the dragster.\
v_f&: & The final speed of the dragster.\
a&: & The constant of acceleration.\
d&: & The distance through which the dragster moved while accelerating.
end{conditions}
And it is given that the dragster was initially at rest and that the constant of acceleration is 48 m/s$^2$ and the distance through which the dragster moved while accelerating is 325 m.
begin{align*}
{v_f}^2 &= 0^2 + 2times 49 times 325\
&= 31850\
intertext{Taking the square root of ${v_f}^2$, we get the final velocity $v_f$}
v_f &= sqrt{31850}\
&= fbox{$178.5 ~ rm{m/s}$}
end{align*}
$$
begin{align*}
v&=12 mathrm{m/s} \
a&=-1.6 mathrm{m/s^2} \
t_a&=6 mathrm{s} \
t_b&=9 mathrm{s}
end{align*}
$$
Unknown:
$$
begin{align*}
d_a&=? \
d_b&=?
end{align*}
$$
$$
begin{align*}
d&=vt+1/2 cdot at^2 \
\
d_a&=vt_a+1/2at^2_a \
&=12 mathrm{m/s} 6 mathrm{s}-1/2cdot 1.6 mathrm{m/s^2} 36 mathrm{s^2} \
&=boxed{43.2 mathrm{m}} \
\
d_b&=vt_b+1/2at^2_b \
&=12 mathrm{m/s} 9 mathrm{s}-1/2cdot 1.6 mathrm{m/s^2} 81 mathrm{s^2} \
&=boxed{43.2 mathrm{m}}
end{align*}
$$
Interestingly, the displacement is the same in both cases, the reason being that after 7.5 seconds the velocity starts to increase in the negative direction that is the car starts to come back.
begin{align*}
a) & d_a=43.2 mathrm{m} \
b) & d_b=43.2 mathrm{m}
end{align*}
$$
textbf{underline{textit{Solution}}}
$$
[d=dfrac{v_f^2 – v_i^2}{2a}tag{1}]
Where,\
newenvironment{conditions}
{parvspace{abovedisplayskip}
noindent
begin{tabular}{>{$}c{${}}c<{{}$} @{} l}}
{end{tabular}parvspace{belowdisplayskip}}
begin{conditions}
v_i&: & The initial speed of the plane.\
v_f&: & The final speed of the plane.\
d&: & The distance traveled by the plane before reaching its final speed.\
a&: & Is the deceleration constant of the car.
end{conditions}
It is given that the initial speed of the race car is 55 m/s and the final speed of the race car is at at rest, and the deceleration constant of the race car is -11 m/s.
enumerate[bfseries (a)]
item Substituting the knowns in equation (1), we can find the distance the plane moved to reach before reaching its final speed, as follows
begin{align*}
d &= dfrac{0^2-55^2}{2timesleft(-11 right)}\
&= fbox{$137.5 ~ rm{m}$}
end{align*}
item If the car was going with an initial speed of 110 m/s, then using equation (1) we find that the distance the car moved through is
begin{align*}
d &= dfrac{0^2-110^2}{2timesleft(-11 right)}\
&= fbox{$550 ~ rm{m}$}
end{align*}
item 140 m
item 550 m\
v_{f}^{2} = v_{i}^{2} + 2ad
$$
0 = (55m/s)^2 + 2(-11m/s^2)(d)
$$
0 = (110m/s)^2 + 2(-11m/s^2)(d)
$$
– Acceleration: $a=-11mathrm{~dfrac{m}{s^2}}$
– Initial velocity: $v_0=55mathrm{~dfrac{m}{s}}$
**Objective**
– $mathrm{bold a)}$ Distance of stoppage $d_{stop1}$ for velocity $v_0$
– $mathrm{bold b)}$ Distance of stoppage $d_{stop2}$ for velocity $2cdot v_0$
In order to solve this problem we need to relate the acceleration of a object $a$ to the initial velocity $v_0$, distance traveled $d$ and final velocity $v_f$ (Which is zero when car stops).
We can do this by using the kinematic relation:
$$begin{align}
v_f^2=v_0^2+2cdot dcdot a
end{align}$$
$$begin{align}
v_f^2&=v_0^2+2cdot dcdot a nonumber
\0&=v_0^2+2cdot d_{stop}cdot arightarrow d_{stop}=-dfrac{v_0^2}{2cdot a}
end{align}$$
Now we can use the equation $(2)$ to solve the problems $mathrm{bold a)}$ and $mathrm{bold b)}$.
Using the equation $(2)$ we get:
$$begin{aligned}
d_{stop1}&=-dfrac{v_0^2}{2cdot a}
\&=dfrac{55^2}{2cdot 11}
\&=boxed{137.5 mathrm{~m}}
end{aligned}$$
Using the equation $(2)$ and $v_0rightarrow 2cdot v_0$ we get:
$$begin{aligned}
d_{stop2}&=-dfrac{(2cdot v_0)^2}{2cdot a}
\&=dfrac{(2cdot 55)^2}{2cdot 11}
\&=boxed{550 mathrm{~m}}
end{aligned}$$
$mathrm{bold b)}$ $d_{stop2}=550 mathrm{~m}$
0 = (20m/s)^2 + 2(-7m/s^2)(d)
$$
a = dfrac{88m/s-66m/s}{12s}
$$
a = 1.83m/s^2
$$
d = (66m/s)(12s) + dfrac{1}{2}(1.83m/s^2)(12s)^2
$$
textbf{underline{textit{Solution}}}
$$
[d=dfrac{1}{2}left(v_f + v_i right)t]
Where,
newenvironment{conditions}
{parvspace{abovedisplayskip}
noindent
begin{tabular}{>{$}c{${}}c<{{}$} @{} l}}
{end{tabular}parvspace{belowdisplayskip}}
begin{conditions}
v_i&: & The initial speed of the plane.\
v_f&: & The final speed of the plane.\
d&: & The distance traveled by the plane before reaching its final speed.\
t&: & Duration of time during which the plane is being decelerated.
end{conditions}
It is given that the initial speed of the plane is 145 m/s and the final speed of the plane is 75 m/s, and the duration of the acceleration is 15 s.
$$
begin{align*}
d &= dfrac{1}{2} left(75+145right) times 15\
&= fbox{$1650 ~ rm{m}$}
end{align*}
$$
(30m/s)(t) = (0m/s)(t) + dfrac{1}{2}(7m/s^2)(t)^2
$$
v_{f} = v_{i} + at
$$
v_{f} = 0 + (7m/s^2)(8.6s)
$$
v_{f} = 60m/s
$$
v_{f} = 60m/s
$$

Since the direction of acceleration and velocity is the same, and the direction of the falling penny is positive, this means that velocity is also positive and thus $mathrm{underline {acceleration~is~positive}}$ as well.
$dfrac{1}{2}at^{2} + v_{i}t – d= 0$
$0.81t^2 + 0t- 1.2= 0$
t = 1.22 sec.
$V_{i}=$ 0 m/s
a= 1.62$m/s^2$
d = 1.2 m
t=?
d = v_{i}t + dfrac{1}{2}at^2
$$
1.2m = 0 + dfrac{1}{2}(1.62m/s^2)(t)^2
$$
t^2 = 1.48148148
$$
– Height: $h=1.2mathrm{~m}$
– Acceleration: $a=1.62mathrm{~dfrac{m}{s^2}}$
**Objective**
– Find time of travel $t$
In order to solve this problem we need to relate the distance traveled $S$ (which in our case is the height $h$), acceleration $a$ and time of travel $t$.
To do this we can use the kinematic relation:
$$begin{align}
S=v_0cdot t+acdotdfrac{t^2}{2}
end{align}$$
Where $v_0$ is the initial velocity.
$$begin{align}
S&=v_0cdot t+acdotdfrac{t^2}{2} nonumber
\&=0cdot t+acdotdfrac{t^2}{2} nonumber
\&=acdotdfrac{t^2}{2}
end{align}$$
$$begin{align}
t^2=dfrac{2cdot S}{a}rightarrow t=sqrtdfrac{2cdot S}{a}
end{align}$$
Now substituting the distance traveled $S$ with height $h$, we can calculate the time of travel.
$$begin{aligned}
t&=sqrtdfrac{2cdot S}{a}
\&=sqrtdfrac{2cdot h}{a}
\&=sqrtdfrac{2cdot 1.2}{1.62}
\&=boxed{1.22mathrm{~sec}}
end{aligned}$$
$v_{f} = 0 + 9.81 x 8$
= 78.48 m/s
$V_{i}=$ 0 m/s
a= 9.81$m/s^2$
d = m
t= 8 sec
$d = 0 x 8 +dfrac{1}{2}$ x 9.81 x 8$^{2}$
d = 313.92 m
$V_{i}=$ 0 m/s
a= 9.81$m/s^2$
d = ? m
t= 8
a = dfrac{v_{f}-v_{i}}{t}
$$
9.81 m/s^2 = dfrac{v_{f}-0}{8s}
$$
d = v_{i}t + dfrac{1}{2}at^2
$$
d = 0 + dfrac{1}{2}(9.81m/s^2)(8s)^2
$$
– Time of travel: $t=8mathrm{~sec}$
**Objective**
$mathrm{bold{a)}}$ Find the velocity $v$ after time $t$
$mathrm{bold{b)}}$ Find the displacement after time $t$
**Approach**
In order to solve this problem, we need to relate the time of travel $t$ to the velocity $v$ and the acceleration $a$. Acceleration due to free fall o Earthis $a=g=9.81$ in the downwards direction.
To do this, we can use the definition of acceleration as change in velocity $varDelta v$ over time interval $t$.
$$begin{align}
a=dfrac{varDelta v}{t}
end{align}$$
$$begin{align}
varDelta v=v_f-v_0
end{align}$$
In our case, the initial velocity $v_0$ is $0$ so the change in velocity is simply:
$$begin{align}
varDelta v=v_f-0=v_f
end{align}$$
We can now plug in this into $(1)$ and find the velocity $v_f$.
$$begin{aligned}
a&=dfrac{varDelta v}{t}
\&=dfrac{ v_f}{t}rightarrow v_f=acdot t
end{aligned}$$
Now we can plug in our knowns and get the $v_f$:
$$begin{aligned}
v_f&=acdot t
\&=9.81cdot8
\&=boxed{78.48mathrm{~dfrac{m}{s}}}
end{aligned}$$
In order to solve this problem, we now need to relate the displacement $d$ to the time of travel $t$ and the acceleration due to gravity $a=9.81$.
We can do this by using the kinematic relation:
$$begin{align}
d=v_0cdot t+dfrac{acdot t^2}{2}
end{align}$$
Where $v_0$ is the initial velocity.
$$begin{align}
d&=v_0cdot t+dfrac{acdot t^2}{2} nonumber
\&=0cdot t+dfrac{acdot t^2}{2} nonumber
\&=dfrac{acdot t^2}{2}
end{align}$$
Now we can calculate the displacement $d$.
$$begin{aligned}
d&=dfrac{acdot t^2}{2}
\&=dfrac{9.81cdot 8^2}{2}
\&=boxed{313.93mathrm{~m}}
end{aligned}$$
$v_{f} = 0 + 9.81 x 2$
= 19.62 m/s
$V_{i}=$ 0 m/s
a= 9.81$m/s^2$
d = m
t= 2 s
$d = 0 x 2 +dfrac{1}{2}$ x 9.81 x 2$^{2}$
d = 19.62 m
$V_{i}=$ 0 m/s
a= 9.81$m/s^2$
d = ? m
t= 2 s
a = dfrac{v_{f}-v_{i}}{t}
$$
9.81 m/s^2 = dfrac{v_{f}-0}{2s}
$$
d = v_{i}t + dfrac{1}{2}at^2
$$
d = 0 + dfrac{1}{2}(9.81m/s^2)(2s)^2
$$
– Time of travel: $t=2mathrm{~sec}$
**Objective**
– Find the velocity of the bag: $v$
– Distnace traveled: $d$
In order to find the velocity $v$ and distance traveled $d$, we need to relate the to the time of travel $t$ and the acceleration due to free fall of Earth $a=9.81$. We can do that by first using the definition of acceleration as change in velocity $varDelta v$ over time interval $t$:
$$begin{align}
a=dfrac{varDelta v}{t}
end{align}$$
$$begin{align}
a=dfrac{varDelta v}{t}=dfrac{v}{t}rightarrow v=acdot t
end{align}$$
Now we can calculate the velocity $v$.
$$begin{aligned}
v&=acdot t nonumber
\&=9.81cdot 2 nonumber
\&=boxed{19.62mathrm{~dfrac{m}{s}}}
end{aligned}$$
$$begin{aligned}
v&=dfrac{d}{t}
\&downarrow
\d&=vcdot t
\&=19.62cdot 2
\&=boxed{39.24mathrm{~m}}
end{aligned}$$
$d=39.24mathrm{~m}$
$V_{f}^{2}$ = $(2.0)^{2}$ + $2(9.8)(2.5)$
$V_{f}^{2}$ = $V_{i}^{2}$ + $2ad$
I picked this equation because it involves everything we’re given to solve this problem: We don’t know $V_{f}$, but we do know $V_{i}$ (our initial velocity, 2.0 m/s), we know “a” (our acceleration due to gravity, 9.8 m/$s^{2}$), and we know “d” (our total displacement, 2.5m).
Everything we know gets plugged into the equation on the left.
$V_{f}^{2}$ = 53
$V_{f}$ = $sqrt{53}$ $approx$ 7.28 m/s
Once you know which equation to use, the problem boils down to plugging in numbers. The trick to these accelerated motion problems is really knowing which equation to use based on which variables you’re given.
$v_f^2 = 2^2 + 2 x 9.81x 2.5$
$sqrt{ 2^2 + 2 x 9.81x 2.5}$
= 7.28 m/s
$V_{f}= ?$
$V_{i}=$ 2 m/s
a= 9.81$m/s^2$
d = 2.5 m
$v_f^2 = 2^2 + 2 x (-9.81) x (-2.5)$
$sqrt{ 4+ 49.05}$
= 7.28 m/s
$V_{f}= ?$
$V_{i}=$ 2 m/s
a= -9.81$m/s^2$
d = -2.5 m
v_{f} = sqrt{v_{i}^{2} + 2gd_{f}}
$$
v_{f} = sqrt{2.0 m/s^{2} + 2left( 9.80 m/s^{2}right)left( 2.5 mright)} = 7.3 m/s
$$
textbf{underline{textit{Solutions}}}
$$
The reason for the time duration being equal in both cases, is that the acceleration work on decreasing the the speed of the beanbag till it reaches zero, where from the following equation we can find the distance at which the beanbag reached a zero velocity, i.e. “the maximum height”
$$
d=dfrac{v_f^2-v_i^2}{2a} tag{1}
$$
Where the final velocity is zero, and the acceleration of gravity is constant, thus the height the beanbag reaches depends solely on the initial speed by which it was thrown.
And at the point of maximum height reached by the beanbag, using equation (1) we find that it will reach a final speed which is same as the initial speed by which it was thrown.
Where by applying equation (1) once again at the point where the beanbag reached the maximum height, where the initial speed is zero and the distance covered when reaching at the same level from where the beanbag was thrown is the same as before.
And as the acceleration of the gravity is the same, then using equation (1) we find that the beanbag $textbf{would have a final speed which is the same speed as it was initially thrown with}$.
knowing that the beanbag is covering the same distance during its journey up and down, and having the same initial and final speed, suggests the symmetry of the motion of the beanbag “a parabolic motion”.
Therefor it spent in equal time moving up to the maximum height till it come to rest and moving down back to the same initial speed from which it was thrown.
And hence the time spent by the beanbag to reach its final speed is 1.1 seconds, and using the following equation we can find the distance traveled by the beanbag to reach its maximum height
$$
d=v_it+dfrac{1}{2}a t^2 tag{1}
$$
And knowing that the initial speed is given by the following equation
$$
v_i = v_f -at tag{2}
$$
Substituting (2) in (1), we get
$$
d= left( v_f -atright)t + dfrac{1}{2}at^2 tag{3}
$$
Therefor, we use equation (3) to find the distance traveled by the ball, $textbf{underline{textit{keeping in mind}}}$ that the acceleration of gravity acts downward thus we assign a negative sign to the acceleration, And and knowing that the final speed is zero thus equation (3) becomes
$$
d =left(-left( -9.8right)t^2 right) – dfrac{1}{2} left( 9.8right)t^2
$$
$$
d= dfrac{1}{2}left( 9.8right) t^2 tag{4}
$$
And, we can find the initial speed by which the ball was thrown using equation (2).
enumerate[bfseries (a)]
item Substituting by the knowns in equation (4), where the final speed is zero and the acceleration of gravity is -9.8 m/s$^2$ and the duration of motion is 1.1 seconds, we can find the distance traveled as follows
begin{align*}
d &= dfrac{1}{2} left(9.8 times 1.1^2 right)\
&= 0.50 left( 9.8 times 1.1 times 1.1 right)\
&= fbox{$5.929 ~ rm{m}$}
end{align*}
Therefor, the maximum height the beanbag reached is 5.9 m.\
textbf{underline{textit{note:}}} Since in the above multiplication process the least number of significant figures is 2, therefor the final answer should have only 2 significant figures, therefor the final result rounded to 2 significant figures is 5.9 m.
item Substituting in equation (2), we can find the initial speed by which the beanbag was thrown, as follows
begin{align*}
v_i &= 0 – (-9.8) (1.1)\
&= 9.8times 1.1 \
&= fbox{$10.78 ~ rm{m/s}$}
end{align*}
textbf{underline{textit{note:}}} Since in the above multiplication process the least number of significant figures is 2, therefor the final answer should have only 2 significant figures therefor the final result rounded to 2 significant figures is 11 m/s.
item 5.9 m
item 11 m/s
textbf{underline{textit{Solution}}}
$$
$$
tag{1} d=dfrac{1}{2}left(v_i+v_f right)t
$$
$$
begin{align*}
d &= dfrac{1}{2}left( 162+65right)times 10\
&= 1135 ~ rm{m}
end{align*}
$$
Therefor the spaceship moved a distance of 1135 m, while uniformly accelerating to reach its final speed.
a = dfrac{4m/s-0m/s}{4s}
$$
a = 1.0m/s^2
$$
d = (0m/s)(10s) + dfrac{1}{2}(1m/s^2)(4s)^2
$$
– Initial velocity: $v_0=0.0mathrm{~dfrac{m}{s}}$
– Final velocity: $v_f=4.0mathrm{~dfrac{m}{s}}$
– Time of travel: $t=4mathrm{~s}$
**Objective**
– Find the distance traveled $d$
In order to solve this problem, we need to relate distance traveled $d$ to the knowns ($v_0$,$v_f$ and $t$).
To do this, we can first find the acceleration $a$, and after that use the kinematic relation:
$$begin{align}
v_f^2=v_0^2+2cdot dcdot a
end{align}$$
Let’s start by finding the acceleration $a$.
$$begin{align}
a=dfrac{varDelta v}{t}
end{align}$$
The change in velocity over interval our given time of travel is equal to the final velocity $v_f$ minus the initial velocity $v_0$, and since the initial velocity $v_0$ is equal to $0$, the change in velocity is: $varDelta v =v_f$.
$$begin{align}
a=dfrac{v_f}{t}
end{align}$$
We can also take in account that the initial velocity $v_0$ is also $0$ in equation $(1)$ and get from $(1)$:
$$begin{align}
v_f^2&=v_0^2+2cdot dcdot a nonumber
\v_f^2&=0^2+2cdot dcdot a nonumber
\v_f^2&=2cdot dcdot a
end{align}$$
$$begin{align}
v_f^2&=2cdot dcdot a nonumber
\v_f^{cancel 2}&=2cdot dcdot dfrac{cancel {v_f}}{t}rightarrow d=dfrac{v_fcdot t}{2}
end{align}$$
Now using $(5)$ we can simply calculate the disntace $d$.
$$begin{aligned}
d&=dfrac{v_fcdot t}{2}
\&=dfrac{4cdot 4}{2}
\&=boxed{8mathrm{~m}}
end{aligned}$$
__a.__ The distance travel of the pack when it releases in a weather balloon that floats at a constant height above Earth and hit the ground with a velocity of $-73.5 m/s$.
__b.__ The total time the pack took to fall.
$$begin{aligned}
&v_f^2 = v_i^2 + 2ad \
&v_f = v_i + at_f \
text{where;} \
&v_f = text{final velocity of the object} \
&v_i = text{initial velocity of the object} \
&a = text{acceleration of the object or the gravity of the Earth if its free fall} \
&d = text{distance travel of the object} \
&t_f = text{total time the object travelled}
end{aligned}$$
$$begin{aligned}
&v_f^2 = v_i^2 + 2ad \
&(-73.5 text{m/s} )^2 = (0)^2 + 2 (9.81 text{ m/s}^2) d \
&5402.25 text{m}^2/ text{s}^2 = 19.62 text{m/s}^2 (d) \
&boxed{d = 275. 34 text{m}}
end{aligned}$$
$$begin{aligned}
&v_f = v_i + at_f \
&-73.5 text{m/s} = 0 + (-9.81 text{m/s}^2 ) t_f \
&t_f = dfrac{-73.5}{-9.81} \
&boxed{t_f =7.49 text{s} }
end{aligned}$$
&textbf{a.} d = 275. 34 text{m} \
&textbf{b.} t_f =7.49 text{s}
end{aligned}$$
$a=dfrac{v_f^2 – v_i^2}{2d}$
=$a=dfrac{ 44^2 – 0^2}{2x 3.5}$
276.57$m/s^2$
$V_{f}= 44 m/s$
$V_{i}=$ 0 m/s
a= ? $m/s^2$
d = 3.5 m
– Final velocity: $v_f=44mathrm{~dfrac{m}{s}}$
– Displacement: $d=3.5mathrm{~m}$
**Objective**
– Find the acceleration $a$ and compare it to the gravity acceleration.
In order to solve this problem, we need to relate the acceleration $a$ to the givens ($v_f$ and $d$). To do this, we can use the kinematic formula:
$$begin{align}
v_f^2=v_0^2+2cdot a cdot d
end{align}$$
Where $v_0$ is the initial velocity and $d$ is the displacement.
$$begin{align}
v_f^2&=v_0^2+2cdot a cdot d nonumber
\v_f^2&=0^2+2cdot a cdot d nonumber
\v_f^2&=2cdot a cdot d rightarrow a=dfrac{v_f^2}{2cdot d}
end{align}$$
Now using $(2)$ we can simply calculate the acceleration.
$$begin{aligned}
a&=dfrac{v_f^2}{2cdot d}
\&=dfrac{44^2}{2cdot3.5}
\&=boxed{277mathrm{~dfrac{m}{s^2}}}
end{aligned}$$
$$begin{align}
dfrac{a}{g}=dfrac{277}{9.81}boxed{approx28}
end{align}$$
So, the acceleration we got $a$ is 28 times bigger than that of Earth’s.
textbf{underline{textit{Solution}}}
$$
item ~\
noindent
{color{white} rule{linewidth}{0.5mm} }\
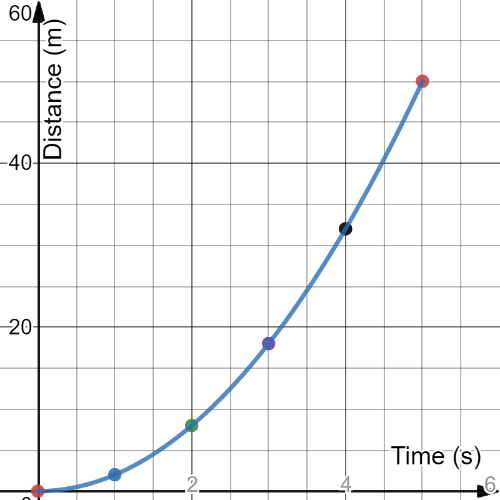
Plotting the given table, where we represent the time on $x$-axis and the distance on $y$-axis yields the following textbf{graph}
item ~\
From the graph, we draw a vertical line from the point $left(2.2,0 right)$ perpendicular to the $x$-axis and find the point of intersection of the curve representing the motion of the ball with this vertical line.\
We find that the point of intersection is nearly $left(2.2,10 right)$.\
And since the $y$-component is 10 m, therefor the ball cut through a distance of 10 m in 2.2 seconds.\
textbf{underline{textit{Or}}} for more accurate result, by carefully examining the given values in the table, we find that the equation representing this values is
[y=2x^2 ]
Substituting in this equation we find that this equation satisfies all the values given in the table, therefor by substituting by $x=2.2$, we find that the distance $y=9.68$
item See graph.
item The ball cut through a distance of $approx$ 10 m.
a. V_{f}^{2}=V_{i}^{2}+2a triangle x
$$
(3500dfrac{m}{s})^{2}=0^{2}+2a(.002m)
$$
a=310000000dfrac{m}{s^{2}}
$$
a=dfrac{v}{t}
$$
310000000dfrac{m}{s^{2}}=dfrac{3500dfrac{m}{s}}{t}
$$
.000011s=t
$$
a. 3.1×10^{8} m/s^{2}; b. 11 microseconds
$$
– Final velocity: $v_f=3.5mathrm{~dfrac{km}{s}}=3500mathrm{~dfrac{m}{s}}$
– Distance of travel: $d=2.0mathrm{~cm}=0.02mathrm{~m}$
**Objective**
$mathrm{bold{a)}}$ Find the acceleration $a$
$mathrm{bold{b)}}$ Time of acceleration $t$
**Approach**
In order to find the acceleration $a$, we need to relate it to the givens ($v_f$ and $d$). To do this, we can use the kinematic formula:
$$begin{align}
v_f^2-v_0^2=2cdot acdot d
end{align}$$
Where $v_0$ is the initial velocity, which for our case is $0$, so $(1)$ becomes:
$$begin{align}
v_f^2=2cdot acdot d
end{align}$$
Now we can find $a$ using $(2)$.
$$begin{align}
a=dfrac{v_f^2}{2cdot d}
end{align}$$
We can now simply calculate:
$$begin{aligned}
a&=dfrac{v_f^2}{2cdot d}
\&=dfrac{3500^2}{2cdot0.02}
\&boxed{approx306times10^6mathrm{~dfrac{m}{s^2}}}
end{aligned}$$
To find the time of acceleration, we can relate it to the givens ($v_f$, $d$) and the acceleration we’ve found in part $mathrm{bold{a)}}$. To do this we can use the definition of acceleration as change in velocity $varDelta v$ over time of travel $t$:
$$begin{align}
a=dfrac{varDelta v}{t}
end{align}$$
$$begin{align}
a=dfrac{varDelta v}{t}=dfrac{v_f}{t}
end{align}$$
From $(5)$ we can express time of travel $t$:
$$begin{align}
t=dfrac{v_f}{a}
end{align}$$
Now we can simply calculate the time of travel $t$ from $(6)$.
$$begin{aligned}
t&=dfrac{v_f}{a}
\&=dfrac{3500}{306times10^6}
\&=boxed{1.14times10^{-5}mathrm{~sec}}
end{aligned}$$
$mathrm{bold{b)}}$ $t=1.14times10^{-5}mathrm{~sec}$
textbf{underline{textit{Solution}}}
$$
And given that it can decelrates from this speed to rest in 2.15 seconds.\
Thus knowing the initial and final speed and duration of time during which the sled reached its final speed, thus we can calculate the acceleration and deceleration constant of the sled using the following equation
[v_f = v_i + at tag{1}]
newenvironment{conditions}
{parvspace{abovedisplayskip}noindent
begin{tabular}{>{$}c{${}}c<{{}$} @{} l}}
{end{tabular}parvspace{belowdisplayskip}}
Where,\
begin{conditions}
v_i & :& Is the initial speed of the sled.\
v_f &:& Is the final speed of the sled.\
a &:& Is the acceleration/deceleration constant of the sled.\
t &:& Time duration during which the sled accelerates/decelerates to its fi- \&& ! nal speed.
end{conditions}
begin{align*}
a &= dfrac{v_f-v_i}{t}\
&= dfrac{444-0}{1.8}\
&approx 250 ~ rm{m/s}^2
intertext{Thus, the acceleration constant of the sled is 250 m/s$^2$.}
intertext{Which is nearly 25.5 times the acceleration of gravity}
end{align*}
And, the deceleration constant using equation (1) but this time the initial speed of the sled is 444 m/s and the final speed is zero, therefor the decelerat-\ion constant is
begin{align*}
a &= dfrac{v_f-v_i}{t}\
&= dfrac{0-444}{2.15}\
&approx – 207 ~ rm{m/s}^2
end{align*}
Thus, the acceleration constant of the sled is 207 m/s$^2$, Which is nearly 21.1 times the acceleration of gravity..\
textbf{underline{textit{note:}}} The negative sign as the sled is decelerating.\
textbf{underline{textit{note:}}} since the least number of significant figures in 207/9.80 is 3 significant figures thus the final answer should have also 3 significant figures.\
textbf{underline{textit{note:}}} The 0 in 9.80 is also a signifcant figures because it tells us the precision of the numerical value.
renewcommand{theinlineenum}{bfseriesarabic{inlineenum}}
newenvironment{inlineenum}
{unskipignorespacessetcounter{inlineenum}{0}%
renewcommand{item}{refstepcounter{inlineenum}{{theinlineenum})~}}}
{ignorespacesafterend}
inlineenum
item 250 m/s$^2$, 25.5 $g$.
item 207 m/s$^2$, 21.1 $g$.
textbf{underline{textit{Solution}}}
$$
item ~\
Plotting the given table for a velocity-time graph, where we represent the velocity on the $y$-axis and the time on $x$-axis yields the following textbf{graph}\
end{enumerate}
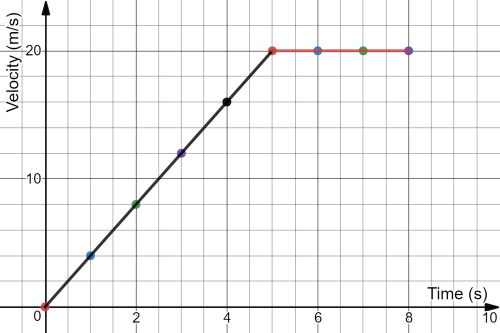
item ~\
The area under the curve in the velocity-time graph represents the displacement of the car, and during the first 2 seconds from the above graph we find that the area under the curve is the area of a right angle triangle, whose height is 8 and its base is 2, and the area of the traingle is given by
[text{Area}= dfrac{1}{2} times base times height = 0.5times 2 times 8 = 8 ~ rm{m} ]
Thus, the total displacement of the car during the first 2 seconds is 8 m.
end{enumerate}
item ~\
During the first 4 seconds the area under the curve representing the motion in the velocity-time graph, from the above graph is the area of a triangle whose height is 16 and base is 4, as before the area of the traingle is thus 32 and therefor the total displacement of the car during the first 4 seconds is 32 m.\
textbf{underline{textit{note:}}} That the height of the traingle in the graph “the $y$-axis” have a unit of m/s and the base of the traingle “the $x$-axis” have a unit of s thus the product would have a unit of displacement.\
end{enumerate}
begin{enumerate}[bfseries (d)]
item ~\
The total displacement during the entire journey of the car, is the area under the curve for the whole 8 seconds, in order to find the total area we divide the are under the curve into two sections.\
The first section is the area under the curve during the time interval [0,5] seconds, where the area under the curve would be a triangle whose base is 5 and height is 20 as before the area would be 50 m.\
The second section is the area under the curve during the time interval [5,8] seconds, which would be represented by the rectangle whose sides are 3 and 20, and since the area of the rectangle is given by
[ text{Area} = text{width} times text{height} = 3 times 20 = 60]
Thus the total area under the curve, is $left(50+60 right)=110 ~ rm{m}$ which means that the total displacement of the car during the entire journey of the car “8 seconds” is 110 m.
end{enumerate}
item ~\
The slope of the line is calculated using the following formula for the slope
[m = dfrac{Delta y}{Delta x} tag{1}]
Using the two points $left(0,0 right)$ and $left( 4,16right)$, the slope would be
[m=dfrac{16-0}{4-0} = 4 ~ rm{m/s}^2]
Therefor the car is uniformly accelerating during the first 4 seconds with a constant of acceleration of 4 m/s$^2$.
end{enumerate}
enumerate[bfseries (f)]
item ~\
Using the formula (1) to calculate the slope as before, and using points $(5,20)$ and $(7,20)$ we get
[m=dfrac{20-20}{7-5}=0 ]
textbf{underline{textit{Or}}} simply from the graph, we observe that the line representing the motion of the car during this time interval is a horizontal straight line and any horizontal line would have a zero slope as the change in $y$-axis is zero.\
item See Graph. quad quad
item 8 m. quad quad
item 32 m. quad quad
item 110 m. quad quad
item 4 m/s. quad quad
item zero.

textbf{underline{textit{Solution}}}
$$
{parvspace{abovedisplayskip}
noindent
begin{tabular}{>{$}l{${}}c<{{}$} @{} l}}
{end{tabular}parvspace{belowdisplayskip}}
textbf{underline{textit{Knowns:}}} Since it is given that barriers decelerates the car with an acceleration constant of $-300$ m/s$^2$, and since the car is going with an initial speed of 110 km/hr.\
And it is required to find the thickness $d$ of the barrier which would bring the car to a final speed of zero, which can be calculated using the following equation
[v_f^2 = v_i^2 + 2 ad tag{1}]
Where,\
begin{conditions}
{v_i}^{2} & : & The initial speed of the car.\
{v_f}^2 & : & The final speed of the car.\
~ a ~ & : & Deceleration constant of the barrier.\
~ d ~ & : & Width of the barrier.\
end{conditions}
And since 1 hr = 3600 seconds, and 1 km = 1000 m therefor we convert the units of 110 km/hr as follows
[110 ~ dfrac{rm{km}}{rm{hr}} ~ dfrac{rm{hr}}{3600 ~ rm{s}} ~ dfrac{1000 ~ rm{m}}{rm{km}}= 110/3.6 ~ dfrac{rm{m}}{rm{s}} approx 31 rm{m/s} ]
textbf{underline{textit{note:}}} to convert the unit of 1 km/hr to m/s we divide by 3.6 and if we want to convert from m/s to km/hr we multiply by 3.6.\
Thus knowing the initial speed of the car in units of m/s and the deceleration constant of the car, we can find the thickness of the barrier that would decelerate the car to a final speed of zero as follows
begin{align*}
v_f^2 &= v_i^2 + 2 ad\
d &= dfrac{v_f^2 – v_i^2}{2a}\
&= dfrac{0^2-31^2}{-2times300}\
&=fbox{$1.6 ~ rm{m}$}
intertext{Thus, the thickness of the barrier should be 1.6 m in order to decelerates the car to rest, textbf{underline{textit{note:}}} we assigned a negative sign to the acceleration as it works on slowing down the car.}
end{align*}
textbf{underline{textit{Solution}}}
$$
The slope of the curve in the velocity-time graph yields the acceleration of the object, where the slope in velocity time graph is given by the following equation
$$
m=a= dfrac{v_f – v_i}{t_f – t_i} tag{1}
$$
And, the area under the velocity time graph represents the distance traveled by the object, where usually we have 3 different shapes for the area bounded between the curve and the $x$-axis. we list them as follows
* ize
* Rectangle: Whose width is $w$ and height is $h$, and its area is given by $wtimes h$
* Triangle: Whose base is $b$ and height is $h$, and its area is given by $dfrac{1}{2} b times h$
* Trapezium: Where we have 2 parallel sides $a$ and $b$, and separated by a distance $h$, and whose area is given by $dfrac{1}{2} (a+b)times h$
item In order to describe the motion of George’s fist, we need first to determine the choice of coordinates by which the two graphs was drown, we do so using the position-time graph first.\
As probably The wooden board is in front of George, thus as the position of George’s fist was initially at 7 cm from the origin, thus probably the board was at the origin and the direction toward which George stand is positive.\
Therefor, as George stands in the positive direction beyond the wooden board and as he is moving his fist toward the board, thus he is moving his fist toward the negative direction thus his fist must have a negative velocity, as he is punching to break the wooden board.\
George acquired his fist speed almost instantly reaching a speed of 13 m/s toward the wooden block “i.e. having negative sign”, and then his fist decelerates to rest breaking the wooden brick in nearly around 5 ms.\
item The acceleration by which George’s fist came to rest when breaking the wooden block is nearly uniform, taking two points along this straight line “during the time interval [3,8] ms”.\
Where the initial speed was around 13 m/s and the final speed is zero, thus by calculating the slope of this line “for simplicity we approximate this line as a perfect straight line”.\
We find that the deceleration constant of George’s first is given by equation (1) but before using this equation we first need to convert time from ms to s, therefor we multiply time by a conversion factor of $10^{-3}$, thus the acceleration constant from the slope is
begin{align*}
m&=dfrac{v_f – v_i }{t_f – t_i}\
&=dfrac{0-(-13)}{(8-3)times 10^{-3}}\
&= 2600 ~ rm{m/s} ^2
end{align*}
We notice, that the deceleration constant is positive as the direction of motion is negative and in order for an object to decelerates then its acceleration must be in a direction opposite to the direction of motion, which emphasis our choice of coordinates.\
end{enumerate}
enumerate[bfseries (c)]
item As we know the constant of deceleration from part (b), we can find how many multiple is it compared with the acceleration of gravity, knowing that the acceleration of the gravity is 9.81 m/s$^2$ thus
[ dfrac{2600}{9.81} = 265 ]
Therefor, the fist decelerates with a constant of acceleration that is 265 time the acceleration of gravity !!
item The area bounded between the curve and the $x$-axis in a velocity-time graph represents the distance moved by the object, hence we can find the distance George’s fist traveled during the first 6 ms.\
During the first 3 ms the area bounded between the curve and the $x$-axis roughly represent area of a rectangle whose width is 3 ms and height is 13 m/s, thus after converting the units of time from ms to s by multiplying by a conversion factor of $10^{-3}$ is
[ Area= 13 times 3 times 10^{-3}= 0.039 ~ rm{m}]
And during the time interval [3,6] ms, the area bounded between the curve and the $x$-axis is a trapezium having 2 parallel sides 13 m/s and 4 m/s, and the distance separating the two sides is 3 m/s, thus the area of the trapezium is
[ Area = dfrac{1}{2} (13+4) times 3 times 10^{-3} = 0.0255 ~ rm{m} ]
Thus, the total area under the curve during the first 6 ms is the sum of the two areas which is
[ text{Total Area} = 0.039 + 0.0255 = 0.0645 ~ rm{m}]
textbf{underline{textit{note:}}} And as the least number of significant figures after the decimal is 2 therefor the final answer should have 2 significant figures after the decimal according to the rules of the significant operations, thus the final answer should be 0.065 m or 6.5 cm.\
Comparing this result with the position-time graph we find that initially the object was at a distance around 7 cm, and finally after the 6 ms the object was nearly at the origin.\
Thus the total distance traveled by the object during this time interval is around 7 cm, which is close to the value obtained calculating the area under the curve, keeping in mind that we made rough estimation concerning the shapes of the areas when calculating them.\
textbf{underline{textit{note:}}} If the curves was perfectly straight then we should expect that the displacement calculating from the position-time graph and the velocity time graph would be exactly the same.\
item From the position-time graph, the coordinates chosen by which the position-time graph was drawn is such that the direction of George’s fist toward the wooden block is negative, thus George’s fist almost instantly reached a velocity of -13 m/s or 13 m/s toward the wooden block, and then his fist decelerates to rest in almost 5 ms after hitting the wooden block.
item 2600 m/s$^2$.
item 265 $g$.\
item From the area under the curve the total displacement of George’s fist is 6.5 cm, while from the position-time graph it is around 7 cm.
textbf{underline{textit{Solution}}}
$$
And since it is required to find the bag velocity after 2 seconds, knowing only the initial velocity $v_i$ and the acceleration of gravity $g$ and the duration during which the bag was falling $t$ we can use the following equation to find the final velocity of the bag $v_f$
$$
v_f=v_i+gt tag{1}
$$
And, knowing the final speed we can use the following equation to find the distance the bag traveled
$$
d= dfrac{v_f^2-v_i^2}{2g} tag{2}
$$
Which is the same equation as the following kinematics equation of motion, in terms of distance $d$
$$
v_f^2 =v_i^2 + 2gd
$$
During the 2 seconds while the bag was falling downward it made a distance $d_{down}$ the helicopter was rising upward cutting a distance $d_{up}$.
Where we will assume the our point of reference from which we are going to measure the distance traveled upward by the helicopter and the distance traveled downward by the bag is at the exact instant at which the bag was fallen.
At this specific moment the helicopter risen a distance $d_{up}$, which can be calculated using the following equation knowing that it have a constant velocity of 5 m/s which also means, that it has no acceleration thus the distance traveled can be calculated using the following equation
$$
d_{up} = v_i t + left( 1/2right)at^2tag{3}
$$
And the downward distance traveled by the bag knowing its initial speed and knowing that it is falling under the influence of the acceleration of gravity and the duration of the fall, can be calculated using the following equation
[d_{down}= v_i t + left(1/2 right) gt^2 tag{4}]
And knowing that the helicopter traveled a distance $d_{up}$ after 2 seconds from our point of reference and the bag traveled a distance $d_{down}$ after 2 seconds from our point of reference, thus we can know that the distance separating the bag and the helicopter by adding both distance, thus
[d_{sep} = d_{up} + d_{down}tag{5}]
Where,
newenvironment{conditions}
{parvspace{abovedisplayskip}noindent
begin{tabular}{>{$}c{${}}c<{{}$} @{} l}}
{end{tabular}parvspace{belowdisplayskip}}
begin{conditions}
v_i &:& The initial speed of the bag and in equation (3) it is the initial sp-\ &&
eed of the helicopter which is also the same as that of the bag.\
v_f &:& The final speed of the bag.\
g &:& The acceleration of gravity.\
t &:& Duration during which the bag was falling.\
d_{up} &:& The upward distance traveled by the helicopter.\
d_{down} &:& The downward distance traveled by the helicopter.\
d_{sep} &:& The distance separating the bag and the helicopter.
end{conditions}
enumerate[bfseries (a)]
item Substituting the knowns in equation (1), we calculate the final velocity of the bag as follows
begin{align*}
v_f &= v_i + gtimes t\
&= 5 – 9.81 times 2\
&= 5 – 20 \
&= – 15 ~ rm{m/s}
end{align*}
textbf{underline{textit{note:}}} we have assigned the positive sign to the initial speed as the bag was initially travelling upward, and the assigned a negative sign to the acceleration as the acceleration is pointing downward, the final speed is downward thus having a negative sign.\
item Knowing the final speed and the initial speed and the acceleration of gravity, we can find the distance traveled by the bag using equation (2)
begin{align*}
d &= dfrac{v_f^2 – v_i^2}{2g}\
&= dfrac{left(-15 right)^2 -left(5 right)^2}{2times left( -9.81right)}\
&= dfrac{200}{-20}\
&= -10 ~ rm{m}
end{align*}
textbf{underline{textit{note:}}} we assigned a negative sign to the acceleration as acts downward, a distance of -ve sign simply means that the bag traveled a distance of 10 m below “downward” the point of reference” the exact moment at which the bag was fallen”.\
Where from equation (3), the upward traveled distance is calculated as follows
begin{align*}
d_{up}&= v_itimes t\
&= 5 times 2\
&= 10 ~ rm{m/s}
intertext{textbf{underline{textit{note:}}} Where we assigned a +ve sign to the velocity because the helicopter is travelling in an upward direction, and the distance is positive which means that it have traveled a distance 10 m beyond the point of reference.}
intertext{ knowing using equation (5) the distance separating the bag and the helicopter is }
d_{sep}&= left|10right| + left|-10right|
&= 20 ~ rm{m}
end{align*}
textbf{underline{textit{note:}}} we have taken the absolute value of both distance in order to find the magnitude of the distance separating them, because the -ve sign only indicates the direction at which the object traveled.\
textbf{underline{textit{Or}}} in other words the bag traveled upward a distance 10 m and the bag traveled downward a distance 10 m, therefor the distance separating them is of course 20 m and not zero.
item – 15 m/s or 15 m/s downward.
item 10 m downward from the moment the bag was dropped.
item 20 m.
$$
begin{align*}
Delta v_C&=10 mathrm{km/h} \
Delta v_B&=10 mathrm{km/h}
end{align*}
$$
Unknown:
$$
a=?
$$
$$
begin{align*}
a&=dfrac{Delta v}{Delta t} \
\
a_{car}&=dfrac{Delta v_c}{Delta t} \
&=dfrac{10 mathrm{km/h}}{Delta t} \
\
a_{bike}&=dfrac{Delta v_b}{Delta t} \
&=dfrac{10 mathrm{km/h}}{Delta t} \
\
a_{car}&=a_{bike}
end{align*}
$$
textbf{underline{textit{Solution}}}
$$
In the given scenario, two trains are moving in the same direction and with different speed with the express train being much faster than the local train with a speed of 36 m/s, and the local train with a speed of 11 m/s.
Of course, as both trains are moving on the same track naturally if the express train doesn’t break it would crash with the local train.
However, the express train driver saw the local train 100 m away and at the moment the express train driver saw the local train he immediately pushed the brakes leading to a deceleration to the train speed with a constant of deceleration of 3 m/s$^2$.
Now, since the local train is moving with a uniform speed it would have cut a given distance after 12 seconds which can be calculated using the following equation
$$
d_1 = v t tag{1}
$$
Knowing both the local train’s speed and the duration of motion, we can find how far would it have traveled.
Knowing the initial speed of the local train, the constant of deceleration, and the duration of motion we can use the following equation
$$
d_2 = v_i t + dfrac{1}{2} at^2 tag{2}
$$
Making the point of origin is the point at which the express train driver observed the local train 100 m away, from this point the local train would be far a way from the origin by the distance already separating between the origin and the local train in addition to the distance traveled by the train during the 12 seconds, i.e. the train position would be at a distance $100+d_1$ from the origin.
While the express train after 12 seconds would be separated by a distance $d_2$ from the origin.
If the distance $d_2$ is greater than the distance $100+d_1$ then the express train would collides with the local train.
enumerate[bfseries (a)]
item Calculating the distance the local train traveled after 12 seconds using equation (1) and substituting by the knowns ,we get
begin{align*}
d_1 &= 11 times 12\
&= 132 ~ rm{m/s}\
end{align*}
And using equation (2) to find the distance the express train traveled and substituting by the knowns in the equation, we get
begin{align*}
d_2 &= 36 times 12 – dfrac{1}{2} times 3 times 12^2\
&= 432 -216\
&= 216 ~ rm{m/s}\
end{align*}
Thus, knowing the distance the express train traveled and the distance the local train traveled, we can find the position of each train from the origin, and hence have some idea whether they would collide or not.\
Since the beginning of the motion for the express train is at the origin, and the distance traveled is $d_2$ therefor the express is at a distance 216 m from the origin.\
And since the local train was 100 m far from the origin, and as it traveled a distance $d_1$ during the 12 seconds, then it is at a distance of $100+132=232 text{m}$ from the origin.\
Since, the local train is at a distance 232 m from the origin, and the express train is at a distance 216 m from the origin, then textbf{underline{no} collision occurs}.\
item In part (a), we didn’t account for the possiblity that the two trains would collides before the 12 seconds, we were only calculating whether or not the two trains would collide after 12 seconds.\
In order to find whether the two trains would collide or not we will table position-time table, where we tabulate the position of each of the two trains at the end of each second during a time interval of 12 seconds.\
And then after tabulating the position-time for each of the two train, we plot the position-time graph for each of the two trains on the same graph, and observe if there is any intersection between the two curves where an intersection would mean that both trains have collided together.\
We begin tabulating the position-time table for the local, train where we know that the local train move with a uniform speed of 11 m/s, thus using equation (1) we can find its position after each second keeping in mind that the local train is separated by a distance 100 m from the origin, thus the table is as follow
begin{center}
begin{tabular}{|c||c|}
hline
Time (s)& Position (m) \
hline
0& 100 \
1& 111\
2& 122\
3& 133\
4& 144\
5& 155\
6& 166\
7& 177\
8& 188\
9& 199\
10& 210\
11& 221\
12& 232\
hline
end{tabular}
end{center}
begin{center}
begin{tabular}{|c||c|}
hline
Time (s)& Position (m) \
hline
0& 0\
1& 34.5\
2& 66\
3& 94.5\
4& 120\
5& 142.5\
6& 162\
7& 178.5\
8& 192\
9& 202.5\
10& 210\
11&214.5 \
12& 216\
hline
end{tabular}
end{center}
Once at time 6.667 seconds at position 173.33 m from the origin, and once at 10 seconds at a position 210 m from the origin “the two points are marked with cross on the graph”.
item From our calculations, the train won’t collide after 12 seconds.
item From part(a), our calculation didn’t put into account the possibility for a collision to occur before the 12 seconds, however from the graph we will find that the the train would collides twice, where the two curves representing the motion of each train intersects twice, the two points are marked with a cross.
– Law of inertia – He helped in describing the fact that constant velocity can be kept even without the presence of external force.
– Ballistic motion – He was one of the first to describe that projectile motion has a parabolic trajectory.
– Many astronomical discoveries, such as Jupiter’s four moons and the invention of a Galilean telescope.
These are just to list a few, there are of course many more.
textbf{underline{textit{Solution}}}
$$
[2.34+2.3=4.6 ]
Where, the second term have only one significant figures after the decimal, therefor the final answer must have only one significant figure after the decimal.\
While in multiplication or division, the final answer must have a number of significant figures as much as the least number of significant figures in the terms being multiplied “or divided”, i.e.
[2.352 times 2 = 5]
Where the least number of significant figures in the terms being multiplied is 1, thus since the final answer should be 4.704 but since the final answer must have only one significant figures then the answer should be 4.$|$7 and is approximated to the nearest 1 significant figure thus the answer is 5.\
Therefor, the final answers for the given algebraic operations is as follows
enumerate[bfseries (a)]
item First, we make both terms being added have the same power of 10, thus we have
[ 0.62 times 10^{-3} ~ rm{m} + 5.7times 10^{-3}~ rm{m} = 6.32 times 10^{-3} ~ rm{m}]
And since the least number of digits after the decimal is 1,hence the final answer is $6.3times 10^{-3} ~ rm{m}$
textbf{underline{textit{Or}}}
If we chosen to make the terms having the same power of -4, thus we have
[ 6.2 times 10^{-4} ~ rm{m} + 57 times 10^{-4}~ rm{m} = 63.2 times 10^{-4} ~ rm{m}]
And since the least number of digits after the decimal is zero, thus we should expect that the final answer should have no decimal, hence the final answer is $63times 10^{-4}~ rm{m}$
item textbf{underline{textit{note:}}} take care that the first term have a unit of km and the second term is in unit of m, therefor before calculating the difference between both numbers we need to unite the exponent, therefor as before we have [8.7 times 10^{11} ~ rm{m} – 3.4 times 10^{7} ~ rm{m} = left( 8.7-0.00034 right)times 10^{7} ~ rm{m} ]
Where the least number of significant figures after the decimal is 1, or in other words we should expect one significant figure after the decimal in our final answer, and therefor the final answer is $8.7 times 10^{11} ~ rm{m}$ rounded to the neareset decimal.
end{enumerate}
begin{enumerate}[bfseries (c)]
item [left( 9.21 times 1.83right) times left( 10^{-5+8} right) ~ rm{cm} = 16.8543 times 10^{3}~ rm{cm}]
And since the final answer should have only 3 significant figures, thus the final answer rounded to the 3 significant figures is $16.9times 10^{3} ~ rm{cm}$
end{enumerate}
enumerate[bfseries (d)]
item [ dfrac{2.63}{4.08} times 10^{-6-6} ~ rm{m/s}= 0.644607 times 10^{-12} ~ rm{m/s}]
And since the final answer should have only 3 significant figures, therefor the final answer should be $0.645 times 10^{-12} ~ rm{m/s}$ rounded to 3 significant figures.
item $63times 10^{-4}~ rm{m}$
item $8.7 times 10^{11} ~ rm{m}$
item $16.9times 10^{3} ~ rm{cm}$
item $0.645 times 10^{-12} ~ rm{m/s}$
textbf{underline{textit{Solution}}}
$$
{parvspace{abovedisplayskip}
noindent
begin{tabular}{>{$}c{${}}c<{{}$} @{} l}}
{end{tabular}parvspace{belowdisplayskip}}
The given equation in the problem describes the distance the object traveled $d$ at a given time $t$, and since the general equation of any straight line is given by the following
[y=mx+c ]
Where,
begin{conditions}
$m$&: &is the slope of the straight line .\
$c$&: &is the $y$ intercept .\
end{conditions}
And comparing the general equation of the straight line with the given equation of the straight line we find that the distance “position'' is represented on the $y$-axis and the time is represented on the $x$-axis and the slope of the straight line is 35 m/s, and the $y$ intercept of the straight line is -5 m.\
Thus, a line that would represent the motion of the object given by the equation in a position-time graph is a straight line that starts at a distance 5 m before the origin at time zero, i.e. a line that begins from point $left( 0,-5right)$ and whose slope is 35 m/s, thus the position-time graphs is as follows
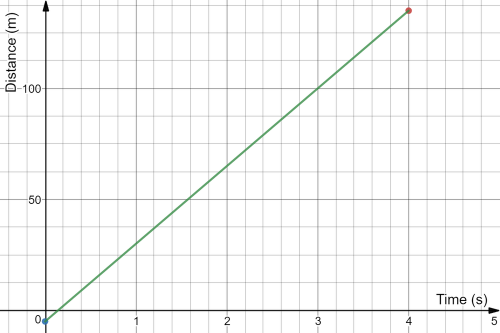
$$
v=35 ~ rm{m/s}
$$
Which is an object whose velocity is constant at all the times whose value is 35 m/s.
$textbf{underline{textit{Or}}}$ simply by comparing the general equation of the straight line with the given equation, we find that the slope of the straight line is 35 m/s.
Thus the motion diagram representing this kind of motion is an equally spaced dots where the time interval between each two consecutive dots is 1 seconds and the arrow coming out from each dot represents the velocity vector, i.e. the direction of the arrow represents the direction of the vector and the length of the arrow represents the magnitude of the vector.
Thus, the arrows coming out from each dots would have the same arrow direction and the same length, as the object is moving with a uniform speed “thus arrow representing the vector would have the same length”.
And since the object started its journey at -5 m before the origin we label the beginning dot at -5 m before the origin which is nearly at a 1/7 the distance between the first two dots, as the the object reaches the origin at nearly 1/7 seconds “from the equation” and since the distance between the two dots is a 1 second therefor the the origin is at 1/7 the distance between the two dots, and hence the motion diagram is