Physics: Principles and Problems
9th Edition
ISBN: 9780078458132
Textbook solutions
All Solutions
Page 770: Assessment
Exercise 23
Step 1
1 of 1
Exercise 24
Step 1
1 of 1
Rutherford has scattered a beam of $alpha$-particles by a thin golden plate and then he observed the distribution of scattering angles. A small number of deflection angle was taking large values (direct deflection) suggesting that the positive charge has to be focused in a very tiny region of space when compared to atom itself.
Exercise 25
Step 1
1 of 1
Bohr postulated that since the energy levels have discrete values the change of the energy in the hydrogen atom has to be accompanied by either emission or absorption of a photon that has the same energy as the given energy difference between the levels.
Exercise 26
Step 1
1 of 1
The main flow of the planetary model is its inconsistency with the electrodynamics since if threated as a particle which follows one circular path eventually it will start radiating and therefore loosing energy which will result in a collapse of the electron into the nucleus.
Exercise 27
Step 1
1 of 1
The main and the principle assumption that Bohr has made was to introduce stationary states of the atom’s energy. In this state the energy is constant and electrons will move without loosing energy.
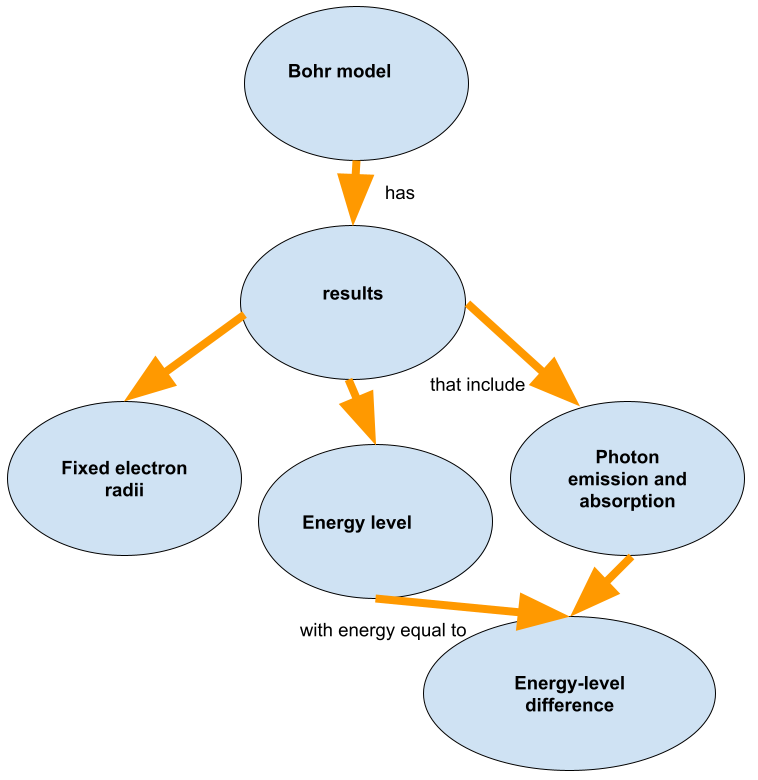
The second assumption was that change in energy happens in discrete jumps between energy levels and it is accompanied by absorption or emission of photons.
The third assumption was that angular momentum is quantized, too.
Exercise 28
Step 1
1 of 2
The gas inside the tube is heated and atoms move faster and collide more frequently causing electrons to move to higher energy levels. Then, while returning to their ground states, atoms will emit photons. These photons will have energies that are equal to atom’s spectral lines.
Result
2 of 2
See explanation.
Exercise 29
Step 1
1 of 1
The position of spectral lines emitted by atoms correspond to wavelengths of emitted photons while atom jumps from higher to lower energy levels and have energies that equal the energy differences between the energy levels.
Exercise 30
Step 1
1 of 1
The spectral lines of hydrogen and helium gas discharge tubes are different because they have different electronic configurations therefore different energy levels.
Exercise 31
Step 1
1 of 1
The reason for this is highly concentrated light over a very small area in laser versus divergent light over a very large area around the lamp.
Exercise 32
Step 1
1 of 1
The acronym MASER stands for the following:
$textbf{Microwave Amplification by Stimulated Emission of Radiation}$
Exercise 33
Step 1
1 of 2
The most distinctive feature that makes lasers perfect for light shows is their directionality, i.e. they are easily manipulated in space and therefore they can be used to create very precise animations. Also, they have sharply defined colors because they are monochromatic.
Result
2 of 2
See the explanations.
Exercise 34
Step 1
1 of 1
As the number of electrons in the shell increases and number of possible states increases the emission spectrum becomes more dense and more complex than for hydrogen like atoms.
Exercise 35
Step 1
1 of 1
The spectrum should be discrete, i.e. should be represented with lines because the air is composed out of three components oxygen molecules, nitrogen molecules and CO2 molecules and these molecules have line spectra. It is worth nothing that the final spectrum will be more dense than usual but definitely a discrete spectrum.
Exercise 36
Step 1
1 of 1
Since the atmosphere consists of gases they will absorb certain wavelengths of the emitted light so the astronaut will see the spectrum with dark lines in it. So the answer is no, it’s not continuous.
Exercise 37
Step 1
1 of 1
Yes, the money is a very good example of quantization because it always has a basic whole value and all amounts of money are always multiples of that value (think of one cent for example. )
The water, in its macroscopic form is not a good example of quantization because it seems like a continuous quantity which can take any value.
Exercise 38
Step 1
1 of 1
No, the photon will not be absorbed since the energy needed for the mercury atom to be excited to $E_4$ is
$$
E_4-E_1=-4.95+10.38=5.43textrm{eV}
$$
and to get to $E_5$ is
$$
E_5-E_1=-3.71+10.38=6.67textrm{eV}
$$
and we need the photon energy to match exactly the transition energy for the excitation to happen.
Exercise 39
Step 1
1 of 2
There are six possible emission lines in this system with the transition $E_{41}$ having the highest energy.
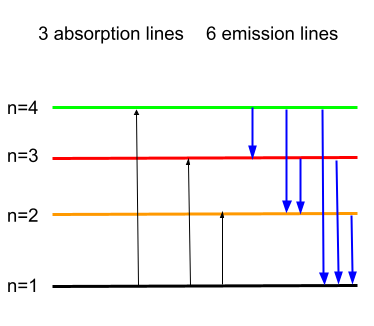
The complete emission and absorption spectrum is given below.
Step 2
2 of 2
Exercise 40
Step 1
1 of 1
The maximum energy, by definition of the hydrogen atom spectrum is 13.6eV and it is equal to ionization energy of the hydrogen. That means that if in the ground state, electron absorbs the photon of this energy, it can escape the hydrogen atom.
Exercise 41
Step 1
1 of 1
The main difference between the Bohr model and the quantum mechanical model is understanding of the electrons trajectory. In the Bohr model, the electron is orbiting on a fixed orbit whereas in the QM model the position of the electron is defined as the probability, i.e. the electron’s position is described with a wave function. This basic difference leads to another major difference where Bohr model can deal only with one-electron systems whereas the QM model can deal with all the atoms, regardless of the number of electrons (of course with some limitations).
Exercise 42
Step 1
1 of 1
In the visible light spectrum, among the given colors, the blue light has the shortest wavelength i.e. the highest energy. The red light photons will have the lowest energy.
Exercise 43
Step 1
1 of 5
In this problem we are given a calcium atom that undergoes a transition to the ground state while emitting a photon. We should find the wavelength of that photon.
Step 2
2 of 5
In order to solve this problem we are first going the determine the energy difference between the two given states which is going to be equal to the energy of the emitted photon since
$$
E_i-E_{ph}=E_f
$$
$$
E_{ph}=E_i-E_f=5.16-2.93=2.23textrm{ eV}
$$
Step 3
3 of 5
Now, we can find the wavelength of the emitted photon by using the Planck equation which is given as
$$
E_{ph}=frac{hc}{lambda}
$$
where we can express $lambda$ as
$$
lambda=frac{hc}{E_{ph}}
$$
where $hc=1240times 10^{-9}$eV$cdot$m.
Step 4
4 of 5
The final step is to substitute the given values in a straightforward manner to obtain that
$$
lambda=frac{1240times 10^{-9}}{2.23}=boxed{556times 10^{-9}textrm{ m}}
$$
Result
5 of 5
$$
lambda=556times 10^{-9}textrm{ m}
$$
lambda=556times 10^{-9}textrm{ m}
$$
Exercise 44
Step 1
1 of 4
In this problem we are given the calcium atom in its first excited state which is hit by photon of a given energy. We should find the final state of the calcium atom.
Step 2
2 of 4
In order to do this we are going to note that the energy state is given relative to the ground state, i.e. we have that $E_{21}=2.93$ eV so we can write that the equation that describes the process is
$$
E_{m1}=E_{21}+E_{ph}=2.93+1.2=4.13textrm{ eV}
$$
Step 3
3 of 4
Now, by looking at the the figure 28-22 we see that energy difference corresponds to the $E_3=4.13$ eV so our answer is $boxed{E_3}$.
Result
4 of 4
The calcium atom ends up at the $E_3$ state.
Exercise 45
Step 1
1 of 4
In this problem we are given a calcium atom which is at $E_6$ energy level and drops to $E_2$ energy level. We want to find how much energy is released in this process.
Step 2
2 of 4
In order to do so, let’s write the equation of the process. We have an emission of a photon so the equation of the process is given as
$$
E_6-E_{ph}=E_2
$$
where we read the $E_6$ and $E_2$ values from the figure 28-22.
Step 3
3 of 4
The released energy is represented by the photon leaving the atom so we have that
$$
E_{ph}=E_6-E_2=5.16-2.93=boxed{2.23textrm{ eV}}
$$
Result
4 of 4
$$
E_{ph}=2.23textrm{ eV}
$$
E_{ph}=2.23textrm{ eV}
$$
Exercise 46
Step 1
1 of 5
In this problem we are given a calcium atom in the $E_6$ state that is being hit by an orange light photon which ionizes it. We want to know the kinetic energy of the electron after the ionization.
Step 2
2 of 5
In order to do this let’s first find how much energy do we we need to ionize the calcium atom in $E_6$ state. The ionization energy of the calcium is 6.08 eV. And the atom in $E_6$ state has 5.16 eV energy. Therefore the ionization energy in $E_6$ becomes
$$
E_{6ion}=E_{ion}-E_{6}=6.08-5.16=0.92textrm{ eV}
$$
Step 3
3 of 5
Now, let’s see how much energy the incident photon has. For that we are using the Planck equation whit $hc=1240times 10^{-9}$ eV$cdot$m.
$$
E_{ph}=frac{hc}{lambda}=frac{1240times 10^{-9}}{600times 10^{-9}}=2.07textrm{ eV}
$$
Step 4
4 of 5
Finally, the kinetic energy of the electron is given as following difference
$$
K_{e}=E_{ph}-E_{6ion}=2.07-0.92=boxed{1.15textrm{ eV}}
$$
Result
5 of 5
$$
K_{e}=1.15textrm{ eV}
$$
K_{e}=1.15textrm{ eV}
$$
Exercise 47
Step 1
1 of 5
In this problem we are given a hydrogen atom with a task to determine the energies of its $E_2$ and $E_7$ state.
Step 2
2 of 5
We can now take the formula that defines the energy levels in the hydrogen atom and is given as
$$
E_{n}=-frac{13.6}{n^2}
$$
Step 3
3 of 5
center{In the case of $E_2$ this becomes}
[E_2=-frac{13.6}{2^2}=boxed{-3.4textrm{ eV}}]
[E_2=-frac{13.6}{2^2}=boxed{-3.4textrm{ eV}}]
Step 4
4 of 5
center{In the case of $E_7$ we have that}
[E_7=-frac{13.6}{7^2}=boxed{-0.278textrm{ eV}}]
[E_7=-frac{13.6}{7^2}=boxed{-0.278textrm{ eV}}]
Result
5 of 5
$$
E_2=-3.4textrm{ eV}
$$
E_2=-3.4textrm{ eV}
$$
$$
E_7=-0.278textrm{ eV}
$$
Exercise 48
Step 1
1 of 6
In this problem we are given a hydrogen atom with a task to determine the energy difference between its $E_2$ and $E_7$ state.
Step 2
2 of 6
Therefore, we should first find the corresponding energies of the two states. We can now take the formula that defines the energy levels in the hydrogen atom and is given as
$$
E_{n}=-frac{13.6}{n^2}
$$
Step 3
3 of 6
center{In the case of $E_2$ this becomes}
[E_2=-frac{13.6}{2^2}=-3.4textrm{ eV}]
[E_2=-frac{13.6}{2^2}=-3.4textrm{ eV}]
Step 4
4 of 6
center{In the case of $E_7$ we have that}
[E_7=-frac{13.6}{7^2}=-0.278textrm{ eV}]
[E_7=-frac{13.6}{7^2}=-0.278textrm{ eV}]
Step 5
5 of 6
center{Now, the energy difference is simply given as}
[E_{7rightarrow2}=E_7-E_2=-0.278+3.4=boxed{3.12textrm{ eV}}]
[E_{7rightarrow2}=E_7-E_2=-0.278+3.4=boxed{3.12textrm{ eV}}]
Result
6 of 6
$$
E_{7rightarrow2}=3.12textrm{ eV}
$$
E_{7rightarrow2}=3.12textrm{ eV}
$$
Exercise 49
Step 1
1 of 4
In this problem we are given a mercury atom which excited to its $E_6$ state. We should find the current ionization energy and the energy released during a drop to $E_2$ state.
Step 2
2 of 4
a) In order to complete the first task, we consult the figure 28-21 which tells us that the ionization energy of the mercury is $E_{ion}=10.38$ eV whereas the energy of $E_6$ state is 7.7 eV. Now, to ionize the atom at $E_6$ we need
$$
E_{6ion}=E_{ion}-E_{6}=10.38-7.7=boxed{2.68 textrm{ eV}}
$$
Step 3
3 of 4
b) Now, the energy released during the deexcitation to $E_2$ state is to be found from the following equation
$$
E_6-E_{ph}=E_2
$$
$$
E_{ph}=E_6-E_2=7.7-4.64=boxed{3.06textrm{ eV}}
$$
Result
4 of 4
$$
textrm{a) }E_{6ion}=2.68textrm{ eV}
$$
textrm{a) }E_{6ion}=2.68textrm{ eV}
$$
$$
textrm{b) }E_{ph}=3.06textrm{ eV}
$$
Exercise 50
Step 1
1 of 4
In this problem we are given a mercury atom which is in an excited state of given energy. After the absorption of a photon, it excites once more to the next energy level and we should find the frequency of the absorbed photon.
Step 2
2 of 4
In order to do so, we consult the figure 28-21 which tells us that the mercury atom is in $E_4$ state and the next level is $E_5$ so the energy of the absorbed photon is
$$
E_{ph}=E_5-E_4=-3.71+4.95=1.24textrm{ eV}
$$
Step 3
3 of 4
Now, we can use the Planck equation $E_{ph}=hf$ to find its frequency. We have that
$$
f=frac{E_{ph}}{h}=frac{1.24times 1.6times 10^{-19}}{6.63times times 10^{-34}}=boxed{3times 10^{14}textrm{ Hz}}
$$
Result
4 of 4
$$
f=3times 10^{14}textrm{ Hz}
$$
f=3times 10^{14}textrm{ Hz}
$$
Exercise 51
Step 1
1 of 8
In this problem we are given a hydrogen atom with a task to determine the energies of its $E_2$, $E_3$, $E_4$, $E_5$ and $E_6$ state.
Step 2
2 of 8
We can now take the formula that defines the energy levels in the hydrogen atom and is given as
$$
E_{n}=-frac{13.6}{n^2}
$$
Step 3
3 of 8
center{In the case of $E_2$ this becomes}
[E_2=-frac{13.6}{2^2}=boxed{-3.4textrm{ eV}}]
[E_2=-frac{13.6}{2^2}=boxed{-3.4textrm{ eV}}]
Step 4
4 of 8
center{In the case of $E_3$ we have that}
[E_3=-frac{13.6}{3^2}=boxed{-1.51textrm{ eV}}]
[E_3=-frac{13.6}{3^2}=boxed{-1.51textrm{ eV}}]
Step 5
5 of 8
center{In the case of $E_4$ we have that}
[E_4=-frac{13.6}{4^2}=boxed{-0.85textrm{ eV}}]
[E_4=-frac{13.6}{4^2}=boxed{-0.85textrm{ eV}}]
Step 6
6 of 8
center{In the case of $E_5$ we have that}
[E_5=-frac{13.6}{5^2}=boxed{-0.544textrm{ eV}}]
[E_5=-frac{13.6}{5^2}=boxed{-0.544textrm{ eV}}]
Step 7
7 of 8
center{In the case of $E_5$ we have that}
[E_6=-frac{13.6}{6^2}=boxed{-0.378textrm{ eV}}]
[E_6=-frac{13.6}{6^2}=boxed{-0.378textrm{ eV}}]
Result
8 of 8
$$
E_2=-3.4textrm{ eV}
$$
E_2=-3.4textrm{ eV}
$$
$$
E_3=-1.51textrm{ eV}
$$
$$
E_4=-0.85textrm{ eV}
$$
$$
E_5=-0.544textrm{ eV}
$$
$$
E_6=-0.378textrm{ eV}
$$
Exercise 52
Step 1
1 of 9
In this problem we are given the hydrogen atom and we should find the following energy differences:
$E_{6rightarrow5}$
$E_{6rightarrow3}$
$E_{4rightarrow2}$
$E_{6rightarrow5}$
$E_{6rightarrow3}$
$E_{4rightarrow2}$
$$
E_{5rightarrow2}
$$
$$
E_{5rightarrow3}
$$
Step 2
2 of 9
In order to do this, we have to find the energies of the involved energy levels and we can do so by employing the following formula:
$$
E_{n}=-frac{13.6}{n^2}
$$
Step 3
3 of 9
center{Now, the energies of different levels are given as:}
[E_2=-frac{13.6}{2^2}=-3.4textrm{ eV}]
[E_3=-frac{13.6}{3^2}=-1.51textrm{ eV}]
[E_4=-frac{13.6}{4^2}=-0.85textrm{ eV}]
[E_5=-frac{13.6}{5^2}=-0.544textrm{ eV}]
[E_6=-frac{13.6}{6^2}=-0.378textrm{ eV}]
[E_2=-frac{13.6}{2^2}=-3.4textrm{ eV}]
[E_3=-frac{13.6}{3^2}=-1.51textrm{ eV}]
[E_4=-frac{13.6}{4^2}=-0.85textrm{ eV}]
[E_5=-frac{13.6}{5^2}=-0.544textrm{ eV}]
[E_6=-frac{13.6}{6^2}=-0.378textrm{ eV}]
Step 4
4 of 9
center{ a) The first energy difference is given as: }
[E_{6rightarrow5}=E_6-E_5=-0.378+0.544=boxed{0.166textrm{ eV}}]
[E_{6rightarrow5}=E_6-E_5=-0.378+0.544=boxed{0.166textrm{ eV}}]
Step 5
5 of 9
center{ b) The second energy difference is given as: }
[E_{6rightarrow3}=E_6-E_3=-0.378+1.51=boxed{1.13textrm{ eV}}]
[E_{6rightarrow3}=E_6-E_3=-0.378+1.51=boxed{1.13textrm{ eV}}]
Step 6
6 of 9
center{ c) The next energy difference is given as: }
[E_{4rightarrow2}=E_4-E_2=-0.85+3.4=boxed{2.55textrm{ eV}}]
[E_{4rightarrow2}=E_4-E_2=-0.85+3.4=boxed{2.55textrm{ eV}}]
Step 7
7 of 9
center{ d) The next energy difference is given as: }
[E_{5rightarrow2}=E_5-E_2=-0.544+3.4=boxed{2.86textrm{ eV}}]
[E_{5rightarrow2}=E_5-E_2=-0.544+3.4=boxed{2.86textrm{ eV}}]
Step 8
8 of 9
center{ e) The next energy difference is given as: }
[E_{5rightarrow3}=E_5-E_3=-0.544+1.51=boxed{0.97textrm{ eV}}]
[E_{5rightarrow3}=E_5-E_3=-0.544+1.51=boxed{0.97textrm{ eV}}]
Result
9 of 9
$$
textrm{a) }E_{6rightarrow5}=0.166textrm{ eV}
$$
textrm{a) }E_{6rightarrow5}=0.166textrm{ eV}
$$
$$
textrm{b) }E_{6rightarrow3}=1.13textrm{ eV}
$$
$$
textrm{c) }E_{4rightarrow2}=2.55textrm{ eV}
$$
$$
textrm{d) }E_{5rightarrow2}=2.86textrm{ eV}
$$
$$
textrm{e) }E_{5rightarrow3}=0.97textrm{ eV}
$$
Exercise 53
Step 1
1 of 14
In this problem we are given the hydrogen atom and we should find the frequencies of the emitted photons during these transitions:
$E_{6rightarrow5}$
$E_{6rightarrow3}$
$E_{4rightarrow2}$
$E_{6rightarrow5}$
$E_{6rightarrow3}$
$E_{4rightarrow2}$
$$
E_{5rightarrow2}
$$
$$
E_{5rightarrow3}
$$
Step 2
2 of 14
In order to do this, we have to find the energies of the involved energy levels and we can do so by employing the following formula:
$$
E_{n}=-frac{13.6}{n^2}
$$
Step 3
3 of 14
center{Now, the energies of different levels are given as:}
[E_2=-frac{13.6}{2^2}=-3.4textrm{ eV}]
[E_3=-frac{13.6}{3^2}=-1.51textrm{ eV}]
[E_4=-frac{13.6}{4^2}=-0.85textrm{ eV}]
[E_5=-frac{13.6}{5^2}=-0.544textrm{ eV}]
[E_6=-frac{13.6}{6^2}=-0.378textrm{ eV}]
[E_2=-frac{13.6}{2^2}=-3.4textrm{ eV}]
[E_3=-frac{13.6}{3^2}=-1.51textrm{ eV}]
[E_4=-frac{13.6}{4^2}=-0.85textrm{ eV}]
[E_5=-frac{13.6}{5^2}=-0.544textrm{ eV}]
[E_6=-frac{13.6}{6^2}=-0.378textrm{ eV}]
Step 4
4 of 14
center{ a) The first energy difference is given as: }
[E_{6rightarrow5}=E_6-E_5=-0.378+0.544=0.166textrm{ eV}]
[E_{6rightarrow5}=E_6-E_5=-0.378+0.544=0.166textrm{ eV}]
Step 5
5 of 14
center{The corresponding frequency is found from}
[f_{6rightarrow5}=frac{E_{6rightarrow5}}{h}=frac{0.166times 1.6times 10^{-19}}{6.63times 10^{-34}}=boxed{4times 10^{13}textrm{ Hz}}]
[f_{6rightarrow5}=frac{E_{6rightarrow5}}{h}=frac{0.166times 1.6times 10^{-19}}{6.63times 10^{-34}}=boxed{4times 10^{13}textrm{ Hz}}]
Step 6
6 of 14
center{ b) The second energy difference is given as: }
[E_{6rightarrow3}=E_6-E_3=-0.378+1.51=1.13textrm{ eV}]
[E_{6rightarrow3}=E_6-E_3=-0.378+1.51=1.13textrm{ eV}]
Step 7
7 of 14
center{The corresponding frequency is found from}
[f_{6rightarrow3}=frac{E_{6rightarrow3}}{h}=frac{1.13times 1.6times 10^{-19}}{6.63times 10^{-34}}=boxed{2.7times 10^{14}textrm{ Hz}}]
[f_{6rightarrow3}=frac{E_{6rightarrow3}}{h}=frac{1.13times 1.6times 10^{-19}}{6.63times 10^{-34}}=boxed{2.7times 10^{14}textrm{ Hz}}]
Step 8
8 of 14
center{ c) The next energy difference is given as: }
[E_{4rightarrow2}=E_4-E_2=-0.85+3.4=2.55textrm{ eV}]
[E_{4rightarrow2}=E_4-E_2=-0.85+3.4=2.55textrm{ eV}]
Step 9
9 of 14
center{The corresponding frequency is found from}
[f_{4rightarrow2}=frac{E_{4rightarrow2}}{h}=frac{2.55times 1.6times 10^{-19}}{6.63times 10^{-34}}=boxed{6.2times 10^{14}textrm{ Hz}}]
[f_{4rightarrow2}=frac{E_{4rightarrow2}}{h}=frac{2.55times 1.6times 10^{-19}}{6.63times 10^{-34}}=boxed{6.2times 10^{14}textrm{ Hz}}]
Step 10
10 of 14
center{ d) The next energy difference is given as: }
[E_{5rightarrow2}=E_5-E_2=-0.544+3.4=2.86textrm{ eV}]
[E_{5rightarrow2}=E_5-E_2=-0.544+3.4=2.86textrm{ eV}]
Step 11
11 of 14
center{The corresponding frequency is found from}
[f_{5rightarrow2}=frac{E_{5rightarrow2}}{h}=frac{2.86times 1.6times 10^{-19}}{6.63times 10^{-34}}=boxed{6.9times 10^{14}textrm{ Hz}}]
[f_{5rightarrow2}=frac{E_{5rightarrow2}}{h}=frac{2.86times 1.6times 10^{-19}}{6.63times 10^{-34}}=boxed{6.9times 10^{14}textrm{ Hz}}]
Step 12
12 of 14
center{ e) The next energy difference is given as: }
[E_{5rightarrow3}=E_5-E_3=-0.544+1.51=0.97textrm{ eV}]
[E_{5rightarrow3}=E_5-E_3=-0.544+1.51=0.97textrm{ eV}]
Step 13
13 of 14
center{The corresponding frequency is found from}
[f_{5rightarrow3}=frac{E_{5rightarrow3}}{h}=frac{0.97times 1.6times 10^{-19}}{6.63times 10^{-34}}=boxed{2.3times 10^{14}textrm{ Hz}}]
[f_{5rightarrow3}=frac{E_{5rightarrow3}}{h}=frac{0.97times 1.6times 10^{-19}}{6.63times 10^{-34}}=boxed{2.3times 10^{14}textrm{ Hz}}]
Result
14 of 14
$$
textrm{a) }f_{6rightarrow2}=4times 10^{13}textrm{ Hz}
$$
textrm{a) }f_{6rightarrow2}=4times 10^{13}textrm{ Hz}
$$
$$
textrm{b) }f_{6rightarrow3}=2.7times 10^{14}textrm{ Hz}
$$
$$
textrm{c) }f_{4rightarrow2}=6.2times 10^{14}textrm{ Hz}
$$
$$
textrm{d) }f_{5rightarrow2}=6.9times 10^{14}textrm{ Hz}
$$
$$
textrm{e) }f_{5rightarrow3}=2.3times 10^{14}textrm{ Hz}
$$
Exercise 54
Step 1
1 of 12
In this problem we are given the hydrogen atom and we should find the wavelengths of the emitted photons during these transitions :
$E_{6rightarrow5}$
$E_{6rightarrow3}$
$E_{4rightarrow2}$
$E_{6rightarrow5}$
$E_{6rightarrow3}$
$E_{4rightarrow2}$
$$
E_{5rightarrow2}
$$
$$
E_{5rightarrow3}
$$
by using their frequencies
Step 2
2 of 12
In order to do this, we have to find the energies of the involved energy levels and we can do so by employing the following formula:
$$
E_{n}=-frac{13.6}{n^2}
$$
Step 3
3 of 12
center{Now, the energies of different levels are given as:}
[E_2=-frac{13.6}{2^2}=-3.4textrm{ eV}]
[E_3=-frac{13.6}{3^2}=-1.51textrm{ eV}]
[E_4=-frac{13.6}{4^2}=-0.85textrm{ eV}]
[E_5=-frac{13.6}{5^2}=-0.544textrm{ eV}]
[E_6=-frac{13.6}{6^2}=-0.378textrm{ eV}]
[E_2=-frac{13.6}{2^2}=-3.4textrm{ eV}]
[E_3=-frac{13.6}{3^2}=-1.51textrm{ eV}]
[E_4=-frac{13.6}{4^2}=-0.85textrm{ eV}]
[E_5=-frac{13.6}{5^2}=-0.544textrm{ eV}]
[E_6=-frac{13.6}{6^2}=-0.378textrm{ eV}]
Step 4
4 of 12
center{Simple algebra then gives us the energy values for the listed transitions}
[textrm{a) }E_{6rightarrow5}=0.166textrm{ eV}]
[textrm{b) }E_{6rightarrow3}=1.13textrm{ eV}]
[textrm{c) }E_{4rightarrow2}=2.55textrm{ eV}]
[textrm{d) }E_{5rightarrow2}=2.86textrm{ eV}]
[textrm{e) }E_{5rightarrow3}=0.97textrm{ eV}]
[textrm{a) }E_{6rightarrow5}=0.166textrm{ eV}]
[textrm{b) }E_{6rightarrow3}=1.13textrm{ eV}]
[textrm{c) }E_{4rightarrow2}=2.55textrm{ eV}]
[textrm{d) }E_{5rightarrow2}=2.86textrm{ eV}]
[textrm{e) }E_{5rightarrow3}=0.97textrm{ eV}]
Step 5
5 of 12
Now, we can apply the Planck equation $E=hf$ to find the frequency of the each photon
$$
textrm{a) }f_{6rightarrow2}=frac{E}{h}=4times 10^{13}textrm{ Hz}
$$
$$
textrm{b) }f_{6rightarrow3}=frac{E}{h}=2.7times 10^{14}textrm{ Hz}
$$
$$
textrm{c) }f_{4rightarrow2}=frac{E}{h}=6.2times 10^{14}textrm{ Hz}
$$
$$
textrm{d) }f_{5rightarrow2}=frac{E}{h}=6.9times 10^{14}textrm{ Hz}
$$
$$
textrm{e) }f_{5rightarrow3}=frac{E}{h}=2.3times 10^{14}textrm{ Hz}
$$
Step 6
6 of 12
Now, we will use the wavelength-frequency relation which is given as follows
$$
c=lambda f
$$
to express the wavelength
$$
lambda=frac{c}{f}
$$
Step 7
7 of 12
center{In the first case we have that }
[lambda_{6rightarrow2}=frac{c}{f_{6rightarrow2}}=frac{3times 10^8}{4times 10^{13}}=boxed{7500times 10^{-9}textrm{ m}}]
[lambda_{6rightarrow2}=frac{c}{f_{6rightarrow2}}=frac{3times 10^8}{4times 10^{13}}=boxed{7500times 10^{-9}textrm{ m}}]
Step 8
8 of 12
center{b) Next }
[lambda_{6rightarrow3}=frac{c}{f_{6rightarrow3}}=frac{3times 10^8}{2.7times 10^{14}}=boxed{1111times 10^{-9}textrm{ m}}]
[lambda_{6rightarrow3}=frac{c}{f_{6rightarrow3}}=frac{3times 10^8}{2.7times 10^{14}}=boxed{1111times 10^{-9}textrm{ m}}]
Step 9
9 of 12
center{c) Next }
[lambda_{4rightarrow2}=frac{c}{f_{4rightarrow2}}=frac{3times 10^8}{6.2times 10^{14}}=boxed{484times 10^{-9}textrm{ m}}]
[lambda_{4rightarrow2}=frac{c}{f_{4rightarrow2}}=frac{3times 10^8}{6.2times 10^{14}}=boxed{484times 10^{-9}textrm{ m}}]
Step 10
10 of 12
center{d) Next }
[lambda_{5rightarrow2}=frac{c}{f_{5rightarrow2}}=frac{3times 10^8}{6.9times 10^{14}}=boxed{435times 10^{-9}textrm{ m}}]
[lambda_{5rightarrow2}=frac{c}{f_{5rightarrow2}}=frac{3times 10^8}{6.9times 10^{14}}=boxed{435times 10^{-9}textrm{ m}}]
Step 11
11 of 12
center{e) Finally }
[lambda_{5rightarrow3}=frac{c}{f_{5rightarrow3}}=frac{3times 10^8}{2.3times 10^{14}}=boxed{1304times 10^{-9}textrm{ m}}]
[lambda_{5rightarrow3}=frac{c}{f_{5rightarrow3}}=frac{3times 10^8}{2.3times 10^{14}}=boxed{1304times 10^{-9}textrm{ m}}]
Result
12 of 12
$$
textrm{a) }lambda_{6rightarrow2}=7500times 10^{-9}textrm{ m}
$$
textrm{a) }lambda_{6rightarrow2}=7500times 10^{-9}textrm{ m}
$$
$$
textrm{b) }lambda_{6rightarrow3}=1111times 10^{-9}textrm{ m}
$$
$$
textrm{c) }lambda_{4rightarrow2}=484times 10^{-9}textrm{ m}
$$
$$
textrm{d) }lambda_{5rightarrow2}=435times 10^{-9}textrm{ m}
$$
$$
textrm{e) }lambda_{5rightarrow3}=1304times 10^{-9}textrm{ m}
$$
Exercise 55
Step 1
1 of 5
In this problem we are given a photon emitted during a transition to the ground state with wavelength of 94.3nm in a hydrogen atom. We should find the initial state of the hydrogen atom.
Step 2
2 of 5
There are several ways how we can find it but let’s first calculate the energy of the photon by using the Planck formula with $hc=1240times 10^{-9}$eV$cdot$m
$$
Delta E=frac{hc}{lambda}=frac{1240times 10^{-9}}{94.3times 10^{-9}}=13.15textrm{ eV}
$$
Step 3
3 of 5
Now, one can take the the simple algebraic procedure to find the energy of the initial state
$$
E_n-Delta E=E_1
$$
$$
E_{n}=E_1+Delta E=-13.6+13.15=-0.45textrm{ eV}
$$
Step 4
4 of 5
Finally, we can use the formula that gives us energies for energy levels in hydrogen-like atoms
$$
E_n=-frac{13.6}{n^2}=-0.45
$$
which can be solved for $n$ to have that
$$
n*2=frac{13.6}{0.45}=30.2
$$
So we see that $n=5.5$ and we are going to take that the level is $boxed{n=6}$.
Result
5 of 5
n=6
Exercise 56
Step 1
1 of 10
In this problem we are given the hydrogen atom in the third Bohr orbital and we are asked to find the radius of the orbital, the Coulomb force between the proton and the electron, the centripetal acceleration of the electron and the orbital speed of the electron.
Step 2
2 of 10
a) In order to find the radius of the orbital we are going to use the Bohr formula which says
$$
r=frac{hbar^2n^2}{Kmq^2}
$$
Step 3
3 of 10
$$
r=frac{1.055^2 times 10^{-68}times 3^2}{9times 10^9times 9.11times 10^{-31}times 1.6^2times 10^{-38}}=boxed{4.77times 10^{-10}textrm{ m}}
$$
r=frac{1.055^2 times 10^{-68}times 3^2}{9times 10^9times 9.11times 10^{-31}times 1.6^2times 10^{-38}}=boxed{4.77times 10^{-10}textrm{ m}}
$$
Step 4
4 of 10
b) The Coulomb formula gives us the force acting between the electron and the proton
$$
F=frac{1}{4pi varepsilon}frac{q^2}{r^2}
$$
Step 5
5 of 10
$$
F=frac{9times10^9times 1.6^2times 10^{-38}}{4.77^2times 10^{-20}}=boxed{1.01times 10^{-9}textrm{ N}}
$$
F=frac{9times10^9times 1.6^2times 10^{-38}}{4.77^2times 10^{-20}}=boxed{1.01times 10^{-9}textrm{ N}}
$$
Step 6
6 of 10
c) Now, the centripetal force has to be equal to the electrostatic force for the stability $F_e=F_c=ma$
so we have that
so we have that
$$
a=frac{F}{m}
$$
Step 7
7 of 10
$$
a=frac{1.01times 10^{-9}}{9.11times 10^{-31}}=boxed{1.11times 10^{21},frac{textrm{m}}{textrm{s}^2}}
$$
a=frac{1.01times 10^{-9}}{9.11times 10^{-31}}=boxed{1.11times 10^{21},frac{textrm{m}}{textrm{s}^2}}
$$
Step 8
8 of 10
Finally, to find the orbital speed we are going to use its relation to the centripetal acceleration
$$
a=frac{v^2}{r}
$$
so we have that
$$
v=sqrt{ar}
$$
Step 9
9 of 10
$$
v=sqrt{1.11times 10^{21}times 4.77times 10^{-10}}=boxed{7.28times 10^5,frac{textrm{m}}{textrm{s}}=frac{1}{412}c}
$$
v=sqrt{1.11times 10^{21}times 4.77times 10^{-10}}=boxed{7.28times 10^5,frac{textrm{m}}{textrm{s}}=frac{1}{412}c}
$$
Result
10 of 10
$$
textrm{a) }r=4.77times 10^{-10}textrm{ m}
$$
textrm{a) }r=4.77times 10^{-10}textrm{ m}
$$
$$
textrm{b) }F=1.01times 10^{-9}textrm{ N}
$$
$$
textrm{c) }a=1.11times 10^{21},frac{textrm{m}}{textrm{s}^2}
$$
$$
textrm{d) }v=7.28times 10^5,frac{textrm{m}}{textrm{s}}=frac{1}{412}c
$$
Exercise 57
Step 1
1 of 4
In this problem we are given a laser that is emitting a given wavelength. We should find the energy difference between the two laser levels.
Step 2
2 of 4
We can solve this problem by employing the Planck relation which is given as
$$
E=frac{hc}{lambda}
$$
where $hc=1240times 10^{-9}$eV$cdot$m.
Step 3
3 of 4
center{Now, we can substitute the values to have that}
[E=frac{1240times 10^{-9}}{840times 10^{-9}}=boxed{1.48textrm{ eV}}]
[E=frac{1240times 10^{-9}}{840times 10^{-9}}=boxed{1.48textrm{ eV}}]
Result
4 of 4
$$
E=1.48textrm{ eV}
$$
E=1.48textrm{ eV}
$$
Exercise 58
Step 1
1 of 4
In this problem we are given a laser that is emitting a light when transitioning between two levels separated by 2.9 eV. We should find the wavelength of the light.
Step 2
2 of 4
In order to do so, are going to use the Planck relation which is given as
$$
E=frac{hc}{lambda}
$$
and it can be used to express the wavelength as
$$
lambda=frac{hc}{E}
$$
where $hc=1240times 10^{-9}$.
Step 3
3 of 4
center{Now, the simple substitution of values gives us that }
[lambda=frac{1240times 10^{-9}}{2.9}=boxed{428times 10^{-9}textrm{ m}}]
and this wavelength belongs to the visible, blue part of the spectrum. \
[lambda=frac{1240times 10^{-9}}{2.9}=boxed{428times 10^{-9}textrm{ m}}]
and this wavelength belongs to the visible, blue part of the spectrum. \
Result
4 of 4
$$
lambda=428times 10^{-9}textrm{ m}
$$
lambda=428times 10^{-9}textrm{ m}
$$
Exercise 59
Step 1
1 of 4
In this problem we are given a laser that is emitting a given wavelength. We should find the energy difference between the two laser levels.
Step 2
2 of 4
We can solve this problem by employing the Planck relation which is given as
$$
E=frac{hc}{lambda}
$$
where $hc=1240times 10^{-9}$eV$cdot$m.
Step 3
3 of 4
center{Now, we read the table 28-1 and substitute the values to have that}
[E=frac{1240times 10^{-9}}{10,600times 10^{-9}}=boxed{0.117textrm{ eV}}]
[E=frac{1240times 10^{-9}}{10,600times 10^{-9}}=boxed{0.117textrm{ eV}}]
Result
4 of 4
$$
E=0.117textrm{ eV}
$$
E=0.117textrm{ eV}
$$
Exercise 60
Step 1
1 of 6
In this problem we are given first two lasers of the same power that are emitting photons of different wavelengths and we should find the ratio of photons emitted per second for two of them. Then we want to find the exact number of emitted photons in a laser of a given power and a given wavelength.
Step 2
2 of 6
a) If we have two lasers of 840 and 427 nm the radio of the number of photons are to be found from the expression for power, i.e. energy.
$$
E=nfrac{hc}{lambda}
$$
so we have that
$$
frac{n_1}{lambda_1}=frac{n_2}{lambda_2}
$$
Step 3
3 of 6
center{Now, we have that the ratio of the emitted photons is given as}
[frac{n_1}{n_2}=frac{lambda_1}{lambda_2}=frac{840}{427}=boxed{1.97}]
[frac{n_1}{n_2}=frac{lambda_1}{lambda_2}=frac{840}{427}=boxed{1.97}]
Step 4
4 of 6
b) The next step is to calculate the number of photons in a laser that is emitting 840 nm photons with 5 mW power. We do this by using the same formula
$$
P=dot nE_{ph}
$$
$$
dot n=frac{P}{E_{ph}}=frac{P}{frac{hc}{lambda}}=frac{lambda P}{hc}
$$
where $hc=1240times 10^{-9}$ eV$cdot$m.
Step 5
5 of 6
center{Now, we can substitute the given values to obtain that }
[dot n=frac{5times 10^{-3}times 840times 10^{-9}}{6.63times 10^{-34}times 3times 10^8}=boxed{21times 10^{15}, frac{textrm{photons}}{textrm{s}}}]
[dot n=frac{5times 10^{-3}times 840times 10^{-9}}{6.63times 10^{-34}times 3times 10^8}=boxed{21times 10^{15}, frac{textrm{photons}}{textrm{s}}}]
Result
6 of 6
$$
textrm{a) }frac{n_1}{n_2}=1.97
$$
textrm{a) }frac{n_1}{n_2}=1.97
$$
$$
textrm{b) }dot n=21times 10^{15}, frac{textrm{photons}}{textrm{s}}
$$
Exercise 61
Step 1
1 of 5
In this problem we are given a laser that can emit three different wavelengths of light. We want to find the respective energy differences between the levels for the three cases and to identify their colors.
Step 2
2 of 5
a) In order to solve this problem we will use the Planck equation which is given as
$$
E_{ph}=frac{hc}{lambda}
$$
where $hc=1240times 10^{-9}$eV$cdot$m.
Step 3
3 of 5
$$
E_{ph1}=frac{1240times 10^{-9}}{632.8times 10^{-9}}=boxed{1.96textrm{eV}}
$$
E_{ph1}=frac{1240times 10^{-9}}{632.8times 10^{-9}}=boxed{1.96textrm{eV}}
$$
$$
E_{ph2}=frac{1240times 10^{-9}}{543.4times 10^{-9}}=boxed{2.28textrm{eV}}
$$
$$
E_{ph3}=frac{1240times 10^{-9}}{1152.3times 10^{-9}}=boxed{1.08textrm{eV}}
$$
Step 4
4 of 5
b) The colors of these three wavelengths are found by taking a look at the EM spectrum graph which tells as that we have red, green and infrared color, respectively.
Result
5 of 5
a) 1.96 eV, 2.28 eV, 1.08 eV
b) red, green, infrared
Exercise 62
Step 1
1 of 4
In this problem, we have a photon of given energy that ionizes a hydrogen atom. We want to find the kinetic energy of the released electron.
Step 2
2 of 4
The ionization energy of the hydrogen atom is 13.6 eV so the kinetic energy can be found as
$$
K=E_{ph}-E_{ion}
$$
Step 3
3 of 4
center{Finally, we can insert the give values to obtain the following}
[K=14-13.6=boxed{0.4textrm{ eV}}]
[K=14-13.6=boxed{0.4textrm{ eV}}]
Result
4 of 4
$$
K=boxed{0.4textrm{ eV}}
$$
K=boxed{0.4textrm{ eV}}
$$
Exercise 63
Step 1
1 of 5
In this problem, we are given $E_5$ and $E_6$ energy levels of the hydrogen atom and we are asked to find the respective orbit radii.
Step 2
2 of 5
In order to do so, we will employ the formula which defines the radii of different energy levels in the hydrogen atom
$$
r_n=frac{hbar^2n^2}{Kmq^2}
$$
Step 3
3 of 5
center{In the case $E_5$ we have that }
[r_5=frac{1.055^2times 10^{-68}times 5^2}{9times 10^{9}times 9.11times 10^{-31}times 1.6^2times 10^{-38}}]
Finally,
[boxed{r_5=1.33times 10^{-9}textrm{ m}}]
[r_5=frac{1.055^2times 10^{-68}times 5^2}{9times 10^{9}times 9.11times 10^{-31}times 1.6^2times 10^{-38}}]
Finally,
[boxed{r_5=1.33times 10^{-9}textrm{ m}}]
Step 4
4 of 5
center{In the case $E_6$ we have that }
[r_6=frac{1.055^2times 10^{-68}times 6^2}{9times 10^{9}times 9.11times 10^{-31}times 1.6^2times 10^{-38}}]
Finally,
[boxed{r_6=1.91times 10^{-9}textrm{ m}}]
[r_6=frac{1.055^2times 10^{-68}times 6^2}{9times 10^{9}times 9.11times 10^{-31}times 1.6^2times 10^{-38}}]
Finally,
[boxed{r_6=1.91times 10^{-9}textrm{ m}}]
Result
5 of 5
$$
r_5=1.33times 10^{-9}textrm{ m}
$$
r_5=1.33times 10^{-9}textrm{ m}
$$
$$
r_6=1.91times 10^{-9}textrm{ m}
$$
Exercise 64
Step 1
1 of 6
In this problem, we are given the hydrogen atom in its second energy level and we are asked to analyze the situation in which a photon of given energy hits the atom. We want to see wheater or not the photon is able to ionize the atom.
Step 2
2 of 6
a) In order to do so we shall find the energy of the hydrogen atom first. The energy of the hydrogen at a certain energy level is given by the following formula
$$
E_n=-frac{13.6}{n^2}textrm{ eV}
$$
So the energy of the second energy level is
$$
E_2=-frac{13.6}{2^2}=-3.4textrm{ eV}
$$
and that makes that the ionization energy (zero level ) is
$$
E_{ion}=3.4textrm{ eV}
$$
Step 3
3 of 6
On the other hand, the energy of the given photon is to be found from Planck’s formula which says
$$
E_{ph}=frac{hc}{lambda}=frac{1240times 10^{-9}}{332times 10^{-9}}=3.73textrm{ eV}
$$
and since $E_{ph}>E_{ion}$ $boxed{textrm{the atom is ionized.}}$
Step 4
4 of 6
b( To find the kinetic energy in Joules we will simply write the expression for the electron’s kinetic energy after the ionization
$$
K=E_{ph}-E_{ion}=3.73-3.4=0.33textrm{ eV}
$$
Step 5
5 of 6
center{Finally, we have that in Joules }
[K=0.33times 1.6times 10^{-19}=boxed{0.53times 10^{-19} textrm{ J}}]
[K=0.33times 1.6times 10^{-19}=boxed{0.53times 10^{-19} textrm{ J}}]
Result
6 of 6
a) The atom is ionized.
b) $K=0.53times 10^{-19} textrm{ J}$
Exercise 65
Step 1
1 of 4
In this problem, we are given a beam of electrons hitting hydrogen atoms and we are asked to find what is the minimum energy needed for the hydrogen to start emitting red light while going from $E_3$ to $E_2$. One should be careful here because at the first glance the answer is the difference between the two given levels but is it? The $E_3rightarrow E_2$ transition doesn’t need an external force to induce it and will happen spontaneously. So we need energy to excite the hydrogen atom from its ground state to $E_3$.
Step 2
2 of 4
So, let’s calculate the energy of the $E_3$ state by using the energy levels formula
$$
E_3=-frac{13.6}{3^2}=-1.51textrm{ eV}
$$
Step 3
3 of 4
Now, the energy that we are looking for can be obtained as following
$$
E_{e}=E_3-E_1=-1.51+13.6=boxed{12.1textrm{ eV}}
$$
Result
4 of 4
$$
E=12.1textrm{ eV}
$$
E=12.1textrm{ eV}
$$
Exercise 66
Step 1
1 of 6
In this problem, we are being introduced to the “two-photon” technique, a powerful spectroscopic tool that allows for very precise measurements of the atomic spectra. We want to know, what photon wavelengths we should use if we want to study the fundamental $E_1rightarrow E_2$ transition.
Step 2
2 of 6
Firstly, let’s characterize the aforementioned transition by determining its energy. We have that
$$
E_{12}=E_2-E_1=-3.4+13.6=10.2textrm { eV}
$$
Step 3
3 of 6
Now, the energy of the photon in the “two-photon” technique is exactly set to be half of this value
$$
E_{ph}=frac{E_{12}}{2}=5.1 textrm{ eV}
$$
Step 4
4 of 6
Finally, we can find the wavelength of the photon by using Planck’s formula where $hc=1240times 10^{-9}$eV$cdot$m
$$
lambda=frac{hc}{E_{ph}}
$$
Step 5
5 of 6
$$
lambda=frac{1240times 10^{-9}}{5.1}=boxed{243times 10^{-9}textrm{ m}}
$$
lambda=frac{1240times 10^{-9}}{5.1}=boxed{243times 10^{-9}textrm{ m}}
$$
Result
6 of 6
$$
lambda=243times 10^{-9}textrm{ m}
$$
lambda=243times 10^{-9}textrm{ m}
$$
Exercise 67
Step 1
1 of 5
In this problem, we are given a snapshot of the mercury vapor spectral lines with their respective wavelengths. We want to find to which transitions these lines belong to
Step 2
2 of 5
To do so, we shall first find separate energies for each spectral line by employing Planck’s relation where we will use $hc=1240times 10^{-9}$eV$cdot$m.
$$
E=frac{hc}{lambda}
$$
Step 3
3 of 5
center{Now, by plugging in the given values we obtain the following energies}
[Delta E_1=frac{1240}{579}=2.14 textrm{ eV}]
[Delta E_2=frac{1240}{546}=2.27 textrm{ eV}]
[Delta E_3=frac{1240}{436}=2.84 textrm{ eV}]
[Delta E_1=frac{1240}{579}=2.14 textrm{ eV}]
[Delta E_2=frac{1240}{546}=2.27 textrm{ eV}]
[Delta E_3=frac{1240}{436}=2.84 textrm{ eV}]
Step 4
4 of 5
Now, by looking at the table of the mercury vapour spectral transitions (also figure 28.21) we see that
$$
boxed{Delta E_1=E_{8rightarrow5}}
$$
$$
boxed{Delta E_2=E_{6rightarrow4}}
$$
$$
boxed{Delta E_3=E_{6rightarrow3}}
$$
Result
5 of 5
$$
Delta E_1=E_{8rightarrow5}
$$
Delta E_1=E_{8rightarrow5}
$$
$$
Delta E_2=E_{6rightarrow4}
$$
$$
Delta E_3=E_{6rightarrow3}
$$
Exercise 68
Step 1
1 of 6
In this problem, we are given the task to analyze the transitions that occur when the mercury atom goes to its ground state from the states that are given as the results of the transitions in problem 67 and to determine whether or not are the photons emitted during their transition to the ground state visible.
Step 2
2 of 6
center{These transitions are respectively given as follows}
[Delta E_1=E_{8rightarrow5}]
[Delta E_2=E_{6rightarrow4}]
[Delta E_3=E_{6rightarrow3}]
so we see that the initial states in our problem are $E_5$, $E_4$ and $E_3$.
[Delta E_1=E_{8rightarrow5}]
[Delta E_2=E_{6rightarrow4}]
[Delta E_3=E_{6rightarrow3}]
so we see that the initial states in our problem are $E_5$, $E_4$ and $E_3$.
Step 3
3 of 6
By consulting Figure 28-21 one sees that the corresponding energies during the transition are
$$
E_{5rightarrow1}=6.67
$$
$$
E_{4rightarrow1}=4.86
$$
$$
E_{3rightarrow1}=4.64
$$
Step 4
4 of 6
Now, we can use the Planck formula to see what is the wavelength of the photon with the least energy available
$$
E=frac{hc}{lambda}
$$
where we know that $hc=1240times 10^{-9}$ eV$cdot$m.
Step 5
5 of 6
Now, we can express the wavelength by using some straightforward algebra
$$
lambda=frac{hc}{E}=frac{1240times 10^{-9}}{4.64}=boxed{267times 10^{-9}textrm{ m}}
$$
which is in the ultraviolet range and therefore invisible which is the final answer.
Result
6 of 6
The emitted photons are not visible.
Exercise 69
Step 1
1 of 6
In this problem, we are given a positronium atom with a task to observe how do radii and energies change if we use the Bohr model to describe this atom while replacing the mass of the electron by $m_e/2$.
Step 2
2 of 6
The formula that gives the radii in the hydrogen model of the atom is given as
$$
r=frac{hbar^2n^2}{Kmq^2}
$$
so we see that the radius of the orbits is inversely proportional to the mass of the electron so if we reduce the mass by a factor of two the radius will increase by a factor of two.
Step 3
3 of 6
The formula that gives the energy in the hydrogen model of the atom is given as
$$
E_n=-frac{K^2q^4m}{2pihbar^2n^2}
$$
so we see that the energy of the orbits is proportional to the mass of the electron so if we reduce the mass by a factor of two the energy will decrease by a factor of two, too.
Step 4
4 of 6
Now, if we take a look at figure 28-11 we see that the $E_{2rightarrow1}$ transition is accompanied by the emission of a 10.2 eV photon so in the positronium, that energy will be twice lower, i.e. it would be 5.1 eV We can use Planck’s formula to get its wavelength
$$
lambda=frac{hc}{E}
$$
Step 5
5 of 6
$$
lambda=frac{1240times 10^{-9}}{5.1}=boxed{243textrm{nm}}
$$
lambda=frac{1240times 10^{-9}}{5.1}=boxed{243textrm{nm}}
$$
Result
6 of 6
$$
textrm{Radii will be twice larger.}
$$
textrm{Radii will be twice larger.}
$$
$$
textrm{Energies will be twice lower.}
$$
$$
lambda=243textrm{nm}
$$
Exercise 70
Step 1
1 of 4
The idea of the atomic structure of the universe is quite old and dates to Ancient Greece where it takes its name from $textit{atomos}$-undividable. It was an important subject of many famous philosophers such as Democritus, Epicurus, and Aristotle.
Step 2
2 of 4
Dark ages of the medieval forgot it but with the renascence rediscovery of the major ancient works it got again in the spotlight. Nevertheless, it took some time and various studies to get the first atomistic model, the Thomsom plum pudding model which assumed that atoms are divisible particles that can be imagined as a positive charge pudding with negatively charged plums floating in it.
Step 3
3 of 4
This model was very fast disproved by Rutherford which suggested something quite opposite, a negative particle circling around a positively charged and very much localized core which represents a so-called planetary model.
Nevertheless, this model had some obvious flaws (violating the conservation of energy, not explaining the experimental data..) which were solved by Niels Bohr who introduced the stationary states, the first step towards the quantum mechanical model of the atom. His model managed to fit well all the experimental results concerning hydrogen and hydrogen-like models but that was its maximum.
Step 4
4 of 4
Finally, de Broglie, Heisenberg, Schroedinger, Born, and others developed a quantum mechanical model of the atom, the one general enough to be able to explain the behavior of all the atoms and most chemical processes that involve atoms electronic structure.
Exercise 71
Step 1
1 of 1
The green laser pointers use a three-step process in order to generate the green light. First, a near-infrared light with a wavelength of 808nm is created by a typical laser diode and it is “injected” into an ND crystal that
converts the 808 nm light into a light with a wavelength of 1064 nm which is well in the infrared part of the spectra. Then, the 1064 nm light uses
a frequency doubling crystal that emits green light at a wavelength of 532nm as a result.
converts the 808 nm light into a light with a wavelength of 1064 nm which is well in the infrared part of the spectra. Then, the 1064 nm light uses
a frequency doubling crystal that emits green light at a wavelength of 532nm as a result.
Exercise 72
Step 1
1 of 4
In this problem, we are given a test charge and the force on it by an external electric field which strength we should find.
Step 2
2 of 4
The force that is acting on a charge when it is in the electric field is given as
$$
F=qE
$$
So the electric field is expressed as
$$
E=frac{F}{q}
$$
Step 3
3 of 4
$$
E=frac{F}{q}=frac{0.027}{3times 10^{-7}}=boxed{9times 10^4, frac{textrm{N}}{textrm{C}}}
$$
E=frac{F}{q}=frac{0.027}{3times 10^{-7}}=boxed{9times 10^4, frac{textrm{N}}{textrm{C}}}
$$
Result
4 of 4
$$
E=9times 10^4, frac{textrm{N}}{textrm{C}}
$$
E=9times 10^4, frac{textrm{N}}{textrm{C}}
$$
Exercise 73
Solution 1
Solution 2
Step 1
1 of 1
Yes. If she connect four of the 1$Omega$ resistors in series, the equivalent resistance will be 4$Omega$.
Step 1
1 of 4
Let’s say we have $n$ number of resistors with resistances:
$$R_1,R_2,R_3,…,R_n$$
$$R_1,R_2,R_3,…,R_n$$
We want to connect these resistors in the circuit and find the total resistance $R_{total}$. Depending on how we put these resistors in the circuit we can have different outcomes for $R_{total}$.
Step 2
2 of 4
– Putting resistors in parallel gives total resistance as:
$$begin{align}
R_{total~parallel}=dfrac{1}{R_1}+dfrac{1}{R_2}+dfrac{1}{R_3}+…+dfrac{1}{R_n}
end{align}$$
– Putting resistors in series gives total resistance as:
$$begin{align}
R_{total~series}=R_1+R_2+R_3+…+R_n
end{align}$$
$$begin{align}
R_{total~parallel}=dfrac{1}{R_1}+dfrac{1}{R_2}+dfrac{1}{R_3}+…+dfrac{1}{R_n}
end{align}$$
– Putting resistors in series gives total resistance as:
$$begin{align}
R_{total~series}=R_1+R_2+R_3+…+R_n
end{align}$$
Step 3
3 of 4
In our case, we have $4$ resistors of equal resistance $R_0=1mathrm{~Omega}$. If we want to combine them into a circuit to get a total resistance of $R_{total}=4mathrm{~Omega}$, we can look at the formulas above and see that we should put them in parallel:
$$begin{aligned}
R_{total}&=R_1+R_2+R_3+…+R_n
\&=R_0+R_0+R_0+R_0
\&=4cdot R_0
\&=4cdot 1mathrm{~Omega}
\&=4mathrm{~Omega} ~checkmark
end{aligned}$$
Step 4
4 of 4
So, in order to replace a $4mathrm{~Omega}$ resistor with four $1mathrm{~Omega}$ resistors, we need to put them in series.
Exercise 74
Step 1
1 of 4
In this problem, we are given a wire that is moving in the Earth’s magnetic field at a given speed. We want to find the induced EMF in the wire.
Step 2
2 of 4
This can be done by employing the well known equation that gives us the the EMF in the conductor that is moving in the external magnetic field
$$
EMF=BLv
$$
Step 3
3 of 4
center{After we plug in the given values we obtain the following }
[EMF=5times 10^{-5}times 1 times 4 =boxed{0.2times 10^{-3} textrm{ V}}]
[EMF=5times 10^{-5}times 1 times 4 =boxed{0.2times 10^{-3} textrm{ V}}]
Result
4 of 4
$$
EMF=0.2times 10^{-3} textrm{V}
$$
EMF=0.2times 10^{-3} textrm{V}
$$
Exercise 75
Step 1
1 of 4
In this problem, we are given a beam of electrons passing through an electric field with a given speed. We want to determine the magnetic field strength at which the electrons are undeflected.
Step 2
2 of 4
We know that in the equilibrium the two forces have to be equal which brings to the identity
$vB=E$
from which the magnetic field is expressed as
$vB=E$
from which the magnetic field is expressed as
$$
B=frac{E}{v}
$$
Step 3
3 of 4
center{After we plug in the values we have that}
[B=frac{1.4times 10^4}{2.8times 10^8}=boxed{50times10^{-6}textrm{ T}}]
[B=frac{1.4times 10^4}{2.8times 10^8}=boxed{50times10^{-6}textrm{ T}}]
Result
4 of 4
$$
B=50times10^{-6}textrm{ T}
$$
B=50times10^{-6}textrm{ T}
$$
Exercise 76
Step 1
1 of 3
In this rather interesting problem, we are given a Thompson’s cathode ray tube which should use protons instead of electrons. Our task is to see whether or not some modifications have to be made if any.
Step 2
2 of 3
a) The magnetic/electric field ratio doesn’t depend on the mass of the charged particle so to select the particles of the given speed nothing would change when compared to electrons.
Step 3
3 of 3
b) When we speak about deflection, i.e. radius of the curvature of the trajectory some modifications have to be made since the magnetic field force is compensated by the centripetal force so we have that
$$
qvB=frac{mv^2}{r}
$$
so we have that
$$
r=frac{mv}{qB}
$$
and in order to keep it constant the magnetic field would have to be increased, and in this case some 2000 times roughly.
Exercise 77
Step 1
1 of 3
In this problem we are given a metal which is used in a photoelectric effect with a given stopping potential. We are asked to find the corresponding maximum kinetic energy.
Step 2
2 of 3
The maximum kinetic energy is by definition equal to the stopping potential and we have that
$$
K_{max}=V_{stop}=7.3times 1.6times 10^{-19}=boxed{11.7times 10^{-19}textrm{ J}}
$$
Result
3 of 3
$$
K_{max}=11.7times 10^{-19}textrm{ J}
$$
K_{max}=11.7times 10^{-19}textrm{ J}
$$
unlock