Home Page Textbooks Physics: Principles and Problems Page 742: Assessment

Physics: Principles and Problems

9th Edition

Elliott, Haase, Harper, Herzog, Margaret Zorn, Nelson, Schuler, Zitzewitz

ISBN: 9780078458132

Textbook solutions

All Solutions

Page 742: Assessment

Exercise 29

Step 1

1 of 2

Result

2 of 2

WE fill the missing field from the top to the bottom and from the left to the right as follows:
dual nature, wave properties, mass, momentum.

Exercise 30

Step 1

1 of 2

The light should move towards red since that is the wavelength in the visible spectrum with the lowest energy.

Result

2 of 2

It will turn more red.

Exercise 31

Step 1

1 of 2

Quantization of energy implies that the energetic states of the system are discrete and the system cannot sample energies in between two given values whatsoever. Basically, all the energy levels are going to be multiples of a given minimal level.

Result

2 of 2

Quantized energy means discrete energy states sampled by a system.

Exercise 32

Step 1

1 of 2

According to Max Planck, during the radiation of an incandescent body its atoms vibrational degrees of freedom get quantized.

Result

2 of 2

Vibrational energy is quantized

Exercise 33

Step 1

1 of 2

The quantum of light is called “photon”.

Result

2 of 2

photon

Exercise 34

Step 1

1 of 2

The number of ejected electrons is directly proportional to the number of photons hitting the plate. On the other hand, the intensity of light is also proportional to the number of photons so higher the intensity, more photons i.e. more ejected electrons.

Result

2 of 2

The intensity of light is proportional to number of photons hitting the plate per second which in turn is proportional to the number of electrons leaving the plate per second.

Exercise 35

Step 1

1 of 2

In photoelectric effect each photon needs to have an energy above a certain value needed for the excitation i.e. ejection of an electron from the metal. If photons are below a certain frequency, i.e. below a certain energy needed for such ejections regardless of their number, i,e, the light intensity, none of them will not be able to eject electrons.

Result

2 of 2

Ejection of electrons happens per photon and if photon’s energy is below a certain value it cannot eject an electron whatsoever.

Exercise 36

Step 1

1 of 2

This can be explained by the fact that red light photons have the lowest energy in visible part of the EM spectrum so they do not have enough energy the ionize the electrons in the film i.e. to cause a chemical reaction that leads to exposure.

Result

2 of 2

Red photons do not have enough energy to excite atoms in the film.

Exercise 37

Step 1

1 of 2

The Compton effect is very well explained by a elastic collision which is based on the conservation of the energy and momentum of the particles colliding therefore, the photon needs to have a momentum in order for the equation to hold since the velocity of a target electron will rise so will its momentum so the momentum of photon should decrease.

Result

2 of 2

The elastic collision equations demand photon to have a momentum in order for them to be satisfied.

Exercise 38

Step 1

1 of 2

No, we cannot because the photons are massless particles so this equation will give that the momentum of a photon is always zero which is not true.

Result

2 of 2

No, we can’t since it would give always zero for the momentum.

Exercise 39

Step 1

1 of 2

a) We can measure the charge in the way Coulomb did, we can hang two charged balls of mass m and let’s say of the same charge and put them close enough so they can start repealing each other. Then we can see how much they are elevated and estimate the charge needed to produce such an elevation.

b( We can estimate the electron’s mass by using the magnetic field in the same way the mass spectrometer is working by balancing the electric field by the magnetic field and knowing the charge of the electron one can estimate its mass in a straight-forward manner.

c) We can aim a beam of electrons into a crystal and then observe the diffraction patterns to get the wavelength.

Result

2 of 2

a) We use the gravitational force.

b) We use the magnetic force.

c) We diffract electrons on a crystal to get the angles of the diffraction.

Exercise 40

Step 1

1 of 2

a) We can measure energy of a photon by using the the photoelectric effect. We should measure the kinetic energy of ejected electrons in a known metal which will give us the energy of the absorbed photon.

b) We can measure the change in the wavelength when X-rays are scattered by some object.

c) We can take a prism with a known index of refraction and measure how much the light bands when passing through the prism.

Result

2 of 2

a) We should use photoelectric effect.

b) X-ray scattering.

c) Bending through the prism.

Exercise 41

Step 1

1 of 2

a) We can read the figure 27-1 where we see that the peak frequencies are

$$
f(4000textrm{ K})=2.5times 10^{14}textrm{ Hz}
$$

$$
f(5800textrm{ K})=3.5times 10^{14}textrm{ Hz}
$$

$$
f(8000textrm{ K})=4.5times 10^{14}textrm{ Hz}
$$

b) We see that the frequency of the peak intensity increases linearly with the temperature.

c) The intensity in the red part of the spectrum rises from 0.5 to 9 which is a 18-fold increase.

Result

2 of 2

$$
textrm{a) }f(4000textrm{ K})=2.5times 10^{14}textrm{ Hz}
$$

$$
textrm{a) }f(5800textrm{ K})=3.5times 10^{14}textrm{ Hz}
$$

$$
textrm{a) }f(8000textrm{ K})=4.5times 10^{14}textrm{ Hz}
$$

$$
textrm{ b) It increases with the temperature.}
$$

$$
textrm{c) It increases 18 times.}
$$

Exercise 42

Step 1

1 of 2

a) According to the peak-intensity law the bar glowing bright orange is hotter.

b) The same holds for radiation of energy, the bright orange bar is radiating more energy.

Result

2 of 2

a) Bright orange bar

b) Bright orange bar

Exercise 43

Step 1

1 of 2

If both lights have frequencies above the threshold frequency, the number of the ejected electrons will not depend on the frequency but exclusively on the intensity of the light. So the high frequency light will not necessarily eject more electrons.

Result

2 of 2

Not necessarily.

Exercise 44

Step 1

1 of 2

a) Since the ultraviolet light has higher frequency than the blue light than we can say that tungsten has a higher threshold frequency.

b) The same reasoning goes for the work function which is directly proportional to the threshold frequency so the answer is tungsten again.

Result

2 of 2

a) Tungsten

b) Tungsten

Exercise 45

Step 1

1 of 2

If we take the given speed the and assume that a baseball weighs $0.2$kg we get that the de Broglie wavelength is given as

$$
lambda=frac{h}{mv}=frac{6.63times 10^{34}}{0.2times 21}
$$

which gives that

$$
lambdaapprox10^{-34}textrm{ m}
$$

Which is $10^{33}$ times less than the diameter of the ball.

Result

2 of 2

The de Broglie wavelength of the ball is $10^{33}$ times less than its diameter.

Exercise 46

Step 1

1 of 2

According to Planck’s theory the energy is quantized as

$$
E=nhf
$$

from where we can express the frequency as

$$
f=frac{E}{nh}=frac{5.44times 10^{-19}}{1times 6.63times 10^{-34}}
$$

Finally, we have that

$$
boxed{f=8.21times 10^{14}textrm{ Hz}}
$$

Result

2 of 2

$$
f=8.21times 10^{14}textrm{ Hz}
$$

Exercise 47

Step 1

1 of 2

When the electrons are stopped the kinetic energy is balanced out by the electrostatic potential completely therefore it has to hold

$$
K=-qV_0
$$

Therefore the stopping potential is given as

$$
V_0=-frac{K}{q}=frac{4.8times 10^{-19}}{1.6times 10^{-19}}
$$

Finally,

$$
boxed{V_0=3textrm{ V}}
$$

Result

2 of 2

$$
V_0=3textrm{ V}
$$

Exercise 48

Step 1

1 of 2

According to quantum theory the momentum of photon is given as

$$
p=frac{h}{lambda}=frac{6.63times 10^{-34}}{4times 10^{-7}}
$$

Finally, one gets that

$$
boxed{p=1.7times 10^{-27}, frac{textrm{kg}cdottextrm{m}}{textrm{s}}}
$$

Result

2 of 2

$$
p=1.7times 10^{-27}, frac{textrm{kg}cdottextrm{m}}{textrm{s}}
$$

Exercise 49

Step 1

1 of 2

In order to solve this problem we have to understand that the maximum kinetic energy of an ejected electron is equal to the stopping potential i.e.

$$
K_{max}=eV_0
$$

a) So in electron-volts we simply have that

$$
K_{max}=etimes5textrm{ V}
$$

$$
boxed{K_{max}=5textrm{ eV}}
$$

b) In joules, the same energy has the following value

$$
K_{max}=5times 1.6times 10^{-19}textrm{ J}
$$

$$
boxed{K_{max}=8times 10^{-19}textrm{ J}}
$$

Result

2 of 2

$$
textrm{a) }K_{max}=5textrm{ eV}
$$

$$
textrm{b) }K_{max}=8times 10^{-19}textrm{ J}
$$

Exercise 50

Step 1

1 of 2

In order to solve this problem, we are going to use the photoelectric effect equation which tells us that the maximum kinetic energy is given as

$$
K_{max}=E_{ph}-W=hf-hf_0
$$

On the other hand the frequency of the light is given as

$$
f=frac{c}{lambda}=frac{3times 10^8}{650times 10^{-9}}
$$

$f=4.6times 10^{14}textrm{ Hz}$
so we have that

$$
K_{max}=h(f-f_0)=6.63times 10^{-34}times(4.6times 10^{14}-3times 10^{14})
$$

Finally, we have that

$$
boxed{K_{max}=1.06times 10^{-19}textrm{ J}}
$$

Result

2 of 2

$$
K_{max}=1.06times 10^{-19}textrm{ J}
$$

Exercise 51

Step 1

1 of 2

By definition, the work needed to be done in order to free an electron from the surface is related to the threshold frequency as follows

$$
W=hf_0=6.63times 10^{-34}times 4.4times 10^{14}
$$

which gives that

$$
boxed{W=2.9times 10^{-19}textrm{ J}}
$$

Result

2 of 2

$$
W=2.9times 10^{-19}textrm{ J}
$$

Exercise 52

Step 1

1 of 2

In order to solve this problem, we are going to use the photoelectric effect equation which tells us that the maximum kinetic energy is given as

$$
K_{max}=E_{ph}-W=hf-hf_0
$$

$$
K_{max}=h(f-f_0)=6.63times 10^{-34}times(1times 10^{15}-4.4times 10^{14})
$$

Finally, we have that

$$
boxed{K_{max}=3.7times 10^{-19}textrm{ J}}
$$

Result

2 of 2

$$
K_{max}=3.7times 10^{-19}textrm{ J}
$$

Exercise 53

Step 1

1 of 2

Because the red light has the longest wavelength among visible light to get the work function it is enough the use the red light wavelength

$$
W=frac{hc}{lambda}=frac{1.24times 10^{-6}}{0.68times 10^{-6}}
$$

This gives that

$$
boxed{W=1.82textrm{ eV}}
$$

Result

2 of 2

$$
W=1.82textrm{ eV}
$$

Exercise 54

Step 1

1 of 4

In order to solve this problem we should check up the recent data on how much solar energy hits the Earth per second. The recent NASA measurements state that $1360$J falls per second per square meter.

Step 2

2 of 4

a) Now, we can calculate the amount that hits the square meter by simple multiplying of the rate by the sun hours

$$
I=1360times 3600times 3000=14.7times 10^9, frac{textrm{ J}}{textrm{m}^2}
$$

Step 3

3 of 4

b) The final step is to find an area that will, with the given efficiency, provide the one year energy of an average US home.

$$
A=frac{E_{home}}{etimes I}=frac{4times 10^{11}}{0.2 times14.7times 10^{9}}=135textrm{ m}^2
$$

Result

4 of 4

$$
textrm{a) }I=14.7times 10^9, frac{textrm{ J}}{textrm{m}^2}
$$

$$
textrm{b) }A=135textrm{ m}^2
$$

Exercise 55

Step 1

1 of 4

This problem involves a moving particle, in this case an electron, for which we should find the corresponding wavelength.

Step 2

2 of 4

In order to solve a problem that involves finding of a wavelength of a particle we are going to use the de Broglie condition

$$
lambda=frac{h}{mv}
$$

Step 3

3 of 4

Now, we can plug in the given values to have that required wavelength is

$$
lambda=frac{6.63times 10^{-34}}{9.11times 10^{-31}times 3times 10^6}
$$

Result

4 of 4

$$
lambda=2.4times 10^{-10}textrm{ m}
$$

Exercise 56

Step 1

1 of 4

This problem involves a moving electron with a given de Broglie wavelength.

Step 2

2 of 4

In order to solve this problem we are going to employ the de Broglie relation which says

$$
lambda=frac{h}{mv}
$$

from where the velocity can be expressed as

$$
v=frac{h}{mlambda}
$$

Step 3

3 of 4

Now, we can plug in the given values to have that the speed of the electron is

$$
v=frac{6.63times 10^{-34}}{9.11times 10^{-31}times 3times 10^{-10}}
$$

Result

4 of 4

$$
v=2.4times 10^{6}, frac{textrm{m}}{textrm{s}}
$$

Exercise 57

Step 1

1 of 5

This problem involves electrons accelerated across a potential difference for which we have to find the speed and de Broglie wavelength.

Step 2

2 of 5

In order to solve it we are going to use the conservation of energy and de Broglie relation.

Step 3

3 of 5

a) We start with the conservation of energy in order to find the electron’s speed

$$
frac{mv^2}{2}=qV
$$

From which the speed is expressed as

$$
v=sqrt{frac{2qV}{m}}=sqrt{frac{2times 1.6times 10^{-19}times 5times 10^3 }{9.11times 10^{-31}}}
$$

Finally, we get that

$$
v=4.2times 10^{7}, frac{textrm{m}}{textrm{s}}
$$

Step 4

4 of 5

b) Now, we use de Broglie relation to find the corresponding wavelength

$$
lambda=frac{h}{mv}=frac{6.63times 10^{-34}}{9.11times 10^{-31}times4.2times 10^7}
$$

$$
lambda=1.7times 10^{-11}textrm{ m}
$$

Result

5 of 5

$$
v=4.2times 10^{7}, frac{textrm{m}}{textrm{s}}
$$

$$
lambda=1.7times 10^{-11}textrm{ m}
$$

Exercise 58

Step 1

1 of 5

This problem involves a neutron of a given kinetic energy from which we should find its velocity and the corresponding de Broglie wavelength.

Step 2

2 of 5

We can do so by applying to formulas, the kinetic energy formula

$$
K=frac{mv^2}{2}
$$

and de Broglie relation

$$
lambda=frac{h}{mv}
$$

Step 3

3 of 5

a) We start with the first relation and from it we can express the velocity as

$$
v=sqrt{frac{2K}{m}}
$$

After plugging the values

$$
v=sqrt{frac{2times0.025times 1.6times 10^{-19}}{1.67times 10^{-27}}}
$$

Finally

$$
v=2.2times 10^3,frac{textrm{m}}{textrm{s}}
$$

Step 4

4 of 5

b) The de Broglie wavelength is then found directly from the second relation

$$
lambda=frac{h}{mv}
$$

After pluging the values

$$
lambda=frac{6.63times 10^{-34}}{1.67times 10^{-27}times2.2times 10^3}
$$

Finally

$$
lambda=1.8times 10^{-10}textrm{ m}
$$

Result

5 of 5

$$
v=2.2times 10^3,frac{textrm{m}}{textrm{s}}
$$

$$
lambda=1.8times 10^{-10}textrm{ m}
$$

Exercise 59

Step 1

1 of 6

This problem involves a hydrogen atom with a given kinetic energy from which we should find its velocity and the corresponding de Broglie wavelength. After this one should find the length of the orbit and compare it with the de Broglie wavelength.

Step 2

2 of 6

We can do so by applying to formulas, the kinetic energy formula

$$
K=frac{mv^2}{2}
$$

and de Broglie relation

$$
lambda=frac{h}{mv}
$$

and with the simple geometric formula

$$
C=2pr
$$

Step 3

3 of 6

a) We start with the first relation and from it we can express the velocity as

$$
v=sqrt{frac{2K}{m}}
$$

After plugging the values

$$
v=sqrt{frac{2times 13.65times 1.6times 10^{-19}}{9.11times 10^{-31}}}
$$

Finally

$$
v=2.19times 10^6,frac{textrm{m}}{textrm{s}}
$$

Step 4

4 of 6

b) The de Broglie wavelength is then found directly from the second relation

$$
lambda=frac{h}{mv}
$$

After pluging the values

$$
lambda=frac{6.63times 10^{-34}}{9.11times 10^{-31}times2.19times 10^6}
$$

Finally

$$
lambda=0.33times 10^{-9}textrm{ m}
$$

Step 5

5 of 6

c) The circumference is found from the given formula and it is equal

$$
C=2pi r=2times 3.14times 0.519times 10^{-9}
$$

$$
C=3.26times 10^{-9} textrm{ m}
$$

Which is one order of magnitude more than the de Broglie wavelength.

Result

6 of 6

$$
v=2.2times 10^6,frac{textrm{m}}{textrm{s}}
$$

$$
lambda=1.8times 10^{-10}textrm{ m}
$$

$$
C=3.26times 10^{-9} textrm{ m}
$$

Exercise 60

Step 1

1 of 7

In this problem we have an electron with a given de Broglie wavelength and our first task is to find what potential difference was used to achieve the corresponding velocity. Then we want to the same for the proton of the equal de Broglie wavelength.

Step 2

2 of 7

In order to solve this problem we are going to start with the conservation of energy. The electrostatic potential energy that is used for acceleration is equal to the kinetic energy at the end of the process
$qV=frac{mv^2}{2}$
from where we can express the voltage as

$$
V=frac{mv^2}{2q}
$$

Step 3

3 of 7

On the other hand, we can use the de Broglie relation to express the speed via the known variables

$$
lambda=frac{h}{mv}
$$

$$
v=frac{h}{lambda m}
$$

Step 4

4 of 7

Now, we can insert the expression obtained for the speed into the expression for the voltage to get that

$$
V=frac{m}{2q}times frac{h^2}{lambda^2 m^2 }=frac{h^2}{2qmlambda^2}
$$

Step 5

5 of 7

a) Let’s now calculate the required voltage in the case of an electron

$$
V=frac{6.63^2times 10^{-68}}{2times 1.6times 10^{-19}times 9.11times 10^{-31}times 0.18^2times 10^{-18}}
$$

Finally, we have that

$$
boxed{V=46.5textrm{ V}}
$$

Step 6

6 of 7

b) The same thing, but with a different mass we do in the case of a proton

$$
V=frac{6.63^2times 10^{-68}}{2times 1.6times 10^{-19}times 1.67times 10^{-27}times 0.18^2times 10^{-18}}
$$

Finally, we have that

$$
boxed{V=0.025textrm{ V}}
$$

Result

7 of 7

$$
textrm{a) }V=46.5textrm{ V}
$$

$$
textrm{b) }V=0.025textrm{ V}
$$

Exercise 61

Step 1

1 of 3

In order to solve this problem, we have to use the photoelectric effect formula which says that the maximum kinetic energy and the stopping potential are related as

$$
K_{max}=-qV_0
$$

Step 2

2 of 3

Now, we can transfer our values from Joules to eVs but we can more elegantly note that eV is a unit charge times one Volt which gives that in our case

$$
K_{max}=-(-1e)times 3.8V
$$

Finally

$$
boxed{K_{max}=3.8textrm{ eV}}
$$

Result

3 of 3

$$
K_{max}=3.8textrm{ eV}
$$

Exercise 62

Step 1

1 of 3

In order to solve this problem we are going to use the fact that the work function is given as

$$
W=hf_0
$$

Step 2

2 of 3

Now, we can plug in the values in the above expression to have that

$$
W=6.63times 10^{-34}times 8times 10^{14}
$$

Finally we have that the work function is given

$$
boxed{W=5.3 times 10^{-19}textrm{ J}}
$$

Result

3 of 3

$$
W=5.3 times 10^{-19}textrm{ J}
$$

Exercise 63

Step 1

1 of 3

This problem involves a metal of a known threshold frequency and the light of a known frequency.
In order to solve this problem, we are going to use the photoelectric effect equation which tells us that the maximum kinetic energy is given as

$$
K_{max}=E_{ph}-W=hf-hf_0
$$

Step 2

2 of 3

Now, we can plug in the given values which gives us that the maximum kinetic energy is

$$
K_{max}=h(f-f_0)=6.63times 10^{-34}times(1.6times 10^{15}-8times 10^{14})
$$

Finally, we have that

$$
boxed{K_{max}=5.3 times 10^{-19}textrm{ J}}
$$

Result

3 of 3

$$
K_{max}=5.3 times 10^{-19}textrm{ J}
$$

Exercise 64

Step 1

1 of 4

This problem involves a moving deuteron for which we should find the de Broglie wavelength.

Step 2

2 of 4

We can do so by using de Broglie relation which is given as follows

$$
lambda=frac{h}{mv}
$$

Step 3

3 of 4

Now, we can plug in the values to obtain that de Broglie wavelength is

$$
lambda=frac{6.63times 10^{-34}}{3.3times 10^{-27}times 2.5times 10^4}
$$

Finally,

$$
boxed{lambda=8times 10^{12}textrm{ m}}
$$

Result

4 of 4

$$
lambda=8times 10^{12}textrm{ m}
$$

Exercise 65

Step 1

1 of 5

This problem involves a metal, namely iron, with a given work function. We should find its threshold wavelength and sequentially the maximum kinetic energy when a light of a given wavelength hits the iron.

Step 2

2 of 5

To do so, we are going to use the work function equation which tells us that
$W=frac{hc}{lambda_0}$
and photoelectric effect equation

$$
K=E_{ph}-W
$$

Step 3

3 of 5

a) Now, let’s find the the threshold wavelength from the first equation. We can express it as

$$
lambda_0=frac{hc}{W}=frac{1240times 10^{-9}}{4.7}
$$

Finally

$$
boxed{lambda=263times 10^{-9}textrm{ m}}
$$

Step 4

4 of 5

b) The final step is to find the maximum kinetic energy from the second equation

$$
K_{max}=E_{ph}-W=frac{hc}{lambda}-W=frac{1240times 10^{-9}}{150times 10^{-9}}-4.7
$$

Which gives

$$
boxed{K_{max}=3.57textrm{ eV}}
$$

Result

5 of 5

$$
lambda=263times 10^{-9}textrm{ m}
$$

$$
K_{max}=3.57textrm{ eV}
$$

Exercise 66

Step 1

1 of 4

In this problem we are looking for a longest (threshold) wavelength that will cause electrons to be ejected from barium.

Step 2

2 of 4

This can be done by employing the work function equation which tells us that

$$
W=frac{hc}{lambda_0}
$$

From where we can express the threshold wavelength as

$$
lambda_0=frac{hc}{W}
$$

Step 3

3 of 4

Now, we can plug in the given values to get that threshold wavelength is

$$
lambda_0=frac{1240times 10^{-9}}{2.48}
$$

Finally, we have

$$
boxed{lambda_0=500times 10^{-9}textrm{ m}}
$$

Result

4 of 4

$$
lambda_0=500times 10^{-9}textrm{ m}
$$

Exercise 67

Step 1

1 of 6

In this problem we have an electron with a given de Broglie wavelength for which we should find the velocity and the kinetic energy in eVs.

Step 2

2 of 6

We can find the value of the electron’s speed mentioned above by using de Broglie relation

$$
lambda=frac{h}{mv}
$$

Step 3

3 of 6

a) We can take now the first equation and express the speed from it as follows

$$
v=frac{h}{mlambda}=frac{6.63times 10^{-34}}{9.11times 10^{-31}times 400times 10^{-9}}
$$

Finally, we have that

$$
boxed{v=1.82times 10^3, frac{textrm{m}}{textrm{s}}}
$$

Step 4

4 of 6

On the other hand we will use the standard kinetic energy equation to find electron’s kinetic energy.

$$
K=frac{mv^2}{2}
$$

Step 5

5 of 6

b) Now, by simply inserting the values into the second equation and dividing by the energy of one eV in Joules we obtain that

$$
K=frac{9.11times 10^{-31}times 1.82^2times 10^6}{2times 1.6times 10^{-19}}
$$

$$
boxed{K=9.43times 10^{-6}{textrm { eV}}}
$$

Result

6 of 6

$$
textrm{a) }v=1.82times 10^3, frac{textrm{m}}{textrm{s}}
$$

$$
textrm{b) }K=9.43times 10^{-6}{textrm{ eV}}
$$

Exercise 68

Step 1

1 of 4

In this problem we are having an electron with a given de Broglie wavelength for which we should find the kinetic energy.

Step 2

2 of 4

We can do so, by first expressing the electron’s speed from its de Broglie wavelength and then inserting it into the kinetic energy expression in the manner as follows

$$
lambda=frac{h}{mv}
$$

so the speed is

$$
v=frac{h}{mlambda}
$$

Now, the kinetic energy is given as

$$
K=frac{mv^2}{2}=frac{m}{2}times frac{h^2}{m^2lambda^2}
$$

Step 3

3 of 4

Now, we can plug in the values into the above’s expression to get that

$$
K=frac{h^2}{2mlambda^2times 1.6times 10^{-19}}=frac{6.63^2times 10^{-68}}{2times 9.11times 10^{-31}times 20^2times 10^{-18}times 1.6times 10^{-19}}
$$

Finally, we have that

$$
boxed{K=3.8times 10^{-3}textrm{ eV}}
$$

Result

4 of 4

$$
K=3.8times 10^{-3}textrm{ eV}
$$

Exercise 69

Step 1

1 of 8

This problem involves the incident light falling on a tin with a given threshold frequency with our task being to find the threshold wavelength of the tin, the work function of the tin and the kinetic energy of the electrons ejected from the tin.

Step 2

2 of 8

a) To find the threshold wavelength, we are going to use the frequency-wavelength relation since the former is given in the problem. We have that

$$
c=lambda f
$$

Step 3

3 of 8

Now, we can use this equation to express the threshold wavelength and after we substitute the given values we have that

$$
lambda=frac{c}{f}=frac{3times 10^{8}}{1.2times 10^{15}}
$$

Which gives that

$$
boxed{lambda=250times 10^{-9}textrm{ m}}
$$

Step 4

4 of 8

b) The next step is finding the work function of the tin which is by definition given as

$$
W=hf_0
$$

Step 5

5 of 8

If we now take the above equation and after we plug in the values we obtain that the work function is

$$
W=6.63times 10^{-34}times 1.2times 10^{15}
$$

that gives us

$$
W=8times 10^{-19}textrm{ J}
$$

or in eV

$$
W=frac{8times 10^{-19}}{1.6times 10^{-19}}=boxed{5textrm{ eV}}
$$

Step 6

6 of 8

a) To find the maximum kinetic energy of the ejected electrons we are going to use the photoelectric effect relation which is given as

$$
K_{max}=frac{hc}{lambda}-W
$$

where $hc=1240times 10^{-9}$ eV$cdot$m.

Step 7

7 of 8

Now, we can plug in the given values to have that the maximum kinetic energy of the ejected electrons is

$$
K_{max}=frac{1240times 10^{-9}}{167times 10^{-9}}-5=7.43-5
$$

Finally, we have that

$$
boxed{K_{max}=2.43textrm{ eV}}
$$

Result

8 of 8

$$
lambda=250times 10^{-9}textrm{ m}
$$

$$
W=5textrm{ eV}
$$

$$
K_{max}=2.43textrm{ eV}
$$

Exercise 70

Step 1

1 of 6

In this problem we have a helium-neon laser of a given power which is emitting photons of a given wavelength. Our task is to find the energy of each photon and the number of photons emitted per second.

Step 2

2 of 6

a) In order to find the energy of a single photon we are going to use the photon energy equation which tells us that

$$
E_{ph}=frac{hc}{lambda}
$$

Step 3

3 of 6

Now, we can simply plug in the given value of the wavelength in the above equation to obtain that

$$
E_{ph}=frac{6.63times 10^{-34}times 3times 10^{8}}{632.8times 10^{-9}}=boxed{3.14times 10^{-19}textrm{ J}}
$$

Step 4

4 of 6

b) To find the number of photons with this energy that are emitted by the laser each second we are going to use the fact that the amount of energy emitted per second is defined as power so we have that

$$
dot n=frac{P}{E_{ph}}
$$

Step 5

5 of 6

Now we can simply plug in the given value of the power and the value obtained for the single photon energy to have that

$$
dot n=frac{5times 10^{-4}}{3.14times 10^{-19}}=boxed{15.9times 10^{14}, frac{textrm{photons}}{textrm{s}}}
$$

Result

6 of 6

$$
textrm{a) }E_{ph}=3.14times 10^{-19}textrm{ J}
$$

$$
textrm{b) }dot n=15.9times 10^{14}, frac{textrm{photons}}{textrm{s}}
$$

Exercise 71

Step 1

1 of 7

In this problem we are supposed to apply the concept learned so far to a very practical problem of the human eye. We aim to find the power of the light entering the eye and the number of photons hitting the pupil each second.

Step 2

2 of 7

Firstly, we should understand that the power of the light hitting a surface equals the product of the intensity and the area of the surface

$$
P=IA=Ipi r^2=1.5times 10^{-11}times 3.14times 3.5^2times 10^{-6}
$$

$$
boxed{P=5.8times 10^{-16}textrm{ W}}
$$

Step 3

3 of 7

a) In order to find the number of photons that each second hit the pupil we need an energy of a single photon so we are going to use the photon energy equation which tells us that

$$
E_{ph}=frac{hc}{lambda}
$$

Step 4

4 of 7

Now, we can simply plug in the given value of the wavelength in the above equation to obtain that

$$
E_{ph}=frac{6.63times 10^{-34}times 3times 10^{8}}{550times 10^{-9}}=boxed{3.6times 10^{-19}textrm{ J}}
$$

Step 5

5 of 7

b) Finally, we can find the number of photons that are received by the eye each second by using the fact that the amount of energy emitted per second is defined as power so we have that

$$
dot n=frac{P}{E_{ph}}
$$

Step 6

6 of 7

Again we can simply plug in the given value of the power and the value obtained for the single photon energy to have that

$$
dot n=frac{5.8times 10^{-16}}{3.6times 10^{-19}}=boxed{1.6times 10^{3}, frac{textrm{photons}}{textrm{s}}}
$$

Result

7 of 7

$$
textrm{a) }E_{ph}=3.6times 10^{-19}textrm{ J}
$$

$$
textrm{b) }dot n=1.6times 10^{3}, frac{textrm{photons}}{textrm{s}}
$$

Exercise 72

Step 1

1 of 8

In this problem we should make a plot from the given data, stopping potential vs frequency but initially we have to convert wavelength to the frequency. Then we should check the plot to find the intercept line, the work function, the slope and $h/q$ value which should be compared to the accepted value.

Step 2

2 of 8

First, let’s convert the wavelengths given in the table to frequencies by using the formula that connects the two parameters

$$
f=clambda
$$

Step 3

3 of 8

begin{table}[]
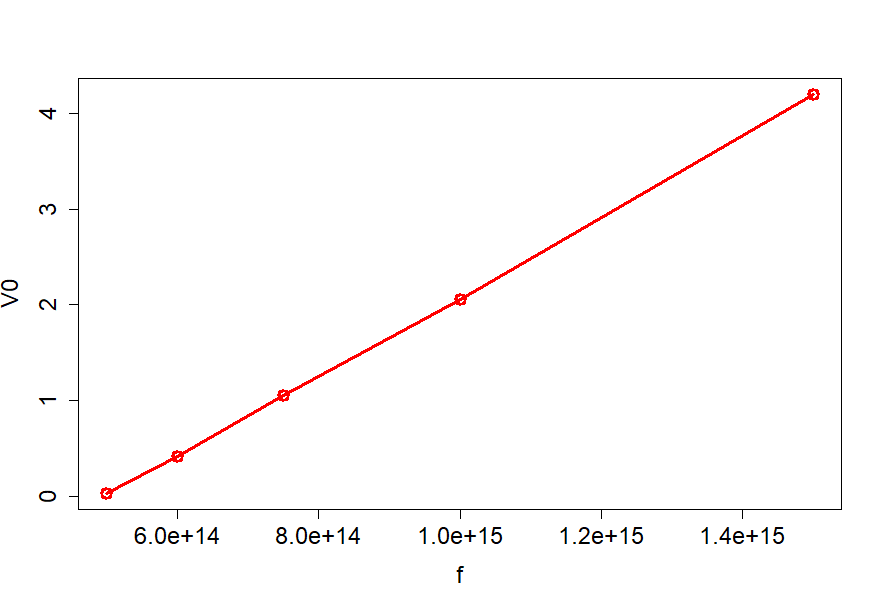
begin{tabular}{|r|r|r|}
hline
multicolumn{1}{|l|}{$lambda$(nm)} & multicolumn{1}{l|}{f(Hz)} & multicolumn{1}{l|}{$V_0$(eV)} \ hline
200 & $15times 10^{14}$ & 4.2 \ hline
300 & $10times 10^{14}$ & 2.06 \ hline
400 & $7.5times 10^{14}$ & 1.05 \ hline
500 & $6times 10^{14}$ & 0.41 \ hline
600 & $5times 10^{14}$ & 0.03 \ hline
end{tabular}
end{table}

Step 4

4 of 8

Now, we can plot the the stopping potential versus frequency as shown in the graph. Exercise scan

Step 5

5 of 8

Now, we can calculate the slope of the function by simply taking any two points and dividing their displacements with each other

$$
Delta V_0=kDelta f
$$

$$
k=frac{Delta V_0}{Delta f}
$$

We can take the last point and the first point that to have

$$
k=frac{4.17}{1times 10^{15}}=4.17times 10^{-15}, frac{textrm{ V}}{textrm{ Hz}}
$$

and since 1V=1J/1C we can write

$$
boxed{k=4.17times 10^{-15}frac{textrm{ J}}{textrm{C}cdottextrm{ Hz}}}
$$

On the other hand the accepted value is set to be

$$
frac{h}{e}=frac{6.63times 10^{-34}}{1.6times 10^{-19}}=boxed{4.14times 10^{-15}frac{textrm{ J}}{textrm{C}cdottextrm{ Hz}}}
$$

we see that the difference is relatively small and equals $approx 10^{-17}$.

Step 6

6 of 8

From the graph we read that the threshold frequency, (the interception point) is approximately given as $f_0=4.99times 10^{14}$. Now, the threshold wavelength can be found as

$$
lambda_0=frac{c}{f_0}=frac{3times 10^8}{4.99times 10^{15}}
$$

$$
boxed{lambda_0=601times 10^{9}textrm{ m}}
$$

Step 7

7 of 8

Finally, the work function can be found from the following well-known formula

$$
W=hf_0=6.63times 10^{-34}times 4.99times 10^{14}
$$

$$
boxed{W=3.3times 10^{-19}textrm{ J}}
$$

Result

8 of 8

$$
k=4.17times 10^{-15}frac{textrm{ J}}{textrm{C}cdottextrm{ Hz}}
$$

$$
lambda_0=601times 10^{9}textrm{ m}
$$

$$
W=3.3times 10^{-19}textrm{ J}
$$

Exercise 73

Step 1

1 of 2

In phthalocyanine molecules that weigh almost 1300 AMU the interference effects were observed by a group of scientists from Vienna Center of Quantum Science and Technology, Faculty of Physics, University of Vienna. They have demonstrated interference effects in a specially devised double slit experiment where they have used a combination of nanofabrication and nano-imaging that provided them with a recording of two-dimensional interference patterns.

Result

2 of 2

Juffmann, Thomas, et al. “Real-time single-molecule imaging of quantum interference.” Nature nanotechnology 7.5 (2012): 297-300.

Exercise 74

Step 1

1 of 3

In this problem we are aiming to find the spring constant for a pogo stick with a given weight and compression distance.

Step 2

2 of 3

We can now use the well known spring equation which gives us the spring force

$$
F=kx
$$

from where we can express the spring constant $k$ as

$$
k=frac{F}{x}=frac{400}{0.15}=boxed{2.7times 10^3, frac{textrm{N}}{textrm{m}}}
$$

Result

3 of 3

$$
k=2.7times 10^3, frac{textrm{N}}{textrm{m}}
$$

Exercise 75

Step 1

1 of 2

The answer to this question is the fact that the pitch depends on the speed of sound which in turn depends directly from the temperature of the air. Therefore, in colder days the speed of sound is lower so is the pitch.

Result

2 of 2

See explanation.

Exercise 76

Step 1

1 of 4

In this problem we have to static charges at a given distance exerting a given force one one another. The value of one charge is known so we should find the second one.

Step 2

2 of 4

In order to solve this problem we are going to apply the Coulomb law which states that the force between two charges is

$$
F=frac{1}{4pi varepsilon_0}cdotfrac{q_1q_2}{r^2}
$$

From where we can express the second charge as

$$
q_2=frac{4pivarepsilon_0cdot Fcdot r^2}{q_1}
$$

Step 3

3 of 4

Now, we can plug in the values in the expression obtained above to have that

$$
q_2=frac{9times 0.02^2}{9times 10^9times 8times 10^{-7}}
$$

Finally, we have that

$$
boxed{q_2=5times 10^{-7}textrm{ C}}
$$

Result

4 of 4

$$
q_2=5times 10^{-7}textrm{ C}
$$

Exercise 77

Step 1

1 of 4

In this problem we are asked to find the the total current when all the light sets are operated simultaneously.

Step 2

2 of 4

For this purpose we are going to use Ohm’s law which gives us the relation between the voltage and the resistance of the circuit

$$
I=frac{V}{R}
$$

Step 3

3 of 4

Now, we have that the total current is equal to twelve times current in the single light set

$$
I=12I_s=12frac{V}{R_s}=12timesfrac{120}{24times 6}
$$

Which gives that the total current is

$$
boxed{I=10 textrm{ A}}
$$

Result

4 of 4

$$
I=10 textrm{ A}
$$

Exercise 78

Step 1

1 of 4

This problem involves Earth’s magnetic force acting on a wire of a given length with an unknown current.

Step 2

2 of 4

We can solve this problem by employing the well known equation that defines the force on a current-carrying wire in a magnetic field

$$
F=ILB
$$

Step 3

3 of 4

From this expression we can express the current in a single step as follows

$$
I=frac{F}{LB}=frac{1.1times 10^{-3}}{1.2times 5times 10^{-5}}
$$

Finally we have that

$$
boxed{I=18.3textrm{ A}}
$$

Result

4 of 4

$$
I=18.3textrm{ A}
$$

unlock

All Solutions

Page 742: Assessment

Haven't found what you were looking for?

Search for samples, answers to your questions and flashcards