All Solutions
Page 64: Section Review
$$
v=v(t)
$$
On the other hand, for lines pointing downward, this slope is negative, so the body is decelerating.
textbf{underline{textit{Solution}}}
$$
Reading the question carefully, we find that both jogger runs with the same magnitude of speed and in the same direction, which means that they also have the same magnitude of the speed with the same sign.
And assuming that the east is the positive side, then the first jogger have an initial position of 15 m beyond the origin, while the second jogger have an initial position of – 15 m or 15 before the origin, and a constant velocity means that the slope of the line representing both jogger in the velocity-time graph is zero “Horizontal line”.
item Since both jogger have the same speed thus, the line representing their motion in the position-time graph would have the same slope of 7.5 but would differ in the initial position, such that the first jogger would have an initial position of +15 m and the second jogger would have an initial position of -15 m, check the following textbf{graph}.\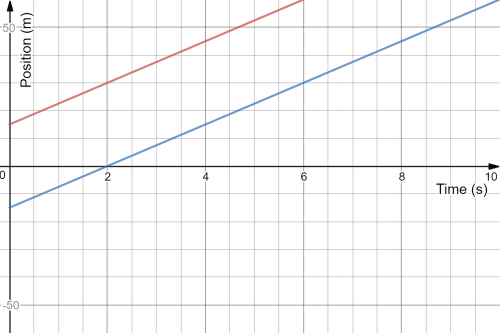
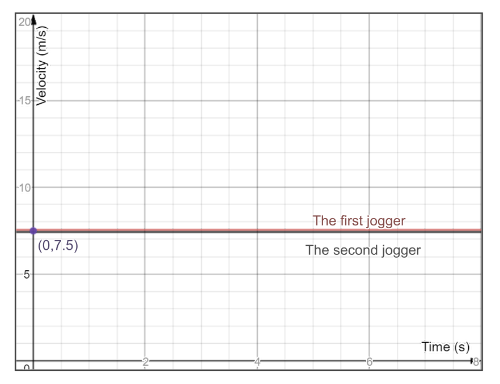
item As both jogger have the same constant speed and in the same direction, thus the line representing the motion of both joggers would be the same, where the line would have a zero slope and its $y$-axis have a value of 7.5 m/s, see the following graph.\
item The line representing the motion of both joggers in the position-time graph, would have the same slope but different initial position, thus the two graphs are not identical, see textbf{graph}.
item Since both joggers are running with the same magnitude and the same direction, thus the line representing the motion of each jogger in the velocity-time graph would be identical, see textbf{graph}.
1. Draw a horizontal line at the velocity in which you would like to find the time.
2. Find the point of intersection between the drawn line, and the velocity-time plot.
3. Draw a line vertically down toward the time axis, and the value in which it hits is the time that you were looking for.
v_{avg}=frac{v_f+v_i}{2}=frac{-4m/s + 2 m/s}{2}=-1m/s
$$
a_{avg}=frac{v_f-v_i}{t_f-t_i}=frac{-4m/s-2m/s}{8s-0s}=frac{-6m/s}{8s}=frac{-3}{4}m/s^2
$$
b. $-3/4 m/s^2$
– The initial speed of the canoe $v_{text{i}}= -2 , frac{text{m}}{text{s}}$ (note the negative sign, since the canoe initially moves upstream, and the positive direction was chosen to point downstream)
– The final speed of the canoe $v_{text{f}}= 4 , frac{text{m}}{text{s}}$ (positive since since the canoe finally moves downstream)
-The time interval needed for the turning around $Delta t=8text{ s}$.
**Required:**
– The average velocity.
– The average acceleration over the given time interval.
The average velocity is found directly as the average value of the two given velocities. We write:
$$
overline{v} = frac{v_{text{i}}+ v_{text{f}}}{2}
tag{1}
$$
$$
begin{align*}
overline{v} &= frac{-2 , frac{text{m}}{text{s}}+ 4 , frac{text{m}}{text{s}}}{2}\
&= boxed{1 , frac{text{m}}{text{s}}}
end{align*}
$$
We know that the average acceleration of a moving object can be expressed via the initial and final velocities and the elapsed time interval as:
$$
begin{split}
overline{a} &= frac{v_{text{f}} – v_{text{i}}}{t_{text{f}} – t_{text{i}}}\
&= frac{v_{text{f}}-v_{text{i}}}{Delta t}
tag{2}
end{split}
$$
Where we introduced the time interval $Delta t$.
$$
begin{align*}
overline{a} &= frac{4 , frac{text{m}}{text{s}} – left(- 2 , frac{text{m}}{text{s}} right)}{8text{ s}}\
&= boxed{0.75 , frac{text{m}}{text{s}^2}}
end{align*}
$$
b) $overline{a} = 0.75 , frac{text{m}}{text{s}^2}$
textbf{underline{textit{Solution}}}
$$
And knowing that the car exceeding the speed limit is next to another car doesn’t mean that it would have the same speed, for both cars to have an equal speed then they both must travel an equal distance at equal time interval, from which we can judge if they both have the same speed or not.
Moreover, moving for enough duration a fast car can by pass a slow one, while a slow car would never by pass a car going faster, therefor we have 3 probabilities whether the car is going faster, at the same speed or slower than the second car.
And since a slow car would never by pass a fast one, therefor since the car exceeding the speed limit by passed the second car, then it can’t be slower than the second car, thus ruling out the possibility that the car is slower.
And under the assumption that both car were moving therefor, since the first car exceeding the speed limit by passed the second car then they both can’t have the same speed, if they did they would always keep an equal distance apart from each other, thus ruling out the possibility that they both have an equal speed.
The only possibility remains is that the first car is much faster than the second car to by pass it, therefor the police-officer and the judge both were wrong to issue a speeding ticket “under the assumption that they $textbf{have the same speed}$” as we just shown that this possibility is rule out.
We draw a sketch, to show the position of the cars and the police officer where the blue dot represents the police officer and the green dot representing the fast car and the yellow dot represent the slow car, we notice that at different time interval the green dot cuts a larger distance, the sketch as follows
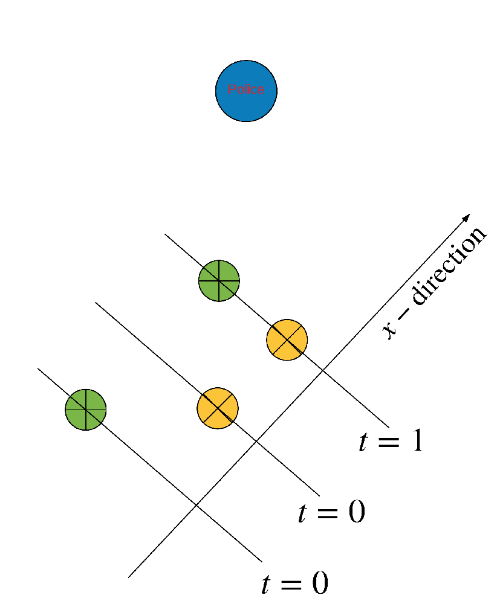
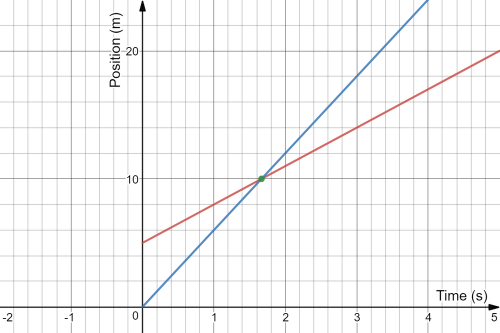
One line for the faster car and the other for the much slower car, for the faster car the dots are much wider a part, while for the slower car the dots are much closer to each other, we would notice that at some time both car would lie at the same distance even though both have a different speeds as in the following $textbf{diagram}$, which means that second car doesn’t necessarily have the same speed even though they are at the same position at some instant of time, thus showing that both the police-officer and the judge have made a wrong decision assuming they both are have the same speed for being at the same position at some instant of time.
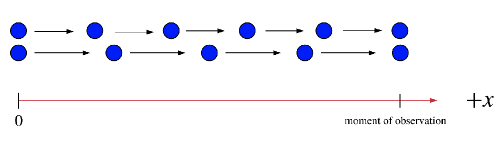
And since the slope of the line represent the speed of the car, then the faster car would have a steep line “a line with a slope of high numerical value”, while the slow car is represented with the shallow line.
And to clarify the idea, we will give the slow car a head-up start such that it start its journey at some point after the origin “+ve $y$-axis”, we would notice that the line representing the faster car would intersect the line representing the slower car which it would by pass the slower car at this instant they both have the same position at that instant of time, but it doesn’t mean that they both have the same speed.