In this problem we have three identical bulbs connected as shown in the figure above. Let $R$ be resistance of the lightbulbs. To compare the brightness of the lightbulbs, we first need to understand that brightess is proportional to the power output on the lightbulb. This means that if we compare the power output on the lightbulbs, we’ll also compare their brightness.
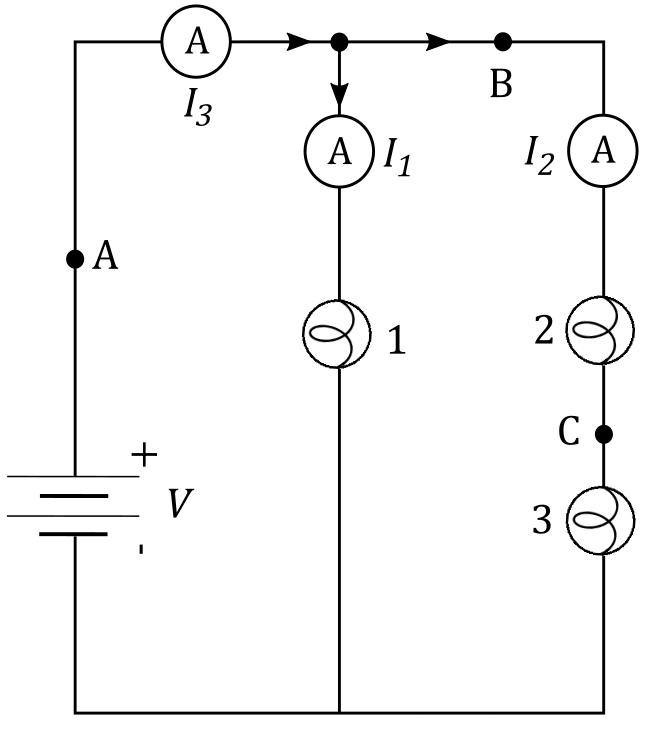
Power output on a resistors with resistance $R$, with current $I$ flowing through it and voltage $V$ across it can be expressed as:

$$
begin{align*}
P &= dfrac{V^2}{R} tag{1} \
end{align*}
$$

As we can see from the figure above, voltage across the lightbulb 1 is equal to voltage $V$ across the battery, since it’s connected in parallel to it. This means that power output $P_1$ on lightbulb 1 can be expressed as:

$$
P_1 = dfrac{V^2}{R}
$$

If we take a look at lightbulbs 2 and 3, we’ll see that they are connected in series to one another, but their combination is connected in parallel to the battery. This means that:

$$
V_2 + V_3 = V
$$

where $V_2$ is voltage across lightbulb 2 and $V_3$ is voltage across lightbulb 3. Since Ohm’s law states that voltage $V$ across a resistor with resistance $R$ and current $I$ flowing through is calculated as:

$$
V = I R
$$

we find that voltage $V_2$ is equal to:

$$
V_2 = I_2 R
$$

and voltage $V_3$ is equal to

$$
V_3 = I_2 R
$$

As we can see, voltages $V_2$ and $V_3$ are equal, which we can plug into the equation above:

$$
begin{align*}
V_2 + V_3 &= V \
tag{plug in $V_2 = I_2 R = V_3 $} \
V_2 + V_2 &= V\
2 V_2 &= V \
tag{express $V_2$ from the equation above} \
V_2 &= dfrac{V}{2}
end{align*}
$$

We can now apply equation $(1)$ to find power output on lightbulbs 2 and 3. Power output $P_2$ on lightbulb 2 is equal to:

$$
begin{align*}
P_2 &= dfrac{V_2^2}{R} \
tag{plug in $V_2 = dfrac{V}{2} $ } \
P_2 &= dfrac{bigg(dfrac{V}{2} bigg)^2}{R} \
P_2 &= dfrac{V^2}{R} dfrac{1}{4} \
tag{plug in $ P_1 = dfrac{V^2}{R} $} \
P_2 &= dfrac{P_1}{4}
end{align*}
$$

Power output $P_3$ on lightbulb 3 is equal to:

$$
begin{align*}
P_3 &= dfrac{V_3^2}{R} \
tag{plug in $V_2 = V_3 $} \
P_3 &= dfrac{V_2^2}{R} \
tag{plug in $ P_2 = dfrac{V_2^2}{R} = dfrac{P_1}{4} $ } \
P_3 &= dfrac{P_1}{4}
end{align*}
$$

As we can see, power output $P_1$ on lightbulb 1 is equal to:

$$
boxed{ P_1 = dfrac{V^2}{R}}
$$

while power output on lightbulbs 2 and 3 are equal to:

$$
boxed{P_2 = P_3 = dfrac{P_1}{4} }
$$

$$
boxed{P_2 = P_3 = dfrac{P_1}{4} }
$$

We need to determine the current $I_2$ if the currents in the shown circuit are $I_3=1.7,,rm{A}$ and $I_1=1.1,,rm{A}$.

Observing junction $D$ we can see that the current $I_3$ enters the junction and $I_1$ and $I_2$ exit. Following the junction rule which states that the sum of all currents entering needs to be equal to the sum of all currents exiting the junction we can set up an equation:
$$I_3=I_1+I_2$$

From the previous equation we can express $I_2$:
$$I_2=I_3-I_1$$

Inserting values into the previous equation we will get:
$$I_2=1.7-1.1$$
Finally, the current $I_2$ is:
$$boxed{I_2=0.6,,rm{A}}$$

$$I_2=0.6,,rm{A}$$

In this problem we have three identical bulbs connected as shown in the figure above. Let $R$ be resistance of the lightbulbs. We need to understand that brightess is proportional to the power output on the lightbulb.
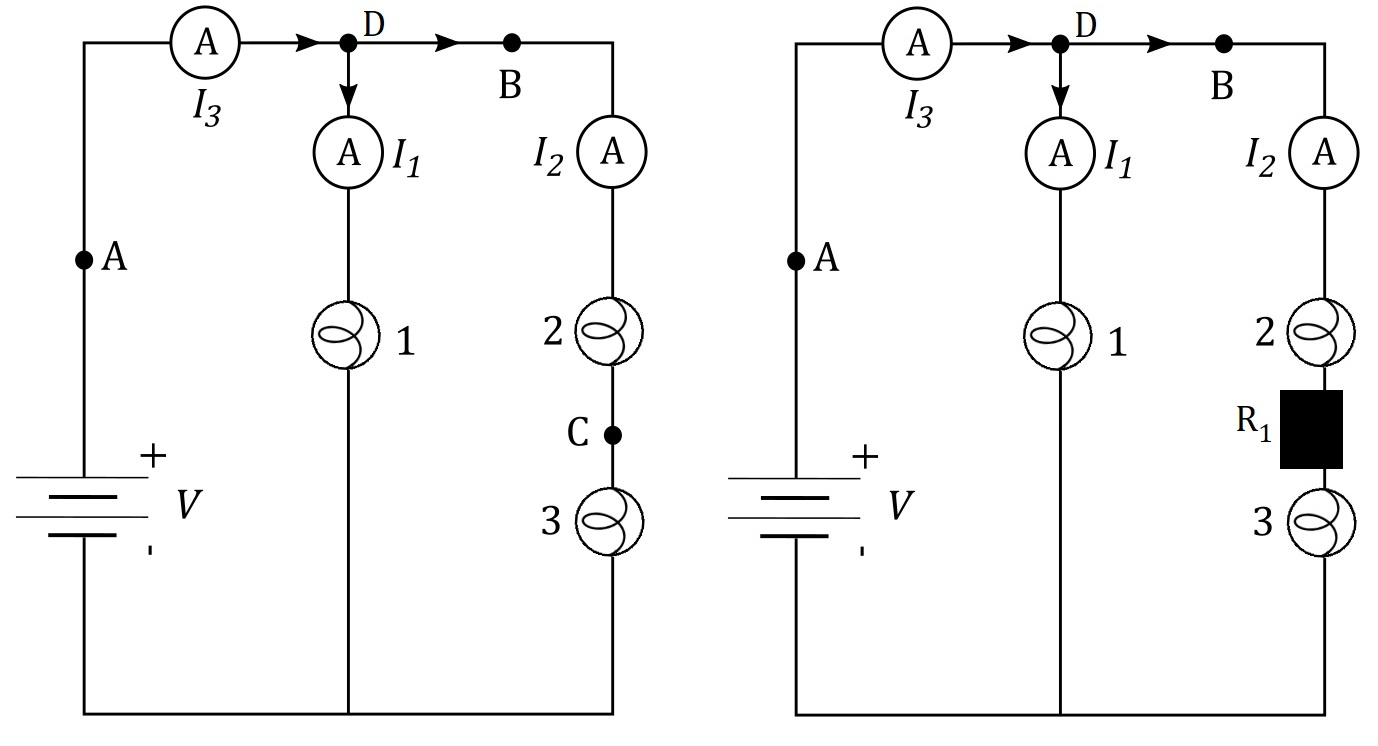
This means that if we compare the power output on the lightbulbs before and after the wire at point C broke, we’ll also compare brightness of the bulbs in the initial case when wire didn’t break and in the final case when it did.
Power output on a resistors with resistance $R$, with current $I$ flowing through it and voltage $V$ across it can be expressed as:

$$
begin{align*}
P &= dfrac{V^2}{R} tag{1} \
end{align*}
$$

However, we don’t yet know the voltagea across the lightbulbs 2 and 3.
If we take a look at lightbulbs 2 and 3, we’ll see that they are connected in series to one another, but their combination is connected in parallel to the battery. This means that:

$$
V_2 + V_3 = V
$$

where $V_2$ is voltage across lightbulb 2 and $V_3$ is voltage across lightbulb 3. Since Ohm’s law states that voltage $V$ across a resistor with resistance $R$ and current $I$ flowing through is calculated as:

$$
V = I R
$$

we find that voltage $V_2$ is equal to:

$$
V_2 = I_2 R
$$

and voltage $V_3$ is equal to

$$
V_3 = I_2 R
$$

As we can see, voltages $V_2$ and $V_3$ are equal, which we can plug into the equation above:

$$
begin{align*}
V_2 + V_3 &= V \
tag{plug in $V_2 = I_2 R = V_3 $} \
V_2 + V_2 &= V\
2 V_2 &= V \
tag{express $V_2$ from the equation above} \
V_2 &= dfrac{V}{2}
end{align*}
$$

We can now apply equation $(1)$ to find power output on lightbulbs 2 and 3 before the wire breaks. Power output $P_{2i}$ on lightbulb 2 is equal to:

$$
begin{align*}
P_{2i} &= dfrac{V_{2i}^2}{R} \
tag{plug in $V_{2i} = dfrac{V}{2} $ } \
P_{2i} &= dfrac{bigg(dfrac{V}{2} bigg)^2}{R} \
P_{2i} &= dfrac{V^2}{R} dfrac{1}{4}
end{align*}
$$

Power output $P_{3i}$ on lightbulb 3 is equal to:

$$
begin{align*}
P_{3i} &= dfrac{V_{3i}^2}{R} \
tag{plug in $V_{2i} = V_{3i} $} \
P_{3i} &= dfrac{V_{2i}^2}{R} \
tag{plug in $P_{2i} = P_{3i}$} \
P_{3i} &= dfrac{V^2}{R} dfrac{1}{4}
end{align*}
$$

As we can see, power output on both of the lightbulbs before the wire breaks is the same and equal to:

$$
boxed{ P_{2i} = P_{3i} = dfrac{V^2}{4R} }
$$

Now that we’ve calculated the power output in the initial case before the wire broke, we can proceed to calculate the power output on the lightbulbs after the wire at point $C$ breaks and we replace it with a resistor with resistance $R_1$. In this case, we have three resistors connected in series, two of which are resistors $R$ on the lightbulbs and the third resistor being $R_1$. In this case, voltage across the battery $V$ is again equal to the sum of voltage across this series combination, stated as:

$$
begin{align*}
V = V_{2f} + V_{3f} + V_1 tag{2}
end{align*}
$$

where $V_{2f}$ and $V_{3f}$ is voltage across lightbulbs 2 and 3, respectively, and $V_1$ is voltage across the new resistor $R_1$. As stated above, since Ohm’s law states that voltage $V$ across a resistor with resistance $R$ and current $I$ flowing through is calculated as:

$$
V = I R
$$

we find that voltage $V_{2f}$ is equal to:

$$
V_{2f} = I_{2f} R
$$

and voltage $V_3$ is equal to

$$
V_{3f} = I_{2f} R
$$

where $R$ is resistance of the lightbulb and $I_{2f}$ is current flowing through this branch of the circuit when resistor $R_1$ is added. As we can see from the two equations above, voltages $V_{2f}$ and $V_{3f}$ are the same, which means that voltage across both of the lightbulbs is the same, which we can plug into equation $(2)$:

$$
begin{align*}
V &= V_{2f} + V_{3f} + V_1 \
V &= V_{2f} + V_{2f} + V_1 \
V &= 2 V_{2f} + V_1 \
tag{express $V_{2f}$ from the equation} \
2 V_{2f} &= V – V_1 \
V_{2f} &= dfrac{V – V_1}{2}
end{align*}
$$

We can now apply equation $(1)$ to find the power output $P_{2f}$ on lightbulbs 2 and 3. Equation $(1)$ states:

$$
P = dfrac{V^2}{R}
$$

We see that since voltage across lightbulbs 2 and 3 is the same and they have the same resistance, power output will be the same on both of them.

$$
begin{align*}
P_{2f} &= dfrac{V_{2f} ^2}{R} \
tag{plug in $V_{2f} = dfrac{V – V_1}{2} $ }\
P_{2f} &= dfrac{ bigg(dfrac{V – V_1}{2} bigg)^2 }{R} \
tag{square the numerator in the equation above} \
P_{2f} &= dfrac{ dfrac{(V – V_1)^2}{4} }{R}
end{align*}
$$

As we can see, power output on lightbulbs 2 and 3 is the same after the wire breaks and gets replaced with a resistor $R_1$ and is equal to:

$$
boxed{ P_{2f} = P_{3f} = dfrac{(V – V_1)^2}{4R} }
$$

As we can see by comparing the power output in the initial case $P_{2i}$ and power output in the final case $P_{2f}$:

$$
begin{align*}
dfrac{ P_{2f} }{ P_{2i}} &= dfrac{ dfrac{(V – V_1)^2 }{4R} }{ dfrac{V^2}{4R} } \
tag{cancel out the $4R$} \
dfrac{ P_{2f} }{ P_{2i}} &= dfrac{(V – V_1)^2 }{V^2} \
tag{group the terms on the right side of the equation} \
dfrac{ P_{2f} }{ P_{2i}} &= left( dfrac{V- V_1}{V} right)^2\
dfrac{ P_{2f} }{ P_{2i}} &= left( 1- dfrac{V_1}{V} right)^2
end{align*}
$$

As we can see, the term on the right side of the equation above is lower than 1, which means:

$$
dfrac{ P_{2f} }{ P_{2i}} < 1
$$

$$
boxed{ P_{2f} < P_{2i} }
$$

Hint: Adding another resistor to the branch will decrease the current through the branch and voltage across both of the lightbulbs.
Since power output on the lightbulbs decreased, their brightness also decreased.

$$
P_{2f} < P_{2i}
$$

Looking at the previously described and shown scheme, we need to determine the voltage of the battery if the voltmeter connected across second bulb measures $V_2=3.8,,rm{V}$ and a voltmeter connected across third bulb shows $V_3=4.2,,rm{V}$.

Looking at the scheme we can see that both bulbs $2$ and $3$ are connected in series on one side of a parallel connection. This means that the voltage on that side is equal to the one on the other side which in turn is **equal** to the one on the **battery**.
$$epsilon =V$$

Voltage on that side of the parallel section can be calculated as a sum of voltages across both bulbs:
$$V=V_2+V_3$$

Combining two previous equations we will get:
$$epsilon =V_2+V_3$$

Inserting given values:
$$epsilon =3.8+4.2$$
Finally:
$$boxed{epsilon =8,,rm{V}}$$

$$epsilon =8,,rm{V}$$

Looking at the results from the previous problem we need to determine if the two bulbs are identical.
The bulbs are connected in series and have a voltage of $V_2=3.8,,rm{V}$ and $V_3=4.2,,rm{V}$

Since they are between themselves connected in series, their currents are equal:
$$I_2=I_3$$

If the bulbs are identical their resistances have to be equal. We can compare resistances using Ohm’s Law:
$$R=frac{V}{I}$$

Comparing the two bulbs:
$$frac{V_2}{I_2}=frac{V_3}{I_3}$$
Since currents are equal we can negate them:
$$V_2=V_3$$
Inserting values, we can see that ti is simply not true. Which also means that resistances are not equal:
$$boxed{R_2 neq R_3}$$
Which finally means that the bulbs are **not identical**.

To make the three bulbs in the figure above burn with equal intensity, power output on each of the lightbulbs must be the same. We’ll see that there are three ways to make this happen, although all the solutions are analogous. We know that the power output $P$ on a resistor $R$, with voltage $V$ across it and current $I$ flowing through it can be expressed in three different ways:

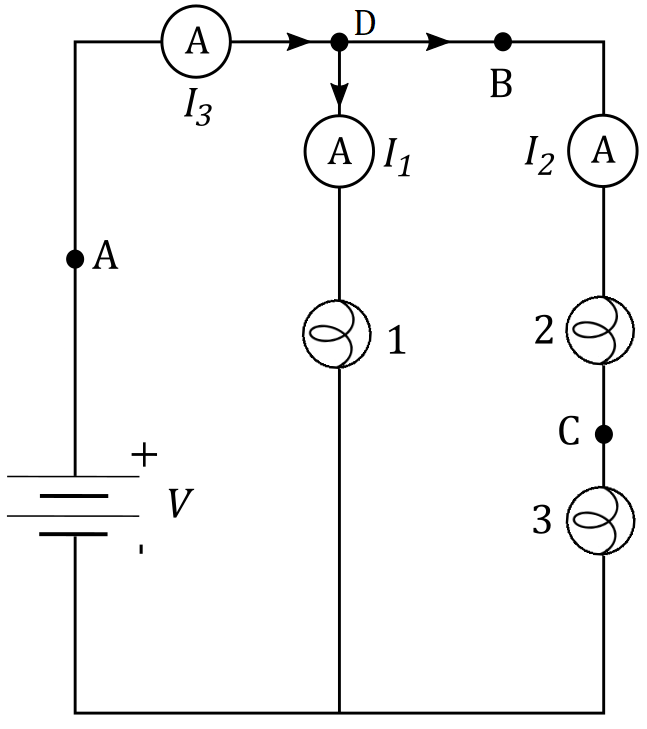
$$
begin{align*}
P &= I V tag{1} \
P &= I^2 R tag{2} \
P &= dfrac{V^2}{R} tag{3} \
end{align*}
$$

Note that in the figure above we aren’t given voltage $V$ across the battery, nor the currents $I_3$, $I_2$ and $I_3$. We also aren’t given resistance $R_1$,$R_2$ and $R_3$
on bulbs 1,2 and 3 respectively, which means that we have all the freedom to make the power outputs $P_1$, $P_2$ and $P_3$ on the three bulbs the same. In other words, we have a following condition:

$$
P_1 = P_2 = P_3
$$

where $P_1$, $P_3$ and $P_3$ are power outputs on bulbs 1,2 and 3 respectively. Let’s try to satisfy the condition above using equation $(1)$.

We see that power output $P_1$ on bulb 1 is:

$$
P_1 = I_1 V_1
$$

where $I_1$ is current flowing through bulb 1 and $V_1$ is voltage across it. We see that this voltage is equal to voltage across the battery, since this bulb is connected in parallel to the battery $V$, which means:

$$
P_1 = I_1 V
$$

We see that bulbs 2 and 3 are connected in series, which means that the same current $I_2$ flows through both of them.
Power output $P_2$ on bulb 2 is given as:

$$
P_2 = I_2 V_2
$$

while power output $P_3$ on bulb 3 is given as:

$$
P_3= I_2 V_3
$$

We see that in order for power outputs $P_2$ and $P_3$ to be equal we have:

$$
begin{align*}
P_3 &= P_2 \
tag{plug in $P_2 = I_2 V_2$ and $P_3= I_2 V_3$ } \
I_2 V_2 &= I_2 V_3 \
tag{cancel out $I_2$} \
V_2 &= V_3
end{align*}
$$

There are multiple ways in which we can make the voltage $V_2$ across bulb 2 and voltage $V_3$ across the bulb 3 equal, one of them being connecting bulbs 2 and 3 in parallel,
but since this would change the whole schematic of circuit, this solution is not viable. We know that Ohm’s law states that voltage $V$ across a resistor $R$ with current $I$ flowing through it is calculated as:

$$
V = IR
$$

From the equation above we see that if the same current $I$ flows through multiple resistors with the same resistance $R$, same voltage $V$ will be applied across all the resistors. In our case, this means that if resistance $R_2$ of bulb 2 and resistance $R_3$ of bulb 3 is the same $R_2 = R_3$, these bulbs would have the same voltage across them:

$$
begin{align*}
V_2 &= I_2 R_2 \
V_3 &= I_2 R_3
end{align*}
$$

As said, since $P_1 = P_2 = P_3$, we have:

$$
begin{align*}
P_1 &= P_2
tag{plug in $P_1 = I_1 V_1$ and $P_2 = I_2 V_2$} \
I_1 V_1 &= I_2 V_2 \
tag{plug in $V_1 = V$} \
I_1 V &= I_2 V_2 \
tag{express $I_1$ from the equation above} \
I_1 &= dfrac{ I_2 }{V} V_2 tag{4}
end{align*}
$$

Keeping it in mind that $V_2 = V_3$ and that since this series combination of bulbs 2 and 3 is connected in parallel to the battery, we know that voltages $V_2$ and $V_3$ will add up to voltage across the battery, stated as:

$$
begin{align*}
V_2 + V_3 &= V \
tag{plug in $V_2 = V_3$} \
V_2 + V_2 &= V \
V_2 cdot 2 &= V \
tag{express $V_2$} \
V_2 &= dfrac{V}{2} tag{5}
end{align*}
$$

We can plug this result for $V_2$ into the equation $(4)$:

$$
begin{align*}
I_1 &= dfrac{I_2 }{V} V_2 \
I_1 &= dfrac{ I_2 }{V} dfrac{V }{2} \
tag{cancel out $V$} \
I_1 &= dfrac{I_2}{2} tag{6}
end{align*}
$$

As we can see, the first solution is to have the same voltage $V_2$ and $V_3$ across bulbs 2 and 3 by having the same resistance $R_2 = R_3$ on these two bulbs, while the current $I_1$ flowing through bulb 1 is calculated as stated above, which means:

$$
boxed{
text{ 1st solution:}~~ R_2 = R_3 ~~ text{and}~~ I_1 = dfrac{I_2 }{2} }
$$

We’ll obtain the second solution from equation $(2)$, which states:

$$
P = I^2 R
$$

This means that in order for the two bulbs to have the same power output, we have:

$$
begin{align*}
P_2 &= P_3 \
tag{apply the equation above to $P_2$ and $P_3$} \
tag{ current $I_2$ flows through bulbs 2 and 3} \
I_2^2 R_2 &= I_2^2 R_3 \
tag{cancel out $I_2^2$} \
R_2 &= R_3
end{align*}
$$

As expected, as in the first solution, we found that in order for the two bulbs connected in series to have the same power output, their resistance must be the same. Now let’s compare the power output $P_1$ on bulb 1 with power output $P_2$ on bulb 2:

$$
begin{align*}
P_1 &= P_2 \
tag{apply the equation $(1)$ to $P_2$ and $P_1$} \
I_1^2 R_1 &= I_2^2 R_2 \
tag{plug in $ I_1 = dfrac{I_2 }{2} $ from equation $(6)$} \
left( dfrac{I_2 }{2} right)^2 R_1 &= I_2^2 R_2 \
dfrac{I_2^2 }{4 } R_1 &= I_2^2 R_2 \
tag{cancel out $I_2^2$} \
dfrac{R_1}{4} &= R_2 \
tag{express $R_1$ from the equation above } \
R_1 &= 4 R_2
end{align*}
$$

As we can see , second solution that satisfies the condition $P_1 = P_2 = P_3$ is to have bulbs 2 and 3 have the same resistance $R_2 = R_3$ while this resistance is 4 times greater than resistance $R_1$ on bulb 1, stated as:

$$
boxed{
text{ 2nd solution:}~~ R_1 = 4 R_2 = 4 R_3 }
$$

We’ll obtain the third solution from equation $(3)$, which states:

$$
P = dfrac{V^2}{R}
$$

We can apply this equation to $P_1$, $P_2$ and $P_3$ to have:

$$
begin{align*}
P_1 &= dfrac{V^2}{R_1} \
P_2 &= dfrac{V_2^2}{R_2} \
P_3 &= dfrac{V_3^2}{R_3}
end{align*}
$$

Let’s compare the power outputs $P_2$ and $P_3$:

$$
begin{align*}
P_2 &= P_3 \
dfrac{V_2^2}{R_2} &= dfrac{V_3^2}{R_3} \
tag{note that $V_2 + V_3 = V$} \
dfrac{V_2^2}{R_2} &= dfrac{(V – V_2) ^2}{R_3} \
tag{find square root of the equation} \
dfrac{V_2}{sqrt{R_2}} &= dfrac{V -V_2}{sqrt{R_3}} \
tag{rewrite the term on the right side as} \
dfrac{V_2}{sqrt{R_2}} &= dfrac{V}{sqrt{R_3}} – dfrac{V_2}{sqrt{R_3}} \
dfrac{V_2}{sqrt{R_2}} + dfrac{V_2}{sqrt{R_3}} &= dfrac{V}{sqrt{R_3}} \
tag{group the terms on the left side of the equation} \
V_2 left( dfrac{1}{sqrt{R_2}} + dfrac{1}{sqrt{R_3}} right) &= dfrac{V}{sqrt{R_3}} \
%
%
V_2 left( dfrac{sqrt{R_2} + sqrt{R_3}}{sqrt{R_2 R_3}} right) &= dfrac{V}{sqrt{R_3 }} \
tag{cancel out $sqrt{R_3}$} \
V_2 left( dfrac{sqrt{R_2} + sqrt{R_3}}{sqrt{R_2 }} right) &= V \
V_2 left( 1 + sqrt{dfrac{R_3}{R_2}} right) &= V tag{7} \
V_2 + V_2 cdot sqrt{dfrac{R_3}{R_2}} &= V \
tag{compare with $V_2 + V_3 = V$} \
V_3 &= V_2 cdot sqrt{dfrac{R_3}{R_2}} tag{8}
end{align*}
$$

Note that the Ohm’s law states that voltage $V_2$ across bulb 2 will be equal to:

$$
V_2 = I_2 R_2
$$

while voltage $V_3$ across bulb 3 will be equal to:

$$
V_3 = I_2 R_3
$$

We can plug this into equation $(8)$:

$$
begin{align*}
V_3 &= V_2 cdot sqrt{dfrac{R_3}{R_2}} \
I_2 R_3 &= I_2 R_2 sqrt{dfrac{R_3}{R_2}} \
tag{cancel out $I_2$} \
R_3 &= R_2 sqrt{dfrac{R_3}{R_2}} \
tag{square the equation} \
R_3^2 &= R_2^2 dfrac{R_3}{R_2}
tag{cancel out $R_3$ and $R_2$} \
R_3 &= R_2
end{align*}
$$