Notice that two terms in fields on the bottom are units of measure. Since the term on the bottom left is unit of measure for current, we conclude that solution for the field on the bottom left is current.

Analogously, since the term on the bottom right is unit of measure for resistance, we conclude that solution for the field on the bottom right is resistance.

Since the terms on the bottom should all be units of measure, this means since the term on the field in the middle is power, solution for field in the bottom centre is unit of measure for power, which is watt.

$$
boxed{text{bottom left: current, ~~ bottom centre: watt, ~~ bottom right: resistance}}
$$

Electric current is defined as a charge that passes a cross-section of conductor in certain period:
$$I=frac{q}{t}$$

Unit of measure for charge is Coulomb (C) and for time is second (s). Unit of measure for electric current is ampere (A) which can then be defined as:
$$boxed{[A]=frac{[C]}{[s]}}$$

$$[A]=frac{[C]}{[s]}$$

In this problem we are asked what is the direction of the conventional current flowing through the motor in the circuit shown in the figure below. As this circuit is a series circuit, there will be only one current $I$ flowing in this circuit and we can measure it by using the ammeter.

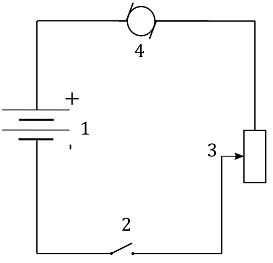
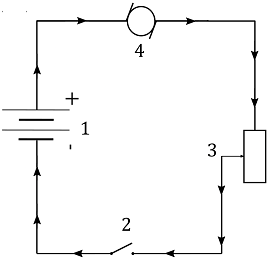
A device that converts electric energy to mechanical is **generator**. In this circuit it is labelled by a number $4$
$$boxed{a) 4}$$

A device that uses electric energy and stores it as a chemical is called a **battery**. In this circuit it is labelled by a number $1$:
$$boxed{b) 1}$$

A device that is used to turn the circuit on and off is called a **switch**. In this circuit it is labelled by a number $2$:
$$boxed{c) 2}$$

A device that is used to adjust the resitance in the circuit is called a **variable resistor**. In this circuit it is labelled by a number $3$:
$$boxed{d) 3}$$

$$a) 4$$
$$b) 1$$
$$c) 2$$
$$d) 3$$

In order to solve this problem, we need to see how does the diameter affect the cross-ssection area of a conductor:
$$A=frac{d^2pi}{4}$$
From this equation we can see that the larger diameter means **larger cross-section area**.

Now, we need to see how does the cross-section area affect the resistance of the wire using the next equation:
$$R=frac{rho L}{A}$$
Where $rho$ is a specific conductivity and is a **property of the material**, meaning that for two wires of the same material it will remain **equal**.
Length $L$ is also not a factor since we are comparing two wires of the equal lengths.

In this problem we are given a simple circuit consisting of a resistor $R$, a battery with arbitrary voltage $V$ and wires that connect this battery to the resistor $R$. We must:

$a)~~$ Draw the circuit diagram

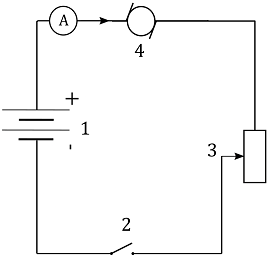
$b)~~$ Connect the ammeter so that it measures the current $I$ flowing in the circuit

$c)~~$ Connect the voltmeter so that it reads the voltage $V$ across the resistor.

Knowing that the resistor and the battery are connected in series, we know that the same current will flow through them and it will be the same current flowing through the circuit. Since ammeter is used to measure current flowing through it, if we connect it in series to both the battery $V$ and resistor $R$, current flowing through the ammeter will be the same current flowing through the battery, the resistor, and circuit overall, which means that reading on ammeter will also show current flowing through the circuit. The end result is shown in the figure below, with ammeter connected in series to the battery and the resistor:

Reading on voltmeter shows voltage $V$ across it. From the definition of parallel connection, we know that the two devices are connected in parallel if they are connected to the same voltage.
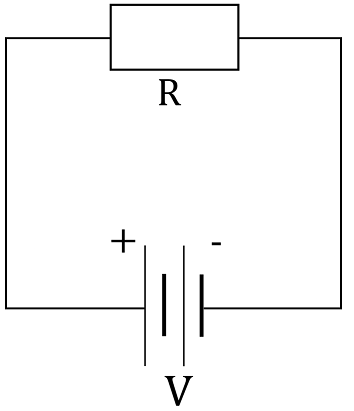
Since voltmeter is used to measure voltage across a certain device, if we connect it in parallel to the resistor $R$, voltage across this resistor will be the same as voltage across the voltmeter and reading on the voltmeter will show us the voltage across the resistor.
The end result is shown in the figure below, with voltmeter connected in parallel to the resistor:

$$
begin{align*}
& a)~~ text{Connect the battery and the resistor in series by using the wires.} \
& b)~~ text{Connect the ammeter in series to the battery.} \
& c)~~ text{Connect the voltmeter in parallel to the resistor.} \
end{align*}
$$

Let’s remember that incandescent light bulbs are built in such a way that less than the quarter of the energy provided to the light bulb is used as energy of the light emitted from the light bulb, while the rest of the energy is given off as heat on the filament. Also note that the filament glows because it reached a temperature high enough to glow. Since light bulb filament reaches this high temperature almost instantaneously after we turn on the light bulb, we see that light bulb requires high current, which is obtained by having a filament with low resistance $R$. Of course, this filament will expand due to its temperature change and since this temperature change is almost instantaneous, it can easily expand too much too fast and break. This is why filament in the light bulb breaks easily just when we turn it on.

While the light bulb is operating, filament in the light bulb already expanded and since it didn’t break during the sudden expanding when we turned it on, there’s no reason for it to break, other than short-circuit or other similar events that make any device burn out.

First we need to write down equation for power:
$$P=frac{V^2}{R}$$
where $V$ is voltage difference on the wire and $R$ is resitance. Copper wire has **low resistance** which then means that the amount of **current** flowing through it will be extremely **high**.

High current, with close to constant resistance, means high power output. This can be shown through the next equation:
$$P=RI^2$$
Where the power is proportional to the square of electric current.
This power needs to leave the wire somehow, and it is done through the heat exchange. The sole mechanism of heat transfer can be explained by a high velocity of high number of **electrons** flowing through the wire, which due to **collisions** between them, increase the temperatuer of the wire.

Power lost to heat, when there’s current $I$ flowing through the wire is equal to

$$
P = I^2 R
$$

where $R$ is resistance of the wire. Of course, to transfer the electric energy over long distances but keep the losses to heat minimal, power expressed in the equation above should be minimal, which means that current $I$ through the wire and its resistance $R$ should be kept small.

$$
text{Current through the wire and its resistance}
$$

Power $P$ can always be defined as rate of change of energy $E$ in time interval $t$, stated as:

$$
P = dfrac{E}{t }
$$

If we take a look at the units of the physical quantities in the equation above, we have:

$$
begin{align*}
mathrm{ W = dfrac{J}{s} } tag{1}
end{align*}
$$

Energy $E$ needed to move an object by a distance $d$ with force $F$ acting on it in the direction of the displacement $d$ is equal to:

$$
E = F d
$$

If we take a look at the units of the physical quantities in the equation above, we have:

$$
mathrm{ J= dfrac{N}{m} }
$$

We can plug in the expression for Joule from the expression above into equation $(1)$ and have:

$$
begin{align*}
mathrm{ W = dfrac{N m }{s} } tag{2}
end{align*}
$$

Force $F$ is defined as a change in the momentum $p$ of an object in a given time interval $Delta t$, stated as:

$$
begin{align*}
F = dfrac{Delta p}{Delta t} tag{3}
end{align*}
$$

whereas momentum is defined as a product of mass $m$ and velocity $upsilon$ of an object, stated as:

$$
p = m upsilon
$$

which means that unit of measurement of momentum is

$$
p ~ [=] ~mathrm{kg ~dfrac{m}{s}}
$$

If we take a look at the units of physical quantities of the units in equation $(3)$ we have:

$$
mathrm{ N = dfrac{dfrac{kg m }{s} }{s} = dfrac{kg m}{s^2 } }
$$

We can plug in the expression for Newtons from the equation above into equation $(2)$ and find that one Watt is equal to:

$$
begin{align*}
mathrm{W} &= mathrm{ dfrac{N m }{s} } \
tag{plug in $ mathrm{ N = dfrac{kg m}{s^2 } } $} \
mathrm{W} &= dfrac{mathrm{ dfrac{kg m }{s^2 } cdot m}}{mathrm{s}}
end{align*}
$$

$$
boxed{ mathrm{W} = mathrm{dfrac{kg m^2}{s^3 } } }
$$

$$
mathrm{W} = mathrm{dfrac{kg m^2}{s^3 } }
$$

Work $W$ needed to move charge $q$ through a potential difference $Delta V$ is equal to:

$$
W = q Delta V
$$

This means that if there is potential difference, work will be done and charges will be moved. If we connect a battery to a complete circuit, this means that charges can flow from one terminal of the battery to the other and since there is potential difference $Delta V$ between the terminals of the battery, this means that charges will start to move and they’ll move through the electric current flowing through this circuit.

Electric fence is connected to some voltage $V$, while electric potential on the ground is zero. When cow touches the electric fence, cow becomes the conductor that connects the higher potential electric fence and ground with zero potential. Since there is potential difference between the ground and the fence and cow is connected to both of the ends of the potential difference, current will flow through the fence and cow will experience an electric shock. Note that greatness of shock will depend on the potential difference which is just enough to shock the cow.

Although voltage on the wires is high, remember that voltage is the potential difference and when we use the term “voltage on the wires”, we refer to the potential difference between the electric potential on the wire $V$ and potential on the ground $V = 0$.
Whole wire is more or less on the same voltage. Voltage drops across great lengths and due to impurities in the wire. Keeping it in mind that birds claws are not far apart, when bird lands on the high-voltage wire, its claws will be on approximately the same electric potential, which makes the potential difference between its claws almost zero. This means that since electric potential difference (Voltage) across its claws is almost zero, there will be no current flowing through the bird. Let’s also add to this conclusion a fact that bird’s claws are made from a highly insulating material which further decreases the possibility of electric shock when bird lands on the wires.

First we need to write down Ohm’s Law:
$$I=frac{V}{R}$$
From this equation we can clearly see correlation between electrical current, voltage and resistance.

We need to determine which of the two lightbulbs connected to the voltage of $V=120,,rm{V}$ has higher resistance; the one with a power consumption of $P_1=50,,rm{W}$ or the one with a power consumption of $P_2=100,,rm{W}$.

We know that the power rating of the lightbulb can be calculated as:
$$P=frac{V^2}{R}$$
From this equation we can calculate the resistance as:
$$R=frac{V^2}{P}$$

From the previous equation we can see that the resistance is inversely proportional to the power rating $P$.
This finally means that the **higher power rating** means **lower resistance**.
This finally means that the bulb with power rating of $P_1=50,,rm{W}$ has higher electric resistance.

The bulb with $P_1=50,,rm{W}$ has higher resistance.

First we can write down Ohm’s Law:
$$I=frac{V}{R}$$
Where $I$ is the current, $V$ is the voltage and $R$ is resitance.

From the previous equation we can notice that the current $I$ is inversely proportional to the resistance $R$:
$$I propto frac{1}{R}$$
Which means that the **increase** in resistance $R$ causes **decrease** in current $I$.

In order to solve this problem we need to write down Ohm’s Law:
$$I=frac{V}{R}$$
which gives relation between current, voltage and resistance of the circuit.

We can write equation for first current:
$$I_1=frac{V_1}{R_1}$$
And for the current in the second scenario:
$$I_2=frac{V_2}{R_2}$$

If we insert the given information that $V_2=2 V_1$ and that $R_2=2 R_1$ we get:
$$I_1=frac{V_1}{R_1}$$
And:
$$I_2=frac{2V_1}{2R_1}$$

When we eliminate $2$ from the second equation we can notice that:
$$boxed{I_2=I_1}$$
Which finally means that the current remains constant

We need to determine whether the device uses Ohm’s Law if the first voltage is $V_1=1.5,,rm{V}$ and current $I_1=45cdot 10^{-6},,rm{A}$. And the second one is $V_2=3,,rm{V}$ and current $I_2=25cdot 10^{-3},,rm{A}$.

In order to determine if the device follows Ohm’s Law we need to write it down:
$$I=frac{V}{R}$$

In order to get a better perspective, we will extract the ratio of voltage and current since those are the information given in the problem:
$$R=frac{V}{I}$$

From the previous equation we can see that the ratio, in this case resistance, should remain equal, if not, the device does not follow Ohm’s Law:
$$R_1=frac{V_1}{I_1}$$
$$R_2=frac{V_2}{R_2}$$

Inserting values we get:
$$R_1=frac{1.5}{45cdot 10^{-6}}$$
$$R_2=frac{3}{25cdot 10^{-3}}$$
Finally:
$$R_1=33.3,,rm{kOmega }$$
And
$$R_2=0.12,,rm{kOmega }$$
Which means that device **does not follow Ohm’s Law** because
$$boxed{R_1 neq R_2}$$

We need to determine which wire of the two wires with different resistance will produce thermal energy at the higher rate if both are connected across terminals of a battery with voltage of $V=6,,rm{V}$

First we need to write down Ohm´s Law which connects current, voltage and resistance:
$$I=frac{V}{R}$$

Next, we need to write down equation for electric power. Rate of production of thermal energy can also be described as power:
$$P=IV$$

Combining the two previously mentioned equations we can get:
$$P=frac{V^2}{R}$$
From this we can see that with constant voltage, the higher the resistance the lower the power.
This means that the **higher rate of thermal energy production** will be with a wire with **lower resistance**.

$a)~~$ As we can see on the figure, voltage $V$ across the motor is $V = 12 ~mathrm{V}$ and current $I$ flowing through it is $I = 1.5 ~mathrm{A}$.
Power output $P$ of an electric component connected to voltage $V$ with current $I$ flowing through it is calculated as:

$$
begin{align*}
P &= VI \
tag{plug in the given values} \
P &= 12 ~mathrm{V} cdot 1.50 ~mathrm{A}
end{align*}
$$

$$
boxed{ P = 18 ~mathrm{W} }
$$

$b)~~$ Energy $E$ converted in time $t$ in the component with power output $P$ can be found from the definition of power, which states that power output $P$ is energy $E$ converted in time interval $t$, stated as:

$$
begin{align*}
P &= dfrac{E}{t} \
tag{express $E$ from the equation above} \
E &= P t \
tag{plug in the given values} \
E &= 18 ~mathrm{W} cdot 15 ~mathrm {min} \
tag{$mathrm{1 min = 60 ~mathrm{s }}$} \
E &= 18 ~mathrm{W} cdot 15 cdot 60 ~mathrm {s}
end{align*}
$$

$$
boxed{ E = 16200 ~mathrm{J} }
$$

$$
a)~~ P = 18 ~mathrm{W}
$$

$$
b)~~ E = 16200 ~mathrm{J}
$$

$a)~~$ Reading on the ammeter is equal to the current $I$ flowing through it. Since it’s connected in series to the resistor $R = 18 ~mathrm{Omega}$, this means that the same current $I$ flows through the resistor and ammeter.
From Ohm’s law we know that the current $I$ flowing through an electric component with resistance $R$ with voltage $V$ across the component is calculated as:

$$
I = dfrac{V}{R}
$$

Keep in mind that voltage across the $R= 18 ~mathrm{Omega}$ resistor is $V = 27 ~mathrm{V}$. Current $I$ through the resistor $R$ is calculated as:

$$
begin{align*}
I &= dfrac{V}{R} \
tag{plug in the given values} \
I &= dfrac{ 27 ~mathrm{V} }{ 18 ~mathrm{Omega}}
end{align*}
$$

$$
boxed{ I = 1.5 ~mathrm{A} }
$$

$b)~~$ Reading on the voltmeter is equal to the voltage across the voltmeter. Since it’s parallel to the resistor $R = 18 ~mathrm{Omega}$ and voltage across the resistor is equal to voltage on the battery $V = 27 ~mathrm{V}$, this means that voltage across the voltmeter is equal to the voltage across this resistor, which is

$$
boxed{ V_{voltmeter} = V = 27 ~mathrm{V} }
$$

$c)~~$ As we can see on the figure, voltage $V$ across the resistor is $V = 27 ~mathrm{V}$ and current $I$ flowing through it is $I = 1.5 ~mathrm{A}$.
Power output $P$ of an electric component connected to voltage $V$ with current $I$ flowing through it is calculated as:

$$
begin{align*}
P &= VI \
tag{plug in the given values} \
P &= 27 ~mathrm{V} cdot 1.5 ~mathrm{A}
end{align*}
$$

$$
boxed{ P = 40.5 ~mathrm{W} }
$$

d)~~ Energy $E$ delivered in time $t$ to the component with power output $P$ can be found from the definition of power, which states that power output $P$ is equal to energy $E$ delivered in time interval $t$, stated as:

$$
begin{align*}
P &= dfrac{E}{t} \
tag{express $E$ from the equation above} \
E &= P t \
tag{we’re interested in energy $E$ delivered in $t = 1 ~mathrm{h}$} \
tag{plug in the given values} \
E &= 40.5 ~mathrm{W} cdot 1 ~mathrm {h} \
tag{$mathrm{1 h = 3600 ~mathrm{s } }$} \
E &= 40.5 ~mathrm{W} cdot 3600 ~mathrm{s }
end{align*}
$$

$$
boxed{ E = 145800 ~mathrm{J} }
$$

$$
a)~~ I = 1.5 ~mathrm{A}
$$

$$
b)~~ V_{voltmeter} = 27 ~mathrm{V}
$$

$$
c)~~ P = 40.5 ~mathrm{W}
$$

$$
d)~~ E = 145800 ~mathrm{J}
$$

$a)~~$ Reading on the ammeter is equal to the current $I$ flowing through it. Since it’s connected in series to the resistor $R = 9 ~mathrm{Omega}$, this means that the same current $I$ flows through the resistor and ammeter.
From Ohm’s law we know that the current $I$ flowing through an electric component with resistance $R$ with voltage $V$ across the component is calculated as:

$$
I = dfrac{V}{R}
$$

Keep in mind that voltage across the $9 ~mathrm{Omega}$ resistor $R$ is $V = 27 ~mathrm{V}$. Current $I$ through the resistor $R$ is calculated as:

$$
begin{align*}
I &= dfrac{V}{R} \
tag{plug in the given values} \
I &= dfrac{ 27 ~mathrm{V} }{ 9 ~mathrm{Omega}}
end{align*}
$$

$$
boxed{ I = 3 ~mathrm{A} }
$$

$b)~~$ Reading on the voltmeter is equal to the voltage across the voltmeter. Since it’s parallel connected in parallel with resistor $R = 9 ~mathrm{Omega}$ and voltage across the resistor is equal to voltage on the battery $V = 27 ~mathrm{V}$, this means that voltage across the voltmeter is equal to the voltage across this resistor, which is

$$
boxed{ V_{voltmeter} = V = 27 ~mathrm{V} }
$$

$c)~~$ As we can see on the figure, voltage $V$ across the resistor is $V = 27 ~mathrm{V}$ and current $I$ flowing through it is $I = 3 ~mathrm{A}$.
Power output $P$ of an electric component connected to voltage $V$ with current $I$ flowing through it is calculated as:

$$
begin{align*}
P &= VI \
tag{plug in the given values} \
P &= 27 ~mathrm{V} cdot 3 ~mathrm{A}
end{align*}
$$

$$
boxed{ P = 81 ~mathrm{W} }
$$

$d)~~$ Energy $E$ delivered in time $t$ to the component with power output $P$ can be found from the definition of power, which states that power output $P$ is equal to energy $E$ delivered in time interval $t$, stated as:

$$
begin{align*}
P &= dfrac{E}{t} \
tag{express $E$ from the equation above} \
E &= P t \
tag{we’re interested in energy $E$ delivered in $t = 1 ~mathrm{h}$} \
tag{plug in the given values} \
E &= 81 ~mathrm{W} cdot 1 ~mathrm {h} \
tag{$mathrm{1 h = 3600 ~mathrm{s } }$} \
E &= 81 ~mathrm{W} cdot 3600 ~mathrm{s }
end{align*}
$$

$$
boxed{ E = 291600 ~mathrm{J} }
$$

$$
a)~~ I = 3 ~mathrm{A}
$$

$$
b)~~ V_{voltmeter} = 27 ~mathrm{V}
$$

$$
c)~~ P = 81 ~mathrm{W}
$$

$$
d)~~ E = 291600 ~mathrm{J}
$$

$a)~~$ Reading on the ammeter is equal to the current $I$ flowing through it. Since it’s connected in series to the resistor $R = 18 ~mathrm{Omega}$, this means that the same current $I$ flows through the resistor and ammeter.
From Ohm’s law we know that the current $I$ flowing through an electric component with resistance $R$ with voltage $V$ across the component is calculated as:

$$
I = dfrac{V}{R}
$$

Keep in mind that voltage across the $18 ~mathrm{Omega}$ resistor $R$ is $V = 9 ~mathrm{V}$. Current $I$ through the resistor $R$ is calculated as:

$$
begin{align*}
I &= dfrac{V}{R} \
tag{plug in the given values} \
I &= dfrac{ 9 ~mathrm{V} }{ 18 ~mathrm{Omega}}
end{align*}
$$

$$
boxed{ I = 0.5 ~mathrm{A} }
$$

$b)~~$ Reading on the voltmeter is equal to the voltage across the voltmeter. Since it’s parallel connected in parallel with resistor $R = 18 ~mathrm{Omega}$ and voltage across the resistor is equal to voltage on the battery $V = 9 ~mathrm{V}$, this means that voltage across the voltmeter is equal to the voltage across this resistor, which is

$$
boxed{ V_{voltmeter} = V = 9 ~mathrm{V} }
$$

$c)~~$ As we can see on the figure, voltage $V$ across the resistor is $V = 9 ~mathrm{V}$ and current $I$ flowing through it is $I = 0.5 ~mathrm{A}$.
Power output $P$ of an electric component connected to voltage $V$ with current $I$ flowing through it is calculated as:

$$
begin{align*}
P &= VI \
tag{plug in the given values} \
P &= 9 ~mathrm{V} cdot 0.5 ~mathrm{A}
end{align*}
$$

$$
boxed{ P = 4.5 ~mathrm{W} }
$$

$d)~~$ Energy $E$ delivered in time $t$ to the component with power output $P$ can be found from the definition of power, which states that power output $P$ is equal to energy $E$ delivered in time interval $t$, stated as:

$$
begin{align*}
P &= dfrac{E}{t} \
tag{express $E$ from the equation above} \
E &= P t \
tag{we’re interested in energy $E$ delivered in $t = 1 ~mathrm{h}$} \
tag{plug in the given values} \
E &= 4.5 ~mathrm{W} cdot 1 ~mathrm {h} \
tag{$mathrm{1 h = 3600 ~mathrm{s } }$} \
E &= 4.5 ~mathrm{W} cdot 3600 ~mathrm{s }
end{align*}
$$

$$
boxed{ E = 16200 ~mathrm{J} }
$$

$$
a)~~ I = 0.5 ~mathrm{A}
$$

$$
b)~~ V_{voltmeter} = V = 9 ~mathrm{V}
$$

$$
c)~~ P = 4.5 ~mathrm{W}
$$

$$
d)~~ E =16200 ~mathrm{J}
$$

We need to determine the power output if a voltage is $V=120,,rm{V}$ and the current $I=8,,rm{A}$

First we need to write down an equation for calculating the electric power:
$$P=VI$$
Where it states that the power is equal to the voltage times current.

No we can insert given values in the previous equation:
$$P=120cdot 8$$
Finally:
$$boxed{P=960,,rm{W}}$$

$$P=960,,rm{W}$$

We need to determine the dissipated power if the voltage is $V=120,,rm{V}$ and current $I=1.2,,rm{A}$.

The dissipated power can be calculated as:
$$P=VI$$
Where $P$ is power, $I$ is current in the bulb and $V$ is the voltage.

Inserting given values we get:
$$P=120cdot 1.2$$
Finally:
$$boxed{P=144,,rm{W}}$$

$$P=144,,rm{W}$$

If a current is $I=0.5,,rm{A}$ and the voltage is $V=120,,rm{V}$ we need to determine the power delivered and energy converted in a period of $t=5,,rm{min}$.

Power output of electric device is calculated as:
$$P=VI$$
Where $P$ is power, $I$ is current and $V$ is voltage.

We can use this equation because in this case **the power delivered is equal to the power output** of the device.

Insering the given values we get:
$$P=120cdot 0.5$$
Finally, the power delivered is
$$boxed{P=60,,rm{W}}$$

Now we can calculate the energy converted in a period $t$. Since we know that power is energy transferred in a period of time:
$$P=frac{E}{t}$$
We can easily extract $E$:
$$E=Pt$$

Inserting given values in the previous equation:
$$E=60cdot 5cdot 60$$
Where $t$ is expressed in SI units, seconds.
Finally we get:
$$boxed{E=18,,rm{kJ}}$$

$$P=60,,rm{W}$$
$$E=18,,rm{kJ}$$

If a voltage is $V=12,,rm{V}$ and the current is $I=210,,rm{A}$ we need to determine how many joules of energ does the battery deliver each second and what is the power of the device, expressed in watts.

First assumption is that the voltage of the source is equal to the voltage across the device.
Energy delivered in a period of time can be calculated as:
$$E=Pt$$
Where, in our case, $t=1,,rm{s}$.
And power can be calculated as:
$$P=VI$$

Combining previous equations we get:
$$E=VIt$$

Inserting given values we get that energy delivered each second is:
$$E=12cdot 210cdot 1$$
Finally:
$$boxed{E=2520,,rm{J}}$$

In this case power supplied is equal to the power output of the electric device:
$$P=VI$$

Inserting given values into the previous equation we get:
$$P=12cdot 210$$
Finally the power output is:
$$boxed{P=2520,,rm{W}}$$

$$E=2520,,rm{J}$$
$$P=2520,,rm{W}$$

We need to determine the current in the device if it’s power output is $P=4200,,rm{W}$ and it’s voltage is $V=220,,rm{V}$.

Power output of electric device can be calculated as:
$$P=VI$$
From this equation we can extract current $I$:
$$I=frac{P}{V}$$

Now we can insert given values into the previous equation:
$$I=frac{4200}{220}$$
Finally, the current on the device is:
$$boxed{I=19.1,,rm{A}}$$

$$I=19.1,,rm{A}$$

We are told that voltage $V$ across the flashlight bulb is $V = 3 ~mathrm{V}$ and that current $I$ flowing through it is $I = 1.5 ~mathrm{A}$.
We need to find the power rating $P$ of the bulb and electric energy $E$ delivered to the flashlight bulb in time interval $t = 11 ~mathrm{min}$.

Power output $P$ of an electric component connected to voltage $V$ with current $I$ flowing through it is calculated as:

$$
begin{align*}
P &= VI \
tag{plug in the given values} \
P &= 3 ~mathrm{V} cdot 1.5 ~mathrm{A}
end{align*}
$$

$$
boxed{ P = 4.5 ~mathrm{W} }
$$

Energy $E$ delivered in time $t$ to the component in the circuit with power output $P$ can be found from the definition of power, which states that power $P$ is energy $E$ delivered in time interval $t$, stated as:

$$
begin{align*}
P &= dfrac{E}{t} \
tag{express $E$ from the equation above} \
E &= P t \
tag{plug in the given values} \
E &= 4.5 ~mathrm{W} cdot 11 ~mathrm{min} \
tag{$mathrm{1 min = 60 ~mathrm{s}}$} \
E &= 4.5 ~mathrm{W} cdot 11 cdot 60 ~mathrm{s}
end{align*}
$$

$$
boxed{ E = 2970 ~mathrm{J} }
$$

$$
a)~~ P = 4.5 ~mathrm{W}
$$

$$
b)~~ E = 2970 ~mathrm{J}
$$

We need to determine the voltage of the source if the device of a resistance of $R=60,,rm{Omega }$ has a current of $I=0.4,,rm{A}$.

In order to solve this equation we need to use the Ohm’s Law which states that the current can be calculated as a ratio of voltage to the resistance:
$$I=frac{V}{R}$$

From the previous equation we can extract voltage:
$$V=IR$$

Inserting given values in the previous equation we get:
$$V=0.4cdot 60$$
Finally the voltage on the battery is:
$$boxed{V=24,,rm{V}}$$

$$V=24,,rm{V}$$

We need to determine the voltage applied to the device that has a resistance of $R=4,,rm{Omega}$ and the current of $I=1.5,,rm{A}$.

In order to solve this problem we need to use the Ohm’s Law which states that the current in the electric circle can be calculated as a ratio of voltage to the resistance:
$$I=frac{V}{R}$$

From the previous equation we can extract voltage:
$$V=IR$$

Inserting the given values in the previous equation we get:
$$V=1.5cdot 4$$
Finally, the voltage applied to the device is:
$$boxed{V=6,,rm{V}}$$

$$V=6,,rm{V}$$

We need to determine the voltage placed on the device that has a resistance of $R=15,,rm{Omega}$ and a current of $I=8,,rm{A}$.

In order to solve this problem we need to use Ohm’s Law which states that the current in the electric circuit can be calculated as a ratio of voltage to the resistance:
$$I=frac{V}{R}$$

From the previous equation we can etract voltage:
$$V=IR$$

Inserting given values into the previous equation we get:
$$V=8cdot 15$$
Finally, the voltage on the device is:
$$boxed{V=120,,rm{V}}$$

$$V=120,,rm{V}$$

We need to determine the current in the resistor if it’s resistance is $R=15,,rm{Omega }$ and a voltage of $V=75,,rm{V}$ is applied to it.

In order to solve this problem we need to use Ohm’s Law which states that the current in the circuit can be calculated as a ratio of voltage to the resistance:
$$I=frac{V}{R}$$

We can directly insert given values:
$$I=frac{75}{15}$$
Finally, the current in the resistor is:
$$boxed{I=5,,rm{A}}$$

$$I=5,,rm{A}$$

In this problem we a nichrome wire connected across a variable power supply with voltage $V$ varying between $0 ~mathrm{V}$ and $10 ~mathrm{V}$.
Students then measured the current $I$ flowing through the nichrome wire for each chosen value of voltage $V$ across the wire. Notice that since wire is the only resistors in the circuit, voltage across the wire is equal to voltage $V$ across the supply. We must:

$a)~~$ Find resistance $R$ of the wire for each measurement

$b)~~$ Graph current $I$ versus voltage $V$

$c)~~$ Determine if the nichrome wire obeys the Ohm’s law.
Ohm’s law states that the current $I$ flowing through a resistor with resistance $R$ can be calculated as:

$$
I = dfrac{V}{R}
$$

where $V$ is voltage across the resistor. In this case, resistor in question is the mentioned nichrome wire.

$a)~~$
We can express resistance $R$ of the nichrome wire from the equation above as:
$$ R = dfrac{V}{I} $$
In this problem, we’ll change the voltage $V$ across the wire, measure the current $I$ flowing through it and determine the resistance $R$ for each of the measurements by plugging in the measured values of voltage $V$ and current $I$. For example, for the first measurement we have:
$$ R_1 = dfrac{V_1}{I_1} $$
where $V_1$ is voltage we’ve applied across the wire in the first measurement, $I_1$ is current measured in the first measurement and $R_1$ is resistance of the nichrome wire in the first scenario, when voltage $V_1$ is applied and current $I_1$ is measured. We find that resistance $R_1$ is equal to:
begin{align*}
R_1 &= dfrac{V_1}{I_1} \
tag{plug in the values} \
R_1 &= dfrac{ 2 ~mathrm{V} }{ 0.014 ~mathrm{A} }
end{align*}
All other values of the resistance for each of the measurements are calculated analogously to the example above.

begin{table}[htb]
begin{tabular}{|l|l|l|ll}
cline{1-3}
Voltage, V (volts) & Current, I (amps) & Resistance, $ R= dfrac{V}{I} $ (ohms) & & \ cline{1-3}
2 & 0.014 & 142.857 & & \ cline{1-3}
4 & 0.027 & 148.148 & & \ cline{1-3}
6 & 0.04 & 150 & & \ cline{1-3}
8 & 0.052 & 153.846 & & \ cline{1-3}
10 & 0.063 & 158.73 & & \ cline{1-3}
-2 & -0.014 & 142.857 & & \ cline{1-3}
-4 & -0.028 & 142.857 & & \ cline{1-3}
-6 & -0.039 & 153.846 & & \ cline{1-3}
-8 & -0.051 & 156.862 & & \ cline{1-3}
-10 & -0.062 & 161.29 & & \ cline{1-3}
end{tabular}
end{table}

$b)~~$ In this part of the problem we must draw the current $I$ versus voltage $V$ graph. This graph actually represents how current $I$ flowing through a given resistor $R$ depends on the voltage $V$ applied across the resistor. To draw this graph, use current $I$ as $y$ axis and use voltage $V$ as $x$ axis. Enter each of the applied voltages $V$ on the graph and also enter the corresponding current $I$ in that same measurement. Each of the measurements will give us one point on the graph which represents the resistance that we found in that measurement. Now connect all of the points obtained from the measurements with one single line so that distance between this line and the points obtained from the measurements is minimal. The end result should look like shown in the figure below:

$c)~~$ In this part of the problem we must determine if the nichrome wire obeys the Ohm’s law. We’ve plotted the current vs voltage graph . Red line in the figure above represents how would this wire behave if it obeyed Ohm’s law for all values of voltage.
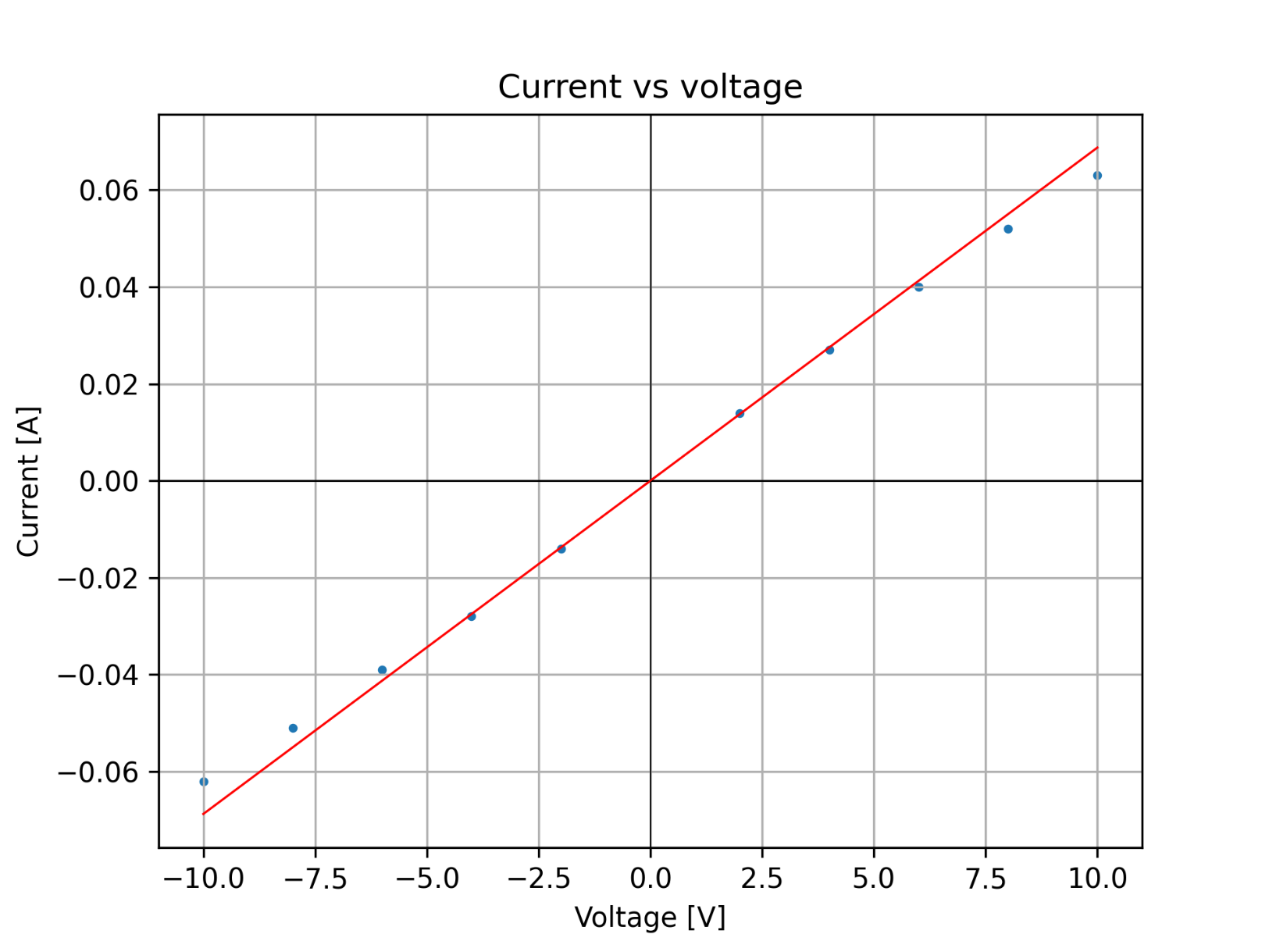
Blue dots represent measured values. We can see that for voltages below $V=-4 mathrm{~V}$ and above $V=4 mathrm{~V}$ measured values are much different than the values that we should have measured. In other words, blue dots are distant to the red line. This means that this wire obeys the Ohm’s law for voltage range between $V=-4 mathrm{~V}$ and $V=4 mathrm{~V}$.

In this problem we must draw a simple circuit diagram consisting of a resistor with resistance $R = 16 ~mathrm{Omega}$, a battery with voltage $V$ and an ammeter that reads a current of $I = 1.75 ~mathrm{A}$. We must also indicate the positive and negative terminal of the battery and its voltage $V$, positive terminal of the ammeter and direction of conventional current $I$ flowing in the circuit.
To draw a circuit diagram, we first conclude that this is a simple circuit, consisting only of a resistor $R$ and battery with voltage $V$ connected in series.

Voltage $V$ across the battery can be calculated by using the Ohm’s law, which states that the current $I$ flowing through a resistor $R$ with voltage $V$ across it can be calculated as:

$$
I = dfrac{V}{R}
$$

We can express voltage $V$ across the battery from the equation above:

$$
begin{align*}
V &= I R \
tag{plug in the values } \
V &= 1.75 ~mathrm{A} cdot 16 ~mathrm{Omega}
end{align*}
$$

$$
boxed{V = 28 ~mathrm{V} }
$$

Now that we have voltage $V$ across the battery, we can draw a battery in the circuit and indicate positive and negative terminal of the battery and direction of the current $I$ accordingly. In other words, current must flow through a circuit from positive to a negative terminal of the battery, as shown in the figure below:

Note that in the figure above we’ve indicated a positive and negative terminal of the ammeter. We did this by taking a look which terminal of the battery is connected to which terminal of the ammeter. Terminal of the ammeter connected to the positive terminal of the battery is positive and vice versa. Also note that in our case current $I$ flows clockwise because it must flow from positive to a negative terminal of the battery.

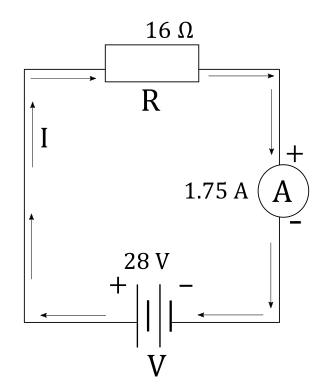
$$
a)~~
$$

Ohm’s law states that
current $I$ flowing through a resistor with resistance $R$ and potential difference $V$ across the terminals of the resistor is equal to:

$$
I = dfrac{V}{R}
$$

We can express resistance $R$ from the equation above as:

$$
R = dfrac{V}{I}
$$

If this device obeys Ohm’s law, ratio of voltage applied in the first case and measured current when that voltage is applied will always be the same, because, as stated in the equation above, resistance is a constant.

In first case, voltage $V_1 = 6 ~mathrm{V}$ was applied to the device and current
$I_1 = 66 ~mathrm{mA}$ was measured. Judging by the two quantities in this measurement, resistance $R_1$ measured in these conditions is:

$$
begin{align*}
R_1 &= dfrac{V_1}{I_1} \
tag{plug in the measured values} \
R_1 &= dfrac{6 ~mathrm{V} }{ 66 ~mathrm{mA} } \
tag{$1~mathrm{mA} = 1 cdot 10^{-3} ~mathrm{A} $} \
R_1 &= dfrac{6 ~mathrm{V} }{ 66 cdot 10^{-3} ~mathrm{A} }
end{align*}
$$

$$
boxed{R_1 = 90.909 ~mathrm{Omega }}
$$

In second case, voltage $V_2 = 9 ~ mathrm{V}$ was applied to the device and current
$I_2 = 75 ~mathrm{mA}$ was measured. Judging by the two quantities in this measurement, resistance $R_2$ measured in these conditions is:

$$
begin{align*}
R_2 &= dfrac{V_2}{I_2} \
tag{plug in the measured values} \
R_2 &= dfrac{9 ~ mathrm{V} }{ 75 ~mathrm{mA} } \
tag{$1~mathrm{mA} = 1 cdot 10^{-3} ~mathrm{A} $} \
R_2 &= dfrac{9 ~ mathrm{V} }{ 75 cdot 10^{-3} ~mathrm{A} }
end{align*}
$$

$$
boxed{R_2 = 120 ~mathrm{ Omega} }
$$

As we can see, resistance $R_1$ and $R_2$ measured in the two cases is not the same, which means that for this device resistance $R$ can’t be calculated by dividing the voltage $V$ applied across it with current $I$ flowing through it, which means that this lamp doesn’t obey the Ohm’s law.

$b)~~$ In this case, we are told that voltage $V$ across the lamp is $V = 6 ~mathrm{V}$ and that current $I$ flowing through it is $I = 66 ~mathrm{m A}$.
Power output $P$ of an electric component connected to voltage $V$ with current $I$ flowing through it is calculated as:

$$
begin{align*}
P_1 &= V_1 I_1 \
tag{plug in the given values} \
P_1 &= 6 ~mathrm{V} cdot 66 ~mathrm{mA} \
tag{$1~mathrm{mA} = 1 cdot 10^{-3} ~mathrm{A} $} \
P_1 &= 6 ~mathrm{V} cdot 66 cdot 10^{-3} ~mathrm{A}
end{align*}
$$

$$
boxed{ P_1 = 0.396 ~mathrm{W} }
$$

$c)~~$ In this case, we are told that voltage $V$ across the lamp is $V = 9 ~mathrm{V}$ and that current $I$ flowing through it is $I =75 ~mathrm{m A}$.
Power output $P$ of an electric component connected to voltage $V$ with current $I$ flowing through it is calculated as:

$$
begin{align*}
P_2 &= V_2 I_2 \
tag{plug in the given values} \
P_2 &= 9 ~mathrm{V} cdot 75 ~mathrm{mA} \
tag{$1~mathrm{mA} = 1 cdot 10^{-3} ~mathrm{A} $} \
P_2 &= 9 ~mathrm{V} cdot 75 cdot 10^{-3} ~mathrm{A}
end{align*}
$$

$$
boxed{ P_2= 0.675 ~mathrm{W} }
$$

$$
text{a)~~ Lamp doesn’t obey the Ohm’s law}
$$

$$
b)~~P_1 = 0.396 ~mathrm{W}
$$

$$
c)~~ P_2= 0.675 ~mathrm{W}
$$

We need to determine the amount of energy used in half an hour if the device has power of $P=60,,rm{W}$. We also need to determine the amount of energy produced in that period if only $f=12,,%$ is converted into light and the rest into heat.

First we need to determine the total energy produced in the half an hour. Power is calculated as:
$$P=frac{E}{t}$$
From this equation we can extract energy:
$$E=Pt$$

Before inserting values, we need to make sure that all units are converted into SI units:
$$t=0.5,,rm{h}=0.5cdot 3600 ,,rm{s}$$
$$t=1800,,rm{s}$$

Now we can calculate energy produced in a period of half an hour:
$$E=60cdot 1800$$
$$boxed{E=108,,rm{kJ}}$$

Now we can calculate the amount converted into thermal energy. If only $12,,%$ is converted into light, that means that:
$$f_t=1-f=1-0.12=0.88$$
is converted into heat.

Finally, calculating the amount converted into thermal energy:
$$E_t=Ecdot f_t$$
Inserting values we get:
$$E_t=108cdot 0.88$$
$$boxed{E_t=95.04,,rm{kJ}}$$

$$E=108,,rm{kJ}$$
$$E_t=95.04,,rm{kJ}$$

$a)~~$ From Ohm’s law we know that the current $I$ flowing through an electric component with resistance $R$ with voltage across the component $V$ is calculated as:

$$
I = dfrac{V}{R}
$$

In this problem we have a current $I = 0.4 ~mathrm{A}$ flowing through a lamp with unknown resistance of $R$ with voltage $V = 120 ~mathrm{V}$ across it.
Current $I$ through the sensor circuit is calculated as:

$$
begin{align*}
I &= dfrac{V}{R} \
tag{express $R$ from the equation above} \
R &= dfrac{V}{I} \
tag{plug in the given values} \
R &= dfrac{120 ~mathrm{V} }{0.4 ~mathrm{A}}
end{align*}
$$

$$
boxed{ R = 300 ~mathrm{Omega} }
$$

$b)~~$ We’re told that when lamp is cold, its resistance is five times lower than its resistance when its hot. To find the lamps cold resistance $R_{cold}$, we’ll divide its hot resistance $R$ calculated above with 5

$$
begin{align*}
R_{cold} &= dfrac{R}{5 } \
tag{plug in the given values}\
R_{cold} &= dfrac{300 ~mathrm{Omega }}{5}
end{align*}
$$

$$
boxed{ R_{cold} = 60 ~mathrm{Omega } }
$$

$c)~~$ For a moment after the lamp was turned on and not yet hot, its resistance is $R_{cold}$ (calculated above) and if we apply voltage of $V = 120 ~mathrm{V}$ across it, its cold current $I_{cold}$ can be calculated by applying the Ohm’s law to this situation:

$$
begin{align*}
I_{cold} &= dfrac{V}{R_{cold}} \
tag{plug in the given values} \
I_{cold} &= dfrac{ 120 ~mathrm{V} }{60 ~mathrm{Omega } }
end{align*}
$$

$$
boxed{ I_{cold} = 2 ~mathrm{A } }
$$

$$
begin{align*}
&a)~~ R = 300 ~mathrm{Omega} \
&b)~~ R_{cold} = 60 ~mathrm{Omega } \
&c)~~ I_{cold} = 2 ~mathrm{A }
end{align*}
$$

In this problem we’re given a graph that shows how current $I$ through the diode depends on the voltage $V$ applied across it.

$a)~~$ If we apply a potential difference (Voltage) of $V_1 = 0.7 ~mathrm{V}$ across the diode, as we can see when we read the corresponding current from the graph, a current of $I_1 = 0.02 ~mathrm{A}$ flows through the diode. To find the resistance of the diode in this situation, we’ll apply the Ohm’s law which states that the current $I$ through an electric device with resistance $R$ connected to voltage $V$ is calculated as:

$$
begin{align*}
I &= dfrac{V }{R} \
tag{If we apply the Ohm’s law to this situation, we have:} \
I_1 &= dfrac{V_1}{R_1} \
tag{express $R_1$ from the equation above } \
R_1 &= dfrac{V_1}{I_1} \
tag{plug in the given values} \
R_1 &= dfrac{ 0.7 ~mathrm{V} }{0.02 ~mathrm{A} }
end{align*}
$$

$$
boxed{ R_1 = 35 ~mathrm{Omega } }
$$

$b)~~$ If we apply a potential difference (Voltage) of $V_2 = 0.6 ~mathrm{V}$ across the diode, as we can see when we read the corresponding current from the graph, a current of $I_2 = 0.006 ~mathrm{A}$ flows through the diode. To find the resistance of the diode in this situation, we’ll apply the Ohm’s law which states that the current $I$ through an electric device with resistance $R$ connected to voltage $V$ is calculated as:

$$
begin{align*}
I &= dfrac{V }{R} \
tag{If we apply the Ohm’s law to this situation, we have:} \
I_2 &= dfrac{V_2}{R_2} \
tag{express $R_2$ from the equation above } \
R_2 &= dfrac{V_2}{I_2} \
tag{plug in the given values} \
R_2 &= dfrac{ 0.6 ~mathrm{V} }{0.006 ~mathrm{A} }
end{align*}
$$

$$
boxed{ R_2 = 100 ~mathrm{Omega } }
$$

$c)~~$ From the graph we can see that the ratio of voltage $V$ and current $I$ is not a constant. If this ratio was a constant, diode would behave like an ohmic resistor and we could apply the Ohm’s law on it. However, as we can see from both the graph and the two results above, Ohm’s law can’t be applied to the diode because its resistance is not a constant, but rather depends on the voltage across it. In other words, current $I$ flowing through the diode is not proportional to the voltage $V$ across it and current $I$ grows exponentially with an increase in voltage. All of this is only possible if diode doesn’t obey the Ohm’s law.

$$
a)~~ R_1 = 35 ~mathrm{Omega }
$$

$$
b)~~ R_2 = 100 ~mathrm{Omega }
$$

$$
c)~~ text{ Hint: Current $I$ grows exponentially with voltage $V$ }
$$

In this problem we must draw a circuit diagram that consists of a battery with voltage $V = 90 ~mathrm{V}$, a resistor with resistance $R = 45 ~mathrm{Omega}$ and an ammeter to measure the current $I$ flowing in the circuit. We must also indicate the reading on the ammeter and direction of the current flowing through the circuit.

This is the simplest circuit, consisting of just a voltage source (battery) and a resistor connected to it in series. This means that the whole circuit is just one loop with one current $I$ flowing in the circuit. Direction of the current $I$ is from positive to a negative terminal of the battery, while magnitude of this current can be calculated by using the Ohm’s law which states that the current $I$ flowing through a resistor $R$ with voltage $V$ across it can be calculated as:

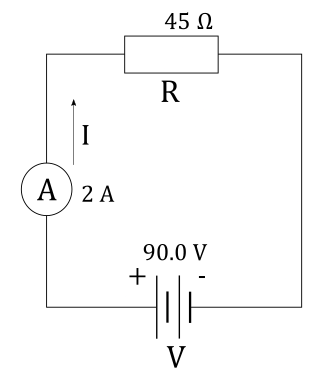
$$
begin{align*}
I &= dfrac{V}{R} \
tag{plug in the values} \
I &= dfrac{90 ~mathrm{V}}{45 ~mathrm{Omega}} \
I &= 2 ~mathrm{A}
end{align*}
$$

Since this is a series circuit, this same current will flow through the whole circuit and reading on the ammeter will show this current. The end result of the circuit diagram is shown in the figure below, where current flows clockwise in order for it to flow from the positive terminal of the battery to negative terminal of the battery.

We’re told that a $V = 9 ~mathrm{V}$ battery costs $Cost = 3 ~mathrm{$}$ and that it supplies $I = 0.025 ~mathrm{A}$ for $t = 26 ~mathrm{h}$ before it runs out of power. To find the $C_{per~kWh}$, its cost per kWh , we’ll divide the total cost of the battery ($3 ~mathrm{$}$) with the total energy $E$ supplied from the battery.

Total energy $E$ supplied from the battery is found as a product of voltage $V$ across its terminals, current $I$ supplied from it and time $t$ that it takes to “empty” the battery, stated as:

$$
begin{align*}
E &= I V t \
tag{plug in the given values} \
E &= 0.025 ~mathrm{A} cdot 9 ~mathrm{V} cdot 26 ~mathrm{h} \
E &= 5.85 ~mathrm{Wh} \
tag{ $ 1 ~mathrm{Wh = 10^{-3} ~mathrm{kWh}}$} \
E &= 5.85 cdot 10^{-3} ~mathrm{kWh}
end{align*}
$$

We found that the total energy stored in the battery, expressed in $~mathrm{kWh}$ is
$E = 5.85 cdot 10^{-3} ~mathrm{kWh}$
Now that we know how much energy is supplied from one battery, to find cost per kWh using the batteries, we’ll divide the cost of one battery with energy stored on it:

$$
begin{align*}
C_{per~kWh} &= dfrac{Cost}{E} \
tag{plug in the values} \
C_{per~kWh} &= dfrac{3 ~mathrm{$} }{5.85 cdot 10^{-3} ~mathrm{kWh}}
end{align*}
$$

$$
boxed{ C_{per~kWh} = 512.82 ~mathrm{dfrac{$}{kWh}} }
$$

$$
C_{per~kWh} = 512.82 ~mathrm{dfrac{$}{kWh}}
$$

We need to determine the maximum current allowed in a resistor with resistance of $R=220,,rm{Omega }$ and a power rating of $P=5,,rm{W}$

First step is writing down equation that combines power, current and resistance:
$$P=I^2R$$

From the previous equation we need to extract current:
$$I^2=frac{P}{R}$$
$$I=sqrt{frac{P}{R}}$$

Now we can insert given valeus:
$$I=sqrt{frac{5}{220}}$$
Finally:
$$boxed{I=0.151,,rm{A}}$$

$$I=0.151,,rm{A}$$

We need to determine the amount of thermal energy developed in an hour by a device that works on a voltage of $V=110,,rm{V}$ and a current of $I=3,,rm{A}$.

First we need to calculate the power of this device using the next equation:
$$P=VI$$

We can directily insert values to get:
$$P=110cdot 3$$
$$P=330,,rm{W}$$

With power and period known we can now calculate the amount of thermal energy produced:
$$P=frac{E}{t}$$

From the previous equation we can extract energy:
$$E=Pt$$

Finally we can insert values in SI units, which means that the period is:
$$t=1,,rm{h}=3600,,rm{s}$$
$$E=330cdot 3600$$
$$boxed{E=1.188,,rm{MJ}}$$

$$E=1.188,,rm{MJ}$$

$a)~~$ We’re told that the maximum safe power is $P_{max}= 50 ~mathrm{W}$. On the figure we see a resistor and its resistance is $R = 40 ~mathrm{ ~Omega }$.
If we apply the maximum safe current $I_{max}$ through the circuit, power output on the resistor $R$ will be equal to its maximum safe power $P _{max}$ given above. This power $P _{max}$ can be calculated as:

$$
P_{max}= I_{max}^2 R
$$

We can express $I_{max}$ from the equation above as:

$$
begin{align*}
I_{max}^2 &= dfrac{P_{max}}{R} \
tag{find square root of the equation} \
I_{max}&= sqrt{dfrac{P_{max}}{R}} \
tag{plug in the given values} \
I_{max}&= sqrt{dfrac{ 50 ~mathrm{W} }{40 ~mathrm{ ~Omega }}} \
I_{max}&= sqrt{1.25 ~mathrm{A^2}}
end{align*}
$$

$$
boxed{ I_{max}= 1.118 ~mathrm{A} }
$$

$b)~~$ When maximum safe current $I _{max}$ is applied, voltage across the resistor and the battery is equal to its maximum safe value $V _{max}$, which can be calculated from the Ohm’s law. We know that the current $I$ flowing through a resistor with resistance $R$ and voltage $V$ across it is equal to:

$$
I = dfrac{V}{R}
$$

If we apply the Ohm’s law to the situation with maximum current $I _{max}$ flowing through the circuit, we have:

$$
begin{align*}
I _{max} &= dfrac{V _{max}}{R} \
tag{express $V _{max}$ from the equation above} \
V _{max} &= R I _{max} \
tag{plug in the given values} \
V _{max} &= 40 ~mathrm{ ~Omega } cdot 1.118 ~mathrm{A}
end{align*}
$$

$$
boxed{ V _{max} = 44.72 ~mathrm{V} }
$$

$$
begin{align*}
I_{max} &= 1.118 ~mathrm{A} \
V _{max} &= 44.72 ~mathrm{V}
end{align*}
$$

As we can see from the figure in the problem text, voltage across the electric furnace is $V = 240 ~mathrm{V}$ and its resistance is $R = 4.8 ~mathrm{Omega }$. We’re told that cost of electricity power $mathrm{kWh}$ is $C_{per~kWh} = 0.1 ~mathrm{dfrac{$}{kWh} }$ and that thermostat was on for one fourth of the whole month (30 days). Of course, this time also represents the time $t$ that furnace was on and converted electric energy to heat. As said, this time interval is equal to 1 fourth of the month, which equals:

$$
begin{align*}
t &= dfrac{1}{4} ~mathrm{month} \
tag{$mathrm{1 ~month = ~30 days}$} \
t &= dfrac{1}{4} cdot 30 ~mathrm{days} \
tag{$ mathrm{1 ~day = ~ 24 h }$} \
t &= dfrac{1}{4} cdot 30 cdot 24 ~mathrm{h}
end{align*}
$$

$$
boxed{ t = 180 ~mathrm{h} }
$$

The reason why we calculated this time interval in $mathrm{h}$ is because when we pay the electric bill, we’re actually paying for the used electric energy, express in $mathrm{kWh}$.

Now that we know for how long did the electric furnace use electric energy over a period of one month, we must find the rate at which electric furnace transforms electric energy to heat, which is its power $P$. We can calculate the power output of the furnace as:

$$
begin{align*}
P &= dfrac{V^2}{R} \
tag{plug in the given values} \
P &= dfrac{(240 ~mathrm{V} )^2}{4.8 ~mathrm{Omega }} \
P &= dfrac{57600 ~mathrm{V^2} }{4.8 ~mathrm{Omega }} \
P &= 12000 ~mathrm{W}
end{align*}
$$

$$
boxed{ P = 12 ~mathrm{kW} }
$$

The reason why we converted the power output $P$ from Watts to kilowatts is due to a fact that when we pay the electric bill, energy is expressed in kilowatt-hours ($mathrm{kWh}$), which means that power $P$ should be expressed in kilowatts and time $t$ should be expressed in hours.

Now that we have a power output $P$ of the furnace and time interval $t$ that the furnace was on and used electric energy $E$ that we must pay, to calculate this energy $E$, we’ll multiply power output $P$ of the furnace with the calculated time interval $t$:

$$
begin{align*}
E &= P t \
tag{plug in the calculated values for $P$ and $t$} \
E &= 12 ~mathrm{kW} cdot 180 ~mathrm{h}
end{align*}
$$

$$
boxed{ E = 2160 ~mathrm{kWh} }
$$

We’ve found the total energy used by the electric furnace in the given time period, expressed in $mathrm{kWh}$ . This is the electric energy that we must pay on our bill. Knowing that price per 1 $mathrm{kWh}$ is $C_{per~kWh} = 0.1 ~mathrm{dfrac{$}{kWh} }$, we find that the total cost $C_{month}$, per month, to use this electric furnace and keep it on for one fourth of a month is equal to a product of the energy $E$ used by the furnace and cost $C_{per~kWh}$ per $mathrm{kWh}$, stated as:

$$
begin{align*}
C_{month} &= E cdot C_{per~kWh} \
tag{plug in the values} \
C_{month} &= 2160 ~mathrm{kWh} cdot 0.1 ~mathrm{dfrac{$}{kWh} }
end{align*}
$$

$$
boxed{C_{month} = 216 ~ $ }
$$

$$
C_{month} = 216 ~ $
$$

Current $I$ that air conditioner will draw from a $V = 120 ~mathrm{V}$ outlet, can be calculated from power $P$ needed for its operation because this power can be found as a product of voltage $V$ across the air conditioner and current $I$ flowing through it, stated as:

$$
P = VI
$$

We are told that the total cost $C_t$ of operating an air conditioner is
$C_t = 50 ~ $$ per 30 days if it runs half of the total time and cost of electricity per one $mathrm{kWh}$ is
$C_p = 0.09 ~mathrm{dfrac{$ }{kWh}}$.
Since we know the total cost of the energy used by the air conditioner $C_t$ and know the cost of electricity per one $mathrm{kWh}$, we can calculate the total energy $E$ used by the air conditioner in a given time interval. Knowing that the total cost of the used energy $C_t$ is equal to a product of energy used by the air conditioner $E$ (expressed in kilowatt-hours) and cost $C_p$ per one kilowatt-hours, we find that the energy $E$ is equal to:

$$
begin{align*}
C_t &= E C_p \
tag{express $E$ from the equation above} \
E &= dfrac{C_t}{C_p} \
tag{plug in the given values} \
E &= dfrac{50 ~ $ }{ 0.09 ~mathrm{dfrac{$ }{kWh}} }
end{align*}
$$

$$
boxed{ E = 555.5555 ~mathrm{kWh} }
$$

Now that we know how much energy $E$ is used by the air conditioner in this time period $t$, equal to half a month, we can find power $P$ needed for the operation of air conditioner from the definition of power, which states that power $P$ is equal to energy $E$ used by the device in time interval $t$, stated as:

$$
P = dfrac{E}{t}
$$

Notice that we aren’t given the time period $t$ explicitly, but we are told that this energy $E$, calculated above, is used by air conditioner in half a month, which means that this time interval $t$ is equal to:

$$
begin{align*}
t &= dfrac{1}{2} ~mathrm{month} \
tag{$mathrm{1 ~month = ~30 days}$} \
t &= dfrac{1}{2} cdot 30 ~mathrm{days} \
tag{$ mathrm{1 ~day = ~ 24 h }$} \
t &= dfrac{1}{2} cdot 30 cdot 24 ~mathrm{h}
end{align*}
$$

$$
boxed{ t = 360 ~mathrm{h} }
$$

This means that power $P$ used by the air conditioner is equal to:

$$
begin{align*}
P &= dfrac{E}{t} \
tag{plug in the calculated values for $E$ and $t$} \
P &= dfrac{ 555.5555 ~mathrm{kWh} }{ 360 ~mathrm{h} } \
P &= 1.54321 ~mathrm{kW}
end{align*}
$$

$$
boxed{ P = 1543.21 ~mathrm{W} }
$$

Now that we have power $P$ needed for operation of the air conditioner, we can calculate current $I$ drawn from a $V = 120 ~mathrm{V}$ outlet from the first equation in the solution:

$$
begin{align*}
P &= V I \
tag{express $I$ from the equation above} \
I &= dfrac{P}{V} \
tag{plug in the calculated value of $P$ and given value of $V$} \
I &= dfrac{ 1543.21 ~mathrm{W} }{ 120 ~mathrm{V}}
end{align*}
$$

$$
boxed{ I = 12.86 ~mathrm{A}}
$$

$$
I = 12.86 ~mathrm{A}
$$

In this problem we have a radio operating at a voltage $V = 9 ~mathrm{V}$ and current of $I = 50 ~mathrm{mA}$. To make any calculation on how much it costs to have this radio run for any time interval $t$, we first need to determine the power $P$ needed for its operation. We find that this power is equal to:

$$
begin{align*}
P &= V I \
P &= 9 ~mathrm{V} cdot 50 ~mathrm{mA} \
tag{$1 ~mathrm{mA} = 1 cdot 10^{-3} ~mathrm{A}$} \
P &= 9 ~mathrm{V} cdot 50 cdot 10^{-3} ~mathrm{A} \
P &= 450 cdot 10^{-3} ~mathrm{W} \
P &= 0.45 ~mathrm{W} \
tag{express power $P$ in kilowatts} \
tag{$mathrm{1 ~ W = 10^{-3} ~kW }$}\
P &= 0.45 cdot 10^{-3} ~mathrm{kW}
end{align*}
$$

$a)~~$ In this part of the problem we used a battery which cost us $C_{battery} = 2.49 $$. This battery can supply the radio for $t_{battery} = 300 ~mathrm{h}$. To calculate the cost $C_{kWh,~ battery}$ per kilowatt-hour by using the battery, we need to divide the total cost $C_{battery}$ of the battery with total energy $E_{battery}$ that we can supply from the battery. Energy supplied from the battery will be equal to a product of power $P$ needed for the operation of the radio and time $t_{battery}$ that battery can supply the radio before it runs out of power, stated as:

$$
begin{align*}
E_{battery} &= P t_{battery} \
tag{plug in the given values} \
E_{battery} &= 0.45 cdot 10^{-3} ~mathrm{kW} cdot 300 ~mathrm{h} \
E_{battery} &= 0.135 ~mathrm{kWh}
end{align*}
$$

As we can see, battery can supply $0.135 ~mathrm{kWh}$ of energy before it runs out of power. If we divide the cost $C_{battery}$ for one battery with the total energy $E_{battery}$ supplied from it, we’ll find the cost $C_{kWh,~ battery}$ per kilowatt-hour when we use the battery:

$$
begin{align*}
C_{kWh,~ battery} &= dfrac{C_{battery}}{E_{battery}} \
C_{kWh,~ battery} &= dfrac{ 2.49 $ }{0.135 ~mathrm{kWh}}
end{align*}
$$

$$
boxed{ C_{kWh,~ battery} = 18.4444 ~mathrm{dfrac{$ }{kWh}} }
$$

$b)~~$ We now plugged in this radio to a household circuit, where price per kilowatt-hour of electric energy is $C_{kWh,~household} = 0.12 ~mathrm{dfrac{$}{kWh}}$. To calculate the cost of having the radio on for the same time interval as in the previous case, the $t = 300 ~mathrm{h}$, we first need to notice that we’ve already calculated the energy used by the radio in this time interval and it’s equal to $E = 0.135 ~mathrm{kWh}$. The difference between this case and the previous case is in the fact that electric power per one kilowatt-hour is much cheaper and equals $C_{kWh,~household}$. To find the total cost $C_{total}$ of the electric energy used by the radio when it runs for the given time period of $t$, we need to understand that this cost will be equal to a product of the total energy $E$ used by the radio in this time interval (expressed in $mathrm{kWh}$) and cost $C_{kWh,~household}$ per one kilowatt-hour of energy, stated as:

$$
begin{align*}
C_{total} &= E C_{kWh,~household} \
tag{plug in the given values} \
C_{total} &= 0.135 ~mathrm{kWh} cdot 0.12 ~mathrm{dfrac{$}{kWh}} \
C_{total} &= 1.62 cdot 10^{-2} ~mathrm{$ }
end{align*}
$$

$$
boxed{ C_{total} = 0.0162 $ }
$$

$$
begin{align*}
&a)~~ C_{kWh,~ battery} = 18.4444 ~mathrm{dfrac{$ }{kWh}} \
&b)~~ C_{total} = 0.0162 $
end{align*}
$$

In this problem we have a stereo with power $P = 200 ~mathrm{W}$ needed for it to operate.
A person wonders how long could the stereo run before it uses enough electric energy $E$ to add up $5$$ to the electric bill, if cost for one $mathrm{kWh}$ of electric energy is $C_p = 0.15 ~mathrm{dfrac{$}{kWh}}$.

In other words, we want to know how much time $t$ will pass until this stereo “spends” a budget of $B = 5 ~mathrm{$ }$.

First, let’s notice that the total cost $C_t$ we need to pay for electric energy is equal to a product of energy $E$ we used (expressed in $mathrm{kWh}$) and cost $C_p$ per one kilowatt-hour, stated as:

$$
C_t = E C_p
$$

Notice that in our case, we know $C_t$ and this is the amount we want to spend, which is $C_t = B = 5 $$. We can calculate the total used energy $E$ from this conclusion and the equation above as:

$$
begin{align*}
C_t &= E C_p \
tag{$B = C_t$} \
B &= E C_p \
tag{express $E$ from the equation above } \
E &= dfrac{B}{C_p} \
E &= dfrac{5 $ }{ 0.15 ~mathrm{dfrac{$}{kWh}} } \
E &= 33.3333 ~mathrm{kWh}
end{align*}
$$

The reason why we calculate the total used energy $E$ is because this total used energy is equal to a product of power rating of the stereo $P = 200 ~mathrm{W}$ given above and time interval $t$ that it took the stereo to use this energy. In other words:

$$
begin{align*}
E &= P t \
tag{express $t$ from the equation above} \
t &= dfrac{E}{P} \
t &= dfrac{ 33.3333 ~mathrm{kWh} }{200 ~mathrm{W}} \
tag{ $ 1 ~mathrm{kWh} = 1000 ~mathrm{Wh} $} \
t &= dfrac{ 33.3333 cdot 1000 ~mathrm{Wh} }{200 W }
end{align*}
$$

$$
boxed{t = 166.6667 ~mathrm{h}}
$$

$$
t = 166.6667 ~mathrm{h}
$$

We need to determine the amount of heat generated if a current of $I=1.2,,rm{A}$ flows through a resistor with resistance of $R=50,,rm{Omega}$ for a period of $t=5,,rm{min}$.

In order to calculate the energy we need power of the device and the time it has been working:
$$E=Pt$$

In order to calculate power, we can use already known equation derived from a equation for power and Ohm’s Law:
$$P=I^2R$$

Combining two previous equations we can get:
$$E=I^2Rt$$

Inserting values in SI units, where $t$ is:
$$t=5cdot 60=300,,rm{s}$$
We get:
$$E=1.2^2cdot 50cdot 300$$
Finally, heat generated is:
$$boxed{E=21600,,rm{J}}$$

$$E=21600,,rm{J}$$

$a)~~$ From Ohm’s law we know that the current $I$ flowing through a resistor with resistance $R$ with voltage $V$ across it is calculated as:

$$
I = dfrac{V}{R}
$$

In this problem we have a resistor with resistance of $R = 6 ~mathrm{Omega}$ with voltage $V = 15 ~mathrm{V}$ across it. Current $I$ through the resistor is calculated as:

$$
begin{align*}
I &= dfrac{V}{R} \
tag{plug in the given values} \
I &= dfrac{ 15 ~mathrm{V} }{ 6 ~mathrm{Omega}}
end{align*}
$$

$$
boxed{ I = 2.5 ~mathrm{A} }
$$

$$
b)~~
$$

Energy $E$ delivered in time $t$ to the resistor in the circuit with power output $P$ can be found from the definition of power, which states that power $P$ is energy $E$ delivered in time interval $t$, stated as:

$$
begin{align*}
P &= dfrac{E}{t} \
tag{express $E$ from the equation above} \
E &= P t \
tag{power $P$ is equal to $P = VI $} \
E &= V I t \
tag{plug in the given values} \
E &= 15 ~mathrm{V} cdot 2.5 ~mathrm{A} cdot 10 ~mathrm{min} \
tag{$1 ~mathrm{min} = 60 ~mathrm{s}$} \
E &= 15 ~mathrm{V} cdot 2.5 ~mathrm{A} cdot 10 cdot 60 ~mathrm{s}
end{align*}
$$

$$
boxed{ E = 22500 ~mathrm{J} }
$$

$$
begin{align*}
& a)~~ I = 2.5 ~mathrm{A} \
& b) ~~ E = 22500 ~mathrm{J}
end{align*}
$$

$a)~~$ We are told that the resistance of the light bulb is lit is $R_{lit} = 40 ~mathrm{Omega}$ and in either case, voltage applied across the light bulb is $V = 120 ~mathrm{V}$.
From Ohm’s law we know that the current $I_{lit}$ flowing through the light bulb when it’s lit , has resistance $R_{lit}$ and it’s connected to voltage $V = 120 ~mathrm{V}$ is calculated as:

$$
begin{align*}
I_{lit} &= dfrac{V}{R_{lit}} \
tag{plug in the given values} \
I_{lit} &= dfrac{ 120 ~mathrm{V} }{ 40 ~mathrm{Omega}}
end{align*}
$$

$$
boxed{ I_{lit} = 3~mathrm{A} }
$$

$b)~~$ We are told that the resistance of the light bulb when it’s not lit is $R_{not~lit} = 10 ~mathrm{Omega}$ and in either case, voltage applied across the light bulb is $V = 120 ~mathrm{V}$.
From Ohm’s law we know that the current $I_{not~lit}$ flowing through the light bulb when it’s not lit, has resistance $R_{not~lit}$ and it’s connected to voltage $V = 120 ~mathrm{V}$ is calculated as:

$$
begin{align*}
I_{not~lit} &= dfrac{V}{R_{not~lit}} \
tag{plug in the given values} \
I_{not~lit} &= dfrac{ 120 ~mathrm{V} }{ 10 ~mathrm{Omega}}
end{align*}
$$

$$
boxed{ I_{not~lit} = 12 ~mathrm{A} }
$$

$c)~~$ Resistance $R_{not~lit}$ of the light bulb is resistance of the light bulb when it’s off and for a brief period of time after we turn it on, until it almost instantaneously increases to $R_{lit}$. When light bulb is off and current through it is zero, power of the light bulb is zero because power is proportional to the current and there is no current. When we turn the light bulb on, it quickly heats up and with an increase in temperature of the filament, resistance increases to $R_{lit}$ and current flowing through it is more or less constant. Now that there is current $I_{lit}$ flowing through the light bulb with voltage $V$ across it, we can calculate its power rating $P$ as:

$$
P = P_{lit} = V I_{lit} = 120 ~mathrm{V} cdot 3~mathrm{A} = 360 ~mathrm{W}
$$

However, if we take a look at power of the light bulb, just at the moment when we turn it $P_{just~on}$, we’ll prove that it’s greater than its power rating.
Power needed $P_{just~on}$ to turn the light bulb on is equal to a product of current $I_{not~lit}$ flowing through it just when it’s turned on, calculated above and voltage across the light bulb:

$$
P_{just~on} = V I_{not~lit} = 120 ~mathrm{V} cdot 10 ~mathrm{A} = 1200 ~mathrm{W}
$$

As we can see, light bulb uses more power just when it’s turned on than it uses when when its filament is already heated up.

$$
a)~~ I_{lit} = 3~mathrm{A}
$$

$$
b)~~ I_{not~lit} = 12 ~mathrm{A}
$$

$$
c)~~ text{ Light bulb uses more power just at the moment when it’s turned on }
$$

We need to determine the range of potentiometer if the device that has a voltage of $V=12,,rm{V}$ uses current that ranges from $I_1=0.02,,rm{A}$ to $I_2=1.2,,rm{A}$

In order to calculate the range of potentiometer, which is expressed as resistance, we need to use Ohm’s Law:
$$R=frac{V}{I}$$

In this problem, we will determine the range by using minimum and maximum values of current:
$$R_{min}=frac{V}{I_2}$$
$$R_{max}=frac{V}{I_1}$$

Inserting given values we get lower limit:
$$R_{min}=frac{12}{1.2}$$
$$boxed{R_{min}=10,,rm{Omega}}$$
And upper limit:
$$R_{max}=frac{12}{0.02}$$
$$boxed{R_{max}=600,,rm{Omega}}$$

$$R_{min}=10,,rm{Omega}$$
$$R_{max}=600,,rm{Omega}$$

We are told that each hour ($t = 1 ~mathrm{h}$), a volume of
$V_0 = 1 cdot 10^4 ~mathrm{L}$ of water is pumped to a vertical distance of
$h = 8 ~mathrm{m}$ to irrigate the crops. We’re also told that motor on the pump has resistance of $R = 22 ~mathrm{Omega }$ and voltage across the pump is
$Delta V = 110 ~mathrm{V}$.

$a)~~$ We’ll apply Ohm’s law to calculate the current $I$ flowing through the pump. Ohm’s law states that current $I$ flowing through a device with resistance $R$ and voltage $V$ across it is calculated as:

$$
begin{align*}
I &= dfrac{Delta V}{R} \
tag{plug in the given values} \
I &= dfrac{ 110 ~mathrm{V} }{22 ~mathrm{Omega } }
end{align*}
$$

$$
boxed{ I = 5 ~mathrm{A} }
$$

$b)~~$ To find the efficiency $e$ of the motor, we essentially need to find the ratio between the useful part of the energy $E_w$ used to pump the water and total electric energy $E_e$ supplied to the pump.

Electric energy $E_e$ supplied to the pump in one hour is equal to a product of its electric power $P_e$ and time $t = 1 ~mathrm{h}$, stated as:

$$
begin{align*}
E_e &= P_e t \
tag{electric power is equal to $P_e = I V $} \
E_e &= I Delta V t \
tag{plug in the given values} \
E_e &= 110 ~mathrm{V} cdot 5 ~mathrm{A} cdot 1 ~mathrm{h} \
tag{$1~mathrm{h} = 3600 ~mathrm{s} $} \
E_e &= 550 ~mathrm{W} cdot 3600 ~mathrm{s} \
E_e &= 1.98 cdot 10^6 ~mathrm{J}
end{align*}
$$

We found the electric energy $E_e$ supplied to the pump in an hour. Now we must find the total energy $E_p$ used to pump the water in one hour. This energy will be equal to change in the gravitational potential energy of water. Gravitational potential energy of an object is given as:

$$
E_g = m g h
$$

where $m$ is mass of an object, $g = 9.81 ~mathrm{dfrac{m}{s^2}}$ is gravitational acceleration and $h$ is vertical distance at which an object is compared to some referent level. Note that mass $m$ of water can be expressed as a product of its density
$rho = 1000 ~mathrm{dfrac{kg}{m^3}}$ and volume $V$ of water, stated as:

$$
m = rho V
$$

Vertical distance $h$ in the equation for gravitational potential energy is actually the height $h$ to which the water is pumped to irrigate the crops. We see that the energy used to irrigate the crops $E_p$ will be equal to the change in gravitational potential energy:

$$
begin{align*}
E_p &= Delta E_g \
tag{change in the gravitational potential energy is $mg(h-h_0)$} \
E_p &= mg h – mgh_0 \
tag{$h_0$ is arbitrary referent level, which we can take as 0} \
E_p &= mg h \
tag{plug in $m = rho V$} \
E_p &= rho V g h
end{align*}
$$

Now that we have an expression for energy used to pump the water $E_p$, we can calculate it keeping it in mind that since we’ll compare the result of this calculation to the electric energy supplied to the pump in one hour, we must also calculate energy used to pump the water in one hour. Given value $V_0 = 1 cdot 10^4 ~mathrm{L} = 10 ~mathrm{m^3}$ represents the volume of water pumped in one hour and out of all the three quantities in $E_p$, only volume of the pumped water depends on a given time interval. This means that if we were to plug in this value into the equation for $E_p$ above, we’d calculate the energy used to pump the water in one hour:

$$
begin{align*}
E_{p, hour} &= rho V_0 gh \
E_{p, hour} &= 1000 ~mathrm{dfrac{kg}{m^3}} cdot 10 ~mathrm{m^3} cdot 9.81 ~mathrm{dfrac{m}{s^2}} cdot 8 ~mathrm{m} \
E_{p, hour} &= 78.48 cdot 10^4 ~mathrm{J}
end{align*}
$$

Efficiency $e$ of the pump is calculated as:

$$
begin{align*}
e &= dfrac{ E_{p, hour} }{E_e} \
tag{plug in the calculated values} \
e &= dfrac{ 78.48 cdot 10^4 ~mathrm{J} }{ 1.98 cdot 10^6 ~mathrm{J} } \
e &= 0.396363
end{align*}
$$

We can express the efficiency $e$ from the equation above as:

$$
boxed{ e = 39.6363 ~% }
$$

$$
begin{align*}
&a)~~ I = 5 ~mathrm{A} \
&b)~~ e = 39.6363 ~%
end{align*}
$$

$a)~~$ In this problem we have a heating coil with resistance $R = 4 ~mathrm{Omega }$ and voltage $V = 120 ~mathrm{V}$ across it. We can find current $I$ flowing through the coil from Ohm’s law, which states that the current $I$ flowing through a device with resistance $R$ and voltage $V$ across it is equal to:

$$
begin{align*}
I &= dfrac{V}{R} \
tag{plug in the given values} \
I &= dfrac{120 ~mathrm{V} }{ 4 ~mathrm{Omega }}
end{align*}
$$

$$
boxed{ I = 30 ~mathrm{A} }
$$

$b)~~$ Energy $E$ supplied to the circuit with power rating $P$ during the time $t$ is given as:

$$
E = P t
$$

Notice that we aren’t given the power rating $P$ of this heating coil but we can calculate it as a product of voltage $V$ across the coil and current $I$ flowing through it, stated as:

$$
P = VI
$$

We can plug in this expression for power into the equation above and calculate energy $E$ supplied to the coil during time $t = 5 ~mathrm{min}$ as:

$$
begin{align*}
E &= P t \
E &= VI t \
tag{plug in the values} \
E &= 120 ~mathrm{V} cdot 30 ~mathrm{A} cdot 5 ~mathrm{min} \
tag{$1 ~mathrm{min } = 60 ~mathrm{s} $} \
E &= 3600 ~mathrm{W} cdot 5 cdot 60 ~mathrm{s} \
E &= 1 080 000 ~mathrm{J} \
E &= 1.08 cdot 10^6 ~mathrm{J}
end{align*}
$$

$$
boxed{ E = 1.08 ~mathrm{MJ} }
$$

$c)~~$ In this part of the problem we’ve put this heating coil into the water, left it on for the same time interval of $t = 5 ~mathrm{min}$ and we must find the temperature change $Delta T$ of $m = 20 ~mathrm{kg}$ of water, assuming that all of the electric energy supplied to the heating coil is absorbed by water. We’ve already calculated energy $E$ supplied by the heating coil above and since all of the energy supplied to the coil is also absorbed by the water as heat, we conclude that heat $Q$ is equal to $E$, stated as:

$$
Q = E
$$

Heat $Q$ needed to increase the temperature $T$ of the substance by $Delta T$ is given as:

$$
Q = m c Delta T
$$

where $m$ is mass of the substance and $c$ is specific heat capacity of the substance. In this case, since we heat up water, we’ll use heat capacity of water

$$
c_{water} = 4200 ~mathrm{dfrac{J}{kg K}}
$$

This means that calculated energy $E$ is equal to:

$$
begin{align*}
E &= Q \
tag{use $Q = m c Delta T $} \
E &= m c Delta T \
tag{express $Delta T$ from the equation above} \
Delta T &= dfrac{E}{mc} \
tag{plug in the values} \
Delta T &= dfrac{ 1.08 cdot 10^6 ~mathrm{J} }{20 ~mathrm{kg} cdot 4200 ~mathrm{dfrac{J}{kg K}} } \
Delta T &= 12.8571 ~mathrm{K}
end{align*}
$$

Note that the change of temperature expressed in Kelvins $mathrm{K}$ is equal to the change of temperature expressed in degrees Celsius $mathrm{^circ C}$, which is why we can express the change of temperature as:

$$
boxed{ Delta T = 12.8571 ~mathrm{^circ C} }
$$

$d)~~$ To find the total cost $C_{total}$ for operating a device with power rating $P$ over a time period $t$, we multiply this time interval $t$, power rating of the device $P$ and cost per kilowatt-hour $C_{per~kWh}$, stated as:

$$
C_{total} = P t C_{per~kWh}
$$

In our case, cost of electric energy per one kilowatt-hour is
$C_{per~kWh} = 0.08 ~mathrm{dfrac{~$}{kWh}}$. Power rating of the heating coil is, as said in part $a)$, equal to a product of voltage $V$ across it and current $I$ flowing through the coil

$$
P = IV
$$

To find the total cost of operating a heating coil for the time interval mentioned in the problem text, we must first express this time interval in hours. If heating coil is on for $30 ~mathrm{min}$ for $30 ~mathrm{days}$, this means that over a whole month, time interval $t$ that the heating coil was on is:

$$
begin{align*}
t &= 30 cdot 30 ~mathrm{min} \
t &= 900 ~mathrm{min} \
tag{$ dfrac{1}{60} ~mathrm{h} = 1 ~mathrm{min}$} \
t &= 900 dfrac{1}{60} ~mathrm{h} \
t &= 15 ~mathrm{h}
end{align*}
$$

We found that heating coil was on for $15 ~mathrm{h}$ a month. We can now calculate the cost of electric energy used by the heating coil over a month as:

$$
begin{align*}
C_{total} = P t C_{per~kWh} \
tag{plug in $P = IV $} \
C_{total} &= IV t C_{per~kWh} \
tag{plug in the calculated values} \
C_{total} &= 30 ~mathrm{A} cdot 120 ~mathrm{V} cdot 15 ~mathrm{h} cdot 0.08 ~mathrm{dfrac{~$}{kWh}} \
C_{total} &= 54000 ~mathrm{Wh} cdot 0.08 ~mathrm{dfrac{~$}{kWh}} \
tag{$1 ~mathrm{kWh} = 1000 ~mathrm{Wh} $} \
C_{total} &= 54 ~mathrm{kWh} cdot 0.08 ~mathrm{dfrac{~$}{kWh}}
end{align*}
$$

$$
boxed{ C_{total} = 4.32 ~$ }
$$

$$
begin{align*}
& a)~~ I = 30 ~mathrm{A} \
& b)~~ E = 1.08 ~mathrm{MJ} \
& c)~~ Delta T = 12.8571 ~mathrm{^circ C} \
& d)~~ C_{total} = 4.32 ~$ \
end{align*}
$$

$a)~~$ In this problem we have a heater with power rating $P = 500 ~mathrm{W}$.
Energy $E$ supplied to the device with power rating $P$ during the time $t$ is given as:

$$
E = P t
$$

We can use the expression above and calculate energy $E$ supplied to the heater during time $t = dfrac{1}{2} ~mathrm{h}$ as:

$$
begin{align*}
E &= P t \
tag{plug in the values} \
E &= 500 ~mathrm{W} cdot dfrac{1}{2} ~mathrm{h} \
tag{$1 ~mathrm{h} = 3600 ~mathrm{s}$} \
E &= 500 ~mathrm{W} cdot dfrac{1}{2} cdot 3600 ~mathrm{s} \
E &= 900 000 ~mathrm{J} \
E &= 0.9 cdot 10^6 ~mathrm{J}
end{align*}
$$

$$
boxed{ E = 0.9~mathrm{MJ} }
$$

$b)~~$ In this part of the problem we’ll us the heater to heat up the air in the room, containing $m = 50 ~mathrm{kg}$ of air. Heater will be turned on for $t = dfrac{1}{2} ~~mathrm{h}$ and only 50% of the thermal energy emitted from the heater will be used to heat up the air in the room. We’ve already calculated energy $E$ supplied to the heater in half an hour and only half of this energy will be used as heat $Q$ heat up the air, stated as:

$$
Q = dfrac{E}{2}
$$

Heat $Q$ mentioned above is the same heat
$Q$ needed to increase the temperature $T$ of the air in the room by $Delta T$, given as:

$$
Q = m c Delta T
$$

where $m$ is mass of the air in the room and
$c = 1.1 ~mathrm{dfrac{kJ}{kgK}} = 1100 ~mathrm{dfrac{J}{kg K}}$ is specific heat capacity of the air.
This means that calculated energy $E$ is equal to:

$$
begin{align*}
Q &= dfrac{E}{2} \
tag{use $Q = m c Delta T $} \
m c Delta T &= dfrac{E}{2} \
tag{express $Delta T$ from the equation above} \
Delta T &= dfrac{ E}{ 2mc} \
tag{plug in the values} \
Delta T &= dfrac{ 0.9 cdot 10^6 ~mathrm{J} }{2 cdot 50 ~mathrm{kg} cdot 1100 ~mathrm{dfrac{J}{kg K}} } \
Delta T &= 8.1818 ~mathrm{K}
end{align*}
$$

Note that the change of temperature expressed in Kelvins $mathrm{K}$ is equal to the change of temperature expressed in degrees Celsius $mathrm{^circ C}$, which is why we can express the change of temperature as:

$$
boxed{ Delta T = 8.1818~mathrm{^circ C} }
$$

$c)~~$ To find the total cost $C_t$ for operating a device with power rating $P$ over a time period $t$, we multiply this time interval $t$, power rating of the device $P$ and cost per kilowatt-hour $C_p$, stated as:

$$
C_t = P t C_p
$$

In our case, cost of electric energy per one kilowatt-hour is
$C_p = 0.08 ~mathrm{dfrac{~$}{kWh}}$.
To find the total cost of operating a heater for the time interval mentioned in the problem text, we must first express this time interval in hours. If heating coil is on for $6 ~mathrm{h}$ for $30 ~mathrm{days}$, this means that over a whole month, time interval $t$ that the heating coil was on is:

$$
begin{align*}
t &= 30 cdot 6 ~mathrm{h} \
t &= 180 ~mathrm{h}
end{align*}
$$

We found that heater was on for $180 ~mathrm{h}$ a month. We can now calculate the cost of electric energy used by the heating coil over a month as:

$$
begin{align*}
C_t &= P t C_p \
tag{plug in the calculated values} \
C_t &= 500 ~mathrm{W} cdot 180 ~mathrm{h} cdot 0.08 ~mathrm{dfrac{~$}{kWh}} \
C_t &= 90 000 ~mathrm{Wh} cdot 0.08 ~mathrm{dfrac{~$}{kWh}} \
tag{$1 ~mathrm{kWh} = 1000 ~mathrm{Wh} $} \
C_t &= 90 ~mathrm{kWh} cdot 0.08 ~mathrm{dfrac{~$}{kWh}}
end{align*}
$$

$$
boxed{ C_t = 7.2 ~$ }
$$

$$
begin{align*}
& a)~~ E = 0.9~mathrm{MJ} \
& b)~~ Delta T = 8.1818~mathrm{^circ C} \
& c)~~ C_t = 7.2 ~$
end{align*}
$$

Resistance $R$ of a resistor depends on its length $L$, cross-sectional area $A$ and resistivity $rho$ of a material from which the resistor is made of, stated as:

$$
R = dfrac{rho L}{A}
$$

we see that the longer the resistor, the higher the resistance because

$$
R propto L
$$

and we see that the larger the cross-sectional area, the lower the resistance because

$$
R propto dfrac{1}{A}
$$

This means that the resistance $R$ depends on the size of the resistor. But do keep in mind that resistance $R$ doesn’t depend only on its size, but also depends on the resistivity $rho$ of the material. Resistivity is a physical quantity which tells us how hard it is for a certain material to conduct current. We see that the higher the resistivity, the higher the resistance because

$$
R propto rho
$$

This means that if two resistors of the same size were build from a different materials with resistivites $rho_1$ and $rho_2$, resistance of these resistors would not be equal:

$$
begin{align*}
R_1 &= rho_1 dfrac{L}{A} \
R_2 &= rho_2 dfrac{L}{A} \
tag{divide the two equations above} \
frac{R_1}{R_2} &= dfrac{rho_1 dfrac{L}{A} }{rho_2 dfrac{L}{A} } \
frac{R_1}{R_2} &= dfrac{rho_1 }{rho_2 } \
tag{Since $ rho_1 ne rho_2 $ we conclude} \
R_1 &ne R_2
end{align*}
$$

Analogously, two resistors can have the same resistance $R_1 = R_2$ even though their cross-sectional areas $A_1$ and $A_2$ are different and/or their lengths $L_1$ and $L_2$ are different if they are built from a different material, which will result in different resistivities of the two resistors:

$$
begin{align*}
R_1 &= R_2 \
rho_1 dfrac{L_1}{A_1} &= rho_2 dfrac{L_2}{A_2} \
tag{multiply the equation above by $ dfrac{A_1 }{rho_2 L_1 } $} \
dfrac{rho_1}{rho_2} &= dfrac{L_2}{L_1} cdot dfrac{A_1}{A_2} \
tag{as said, $A_1 ne A_2 $ and $L_1 ne L_2$} \
tag{this means that $ dfrac{L_2}{L_1} ne 1 $ and $dfrac{A_1}{A_2} ne 1 $} \
dfrac{rho_1}{rho_2} ne 1
rho_1 &= rho_2
end{align*}
$$

As we can see, two resistors can have the same resistance (for example $R = 10 ~mathrm{Omega }$, even though these two resistors don’t have the same length or cross sectional area if they are built from a different material, so that their resistiviteis are different.

Hint: Resistance $R$ of a resistor depends on its length $L$, cross-sectional area $A$ and resistivity $rho$ of a material from which the resistor is made of, stated as:

$$
R = dfrac{rho L}{A}
$$

Diode graph shown in Figure 22-17 represents how current $I$ through the diode depends on voltage $V$ across the diode. We can see that current $I$ increases exponentially with an increase in voltage $V$ across the diode, or in other words, current $I$ rapidly increases with a small increase in voltage $V$.

If we now take a look at the Ohm’s law, it states that current $I$ flowing through a device with resistance $R$ and voltage $V$ across the device is equal to

$$
I = dfrac{1}{R} cdot V
$$

Knowing that resistance $R$ is constant and depends on the temperature of the resistor, we conclude that Ohm’s law say that current $I$ through a resistor $R$ is a linear function of voltage $V$ across the resistor.

We can see that for diode, this isn’t the case. As said, current through the diode is an exponential function of voltage $V$ across the diode and Ohm’s law can’t be applied to the diode because in diode, as said, current is not a linear function of voltage. This is why graph shown in Figure 22-17 is more useful than the linear function graph of the Ohm’s law.

In this problem we need to calculate the pressure change caused by a change in height of $h=150,,rm{m}$ if the density of air is $rho =1.3,,rm{kg/m^3}$.

In order to calculate the change in pressure we need to use the next equation:
$$Delta p=-rho gDelta h$$
Which connects change in pressure $Delta p$, density $rho$ and change in height $Delta h$.
Notice the ‘-‘ sign in front of the equation. It simply states that the pressure drops by **increase in height**.

Inserting given values we get:
$$Delta p=1.3cdot 9.81cdot 150$$
Finally, change in pressure is:
$$boxed{Delta p=-1912,,rm{Pa}}$$

$$Delta p=-1912,,rm{Pa}$$

We need to calculate the wavelength of a sound witha frequency of $f=17,,rm{kHz}$ if it moves through air.

First assumption is that the speed of sound in the air is the default one:
$$v=343,,rm{m/s}$$

Now we can calulate the wavelength by using the next equation:
$$v=lambda f$$
Where $v$ is the speed of sound, $lambda $ is a wavelength and $f$ is frequency.

From the previous equation we can extract $lambda $:
$$lambda =frac{v}{f}$$

Inserting given values we get:
$$lambda =frac{343}{17cdot 10^3}$$
Finally:
$$boxed{lambda =0.02,,rm{m}}$$

$$lambda =0.02,,rm{m}$$

We need to calculate the distance between the slits if the wavelength is $lambda =478,,rm{nm}$ and first order band appears $y=3,,rm{mm}$ from the central band and the screen is at a distance of $L=0.91,,rm{m}$ from the slits.

In order to solve this problem we can us the equation for interference:
$$d sin (theta )=mlambda$$

Where we can substitute the part of the equation:
$$sin (theta )=frac{y}{L}$$

Combining two previous equations we can get:
$$d frac{y}{L}=mlambda $$
$$d=frac{mlambda y}{L}$$

Inserting given values we get:
$$d=frac{1cdot 378cdot 10^{-9} cdot 3cdot 10^{-3}}{0.91}$$
Finally, the distance is:
$$boxed{d=1.6,,rm{nm}}$$

$$d=1.6,,rm{nm}$$

We need to calculate the magnitude of force between a charge of $q_1=3cdot 10^{-6},,rm{C}$ and a charge of $q_2=6cdot 10^{-5},,rm{C}$ at a distance of $d=2,,rm{m}$.

In order to solve this problem we need to use an equation for an electromagnetic force between two charges:
$$F_e=frac{kq_1q_2}{r^2}$$
Where $k=9cdot 10^9,,rm{Nm^2/C^2}$ is a Coulomb constant.

Inserting values in the previous equation we get:
$$F_e=frac{9cdot 10^9cdot 3cdot 10^{-6} cdot 6cdot 10^{-5}}{2^2}$$
Finally, the force is:
$$boxed{F_e=0.405,,rm{N}}$$

$$F_e=0.405,,rm{N}$$