All Solutions
Page 558: Assessment
$$
F = dfrac{kq_1q_2}{r^2}
$$
where $k= 9 cdot 10^9 ~mathrm{dfrac{Nm^2}{C^2}}$ is Coulomb constant. We see that the Coulomb (electrostatic) force is connected to charges, since charges either attract or repel, described in the equation above. We also see that Coulomb force is connected to the distance $r$ between the two charges and we thus conclude that the two terms with which Coulomb’s law is connected is distance and charge.
$$
F = dfrac{kq_1q_2}{r^2}
$$
Elementary charge is the least amount of charge in nature.
An object can become charged through conduction.
tap water, sea water, wet wood, graphite, human body and any metal (gold, silver, copper, aluminum, platinum etc).
Some examples of insulators are:
plastic, dry wood, distilled water, dry air, rubber, styrofoam, ceramic and glass.
these free electrons will start to move around and we’ll have a current in this conductor.
There is not much (if any) free electrons in rubber or any other insulator, which means that when we bring in the same voltage across a piece of rubber, there will not be a lot of electrons flowing through the rubber because there weren’t many free electrons in rubber.
$$
q = (N_+ – N_-) cdot e
$$
where $e = 1.6 cdot 10^{-19} ~mathrm{C}$
As we can see from the equation above, if number of protons is greater than number of electrons, charge $q$ of the coin is positive, whereas if number of electrons is greater than number of protons, charge $q$ on the coin is negative.
$$
F = dfrac{k q_1 q_2}{r^2}
$$
where $k = 9 cdot 10^9 ~mathrm{dfrac{N m^2}{C^2}}$ is Coulomb constant.
We see that magnitude of the force between the two charges is proportional to those two charges and inversely proportional to the square of the distance between them.
This means that if, for example, distance between the two charges tripled, force between the same two charges would decrease by a factor of $3^2$, which is $9$. We can prove this. Let $F_i$ be the electric force between charges $q_1$ and $q_2$ that are initially at a distance $r_i$. In this case, force $F_i$ between these two charges is given as:
$$
begin{equation}
F_i = dfrac{k q_1 q_2}{r_i^2}
end{equation}
$$
Let’s now move these same charges further apart to a distance 3 times larger than the initial distance. This final distance between the charges will be given as $r_f = 3 r_i$. Force $F_f$ between these two charges in the final case is given as:
$$
begin{equation}
F_f = dfrac{k q_1 q_2}{r_f^2} = dfrac{k q_1 q_2}{(3r_i)^2}
end{equation}
$$
$$
begin{align*}
dfrac{F_f}{F_i} &= dfrac{dfrac{k q_1 q_2}{(3r_i)^2}}{dfrac{k q_1 q_2}{r_i^2} } \
dfrac{F_f}{F_i} &= dfrac{dfrac{1}{9r_i^2}}{dfrac{1}{r_i^2} } \
dfrac{F_f}{F_i} &= dfrac{ r_i^2 }{ 9 r_i^2 } \
dfrac{F_f}{F_i} &= dfrac{ 1 }{ 9 }
end{align*}
$$
$$
boxed{F_f = dfrac{F_i}{9}}
$$
Bringing in this positively charged rod in close proximity of the uncharged rod will result in redistribution of negative charges from ground which will flow to a conductor and set near to a positively charged rod. Now we disconnect conductor from the ground and remove positively charged rod from proximity of the conductor. Conductor was charged negatively by induction.
$$
q_p = e = 1.6 cdot 10^{-19} ~mathrm{C}
$$
whereas charge of electron $q_e$ is negative but equal in magnitude to the charge of proton
$$
q_e = – e = – 1.6 cdot 10^{-19} ~mathrm{C}
$$
In other words, charge of proton and electron are same in magnitude, but charge of electron is negative.
We need to place an object in contact with the knob of the electroscope.
Next step is to touch opposite part of the object with the charged rod. If the object in question is a conductor, charges from the charged rod would flow through the object and to the knob of the electroscope.
If we bring in a positive charge near the electroscope, electroscope will become even more positively charged and leaves on the electroscope will move farther apart.
If we bring in a negative charge near the electroscope, electroscope will lose some of its positive charge, become less and less positively charged and leaves on the electroscope will move closer together.
$$
F_g = G dfrac{m_Am_B}{r^2}
$$
where $G = 6.67 cdot 10^{-11} ~mathrm{dfrac{Nm^2}{kg^2}}$ is gravitational constant.
We see that magnitude of the force between the two objects is proportional to mass of both of the objects and inversely proportional to the square of the distance between them, stated as:
$$
F propto m_A m_B
$$
$$
F propto dfrac{1}{r^2}
$$
$$
F = dfrac{k q_A q_B}{r^2}
$$
where $k = 9 cdot 10^9 ~mathrm{dfrac{N m^2}{C^2}}$ is Coulomb constant.
We see that magnitude of the force between the two charges is proportional to those two charges and inversely proportional to the square of the distance between them, stated as:
$$
F propto q_A q_B
$$
$$
F propto dfrac{1}{r^2}
$$
Both of the forces are proportional to a constant which is the same anywhere in the universe.
Both of the forces are inversely proportional to the distance between the two objects, which in case of gravitational force are two objects with mass, whereas in case of electric force, they’re objects with charge.
the gravitational force.
textit{color{#c34632} $See$ $Explanation$}
$$
$$ F = K frac{ q_1q_2}{r^2} $$
Where:
– $K$ is Coulomb’s constant $K = 9 times 10^9 ,frac{text{N} cdot text{m}^2}{text{C}^{2}}$;
– $q_1$ and $q_2$ are charges between which the force acts;
– $r$ is the distance between the charges;
$$begin{align*}
F &= G frac{m_1m_2}{r^2} \
end{align*}$$
Where:
– $G$ is a gravitational constant $G = 6.67 times 10^{-11} ,frac{text{Nm}^2}{text{kg}^2}$;
– $m_1$ and $m_2$ are masses of objects between which the force acts;
– $r$ is the distance between the charges;
$$
q_A = q_B
$$
Due to law of charge conservation, we have know that total charge $q$ before the spheres touched is equal to the total charge after they touched:
$$
begin{align*}
q &= q_A + q_B \
q &= 2 q_A \
q_A &= dfrac{q}{2} \
q_B &= dfrac{q}{2}
end{align*}
$$
As said, charge on both of the spheres will be identical because spheres themselves are identical and we also proved that charge on both of them will be equal to half the total charge.
$$
q_A = q_B = q_C
$$
Due to law of charge conservation, we have know that total charge $q$ before the spheres touched is equal to the total charge after they touched:
$$
begin{align*}
q &= q_A + q_B + q_C \
q &= 3 q_A \
q_A &= dfrac{q}{3} \
q_B &= dfrac{q}{3} \
q_C &= dfrac{q}{3}
end{align*}
$$
As said, charge on both of the spheres will be identical because spheres themselves are identical and we also proved that charge on each of them will be equal to third of the total charge.
$$
F = dfrac{k q_A q_B}{r^2}
$$
where $k = 9 cdot 10^9 ~mathrm{dfrac{N m^2}{C^2}}$ is Coulomb constant.
$$
begin{equation}
F_i = dfrac{k q q}{r_i^2}
end{equation}
$$
In the final case, charge on sphere $A$ is $q_A = q$, whereas charge on sphere $B$ is equal $q_B = dfrac{1}{3} q_A = dfrac{q}{3}$ and distance between the two sphere is $r_f$, which makes the force $F_f$ in the final case equal to:
$$
F_f = dfrac{k q dfrac{q}{3} }{r_f^2}
$$
$$
begin{equation}
F_f = dfrac{kqq}{3 r_f^2 }
end{equation}
$$
$$
begin{align*}
dfrac{F_f}{F_i} &= dfrac{dfrac{kqq}{3 r_f^2 }}{dfrac{k q q}{r_i^2}} \
1 &= dfrac{r_i^2}{3 r_f^2 } \
3 r_f^2 &= r_i^2 \
r_f^2 &= dfrac{r_i^2}{3} \
r_f &= dfrac{r_i}{sqrt{3}} \
end{align*}
$$
$$
boxed{ r_f approx 0.57735 r_i }
$$
As it can be seen from the equation above, distance $r_f$ at which the two spheres will have a same deflection will be equal to approximately $0.57735$ of the initial distance between the spheres.
r_f approx 0.57735 ~ r_i
$$
Electric force $F$ between charges $q_1$ and $q_2$ at a distance $r$ from each other is given as:
$$
F = dfrac{k q_1 q_2}{r^2}
$$
where $k = 9 cdot 10^9 ~mathrm{dfrac{N m^2}{C^2}}$ is Coulomb constant.
We see that magnitude of the force between the two charges is proportional to those two charges and inversely proportional to the square of the distance between them.
$$
begin{equation}
F_i = dfrac{k q_1 q_2}{r_i^2}
end{equation}
$$
Let’s now move these same charges closer together equal to one fourth of the initial distance. This final distance between the charges will be given as $r_f = dfrac{r_i}{4}$. Force $F_f$ between these two charges in the final case is given as:
$$
begin{align*}
F_f &= dfrac{k q_1 q_2}{r_f^2} \
F_f &= dfrac{k q_1 q_2}{ bigg( dfrac{r_i}{4} bigg)^2}
end{align*}
$$
$$
begin{equation}
F_f = dfrac{16 k q_1 q_2}{r_i^2 }
end{equation}
$$
$$
begin{align*}
dfrac{F_f}{F_i} &= dfrac{ dfrac{16 k q_1 q_2}{r_i^2 }}{ dfrac{k q_1 q_2}{r_i^2} } \
dfrac{F_f}{F_i} &= 16 \
F_f &= 16 F_i cdot 0.145 ~mathrm{N}
end{align*}
$$
$$
boxed{F_f = 2.32 ~mathrm{N} }
$$
$$
F_f = 2.32 ~mathrm{N}
$$
Gravitational force, however, doesn’t depend on our charge or charge of our surroundings and it is always present. Moreover, mass of Earth is humongous and equal to $m_{Earth} = 5.972 cdot 10^{24} ~mathrm{kg}$, which makes the gravitational force between us and the Earth easy to feel.
Electric force $F$ between charges $q_A$ and $q_B$ at a distance $r$ from each other is given as:
$$
begin{equation}
F = dfrac{k q_A q_B}{r_i^2}
end{equation}
$$
where $k = 9 cdot 10^9 ~mathrm{dfrac{N m^2}{C^2}}$ is Coulomb constant.
We see that magnitude of the force between the two charges is proportional to those two charges and inversely proportional to the square of the distance between them.
$$
begin{align*}
F_f &= dfrac{k cdot 2 q_A cdot q_b}{r^2} \
F_f &= 2 dfrac{k cdot q_A cdot q_b}{r^2}
end{align*}
$$
We’ve calculated that when one of the charges doubled, force between the charges doubled, which we could expect from the fact that force between the charges is proportional to the charges.
$$
boxed{ a )~~ F_f = 2 F }
$$
$$
q_A rightarrow dfrac{q_A }{2} ~~~~text{and}~~~ q_B rightarrow dfrac{q_B }{2}
$$
This means that instead of plugging in $q_A$ and $q_B$ in equation $(1)$, to calculate the new force, we’d plug in $dfrac{q_A }{2}$ and $dfrac{q_B }{2}$. This means that the final force $F_f$ in this part of the problem is equal to:
$$
begin{align*}
F_f &= dfrac{k cdot dfrac{q_A }{2} cdot dfrac{q_B }{2}}{r^2} \
F_f &= dfrac{1}{4} dfrac{k cdot q_A cdot q_b}{r^2}
end{align*}
$$
We’ve calculated that when both of the charges were cut in half, force between the charges was decreased by a factor of 4, which we could expect from the fact that force between the charges is proportional to the charges.
$$
boxed{ b )~~ F_f = dfrac{F}{4}}
$$
If distance between the two charges tripled, force between the same two charges would decrease by a factor of $3^2$, which is $9$. We can prove this. Initial force between the charges is given with equation $(1)$:
$$
F = dfrac{k q_A q_B}{r_i^2}
$$
Let’s now move these same charges further apart to a distance 3 times larger than the initial distance. This final distance between the charges will be given as $r_f = 3 r_i$. Force $F_f$ between these two charges in the final case is given as:
$$
F_f = dfrac{k q_A q_B}{r_f^2} = dfrac{k q_A q_B}{(3r_i)^2}
$$
Let’s divide the two equations stated in this part of the problem:
$$
begin{align*}
dfrac{F_f}{F} &= dfrac{dfrac{k q_A q_B}{(3r_i)^2}}{dfrac{k q_A q_B}{r_i^2} } \
dfrac{F_f}{F} &= dfrac{dfrac{1}{9r_i^2}}{dfrac{1}{r_i^2} } \
dfrac{F_f}{F} &= dfrac{ r_i^2 }{ 9 r_i^2 } \
dfrac{F_f}{F} &= dfrac{ 1 }{ 9 }
end{align*}
$$
$$
boxed{ c )~~ F_f = dfrac{F}{9}}
$$
We have calculated that if distance between the charges tripled, force between the charges would decrease by a factor of 9, which we could expect from the fact that force between the two charges is inversely proportional to the square of the distance between them.
From equation $(1)$ we see that magnitude of the force between the two charges inversely proportional to the square of the distance between them.
This means that if charges are brought closer at a distance equal to a distance equal to half the initial distance, force between the same two charges would increase by a factor of $2^2$, which is $4$. We can prove this. Initial force between the two charges is given with equation $(1)$.
$$
F = dfrac{k q_A q_B}{r_i^2}
$$
Let’s now move these same charges closer together to a distance equal to $r_f = dfrac{r_i}{2}$. Force $F_f$ between these two charges in the final case is given as:
$$
begin{align*}
F_f &= dfrac{k q_A q_B}{r_f^2} \
F_f &= dfrac{k q_A q_B}{ bigg( dfrac{r_i}{2} bigg)^2} \
F_f &= dfrac{4 k q_A q_B}{r_i^2 }
end{align*}
$$
Let’s divide the equation above with equation $(1)$. We have:
$$
begin{align*}
dfrac{F_f}{F} &= dfrac{ dfrac{4 k q_A q_B}{r_i^2 }}{ dfrac{k q_A q_B}{r_i^2} }
end{align*}
$$
We have calculated that when distance between the charges was cut in half, force is increased by a factor of 4, which we could expect from the fact that electric force between the two charges is inversely proportional to the distance between the charges.
$$
boxed{ d )~~ dfrac{F_f}{F} = 4 }
$$
In this part of the problem $q_A$ is tripled, which means that instead of plugging in $q_A$ in equation $(1)$, to calculate the new force, we’d plug in $3 q_A$. We are also told that the distance between the charges is doubled, which means that in order to find the force between the charges, we need to plug in $r_f = 2 r_i$ instead of $r_i$. We conclude that the force between the charges is now equal to:
$$
begin{align*}
F_f &= dfrac{ k 3 q_A q_B }{(2 r_i)^2} \
F_f &= dfrac{3}{4} dfrac{k q_A q_B}{r_i^2}
end{align*}
$$
$$
boxed{ e )~~ F_f = dfrac{3}{4} F}
$$
a )~~ F_f = 2 F
$$
$$
b )~~ F_f = dfrac{F}{4 }
$$
$$
c )~~ F_f = dfrac{F}{9 }
$$
$$
d )~~ dfrac{F_f}{F} = 4
$$
$$
e )~~ F_f = dfrac{3}{4} F
$$
$$
begin{align*}
q &= N |e| \
&text{We can express $N$ from the equation above as:}\
N &= dfrac{q}{|e|} \
N &= dfrac{25 ~mathrm{C} }{1.6 cdot 10^{-19} ~mathrm{C}}
end{align*}
$$
$$
boxed{ N = 15.625 cdot 10^{19} }
$$
Note that we stated that charge $q_e$ of one electron is equal to negative value of elementary charge, but we used the absolute value of elementary charge in order to calculate the positive number of electrons.
N = 15.625 cdot 10^{19}
$$
$$
begin{equation}
F = dfrac{k q_A q_B}{r^2}
end{equation}
$$
where $k = 9 cdot 10^9 ~mathrm{dfrac{N m^2}{C^2}}$ is Coulomb constant.
We are told that the distance $r$ between the electrons is $r = 1.5 cdot 10^{-10} ~mathrm{m}$ and we know that charge of an electron $q_e$ is equal to negative value of the elementary charge $q_e = – e = – 1.6 cdot 10^{-19} ~mathrm{C}$.
We can plug in this data into equation $(1)$, a general equation for force between the two charges and find that the force between these two electrons is equal to:
$$
begin{align*}
F &= dfrac{k q_e q_e }{r^2} \
F &= dfrac{k e^2 }{r^2} \
F &= 9 cdot 10^9 ~mathrm{dfrac{N m^2}{C^2}} cdot dfrac{ (1.6 cdot 10^{-19})^2 ~mathrm{C^2} }{(1.5 cdot 10^{-10})^2 ~mathrm{m^2} }
end{align*}
$$
$$
boxed{F = 1.024 cdot 10^{-8} ~mathrm{N}}
$$
F = 1.024 cdot 10^{-8} ~mathrm{N}
$$
$$
begin{equation}
F = dfrac{k q_A q_B}{r^2}
end{equation}
$$
where $k = 9 cdot 10^9 ~mathrm{dfrac{N m^2}{C^2}}$ is Coulomb constant.
We are told that the distance $r$ between the charges is $r = 15 ~mathrm{cm} = 0.15 ~mathrm{m}$ and we know both charges have the same magnitude $q = 2.5 cdot 10^{-5} ~mathrm{C}$, but one charge is positive, while the other one is negative, which means that two charges are equal to:
$$
q_A = q ~~~~~~ q_B = -q
$$
We can plug in this data into equation $(1)$, a general equation for force between the two charges and find that the force between these two charges is equal to:
$$
begin{align*}
F &= dfrac{k q_A q_B }{r^2} \
F &= dfrac{k q cdot (- q) }{r^2} \
F &= – dfrac{k q^2 }{r^2} \
F &= -9 cdot 10^9 ~mathrm{dfrac{N m^2}{C^2}} cdot dfrac{ ( 2.5 cdot 10^{-5})^2 ~mathrm{C^2} }{( 0.15 ~mathrm{m} )^2 ~mathrm{m^2} }
end{align*}
$$
$$
boxed{F = 250 ~mathrm{N}}
$$
F = 250 ~mathrm{N}
$$
$$
begin{equation}
F = dfrac{k q_1 q_2}{r^2}
end{equation}
$$
where $k = 9 cdot 10^9 ~mathrm{dfrac{N m^2}{C^2}}$ is Coulomb constant.
We are told that the magnitude of the force $F$ between charges $q_1 = 8 cdot 10^{-5} ~mathrm{C}$ and $q_2 = 3 cdot 10^{-5} ~mathrm{C}$ is $F= 2.4 cdot 10^2 ~mathrm{N}$ and we must find the distance between the two charges. We’ll express distance from equation $(1)$ and plug in the given values to the resulting equation:
$$
begin{align*}
F &= dfrac{k q_1 q_2 }{r^2} \
r^2 &= dfrac{k q_1 q_2 }{F} \
r &= sqrt{dfrac{k q_1 q_2 }{F}} \
r &= sqrt{dfrac{ 9 cdot 10^9 ~mathrm{dfrac{N m^2}{C^2}} cdot 8 cdot 10^{-5} ~mathrm{C} cdot 3 cdot 10^{-5} ~mathrm{C} }{2.4 cdot 10^2 ~mathrm{N}}} \
r &= sqrt{0.09 ~mathrm{m^2}}
end{align*}
$$
$$
boxed{ r = 0.3 ~mathrm{m} }
$$
r = 0.3 ~mathrm{m}
$$
$$
begin{equation}
F = dfrac{k q_A q_B}{r^2}
end{equation}
$$
where $k = 9 cdot 10^9 ~mathrm{dfrac{N m^2}{C^2}}$ is Coulomb constant.
We are told that when distance between the charges is $r = 3.8 cdot 10^{-10} ~mathrm{m}$, there is a repulsive force of magnitude $F = 6.4 cdot 10^{-9} ~mathrm{N}$ between these two charges. Knowing that both charges are positive and same in magnitude, we must find charge $q$ on them.
We can express charge $q$ from equation $(1)$, a general equation for force between the two charges and solve for $q$:
$$
begin{align*}
F &= dfrac{k q_A q_B }{r^2} \
F &= dfrac{k q q }{r^2} \
F &= dfrac{k q^2 }{r^2} \
F r^2 &= k q^2 \
q^2 &= dfrac{F r^2}{k} \
q &= sqrt{ dfrac{F r^2}{k} } \
q &= sqrt{dfrac{ 6.4 cdot 10^{-9} ~mathrm{N} cdot (3.8 cdot 10^{-10} ~mathrm{m})^2 }{9 cdot 10^9 ~mathrm{dfrac{N m^2}{C^2}} }} \
%
%
q &= sqrt{dfrac{ 6.4 cdot 10^{-9} ~mathrm{N} cdot 14.4 cdot 10^{-20} ~mathrm{m^2} }{9 cdot 10^9 ~mathrm{dfrac{N m^2}{C^2}} }} \
end{align*}
$$
$$
boxed{ q = 3.2 cdot 10^{-19} ~mathrm{C} }
$$
q = 3.2 cdot 10^{-19} ~mathrm{C}
$$
First negative charge is $q_1 = -2 ~mathrm{mu C}$ and it is placed at a distance $r_1 = 0.05 ~mathrm{m}$ to the west from the positive charge.
Second negative charge is $q_2 = -4 ~mathrm{mu C}$ and it is placed at a distance $r_2 = 0.03 ~mathrm{m}$ to the west from the positive charge.
What happens in this problem is that positive charge $q$ will be attracted to both of the charges and thus it will be pulled in the direction of both of the charges. However, since it can’t move to both of the charges, resulting force $F$ is what’s going to decide the direction of overall attraction between positive charge and the other charges.
Since we have two forces acting in the opposite direction, magnitude of the resulting force $F$ will be calculated as:
$$
begin{equation}
|F| = |F_2| – |F_1|
end{equation}
$$
where $F_1$ is magnitude of the attractive force between the positive charge and the first negative charge $q_1$, whereas $F_2$ is attractive force between the positive charge and the second negative charge $q_2$. We know that the electric force $F$ between charges $q_A$ and $q_B$ at a distance $r$ from each other is given as:
$$
begin{equation}
F_{AB} = dfrac{k q_A q_B}{r^2}
end{equation}
$$
where $k = 9 cdot 10^9 ~mathrm{dfrac{N m^2}{C^2}}$ is Coulomb constant.
$$
F_1 = dfrac{k q_1 q}{r_1^2}
$$
We are given distance $r_2$ between the second negative charge $q_2$ and positive charge $q$ and we are also given $q$ and $q_2$, which means that we can calculate the magnitude of the force $F_2$ between these two charges as:
$$
F_2 = dfrac{k q_2 q}{r_2^2}
$$
$$
begin{align*}
|F| &= bigg| dfrac{k q_2 q}{r_2^2}bigg| – bigg| dfrac{k q_1 q}{r_1^2}bigg| \
|F| &= kq bigg( dfrac{|q_2|}{r_2^2} – dfrac{|q_1|}{r_1^2} bigg) \
%
%
|F| &= 3 ~mathrm{mu C} cdot 9 cdot 10^9 ~mathrm{dfrac{N m^2}{C^2}}
bigg( dfrac{ 4 ~mathrm{mu C}}{( 0.03 ~mathrm{m} )^2} – dfrac{ 2 ~mathrm{mu C}}{ (0.05 ~mathrm{m})^2 } bigg) \
%
%
|F| &= 3 cdot 10^{-6} ~mathrm{C} cdot 9 cdot 10^9 ~mathrm{dfrac{N m^2}{C^2}}
bigg( dfrac{ 4 cdot 10^{-6} ~mathrm{ C}}{( 0.03 ~mathrm{m} )^2} – dfrac{ 2 cdot 10^{-6} ~mathrm{ C}}{ (0.05 ~mathrm{m})^2 } bigg) \
|F| &= 27 cdot 10^{-3} ~mathrm{N} cdot bigg( dfrac{ 4 }{( 0.03 )^2} – dfrac{ 2 }{ (0.05 )^2 } bigg)
end{align*}
$$
$$
boxed{|F| = |F_2| – |F_1|= 98.4 ~mathrm{N}}
$$
|F| = |F_2| – |F_1|= 98.4 ~mathrm{N}
$$
$$
begin{equation}
F = dfrac{k q_A q_B}{r^2}
end{equation}
$$
where $k = 9 cdot 10^9 ~mathrm{dfrac{N m^2}{C^2}}$ is Coulomb constant.
After we apply the equation above to the two charged spheres in our problem we have:
$$
F = dfrac{k q cdot 3q}{r^2}
$$
$$
begin{equation}
F = dfrac{3 k q^2}{r^2}
end{equation}
$$
$$
begin{align*}
F &= dfrac{3 k q^2}{r^2} \
F r^2 &= 3 k q^2 \
q^2 &= dfrac{F r^2}{3k} \
q &= sqrt{ dfrac{F r^2}{3k} } \
q &= sqrt{dfrac{ 0.28 ~mathrm{N}cdot (0.16 ~mathrm{m})^2 }{ 3 cdot 9 cdot 10^9 ~mathrm{dfrac{N m^2}{C^2}} }} \
q &= sqrt{dfrac{ 0.28 ~mathrm{N}cdot 0.0256 ~mathrm{m^2} }{ 3 cdot 9 cdot 10^9 ~mathrm{dfrac{N m^2}{C^2}} }} \
q &= 5.1525 cdot 10^{-7} ~mathrm{C}
end{align*}
$$
We found $q$ and we know that this is charge on one of the spheres, stated as $q_1 = q$, whereas charge on the other sphere is three times the charge on the first sphere, stated as $q_2 = 3q$. We fin that charge on the spheres is:
$$
boxed{ q_1 = q = 5.1525 cdot 10^{-7} ~mathrm{C} }
$$
$$
boxed{ q_2 = 3q = 15.456 cdot 10^{-7} ~mathrm{C} }
$$
q_1 = q = 5.1525 cdot 10^{-7} ~mathrm{C}
$$
$$
q_2 = 3q = 15.456 cdot 10^{-7} ~mathrm{C}
$$
We can use this data to calculate the number of moles $n$ of coin’s atoms in a coin and calculate number $N_{atoms}$ of atoms in a coin.
We know that amount of substance (number of moles) $n$ in a sample of a substance is equal to a mass $m$ of that sample divided by the molar mass $M$ of the substance:
is given as:
$$
begin{align*}
n &= dfrac{m}{M} \
n &= dfrac{5 ~mathrm{g}}{62 ~mathrm{dfrac{g}{mol}}} \
n &= 0.080645 ~mathrm{mol}
end{align*}
$$
We also know that amount of substance (number of moles) $n$ in a sample of a substance is equal to a number $N$ of atoms in that sample divided by the Avogadro’s number $N_A = 6.022 cdot 10^{23} ~mathrm{dfrac{atoms}{mol}}$, stated as:
$$
begin{align*}
n &= dfrac{N}{N_A} \
N &= n N_A \
N &= 0.080645 ~mathrm{mol} cdot 6.022 cdot 10^{23} ~mathrm{dfrac{atoms}{mol}} \
N &= 4.85645 cdot 10^{22}
end{align*}
$$
$$
begin{align*}
N_{electrons} &= 28.75 cdot N \
N_{electrons} &= 28.75 cdot 4.85645 cdot 10^{22} \
N_{electrons} &= 1.3962 cdot 10^{24} \
end{align*}
$$
$$
begin{align*}
q &= N_{electrons} cdot q_e \
q &= 1.3962 cdot 10^{24} cdot (-1.6) cdot 10^{-19} ~mathrm{C}
end{align*}
$$
$$
boxed{q = 223392 ~mathrm{C}}
$$
q = 223392 ~mathrm{C}
$$
Charge on the leftmost particle (the first negatively charged particle) is $q_1 = -55 ~mathrm{mu C}$, whereas charge on the positively charged particle in the middle is
$q = 45 ~mathrm{mu C}$ and charge on the rightmost particle (the second negatively charged particle) is $q_2 = -78 ~mathrm{mu C}$.
Middle particle, the one with charge $q$ is at a distance of $r = 72 ~mathrm{cm} = 0.72 ~mathrm{m}$ from the other charged particles.
What happens in this part of the problem is that positive charge $q$ will be attracted to both of the charges and thus it will be pulled in the direction of both of the charges. However, since it can’t move to both of the charges, resulting force $F$ is what’s going to decide the direction of overall attraction between positive charge and the other charges.
Since we have two forces acting in the opposite direction, magnitude of the resulting force $F$ will be calculated as:
$$
begin{equation}
|F| = |F_2| – |F_{12}|
end{equation}
$$
where $F_{12}$ is magnitude of the attractive force between the positive charge $q$ and the first negative charge $q_1$, whereas $F_2$ is attractive force between the positive charge $q$ and the second negative charge $q_2$. We know that the electric force $F$ between charges $q_A$ and $q_B$ at a distance $r$ from each other is given as:
$$
begin{equation}
F_{AB} = dfrac{k q_A q_B}{r^2}
end{equation}
$$
where $k = 9 cdot 10^9 ~mathrm{dfrac{N m^2}{C^2}}$ is Coulomb constant.
We are given distance $r$ between the first negative charge $q_1$ and positive charge $q$ and we are also given $q$ and $q_1$, which means that we can calculate the magnitude of the force $F_{12}$ between these two charges as:
$$
F_{12} = dfrac{k q_1 q}{r^2}
$$
We are given distance $r$ between the second negative charge $q_2$ and positive charge $q$ and we are also given $q$ and $q_2$, which means that we can calculate the magnitude of the force $F_2$ between these two charges as:
$$
F_2 = dfrac{k q_2 q}{r^2}
$$
$$
begin{align*}
|F| &= bigg| dfrac{k q_2 q}{r^2}bigg| -bigg| dfrac{k q_1 q}{r^2} bigg| \
|F| &= kq bigg( dfrac{|q_2|}{r^2} – dfrac{|q_1|}{r^2} bigg) \
%
%
|F| &= dfrac{kq}{r^2} ( |q_2| – |q_1| ) \
%
%
|F| &= dfrac{ 9 cdot 10^9 ~mathrm{dfrac{N m^2}{C^2}} cdot 45 ~mathrm{mu C} }{(0.72 ~mathrm{m})^2} ( 78 ~mathrm{mu C} -55 ~mathrm{mu C} ) \
%
%
|F| &= dfrac{ 9 cdot 10^9 ~mathrm{dfrac{N m^2}{C^2}} cdot 45 cdot 10^{-6}~mathrm{ C} }{ 0.5184 ~mathrm{m^2}} ( 78 cdot 10^{-6}~mathrm{ C} -55 cdot 10^{-6}~mathrm{ C} ) \
end{align*}
$$
$$
boxed{a)~ |F| = |F_2| – |F_{12}| = 17.96875 ~mathrm{N}}
$$
Notice that since we assumed magnitude of the force to be calculated as $|F| = |F_2| – |F_{12}|$ and we calculated a positive value of $|F|$, this means magnitude of force $F_2$ is higher than magnitude of force $F_{12}$, which means that direction of force $F$ is in the direction from positive charge $q$ to charge $q_2$, to the right.
Charge on the leftmost particle (the first negatively charged particle) is $q_1 = -55 ~mathrm{mu C}$, whereas charge on the positively charged particle in the middle is
$q = 45 ~mathrm{mu C}$ and charge on the rightmost particle (the second negatively charged particle) is $q_2 = -78 ~mathrm{mu C}$.
Middle particle, the one with charge $q$ is at a distance of $r = 72 ~mathrm{cm} = 0.72 ~mathrm{m}$ from the other charged particles.
What happens in this part of the problem is that negative charge $q_2$ on the right will be attracted to charged particle $q$ in the middle, but it will be repelled by the charged particle $q_1$ on the left.
Since we have two forces acting in the opposite direction, magnitude of the resulting force $F$ will be calculated as:
$$
begin{equation}
|F| = |F_2| – |F_{12}|
end{equation}
$$
where $F_{12}$ is magnitude of the force between the first negative charge $q_1$ and the second negative charge $q_2$, whereas $F_2$ is attractive force between the positive charge $q$ and the second negative charge $q_2$. We know that the electric force $F$ between charges $q_A$ and $q_B$ at a distance $r$ from each other is given as:
$$
begin{equation}
F_{AB} = dfrac{k q_A q_B}{r^2}
end{equation}
$$
where $k = 9 cdot 10^9 ~mathrm{dfrac{N m^2}{C^2}}$ is Coulomb constant.
We are given distance $r$ between the second negative charge $q_2$ and positive charge $q$ and we are also given $q$ and $q_2$, which means that we can calculate the magnitude of the force $F_2$ between these two charges as:
$$
F_2 = dfrac{k q_2 q}{r^2}
$$
We are given distance $r$ between the second negative charge $q_2$ and positive charge $q$. As it can be seen from the figure accompanying the problem, distance between charges $q_1$ and $q_2$ is equal to $r_{12} = 2r$. We are also given $q_1$ and $q_2$, which means that we can calculate the magnitude of the force $F_{12}$ between these two charges as:
$$
F_{12} = dfrac{k q_2 q_1}{r^2}
$$
$$
begin{align*}
|F| &= bigg| dfrac{k q_2 q}{r^2}bigg| -bigg| dfrac{k q_1 q_2}{(2r)^2} bigg| \
|F| &= k|q_2| bigg( dfrac{|q|}{r^2} – dfrac{|q_1|}{4r^2} bigg) \
%
%
|F| &= dfrac{k|q_2|}{r^2} ( |q| – dfrac{|q_1|}{4} ) \
%
%
|F| &= dfrac{ 9 cdot 10^9 ~mathrm{dfrac{N m^2}{C^2}} cdot 78 ~mathrm{mu C} }{(0.72 ~mathrm{m})^2} bigg( 45 ~mathrm{mu C} – dfrac{ 55 ~mathrm{mu C} }{4} bigg) \
%
%
|F| &= dfrac{ 9 cdot 10^9 ~mathrm{dfrac{N m^2}{C^2}} cdot 78 cdot 10^{-6} ~mathrm{C} }{0.5184 ~mathrm{m^2}} bigg( 45cdot 10^{-6} ~mathrm{C} – dfrac{ 55 cdot 10^{-6} ~mathrm{C} }{4} bigg) \
end{align*}
$$
$$
boxed{b)~ |F| = |F_2| – |F_{12}| = 42.3177 ~mathrm{N}}
$$
Notice that since we assumed magnitude of the force to be calculated as $|F| = |F_2| – |F_{12}|$ and we calculated a positive value of $|F|$, this means magnitude of force $F_2$ is higher than magnitude of force $F_{12}$, which means that direction of force $F$ is in the direction from positive charge $q$ to charge $q_2$, to the left. This is because attractive pull from the positive charge in the middle to the rightmost charge is higher than repulsive push from the leftmost charge.
a)~ |F| = |F_2| – |F_{12}| = 17.96875 ~mathrm{N}, ~text{to the right}
$$
$$
b)~ |F| = |F_2| – |F_{12}| = 42.3177 ~mathrm{N}, ~text{to the left}
$$
$$
q = q_1 + q_2
$$
where $q_1$ is charge on the first sphere after they touched and $q_2$ is charge on the second sphere after they touched. Since the two spheres are identical, charge on both of them will become the same, which means $q_1 = q_2$. If we plug in this conclusion into a law of charge conservation, we have:
$$
q = q_1 + q_1 ~~ rightarrow~~~ q_1 = q_2 = dfrac{q}{2} = 0.6 cdot 10^{-5} ~mathrm{C}
$$
$$
begin{equation}
F = dfrac{k q_A q_B}{r^2}
end{equation}
$$
where $k = 9 cdot 10^9 ~mathrm{dfrac{N m^2}{C^2}}$ is Coulomb constant.
We are told that the distance $r$ between the charges is $r = 0.15 ~mathrm{m}$ and we know both charges have the same magnitude $q = 0.6 cdot 10^{-5} ~mathrm{C}$.
We can plug in this data into equation $(1)$, a general equation for force between the two charges and find that the force between these two charges is equal to:
$$
begin{align*}
F &= dfrac{k q_A q_B }{r^2} \
F &= dfrac{k q cdot q }{r^2} \
F &= dfrac{k q^2 }{r^2} \
F &= 9 cdot 10^9 ~mathrm{dfrac{N m^2}{C^2}} cdot dfrac{ ( 0.6 cdot 10^{-5})^2 ~mathrm{C^2} }{( 0.15 ~mathrm{m} )^2 ~mathrm{m^2} } \
%
%
F &= 9 cdot 10^9 ~mathrm{dfrac{N m^2}{C^2}} cdot dfrac{ 0.36 cdot 10^{-10} ~mathrm{C^2} }{ 0.0225 ~mathrm{m^2} }
end{align*}
$$
$$
boxed{F = 14.4 ~mathrm{N}}
$$
F = 14.4 ~mathrm{N}
$$
$$
begin{equation}
F = dfrac{k q_A q_B}{r^2}
end{equation}
$$
where $k = 9 cdot 10^9 ~mathrm{dfrac{N m^2}{C^2}}$ is Coulomb constant.
Charges in this problem are proton and electron and both of them have the same magnitude of charge, equal to elementary charge $e = 1.6 cdot 10^{-19} ~mathrm{C}$, but charge of the proton $q_p= e$ is positive, whereas charge on the electron is negative $q_e = -e$. Proton and electron are at a distance $r = 5.3cdot 10^{-11} ~mathrm{m}$.
We can plug in this data into equation $(1)$, a general equation for force between the two charges and find that the force between proton and electron at distance $r$ is equal to:
$$
begin{align*}
F &= dfrac{k q_p q_e }{r^2} \
F &= dfrac{k e cdot (-e) }{r^2} \
F &= – dfrac{k e^2 }{r^2} \
F &= -9 cdot 10^9 ~mathrm{dfrac{N m^2}{C^2}} cdot dfrac{ ( 1.6 cdot 10^{-19})^2 ~mathrm{C^2} }{( 5.3cdot 10^{-11})^2 ~mathrm{m}^2 } \
%
%
F &= -9 cdot 10^9 ~mathrm{dfrac{N m^2}{C^2}} cdot dfrac{ 2.56 cdot 10^{-38} ~mathrm{C^2} }{ 28.09 cdot 10^{-22} ~mathrm{m^2} }
end{align*}
$$
$$
boxed{F = – 8.2022 cdot 10^{-8} ~mathrm{N}}
$$
Note that the minus sign in the result above means that the force between proton and electron is attractive, which we could assume directly, knowing that one charge is positive, while the other one is negative.
F = – 8.2022 cdot 10^{-8} ~mathrm{N}
$$
$$
begin{equation}
F = dfrac{k q_A q_B}{r^2}
end{equation}
$$
where $k = 9 cdot 10^9 ~mathrm{dfrac{N m^2}{C^2}}$ is Coulomb constant.
In this problem we are given two charged spheres. Charge $q_1$ on one of the spheres is known and is equal to $q_1 = 2.4 mathrm{mu C} = 2.4 cdot 10^{-6} ~mathrm{C}$, while the other charge $q_2$ must be calculated.Charges are at a distance of $r = 5.5 ~mathrm{cm} = 0.055 ~mathrm{m}$ and force between the two charges is $F = 0.36 ~mathrm{N}$.
We can plug in this data into equation $(1)$, a general equation for force between the two charges and find that the force between these two charges is equal to:
$$
begin{align*}
F &= dfrac{k q_A q_B }{r^2} \
text{apply the equation for our problem:}\
F &= dfrac{k q_1 cdot q_2 }{r^2} \
text{express $q_2$ from the equation above}\
F r^2 &= k q_1 q_2 \
q_2 &= dfrac{F r^2}{k q_1 } \
q_2 &= dfrac{ 0.36 ~mathrm{N} cdot (0.055 ~mathrm{m} )^2 }{ 9 cdot 10^9 ~mathrm{dfrac{N m^2}{C^2}} cdot 2.4 cdot 10^{-6} ~mathrm{C} }
end{align*}
$$
$$
boxed{q_2 = 5.042 cdot 10^{-8} ~mathrm{C}}
$$
q_2 = 5.042 cdot 10^{-8} ~mathrm{C}
$$
$$
begin{equation}
F = dfrac{k q_A q_B}{r^2}
end{equation}
$$
where $k = 9 cdot 10^9 ~mathrm{dfrac{N m^2}{C^2}}$ is Coulomb constant.
We are told that distance between the charges is $r = 12 ~mathrm{cm} = 0.12 ~mathrm{m}$ and there is a force of magnitude $F = 0.28 ~mathrm{N}$ between these two charges. Since both of the charges are identical, this means that sign of charge on each of them is same and that magnitude of the charge is same, which will result in a repulsive force.
We can express charge $q$ from equation $(1)$, a general equation for force between the two charges and solve for $q$:
$$
begin{align*}
F &= dfrac{k q_A q_B }{r^2} \
F &= dfrac{k q q }{r^2} \
F &= dfrac{k q^2 }{r^2} \
F r^2 &= k q^2 \
q^2 &= dfrac{F r^2}{k} \
q &= sqrt{ dfrac{F r^2}{k} } \
q &= sqrt{dfrac{ 0.28 ~mathrm{N} cdot ( 0.12 ~mathrm{m})^2 }{9 cdot 10^9 ~mathrm{dfrac{N m^2}{C^2}} }} \
%
%
q &= sqrt{dfrac{ 0.28 ~mathrm{N}cdot 0.0144 ~mathrm{m^2} }{9 cdot 10^9 ~mathrm{dfrac{N m^2}{C^2}} }}
end{align*}
$$
$$
boxed{ q = pm~ 6.6933 cdot 10^{-7} ~mathrm{C} }
$$
Note that we can’t be sure if charges are either both positive or both negative, which is why we used the $pm$ sign.
q = pm~ 6.6933 cdot 10^{-7} ~mathrm{C}
$$
$$
begin{equation}
F = dfrac{k q_A q_B}{r^2}
end{equation}
$$
where $k = 9 cdot 10^9 ~mathrm{dfrac{N m^2}{C^2}}$ is Coulomb constant.
In this problem we are given two charged spheres. Charge $q_1$ on one of the spheres is known and is equal to $q_1 = 3.6 cdot 10^{-8} ~mathrm{ C}$, while the other charge $q_2$ must be calculated. Charges are at a distance of $r = 1.4 ~mathrm{cm} = 0.014 ~mathrm{m}$ and force between the two charges is $F = 2.7 cdot 10^{-2} ~mathrm{N}$.
We can plug in this data into equation $(1)$, a general equation for force between the two charges and find that the force between these two charges is equal to:
$$
begin{align*}
F &= dfrac{k q_A q_B }{r^2} \
text{apply the equation for our problem:}\
F &= dfrac{k q_1 cdot q_2 }{r^2} \
text{express $q_2$ from the equation above}\
F r^2 &= k q_1 q_2 \
q_2 &= dfrac{F r^2}{k q_1 } \
q_2 &= dfrac{ 2.7 cdot 10^{-2} ~mathrm{N} cdot (0.014 ~mathrm{m} )^2 }{ 9 cdot 10^9 ~mathrm{dfrac{N m^2}{C^2}} cdot 3.6 cdot 10^{-8} ~mathrm{ C} }
end{align*}
$$
$$
boxed{ q_2 = 1.6333 cdot 10^{-8} ~mathrm{C} }
$$
q_2 = 1.6333 cdot 10^{-8} ~mathrm{C}
$$
$$
begin{equation}
F = dfrac{k q_1 q_2}{r^2}
end{equation}
$$
where $k = 9 cdot 10^9 ~mathrm{dfrac{N m^2}{C^2}}$ is Coulomb constant.
We are told that the magnitude of the force $F$ between proton and an electron is $F= 3.5 cdot 10^{-10} ~mathrm{N}$ and we must find the distance between them.
Keep in mind that absolute value of charge of both proton and electron is equal to elementary charge $e = 1.6 cdot 10^{-19} ~mathrm{C}$.
We’ll express distance from equation $(1)$ and plug in the given values:
$$
begin{align*}
F &= dfrac{k q_1 q_2 }{r^2} \
r^2 &= dfrac{k e^2}{F} \
r &= sqrt{dfrac{k e^2 }{F}} \
r &= e sqrt{dfrac{k }{F}} \
r &= 1.6 cdot 10^{-19} ~mathrm{C} cdot sqrt{dfrac{ 9 cdot 10^9 ~mathrm{dfrac{N m^2}{C^2}} }{ 3.5 cdot 10^{-10} ~mathrm{N}}}
end{align*}
$$
$$
boxed{ r = 8.1135 cdot 10^{-10} ~mathrm{m} }
$$
r = 8.1135 cdot 10^{-10} ~mathrm{m}
$$
$$
F_g = G dfrac{m_A m_B}{r^2}
$$
where $G = 6.67 cdot 10^{-11} ~mathrm{dfrac{Nm^2}{kg^2}}$ is gravitational constant.
This means that gravitational force between a proton and an electron in a hydrogen atom is equal to:
$$
begin{equation}
F_g = G dfrac{m_p m_e}{r^2}
end{equation}
$$
where $r$ is distance between a proton and an electron and $m_p$ and $m_e$ are mass of proton and electron, respectfully.
Coulomb’s law states that the electric force $F$ between charges $q_A$ and $q_B$ at a distance $r$ from each other is given as:
$$
F_e = dfrac{k q_A q_B}{r^2}
$$
where $k = 9 cdot 10^9 ~mathrm{dfrac{N m^2}{C^2}}$ is Coulomb constant.
This means that electric force between a proton and an electron in a hydrogen atom is equal to:
$$
begin{equation}
F_e = k dfrac{q_p q_e}{r^2}
end{equation}
$$
where $r$ is distance between a proton and an electron and $q_p$ and $q_e$ are charge of proton and electron, respectfully, which in both cases is equal to elementary charge $e = 1.6 cdot 10^{-19} ~mathrm{C}$
Keep in mind that charge on the electron is negative $q_e = -e$ and charge of proton is positive $q_p = e$, but since we only care about a ratio between the two forces above, we can use a positive sign for charge of an electron.
$$
begin{align*}
dfrac{ F_e }{ F_g} &= dfrac{ dfrac{k q_p q_e }{r^2} }{ G dfrac{m_p m_e}{r^2} } \
dfrac{ F_e }{ F_g} &= dfrac{ k q_p q_e }{ G m_p m_e } \
dfrac{ F_e }{ F_g} &= dfrac{ k e^2 }{ G m_p m_e } \
%
%
&text{mass of proton is $m_p = 1.67 cdot 10^{-27} ~mathrm{kg} $ } \
& text{mass of electron is $m_e = 9.1 cdot 10^{-31} ~mathrm{kg} $ } \
%
%
dfrac{ F_e }{ F_g} &= dfrac{ 9 cdot 10^9 ~mathrm{dfrac{N m^2}{C^2}} cdot (1.6 cdot 10^{-19} ~mathrm{C})^2 }{ 6.67 cdot 10^{-11} ~mathrm{dfrac{Nm^2}{kg^2}} cdot 1.67 cdot 10^{-27} ~mathrm{kg} cdot 9.1 cdot 10^{-31} ~mathrm{kg} } \
%
%
dfrac{ F_e }{ F_g} &= dfrac{ 9 cdot 10^9 ~mathrm{dfrac{N m^2}{C^2}} cdot 2.56 cdot 10^{-38} ~mathrm{C^2} }{ 6.67 cdot 10^{-11} ~mathrm{dfrac{Nm^2}{kg^2}} cdot 1.67 cdot 10^{-27} ~mathrm{kg} cdot 9.1 cdot 10^{-31} ~mathrm{kg} } \
%
%
dfrac{ F_e }{ F_g} &= dfrac{2.304 cdot 10^{-28} }{ 1.0136 cdot 10^{-67} }
end{align*}
$$
$$
boxed{ dfrac{ F_e }{ F_g} = 2.273 cdot 10^{39}}
$$
dfrac{ F_e }{ F_g} = 2.273 cdot 10^{39}
$$

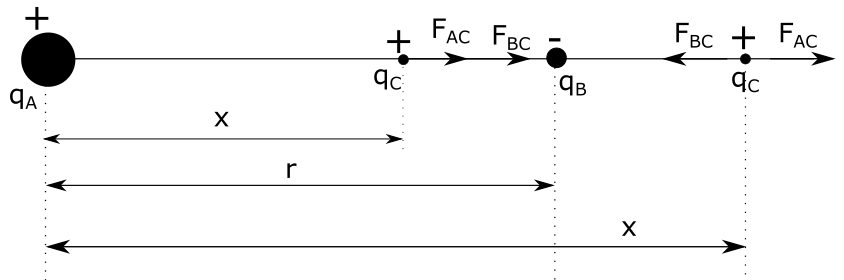
We’ll see that there are actually two positions $x_1$ and $x_2$, as shown in the figure above, although one of these solutions won’t make physical sense.
In order for net force on third charged sphere to be equal to zero,
center of all the three spheres must be at a same line. This means that the third sphere must be placed somewhere on the $x$-axis.
We know that the electrostatic force acting between charges $q_1$ and $q_2$, at a distance $r$ from each other is equal to:
$$
F_e = k dfrac{q_1 q_2}{r^2}
$$
where $k = 9 cdot 10^9 ~mathrm{dfrac{N m^2}{C^2}}$.
Let’s assume that the charges are positioned as in the figure above.
We can now use the equation above to find force $F_{AC}$ acting between charges $q_A$ and $q_C$ and force $F_{BC}$ acting between charges $q_B$ and $q_C$.
Forces acting on the third charged sphere $q_{C}$ are:
$$
begin{align*}
F_{AC} &= k cdot dfrac{q_A cdot q_{C}}{x^{2}}\
F_{BC} &= k cdot dfrac{q_B cdot q_{C}}{(r-x)^{2}}\
end{align*}
$$
Condition above states that the net force at a point where third charged sphere $q_C$ is placed is zero which means that forces that act on third sphere are equal in magnitude. We thus write:
$$
begin{align*}
F_{AC}&=F_{BC}\
tag{plug in the expressions for these forces} \
k cdot dfrac{q_A cdot q_{C}}{x^{2}}&=k cdot dfrac{q_B cdot q_{C}}{(r-x)^{2}}\
tag{We can divide both sides by $k cdot q_{C}$}\
dfrac{q_A}{x^{2}}&=dfrac{q_B}{(r-x)^{2}}tag{1}\
tag{multiply by $ x^2$ and $(r-x)^2$} \
q_A cdot (r-x)^{2}&=q_B cdot x^{2}\
tag{calculate the term $(r-x)^2$} \
q_A cdot (r^{2}-2cdot r cdot x+x^{2})&=q_B cdot x^{2}\
tag{distribute the term on the left side of the equation} \
q_A cdot r^{2}- q_Acdot 2cdot r cdot x+ q_A cdot x^{2}&=q_B cdot x^{2}\
q_A cdot r^{2}- q_Acdot 2cdot r cdot x+ q_A cdot x^{2}-q_B cdot x^{2}&=0\
tag{group the terms containing $x^2$} \
(q_A-q_B) cdot x^{2} – 2 cdot q_A cdot r cdot x+ q_A cdot r^{2}&=0\
end{align*}
$$
Notice that the equation above is quadratic equation in terms of $x$.
Any quadratic equation is written as:
$$
ax^2 + bx + c = 0
$$
Notice that in our case:
$$
begin{align*}
a &= (q_A-q_B) \
b &= – 2 cdot q_A cdot r \
c &= q_A cdot r^{2}
end{align*}
$$
$$
x_{1,2} =dfrac{-b pm sqrt{ b^2-4ac }}{2 a }
$$
The equation above is quadratic formula.
We will apply the quadratic formula to solve for $x$:
$$
begin{align*}
tag{apply quadratic formula} \
x_{1,2}&=dfrac{2cdot q_A cdot r pm sqrt{4 cdot q_A^{2} cdot r^{2}-4(q_A-q_B) cdot q_A cdot r^{2}}}{2 cdot (q_A-q_B)}\
tag{group the terms containing $4 r^2$} \
x_{1,2}&=dfrac{2cdot q_A cdot r pm sqrt{4 cdot r^{2} cdot [q_A^{2}-(q_A-q_B) cdot q_A]}}{2 cdot (q_A-q_B)}\
tag{Notice $sqrt{4 cdot r^{2} cdot [q_A^{2}-(q_A-q_B) cdot q_A]} = sqrt{4 r^2} cdot sqrt{q_A^{2}-(q_A-q_B) cdot q_A} $ } \
x_{1,2}&=dfrac{2cdot q_A cdot r pm 2 cdot r cdot sqrt{q_A^{2}-(q_A-q_B) cdot q_A}}{2 cdot (q_A-q_B)}\
tag{factor out $2r$ from the equation} \
x_{1,2}&=2r cdot dfrac{q_A pm sqrt{q_A^{2}-(q_A-q_B) cdot q_A}}{2(q_A-q_B)}\
tag{cancel out $2$} \
x_{1,2}&=r cdot dfrac{q_A pm sqrt{q_A^{2}-(q_A-q_B) cdot q_A}}{(q_A-q_B)}\
tag{notice that $ (q_A-q_B) cdot q_A = q_A^{2} -q_B cdot q_A $} \
x_{1,2}&=r cdot dfrac{q_A pm sqrt{q_A^{2}-(q_A^{2} -q_B cdot q_A)}}{(q_A-q_B)}\
x_{1,2}&=r cdot dfrac{q_A pm sqrt{q_A^{2}-q_A^{2} +q_B cdot q_A)}}{(q_A-q_B)}\
x_{1,2}&=r cdot dfrac{q_A pm sqrt{q_B cdot q_A}}{(q_A-q_B)}
end{align*}
$$
$$
begin{align*}
x_1&=1 mathrm{~m} cdot dfrac{64 mathrm{~mu C} – sqrt{16mathrm{~mu C} cdot 64 mathrm{~mu C}}}{(64 mathrm{~mu C}-16mathrm{~mu C})}\
tag{ $ 1 ~mathrm{mu C} = 10^{-6 } ~mathrm{C} $ } \
x_1&=1 mathrm{~m} cdot dfrac{64 cdot 10^{-6} mathrm{~C} – sqrt{16 cdot 10^{-6} mathrm{~C} cdot 64 cdot 10^{-6} mathrm{~C}}}{(64 cdot 10^{-6} mathrm{~C}-16 cdot 10^{-6}mathrm{~C})}\
x_1&=1 mathrm{~m} cdot dfrac{64 cdot 10^{-6} mathrm{~C} – 32 cdot 10^{-6} mathrm{~C}}{48 cdot 10^{-6} mathrm{~C}}
end{align*}
$$
$$
boxed{ x_1=0.66 mathrm{~m} }
$$
And we also find that $x_2$ is equal to:
$$
begin{align*}
x_2 &=1 mathrm{~m} cdot dfrac{64 mathrm{~mu C} + sqrt{16mathrm{~mu C} cdot 64 mathrm{~mu C}}}{(64 mathrm{~mu C}-16mathrm{~mu C})}\
tag{ $ 1 ~mathrm{mu C} = 10^{-6 } ~mathrm{C} $ } \
x_2&=1 mathrm{~m} cdot dfrac{64 cdot 10^{-6} mathrm{~C}+ sqrt{16 cdot 10^{-6} mathrm{~C} cdot 64 cdot 10^{-6} mathrm{~C}}}{(64 cdot 10^{-6} mathrm{~C}-16 cdot 10^{-6}mathrm{~C})}\
x_2&=1 mathrm{~m} cdot dfrac{64 cdot 10^{-6} mathrm{~C} + 32 cdot 10^{-6} mathrm{~C}}{48 cdot 10^{-6} mathrm{~C}}
end{align*}
$$
$$
boxed{ x_2= 2 mathrm{~m} }
$$
$$
x_1=0.66 mathrm{~m}
$$
$$
text{and}
$$
$$
x_2= 2 mathrm{~m}
$$
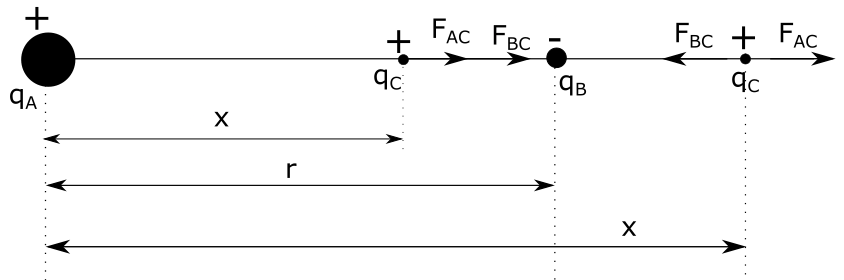
We must take a look at these solutions to determine if both of the solutions make physical sense. As we can see, the first solution
$x_1=0.66 mathrm{~m}$ requires the charge $q_C$ to be placed between charges $q_A$ and $q_B$ and as we can see from from the figure above, charge $q_A$ will push charge $q_C$ to the right, while charge $q_B$ will attract charge $q_C$ to the right, which means that if we place charge $q_C$ between the two other charges, it will get pushed to the right, which means that net force acting on charge $q_C$ won’t be zero in this point. This means that the solution $x_1=0.66 mathrm{~m}$ doesn’t make physical sense and is thus rejected. If we take a look at the other position of charge $q_C$, being $x_2= 2 mathrm{~m}$, we see that at this point, charge $q_C$ is being attracted by charge $q_B$ and pushed to the left, while at the same time, it is repelled by charge $q_A$ and pushed to the right, which means that at this point, we can actually have a zero net force acting on charge $q_C$.
First solution of this quadratic equation doesn’t have physical sense, thus:
$$
boxed{ a)~~ x= 2 mathrm{~m} }
$$
$$
dfrac{q_A}{x^{2}} =dfrac{q_B}{(r-x)^{2}}
$$
From equation $(1)$ it follows that the points in which net force is zero doesn’t depend on the charge of the third sphere $q_C$.
There are two possible points where net force acting on charge $q_C$ could equal zero, being:
$$
x_1=0.66 mathrm{~m}
$$
$$
text{and}
$$
$$
x_2= 2 mathrm{~m}
$$
If we place a positively charged sphere with charge
$q_{C}=+6 mathrm{~mu C}$, a point on the $x$-axis where net force on this charge will be zero is:
$$
boxed{ x= 2 mathrm{~m} }
$$
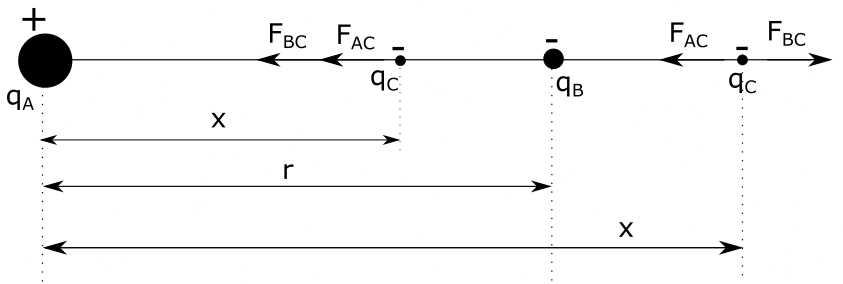
As we can see, if we place charge $q_C$ between charges $q_A$ and $q_B$, charge $q_A$ will attract charge $q_C$, pulling it to the left, while charge $q_B$ will push this charge to the left. This means that the point between these two charges is not a valid solution for this case either. Now let’s see what happens with the equations when we put a negative charge between charges $q_A$ and $q_B$. Same principle applies, we want the net force acting on charge $q_C$ to be zero, which is only possible if magnitude of these forces is the same, while their direction is opposite. Magnitude of these forces is:
$$
begin{align*}
F_{AC} &= k cdot dfrac{q_A cdot q_{C}}{x^{2}}\
F_{BC} &= k cdot dfrac{q_B cdot q_{C}}{(r-x)^{2}}\
end{align*}
$$
As we can see, since magnitude of these forces must be equal, we have:
$$
begin{align*}
F_{AC} &= F_{BC} \
tag{plug in the magnitude of these forces} \
k cdot dfrac{q_A cdot q_{C}}{x^{2}} &= k cdot dfrac{q_B cdot q_{C}}{(r-x)^{2}} \
tag{cancel out $k$ and $q_C$} \
dfrac{q_A}{x^{2}}&=dfrac{q_B}{(r-x)^{2}}
end{align*}
$$
As we can see, as expected, the equation above is actually equation $(1)$, which means that adding any charge $q_C$ won’t affect the points where net force between charges $q_1$ and $q_B$ is zero. This means that in this case, we have the same system of solutions, being:
$$
x_1=0.66 mathrm{~m}
$$
$$
text{and}
$$
$$
x_2= 2 mathrm{~m}
$$
However, since $x_1$ is between charges $q_1$ and $q_B$, we see that this solution doesn’t make physical sense and that the real solution is:
$$
boxed{ x= 2 mathrm{~m} }
$$
begin{align*}
a)~~ x = 2 mathrm{~m} \
b)~~ x = 2 mathrm{~m} \
c)~~ x = 2 ~mathrm{m}
end{align*}
$$
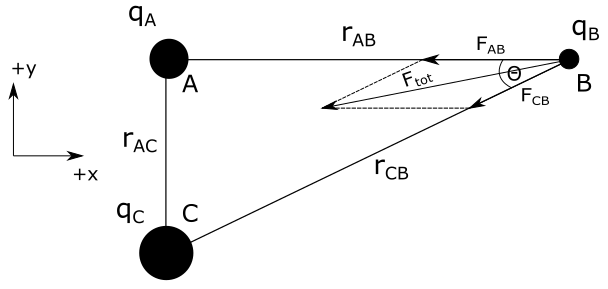
Distances between charged spheres given in problem are $r_{AB}=4.0 mathrm{~cm}$ and $r_{AC}=3.0 mathrm{~cm}$. We need to determine total force acting on sphere $B$.
We know that the electrostatic force acting between charges $q_1$ and $q_2$, at a distance $r$ from each other is equal to:
$$
F_e = k dfrac{q_1 q_2}{r^2}
$$
where $k = 9 cdot 10^9 ~mathrm{dfrac{N m^2}{C^2}}$.
To find total force on charged sphere $B$ we need to find all forces that act on the charged sphere $B$. Charged sphere $A$ acts on charged sphere $B$ with attractive electric force. Direction of this force is shown in the figure above. Magnitude of this force is equal to:
$$
begin{align*}
F_{AB}&=k cdot dfrac{q_{A}cdot q_{B}}{r_{AB}^{2}}\
tag{plug in the values} \
F_{AB}&=8.99 cdot 10^9 mathrm{~dfrac{Nm^2}{C^2}} cdot dfrac{4.5 mathrm{~mu C}cdot 8.2 mathrm{~mu C}}{(4.0 mathrm{~cm})^{2}}\
tag{ $ 1 ~mathrm{mu C} = 10^{-6 } ~mathrm{C} $ } \
tag{$ 1 ~mathrm{cm} = 10^{-2} ~mathrm{m} $} \
F_{AB}&=8.99 cdot 10^9 mathrm{~dfrac{Nm^2}{C^2}} cdot dfrac{4.5 cdot 10^{-6} mathrm{~C}cdot 8.2 cdot 10^{-6} mathrm{~C}}{(0.04 mathrm{~m})^{2}}\
F_{AB}&=207.56 mathrm{~N}
end{align*}
$$
$$
begin{align*}
F_{CB}&=k cdot dfrac{q_{C}cdot q_{B}}{r_{CB}^{2}}\
end{align*}
$$
All the quantities on the right side of equation above are known except for $r_{CB}$. We can determine $r_{CB}$ from Pythagorean theorem. From figure we have:
$$
begin{align*}
r_{CB}^{2}&=r_{AB}^{2} + r_{AC}^{2}\
tag{find square root of the equation above} \
r_{CB}&=sqrt{r_{AB}^{2} + r_{AC}^{2}}\
tag{plug in the values} \
r_{CB}&=sqrt{(4.0 mathrm{~cm})^{2} + (3.0 mathrm{~cm})^{2}}\
tag{$ 1 ~mathrm{cm} = 10^{-2} ~mathrm{m} $} \
r_{CB}&=sqrt{(0.04 mathrm{~m})^{2} + (0.03 mathrm{~m})^{2}}\
r_{CB}&=sqrt{0.0016 mathrm{~m^{2}} + 0.0009 mathrm{~m^{2}}}\
r_{CB}&=sqrt{0.0025 mathrm{~m^{2}}}\
r_{CB}&=0.05 mathrm{~m}\
end{align*}
$$
$$
begin{align*}
F_{CB}&=8.99cdot 10^9 mathrm{ ~dfrac{Nm^2}{C^2} } cdot dfrac{6.0 mathrm{~mu C}cdot 8.2 mathrm{~mu C}}{(0.05 mathrm{~m})^{2}}\
F_{CB}&=8.99cdot 10^9 mathrm{ ~dfrac{Nm^2}{C^2} } cdot dfrac{6.0 cdot 10^{-6} mathrm{~C}cdot 8.2 cdot 10^{-6} mathrm{~C}}{(0.05 mathrm{~m})^{2}}\
F_{CB}&=177.12 mathrm{~N}
end{align*}
$$
$$
begin{align*}
vec{F}_{tot}=vec{F}_{AB}+vec{F}_{CB}
end{align*}
$$
By squaring equation above we can determine magnitude of force $F_{tot}$. Direction of this force is shown in the figure above.
$$
begin{align*}
(vec{F}_{tot})^{2}&=(vec{F}_{AB}+vec{F}_{CB})^{2}\
tag{note that dot product of any vector $vec{a}$ with itself is: $vec{a } cdot vec{a} = a^2 $ } \
F_{tot}^{2}&=F_{AB}^{2}+F_{CB}^{2}+2 cdot vec{F}_{AB} cdot vec{F}_{CB} \
tag{find square root of the equation above} \
F_{tot}&=sqrt{F_{AB}^{2}+F_{CB}^{2}+2 cdot vec{F}_{AB} cdot vec{F}_{CB} }tag{1}
end{align*}
$$
$$
vec{F}_{AB} cdot vec{F}_{CB} =F_{AB} cdot F_{CB} cdot cos theta
$$
where $theta$ is angle between vectors $vec{F}_{AB}$ and $vec{F}_{CB}$, which is the same angle as angle between $r_{AB}$ and $r_{CB}$. From this, we can write:
$$
cos theta = dfrac{r_{AB}}{r_{CB}}
$$
By plugging in this with other quantities into equation $(1)$:
$$
begin{align*}
F_{tot}&=sqrt{F_{AB}^{2}+F_{CB}^{2}+2 cdot vec{F}_{AB} cdot vec{F}_{CB} } \
F_{tot}&=sqrt{F_{AB}^{2}+F_{CB}^{2}+2 cdot F_{AB} cdot F_{CB} cdot dfrac{r_{AB}}{r_{CB}}}\
F_{tot}&=sqrt{(207.56 mathrm{~N})^{2}+(177.12 mathrm{~N})^{2}+2 cdot 207.56 mathrm{~N} cdot 177.12 mathrm{~N} cdot dfrac{0.04 mathrm{~m}}{0.05 mathrm{~m}}}
end{align*}
$$
$$
boxed{ F_{tot} =365.066 mathrm{~N} }
$$
F_{tot} =365.066 mathrm{~N}
$$
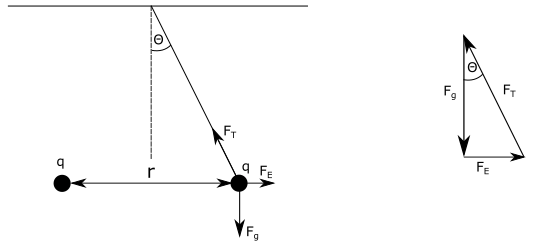
$a)$ We need to determine the weight $F_{g}$ of the pith ball, acting on the suspended pith ball. $F_{g}$ is equal to the mass of the ball multiplied by gravitational acceleration $g=9.81 mathrm{~dfrac{m}{s^{2}}}$, stated as:
$$
begin{align*}
F_{g} &= m cdot g\
tag{plug in the values} \
F_{g} &= 1 mathrm{~g} cdot 9.81 mathrm{~dfrac{m}{s^{2}}}\
tag{ $ 1 mathrm{~g} = 0.001 mathrm{~kg} $ } \
F_{g} &= 0.001 mathrm{~kg} cdot 9.81 mathrm{~dfrac{m}{s^{2}}}
end{align*}
$$
$$
boxed{F_{g}=0.00981 mathrm{~N}}
$$
$$
begin{align*}
vec{F_{g}}+vec{F_{E}}+vec{F_{T}}&=0\
tag{by rearranging:}\
vec{F_{g}}+vec{F_{E}}&=-vec{F_{T}}
end{align*}
$$
where $F_g$ is gravitational force acting on the pith ball (its weight), $F_e$ is electrostatic force between the pith balls and $F_T$ is tension force acting on the insulating thread.
From the last equation we see that vector sum of vectors $vec{F_{g}}$ and $vec{F_{E}}$ has same magnitude as tension force vector $vec{F_{T}}$, but it has a different direction. From this we can construct triangle using force vectors. Triangle is shown on the left side of the figure above. From it this triangle we can see the following:
$$
begin{align*}
tan theta = dfrac{F_{E}}{F_{g}}
end{align*}
$$
From the equation above we can express and calculate $F_{E}$ as:
$$
begin{align*}
F_{E} &= tan theta cdot F_{g}\
tag{ $ theta=30^{circ} $ } \
F_{E} &= tan (30^{circ}) cdot 0.00981 mathrm{~N}\
tag{ $ tan(30^{circ})=0.577 $ } \
F_{E} &= 0.577 cdot 0.00981 mathrm{~N}
end{align*}
$$
$$
boxed{F_{E}=0.00566 mathrm{~N}}
$$
$$
begin{align*}
F_{E}&=k cdot dfrac{qcdot q}{r^{2}}\
& text{where $k = 8.99cdot 10^9 mathrm{ ~ dfrac{Nm^2}{C^2} }$ is Coulomb’s constant} \
& text{and $q$ is charge carried by each of the pith balls} \
F_{E}&=k cdot dfrac{q^{2}}{r^{2}} \
tag{multiply by $r^2$} \
F_{E}cdot r^{2}&=k cdot q^{2}
end{align*}
$$
From the last equation we can express charge $q$ on each of the pith balls as:
$$
begin{align*}
F_{E}cdot r^{2}&=k cdot q^{2}\
tag{we divide everything by $k$}\
q^{2}&=dfrac{F_{E}cdot r^{2}}{k}\
tag{we take square root of both sides}\
q&=sqrt{dfrac{F_{E}cdot r^{2}}{k}}\
tag{plug in the values}\
q&=sqrt{dfrac{0.00566 mathrm{~N}cdot (3 mathrm{~cm})^{2}}{8.99cdot 10^9 mathrm{ ~ dfrac{Nm^2}{C^2} }}}\
tag{$3 mathrm{~cm}=0.03 mathrm{~m}$} \
q&=sqrt{dfrac{0.00566 mathrm{~N}cdot (0.03 mathrm{~m})^{2}}{8.99cdot 10^9 mathrm{ ~ dfrac{Nm^2}{C^2} }}}\
q&=sqrt{dfrac{0.00566 mathrm{~N}cdot 0.0009 mathrm{~m^{2}}}{8.99cdot 10^9 mathrm{ ~ dfrac{Nm^2}{C^2} }}}
end{align*}
$$
$$
boxed{q=2.38 cdot 10^{-8}mathrm{~C}}
$$
begin{align*}
& a)~~F_{g}=0.00981 mathrm{~N}\
& b)~~ F_{E}=0.00566 mathrm{~N}\
& c)~~ q=2.38 cdot 10^{-8}mathrm{~C} \
end{align*}
$$
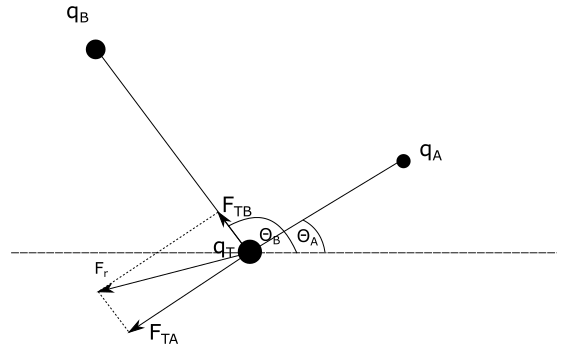
We are given:
$$
begin{align*}
text{Charge of the test charge}~q_{T}&=+7.2 mathrm{~mu C} \
text{Charge of the first charge}~q_{A}&= +3.6 mathrm{~mu C} \
text{Charge of the second charge}~q_{B}&=-6.6 mathrm{~mu C} \
text{Distance between test charge and first charge}~r_{TA}&=2.5 mathrm{~cm} \
text{Distance between test charge and second charge}~r_{TB}&=6.8 mathrm{~cm} \
text{Angle at which $q_{A}$ is placed with respect to the horizontal }~ theta_{A}&=35^{circ} \
text{Angle at which $q_{B}$ is placed with respect to the horizontal }~ theta_{B}&=125^{circ} \
end{align*}
$$
First charge $q_{A}$ acts on test charge $q_{T}$ with repulsive electric force because both charges have the same sign. Magnitude of this force is equal to:
$$
begin{align*}
F_{TA}&=k cdot dfrac{q_{T}cdot q_{A}}{r_{TA}^{2}}\
&text{where $k = 8.99cdot 10^9 mathrm{ ~ dfrac{Nm^2}{C^{2}}}$ is Coulomb’s constant} \
tag{plug in the given values }\
F_{TA}&=8.99cdot 10^9 mathrm{~dfrac{Nm^2}{C^{2}}} cdot dfrac{7.2 mathrm{~mu C}cdot 3.6 mathrm{~mu C} }{(2.5 mathrm{~cm})^{2}}\
tag{$7.2 mathrm{~mu C} = 7.2 cdot 10^{-6} mathrm{~C}$}\
tag{$3.6 mathrm{~mu C} = 3.6 cdot 10^{-6} mathrm{~C}$}\
tag{$2.5 mathrm{~cm} = 0.025 mathrm{~m}$}\
F_{TA}&=8.99cdot 10^9 mathrm{~dfrac{Nm^2}{C^{2}}} cdot dfrac{7.2 cdot 10^{-6} mathrm{~C}cdot 3.6 cdot 10^{-6}mathrm{~C} }{(0.025 mathrm{~m})^{2}}\
F_{TA}&=8.99cdot 10^9 mathrm{~dfrac{Nm^2}{C^{2}}} cdot dfrac{7.2 cdot 10^{-6} mathrm{~C}cdot 3.6 cdot 10^{-6}mathrm{~C} }{0.000625 mathrm{~m^{2}}}
end{align*}
$$
$$
boxed{F_{TA}=372.8 mathrm{~N}}
$$
Second charge $q_{B}$ acts on test charge $q_{T}$ with attractive electric force because these charges have a different signs. Magnitude of this force is equal to:
$$
begin{align*}
F_{TB}&=k cdot dfrac{q_{T}cdot q_{B}}{r_{TB}^{2}}\
tag{plug in values given in problem}\
F_{TB}&=8.99cdot 10^9 mathrm{~dfrac{Nm^2}{C^{2}}} cdot dfrac{7.2 mathrm{~mu C}cdot 6.6 mathrm{~mu C} }{(6.8mathrm{~cm})^{2}}\
tag{$7.2 mathrm{~mu C} = 7.2 cdot 10^{-6} mathrm{~C}$}\
tag{$3.6 mathrm{~mu C} = 6.6 cdot 10^{-6} mathrm{~C}$}\
tag{$6.8 mathrm{~cm} = 0.068 mathrm{~m}$}\
F_{TB}&=8.99cdot 10^9 mathrm{~dfrac{Nm^2}{C^{2}}} cdot dfrac{7.2 cdot 10^{-6} mathrm{~C}cdot 6.6 cdot 10^{-6}mathrm{~C} }{(0.068 mathrm{~m})^{2}}\
F_{TB}&=8.99cdot 10^9 mathrm{~dfrac{Nm^2}{C^{2}}} cdot dfrac{7.2 cdot 10^{-6} mathrm{~C}cdot 6.6 cdot 10^{-6}mathrm{~C} }{0.004624 mathrm{~m^{2}}}
end{align*}
$$
$$
boxed{F_{TB}=92.3 mathrm{~N}}
$$

b)
$$
We need to sketch force diagram of all forces that act on $q_{T}$. Force diagram is visible on the figure above. Force between charges $q_{B}$ and $q_{T}$ is attractive and that’s why force $F_{TB}$ is pointing towards charge $q_{B}$ on the line that connects these two charges. Force between charges $q_{A}$ and $q_{T}$ is repulsive and that’s why force $F_{TA}$ is pointing away from charge $q_{T}$ on the line that connects these two charges.
Vector of the resulting force $F_r$ is found by vector addition of vectors
of forces $F_{TA}$ and $F_{TB}$.
c)
$$
We can see that vectors $F_{TA}$, $F_{TB}$ and resultant force vector $F_{r}$ form a right triangle. By using Pythagorean theorem we can write:
$$
begin{align*}
F_{r}^{2}&=F_{TA}^{2}+F_{TB}^{2}\
tag{find square root of the equation above} \
F_{r}&=sqrt{F_{TA}^{2}+F_{TB}^{2}}\
tag{plug in the values} \
F_{r}&=sqrt{(372.8 mathrm{~N})^{2}+(92.3 mathrm{~N})^{2}}\
F_{r}&=sqrt{147499.13 mathrm{~N}^{2}}
end{align*}
$$
$$
boxed{F_{r}=384.05 mathrm{~N}}
$$
begin{align*}
&a)~~ F_{TA}=372.8 mathrm{~N} \
& a)~~ F_{TB}=92.3 mathrm{~N} \
& b)~~ text{Hint: Draw the direction of forces acting on test charge.} \
& c)~~ F_{r}=384.05 mathrm{~N} \
end{align*}
$$
Neutralizer connects electrically charged diagonal sectors on both of the disks.
In this process, positive and negative charged are separated on two halves of each of the disks. Charges are then collected from the sectors by electrodes called collectors. Each Wimshurst machine also has two previously described Leyden jars for collecting induced charges. These two Leyden jars have a common electrode. Two non-common electrodes are connected to a spark gap. When enough charges are stored in Leyden jars, electric discharge occurs at the spark gap.
$$
begin{align*}
T=2 cdot pi sqrt{dfrac{l}{g}}
end{align*}
$$
where $l$ is length of thread that we used to make a pendulum and $T$ is period of oscillation of pendulum.
Let’s square the equation above:
$$
T^2 = 4 pi^2 dfrac{l}{g}
$$
Note that we can easily measure the length of a pendulum by using a meter. Also note that the equation above only works if maximum angle that the pendulum reaches during an oscillation is a very small angle, less than $6 ^circ$
We can express the gravitational acceleration from the equation above as:
$$
begin{align*}
g=4cdot pi^{2} cdot dfrac{l}{T^{2}}tag{1}
end{align*}
$$
By measuring time $t$ in which these oscillations happen and number $N$ of oscillations during this time interval, we can calculate a period $T$ of a single oscillation of pendulum with equation:
$$
T=dfrac{t}{N}
$$
By plugging in the last expression for period of oscillation of a pendulum into equation $(1)$, we find an expression for local gravitational acceleration:
$$
begin{align*}
g=4cdot pi^{2} cdot dfrac{l}{(dfrac{t}{N})^{2}}
end{align*}
$$
$$
boxed{g=4cdot pi^{2} cdot dfrac{lcdot N^{2}}{t^{2}}}
$$
Now that we have an equation that we can use to find gravitational acceleration $g$, we can measure the time $t$ that it takes for pendulum to make 10 full oscillations (N= 10). We can easily measure the length $L$ of the thread on the pendulum and plug in our results into the equation above.
$$
T=2 cdot pi sqrt{dfrac{l}{g}}
$$
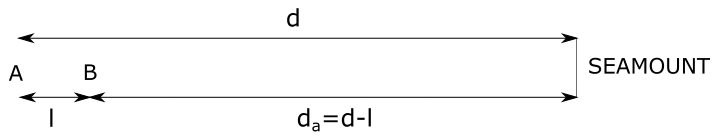
$a)$ We need to determine distance of the submarine from the seamount $d_{a}$. Submarine is at a distance $d$ from the seamount when it sends ping towards it. From the figure we see that in time $t$ submarine travels a distance $l$ from point $A$ to point $B$ and that the ping travels a distance:
$$
begin{align*}
d+d_{a}&= 2cdot d-l
end{align*}
$$
during this same time interval $t$.
From the equation above we can express distance $d_{a}$ that we need to determine:
$$
begin{align*}
d_{a}&= 2cdot d-l-d\
d_{a}&= d-l tag{1}
end{align*}
$$
Distance $l$ from point $A$ to point $B$ that the submarine travels
is equal to a product of speed $upsilon$ of submarine and time $t$ in which submarine travels from point $A$ to point $B$, stated as:
$$
begin{align*}
l &= upsilon t \
tag{plug in the values} \
l&=12 mathrm{~dfrac{m}{s}} cdot 1.8 mathrm{~s}\
l&=21.6 mathrm{~m} tag{2}
end{align*}
$$
$$
begin{align*}
2d – l &= upsilon_{sound} cdot t
end{align*}
$$
We need to determine distance $d_{a}$, so we will first calculate distance $d$, and use it to calculate $d_{a}$ sometime later. Let’s rewrite the equation above:
$$
begin{align*}
2d – l &= upsilon_{sound} cdot t \
tag{move $l$ to the right side of the equation} \
2cdot d&= upsilon_{sound} cdot t +l\
tag{divide the equation by 2} \
d&= dfrac{ upsilon_{sound} cdot t +l}{2}
end{align*}
$$
By plugging in values into the equation above, we can calculate the distance $d$:
$$
begin{align*}
d&=dfrac{1533 mathrm{~dfrac{m}{s}} cdot 1.8 mathrm{~s}+21.6 mathrm{~m}}{2}\
d&=1390.5 mathrm{~m}
end{align*}
$$
We will plug in value for $d$ from the equation above and value for $l$ from $(2)$ into equation $(1)$ to calculate $d_{a}$:
$$
begin{align*}
d_a &= d – l \
tag{plug in the values} \
d_{a}&=1390.5 mathrm{~m}-21.6 mathrm{~m}
end{align*}
$$
$$
boxed{d_{a} =1368.9 mathrm{~m}}
$$
b)
$$
We need to determine frequency of the sound wave sent from the submarine when the sound wave reaches seamount. Frequency of the sound wave will be altered because we have relative motion of source of the sound wave (submarine) and detector (seamount). We will use the equation that describes Doppler shift of the wave:
$$
begin{align*}
f_{d}&=f_{s} cdot dfrac{upsilon_{sound} pm upsilon_{detector}}{upsilon_{sound} mp upsilon_{source}}
end{align*}
$$
Where $f_{d}$ is frequency that we measure at the point of detector, $f_{s}$ is frequency that we measure at the source of the sound wave, $upsilon_{sound}$ is speed of sound in a certain medium (in our case medium seawater with $upsilon_{sound}=1533 mathrm{dfrac{m}{s}}$), $upsilon_{source}$ is speed of the source and $upsilon_{detector}$ is speed of the detector.
If sound source and sound detector approach one another we have $+$ in the numerator and $-$ in the denominator.
Frequency $f_{d}$ of the sound wave when it hits the seamount is equal to:
$$
begin{align*}
f_{d}&=f_{s} cdot dfrac{upsilon_{sound} + upsilon_{detector}}{upsilon_{sound} – upsilon_{source}}
end{align*}
$$
We are given $f_{s}=1500 mathrm{~Hz}$, $upsilon_{detector}=0$ because seamount is stationary, $upsilon_{source}= ~text{speed of the submarine}~ = 12 mathrm{~dfrac{m}{s}}$
and $upsilon_{sound}=1533 mathrm{dfrac{m}{s}}$. We can now plug in these values into the equation above:
$$
begin{align*}
f_{d}&=f_{s} cdot dfrac{upsilon_{sound} + upsilon_{detector}}{upsilon_{sound} – upsilon_{source}} \
f_{d}&=1500 mathrm{~Hz} cdot dfrac{1533 mathrm{dfrac{m}{s}} + 0}{1533 mathrm{dfrac{m}{s}} – 12 mathrm{~dfrac{m}{s}}}
end{align*}
$$
$$
boxed{f_{d} =1511.83 mathrm{~Hz}}
$$
The equation for Doppler shift states:
$$
begin{align*}
f_{d}&=f_{s} cdot dfrac{upsilon_{sound} + upsilon_{detector}}{upsilon_{sound} – upsilon_{source}} \
tag{plug in the values} \
f_{d}&=1511.83 mathrm{~Hz} cdot dfrac{1533 mathrm{dfrac{m}{s}} + 12 mathrm{~dfrac{m}{s}}}{1533 mathrm{dfrac{m}{s}} – 0}
end{align*}
$$
$$
boxed{f_{d}=1523.66 mathrm{~Hz}}
$$
begin{align*}
& a)~~ d_{a} =1368.9 mathrm{~m} \
& b)~~ f_{d} =1511.83 mathrm{~Hz} \
& c)~~ f_{d}=1523.66 mathrm{~Hz} \
end{align*}
$$
$$
begin{align*}
m&=dfrac{-d_{i}}{d_{o}}
end{align*}
$$
where $d_o$ is distance from an object to the centre of the mirror and $d_i$ is distance from the image to the centre of the mirror.
We are given distance of the image $d_{i}= – 12 mathrm{~cm}$ and magnification $m=dfrac{3}{4}$. From the equation above and given quantities we can calculate distance of the object from the mirror as:
$$
begin{align*}
d_{o}&=dfrac{-d_{i}}{m}\
tag{plug in the values} \
d_{o}&=dfrac{-(-12mathrm{~cm})}{dfrac{3}{4}}\
d_{o}&=dfrac{12mathrm{~cm} cdot 4}{ 3 }\
d_{o}&=16 mathrm{~cm}
end{align*}
$$
$$
begin{align*}
dfrac{1}{f}&=dfrac{1}{d_{i}}+dfrac{1}{d_{o}}\
tag{plug in the values} \
dfrac{1}{f}&=dfrac{1}{(-12mathrm{~cm})}+dfrac{1}{16 mathrm{~cm}}\
dfrac{1}{f}&=-dfrac{1}{(12mathrm{~cm})}+dfrac{1}{16 mathrm{~cm}}\
dfrac{1}{f}&=dfrac{1}{16 mathrm{~cm}}-dfrac{1}{12mathrm{~cm}}\
tag{calculate each of the fractions} \
dfrac{1}{f}&=0.0625 mathrm{~cm^{-1}}-0.0833 mathrm{~cm^{-1}}\
dfrac{1}{f}&=-0.02083333 mathrm{~cm^{-1}}\
tag{find reciprocal value of the equation above} \
f&=dfrac{1}{-0.02083333} mathrm{~cm}
end{align*}
$$
$$
boxed{f=-48 mathrm{~cm}}
$$
f=-48 mathrm{~cm}
$$
Note that the focal length $f$ is taken as negative since we talk about a diverging (concave) lens.
$$
dfrac{1}{f} =dfrac{1}{d_i}+dfrac{1}{d_o}
$$
where $f$ is focal length of the lens, $d_i$ is distance from the center of the lens to the image and $d_o$ is distance from the lens to the object.
We will use the equation above to determine distance of the image:
$$
begin{align*}
dfrac{1}{f}&=dfrac{1}{d_i}+dfrac{1}{d_o}\
tag{express $dfrac{1}{d_i}$ from the equation above} \
dfrac{1}{d_i}&=dfrac{1}{f}-dfrac{1}{d_o}\
tag{plug in the values} \
dfrac{1}{d_i}&=dfrac{1}{(-24 mathrm{~cm})}-dfrac{1}{20 mathrm{~cm}}\
dfrac{1}{d_i}&=-0.0416 mathrm{~cm^{-1}}-0.05 mathrm{~cm^{-1}}\
dfrac{1}{d_i}&=-0.0916 mathrm{~cm^{-1}}\
tag{find reciprocal value of the equation} \
d_i &=dfrac{1}{-0.0916 mathrm{~cm^{-1}} }\
d_i &=dfrac{1}{-0.0916} mathrm{~cm}
end{align*}
$$
$$
boxed{d_i= -10.91 mathrm{~cm}}
$$
$$
begin{align*}
m equiv dfrac{h_i}{h_o} = dfrac{-d_i}{d_o}
end{align*}
$$
From the equation above we can express height of the image $h_i$ in terms of distance of the image $d_i$, height of the object $h_o$ and distance of the object $d_o$:
$$
begin{align*}
dfrac{h_i}{h_o} &= dfrac{-d_i}{d_o} \
tag{express $h_i$ from the equation above} \
h_i &= dfrac{-d_i cdot h_o }{d_o}\
tag{plug in the values} \
h_i &= dfrac{-(-10.91 mathrm{~cm}) cdot 2 mathrm{~cm} }{20 mathrm{~cm}}\
h_i &= dfrac{10.91 mathrm{~cm} cdot 2 mathrm{~cm} }{20 mathrm{~cm}}
end{align*}
$$
$$
boxed{h_i=1.091 mathrm{~cm}}
$$
Diverging (concave) always gives us an upright, virtual image.
d_{i}=-10.91 mathrm{~cm}
$$
$$
h_{i}=1.091 mathrm{~cm}
$$
Diverging (concave) always gives us an upright virtual image.
Diffraction maximum, for light with wavelength $lambda$ is determined from the following equation equation:
$$
begin{align*}
m cdot lambda = d cdot sin theta tag{1}
end{align*}
$$
where $m$ is order of the bright band, $d$ is grate spacing and $theta$ is angle at which we see the given maximum of diffraction.
In our case we are observe the first-order bright band, which means $m=1$. Grate spacing $d$ is equal to the reciprocal value of the number $N$ of lines per unit length which is given in the problem ($N = 11500 mathrm{~dfrac{slits}{cm}}$). We can thus calculate the grate spacing $d$ by finding reciprocal value of number $N$ of lines per unit length:
$$
begin{align*}
d &= dfrac{1}{N} \
tag{plug in the values} \
d&=dfrac{1}{11500 mathrm{~dfrac{slits}{cm}}}\
tag{ $ 1 ~mathrm{cm} = 100 ~mathrm{m} $} \
d&=dfrac{1}{1150000 mathrm{~dfrac{slits}{m}}}\
d&=8.69 cdot 10^{-7} mathrm{~m}
end{align*}
$$
$$
begin{align*}
m cdot lambda &= d cdot sin theta \
tag{express $sin theta $ from the equation above} \
sin theta &= dfrac{m cdot lambda}{d}\
tag{find $arcsin $ of the equation above} \
theta&=arcsin left( dfrac{m cdot lambda}{d} right)\
tag{plug in the values} \
theta&=arcsin left( dfrac{1 cdot 527 mathrm{~nm}}{8.69 cdot 10^{-7} mathrm{~m}} right)\
tag{$527 mathrm{~nm}=527 cdot 10^{-9}mathrm{~m}$}\
theta&=arcsin left( dfrac{1 cdot 527 cdot 10^{-9} mathrm{~m}}{8.69 cdot 10^{-7} mathrm{~m}} right)\
theta&=arcsin left( dfrac{527 cdot 10^{-2}}{8.69} right)\
theta&=arcsin(0.606)
end{align*}
$$
$$
boxed{theta=37.33^{circ}}
$$
theta=37.33^{circ}
$$

