First, I would measure the distance between slits and screen $L$, then I would light slits to make an interference pattern on the screen and measure the distance between first-order bright band and a central one $x$.

Since I would use the light with know wavelength, in this moment I could use equation

$$
begin{align}
d=frac{lambdacdot L}{x}
end{align}
$$

to calculate the distance $d$.

Since we know the definition

$$
begin{align}
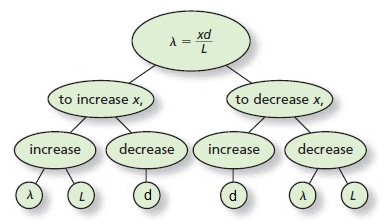
lambda&=frac{xcdot d}{L} \
end{align}
$$

we conclude that a wavelength is proportional to the distance between lines.

Because $lambda_r>lambda_v$ spacing between red lines will be greater than between violet lines.

Since we know the definition

$$
begin{align}
lambda&=frac{xcdot d}{L} \
end{align}
$$

we conclude that a wavelength is proportional to the distance between lines.

Since violet light has the smallest wavelength, bright lines will be the closest.

We see colors on objects because of many reasons.

$textbf{a.}$ colors on soap bubbles are the product of $interference$ on its extremely thin film of soapy water

$textbf{b.}$ rose petals are composed of $pigment$-containing cells

$textbf{c.}$ on oil films, just like on soap bubbles, light $interferes$

$textbf{d.}$ a rainbow appears when Sun light $refracts$ in rain drops

$textbf{a.}$ If the film thickness is doubled, then there is complete destructive interference.

$textbf{b.}$ If the film thickness was increased by half a wavelength of the illuminating light, then there is complete constructive interference.

$textbf{c.}$ If the film thickness was decreased by 1/4 of the wavelength of the illuminating light, then there is complete destructive interference.

A diffraction grating has $a=10^{4}frac{slit}{cm}$ or $b=10^{5}frac{slit}{cm}$ which means one slit is $frac{1}{10^{4}}text{ cm}$ or $frac{1}{10^{5}}text{ cm}$ wide. So $d_a=10^{-4}text{ m}$ or $d_b=10^{-5}text{ m}$.

Form the definition of the wavelength from a diffraction grating

$$
begin{align}
lambda=dcdotsintheta
end{align}
$$

We can conclude that an angle of diffraction is inversely proportional to the size of grating, so for situation $a$ diffraction patter will be more rare and for $b$ narrower.

Let’s first remember we know the definition of the wavelength from a diffraction grating

$$
begin{align}
lambda=dcdotsintheta
end{align}
$$

We see that wavelength is proportional to angle $theta$.

If they light a diffraction grating with green light, a pattern will be narrower which means $theta$ is smaller for the green light, also a wavelength.

In this problem we have two slits separated by $d=1.9times 10^{-5}text{ m}$, the distance between slits and the screen $L=0.8text{ m}$ and distance between first-order bright band and the central bright band on the screen $x=1.9times 10^{-2}text{ m}$. What we need to find is wavelength for double-slit experiment.

As we can see, this problem is an example of Young’s double slit experiment so we will find the solution by using the definition for wavelength.

$$
begin{align}
lambda&=frac{xcdot d}{L} \
lambda&=frac{1.9times 10^{-5}mcdot 1.9times 10^{-2}m}{0.8m} \
&boxed{lambda=4.51times 10^{-7}m}
end{align}
$$

$$
lambda=4.51times 10^{-7}m
$$

The light ray goes through the air, $n=1$, and hits the film of oil, $n_f=1.45$. Here the reflection and phase inversion happens because $n<n_f$.

The light that is used in this problem has a wavelength $lambda=5.45times10^{-7}text{ m}$

The definition of thickness when stripe appears is

$$
begin{align}
d=frac{1}{2}cdot (m+frac{1}{2})cdotfrac{lambda}{n_f}
end{align}
$$

For a thinnest film $m=0$. So, we have

$$
begin{align}
d&=frac{1}{2}cdot (0+frac{1}{2})cdotfrac{5.45times10^{-7}text{ m}}{1.45} \
&boxed{d=9.4times 10^{-8}m}
end{align}
$$

$$
d=9.4times 10^{-8}m
$$

Here we have the light of wavelength $lambda=5.42times10^{-7}text{ m}$ that appears on the screen moved $L=1.2text{ m}$ from the slits. The first-order bright band appears at the $x=4times10^{-2}m$ from the central band.
We need to calculate the distance between two slits.

As we can see, this problem is an example of Young’s double slit experiment so we will find the solution by using the definition for wavelength.

$$
begin{align}
lambda&=frac{xcdot d}{L} \
d&=frac{lambdacdot L}{x} \
d&=frac{5.42times10^{-7}mcdot 1.2m}{4times10^{-2}m} \
&boxed{d=1.63times 10^{-5}m}
end{align}
$$

$$
d=1.63times 10^{-5}m
$$

The light ray goes through the air, $n=1$, and hits the film of oil, $n_f=1.81$. Here the reflection and phase inversion happens because $n<n_f$.

The light that produces stripes in this problem has a wavelength $lambda=4.4times10^{-7}text{ m}$

The definition of thickness when stripe appears is

$$
begin{align}
d=frac{1}{2}cdot (m+frac{1}{2})cdotfrac{lambda}{n_f}
end{align}
$$

Three possible thicknesses of the portion occur at $m=0,1,2$.

For a thinnest film $m=0$. So, we have

$$
begin{align}
d&=frac{1}{2}cdot (0+frac{1}{2})cdotfrac{4.4times10^{-7}text{ m}}{1.81} \
&boxed{d=6.08times 10^{-8}m}
end{align}
$$

Then we have $m=1$. So, we write

$$
begin{align}
d&=frac{1}{2}cdot (1+frac{1}{2})cdotfrac{4.4times10^{-7}text{ m}}{1.81} \
&boxed{d=1.82times 10^{-7}m}
end{align}
$$

And in the end $m=2$.

$$
begin{align}
d&=frac{1}{2}cdot (2+frac{1}{2})cdotfrac{4.4times10^{-7}text{ m}}{1.81} \
&boxed{d=3.04times 10^{-7}m}
end{align}
$$

$d=6.08times 10^{-8}m$, $d=1.82times 10^{-7}m$, $d=3.04times 10^{-7}m$

In this problem we have three different double-slit setups. In setup $A$ we have $d=1.5times10^{-4}m$ and $L=0.6text{ m}$, in $B$ $d=1.75times10^{-4}m$ and $L=0.8text{ m}$ and in $C$ we have $d=1.5times10^{-4}m$ and $L=0.8text{ m}$. We need to calculate the distance between the central bright band and the first-order bright band.

As we can see, this problem is an example of Young’s double slit experiment so we will find the solution by using the definition for wavelength.

$$
begin{align}
lambda&=frac{xcdot d}{L} \
end{align}
$$

But since the wavelength is same in all setups, we will modify our equation to

$$
begin{align}
frac{x}{lambda}&=frac{L}{d} \
end{align}
$$

So we write

$$
(A)
$$

$$
begin{align}
frac{x_A}{lambda}&=frac{0.6text{ m}}{1.5times10^{-4}m} \
frac{x_A}{lambda}&=4times10^{3} \
end{align}
$$

$$
(B)
$$

$$
begin{align}
frac{x_B}{lambda}&=frac{0.8text{ m}}{1.75times10^{-4}m} \
frac{x_B}{lambda}&=4.57times10^{3} \
end{align}
$$

$$
(C)
$$

$$
begin{align}
frac{x_C}{lambda}&=frac{0.8text{ m}}{1.5times10^{-4}m} \
frac{x_C}{lambda}&=5.33times10^{3} \
end{align}
$$

Our solution is

$$
begin{align}
{x_A<x_B<x_C}
end{align}
$$

$$
x_A<x_B<x_C
$$

Monochromatic light passes through a slit $w=1times 10^{-4}text{ m}$. A screen is $L=1text{ m}$ away and the width of the central band is $2cdot x=1.2times 10^{-2}text{ m}$. We will use the definition of the width of the bright band in single slit diffraction.

$$
begin{align}
2cdot x&=frac{2cdotlambdacdot L}{w} \
lambda&=frac{2cdot xcdot w}{2cdot L} \
lambda&=frac{1.2times 10^{-2}text{ m}cdot 1times 10^{-4}text{ m}}{2cdot 1m} \
&boxed{lambda=6times 10^{-7}m}
end{align}
$$

$$
lambda=6times 10^{-7}m
$$

We will solve this problem by using equation

$$
begin{align}
d=frac{1}{N}
end{align}
$$

Since $N=2.5times10^{3} frac{lines}{cm}$, we write

$$
begin{align}
d&=frac{1}{2.5times10^{3} frac{lines}{cm}} \
&boxed{d=4times10^{-6}m}
end{align}
$$

$$
d=4times10^{-6}m
$$

Light $lambda_b=4.5times10^{-7}text{ m}$ passes through a slit of width $w=1.5times 10^{-4}text{ m}$. A screen is $L=1text{ m}$. We will use the definition of the width of the bright band in single slit diffraction.

The definition of the bright band in single slit diffraction is

$$
begin{align}
2cdot x=frac{2cdot lambdacdot L}{w} \
end{align}
$$

$2cdot x$ represent the width of the bright band so since we want the distance from the center to the first dark band, we need to divide equation by 2.

$$
begin{align}
x&=frac{lambda_bcdot L}{w} \
x&=frac{4.5times 10^{-7}mcdot 1text{ m}}{1.5times 10^{-4}m} \
&boxed{x=3times 10^{-3}m}
end{align}
$$

$$
x=3times 10^{-3}m
$$

In this problem we have to find how large i Earth seen by the $Hubble$ $Space$ $Telescope$. We will define that size with radius and sing with $x_{obj}$. We know the diameter of a telecope $D=2.4text{m}$, the position of a telescope is $L_{obj}=1times10^{5}text{ m}$ and use the wavelength $lambda=5.1times10^{-7}text{ m}$.

We will use The Rayleigh criterion to solve this problem.

$$
begin{align}
{x_{obj}}&=frac{1.22cdotlambdacdot L_{obj}}{D} \
{x_{obj}}&=frac{1.22cdot5.1times10^{-7}text{ m}cdot 1times10^{5}text{m}}{2.4text{m}} \
&boxed{x_{obj}=2.26times10^{-2}text{m}}
end{align}
$$

$$
x_{obj}=2.26times10^{-2}text{m}
$$

Light $lambda_b=4.25times10^{-7}text{ m}$ passes through a slit. A screen is $L=7.5times 10^{-1}text{ m}$ and the central bright band is $2cdot x=6times 10^{-1}text{ m}$. We will use the definition of the width of the bright band in single slit diffraction.

The definition of the bright band in single slit diffraction is

$$
begin{align}
2cdot x=frac{2cdot lambdacdot L}{w} \
end{align}
$$

$2cdot x$ represent the width of the bright band so since we want the distance from the center to the first dark band, we need to divide equation by 2.

$$
begin{align}
w&=frac{lambdacdot L}{x} \
w&=frac{4.25times 10^{-7}mcdot 7.5times 10^{-1}text{ m}}{3times 10^{-1}m} \
&boxed{w=1.06times 10^{-6}m}
end{align}
$$

$$
w=1.06times 10^{-6}m
$$

The diameter of a eyehole is $D=7times10^{-3}text{m}$. Two specks are separated $x_{obj}=4times10^{-5}text{m}$ and use the wavelength $lambda=6.5times10^{-7}text{ m}$.

We will use The Rayleigh criterion to solve this problem.

$$
begin{align}
{x_{obj}}&=frac{1.22cdotlambdacdot L_{obj}}{D} \
{L_{obj}}&=frac{Dcdot x_{obj}}{1.22cdotlambda} \
{L_{obj}}&=frac{4times10^{-5}text{ m}cdot 7times10^{-3}text{m}}{1.22cdot 6.5times10^{-7}text{ m}} \
&boxed{L_{obj}=3.53times10^{-1}text{m}}
end{align}
$$

$$
L_{obj}=3.53times10^{-1}text{m}
$$

We need to find angles at which red light $lambda_r=6.32times10^{-7}text{ m}$ and blue light $lambda_b=4.21times10^{-7}text{ m}$ have first-order lines if we know that spectroscope uses a grating with $N=1.2times10^{4}text{$frac{lines}{cm}$}$.

The definition of the wavelength from a diffraction grating is

$$
begin{align}
lambda=dcdotsintheta
end{align}
$$

To find $theta$, first we need to calculate $d$.

We will use following equation

$$
begin{align}
d&=frac{1}{N} \
d&=frac{1}{1.2times10^{4} frac{lines}{cm}} \
&boxed{d=8.33times10^{-7}m}
end{align}
$$

Now we can use the definition from the second step.

For red light we have

$$
begin{align}
sintheta&=frac{lambda}{d} \
theta_r&=arcsin{frac{lambda_r}{d}} \
theta_r&=arcsin{left(frac{lambda_r}{d}right)} \
theta_r&=arcsin{left(frac{6.32times10^{-7}text{ m}}{8.33times10^{-7}m}right)} \
&boxed{theta_r=49^circ 21′}
end{align}
$$

And for blue light we have

$$
begin{align}
sintheta&=frac{lambda}{d} \
theta_b&=arcsin{frac{lambda_b}{d}} \
theta_b&=arcsin{left(frac{lambda_b}{d}right)} \
theta_b&=arcsin{left(frac{4.21times10^{-7}text{ m}}{8.33times10^{-7}m}right)} \
&boxed{theta_b=30^circ 22′}
end{align}
$$

$theta_r=49^circ 21’$ and $theta_b=30^circ 22’$

Marie shines $lambda_r=6.328times10^{-7}text{ m}$ laser light on a record and it appears on a screen $L=4text{ m}$ away from the record, used as a diffraction grating. Dots are $x=2.1times10^{-2}text{ m}$ separated

The definition of the wavelength from a diffraction grating is

$$
begin{align}
lambda=dcdotsintheta
end{align}
$$

So we write

$$
begin{align}
d=frac{lambda}{sintheta}
end{align}
$$

But we don’t know $theta$.

From basic geometry, we can conclude

$$
begin{align}
tantheta&=frac{x}{L} \
theta&=arctan {frac{x}{L}}
end{align}
$$

So we write

$$
begin{align}
d&=frac{lambda}{sin{left(arctan {frac{x}{L}}right)}} \
d&=frac{6.328times10^{-7}text{ m}}{sin{left(arctan {frac{2.1times 10^{-2}text{ m}}{4text{ m}}}right)}} \
d&=1.21times 10^{-4}m \
d&=1.21times 10^{-2}cm \
end{align}
$$

Therefore our solution is

$$
begin{align}
&N=frac{1 ridge}{d} \
&N=frac{1 ridge}{1.21times 10^{-2}cm} \
&boxed{N=83frac{ridge}{cm}}
end{align}
$$

$b)$ Song plays $t=4.01text{min}$ and takes $s=1.6text{cm}$. Also we know that the record is $33.3text{rpm}$ (signed with $r$).
First, we will find a number of ridges by using the equation

$$
begin{align}
n&={t}cdot{r} \
n&={4.01text{min}}cdot{33.3text{rpm}} \
n&=134 ridges
end{align}
$$

Now, when we know how many ridges are turned during a song, we can rind $N$.

$$
begin{align}
&N=frac{n}{s} \
&N=frac{134 ridge}{1.6cm} \
&boxed{N=84frac{ridge}{cm}}
end{align}
$$

$a)$ $N=83frac{ridge}{cm}$

$b)$ $N=84frac{ridge}{cm}$

The light ray goes through the air, $n=1$, and hits the film, $n_f=1.2$. The thickness of a film is $d=1.25times 10^{-7}text{ m}$. Here the first reflection and phase inversion happens because $n<n_f$.

Other situation is when ray goes through a film and hits the glass lens, $n_g=1.52$. Since $n_f<n_g$, on the second reflection the phase inversion happens.

What we need here is to find wavelength of light that makes destructive interference.

The definition of thickness when black stripe appears is

$$
begin{align}
d=frac{1}{2}cdot left(m+frac{1}{2}right)cdotfrac{lambda}{n_f}
end{align}
$$

First we use a thinnest film, $m=0$. So, we write

$$
begin{align}
lambda&=frac{2cdot dcdot n_f}{m+frac{1}{2}} \
lambda&=frac{2cdot 1.25times 10^{-7}text{ m}cdot 1.2}{0+frac{1}{2}} \
&boxed{lambda=6times 10^{-7}m}
end{align}
$$

This wavelength is particular for $textbf{reddish-orange color}$.