All Solutions
Page 508: Assessment
$n_{g}>n_{a}$
$textbf{Solution}$
The definition of Snell’s law of refraction is
$$
begin{align}
{n_1cdot sin theta_1}={n_2cdot sin theta_2}
end{align}
$$
so we write
$$
begin{align}
{n_{a}cdotsintheta_{a}}&={n_{g}cdotsintheta_{g}} \
frac{n_{a}}{n_{g}}&=frac{sintheta_{g}}{sintheta_{a}}
end{align}
$$
If $n_{g}>n_{a}$ than the angle of incidence $theta_{a}$ is larger than the angle of refraction $theta_{g}$.
$$
begin{align}
sin&theta_{a}>sintheta_{g} \
&theta_{a}>theta_{g} \
&boxed{theta_{i}>theta_{r}}
end{align}
$$
theta_{i}>theta_{r}
$$
$n_{g}>n_{a}$
$textbf{Solution}$
The definition of Snell’s law of refraction is
$$
begin{align}
{n_1cdot sin theta_1}={n_2cdot sin theta_2}
end{align}
$$
so we write
$$
begin{align}
{n_{g}cdotsintheta_{g}}&={n_{a}cdotsintheta_{a}} \
frac{n_{g}}{n_{a}}&=frac{sintheta_{a}}{sintheta_{g}}
end{align}
$$
If $n_{g}>n_{a}$ than the angle of refraction $theta_{a}$ is larger than the angle of incidence $theta_{g}$.
$$
begin{align}
sin&theta_{a}>sintheta_{g} \
&theta_{a}>theta_{g} \
&boxed{theta_{r}>theta_{i}}
end{align}
$$
theta_{r}>theta_{i}
$$
If we look at the Snell’s law, that means that the angle of refraction $theta_2$ is equal to $90^circ$ so we can define the critical angle as
$$
begin{align}
{sintheta_c}=frac{n_2}{n_1}
end{align}
$$
{sintheta_c}=frac{n_2}{n_1}
$$
We also need to state what this implies about the speeds of different colors of light when traveling through the air.
Hence, the difference in indices of refraction for different colors is even smaller.
For a sense of scale $n_{text{vacuum}}=1$ and $n_{text{air}} sim 1.0003$
This difference is too small to lead to a separation into a spectrum.
The fact that there is no separation into a spectrum implies that the speeds of different colors of light when passing through the air are very similar.
This means that image is not focused. To manage the precision in focusing the picture when using precise optical instruments, we use $textbf{achromatic lens}$ which is a system of two or more lenses.
surrounded with eye muscles that help to change the shape of the lens so eye can focus on objects on different positions.
To correct this we use concave lens.
$theta_{B}>theta_{A}$
$textbf{Approach}$
In this problem we are going to use Snell’s law.
$textbf{Solution}$
The definition of Snell’s law of refraction is
$$
begin{align}
{n_1cdot sin theta_1}={n_2cdot sin theta_2}
end{align}
$$
so we write
$$
begin{align}
{n_{A}cdotsintheta_{A}}&={n_{B}cdotsintheta_{B}} \
frac{n_{A}}{n_{B}}&=frac{sintheta_{B}}{sintheta_{A}}
end{align}
$$
From the picture we see that $theta_{B}>theta_{A}$ which means that the index of refraction of substance A, $theta_{A}$, is larger than the index of refraction of substance B, $theta_{B}$.
$$
begin{align}
&boxed{n_{A}>n_{B}}
end{align}
$$
n_{A}>n_{B}
$$
$$
begin{align}
{n}=frac{c}{v}
end{align}
$$
where indexes $c$ is the speed of light and $v$ is the speed in the medium.
Now we write
$$
begin{align}
{v}=frac{c}{n}
end{align}
$$
Since the speed of light in a vacuum $c$ is constant, if the index of refraction of a material $n$ is increased, the speed of light in the material $v$ will be decreased.
$$
begin{align}
sintheta_{c}=frac{n_2}{n_1}
end{align}
$$
so the critical angle is
$$
begin{align}
theta_{c}=arcsin{left(frac{n_2}{n_1}right)}
end{align}
$$
Let’s say that one medium is air $n_a=1$ so for other one we have $n_a<n_m$.
In first situation let's say we have $n_1=n_a$ and $n_2=n_m$. Here we can easely see that (2) does not exist.
Now, we say $n_2=n_a$ and $n_1=n_m$. This solution exists and since the ciritcal angle is inversely proportional to $n_1$, it increases as the index $n_1$ decreases.
$n_{a}=1$
$n_{w}=1.33$
$n_{g}=1.52$
$textbf{Approach}$
In this problem we will use the definition for the critical angle for total internal reflection.
$textbf{Solution}$
The definition for the critical angle for total internal reflection is
$$
begin{align}
sintheta_{C}=frac{n_2}{n_1}
end{align}
$$
so we the critical angle is
$$
begin{align}
theta_{C}=arcsin{left(frac{n_2}{n_1}right)}
end{align}
$$
In the first place, lets see the critical angle for air and water.
$$
begin{align}
theta_{C,a-w}&=arcsin{left(frac{n_a}{n_w}right)} \
theta_{C,a-w}&=arcsin{left(frac{1}{1.33}right)} \
theta_{C,a-w}&=48^circ 45′
end{align}
$$
Now, we calculate the critical angle for air and glass in the same way.
$$
begin{align}
theta_{C,a-g}&=arcsin{left(frac{n_a}{n_g}right)} \
theta_{C,a-g}&=arcsin{left(frac{1}{1.52}right)} \
theta_{C,a-g}&=41^circ 8′
end{align}
$$
Now, we see that the critical angle for air and glass $theta_{C,a-g}$ is smaller that the critical angle for air and water $theta_{C,a-w}$.
$$
begin{align}
boxed{theta_{C,a-g}<theta_{C,a-w}}
end{align}
$$
theta_{C,a-g} < theta_{C,a-w}
$$
$$
begin{align}
sintheta_{i}>sintheta_{c}=frac{n_a}{n_g}
end{align}
$$
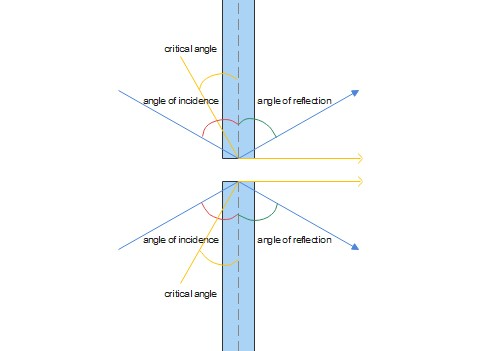
Remember first the mirage that occurs when traveling on a hot road or in the desert.
Because of its high temperature, the ground keeps the air above it warm. This means that the air closer to the ground has a smaller refractive index than the higher air.
Well in the case of the sea, the air closer to the surface is cooler than the air above it. This means that its refractive index is larger.
So light traveling above the surface will actually bend towards the surface. This is the opposite of what occurs on a hot road.
This means that something that is actually located below the horizon could be seen!
Light coming from the yet distant Greenland would bend while traveling through the atmosphere, and reach the eye of the observer.
$$
begin{align}
{lambda}=frac{v}{f}
end{align}
$$
We can also write it like
$$
begin{align}
v=lambda cdot f
end{align}
$$
where $lambda$ is wavelength, $v$ is the speed of light in a medium and $f$ is the frequency of light.
Violet light has smaller wavelength and frequency than red light, so it travels slower than the red light.
The brightness of the image will increase.
$n_{a}=1$
$n_{w}=1.33$
$n_{g}=1.52$
$textbf{Solution}$
Here we have two situations. First, refraction in system air-glass and second, in system water-glass.
Magnification is proportional to the refraction. The difference between indexes of refraction $n_w$ and $n_g$ is much smaller than the difference between $n_a$ and $n_w$ which means that refraction for system water-glass is smaller.
Reflection, that happens on mirrors, does not depend on the refractive index. Hence the reflection does not depend on the wavelength and hence no chromatic aberration.
|
$theta_{1}=30text{ $^circ$}$
$theta_{2}=22text{ $^circ$}$
$n_{a}=1$
$textbf{Approach}$
In this problem we are going to use Snell’s law.
$textbf{Solution}$
$a)$ The definition of Snell’s law of refraction is
$$
begin{align}
{n_1cdot sin theta_1}={n_2cdot sin theta_2}
end{align}
$$
so we write
$$
begin{align}
{n_{a}cdotsintheta_{a}}&={n_{l}cdotsintheta_{l}} \
{n_l}&={n_a}cdot frac{sintheta_{a}}{sintheta_{l}} \
{n_l}&=1cdot frac{sin 30^circ}{sin 22^circ} \
&boxed{{n_l}=1.33}
end{align}
$$
$b)$ Due to solution in $a)$, the liquid from in this problem is $textbf{water}$.
$b)$ It is water.
$n_{fg}=1.62$
$n_{e}=1.36$
$theta_{e}=25text{ $^circ$}$
$textbf{Approach}$
In this problem we will use Snell’s law.
$textbf{Solution}$
$a)$ The definition of Snell’s law of refraction is
$$
begin{align}
{n_1cdot sin theta_1}={n_2cdot sin theta_2}
end{align}
$$
so we write
$$
begin{align}
{n_{fg}cdotsintheta_{fg}}&={n_{e}cdotsintheta_{e}} \
{theta_{fg}}&=arcsin{left( frac{n_e}{n_{fg}} cdot sintheta_e right)} \
{theta_{fg}}&=arcsin{left( frac{1.36}{1.62} cdot sin 25^circ right)} \
&boxed{{theta_{fg}}=20^circ47′}
end{align}
$$
{theta_{fg}}=20^circ47′
$$
$n_{a}=1$
$n_{g}=1.5$
$n_{w}=1.33$
$theta_{a}=40text{ $^circ$}$
$textbf{Approach}$
In this problem we will use Snell’s law.
$textbf{Solution}$
$a)$ The definition of Snell’s law of refraction is
$$
begin{align}
{n_1cdot sin theta_1}={n_2cdot sin theta_2}
end{align}
$$
so we write
$$
begin{align}
{n_{a}cdotsintheta_{a}}&={n_{g}cdotsintheta_{g}} \
{theta_{g}}&=arcsin{left( frac{n_g}{n_{a}} cdot sintheta_a right)} \
{theta_{g}}&=arcsin{left( frac{1}{1.5} cdot sin 40^circ right)} \
&boxed{{theta_{g}}=25^circ 22′}
end{align}
$$
$b)$ Now, we have the same problem but with two different media.
$$
begin{align}
{n_{g}cdotsintheta_{g}}&={n_{w}cdotsintheta_{w}} \
{theta_{w}}&=arcsin{left( frac{n_g}{n_{w}} cdot sintheta_g right)} \
{theta_{w}}&=arcsin{left( frac{1.5}{1.33} cdot sin 25^circ 22′ right)} \
&boxed{{theta_{w}}=28^circ 54′}
end{align}
$$
$b)$ ${theta_{w}}=28^circ 54’$
$n=2.42$
$c=3times10^8frac{text{ m}}{text{ s}}$
$textbf{Approach}$
In this problem we will use a definition of index of refraction.
$textbf{Solution}$
The definition of index of refraction is
$$
begin{align}
{n}=frac{c}{v}
end{align}
$$
where indexes $c$ is the speed of light and $v$ is the speed in the medium.
$$
begin{align}
&{v}=frac{c}{n} \
&{v}=frac{3times10^8frac{ m}{ s}}{2.42} \
&boxed{{v}=1.24times10^8frac{ m}{ s} }
end{align}
$$
{v}=1.24times10^8frac{ m}{ s}
$$
$n_{a}=1$
$n_{d}=2.42$
$textbf{Approach}$
In this problem we will use the definition for the critical angle.
$textbf{Solution}$
The definition for the critical angle for total internal reflection is
$$
begin{align}
sintheta_{C}=frac{n_2}{n_1}
end{align}
$$
so the critical angle is
$$
begin{align}
&theta_{C}=arcsin{left(frac{1}{2.42}right)} \
&boxed{theta_{C}=24^circ 24′}
end{align}
$$
theta_{C}=24^circ 24′
$$
$n_{w}=1.33$
$n_{p}=1.5$
$theta_{e}=35text{ $^circ$}$
$textbf{Approach}$
In this problem we will use Snell’s law.
$textbf{Solution}$
The definition of Snell’s law of refraction is
$$
begin{align}
{n_1cdot sin theta_1}={n_2cdot sin theta_2}
end{align}
$$
First, the light ray goes from fish through water to the plastic sheet, so we write
$$
begin{align}
{n_{w}cdotsintheta_{w}}&={n_{p}cdotsintheta_{p}} \
{theta_{p}}&=arcsin{left( frac{n_w}{n_{p}} cdot sintheta_w right)} \
{theta_{p}}&=arcsin{left( frac{1.33}{1.5} cdot sin 35^circ right)} \
{theta_{p}}&=30^circ34′
end{align}
$$
Then, it goes through the plastic sheet in the air.
$$
begin{align}
{n_{p}cdotsintheta_{p}}&={n_{a}cdotsintheta_{a}} \
{theta_{a}}&=arcsin{left( frac{n_p}{n_{a}} cdot sintheta_p right)} \
{theta_{a}}&=arcsin{left( frac{1.5}{1} cdot sin 30^circ 34’right)} \
&boxed{{theta_{a}}=49^circ43′}
end{align}
$$
{theta_{a}}=49^circ43′
$$
$d=1.5text{m}$
$h=2text{m}$
$n_{a}=1$
$n_{w}=1.33$
$textbf{Approach}$
In this problem, we will use Snell’s law and trigonometry.
$textbf{Solution}$
$a)$ To find the angle at which light leaves the water, first we need to find the angle of incidence in the water.
$$
begin{align}
{tan theta_w}&=frac{d}{h} \
{theta_w}&=arctan {left( frac{1.5m}{2m}right)} \
{theta_{w}}&=36.87^circ
end{align}
$$
Now, from the definition for Snell’s law, we can find the angle of refraction
$$
begin{align}
{n_{w}cdotsintheta_{w}}&={n_{a}cdotsintheta_{a}} \
{theta_{a}}&=arcsin{left( frac{n_w}{n_{a}} cdot sintheta_w right)} \
{theta_{a}}&=arcsin{left( frac{1.33}{1} cdot sin 36.87^circ right)} \
&boxed{{theta_{a}}=52.94^circ}
end{align}
$$
$b)$ When we watch the light from angle $theta_{a}$, we will have the feeling that a light source is not placed on $2m$ beneath the water but on the $h_i$.
$$
begin{align}
{tan theta_a}&=frac{d}{h_i} \
{h_i}&=frac{d}{tan theta_a} \
{h_i}&=frac{1.5m}{tan 52.94^circ } \
&boxed{h_i=1.13m}
end{align}
$$
Since $h_i<h$, the light viewed from angle $theta_i$ will appear shallower than it actually is.
$b)$ Shallower.
$n_{r}=2.41$
$n_{b}=2.45$
$n_{a}=1$
$lambda_{r}=656text{nm}$
$lambda_{b}=434text{nm}$
$theta_{w}=30text{ $^circ$}$
$textbf{Approach}$
In this problem, we will use Snell’s law.
$textbf{Solution}$
Lights of different wavelenght will refract at different angles.We will strat with a definition for Snell’s law.
$$
begin{align}
{n_1cdot sin theta_1}={n_2cdot sin theta_2}
end{align}
$$
For first situation we write
$$
begin{align}
{n_{a}cdotsintheta_{a}}&={n_{r}cdotsintheta_{r}} \
{theta_{r}}&=arcsin{left( frac{n_a}{n_{r}} cdot sintheta_a right)} \
{theta_{r}}&=arcsin{left( frac{1}{2.41} cdot sin 30^circ right)} \
&boxed{{theta_{r}}=11.97^circ}
end{align}
$$
And for situation with blue light, we have
$$
begin{align}
{n_{a}cdotsintheta_{a}}&={n_{b}cdotsintheta_{b}} \
{theta_{b}}&=arcsin{left( frac{n_a}{n_{b}} cdot sintheta_a right)} \
{theta_{b}}&=arcsin{left( frac{1}{2.45} cdot sin 30^circ right)} \
&boxed{{theta_{b}}=11.77^circ}
end{align}
$$
$$
{theta_{b}}=11.77^circ
$$
$n_{r}=1.51$
$n_{v}=1.53$
$c=3times10^8frac{text{ m}}{text{ s}}$
$textbf{Approach}$
In this problem, we will use a definition of the index of refraction.
$textbf{Solution}$
$a)$ The definition of index of refraction is
$$
begin{align}
{n}=frac{c}{v}
end{align}
$$
We need to calculate the speed of violet light so we write
$$
begin{align}
&{v_v}=frac{c}{n} \
&{v_v}=frac{3times10^8frac{ m}{ s} }{1.53} \
&boxed{{v_v}=1.96times10^8frac{ m}{ s}}
end{align}
$$
$b)$ We do the same for red light.
$$
begin{align}
&{v_r}=frac{c}{n} \
&{v_r}=frac{3times10^8frac{ m}{ s} }{1.51} \
&boxed{{v_r}=1.99times10^8frac{ m}{ s}}
end{align}
$$
$$
{v_r}=1.99times10^8frac{ m}{ s}
$$
$theta_c=41text{$^circ$}$
$n_{a}=1$
$n_{w}=1.33$
$textbf{Approach}$
In this problem, we will use the definition for the critical angle for total internal reflection.
$textbf{Solution}$
The definition for the critical angle for total internal reflection is
$$
begin{align}
sintheta_{c}=frac{n_2}{n_1}
end{align}
$$
First, we need to find the index of refraction for a special glass.
$$
begin{align}
sintheta_{c,a}&=frac{n_a}{n_g} \
{n_g}&=frac{n_a}{sintheta_{c,a}} \
n_g&=1.52
end{align}
$$
Now, when we know $n_g$, we can find the solution.
$$
begin{align}
sintheta_{c,w}&=frac{n_w}{n_g} \
theta_{c,w}&=arcsin{left(frac{n_w}{n_g}right)} \
&boxed{theta_{c,w}=61.04^circ}
end{align}
$$
theta_{c,w}=61.04^circ
$$
$theta_i=55text{$^circ$}$
$n_{a}=1$
$n_{w}=1.33$
$textbf{Approach}$
In this problem, we will use Snell’s law.
$textbf{Solution}$
The definition of Snell’s law of refraction is
$$
begin{align}
{n_1cdotsin theta_1}={n_2cdot sin theta_2}
end{align}
$$
so we write
$$
begin{align}
{n_{w}cdotsintheta_{w}}&={n_{a}cdotsintheta_{a}} \
{theta_{a}}&=arcsin{left( frac{n_w}{n_{a}} cdot sintheta_w right)} \
{theta_{w}}&=arcsin{left( frac{1.33}{1} cdot sin 55^circ right)} \
&boxed{{theta_{w}}=arcsin{1.09}}
end{align}
$$
The value for $sin$ is defined from $0$ to $1$ which means that here we have a total internal reflection.
$theta_a=45text{$^circ$}$
$n_{a}=1$
$n_{g}=1.5$
$textbf{Approach}$
In this problem, we will use Snell’s law and elementary geometry.
$textbf{Solution}$
$a)$ The definition of Snell’s law of refraction is
$$
begin{align}
{n_1sin theta_1}={n_2 sin theta_2}
end{align}
$$
Since the prism is made of glass, we write
$$
begin{align}
{n_{a}cdotsintheta_{a}}&={n_{g}cdotsintheta_{g}} \
{theta_{g}}&=arcsin{left( frac{n_a}{n_{g}} cdot sintheta_a right)} \
{theta_{g}}&=arcsin{left( frac{1}{1.5} cdot sin 45^circ right)} \
&boxed{{theta_{g}}={28.13^circ}}
end{align}
$$
$$
begin{align}
&{theta_P}={90^circ}-theta_2 \
&{theta_P}={90^circ}-{28.13^circ} \
&{theta_P}=61.86^circ
end{align}
$$
and $Q$.
$$
begin{align}
&{theta_Q}={180^circ}-theta_P-{60^circ} \
&{theta_Q}={180^circ}-{61.86^circ}-{60^circ} \
&{theta_Q}=58.14^circ
end{align}
$$
And in the end we have solution
$$
begin{align}
&{theta_1′}={90^circ}-theta_Q \
&{theta_1′}={90^circ}-{58.14^circ} \
&boxed{{theta_1′}=31.86^circ}
end{align}
$$
$$
begin{align}
{n_{g}cdotsintheta_{g}}&={n_{a}cdotsintheta_{a}} \
{theta_2′}&=arcsin{left( frac{n_a}{n_{g}} cdot sintheta_1′ right)} \
{theta_2′}&=arcsin{left( frac{1.5}{1} cdot sin 31.86^circ right)} \
&boxed{{theta_2′}={52.35^circ}}
end{align}
$$
$b)$ ${theta_1′}=31.86^circ$
$c)$ ${theta_2′}={52.35^circ}$
$n_{a}=1$
$theta_a=22text{$^circ$}$
$v_{p}=1.9times10^8frac{text{ m}}{text{ s}}$
$c=3times10^8frac{text{ m}}{text{ s}}$
$textbf{Approach}$
In this problem, we will use a definition of the index of refraction and Snell’s law.
$textbf{Solution}$
Let’s start with the definition of index of refraction
$$
begin{align}
{n}&=frac{c}{v} \
{n_p}&=frac{c}{v_p} \
{n_p}&=frac{3times10^8 frac{m}{s}}{1.9times10^8 frac{m}{s}} \
{n_p}&=1.57
end{align}
$$
From Snell’s law, we can find a solution.
$$
begin{align}
{n_{a}cdotsintheta_{a}}&={n_{p}cdotsintheta_{p}} \
{theta_{p}}&=arcsin{left( frac{n_a}{n_{p}} cdot sintheta_a right)} \
{theta_{p}}&=arcsin{left( frac{1}{1.57} cdot sin 22^circ right)} \
&boxed{{theta_{g}}=13.8^circ}
end{align}
$$
{theta_{g}}=13.8^circ
$$
Firs we start with a Snell’s law where we use $theta_i=45^circ$.
$$
begin{align}
{n_1cdot sin theta_1}&={n_2cdot sin theta_2} \
{n_{a}cdotsintheta_{a}}&={n_{g}cdotsintheta_{g}} \
{theta_{g}}&=arcsin{left( frac{n_a}{n_{g}} cdot sintheta_a right)} \
{theta_{g}}&=arcsin{left( frac{1}{1.52} cdot sin 45^circ right)} \
theta_{g}&=27^circ43′
end{align}
$$
$$
begin{align}
90^circ&=theta_{g,r}+theta_{g,i} \
theta_{g,i}&=90^circ-27^circ43′ \
theta_{g,i}&=62^circ27′
end{align}
$$
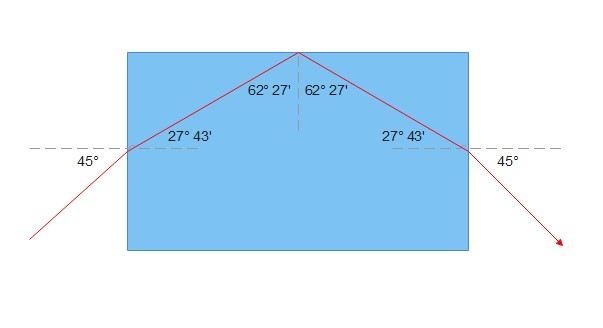
But, is this angle a critical angle, an angle of refraction or an angle of reflection?
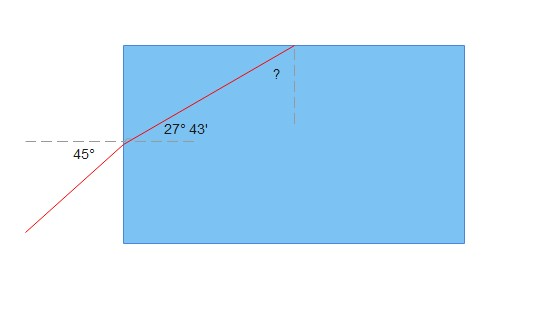
$$
begin{align}
sintheta_{c}&=frac{n_a}{n_g} \
theta_{c}&=arcsin{left(frac{n_a}{n_g}right)} \
theta_{c}&=arcsin{left(frac{1}{1.52}right)} \
theta_{c}&=41^circ8′
end{align}
$$
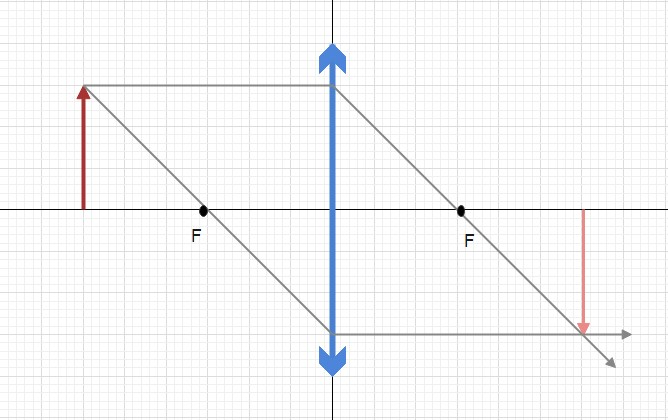
$d_{o}=72.5times10^{-2}text{ m}$
$f=25.5times10^{-2}text{ m}$
$textbf{Approach}$
We will find the solutions by using the definition of thin lens equation.
$textbf{Solution}$
Thin lens equation is defined as
$$
begin{align}
frac{1}{f}=frac{1}{d_i}+frac{1}{d_o}
end{align}
$$
so for image position $d_i$ we have
$$
begin{align}
{d_i}&=frac{d_ocdot f}{d_o -f} \
{d_i}&=frac{72.5times10^{-2}mcdot 25.5times10^{-2}m}{72.5times10^{-2}m- 25.5times10^{-2}m}{} \
&boxed{{d_i}=39.34times10^{-2}m}
end{align}
$$
$d_{o}=10times10^{-2}text{ m}$
$f=5times10^{-2}text{ m}$
$textbf{Approach}$
We will find the solutions by using the definition of thin lens equation.
$textbf{Solution}$
Thin lens equation is defined as
$$
begin{align}
frac{1}{f}=frac{1}{d_i}+frac{1}{d_o}
end{align}
$$
so for image position $d_i$ we have
$$
begin{align}
{d_i}&=frac{d_ocdot f}{d_o -f} \
{d_i}&=frac{10times10^{-2}mcdot 5times10^{-2}m}{10times10^{-2}m- 5times10^{-2}m}{} \
&boxed{{d_i}=10times10^{-2}m}
end{align}
$$
$m=-0.75$
$d_{i}=24times10^{-2}text{ m}$
$f=5.5times10^{-2}text{ m}$
$textbf{Approach}$
We will find the solutions by using the definition of the thin lens equation and the definition of the magnification.
$textbf{Solution}$
The magnification is defined as the ratio of positions.
$$
begin{align}
{m}&=frac{-d_i}{d_o}
end{align}
$$
The magnification is negative because an image is located on the other side of the lens than the object.
$$
begin{align}
{d_o}&=frac{-d_i}{m} \
{d_o}&=frac{-24times10^{-2}m}{-0.75} \
{d_o}&=32times10^{-2}m
end{align}
$$
Thin lens equation is defined as
$$
begin{align}
frac{1}{f}=frac{1}{d_i}+frac{1}{d_o}
end{align}
$$
so for focal length $f$ we have
$$
begin{align}
{f}&=frac{d_ocdot d_i}{d_o + d_i} \
{f}&=frac{32times10^{-2}mcdot 24times10^{-2}m}{32times10^{-2}m+24times10^{-2}m} \
&boxed{{f}=13.71times10^{-2}m}
end{align}
$$
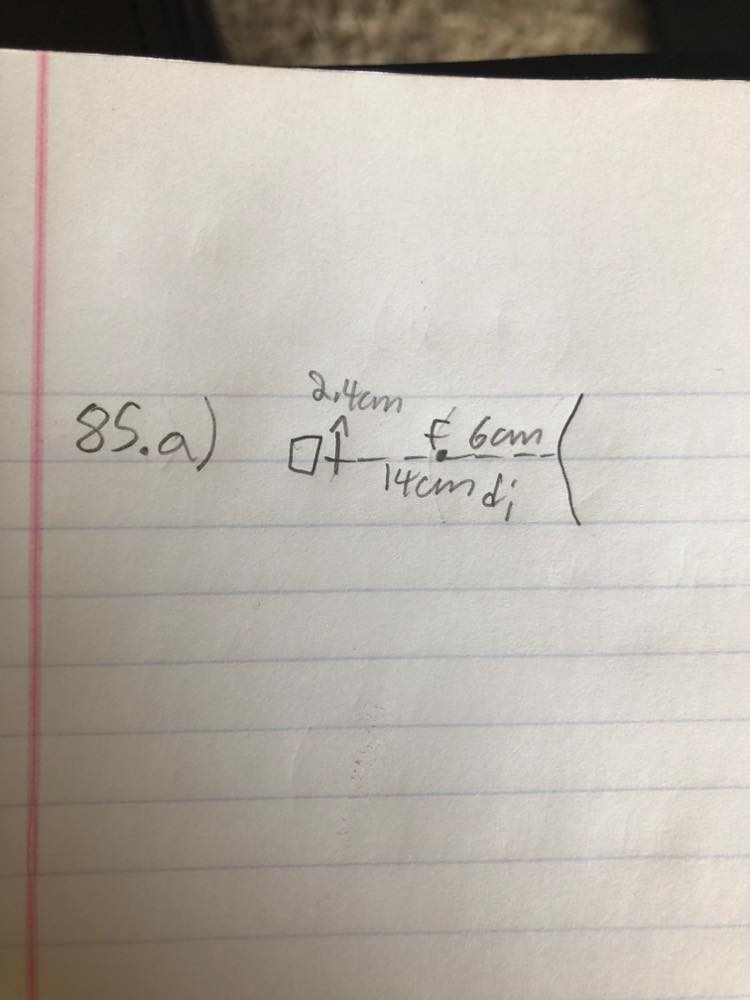
$h_{o}=3times10^{-2}text{ m}$
$d_{o}=22times10^{-2}text{ m}$
$d_{i}=11times10^{-2}text{ m}$
$textbf{Approach}$
We will find the solutions by using the equality of ratios of image and object height and position respectively the magnification.
$textbf{Solution}$
Let’s start with equality of ratios of image and object height and position
$$
begin{align}
frac{h_i}{h_o}&=frac{-d_i}{d_o} \
{h_i}&=frac{-d_i cdot h_o}{d_o} \
{h_i}&=frac{-11times10^{-2}m cdot 3times10^{-2}m}{22times10^{-2}m} \
{h_i}&=-1.5times10^{-2}m \
&boxed{{mid h_i mid}=1.5times10^{-2}m}
end{align}
$$
Minus in solution means that the image is inverted.
$h_{o}=3times10^{-2}text{ m}$
$d_{o}=15times10^{-2}text{ m}$
$d_{i}=10times10^{-2}text{ m}$
$textbf{Approach}$
We will find the solutions by using the definition of the thin lens equation and equality of ratios of image and object height and position respectively the definition of the magnification.
$textbf{Solution}$
$a)$ To find the focal length we will use the thin lens equation.
$$
begin{align}
frac{1}{f}=frac{1}{d_i}+frac{1}{d_o}
{f}&=frac{d_ocdot d_i}{d_o + d_i} \
{f}&=frac{15times10^{-2}mcdot 10times10^{-2}m}{15times10^{-2}m+ 10times10^{-2}m}{} \
&boxed{f=6times10^{-2}m}
end{align}
$$
$$
begin{align}
{f_n}&=2cdot{6m} \
{f_n}&=12m
end{align}
$$
Now, we use equation for thin lens.
$$
begin{align}
{d_{i,n}}&=frac{d_ocdot f_n}{d_o -f_n} \
{d_{i,n}}&=frac{15times10^{-2}mcdot 12times10^{-2}m}{15times10^{-2}m- 12times10^{-2}m}{} \
&boxed{{d_{i,n}}=60times10^{-2}m}
end{align}
$$
In the end, when we have new position of image, we can find size.
$$
begin{align}
frac{h_i}{h_o}&=frac{-d_{i,n}}{d_o} \
{h_{i,n}}&=frac{-d_{i,n} cdot h_o}{d_o} \
{h_{i,n}}&=frac{-60times10^{-2}m cdot 3times10^{-2}m}{15times10^{-2}m} \
&boxed{{h_{i,n}}=-12times10^{-2}m}
end{align}
$$
Minus in solution means that image is $textbf{inverted}$.
$b)$ ${d_{i,n}}=60 times10^{-2}m$ and ${h_{i,n}}=-12times10^{-2}m$ (Image is inverted.)
$h_{i}=2times10^{-2}text{ m}$
$d_{i}=-5times10^{-2}text{ m}$
$f=-15times,
10^{-2}text{ m}$
$textbf{Approach}$
We will find the solutions by using the definition of thin lens equation and equality of ratios of image and object height and position respectively the definition of the magnification.
$textbf{Solution}$
$a)$ To find the position of the image we will use the thin lens equation. The object is placed on the opposite side and here we have a diverging lens, that is why $d_i$ and $f$ have negative signs.
$$
begin{align}
frac{1}{f}&=frac{1}{d_i}+frac{1}{d_o} \
{d_o}&=frac{d_icdot f}{d_i -f} \
{d_o}&=frac{-5times10^{-2}mcdot (-15)times10^{-2}m}{-5times10^{-2}m- (-15)times10^{-2}m} \
&boxed{{d_o}=7.5times10^{-2}m}
end{align}
$$
We will find a new position from the equality of ratios of image and object height and position.
$$
begin{align}
frac{h_i}{h_o}&=frac{-d_i}{d_o} \
{h_{o}}&=frac{-d_o cdot h_i}{d_i} \
{h_{o}}&=frac{-7.5times10^{-2}m cdot 2times10^{-2}m}{-5times10^{-2}m} \
&boxed{h_{o}=3times10^{-2}m}
end{align}
$$
Now, we use equation for thin lens.
$$
begin{align}
frac{1}{f}=frac{1}{d_i}+frac{1}{d_o} \
{d_{i,n}}&=frac{d_ocdot f_n}{d_o -f_n} \
{d_{i,n}}&=frac{7.5times10^{-2}mcdot 15times10^{-2}m}{7.5times10^{-2}m- 15times10^{-2}m} \
&boxed{{d_{i,n}}=-15times10^{-2}m}
end{align}
$$
In the end, when we have new position of image, we can find size.
$$
begin{align}
frac{h_i}{h_o}&=frac{-d_{i,n}}{d_o} \
{h_{i,n}}&=frac{-d_{i,n} cdot h_o}{d_o} \
{h_{i,n}}&=frac{-(-15)times10^{-2}m cdot 3times10^{-2}m}{7.5times10^{-2}m} \
&boxed{{h_{i,n}}=6times10^{-2}m}
end{align}
$$
Image is $textbf{virtual and upright}$.
$b)$ ${d_{i,n}}=-15times10^{-2}m$ and ${h_{i,n}}=6times10^{-2}m$ (Image is upright and virtual.)
$a)$ $d_{o}=3text{ m}$
$f=5text{ m}$
$b)$ $d_{o}=125text{ m}$
$f=1text{ m}$
$textbf{Approach}$
We will find solutions by using the definition of the thin lens equation.
$textbf{Solution}$
$a)$ To find the position of the image we will use the thin lens equation.
$$
begin{align}
frac{1}{f}&=frac{1}{d_i}+frac{1}{d_o} \
{d_i}&=frac{d_ocdot f}{d_o -f} \
{d_i}&=frac{3mcdot 5times10^{-2}m}{3m- 5times10^{-2}m} \
&boxed{{d_i}=5.08times10^{-2}m}
end{align}
$$
$b)$ Here, we do the same as in $a)$.
$$
begin{align}
frac{1}{f}&=frac{1}{d_i}+frac{1}{d_o} \
{d_i}&=frac{d_ocdot f}{d_o -f} \
{d_i}&=frac{125mcdot 1m}{125m- 1m} \
&boxed{{d_i}=1.01m}
end{align}
$$
$b)$ ${d_i}=1.01m$
$d_{o}=25times10^{-2}text{ m}$
$d_{i}=-45times10^{-2}text{ m}$
$textbf{Approach}$
We will find the solutions by using the definition of the thin lens equation.
$textbf{Solution}$
To find the focal length we will use the thin lens equation.
$$
begin{align}
frac{1}{f}&=frac{1}{d_i}+frac{1}{d_o} \
{f}&=frac{d_ocdot d_i}{d_o + d_i} \
{f}&=frac{25times10^{-2}mcdot (-45)times10^{-2}m}{25times10^{-2}m+ (-45)times10^{-2}m}{} \
&boxed{f=56.25times10^{-2}m}
end{align}
$$
f=56.25times10^{-2}m
$$
$f=25times10^{-2}text{ m}$
$d_{o}=40times10^{-2}text{ m}$
$textbf{Approach}$
We will find the solutions by using the definition of the thin lens equation and equality of ratios of image and object height and position respectively the definition of the magnification.
$textbf{Solution}$
$a)$ To find the focal length we will use the thin lens equation.
$$
begin{align}
frac{1}{f}&=frac{1}{d_i}+frac{1}{d_o} \
{d_i}&=frac{d_ocdot f}{d_o -f} \
{d_i}&=frac{40times10^{-2}mcdot 25times10^{-2}m}{40times10^{-2}m- 25times10^{-2}m}{} \
&boxed{{d_i}=66.67times10^{-2}m}
end{align}
$$
$b)$ The copy represents the size of image $h_i$.
$$
begin{align}
frac{h_i}{h_o}&=frac{-d_i}{d_o} \
{h_i}&=frac{-d_i cdot h_o}{d_o} \
{h_i}&=frac{-66.67times10^{-2}m cdot h_o}{40times10^{-2}m} \
&boxed{{h_i}=-1.67cdot h_o}
end{align}
$$
The image is $textbf{inverted and enlarged}$.
$b)$ ${h_i}=-1.67cdot h_o$ (The image is inverted and enlarged.)
$a)$
$f=1times10^{-2}text{ m}$
$d_{o}=1.2times10^{-2}text{ m}$
$c)$
$f=2times10^{-2}text{ m}$
$d_{o}=1times10^{-2}text{ m}$
$textbf{Approach}$
We will find the solutions by using the definition of the thin lens equation and equality of ratios of image and object height and position respectively the definition of the magnification.
$textbf{Solution}$
$a)$ To find the focal length we will use the thin lens equation.
$$
begin{align}
frac{1}{f}&=frac{1}{d_i}+frac{1}{d_o} \
{d_i}&=frac{d_ocdot f}{d_o -f} \
{d_i}&=frac{1.2times10^{-2}mcdot 1times10^{-2}m}{1.2times10^{-2}m- 1times10^{-2}m}{} \
&boxed{{d_i}=6times10^{-2}m}
end{align}
$$
$$
begin{align}
&m=frac{-d_i}{d_o} \
&m=frac{-6times10^{-2}m}{1.2times10^{-2}m} \
&boxed{m=-5}
end{align}
$$
$$
begin{align}
frac{1}{f}&=frac{1}{d_i}+frac{1}{d_o} \
{d_i}&=frac{d_ocdot f}{d_o -f} \
{d_i}&=frac{1times10^{-2}mcdot 2times10^{-2}m}{1times10^{-2}m- 2times10^{-2}m}{} \
&boxed{{d_i}=-2times10^{-2}m}
end{align}
$$
Minus in the solution means that an image is also beneath the eyepiece.
$$
begin{align}
&{m_d}=frac{-d_i}{d_o} \
&{m_d}=frac{-(-2)times10^{-2}m}{1times10^{-2}m} \
&{m_d}=2
end{align}
$$
Total magnification is a multiplication of the magnification of the image in $b$ and the magnification of the real image from $c)$.
$$
begin{align}
&{m_{tot}}={m_d}cdot m \
&{m_{tot}}=2cdot(-5) \
&boxed{m_{tot}=-10}
end{align}
$$
$b)$ $m=-5$
$c)$ ${d_i}=-2times10^{-2}m$
$d)$ $m_{tot}=-10$
$a)$
$f=20times10^{-2}text{ m}$
$h_{o}=10times10^{-2}text{ m}$
$d_{o}=425times10^{-2}text{ m}$
$b)$
$l=25times10^{-2}text{ m}$
$f_n=4.05times10^{-2}text{ m}$
$textbf{Approach}$
We will find the solutions by using the definition of the thin lens equation and equality of ratios of image and object height and position respectively the definition of the magnification.
$textbf{Solution}$
$a)$ To find the image position we will use the thin lens equation.
$$
begin{align}
frac{1}{f}&=frac{1}{d_i}+frac{1}{d_o} \
{d_i}&=frac{d_ocdot f}{d_o -f} \
{d_i}&=frac{425times10^{-2}mcdot 20times10^{-2}m}{425times10^{-2}m- 20times10^{-2}m} \
&boxed{{d_i}=20.99times10^{-2}m}
end{align}
$$
To find the height we will use equality of ratios of image and object height and position.
$$
begin{align}
frac{h_i}{h_o}&=frac{-d_i}{d_o} \
{h_i}&=frac{-d_i cdot h_o}{d_o} \
{h_i}&=frac{-20.99times10^{-2}m cdot 10times10^{-2}m}{425times10^{-2}m} \
&boxed{{h_i}=-0.49times10^{-2}m}
end{align}
$$
The image is $textbf{real and inverted}$.
$$
begin{align}
d_{o,n}&=l-{d_i} \
d_{o,n}&=25times10^{-2}m-21times10^{-2}m \
d_{o,n}&=4times10^{-2}m \
end{align}
$$
Since the object changed, all parameters in lens equation have to change.
$$
begin{align}
frac{1}{f_n}&=frac{1}{d_{i,n}}+frac{1}{d_{o,n}} \
{d_{i,n}}&=frac{d_{o,n}cdot f_n}{d_{o,n} -f_n} \
{d_{i,n}}&=frac{4times10^{-2}mcdot 4.05times10^{-2}m}{4times10^{-2}m- 4.05times10^{-2}m} \
&boxed{{d_{i,n}}=-324times10^{-2}m}
end{align}
$$
New high of object $h_{o,n}$ is equal to image high $h_i$ in $a)$.
$$
begin{align}
frac{h_{i,n}}{h_{o,n}}&=frac{-d_{i,n}}{d_{o,n}} \
{h_{i,n}}&=frac{-d_{i,n} cdot h_{o,n}}{d_{o,n}} \
{h_{i,n}}&=frac{-(324)times10^{-2}m cdot (-0.49)times10^{-2}m}{4times10^{-2}m} \
&boxed{{h_{i,n}}=-39.69times10^{-2}m}
end{align}
$$
The image is $textbf{virtual and inverted}$.
$$
begin{align}
&{m}=frac{h_{i,n}}{h_o} \
&{m}=frac{-39.69times10^{-2}m}{10times10^{-2}m} \
&boxed{{m}=-3.97}
end{align}
$$
$b)$ $d_{i,n}=-324times10^{-2}m$, ${h_{i,n}}=-39.69times10^{-2}m$ (The image is virtual and inverted.)
$c)$ $m=-3.97$
$theta_{c}=45text{ $^circ$}$
$n_{a}=1$
$textbf{Approach}$
In this problem, we will use the definition for the critical angle for total internal reflection.
$textbf{Solution}$
The definition for the critical angle for total internal reflection is
$$
begin{align}
sintheta_{c}=frac{n_2}{n_1}
end{align}
$$
so we write
$$
begin{align}
sintheta_{c}&=frac{n_a}{n_g} \
{n_g}&=frac{n_a}{sintheta_{c}} \
{n_g}&=frac{1}{sin45^circ} \
&boxed{n_g=1.41}
end{align}
$$
n_g=1.41
$$
$n=2.35$
$c=3times10^8frac{text{ m}}{text{ s}}$
$textbf{Approach}$
In this problem, we will use a definition of the index of refraction.
$textbf{Solution}$
The definition of index of refraction is
$$
begin{align}
{n}=frac{c}{v}
end{align}
$$
We need to calculate the speed of light in medium, so we write
$$
begin{align}
&{v}=frac{c}{n} \
&{v}=frac{3times10^8frac{text{ m}}{text{ s}}}{2.35} \
&boxed{{v}=1.28times10^8frac{ m}{text{ s}}}
end{align}
$$
{v}=1.28times10^8frac{ m}{text{ s}}
$$
$h_{o}=3times10^{-2}text{ m}$
$d_{o}=20times10^{-2}text{ m}$
$d_{i}=10times10^{-2}text{ m}$
$textbf{Approach}$
We will find the solutions by using the definition of the thin lens equation.
$textbf{Solution}$
Thin lens equation is defined as
$$
begin{align}
frac{1}{f}=frac{1}{d_i}+frac{1}{d_o}
end{align}
$$
so for focal length we write
$$
begin{align}
{f}&=frac{d_ocdot d_i}{d_o +d_i} \
{f}&=frac{20times10^{-2}mcdot 10times10^{-2}m}{20times10^{-2}m +10times10^{-2}m}{} \
&boxed{{f}=6.67times10^{-2}m}
end{align}
$$
{f}=6.67 times10^{-2}m
$$
$$
begin{align}
{n_1cdot sin theta_1}={n_2cdot sin theta_2}
end{align}
$$
We want to achieve
$$
begin{align}
{n}=cdot frac{sin theta_1}{sin theta_2}
end{align}
$$
(2) can be written like that only if $n_2=n_{air}$ respectievly $n_2=1$ and $n_1=n$.
$n=1.33$
$d=1.5times10^{11}text{m}$
$c=3times10^8frac{text{ m}}{text{ s}}$
$textbf{Approach}$
In this problem, we will use a definition of the index of refraction and equation for speed.
$textbf{Solution}$
First, we will find time for light to travel from Sun to the Earth trough vacuum.
$$
begin{align}
{t_v}&=frac{d}{c} \
{t_v}&=frac{1.5times10^{11}text{m}}{3times10^8frac{text{ m}}{text{ s}}} \
{t_v}&=500{s}
end{align}
$$
Now, to find the speed trough water we need the definition of index of refraction
$$
begin{align}
{n}&=frac{c}{v} \
{v}&=frac{c}{n} \
{v}&=frac{3times10^8frac{text{ m}}{text{ s}}}{1.33} \
{v}&=2.26times10^8frac{ m}{text{ s}}
end{align}
$$
and same equation as (1)
$$
begin{align}
{t_w}&=frac{d}{v} \
{t_w}&=frac{1.5times10^{11}text{m}}{2.26times10^8frac{text{ m}}{text{ s}}} \
{t_w}&=663.72s
end{align}
$$
Our solution is difference between (2) and (4).
$$
begin{align}
{Delta t}&={t_w – t_v} \
{Delta t}&={663s – 500s} \
&boxed{{Delta t}=163.72s}
end{align}
$$
{Delta t}=163.72s
$$
$d_{o}=35times10^{-2}text{ m}$
$d_{i}=1.9times10^{-4}text{ m}$
$textbf{Approach}$
We will find the solutions by using the definition of the thin lens equation.
$textbf{Solution}$
Thin lens equation is defined as
$$
begin{align}
frac{1}{f}=frac{1}{d_i}+frac{1}{d_o}
end{align}
$$
so for focal length we write
$$
begin{align}
{f}&=frac{d_ocdot d_i}{d_o +d_i} \
{f}&=frac{35times10^{-2}mcdot 1.9times10^{-4}m}{35times10^{-2}m +1.9times10^{-4}m}{} \
&boxed{{f}=1.9times10^{-4}m}
end{align}
$$
{f}=1.9times10^{-4}m
$$
$n_{w}=1.33$
$n_{a}=1$
$d=12times10^{-2}text{ m}$
$theta_{w}=5text{ $^circ$}$
$textbf{Approach}$
In this problem, we will use Snell’s law and basic trigonometry.
$textbf{Solution}$
$a)$ The definition of Snell’s law of refraction is
$$
begin{align}
{n_1cdot sin theta_1}={n_2cdot sin theta_2}
end{align}
$$
so we write
$$
begin{align}
{n_{a}cdotsintheta_{a}}&={n_{w}cdotsintheta_{w}} \
{theta_{a}}&=arcsin{left( frac{n_w}{n_{a}} cdot sintheta_w right)} \
{theta_{a}}&=arcsin{left( frac{1.33}{1} cdot sin 5^circ right)} \
&boxed{{theta_{a}}=6^circ39′}
end{align}
$$
$$
begin{align}
tan 5^circ&=frac{l}{d} \
tan theta_2&=frac{l}{d_n} \
tan 6^circ39’&=frac{l}{d_n}
end{align}
$$
When we equalize (3) and (4), we have the solution $d_n$.
$$
begin{align}
{d}cdot tan 5^circ &={d_n}cdot tan 6^circ39′ \
{d_n}&=dcdot frac{tan 5^circ}{tan 6^circ39′} \
{d_n}&=12times10^{-2}{ m}cdot frac{tan 5^circ}{tan 6^circ39′} \
&boxed{{d_n}=9times10^{-2}m}
end{align}
$$
Now, we need to compare two depths with indexes of refraction.
$$
begin{align}
frac{d_n}{d}&=frac{9times10^{-2}}{12times10^{-2}}=0.75 \
frac{n_a}{n_w}&=frac{1}{1.33}=0.75 \
&boxed{frac{d_n}{d}=frac{n_a}{n_w}}
end{align}
$$
$b)$ ${d_n}=9times10^{-2}m$, $frac{d_n}{d}=frac{n_a}{n_w}$
$n_{g}=1.5$
$n_{a}=1$
$theta_{a}=theta_1=90text{ $^circ$}$
$textbf{Approach}$
In this problem, we will use Snell’s law.
$textbf{Solution}$
We need to prove that if light ray acts like it is shown in the picture, angle $theta_1’$ will not be the critical angle. Let’s start with the definition of Snell’s law of refraction.
$$
begin{align}
{n_1cdot sin theta_1}={n_2cdot sin theta_2}
end{align}
$$
For the first refraction we write
$$
begin{align}
{n_{a}cdotsintheta_{a}}&={n_{g}cdotsintheta_{g}} \
{theta_{g}}&=arcsin{left( frac{n_a}{n_{g}} cdot sintheta_a right)} \
{theta_{g}}&=arcsin{left( frac{1}{1.5} cdot sin 90^circ right)} \
&boxed{{theta_{g}}=41^circ49′}
end{align}
$$
Where $theta_2=theta_g$.
Using knowledge of geometry we can calculate $theta_1’$.
$$
begin{align}
{theta_1′}&={90^circ}-{theta_2} \
{theta_1′}&=48^circ11′
end{align}
$$
Now, let’s find a critical angle from the definition.
$$
begin{align}
theta_{c}&=arcsin{left(frac{n_a}{n_g}right)} \
theta_{c}&=arcsin{left(frac{1}{1.5}right)} \
theta_{c}&=41^circ49′
end{align}
$$
We can conclude from the fact $theta_{c}<{theta_1'}$ that light will not leave the glass, actually it will reflect back into the glass.
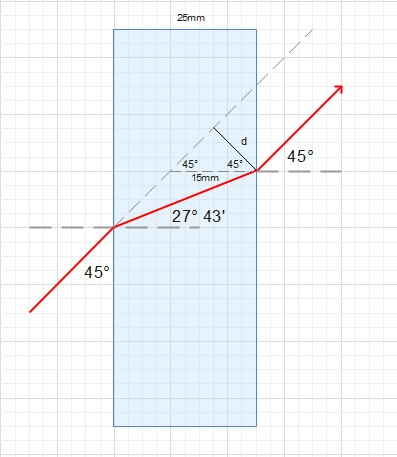
$$
begin{align}
frac{15mm}{sin 90^circ}&=frac{d}{sin 45^circ} \
d&=frac{15mm cdot sin 45^circ}{sin 90^circ} \
&boxed{d=10.6mm}
end{align}
$$
$n_{a}=1.0003$
$n_{g,b}=1.7708$
$n_{g,r}=1.7273$
$theta_{a}=45text{ $^circ$}$
$textbf{Approach}$
In this problem we will use Snell’s law.
$textbf{Solution}$
The angle of dispersion will be different for red end blue light. Let’s start with the definition of Snell’s law of refraction.
$$
begin{align}
{n_1cdot sin theta_1}={n_2cdot sin theta_2}
end{align}
$$
For blue light we write
$$
begin{align}
{n_{a}cdotsintheta_{a}}&={n_{g,b}cdotsintheta_{g,b}} \
{theta_{g,b}}&=arcsin{left( frac{n_a}{n_{g,b}} cdot sintheta_a right)} \
{theta_{g,b}}&=arcsin{left( frac{1.0003}{1.7708} cdot sin 45^circ right)} \
&boxed{{theta_{g,b}}=23^circ32′}
end{align}
$$
For red light we write
$$
begin{align}
{n_{a}cdotsintheta_{a}}&={n_{g,r}cdotsintheta_{g,r}} \
{theta_{g,r}}&=arcsin{left( frac{n_a}{n_{g,r}} cdot sintheta_a right)} \
{theta_{g,r}}&=arcsin{left( frac{1.0003}{1.7273} cdot sin 45^circ right)} \
&boxed{{theta_{g,r}}=24^circ10′}
end{align}
$$
$$
{theta_{g,r}}=24^circ10′
$$
$n_{a}=1$
$n_{i}=1.31$
$textbf{Approach}$
In this problem, we will use the definition for the critical angle.
$textbf{Solution}$
The definition for the critical angle for total internal reflection is
$$
begin{align}
sintheta_{c}=frac{n_2}{n_1}
end{align}
$$
so we have
$$
begin{align}
sintheta_{c}&=frac{n_a}{n_i} \
theta_{c}&=arcsin{left(frac{n_a}{n_i}right)} \
theta_{c}&=arcsin{left(frac{1}{1.31}right)} \
&boxed{theta_{c}=49^circ46′}
end{align}
$$
The index of refraction of glass is $n=1.54$ and it is greater than the index of the ice. Because of that, the critical angle for glass will be smaller which means more light rays will reflect back into the cable, and $textbf{the glass is a better}$ material for fiber-optic cables.
$h_{i}=4times10^{-2}text{ m}$
$d_{i}=25times10^{-2}text{ m}$
$f=-15times10^{-2}text{ m}$
$d_{o,n}=-10times10^{-2}text{ m}$
$textbf{Approach}$
We will find the solutions by using the definition of the thin lens equation and magnification.
$textbf{Solution}$
$h_i$ and $d_i$ represent information about the image produced by the convex lens. After we put a concave lens between the convex lens and its image, the image becomes an object for the concave lens. Because of that, information for the object and image of the concave lens will be written with index $n$.
Let’s start with thin lens equation.
$$
begin{align}
frac{1}{f}&=frac{1}{d_i}+frac{1}{d_o} \
{d_{i,n}}&=frac{d_{o,n}cdot f}{d_{o,n} -f} \
{d_{i,n}}&=frac{-15times10^{-2}mcdot (-10)times10^{-2}m}{-10times10^{-2}m- (-15)times10^{-2}m}{} \
&boxed{{d_{i,n}}=30times10^{-2}m}
end{align}
$$
The ratio of high of image and object is equal to negative ratio of theirs positions.
$$
begin{align}
frac{h_{i,n}}{h_{o,n}}&=frac{-d_{i,n}}{d_{o,n}} \
{h_{i,n}}&=frac{-d_{i,n} cdot h_{o,n}}{d_{o,n}} \
{h_{i,n}}&=frac{-30times10^{-2}m cdot 4times10^{-2}m}{-10times10^{-2}m} \
&boxed{{h_{i,n}}=12times10^{-2}m}
end{align}
$$
The result is positive which means the orientation of image is not changed.
${h_{i,n}}=12times10^{-2}m$
Also, animals who are active during the day and have to be on alert all the time, have wide horizontal pupils. It makes them see a wide field of vision.
For example, eagles can see clearly eight times as far as humans can, deers and horses see wider than humans, and deepwater fishes have eyes with few cone cells so they can see in the darkness of a deep sea,
$h=1.5text{ m}$
$m=2text{ kg}$
$Delta T=10text{$K$}$
$g=9.8 frac{text{ m}}{text{ $s^2$}}$
$C=130frac{text{ J}}{text{ $kg K$}}$
$textbf{Approach}$
We will solve this problem with the definition of gravitation potential energy and the heat equation.
$textbf{Solution}$
When we drop the bag, its potential energy changes.
$$
begin{align}
PE&=mcdot gcdot h \
PE&={2kg}cdot {9.8 frac{m}{s^2}}cdot {1.5m} \
PE&={29.4 J}
end{align}
$$
To change the temperature by $10^circ C$, the bag needs to receive $Delta Q$ heat.
$$
begin{align}
Delta Q&=mcdot Ccdot Delta T \
Delta Q&={2kg}cdot 130 frac{J}{kgcdot K}cdot {10 K} \
end{align}
$$
The number of drops is the ratio of half of $PE$ and $Q$.
$$
begin{align}
N&=frac{Q}{frac{1}{2}cdot PE} \
N&=frac{2600J}{frac{1}{2}cdot 29.4 J} \
&boxed{N=177}
end{align}
$$
N=177
$$
$L_{1}=1text{ m}$
$L_{2}=0.995text{ m}$
$alpha_{iron}=12times 10^{-6}frac{text{ 1}}{text{ $^circ C$}}$
$textbf{Approach}$
Here we will use the definition of linear thermal expansion.
$textbf{Solution}$
The definition of linear thermal expansion is
$$
begin{align}
Delta L=alphacdot LcdotDelta T
end{align}
$$
Where $Delta L={L_1}-{L_2}$ and $L$ is the diameter of the iron hoop.
$$
begin{align}
Delta L&=alpha_{iron}cdot {L_2}cdotDelta T \
Delta T&=frac{Delta L}{alpha_{iron}cdot L_2} \
Delta T&=frac{1m-0.995m}{12times10^{-6}frac{1}{^circ C}cdot 0.995m} \
&boxed{Delta T=419^circ C}
end{align}
$$
Delta T=419^circ C
$$
$$
begin{align}
f=f_0cdotleft(1+frac{Delta v}{c} right)
end{align}
$$
Where $c$ is the speed of sound in a vacuum, $Delta v$ is the speed of a car and $f_0$ is the frequency of the horn. As the car slows down, the frequency $f$ will decrease.
$$
begin{align}
{F_r}&={F_R} \
frac{Gcdot Mcdot m}{R^2}&=frac{Gcdot Mcdot m}{r^2} \
frac{Gcdot Mcdot m}{R^2}&=frac{Gcdot Mcdot m}{1000^2cdot R^2}
end{align}
$$
We conclude
$$
begin{align}
&boxed{frac{F_R}{F_r}=10^6}
end{align}
$$
Therefore, a force that would act on us on the Sun’s surface is $10^6$ times larger than a force that would act on us at the distance $r$.
$$
begin{align}
E=frac{P}{4cdotpicdot r^2}
end{align}
$$
Here, $P$ represents the power of a source, the Sun. We can use the same logic as we did in $a)$.
begin{align}
{E_r}&={E_R} \
frac{P}{4cdotpicdot r^2}&=frac{P}{4cdotpicdot R^2} \
frac{P}{4cdotpicdot 1000^2cdot R^2}&=frac{1}{4cdotpicdot R^2} \
&boxed{frac{E_R}{E_r}=10^6}
end{align}
$$
Therefore, an illuminance on the distance $R$ is $10^6$ times larger than a force on the distance $r$.
$b)$ $frac{E_R}{E_r}=10^6$
$c)$ See the explanation.
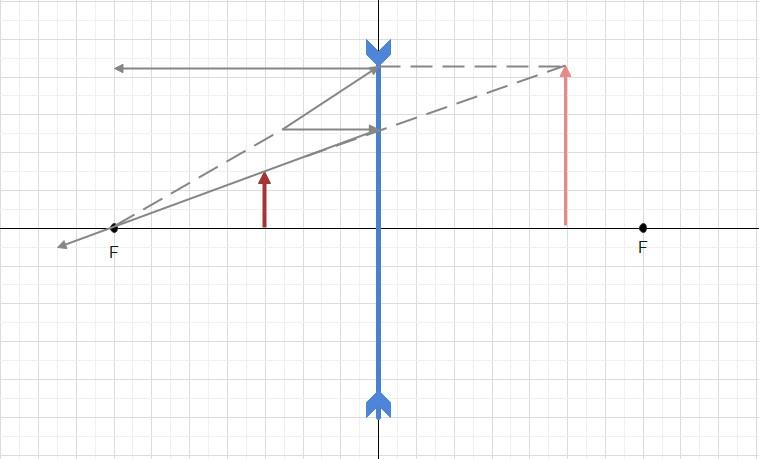
begin{align}
frac{1}{f}&=frac{1}{d_i}+frac{1}{d_o} \
{d_i}&=frac{d_ocdot f}{d_o -f} \
{d_i}&=frac{6times10^{-2}mcdot 14times10^{-2}m}{6times10^{-2}m- 14times10^{-2}m}{} \
&boxed{{d_i}=-10.5times10^{-2}m}
end{align}
$$
$$
begin{align}
frac{h_i}{h_o}&=frac{-d_i}{d_o} \
{h_i}&=frac{-d_i cdot h_o}{d_o} \
{h_i}&=frac{-(-10.5)times10^{-2}m cdot 3}{6times10^{-2}m} \
&boxed{{h_i}=5.25times10^{-2}m}
end{align}
$$

