Concave mirrors’ magnification depends on the objects position relative to the center of curvature.

Magnification is smaller than $1$ if the image is **smaller than the object**.
This will happen only if the object is **past the center of curvature**.

In this problem, we have a concave mirror. To solve this problem, we are going to use two equations, the mirror equation $frac{1}{f} = frac{1}{d_{o}}+ frac{1}{d_{i}}$ where $f$ is the focal length of mirror, $d_{o}$ is the position of our object, and $d_{i}$ is the position of the image. Also, we are going to use the magnification equation to find the image height $M= -frac{d_{i}}{d_{o}}$

First, we are going to find the image position from the magnification equation. We can multiply both sides with $-d_{o}$, and substitute the values hfill textcolor{white}{.}
begin{align*}
M&=- frac{d_{i}}{d_{o}}/ cdot -d_{o}\
d_{i}&=-Md_{o}\
d_{i}&=- (+3.2) cdot 30 hspace{0.5mm} mathrm{cm}\
d_{i}&=- 96 hspace{0.5mm} mathrm{cm}
end{align*}

Now, we can find the focal length. In this step, we need to find the least common multipe for $frac{1}{d_{i}}$ and $frac{1}{d_{o}}$ hfill textcolor{white}{.}
begin{align*}
frac{1}{f}&= frac{1}{d_{i}} + frac{1}{d_{o}} \
frac{1}{f}&= frac{d_{o}+d_{i}}{d_{i} cdot d_{o}}
end{align*}

We have found the final expression for the focal length, and now, we can substitute the values

$$
begin{align*}
f&=frac{d_{i} d_{o}}{d_{o}+d_{i}}\
f&=frac{(-96 hspace{0.5mm} mathrm{cm}) 30 hspace{0.5mm} mathrm{cm}}{30 hspace{0.5mm} mathrm{cm}-96 hspace{0.5mm} mathrm{cm}}\
f&=frac{-2880 hspace{0.5mm} mathrm{cm^{2}}}{-66 hspace{0.5mm} mathrm{cm}}\
f&=43.4 hspace{0.5mm} mathrm{cm}\
f& approx 44 hspace{0.5mm} mathrm{cm}
end{align*}
$$

$C.$ $44 hspace{0.5mm} mathrm{cm}$

In this problem, we have a concave mirror. To solve this problem, we are going to use the mirror equation $frac{1}{f} = frac{1}{d_{o}}+ frac{1}{d_{i}}$ where $f$ is the focal length of mirror, $d_{o}$ is the position of our object, and $d_{i}$ is the position of the image.

To find the position of the image from the mirror equation, first we are going to subtract $frac{1}{d_{o}}$ on the both sides.

$$
begin{align*}
frac{1}{f} &= frac{1}{d_{o}}+ frac{1}{d_{i}} / – frac{1}{d_{o}} \
frac{1}{d_{i}}&= frac{1}{f} – frac{1}{d_{o}}
end{align*}
$$

In this step, we need to find the least common multipe for $frac{1}{f}$ and $frac{1}{d_{o}}$ hfill textcolor{white}{.}
begin{align*}
frac{1}{d_{i}}&= frac{1}{f} – frac{1}{d_{o}} \
frac{1}{d_{i}}&= frac{d_{o}- f}{f cdot d_{o}}
end{align*}

We have found the final expression for the image position, and now, we can substitue the values and calculate the position

$$
begin{align*}
d_{i}&= frac{f cdot d_{o}}{d_{o}- f}\
d_{i}&= frac{14 hspace{0.5mm} mathrm{cm} cdot 21 hspace{0.5mm} mathrm{cm}}{21 hspace{0.5mm} mathrm{cm}- 14 hspace{0.5mm} mathrm{cm}}\
d_{i}&= frac{294 hspace{0.5mm} mathrm{cm^{2}}}{7 hspace{0.5mm} mathrm{cm}}\
d_{i}&= 42 hspace{0.5mm} mathrm{cm}
end{align*}
$$

$D.$ $42 hspace{0.5mm} mathrm{cm}$

Answers $A$ and $B$ are discarded because we know that there are some kinds of both spherical and parabolic mirrors that do focus light rays on the focal point.

Answer $D$ is disregarded because the difference between spherical and parabolic mirrors is that parabolic mirror will focus parallel rays into a point, but a spherical mirror **only focuses at a point when the object is at the center of the curve.**
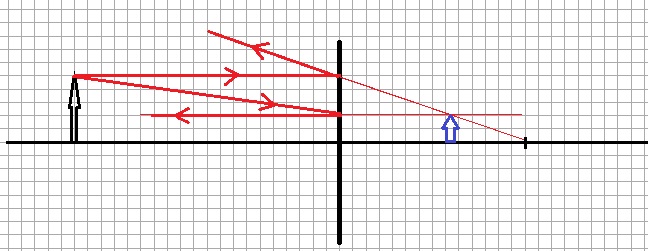
Which further means that defective spherical mirror will not properly focus rays at the focal point.

We need to determine the angle between reflected ray and the mirror if the light ray strikes a plane mirror at an angle of $theta_i=23^o$ to the normal.

First, we need to calculate the angle of reflection. It is the angle between normal of the mirror and the reflected ray. In a plane mirror, that angle is equal to the angle of incidence:
$$theta_r=theta_i$$
$$theta_r=23^o$$

Now we can calculate the angle between reflected ray and plane mirror, $alpha$. That angle can be calculate as a difference between an angle between normal and the plane and the angle of reflection:
$$alpha=90^o-theta_r$$
Inserting values we get:
$$alpha=90^o- 23^o$$
Finally:
$$boxed{alpha=67^o}$$

c) $alpha=67^o$

We need to determine the height of the object if the inverted image is tall $h_i=8.5,,rm{cm}$, located at a distance of $d_i=34.5,,rm{cm}$ from the mirror with a focal length of $f=24,,rm{cm}$

In order to solve the problem, we are going to use the equation:
$$frac{1}{d_o}+frac{1}{d_i}=frac{1}{f}$$

From the previous equation we can express $d_o$:
$$frac{1}{d_o}=frac{1}{f}-frac{1}{d_i}$$
$$frac{q}{d_o}=frac{d_i-f}{fd_i}$$
And finally:
$$d_o=frac{fd_i}{d_i-f}$$

Inserting values we get:
$$d_o=frac{24cdot 34.5}{34.5-24}$$
$$d_o=78.86,,rm{cm}$$

Now we can calculate the height of the object using the equation for magnification:
$$frac{h_i}{h_o}=-frac{d_i}{d_o}$$
$$h_o=h_ifrac{d_o}{d_i}$$
Inserting values we get:
$$h_o=-(-8.5)cdot frac{78.86}{34.5}$$
$$boxed{h_o=19,,rm{cm}}$$

$$h_o=19,,rm{cm}$$

In this problem, we have a concave mirror. To solve this problem, we are going to use the mirror equation $frac{1}{f} = frac{1}{d_{o}}+ frac{1}{d_{i}}$ where $f$ is the focal length of mirror, $d_{o}$ is the position of our object, and $d_{i}$ is the position of the image.

To find the position of the object from the mirror equation, first we are going to subtract $frac{1}{d_{i}}$ on the both sides.

$$
begin{align*}
frac{1}{f} &= frac{1}{d_{o}}+ frac{1}{d_{i}} / – frac{1}{d_{i}} \
frac{1}{d_{o}}&= frac{1}{f} – frac{1}{d_{i}}
end{align*}
$$

In this step, we need to find the least common multipe for $frac{1}{f}$ and $frac{1}{d_{i}}$ hfill textcolor{white}{.}
begin{align*}
frac{1}{d_{o}}&= frac{1}{f} – frac{1}{d_{i}} \
frac{1}{d_{o}}&= frac{d_{i}- f}{f cdot d_{i}}
end{align*}

We have found the final expression for the object position, and now, we can substitute the values

$$
begin{align*}
d_{o}&= frac{f cdot d_{i}}{d_{i}- f}\
d_{o}&= frac{16.0 hspace{0.5mm} mathrm{cm} cdot 38.6 hspace{0.5mm} mathrm{cm}}{38.6 hspace{0.5mm} mathrm{cm}- 16.0 hspace{0.5mm} mathrm{cm}}\
d_{o}&= frac{617.6 hspace{0.5mm} mathrm{cm^{2}}}{22.6 hspace{0.5mm} mathrm{cm}}\
d_{o}&= 27.3 hspace{0.5mm} mathrm{cm}
end{align*}
$$

$D.$ $27.3 hspace{0.5mm} mathrm{cm}$

In this problem, we have a convex mirror, where we need to find the focal length of the mirror. We are going to use the mirror equation $frac{1}{f} = frac{1}{d_{o}}+ frac{1}{d_{i}}$ where $f$ is the focal length of mirror, $d_{o}$ is the position of our object, and $d_{i}$ is the position of the image. Also, we are going to use the magnification equation to find the image position $M= -frac{d_{i}}{d_{o}}$

First, we are going to find the object position from the magnification equation. We can multiply both sides with $-d_{i}/M$, and substitute the values hfill textcolor{white}{.}
begin{align*}
M&=- frac{d_{i}}{d_{o}}/ cdot -(d_{o}/M)\
d_{o}&=-frac{d_{i}}{M}\
d_{o}&=-frac{-8.4 hspace{0.5mm} mathrm{cm}}{0.75}\
d_{o}&=11.2 hspace{0.5mm} mathrm{cm}
end{align*}

Now, we can find the focal length. In this step, we need to find the least common multipe for $frac{1}{d_{i}}$ and $frac{1}{d_{o}}$ hfill textcolor{white}{.}
begin{align*}
frac{1}{f}&= frac{1}{d_{i}} + frac{1}{d_{o}} \
frac{1}{f}&= frac{d_{o}+d_{i}}{d_{i} cdot d_{o}}
end{align*}

We have found the final expression for the focal length, and now, we can substitute the values

$$
begin{align*}
f&= frac{d_{i} d_{o}}{d_{o}+d_{i}}\
f&= frac{-8.4 hspace{0.5mm} mathrm{cm} cdot 11.2 hspace{0.5mm} mathrm{cm}}{11.2 hspace{0.5mm} mathrm{cm}- 8.4 hspace{0.5mm} mathrm{cm}}\
f&= frac{-94.8 hspace{0.5mm} mathrm{cm^{2}}}{2.8 hspace{0.5mm} mathrm{cm}}\
f&= -33.6 hspace{0.5mm} mathrm{cm}\
f& approx -34 hspace{0.5mm} mathrm{cm}
end{align*}
$$

$A.$ $-34 hspace{0.5mm} mathrm{cm}$

$m = dfrac{-d_i}{d_o} = -dfrac{34}{17} = -2.0$

The magnification is negative, therefore the image is inverted.