First, from the text of the problem we can take some information:
– the mirror is concave, which means that $f>0$
– image is upright, which means that $h_i>0$
– image is larger than object, which means that $M=-frac{d_i}{d_o}>1$

From the last equation we can get relation:
$$d_i<-d_o$$
The position of object is real, which means that the position of image is **virtual**.

Using the equation for mirrors:
$$frac{1}{d_o}+frac{1}{d_i}=frac{1}{f}$$
Using previous equations we can get:
$$frac{1}{d_i}<0/+frac{1}{d_o}$$
$$frac{1}{d_o}+frac{1}{d_i}<frac{1}{d_o}$$
And further combining them:
$$frac{1}{f}<frac{1}{d_o}$$
Which finally means:
$$boxed{d_o<f}$$

$$d_o<f$$
Image will be virtual.

We need to determine the magnification if a object is placed $d_o=20,,rm{cm}$ in front of a concave mirror that has a focal length of $f=9,,rm{cm}$.

In order to solve the problem, we need to use the next equation:
$$frac{1}{d_o}+frac{1}{d_i}=frac{1}{f}$$
Where $f$ is positive for the concave mirror.

From the previous equation we can express $d_i$:
$$frac{1}{d_i}=frac{1}{f}-frac{1}{d_o}$$
$$frac{q}{d_i}=frac{d_o-f}{fd_o}$$
And finally:
$$d_i=frac{fd_o}{d_o-f}$$

Inserting values we get:
$$d_i=frac{9cdot 20}{20-9}$$
$$d_i=16.36,,rm{cm}$$

Finally we can calculate magnification:
$$M=-frac{d_i}{d_o}$$
Inserting values:
$$M=-frac{16.36}{20}$$
$$boxed{M=-0.82}$$

$$M=-0.82$$

We need to determine the position of an object if a mirror with focal length of $f=12,,rm{cm}$ creates an image at a distance of $d_i=22.3,,rm{cm}$.

Main equation that we will use is mirror equation:
$$frac{1}{d_o}+frac{1}{d_i}=frac{1}{f}$$

From the previous equation we can express $d_o$:
$$frac{1}{d_o}=frac{1}{f}-frac{1}{d_i}$$
$$frac{q}{d_o}=frac{d_i-f}{fd_i}$$
And finally:
$$d_o=frac{fd_i}{d_i-f}$$

Now we can insert values:
$$d_o=frac{12cdot 22.3}{22.3-12}$$
$$boxed{d_o=26,,rm{cm}}$$

$$d_o=26,,rm{cm}$$

In this case, we have a concave mirror with the focal length of $f= 12.0 hspace{0.5mm} mathrm{cm}$, and the object that is at the position of $d_{o} = 22.0 hspace{0.5mm} mathrm{cm}$. Also, that object is $h_{o}= 3.0 hspace{0.5mm} mathrm{cm}$ high. To find the position and the height of the image, we are going to use two methods. First one, where we use a ray diagram in scale of $1:3$. And the second one, where we use the mirror and the magnification equation.

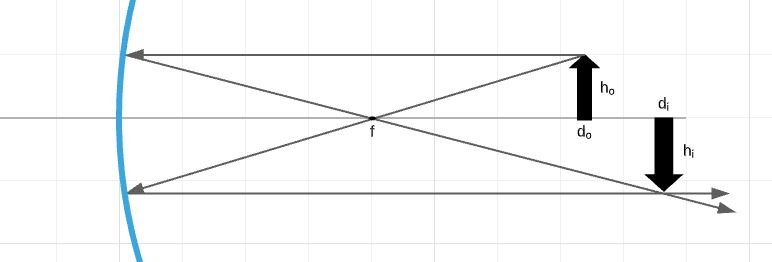
The diagram below is in scale of $1:3$, We can see that the image is real and inverted, so its height will be lesser than zero. Also, from diagram we can see that height is about $h_{i}= -1.2 hspace{0.5mm} mathrm{cm}$, or in real size $h_{i}= -3.6 hspace{0.5mm} mathrm{cm}$. For the position of the image, we can see that the image is at $8.0 hspace{0.5mm} mathrm{cm}$ and about $3/4$ of the square. So in the total, the position of the image is $d_{i}=8.75 hspace{0.5mm} mathrm{cm}$, or in real size $d_{i}=26.25 hspace{0.5mm} mathrm{cm}$.

Now, we are verify our result of the position of the image with the mirror equation
begin{align*}
frac{1}{d_{o}}+ frac{1}{d_{i}}&= frac{1}{f}\
frac{1}{d_{i}}&= frac{1}{f} – frac{1}{d_{o}}\
frac{1}{d_{i}}&= frac{d_{o} – f}{f hspace{0.5mm} d_{o}} \
d_{i}&= frac{f hspace{0.5mm} d_{o}}{d_{o} – f}\
d_{i}&= frac{12.0 hspace{0.5mm} mathrm{cm} cdot 22.0 hspace{0.5mm} mathrm{cm}}{22.0 hspace{0.5mm} mathrm{cm} – 12.0 hspace{0.5mm} mathrm{cm}}\
d_{i}&= 26.4 hspace{0.5mm} mathrm{cm}
end{align*}
So, the position of the image is [ framebox[1.1width]{$ therefore d_{i} = 26.4 hspace{0.5mm} mathrm{cm} $}]
Now, we are going to use the magnification equation to find the height of the image
begin{align*}
M&=- frac{d_{i}}{d_{o}}= frac{h_{i}}{h_{o}} \
frac{h_{i}}{h_{o}} &= – frac{d_{i}}{d_{o}} \
h_{i} &=- h_{o} frac{d_{i}}{d_{o}} \
h_{i} &=- 3.0 hspace{0.5mm} mathrm{cm} hspace{0.5mm} frac{26.4 hspace{0.5mm} mathrm{cm}}{22.0 hspace{0.5mm} mathrm{cm}} \
h_{i} &=- 3.0 hspace{0.5mm} mathrm{cm} cdot 1.2 \
h_{i} &=- 3.6 hspace{0.5mm} mathrm{cm}
end{align*}
So, the height of the image is [ framebox[1.1width]{$ therefore h_{i} = -3.6 hspace{0.5mm} mathrm{cm} $}]

$d_{i} = 26.4 hspace{0.5mm} mathrm{cm}$

$$
h_{i} = -3.6 hspace{0.5mm} mathrm{cm}
$$

This is the case of convex mirror with the focal length of $f= -12.0 hspace{0.5mm} mathrm{cm}$, and the object that has the position of $d_{o} = 14.0 hspace{0.5mm} mathrm{cm}$. Also, that object is $h_{o}= 3.0 hspace{0.5mm} mathrm{cm}$ high. To find the position and the height of the image, we are going to use two methods. First one, where we use a ray diagram in scale of $1:3$. And the second one, where we use the mirror and the magnification equation.

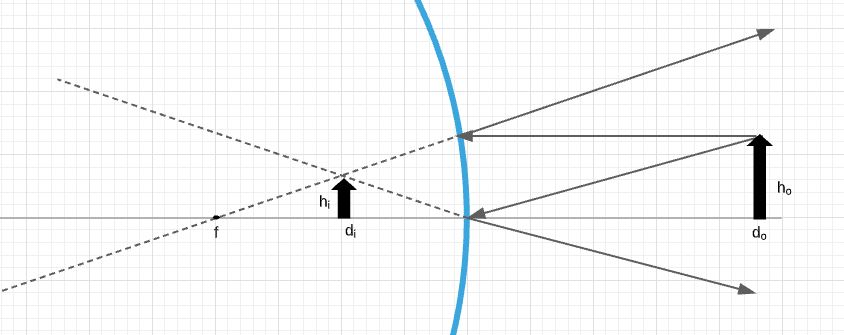
The diagram below is in scale of $1:3$. We can see that the image is upright and virtual, so its height will be greater than zero, but the position willl be lesser than zero. Also, from diagram we can see that height is about $h_{i}= 0.6 hspace{0.5mm} mathrm{cm}$, or in real size $h_{i}= 1.8 hspace{0.5mm} mathrm{cm}$. For the position of the image, we can see that the image is at $-2.0 hspace{0.5mm} mathrm{cm}$. So the position of the image in real size is $d_{i}=6.0 hspace{0.5mm} mathrm{cm}$. Also, on the diagram below, the big square has sides of length $1.0 hspace{0.5mm} mathrm{cm}$.

Now, we are verify our result of the position of the image with the mirror equation
begin{align*}
frac{1}{d_{o}}+ frac{1}{d_{i}}&= frac{1}{f}\
frac{1}{d_{i}}&= frac{1}{f} – frac{1}{d_{o}}\
frac{1}{d_{i}}&= frac{d_{o} – f}{f hspace{0.5mm} d_{o}} \
d_{i}&= frac{f hspace{0.5mm} d_{o}}{d_{o} – f}\
d_{i}&= frac{-12.0 hspace{0.5mm} mathrm{cm} cdot 14.0 hspace{0.5mm} mathrm{cm}}{14.0 hspace{0.5mm} mathrm{cm} + 12.0 hspace{0.5mm} mathrm{cm}}\
d_{i}&= -6.5 hspace{0.5mm} mathrm{cm}
end{align*}
So, the position of the image is [ framebox[1.1width]{$ therefore d_{i} = -6.5 hspace{0.5mm} mathrm{cm} $}]
Now, we are going to use the magnification equation to find the height of the image
begin{align*}
M&=- frac{d_{i}}{d_{o}}= frac{h_{i}}{h_{o}} \
frac{h_{i}}{h_{o}} &= – frac{d_{i}}{d_{o}} \
h_{i} &=- h_{o} frac{d_{i}}{d_{o}} \
h_{i} &=- 4.0 hspace{0.5mm} mathrm{cm} frac{-6.5 hspace{0.5mm} mathrm{cm}}{14.0 hspace{0.5mm} mathrm{cm}} \
h_{i} &=- 4.0 hspace{0.5mm} mathrm{cm} cdot (-0.46) \
h_{i} &= 1.85 hspace{0.5mm} mathrm{cm}
end{align*}
So, the height of the image is [ framebox[1.1width]{$ therefore h_{i} =1.85 hspace{0.5mm} mathrm{cm} $}]

$d_{i} =-6.5 hspace{0.5mm} mathrm{cm}$

$$
h_{i} =1.85 hspace{0.5mm} mathrm{cm}
$$

An object with a height of $h_o=6,,rm{cm}$ is at a distance of $d_o=16.4,,rm{cm}$ in front of the convex mirror. We need to determine the curvature of the mirror if the imahe is $h_i=2.8,,rm{cm}$ tall.

In order to solve this problem, we need to use the next equation:
$$frac{h_i}{h_o}=-frac{d_i}{d_o}$$
And we can get:
$$d_i=-d_ofrac{h_i}{h_o}$$

inserting values we get.
$$d_i=-16.4cdot frac{2.8}{6}$$
$$d_i=-7.65,,rm{cm}$$

Next, we will use an equation for mirrors:
$$frac{1}{d_o}+frac{1}{d_i}=frac{1}{f}$$

From the previous equation we can express $f$:
$$frac{1}{f}=frac{d_i-d_o}{d_id_o}$$
And finally:
$$f=frac{d_id_o}{d_i-d_o}$$

Inserting values we get:
$$f=frac{16.4cdot 7.65}{7.65-16.4}$$
$$f=14.34,,rm{cm}$$

And finally, radius of the curvature can be calculated as:
$$r=2|f|$$
Inserting values:
$$r=2cdot 14.34$$
$$boxed{r=28.7,,rm{cm}}$$

$$r=28.7,,rm{cm}$$

To sovle this problem, we are going to use the mirror equation [frac{1}{d_{o}}+ frac{1}{d_{i}}= frac{1}{f}] and the magnification equation [M=- frac{d_{i}}{d_{o}}= frac{h_{i}}{h_{o}} ] We know that the magnification is $M= frac{2}{3}$, and the image has a position of $d_{i}=-12 hspace{0.5mm} mathrm{cm}$. Firstly, we are going to find the position of the object
begin{align*}
M&=- frac{d_{i}}{d_{o}} \
d_{o}&= – frac{d_{i}}{M}\
d_{o}&= – frac{-12 hspace{0.5mm} mathrm{cm}}{ frac{2}{3}}\
d_{o}&= frac{3 cdot 12 hspace{0.5mm} mathrm{cm}}{ 2}\
d_{o}&= 18 hspace{0.5mm} mathrm{cm}
end{align*}
Now, we can find the focal length of the mirror with the previous information and the mirror equation
begin{align*}
frac{1}{f} &= frac{1}{d_{o}}+ frac{1}{d_{i}}\
frac{1}{f} &= frac{d_{o}+d_{i}}{ d_{o} hspace{0.5mm} d_{i}}\
frac{1}{f} &= frac{d_{o}+d_{i}}{ d_{o} hspace{0.5mm} d_{i}}\
f &= frac{ d_{o} hspace{0.5mm} d_{i}}{ d_{o}+d_{i}} \
f &= frac{ 18 hspace{0.5mm} mathrm{cm} hspace{0.5mm}(-12 hspace{0.5mm} mathrm{cm})}{ 18 hspace{0.5mm} mathrm{cm}-12 hspace{0.5mm} mathrm{cm}} \
f&= -36 hspace{0.5mm} mathrm{cm}
end{align*}
The focal length is [ framebox[1.1width]{$ therefore f = -36 hspace{0.5mm} mathrm{cm} $}]

$$
f = -36 hspace{0.5mm} mathrm{cm}
$$

Spherical mirrors have an aberration. There is an intrinsic defect with any mirror that takes on the shape of a sphere.

This defect prohibits the mirror from focusing all the incident light from the same location on an object to a precise point.

$$
text{color{#4257b2}The defect is most noticeable for light rays striking the outer edges of the mirror.

$ $

Rays that strike the outer edges of the mirror fail to focus in the same precise location as light rays that strike the inner portions of the mirror.}
$$

$$
text{color{#c34632}Therefore spherical aberration will be less for a mirror whose height is small compared to its radius of curvature }
$$