All Solutions
Page 469: Practice Problems
begin{center}
begin{tabular}{| c | c | c | }
hline
& Real case & The diagram\
hline
The original height & $2.0 hspace{0.5mm} mathrm{cm}$ & $0.5 hspace{0.5mm} mathrm{cm}$ \
The image height & $-1.0 hspace{0.5mm} mathrm{cm}$ & $-0.25 hspace{0.5mm} mathrm{cm}$ \
The original distance & $30.0 hspace{0.5mm} mathrm{cm}$ & $7.5 hspace{0.5mm} mathrm{cm}$ \
The image distance & $15.0 hspace{0.5mm} mathrm{cm}$ & $3.75 hspace{0.5mm} mathrm{cm}$ \
The radius & $20.0 hspace{0.5mm} mathrm{cm}$ & $5.0 hspace{0.5mm} mathrm{cm}$ \
The focal length & $10.0 hspace{0.5mm} mathrm{cm}$ & $2.5 hspace{0.5mm} mathrm{cm}$ \
hline
end{tabular}
end{center}
Also, in the diagram below, one square has length side of $1.0 hspace{0.5mm} mathrm{cm}$.
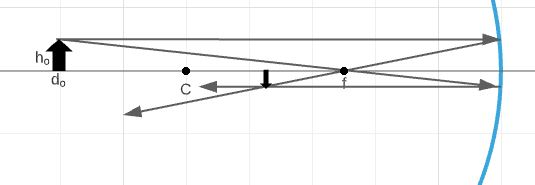
$$frac{1}{d_o}+frac{1}{d_i}=frac{1}{f}$$
Where $d_o$ is distance of an object, $d_i$ distance of the image and $f$ a focal length of the mirror.
$$frac{1}{d_i}=frac{1}{f}-frac{1}{d_o}$$
$$frac{q}{d_i}=frac{d_o-f}{fd_o}$$
And finally:
$$d_i=frac{fd_o}{d_o-f}$$
$$d_i=frac{0.16cdot 0.36}{0.36-0.16}$$
Finally:
$$boxed{d_i=28.8,,rm{cm}}$$
begin{align*}
frac{1}{d_{o}}+ frac{1}{d_{i}}&= frac{1}{f}\
frac{1}{d_{i}}&= frac{1}{f} – frac{1}{d_{o}}\
frac{1}{d_{i}}&= frac{d_{o} – f}{f hspace{0.5mm} d_{o}} \
d_{i}&= frac{f hspace{0.5mm} d_{o}}{d_{o} – f}\
d_{i}&= frac{16.0 hspace{0.5mm} mathrm{cm} cdot 36.0 hspace{0.5mm} mathrm{cm}}{36.0 hspace{0.5mm} mathrm{cm} – 16.0 hspace{0.5mm} mathrm{cm}}\
d_{i}&= 28.8 hspace{0.5mm} mathrm{cm}
end{align*}
The image position is [ framebox[1.1width]{$ therefore d_{i}= 28.8 hspace{0.5mm} mathrm{cm} $}]
d_{i}= 28.8 hspace{0.5mm} mathrm{cm}
$$
– the image is real
– the image is smaller than original
– the image is inverted
$$f=frac{r}{2}$$
Inserting values we get:
$$f=frac{0.16}{2}$$
$$f=8,,rm{cm}$$
$$frac{1}{d_o}+frac{1}{d_i}=frac{1}{f}$$
From this equation we can express $d_i$:
$$frac{1}{d_i}=frac{1}{f}-frac{1}{d_o}$$
$$frac{q}{d_i}=frac{d_o-f}{fd_o}$$
And finally:
$$d_i=frac{fd_o}{d_o-f}$$
$$d_i=frac{0.08cdot 0.2}{0.2-0.08}$$
$$boxed{d_i=13.3,,rm{cm}}$$
$$m=-frac{d_i}{d_o}=frac{h_i}{h_o}$$
Where $m$ is magnification and $h_o$ is height of an object.
From the previous equation we can get:
$$h_i=-h_ofrac{d_i}{d_o}$$
$$h_i=-0.03cdot frac{0.133}{0.2}$$
$$boxed{h_i=-2,,rm{cm}}$$
$$h_i=-2,,rm{cm}$$
$$
begin{align*}
r&= 2f\
f&= frac{r}{2}\
f&= frac{16.0 hspace{0.5mm} mathrm{cm}}{2}\
f&= 8.0 hspace{0.5mm} mathrm{cm}
end{align*}
$$
Now, we can find the position of the image
$$
begin{align*}
frac{1}{d_{o}}+ frac{1}{d_{i}}&= frac{1}{f}\
frac{1}{d_{i}}&= frac{1}{f} – frac{1}{d_{o}}\
frac{1}{d_{i}}&= frac{d_{o} – f}{f hspace{0.5mm} d_{o}} \
d_{i}&= frac{f hspace{0.5mm} d_{o}}{d_{o} – f}\
d_{i}&= frac{8.0 hspace{0.5mm} mathrm{cm} cdot 20.0 hspace{0.5mm} mathrm{cm}}{20.0 hspace{0.5mm} mathrm{cm} – 8.0 hspace{0.5mm} mathrm{cm}}\
d_{i}&= 13.3 hspace{0.5mm} mathrm{cm}
end{align*}
$$
begin{align*}
frac{h_{i}}{h_{o}} &= – frac{d_{i}}{d_{o}}\
h_{i} &= -h_{o} frac{d_{i}}{d_{o}}\
h_{i} &= -3.0 hspace{0.5mm} mathrm{cm} frac{13.3 hspace{0.5mm} mathrm{cm}}{20.0 hspace{0.5mm} mathrm{cm}}\
h_{i} &= -1.995 hspace{0.5mm} mathrm{cm} \
h_{i} &= -2.0 hspace{0.5mm} mathrm{cm}
end{align*}
So, the position of the image is [ framebox[1.1width]{$ therefore d_{i}= 13.3 hspace{0.5mm} mathrm{cm} $}] and the height of the image is [ framebox[1.1width]{$ therefore h_{i} = -2.0 hspace{0.5mm} mathrm{cm} $}]
$$
h_{i} = -2.0 hspace{0.5mm} mathrm{cm}
$$
$$frac{1}{d_o}+frac{1}{d_i}=frac{1}{f}$$
From the previous equation we can express $d_i$:
$$frac{1}{d_i}=frac{1}{f}-frac{1}{d_o}$$
$$frac{q}{d_i}=frac{d_o-f}{fd_o}$$
And finally:
$$d_i=frac{fd_o}{d_o-f}$$
$$d_i=frac{0.07cdot 0.16}{0.16-0.07}$$
$$boxed{d_i=12.44,,rm{cm}}$$
$$-frac{d_i}{d_o}=frac{h_i}{h_o}$$
From this we can get:
$$h_i=-h_o frac{d_i}{d_o}$$
Inserting values:
$$h_i=- 0.024cdot frac{0.1244}{0.16}$$
$$boxed{h_i=-1.867,,rm{cm}}$$
Where negative value means that the image is inverted.
$$h_i=-1.867,,rm{cm}$$
The positive sign means that the Image is formed in front of the mirror }$
$$
text{color{#c34632}Recall that : $$m = -dfrac{d_i}{d_o}$$}
$$
$$
m = -dfrac{12.44}{16} = -0.778
$$
The negative sign means that the Image will be Inverted
The height of the image will be $mtimestext{Object Height} =-0.778times2.4 = -1.867$
text{color{#4257b2}The Image is formed 12.44 cm in front of the mirror
$ $
The height of the image is $-1.867$ cm
$ $
The negative sign means that the Image is Inverted }
$$
$$frac{1}{d_o}+frac{1}{d_i}=frac{1}{f}$$
From the previous equation we can express $d_o$:
$$frac{1}{d_o}=frac{1}{f}-frac{1}{d_i}$$
$$frac{q}{d_o}=frac{d_i-f}{fd_i}$$
And finally:
$$d_o=frac{fd_i}{d_i-f}$$
$$d_o=frac{0.10cdot 0.16}{0.16-0.10}$$
$$boxed{d_o=26.67,,rm{cm}}$$
$$-frac{d_o}{d_i}=frac{h_o}{h_i}$$
From this we can get:
$$h_o=-h_ifrac{d_o}{d_i}$$
inserting values we get.
$$h_o=-(-3)cdot frac{26.67}{16}$$
$$boxed{h_o=5,,rm{cm}}$$
$$h_0=5,,rm{cm}$$
}$
dfrac{3}{80} = dfrac{1}{d_o}
$$
Take Reciprocal of both sides
$$
dfrac{80}{3} = d_o
$$
$$
d_oapprox 26.67
$$
To find the object height we need to find magnification first
$$
text{color{#c34632}Recall that : $$m = -dfrac{d_i}{d_o}$$}
$$
$$
m = -dfrac{16}{26.67} = -0.6
$$
$$
text{color{#4257b2}Recall that : $m=dfrac{h_i}{h_o}$}
$$
$$
-0.6=dfrac{-3}{h_o}
$$
$$
h_o=dfrac{-3}{-0.6} = +5
$$
text{color{#4257b2}Height of the Object is 5 cm
$ $
It is placed 26.67 cm in front of the mirror }
$$
begin{align*}
frac{1}{d_{o}}+ frac{1}{d_{i}}&= frac{1}{f}\
frac{1}{d_{i}}&= frac{1}{f} – frac{1}{d_{o}}\
frac{1}{d_{i}}&= frac{d_{o} – f}{f hspace{0.5mm} d_{o}} \
d_{i}&= frac{f hspace{0.5mm} d_{o}}{d_{o} – f}\
d_{i}&= frac{-15.0 hspace{0.5mm} mathrm{cm} cdot 20.0 hspace{0.5mm} mathrm{cm}}{20.0 hspace{0.5mm} mathrm{cm} + 15.0 hspace{0.5mm} mathrm{cm}}\
d_{i}&= -8.6 hspace{0.5mm} mathrm{cm}
end{align*}
So, the distance of the image is [ framebox[1.1width]{$ therefore d_{i} = -8.6 hspace{0.5mm} mathrm{cm} $}]
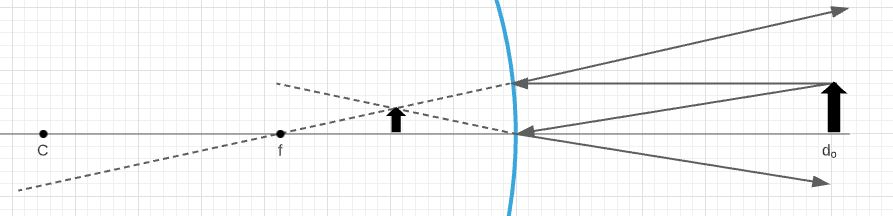
d_{i} = -8.6 hspace{0.5mm} mathrm{cm}
$$
We can use the next equation in order to calculate the distance of an image:
$$frac{1}{d_o}+frac{1}{d_i}=frac{1}{f}$$
From the previous equation we can express $d_i$:
$$frac{1}{d_i}=frac{1}{f}-frac{1}{d_o}$$
$$frac{q}{d_i}=frac{d_o-f}{fd_o}$$
And finally:
$$d_i=frac{fd_o}{d_o-f}$$
$$d_i=frac{-13cdot 60}{60+13}$$
$$boxed{d_i=-10.7,,rm{cm}}$$
$$frac{h_i}{h_o}=-frac{d_i}{d_o}$$
From this we can get:
$$h_i=h_ofrac{d_i}{d_o}$$
$$h_i=-6cdot frac{-10.7}{60}$$
$$boxed{h_i=1.07,,rm{cm}}$$
$$h_i=1.07,,rm{cm}$$
begin{align*}
frac{1}{d_{o}}+ frac{1}{d_{i}}&= frac{1}{f}\
frac{1}{d_{i}}&= frac{1}{f} – frac{1}{d_{o}}\
frac{1}{d_{i}}&= frac{d_{o} – f}{f hspace{0.5mm} d_{o}} \
d_{i}&= frac{f hspace{0.5mm} d_{o}}{d_{o} – f}\
d_{i}&= frac{-13.0 hspace{0.5mm} mathrm{cm} cdot 60.0 hspace{0.5mm} mathrm{cm}}{60.0 hspace{0.5mm} mathrm{cm} + 13.0 hspace{0.5mm} mathrm{cm}}\
d_{i}&= -10.7 hspace{0.5mm} mathrm{cm}
end{align*}
So, the distance of the image is [ framebox[1.1width]{$ therefore d_{i} = -10.7 hspace{0.5mm} mathrm{cm} $}]
To calculate the height of the image, we use the equation [ frac{h_{i}}{h_{o}} =- frac{d_{i}}{d_{o}} ] where $h_{i}$ is the image of the diameter, so we can write
begin{align*}
frac{h_{i}}{h_{o}} &=- frac{d_{i}}{d_{o}} \
h_{i} &=-h_{o} frac{d_{i}}{d_{o}} \
h_{i} &=-6.0 hspace{0.5mm} mathrm{cm} frac{-10.7 hspace{0.5mm} mathrm{cm}}{60.0 hspace{0.5mm} mathrm{cm}} \
h_{i} &=-6.0 hspace{0.5mm} mathrm{cm} cdot (-0.18) \
h_{i} &=1.07 hspace{0.5mm} mathrm{cm}
end{align*}
The diameter of the image is [ framebox[1.1width]{$ therefore h_{i} =1.07 hspace{0.5mm} mathrm{cm} $}]
$$
h_{i} =1.07 hspace{0.5mm} mathrm{cm}
$$
$$M=-frac{d_i}{d_o}$$
From this we can get.
$$d_o=-frac{24}{0.75}$$
$$d_o=32,,rm{cm}$$
$$frac{1}{d_o}+frac{1}{d_i}=frac{1}{f}$$
From this we can extract $f$:
$$frac{1}{f}=frac{d_o+d_i}{d_od_i}$$
$$f=frac{d_od_i}{d_o+d_i}$$
$$f=frac{32cdot (-24)}{32-24}$$
$$boxed{f=-96,,rm{cm}}$$
begin{align*}
M&=- frac{d_{i}}{d_{o}}\
d_{o}&= – frac{d_{i}}{M}\
d_{o}&= – frac{-24 hspace{0.5mm} mathrm{cm}}{ frac{3}{4}}\
d_{o}&= frac{4 cdot 24 hspace{0.5mm} mathrm{cm}}{ 3}\
d_{o}&= 32 hspace{0.5mm} mathrm{cm}
end{align*}
To find the focal length, we will use the mirror equation [ frac{1}{d_{o}}+ frac{1}{d_{i}}= frac{1}{f}] so we are going to write
begin{align*}
frac{1}{f} &= frac{1}{d_{o}}+ frac{1}{d_{i}}\
frac{1}{f} &= frac{d_{o}+d_{i}}{ d_{o} hspace{0.5mm} d_{i}}\
frac{1}{f} &= frac{d_{o}+d_{i}}{ d_{o} hspace{0.5mm} d_{i}}\
f &= frac{ d_{o} hspace{0.5mm} d_{i}}{ d_{o}+d_{i}} \
f &= frac{ 32 hspace{0.5mm} mathrm{cm} hspace{0.5mm}(-24 hspace{0.5mm} mathrm{cm})}{ 32 hspace{0.5mm} mathrm{cm}-24 hspace{0.5mm} mathrm{cm}} \
f&= -96 hspace{0.5mm} mathrm{cm}
end{align*}
The focal length is [ framebox[1.1width]{$ therefore f = -96 hspace{0.5mm} mathrm{cm} $}]
f = -96 hspace{0.5mm} mathrm{cm}
$$
$$f=frac{r}{2}$$
$$f=frac{60}{2}$$
$$f=30,,rm{cm}$$
$$frac{1}{d_o}+frac{1}{d_i}=frac{1}{f}$$
From the previous equation we can express $d_i$:
$$frac{1}{d_i}=frac{1}{f}-frac{1}{d_o}$$
$$frac{q}{d_i}=frac{d_o-f}{fd_o}$$
And finally:
$$d_i=frac{fd_o}{d_o-f}$$
$$d_i=-frac{30cdot 22}{30+22}$$
$$boxed{d_i=12.7,,rm{cm}}$$
$$frac{h_i}{h_o}=-frac{d_i}{d_o}$$
$$h_i=h_ofrac{d_i}{d_o}$$
$$h_i=7.6cdot frac{12.7}{22}$$
$$boxed{h_i=4.4,,rm{cm}}$$
$$h_i=4.4,,rm{cm}$$
text{color{#4257b2}Recall that : Focal length = $dfrac{text{Radius of Curvature}}{2} color{Black}= dfrac{60}{2}$}
$$
Therefore $f = -30$
Note that $f$ is negative because the mirror is convex
$$
text{color{#c34632}Recall that : $$dfrac{1}{f} = dfrac{1}{d_o}+dfrac{1}{d_i}$$}
$$
Substitute $f = -30$ and $d_o = 22$
$$
dfrac{1}{-30} = dfrac{1}{22}+dfrac{1}{d_i}
$$
$$
-dfrac{1}{30} – dfrac{1}{22}=dfrac{1}{d_i}
$$
$$
-dfrac{1}{30}times dfrac{11}{11} – dfrac{1}{22}times dfrac{15}{15}=dfrac{1}{d_i}
$$
$$
-dfrac{11}{330} – dfrac{15}{330}=dfrac{1}{d_i}
$$
$$
-dfrac{26}{330}=dfrac{1}{d_i}
$$
Take Reciprocal of both sides
$$
-dfrac{330}{26}=d_i
$$
$$
d_i = -dfrac{330}{26}approx -12.69
$$
The image is formed 12.69 cm behind the mirror
text{color{#4257b2}Recall that : $$m = -dfrac{q}{p}= dfrac{text{Image Height}}{text{Object Height}}$$}
$$
Substitute $q = -12.69$ and $p = 22$ and Object Height = 7.6
$$
-dfrac{-12.69}{22}= dfrac{text{Image Height}}{7.6}
$$
Multiply both sides by 7.6
$$
dfrac{12.69times7.6}{22}= text{Image Height}
$$
$$
text{Image Height} = dfrac{12.69times7.6}{22}approx 4.38
$$
Note that diameter is same as the height
text{color{#4257b2}The image is formed 12.69 cm behind the mirror
$ $
Diameter of the image is 4.38 cm }
$$
text{color{#c34632}Recall that : $$text{Magnification} = dfrac{text{Image Height}}{text{Object Height}} = -dfrac{d_i}{d_o}$$}
$$
Substitute : Object Height = 1.8 m and Image Height = 0.36 m
And $d_o = 2.4$
$$
dfrac{0.36}{1.8} = -dfrac{d_i}{2.4}
$$
$$
– dfrac{0.36times 2.4}{1.8} = d_i
$$
$$
d_i= – dfrac{0.36times 2.4}{1.8} approx -0.48
$$
text{color{#4257b2}Recall that : $$dfrac{1}{f} = dfrac{1}{d_o}+dfrac{1}{d_i}$$}
$$
Substitute $d_o = 2.4$ and $d_i = -0.48$
$$
dfrac{1}{f} = dfrac{1}{2.4}+dfrac{1}{-0.48}
$$
$$
dfrac{1}{f} = dfrac{1}{2.4}-dfrac{1}{0.48}times dfrac{5}{5}
$$
$$
dfrac{1}{f} = dfrac{1}{2.4}-dfrac{5}{2.4}
$$
$$
dfrac{1}{f} = -dfrac{4}{2.4}
$$
Take Reciprocal of both sides
$$
f = -dfrac{2.4}{4} = -0.6
$$
text{color{#4257b2}$f = -0.6$ m
$ $
The negative sign means that the mirror is convex }
$$
$$frac{h_i}{h_o}=-frac{d_i}{d_o}$$
$$d_i=-d_ofrac{h_i}{h_o}$$
$$d_i=-2.4cdot frac{0.36}{1.8}$$
$$d_i=-0.48,,rm{m}$$
$$frac{1}{d_o}+frac{1}{d_i}=frac{1}{f}$$
$$frac{1}{f}=frac{d_i+d_o}{d_id_o}$$
From that we can get:
$$f=frac{d_od_i}{d_o+d_i}$$
$$f=frac{2.4cdot (-0.48)}{2.4-0.48}$$
$$boxed{f=-0.6,,rm{m}}$$

