All Solutions
Page 306: Assessment
Difference in energy can help us determine amount of work that was done, and in a thermo-isolated system it can be expressed as:
$$
W=E_1-E_2
$$
Where a positive work means that a work has been done by a body, and will therefore have lower final energy that the initial one and vice versa.
The form of energy in a wound-up watch spring is mainly elastic potential energy.\
noindent
A mechanical watch is driven primarily by gears but source of its energy is still wound-up watch spring. Thus, the forms of energy in a mechanical watch are rotational kinetic energy and elastic potential energy.\
noindent
Most of the energy generated by wound-up watch spring is converted to rotational kinetic energy that drives arms of the watch. However, due to friction, some of it is converted to thermal energy
Mechanical watch: Rotational kinetic energy and elastic potential energy
It is converted to thermal energy.
work, which produces a change in energy.
textit{color{#c34632} $See$ $Explanation$}
$$
b. Same. Even though the relative measurements of height is different, the change in height, measured at the two different reference level, is the same thus the change in potential energy is also the same.
c. Same. The speed of the ball measured at the two different reference level is the same thus the kinetic energy is also the same.
b. Same
c. Same
never be negative because the kinetic
energy depends on the square of the
velocity, which is always positive.
textit{color{#c34632} $See$ $Explanation$}
$$
K = dfrac{1}{2} mv^{2}
$$
$$
KE = frac{1}{2}mv^2
$$
Since both the mass $m$ and the squared velocity $v^2$ can’t be negative, the kinetic energy will always be positive.
baseball can be negative if the height of
the ball is lower than the reference level.
textit{color{#c34632} $See$ $Explanation$}
$$
$$
E_k=frac{mv^2}{2}
$$
k=9
$$
$$
begin{equation}
KE = frac{1}{2}mv^2
end{equation}
$$
Increasing the sprinter’s velocity by a factor of 3
$$
frac{1}{2}m(3v)^2 = frac{1}{2}m(9v^2) = 9left(frac{1}{2}mv^2right) = 9KE
$$
Thus, $boxed{text{the kinetic energy increases by a factor of 9}}$
First one is that the ability to bend allowed pole-vaulters to change their trajectory more smoothly therefore $textbf{decreasing the losses of energy}$ due to the sudden changes of direction of movement and secondly:
The elasticity of the fiberglass poles allowed them to $textbf{store more elastic potential energy}$ that came in the form of horizontally directed kinetic energy into the gravitational potential energy that was vertically directed allowing the vaulters to conquer bigger heights.
b. Since the collision is inelastic (the smashed clay ball stick to the hockey puck), the kinetic energy is not conserved.
b. Kinetic energy is not conserved
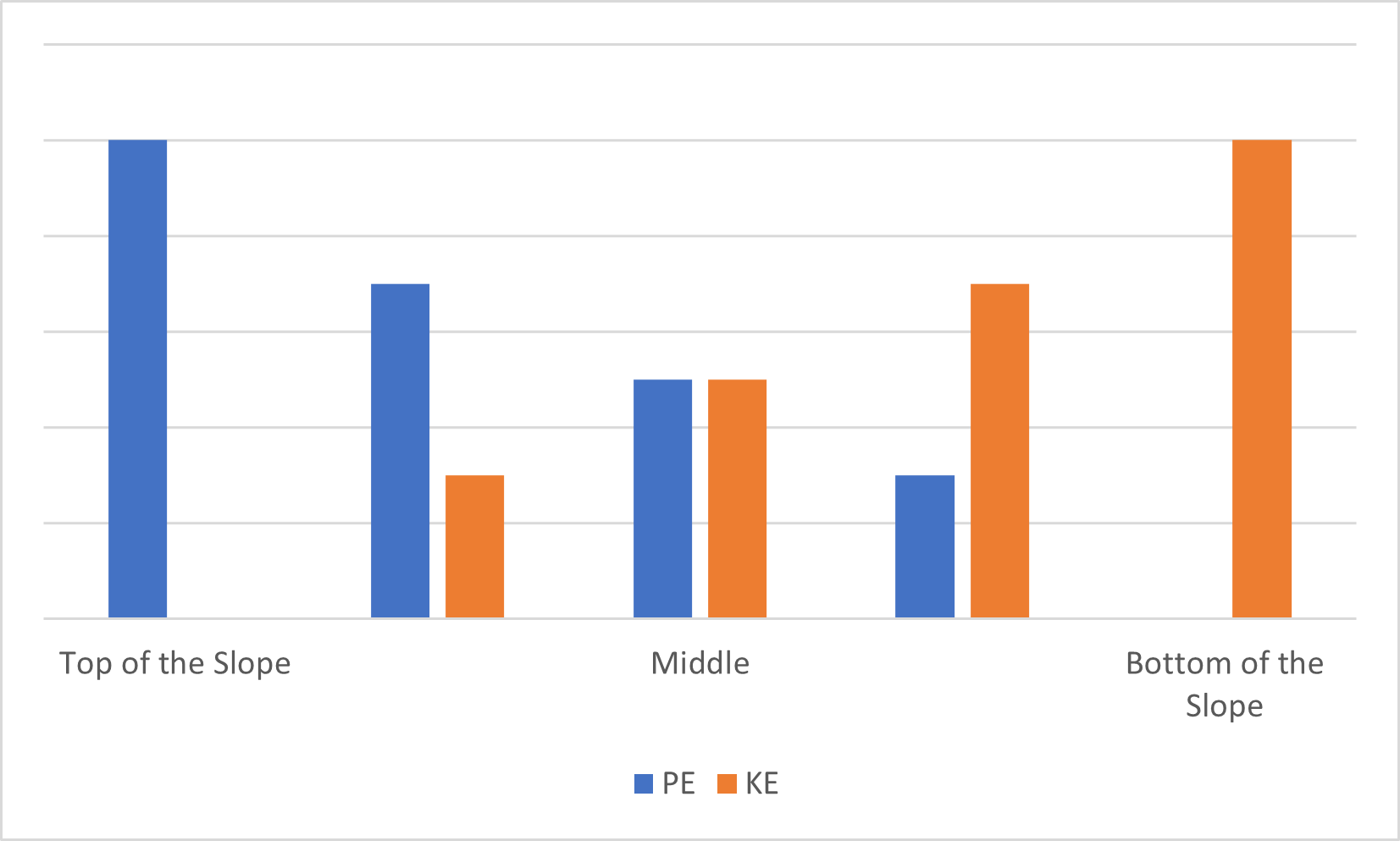
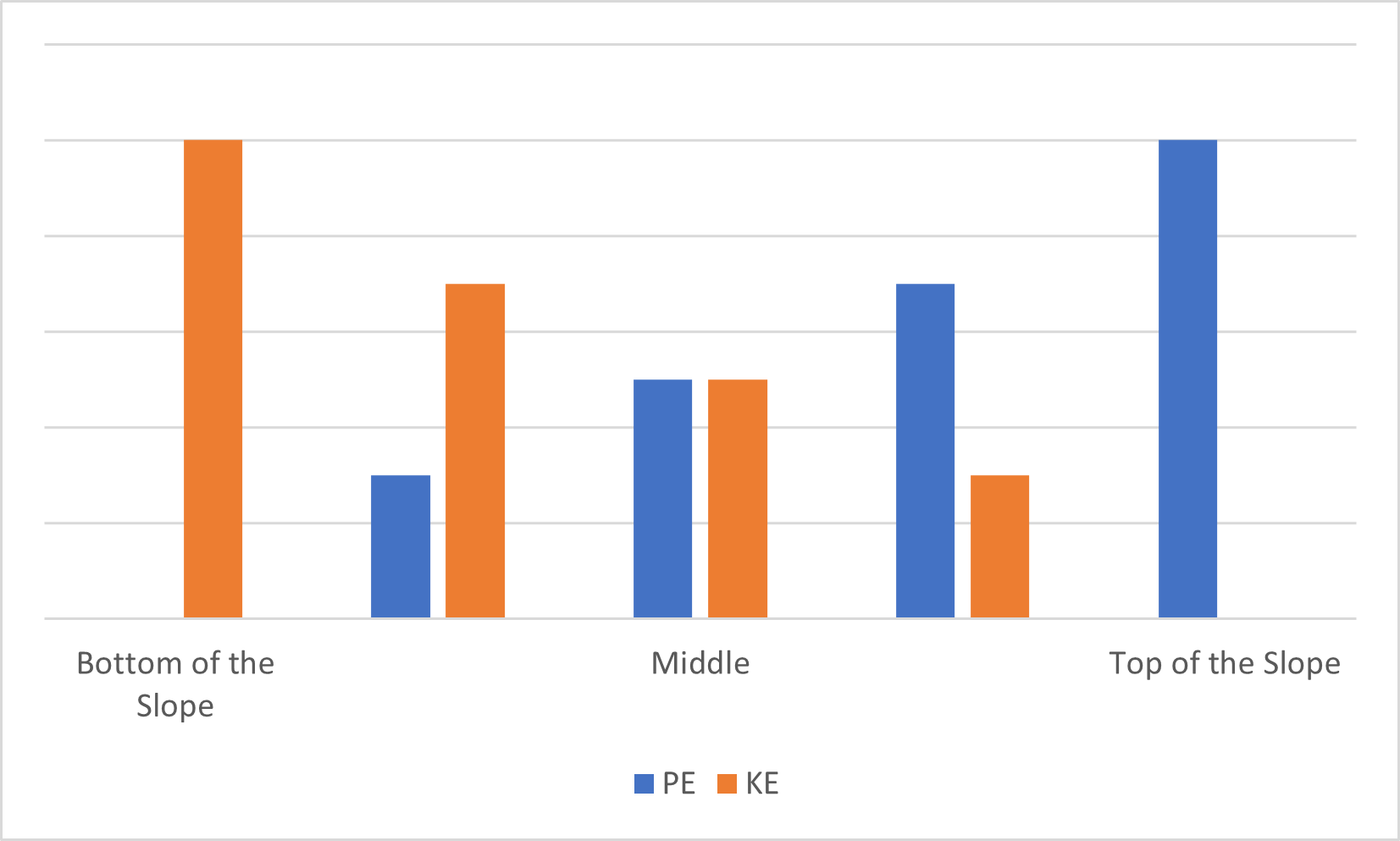
(b) The kinetic energy of the block decreases as it moves upward the slope and gain potential energy. At the top of the slope, the potential energy is at the maximum and the kinetic energy is 0.
(b) The work applied by the breaks is less than the kinetic energy of the car. Thus, the car’s wheels still skid despite the breaks being applied.
(b) The work applied by the breaks to stop the car from moving is greater than or equal to the kinetic energy of the car.
$$
W=E_k
$$
Kinetic energy can be expressed as:
$$
E_k=frac{mv^2}{2}
$$
From this equation we can see that for the same velocity, greater kinetic energy will have an object with $textbf{higher mass}$. In our case that is $textbf{truck}$, which means that we need to put in more work for the truck to reach that velocity than we have to for a car.
There are two significant mechanisms of that transformation; one is by $textbf{plastic deformation}$ of material, and the other is by $textbf{vibration}$ of molecules in the material. Both of the mechanisms in the end result in the energy being dissipated as a $textbf{heat}$.
Therefore we can write the total energy equation as:
$$
E_{total}=E_k+E_p
$$
Total energy of a system $textbf{doesn’t change}$ by itself, but if we set the limits of our system in a way that it includes the work being done on our system we can see that the total energy needs to increase:
$$
W=Delta E_{total}
$$
With positive work (work done on a system) the total energy of that system increases. With potential energy decreasing, the only possible solution is that $textbf{kinetic energy increases}$ by the sum of the amounts that potential energy decreases plus the amount of the work done.
Therefore we can write the total energy equation as:
$$
E_{total}=E_k+E_p
$$
Total energy of a system $textbf{doesn’t change}$ by itself, but if we set the limits of our system in a way that it includes the work being done on our system we can see that the total energy needs to increase:
$$
W=Delta E_{total}
$$
With positive work (work done on a system) the total energy of that system increases.
We cannot however determine what happens to the kinetic energy because we don’t know the amount of work done on the system and the increase in potential energy which leaves the next equation with insufficient data:
$$
Delta E_k=W – Delta E_p
$$
W =Delta Kinetic Energy + Potential Energy
$$
The skater with larger mass will have larger kinetic energy thus the work needed to stop it must also be larger. Since the stopping distance is directly proportional to work done by the friction as shown in the equation below, the skater with the larger mass will have longer stopping distance.
$$
W = Fd
$$
b. Yes, since no work is done by the tension of the string on the mass, there is no change in its kinetic energy.
b. Yes
b. Dropping an object at a certain height. The potential energy stored by raising the object at a certain height is converted to kinetic energy as it drops.
c. Winding wound-up watch spring. The work is done by winding the wound-up watch spring, which, in turn, stores elastic potential energy.
d. An ideal gas pushing a piston upward. The work is done by the kinetic energy of the molecules of the ideal gas on the piston as it moves upward. This significantly reduces the kinetic energy of the ideal gas without decreasing its potential energy.
b. Dropping an object at a certain height
c. Winding wound-up watch spring
d. An ideal gas pushing a piston upward
$$
E_k=E_p
$$
When we insert equations for kinetic and potential energy we get:
$$
0.5cdot mv^2=mgh
$$
$$
h_0=frac{v^2}{2g}
$$
When we insert twice the bigger velocity we get:
$$
h=frac{(2v)^2}{2g}
$$
$$
h=4cdot frac{v^2}{2g}
$$
We can notice that we have $h_0$ and isolate it:
$$
boxed{h=4cdot h_0}
$$
Which means that height needs to be $textbf{four times greater.}$
h=4cdot h_0
$$
Since the kinetic energy of the roller coaster at the bottom of the track is equal to its potential energy at the top of the track, we can express it as follows
$$
KE_{text{max}} = PE_{text{max}}
$$
$$
frac{1}{2}mv^2 = mgh
$$
noindent
Isolating $h$ on one side of the equation
$$
h = frac{v^2}{2g}
$$
noindent
By doubling the speed of the roller coaster
$$
frac{(2v)^2}{2g} = frac{4v^2}{2g} = 4 left( frac{v^2}{2g} right) = 4h
$$
noindent
Thus, to double the speed of the roller coaster, the height of the top of the track must increase by a factor of 4
First we determine the kinetic energy of the ball thrown straight down (we will refer to this as the first ball). The maximum kinetic energy of the first ball can be expressed as
begin{equation}
KE_1 = mgh + frac{1}{2}mv^2
end{equation}
noindent
We then compute for the kinetic energy of the ball thrown straight up (we will refer to this as the second ball). The maximum kinetic energy of the second ball can be expressed as
begin{equation}
KE_2 = mg(h+d)
end{equation}
noindent
where $d$ is the distance travelled by the ball as it was thrown straight up. We will compute for this as follows
begin{equation}
d = vt – frac{1}{2}gt^2
end{equation}
noindent
Since we know that $v = gt$, then we can plug in $t = frac{v}{g}$ to Equation (3)
$$
d = vleft( frac{v}{g} right) – frac{1}{2}gleft( frac{v}{g} right)^2
$$
$$
d = left( frac{v^2}{g} right) – frac{1}{2}gleft( frac{v^2}{g^2} right)
$$
$$
d = left( frac{v^2}{g} right) – left( frac{v^2}{2g} right)
$$
begin{equation}
d = frac{v^2}{2g}
end{equation}
noindent
Pluggin in Equation (4) to Equation (2), we now have
$$
KE_2 = mg(h+frac{v^2}{2g})
$$
begin{equation}
KE_2 = mgh + frac{1}{2}mv^2
end{equation}
noindent
Comparing Equation (1) and (5), we can conclude that the kinetic energies of the balls are the same. Since the kinetic energies and the masses of the ball is similar, their speeds as they strike the ground is also the same.
$$
E_k=frac{mv^2}{2}
$$
When we insert values we get:
$$
E_k=frac{1600cdot 12.5^2}{2}
$$
$$
boxed{E_k=125000,,rm{J}}
$$
E_k=125000,,rm{J}
$$
$$
v=108,,rm{km/h}cdot frac{1000,,rm{m/km}}{3600,,rm{s/h}}
$$
$$
v=30,,rm{m/s}
$$
$$
E_k=frac{mv^2}{2}
$$
When we insert values we get:
$$
E_k=frac{1525cdot 30^2}{2}
$$
$$
boxed{E_k=686250,,rm{J}}
$$
E_k=686250,,rm{J}
$$
$$
v=frac{s}{t}
$$
Inserting values in SI units we get:
$$
v=frac{1.8cdot 1000}{10cdot 60}
$$
$$
v=3,,rm{m/s}
$$
$$
E_k=frac{mv^2}{2}
$$
Inserting values we get:
$$
E_k=frac{45cdot 3^2}{2}
$$
Finally the kinetic energy is:
$$
boxed{E_k=203,,rm{J}}
$$
E_k=203,,rm{J}
$$
$$
E_{k1}=frac{mv^2}{2}
$$
Inserting values we get:
$$
E_{k1}=frac{45cdot 10^2}{2}
$$
$$
boxed{E_{k1}=2250,,rm{J}}
$$
$$
E_{k2}=frac{mv_2^2}{2}
$$
Inserting values we get:
$$
E_{k2}=frac{45cdot 5^2}{2}
$$
$$
boxed{E_{k2}=562.5,,rm{J}}
$$
$$
frac{E_{k1}}{E_{k2}}=frac{2250}{562.5}
$$
$$
boxed{frac{E_{k1}}{E_{k2}}=4}
$$
We can se that the ratio is $4$ which is square of the increase of velocity ($2$) which makes sense because the velocity is under the square in the equation for the kinetic energy.
E_{k1}=2250,,rm{J}
$$
$$
E_{k2}=562.5,,rm{J}
$$
$$
frac{E_{k1}}{E_{k2}}=4
$$
The kinetic energy:
$K_a = (1/2) m v_a^2$
$K_a = (1/2) * (45) * (10.0)^2$
$K_a = 2250 J$
b)
$K_b = (1/2) m v_b^2$
$K_b = (1/2) * (45) * (5.0)^2$
$K_b = 563 J$
c)
$ratio = dfrac{K_b}{K_a} = dfrac{563}{2250} = dfrac{1}{4}$
The kinetic energy is proportional to $v^2$ and the ratio of $v_b$ to $v_a$ is $dfrac{1}{2}$, therefore the ratio of the $dfrac{K_b}{K_a}$ will be $(dfrac{1}{2})^2 = dfrac{1}{4}$.
b) 563 J
c) $dfrac{1}{4}$
$$
E_{comb}=frac{(2m)v^2}{2}
$$
The mass is taken as $2m$ since that is their combined mass. Now we can insert values:
$$
E_{comb}=frac{(2cdot 45)cdot 10^2}{2}
$$
$$
boxed{E_{comb}=4500,,rm{J}}
$$
$$
m_{comb}=2cdot m
$$
Because we combined masses of both girls and each of them weights $m$. Now we can proceed to the ratio:
$$
frac{m_{comb}}{m_{Katia}}=frac{2cdot m}{m}
$$
We don’t even have to insert values to get:
$$
boxed{frac{m_{comb}}{m_{Katia}}=2}
$$
$$
frac{E_{comb}}{E_{Katia}}=frac{0.5cdot (2cdot m)cdot v^2}{0.5cdot mcdot v^2}
$$
We can eliminate $0.5$ multiplier, $m$ and $v^2$ to get:
$$
boxed{frac{E_{comb}}{E_{Katia}}=2}
$$
E_{comb}=4500,,rm{J}
$$
$$
frac{m_{comb}}{m_{Katia}}=2
$$
$$
frac{E_{comb}}{E_{Katia}}=2
$$
$$
W=Fd
$$
Inserting values we get:
$$
W=5cdot 10^5 cdot 509
$$
$$
boxed{W=2.55cdot 10^8,,rm{J}}
$$
$$
Delta E_k=W
$$
$$
boxed{Delta E_k=2.55cdot 10^8,,rm{J}}
$$
$$
E_{kf}=E_{ki}+Delta E_k
$$
Inserting values we get:
$$
E_{kf}=0 + 2.55cdot 10^8
$$
Where inital kinetic energy is equal to zero because the train was at rest. Finally we get:
$$
boxed{E_{kf}=2.55cdot 10^8,,rm{J}}
$$
$$
E_{kf}=frac{mv^2}{2}
$$
From this we can get speed:
$$
v=sqrt{frac{2cdot E_{kf}}{m}}
$$
Inserting values we get:
$$
v=sqrt{frac{2cdot 2.55cdot 10^8}{2.5cdot 10^4}}
$$
$$
boxed{v=143,,rm{m/s}}
$$
W=2.55cdot 10^8,,rm{J}
$$
$$
Delta E_k=2.55cdot 10^8,,rm{J}
$$
$$
E_{kf}=2.55cdot 10^8,,rm{J}
$$
$$
v=143,,rm{m/s}
$$
textbf{Given:}\
$m = 2.50 times 10^4 text{kg}$ \
$F = 5.00 times 10^5 text{N}$ \
$d = 509 text{m}$\
$KE_text{initial} = 0 text{J}$\
noindent
(a) \
To solve for the work done on the train, we will use the equation below
$$
W = Fd
$$
noindent
Plugging in the given the values, we now have
$$
W = (5.00 times 10^5)(509)
$$
$$
boxed{W = 2.55 times 10^8 text{J}}
$$
noindent
(b) \
Since the change in kinetic energy is equal to the work done on the train. we have
$$
Delta KE = W
$$
$$
boxed{Delta KE = 2.55 times 10^8 text{J}}
$$
(c) \
To solve for the final kinetic energy of the train, we will use the equation below
$$
KE_text{final} = KE_text{initial} + Delta KE
$$
noindent
Plugging in the given values and our result from part (a), we now have
$$
KE_text{final} = 0 + 2.55 times 10^8
$$
$$
boxed{KE_text{final} = 2.55 times 10^8}
$$
noindent
(d) \
We know that the kinetic energy is given by the equation below
$$
KE = frac{1}{2}mv^2
$$
noindent
Isolating velocity $v$ on one side of the equation, we now have
$$
v_text{final} = sqrt{frac{2KE_text{final}}{m}}
$$
noindent
Plugging in the given values and our result from part (c), we now have
$$
v_text{final} = sqrt{frac{2cdot(2.55 times 10^8)}{2.50 times 10^4}}
$$
$$
boxed{v_text{final} = 143 frac{text{m}}{text{s}}}
$$
(b) $Delta KE = 2.55 times 10^8 text{J}$
(c) $KE_text{final} = 2.55 times 10^8$
(d) $v_text{final} = 143 frac{text{m}}{text{s}}$
But first we need to calculate the mass of the car because we will use that value in many other equations:
$$
m=frac{m_w}{g}
$$
$$
m=frac{14700}{9.81}
$$
$$
m=1500,,rm{kg}
$$
$$
W=frac{mv^2}{2}
$$
We can insert values:
$$
W=frac{1500cdot 25^2}{2}
$$
$$
W=468750,,rm{J}
$$
$$
W=F_bd
$$
From this we can get breaking distance $d$:
$$
d=frac{W}{F_b}
$$
Inserting values we get:
$$
d=frac{468750}{7100}
$$
$$
boxed{d=66,,rm{m}}
$$
d=66,,rm{m}
$$
textbf{Given:}\
$F_g = 14,700 text{N}$\
$v = 25 frac{text{m}}{text{s}}$\
$F_text{break} = 7100 text{N}$ \
$g = 9.8 frac{text{m}}{text{s}^2}$ \
noindent
textbf{Calculation:}\
Since the work needed to stop the car is equal to the kinetic energy of the car, we can express it as follows
begin{equation}
W = KE = frac{1}{2}mv^2
end{equation}
noindent
To solve for the mass of the car, we use the equation below
$$
F_g = mg
$$
$$
m = frac{F_g}{g}
$$
noindent
Plugging in the given values, we now have
$$
m = frac{14,700}{9.8}
$$
$$
m = 1.50 times 10^3 text{kg}
$$
Plugging in the calculated mass and the given values to Equation (1)
$$
W = frac{1}{2}(1.50 times 10^3)(25)^2
$$
$$
W = 468750 text{J}
$$
noindent
To determine the distance $d$, we will use the equation below
$$
W = F_text{break}d
$$
begin{equation} tag{2}
d = frac{W}{F_text{break}}
end{equation}
noindent
Plugging in the calculated work and the given values
$$
d = frac{468750}{7100}
$$
$$
boxed{d = 66 text{m}}
$$
d = 66 text{m}
$$
$$
Delta E_k=E_{k2}-E_{k1}
$$
Combinint that equation with equation for kinetic energy we get:
$$
Delta E_k=frac{mcdot (v_2^2-v^2)}{2}
$$
Inserting values:
$$
Delta E_k=frac{15cdot (3.2^2-7.5^2)}{2}
$$
Finally:
$$
boxed{Delta E_k=-345,,rm{J}}
$$
$$
W=Delta E_k
$$
Inserting values we get:
$$
boxed{W=-345,,rm{J}}
$$
$$
W=Fd
$$
From this we can calculate the distance that cart traveled while the force acted:
$$
d=frac{W}{F}
$$
Inserting values:
$$
d=frac{-345}{-10}
$$
Where force is applied as negative value because it is acting in the opposite direction of the movement of the cart. We can conclude it is acting in that direction because it is $textbf{deccelerating}$ the cart.
$$
boxed{d=34.5,,rm{m}}
$$
Delta E_k=-345,,rm{J}
$$
$$
W=-345,,rm{J}
$$
$$
d=34.5,,rm{m}
$$
textbf{Given:} \
$m = 15.0 text{kg}$ \
$v_i = 7.50 frac{text{m}}{text{s}}$ \
$F = -10.0 text{N}$ \
$v_f = 3.20 frac{text{m}}{text{s}}$ \
noindent
textbf{Calculation:} \
(a) \
The change in the kinetic energy of the cart is given by
$$
Delta KE = KE_f – KE_i
$$
$$
Delta KE = frac{1}{2}mv_f^2 – frac{1}{2}mv_i^2
$$
$$
Delta KE = frac{1}{2}(15.0)(3.20)^2 – frac{1}{2}(15.0)(7.50)^2
$$
$$
boxed{Delta KE = -345 text{J}}
$$
noindent
(b) \
Since the work done on the cart causes the change in kinetic energy, we can express it as follows
$$
W = Delta KE
$$
$$
boxed{W = -345 text{J}}
$$
noindent
(c) \
To calculate the distance travelled by the cart, we use the equation below
$$
W = Fd
$$
$$
d = frac{-345}{-10.0}
$$
$$
boxed{d = 34.5 text{m}}
$$
(b) $W = -345 text{J}$
(c) $d = 34.5 text{m}$
$$
Delta E_p=mgh
$$
Inserting values we get:
$$
Delta E_p=60cdot 9.8cdot 3.5
$$
Finally:
$$
boxed{Delta E_p=2058,,rm{J}}
$$
Delta E_p=2058,,rm{J}
$$
textbf{Given:} \
$m = 60.0 text{kg}$ \
$h = 3.5 text{m}$ \
$g = 9.8 frac{text{m}}{text{s}}$
noindent
textbf{Calculation:} \
To solve for the potential energy, we will use the equation below
$$
PE = mgh
$$
noindent
Plugging in the given values
$$
PE = (60.0)cdot(3.5)cdot(9.8)
$$
$$
boxed{PE = 2.06 times 10^3 text{J}}
$$
PE = 2.06 times 10^3 text{J}
$$
$$
Delta E_p=mgh
$$
Inserting values we get:
$$
Delta E_p=6.4cdot 9.8cdot 2.1
$$
Finally:
$$
boxed{Delta E_p=132,,rm{J}}
$$
Delta E_p=132,,rm{J}
$$
$$
Delta E_p=m_w Delta h
$$
Inserting values we get:
$$
Delta E_p=505cdot (-5.5)
$$
Which finally gives:
$$
boxed{Delta E_p=-2780,,rm{J}}
$$
Delta E_p=-2780,,rm{J}
$$
$$
Delta E_p=mg(h-h_0)
$$
Where $h_0$ is assumed to be zero because it is a referent value which in this case is set for a floor. Inserting values we get:
$$
Delta E_p=180cdot 9.8cdot (1.95-0)
$$
Finally we get:
$$
boxed{Delta E_p=3440,,rm{J}}
$$
Delta E_p=3440,,rm{J}
$$
textbf{Given:} \
$m = 180 text{kg}$ \
$h = 1.95 text{m}$ \
$g = 9.8 frac{text{m}}{text{s}^2}$\
noindent
textbf{Calculation:}\
To solve for the increase in potential energy, we will use the equation below
$$
PE = mgh
$$
$$
PE = (180 cdot (9.8) cdot (1.95)
$$
$$
boxed{PE = 3.44 times 10^3 text{J}}
$$
PE = 3.44 times 10^3 text{J}
$$
That means that we can calculate the potential energy at that point as:
$$
E_p=E_k
$$
$$
E_p=1960,,rm{J}
$$
$$
E_p=mgh
$$
From this we can extract $h$:
$$
h=frac{E_p}{mg}
$$
Inserting values we get:
$$
h=frac{1960}{10cdot 9.8}
$$
Finally the maximum height is:
$$
boxed{h=20,,rm{m}}
$$
h=20,,rm{m}
$$
textbf{Given:} \
$m = 10.0 text{kg}$ \
$W = 1960 text{J}$ \
$g = 9.8 frac{text{m}}{text{s}^2}$ \
noindent
textbf{Calculation:}
To solve the height travelled by the rocket due to the kinetic energy of the fuel, we use the equation below
$$
W = mgh
$$
$$
h = frac{W}{mg}
$$
noindent
Plugging in the given values
$$
h = frac{1960}{(10.0)cdot(9.8)}
$$
$$
boxed{h = 20.0 text{m}}
$$
h = 20.0 text{m}
$$
In order to solve this problem, we must convert values to SI units:
$$
h_t=75,,rm{cm}cdot frac{1,,rm{m}}{100,,rm{cm}}=0.75,,rm{m}
$$
$$
Delta E_p=m_wcdot (h_s-h_t)
$$
Inserting values we get:
$$
Delta E_p=12cdot (2.15-0.75)
$$
Finally, the change in potential energy is:
$$
boxed{Delta E_p=16.8,,rm{J}}
$$
Delta E_p=16.8,,rm{J}
$$
$$
W=Delta E_p
$$
Potential energy of an object depends on its weight and $textbf{vertical}$ displacement.
$$
Delta E_p=mgh
$$
Inserting previous equation we get:
$$
W=mgh
$$
From this we can extract mass:
$$
m=frac{W}{gh}
$$
Inserting values we get:
$$
m=frac{1}{9.8cdot 1}
$$
Finally we get:
$$
boxed{m=0.102,,rm{kg}}
$$
m=0.102,,rm{kg}
$$
Thus:
$W = m g (h_f – h_i)$
Solve for m:
$$
m = dfrac{W}{g (h_f – h_i)} = dfrac{1.00}{(9.80)*(1.00 – 0.00)} = 0.102 kg
$$
0.102 kg
$$
We can calculate the velocity of the ball using the equation for force:
$$
F=ma
$$
And equation for acceleration:
$$
a=frac{v}{t}
$$
Combining equations we get:
$$
F=mfrac{v}{t}
$$
$$
v=frac{Ft}{m}
$$
Inserting values we get:
$$
v=frac{150cdot 0.03}{0.06}
$$
$$
v=75,,rm{m/s}
$$
$$
E_k=frac{mv^2}{2}
$$
Inserting values we get:
$$
E_k=frac{0.06cdot 75^2}{2}
$$
$$
boxed{E_k=170,,rm{J}}
$$
E_k=170,,rm{J}
$$
textbf{Given:} \
$F = 150.0 text{N}$ \
$m = 0.060 text{kg}$ \
$t = 0.030 text{s}$ \
noindent
textbf{Calculation:} \
To solve for kinetic energy, we will use the equation below
begin{equation}
KE = frac{1}{2}mv^2
end{equation}
noindent
To solve for the velocity of the ball as it leaves the racket, we will use Newton’s Second Law
$$
F = ma = mfrac{v}{t}
$$
$$
v = frac{Ft}{m}
$$
$$
v = frac{(150.0) cdot (0.030)}{(0.060)}
$$
$$
v = 75 frac{text{m}}{text{s}}
$$
noindent
Plugging in the value of $v$ to Equation (1)
$$
KE = frac{1}{2}(0.060)(75)^2
$$
$$
boxed{KE = 170 text{J}}
$$
KE = 170 text{J}
$$
$$
W=E_k
$$
Where work is:
$$
W=Fd
$$
and kinetic energy is:
$$
E_k=frac{mv^2}{2}
$$
Combined we can get:
$$
Fd=frac{mv^2}{2}
$$
$$
F=frac{mv^2}{2cdot d}
$$
Inserting values we get:
$$
F=frac{45cdot 62^2}{2cdot 22}
$$
$$
boxed{F=3900,,rm{N}}
$$
$$
E_k=frac{mv^2}{2}
$$
Inserting values we get:
$$
E_k=frac{45cdot 62^2}{2}
$$
$$
boxed{E_k=86000,,rm{J}}
$$
F=3900,,rm{N}
$$
$$
E_k=86000,,rm{J}
$$
textbf{Given:} \
$m = 45 text{kg}$ \
$d = 22.0 text{m}$ \
$v = 62.0 frac{text{m}}{text{s}}$ \
noindent
textbf{Calculation:} \
(a)\
The work done by the rocket pack is equal to the kinetic energy acquired by Pam. We can express this as follows:
begin{equation}
W = KE
end{equation}
noindent
We know that work and kinetic energy are given by the equations below
$$
W = Fd
$$
$$
KE = frac{1}{2}mv^2
$$
noindent
Plugging in these equations to Equation (1), we now have
$$
Fd = frac{1}{2}mv^2
$$
noindent
Isolating the force $F$ on one side of the equation
$$
F = frac{mv^2}{2d}
$$
noindent
Plugging in the given values, we now have
$$
F = frac{(45)cdot(62.0)^2}{2cdot(22.0)}
$$
$$
boxed{F = 3900 text{N}}
$$
(b)\
To solve for the Pam’s final kinetic energy, we will use the equation below
$$
KE = frac{1}{2}mv^2
$$
noindent
Plugging in the given values, we now have
$$
KE = frac{1}{2}(45)(62.0)^2
$$
$$
boxed{KE = 86000 text{J}}
$$
(b) $KE = 86000 text{J}$
$$
Delta E_k=E_{kf}-E_{ki}
$$
$$
Delta E_k=frac{mv_2^2}{2}-frac{mv^2}{2}
$$
Inserting values we get:
$$
Delta E_k=frac{2000cdot 0^2}{2}-frac{2000cdot 12^2}{2}
$$
Finally:
$$
boxed{Delta E_k=-144000,,rm{J}}
$$
$$
W=Delta E_k
$$
Inserting values:
$$
boxed{W=-144000,,rm{J}}
$$
Where work is negative because it is done to the car, not done by the car.
$$
d=50cdot 10^{-2}=0.5,,rm{m}
$$
Work done by a force is defined as a force acting over a certain distance:
$$
W=Fd
$$
From this we can extract force:
$$
F=frac{W}{d}
$$
Inserting values:
$$
F=frac{-144000}{0.5}
$$
$$
boxed{F=-288000,,rm{N}}
$$
Where force is negative because it is acting in the opposite direction of the movement of the car, deccelerating it.
Delta E_k=-144000,,rm{J}
$$
$$
W=-144000,,rm{J}
$$
$$
F=-288000,,rm{N}
$$
textbf{Given:} \
$m = 2.00 times 10^3 text{kg}$ \
$v_text{i} = 12.0 frac{text{m}}{text{s}}$ \
$v_text{f} = 0.00 frac{text{m}}{text{s}}$ \
$d = 0.500 text{m}$ \
noindent
textbf{Calculation:} \
(a) \
The change in kinetic energy can be expressed as follows
$$
Delta KE = KE_text{f} – KE_text{i} = frac{1}{2}mv_text{f}^2 – frac{1}{2}mv_text{i}^2
$$
$$
Delta KE = frac{1}{2}m(v_text{f}^2 – v_text{i}^2)
$$
noindent
Plugging in the given values, we now have
$$
Delta KE = frac{1}{2}(2.00 times 10^3)((0.00)^2 – (12.0)^2)
$$
$$
boxed{Delta KE = -144000 text{J}}
$$
noindent
(b) \
Since the work done on the front of the car is what causes the change in kinetic energy, then
$$
W = Delta KE
$$
$$
boxed{W = -144000 text{J}}
$$
(c) \
To solve for the force that pushed the front of the car, we use the equation below
$$
W = Fd
$$
noindent
Isolating the force $F$ on one side of the equation, we now have
$$
F = frac{W}{d}
$$
noindent
Plugging in the given values
$$
F = frac{-144000}{0.500}
$$
$$
boxed{F = -288000 text{N}}
$$
(b) $W = -144000 text{J}$
(c) $F = -288000 text{N}$
$$
W=Delta E_p
$$
Work of a force $F$ on a distance $d$ is defined as
$$
W=Fd
$$
And change in potential energy as:
$$
Delta E_p=mgh
$$
Combined we get:
$$
Fd=mgh
$$
$$
h=frac{Fd}{mg}
$$
Inserting values we get:
$$
h=frac{410cdot 2}{32}
$$
Finally:
$$
boxed{h=26,,rm{m}}
$$
h=26,,rm{m}
$$
textbf{Given:} \
$F = 410 text{N}$ \
$F_text{g} = 32 text{N}$ \
$d = 2.0 text{m}$ \
noindent
textbf{Calculation:} \
The work done on the stone causes the change in its potential energy. This can be expressed as follows
begin{equation}
W = Delta PE
end{equation}
noindent
We know that work and potential energy are given by the equations below
$$
W = Fd
$$
$$
PE = mgh = F_text{g}h
$$
noindent
Plugging in these equations to Equation (1)
$$
Fd = F_text{g}Delta h
$$
noindent
Isolating $Delta h$ on one side of the equation
$$
Delta h = frac{Fd}{F_text{g}}
$$
noindent
Plugging in the given values, we now have
$$
Delta h = frac{(410)cdot(2.0)}{(32)}
$$
$$
boxed{Delta h = 26 text{m}}
$$
Delta h = 26 text{m}
$$
$$
W=Fd
$$
Where the force needed to conquer the weight of the sack is equal to its weight and the distance on which the force acts is equal to the height:
$$
W=mgh
$$
Inserting values we get:
$$
W=98cdot 50
$$
$$
boxed{W=4900,,rm{J}}
$$
$$
Delta E_p=W
$$
$$
boxed{Delta E_p=4900,,rm{J}}
$$
Since all of it is now converted to kinetic energy, we can write down an equation:
$$
E_k=Delta E_p
$$
$$
boxed{E_k=4900,,rm{J}}
$$
W=4900,,rm{J}
$$
$$
Delta E_p=4900,,rm{J}
$$
$$
E_k=4900,,rm{J}
$$
textbf{Given:} \
$F = 98.0 text{N}$ \
$h = 50.0 text{m}$ \
noindent
textbf{Calculation:} \
(a) \
To solve for work done on the sack of grain, we use the equation below
$$
W = Fd
$$
noindent
Plugging in the given values
$$
W = (98.0) cdot (50.0)
$$
$$
boxed{W = 4.90 times 10^3 text{J}}
$$
noindent
(b) \
Since the work done on the sack of grain causes the change in potential energy, then
$$
Delta PE = W
$$
$$
boxed{Delta PE = 4.90 times 10^3 text{J}}
$$
noindent
(c) \
Since the mechanical energy is conserved, the maximum potential energy is equal to the maximum kinetic energy
$$
KE = Delta PE
$$
$$
boxed{KE = 4.90 times 10^3 text{J}}
$$
(b) $Delta PE = 4.90 times 10^3 text{J}$
(c) $KE = 4.90 times 10^3 text{J}$
$$
E_p=mgh
$$
Where $h$ is the difference in the height.
We can insert values to get:
$$
E_p=20cdot 9.8cdot 100
$$
Potential energy of the rock is:
$$
boxed{E_p=19600,,rm{J}}
$$
$$
E_p=E_k
$$
Where $E_p$ is potential energy at the top, and $E_k$ is kinetic energy just before hitting the ground.
$$
boxed{E_k=19600,,rm{J}}
$$
$$
E_k=frac{mv^2}{2}
$$
From this we can extract speed $v$:
$$
v=sqrt{frac{2cdot E_k}{m}}
$$
Inserting values we get:
$$
v=sqrt{frac{2cdot 19600}{20}}
$$
Finally:
$$
boxed{v=44.3,,rm{m/s}}
$$
E_p=19600,,rm{J}
$$
$$
E_k=19600,,rm{J}
$$
$$
v=44.3,,rm{m/s}
$$
$PE = m g h = (20)*(9.8)*(100) = 19600 J$
b)
Its kinetic energy is equal to its initial potential energy.
c)
$KE_f = PE_i$
$(1/2) m v^2 = m g h$
$v = sqrt{2 g h} = sqrt{(2)*(9.8)*(100)} = 44 m/s$
b) $19600 J$
c) $44 m/s$
$$
W=E_k
$$
Where work done by a force of the string is defined as:
$$
W=Fd
$$
and kinetic energy can be calculated as:
$$
E_k=frac{mv^2}{2}
$$
Combined we get:
$$
Fd=frac{mv^2}{2}
$$
$$
v=sqrt{frac{2cdot Fd}{m}}
$$
Inserting values we get:
$$
v=sqrt{frac{2cdot 201cdot 1.3}{0.3}}
$$
Finally the speed is:
$$
boxed{v=41.7,,rm{m/s}}
$$
$$
E_k=E_p
$$
Combined with previous equation:
$$
W=E_k
$$
We get that elastic potential energy will in the end be converted to the gravitational potential energy:
$$
W=E_p
$$
Where gravitational potential energy can be calculated as:
$$
E_p=mgh
$$
Combined we get:
$$
Fd=mgh
$$
$$
h=frac{Fd}{mg}
$$
Inserting values we get:
$$
h=frac{201cdot 1.3}{0.3cdot 9.8}
$$
Finally the height is:
$$
boxed{h=89,,rm{m}}
$$
v=41.7,,rm{m/s}
$$
$$
h=89,,rm{m}
$$
textbf{Given:} \
$m = 0.30 text{kg}$ \
$F = 201 text{N}$ \
$d = 1.3 text{m}$ \
$g = 9.8 frac{text{m}}{text{s}^2}$ \
noindent
textbf{Calculation:} \
(a) \
The maximum kinetic energy of the arrow comes from the work done by the archer. We can express this as follows
begin{equation}
KE = W
end{equation}
noindent
We know that work and kinetic energy are given by the equations below
$$
KE = frac{1}{2}mv^2
$$
$$
W = Fd
$$
noindent
Plugging in the these equations to Equation (1), we have
$$
frac{1}{2}mv^2 = Fd
$$
noindent
Isolating velocity $v$ on one side of the equation
$$
v = sqrt{frac{2Fd}{m}}
$$
noindent
Plugging in the given values
$$
v = sqrt{frac{2 cdot (201) cdot (1.3)}{(0.30)}}
$$
$$
boxed{v = 42 frac{text{m}}{text{s}}}
$$
(b) \
The maximum potential energy of the arrow comes from the work done by the archer. This can be expressed as follows
begin{equation} tag{2}
PE = W
end{equation}
noindent
We know that work and potential energy are given by the equations below
$$
W = Fd
$$
$$
PE = mgh
$$
noindent
Plugging in these equations to Equation (2), we now have
$$
mgh = Fd
$$
noindent
Isolating height $h$ on one side of the equation, we now have
$$
h = frac{Fd}{mg}
$$
noindent
Plugging in the given values
$$
h = frac{(201)(1.3)}{(0.30)(9.8)}
$$
$$
boxed{h = 89 text{m}}
$$
(b) $h = 89 text{m}$
$$
Delta E_p=E_k
$$
$$
boxed{E_k=407,,rm{J}}
$$
$$
E_k=frac{mv^2}{2}
$$
From this we can get speed:
$$
v=sqrt{frac{2cdot E_k}{m}}
$$
Inserting values:
$$
v=sqrt{frac{2cdot 407}{2}}
$$
Finally the speed is:
$$
boxed{v=20,,rm{m/s}}
$$
E_k=407,,rm{J}
$$
$$
v=20,,rm{m/s}
$$
$$
Delta E_p=E_k
$$
Since change in potential energy is:
$$
Delta E_p=mgDelta h
$$
And kinetic energy is:
$$
E_k=frac{mv^2}{2}
$$
We can combine these equations to get:
$$
frac{mv^2}{2}=mgDelta h
$$
$$
v=sqrt{frac{2cdot mgDelta h}{m}}
$$
Eliminating $m$:
$$
v=sqrt{2cdot gDelta h}
$$
Inserting values we get:
$$
v=sqrt{2cdot 9.8cdot 4.5}
$$
Finally the speed just before it hits the ground is:
$$
boxed{v=9.39,,rm{m/s}}
$$
v=9.39,,rm{m/s}
$$
$$
begin{align*}
p &= mv_i\
&= (5.0 times 10^{5})(8.0,mathrm{frac{m}{s}})\
&= boxed{4.0 times 10 ^{6} ,mathrm{kg} cdot mathrm{frac{m}{s}}}
end{align*}
$$
$$
begin{align*}
p &= mv_i\
&= (5.0 times 10^{5})(8.0,mathrm{frac{m}{s}})\
&= boxed{4.0 times 10 ^{6} ,mathrm{kg} cdot mathrm{frac{m}{s}}}
end{align*}
$$
begin{align*}
intertext{textbf{Before collision:}}
KE_i &= frac{1}{2} mv_{i}^2\
&= frac{1}{2} (5.0 times 10^5 kg)(8.0,mathrm{frac{m}{s}})^2\
&= boxed{1.6 times 10^7 ,mathrm{J}}
end{align*}
begin{align*}
intertext{textbf{After collision:}}
KE_f &= frac{1}{2} mv_{f}^2\
&= frac{1}{2} (5.0 times 10^{5} kg + 5.0 times 10^{5})(4.0,mathrm{frac{m}{s}})^2\
&= boxed{8.0 times 10^6 ,mathrm{J}}
end{align*}
$textbf{b.)}p = 4.0 times 10 ^{6} ,mathrm{kg} cdot mathrm{frac{m}{s}}$
$textbf{c.)}KE_i = 1.6 times 10^7 ,mathrm{J}$ and $KE_f = 8.0 times 10^6 ,mathrm{J}$
$textbf{d.)}$kinetic energy was $textit{textbf{not conserved}}$.
$$
E_p=E_k
$$
Where potential energy can be calculated as:
$$
E_p=mgh
$$
and kinetic energy as:
$$
E_k=frac{mv^2}{2}
$$
Combining these equations we get:
$$
mgh=frac{mv^2}{2}
$$
We can cancel out $m$ on both sides to get:
$$
gh=frac{v^2}{2}
$$
$$
h=frac{v^2}{2cdot g}
$$
before we insert values, we need to convert speed to SI units:
$$
v=100,,rm{km/h}cdot frac{1000,,rm{m/km}}{3600,,rm{s/h}}=27.78,,rm{m/s}
$$
Now we can insert values:
$$
h=frac{27.78^2}{2cdot 9.8}
$$
$$
boxed{h=39.4,,rm{m}}
$$
h=39.4,,rm{m}
$$
textbf{Given:} \
$v = 1.00 times 10^2 frac{text{km}}{text{h}}$ \
$g = 9.8 frac{text{m}}{text{s}^2}$ \
noindent
textbf{Calculation:} \
We first convert the velocity to standard units
$$
v = 1.00 times 10^2 frac{text{km}}{text{h}} cdot left( frac{1000 text{m}}{1 text{km}} right) cdot left( frac{1 text{h}}{3600 text{s}} right)
$$
$$
v = 27.8 frac{text{m}}{text{s}}
$$
noindent
We know that the maximum kinetic energy is equal to the maximum potential energy thus we can express it as follows
begin{equation}
KE = PE
end{equation}
noindent
We know that kinetic energy and potential energy are given by the following equations
$$
KE = frac{1}{2}mv^2
$$
$$
PE = mgh
$$
noindent
Plugging in these equations to Equation (1), we have
$$
frac{1}{2}mv^2 = mgh
$$
noindent
Isolating height $h$ on one side of the equation
$$
h = frac{v^2}{2g}
$$
noindent
Plugging in the given values
$$
h = frac{(27.8)^2}{2cdot(9.8)}
$$
$$
boxed{h = 39.4 text{m}}
$$
h = 39.4 text{m}
$$
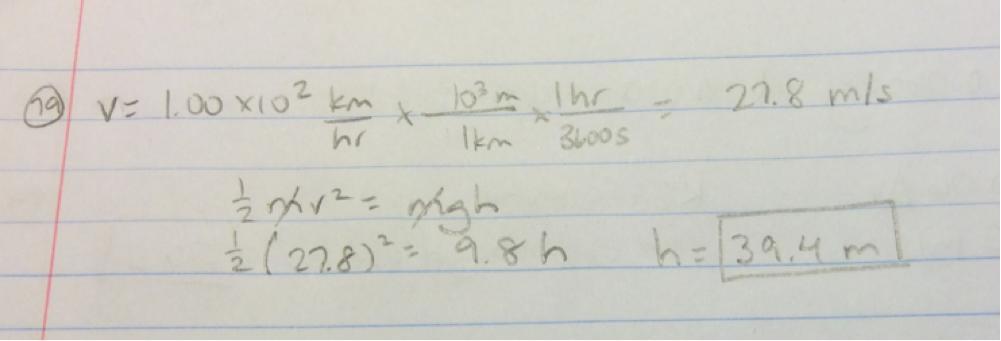
$$
Delta E_p=E_k
$$
Where change in potential energy is defined as:
$$
Delta E_p=mgcdot (h-h_0)
$$
And kinetic energy as:
$$
E_k=frac{mv^2}{2}
$$
Combining these equations we get:
$$
frac{mv^2}{2}=mgcdot (h-h_0)
$$
$$
v=sqrt{2cdot gcdot (h-h_0)}
$$
Inserting values we get:
$$
v=sqrt{2cdot 9.8cdot (1-0.4)}
$$
Finally the speed at the lowest point is:
$$
boxed{v=3.4,,rm{m/s}}
$$
$$
W=E_k-E_{kf}
$$
Where $E_k$ is kinetic energy in the case with friction present and can be calculated as:
$$
E_{kf}=frac{mv_f^2}{2}
$$
But, first we need to calculate Kelly’s mass:
$$
m=frac{mg}{g}
$$
$$
m=frac{420}{9.8}
$$
$$
m=42.9,,rm{kg}
$$
Now, we can calculate the work of the friction:
$$
W=frac{mv^2}{2}-frac{mv_f^2}{2}
$$
$$
W=frac{42.9cdot 3.4^2}{2}-frac{42.9cdot 2^2}{2}
$$
$$
boxed{W=160,,rm{J}}
$$
v=3.4,,rm{m/s}
$$
$$
W=160,,rm{J}
$$
textbf{Given:} \
$F_g = 420 text{N}$ \
$h_text{lowest} = 0.40 text{m}$ \
$h_text{highest} = 1.00 text{m}$ \
$v_text{actual} = 2.0 frac{text{m}}{text{s}}$ \
$g = 9.8 frac{text{m}}{text{s}^2}$ \
noindent
textbf{Calculation:} \
(a) \
The maximum kinetic energy of the swing is equal to its maximum potential energy. We can express this as follows
begin{equation}
KE = PE
end{equation}
noindent
We know that kinetic energy and potential energy are given by the equations below
$$
KE = frac{1}{2}mv^2
$$
$$
PE = mgh
$$
noindent
Plugging in these equations to Equation (1), we now have
$$
frac{1}{2}mv^2 = mgh
$$
$$
frac{1}{2}mv^2 = mg(h_text{highest} – h_text{lowest})
$$
noindent
Isolating velocity $v$ on one side of the equation
$$
v = sqrt{2g(h_text{highest} – h_text{lowest})}
$$
noindent
Plugging in the given values
$$
v = sqrt{2 cdot (9.8) cdot (1.00 – 0.40)}
$$
$$
boxed{v = 3.4 frac{text{m}}{text{s}}}
$$
(b) \
The work done by the friction on the swing is given by the eqution below
$$
W = KE_text{expected} – KE_text{actual}
$$
begin{equation} tag{2}
W = frac{1}{2}mv_text{expected}^2 – frac{1}{2}mv_text{actual}^2
end{equation}
noindent
To solve for Kelli’s mass, we will use the equation below
$$
F_g = mg
$$
$$
m = frac{F_g}{g}
$$
noindent
Plugging in the given values, we now have
$$
m = frac{420}{9.8}
$$
$$
m = 43 text{kg}
$$
noindent
Plugging in the given values and the velocity we calculated from part (a) $v_text{expected} = 3.4 frac{text{m}}{text{s}}$ to Equation (2)
$$
W = frac{1}{2}cdot(43)cdot(3.4)^2 – frac{1}{2}cdot(43)cdot(2.00)^2
$$
$$
boxed{W = 160 text{J}}
$$
(b) $W = 160 text{J}$
$$
E_{ki}+E_{pi}=E_{kf}
$$
$$
E_{ki}=frac{mv_0^2}{2}
$$
Initial potential energy as:
$$
E_{pi}=mgh
$$
and final kinetic energy as:
$$
E_{kf}=frac{mv^2}{2}
$$
Combining previous equations we can get:
$$
frac{mv_0^2}{2}+mgh=frac{mv^2}{2}
$$
We can cancel out $m$ to get:
$$
frac{v_0^2}{2}+gh=frac{v^2}{2}
$$
Now we can extract $v_0$:
$$
v_0=sqrt{v^2-2cdot gh}
$$
$$
v_0=sqrt{7.5^2-2cdot 9.8cdot 2}
$$
$$
boxed{v_0=4.1,,rm{m/s}}
$$
v_0=4.1,,rm{m/s}
$$
textbf{Given:} \
$m = 0.010 text{kg}$ \
$h = 2.0 text{m}$ \
$v_text{max} = 7.5 frac{text{m}}{text{s}}$ \
noindent
textbf{Calculation:} \
We know that the total mechanical energy (sum of kinetic and potential energy) is equal to the maximum kinetic energy. We can express this relationship as follows
begin{equation}
KE_i + PE_i = KE_text{max}
end{equation}
noindent
We know that kinetic energy and potential energy are given by equations below
$$
KE = frac{1}{2}mv^2
$$
$$
PE = mgh
$$
noindent
Plugging in these equations to Equation (1), we now have
$$
frac{1}{2}mv_i^2 + mgh = frac{1}{2}mv_text{max}^2
$$
noindent
Isolating the initial velocity $v_i$ on one side of the equation
$$
v_i = sqrt{v_text{max}^2 – 2gh}
$$
noindent
Plugging in the given values
$$
v_i = sqrt{(7.5)^2 – 2 cdot (9.8) cdot (2.0)}
$$
$$
boxed{v_i = 4.1 frac{text{m}}{text{s}}}
$$
v_i = 4.1 frac{text{m}}{text{s}}
$$
$$
W_f=E_p-E_k
$$
$$
E_p=mgh
$$
And her kinetic energy as:
$$
E_k=frac{mv^2}{2}
$$
Combining equations we get:
$$
W_f=mgh-frac{mv^2}{2}
$$
Inserting values we get:
$$
W_f=28cdot 9.8cdot 4.8 – frac{28cdot 3.2^2}{2}
$$
Finally, the work done by friction is:
$$
boxed{W_f=1200,,rm{J}}
$$
W_f=1200,,rm{J}
$$
$E_i = PE = m g h = (28)*(9.8)*(4.8) = 1317 J$
The Lorena’s final energy is equal to her kinetic energy at the bottom of the slide:
$E_f = KE = (1/2) m v^2 = (1/2) * (28) * (3.2)^2 = 143 J$
The work done by friction on Lorena:
$$
W_{friction} = E_f – E_i = (1317) – (143) = 1200 J
$$
1200 J
$$
textbf{Given:} \
$F_g = 635 text{N}$ \
$h = 5.0 text{m}$ \
noindent
textbf{Calculation:} \
(a) \
The mechanical energy of the system changed equivalent to the increase in potential energy of the person given by the equation below.
$$
Delta ME = Delta PE = F_gh
$$
noindent
Plugging in the given values
$$
Delta ME = (635) cdot (5.0)
$$
$$
Delta ME = 3175 text{J}
$$

(b) \
The increase in mechanical energy came from the work done by the person as he/she climbs up the ladder
(b) The increase in mechanical energy came from the work done by the person as he/she climbs up the ladder.
The problem asked us to solve for the chimp’s velocity $(v)$ before it reaches the ground. We will get $v$ from the maximum kinetic energy $(KE)$ of the chimp that we will relate to its maximum potential energy $(PE)$ using the equation below. \
begin{equation}
KE = PE
end{equation}
We first solve for the maximum potential energy of the chimp using the equation below
begin{equation} tag{2}
PE = mgh
end{equation}
From the problem, we know that the chimp is on a vine with length $L = 13 text{m}$, swinging at an angle $theta = 45^circ$. To solve for the vertical component $(h)$ of the vine we will use the equation below
$$
h = L sin(theta)
$$
noindent
Plugging in this equation to Equation (2), we now have
begin{equation} tag{3}
PE = mgL sin(theta)
end{equation}
We know that kinetic energy is given by the equation below
begin{equation} tag{4}
KE = frac{1}{2}mv^2
end{equation}
noindent
Plugging in Equation (3) and (4) to Equation (1), we now have
$$
frac{1}{2}mv^2 = mgL sin(theta)
$$
Isolating $v$ on one side of the equation
$$
v = sqrt{2gL sin(theta)}
$$
noindent
Plugging in the given values and the acceleration due to gravity $g = 9.8 frac{text{m}}{text{s}^2}$
$$
v = sqrt{2(9.8)(13) sin(45)}
$$
$$
boxed{v = 13 frac{text{m}}{text{s}}}
$$
v = 13 frac{text{m}}{text{s}}
$$
$(1/2) m v^2 = m g d sin(theta)$
$v = sqrt{2 g d sin(theta)}$
$v = sqrt{2 (9.8) (13) sin(45)}$
$$
v = 13 m/s
$$
13 m/s
$$
$$
begin{equation}
PE = mgh
end{equation}
$$
$$
PE = (0.80)(0.32)(9.8)
$$
$$
PE = 2.5088 text{J}
$$
$$
begin{equation} tag{2}
W = F_fd
end{equation}
$$
Since the work needed to stop the cart is equal to the stored potential energy of the cart, we can express Equation (2) as follows
$$
PE = F_fd
$$
$$
begin{equation} tag{3}
d = frac{PE}{F_f}
end{equation}
$$
$$
d = frac{2.5088}{2.0}
$$
$$
boxed{d = 1.3 text{m}}
$$
d = 1.3 text{m}
$$
$E = PE = m g h = (0.80)*(9.8)*(0.32) = 2.51 J$
The force of friction decreases the energy of the cart to zero:
$F_{friction} d = PE$
Solve for d:
$$
d = dfrac{PE}{F_{friction}} = dfrac{2.51}{2.0} = 1.3 m
$$
1.3 m
$$
$$
W=Delta E_p
$$
Where change in potential energy can be calculated as:
$$
Delta E_p=mgh
$$
$$
W=mgh
$$
Inserting values we get:
$$
W=73cdot 9.8cdot 2.45
$$
$$
boxed{W=1750,,rm{J}}
$$
W=1750,,rm{J}
$$
$$
begin{equation}
W_text{break} = PE
end{equation}
$$
$$
W = Fd
$$
$$
PE = mgh
$$
Plugging in these equations to Equation (1), we now have
$$
F_text{break}d = mgh
$$
$$
begin{equation} tag{2}
d = frac{mgh}{F_text{break}}
end{equation}
$$
$$
d_1 = frac{mgh_1}{F_text{break}}
$$
Plugging in the height of the building $h_1 = h$
$$
d_1 = frac{mgh}{F_text{break}}
$$
$$
d_2 = frac{mgh_2}{F_text{break}}
$$
$$
begin{equation} tag{3}
d_2 = frac{mg(5h)}{F_text{break}}
end{equation}
$$
$$
d_2 = 5left(frac{mgh}{F_text{break}}right)
$$
$$
d_2 = 5d_1
$$
We know that $d_1 = 1 text{m}$, thus we have
$$
d_2 = 5 cdot (1)
$$
$$
boxed{d_2 = 5 text{m}}
$$
d_2 = 5 text{m}
$$
$$
begin{equation}
boxed{p_1 = p_2}
end{equation}
$$
$$
p = mv
$$
Plugging this into Equation (1)
$$
begin{equation}
m_1v_1 = m_2v_2
end{equation}
$$
$$
(110)v_1 = (150)v_2
$$
$$
v_1 = 1.4 v_2
$$
$$
KE = frac{1}{2}mv^2
$$
For the linebacker, we have
$$
KE_1 = frac{1}{2}m_1v_1^2 = frac{1}{2}(110)(1.4v_2)^2
$$
$$
KE_1 = 108 v_2^2
$$
For the defensive end, we have
$$
KE_2 = frac{1}{2}m_2v_2^2 = frac{1}{2}(150)v_2^2
$$
$$
KE_2 = 75 v_2^2
$$
By examining the calculated $KE_1$ and $KE_2$, we can conclude that the kinetic energy of the linebacker is greater than the defensive end
$$
boxed{KE_1 > KE_2}
$$
(b) $KE_1 = KE_2$; The kinetic energy of the linebacker is greater than the defensive end.
$$
begin{equation}
Delta E = E_f – E_i
end{equation}
$$
$$
E_i = KE_{1i} + KE_{2i}
$$
$$
begin{equation} tag{2}
E_i = frac{1}{2}m_1v_{1i}^2 + frac{1}{2}m_2v_{2i}^2
end{equation}
$$
$$
E_i = frac{1}{2}(2.0)(2.1)^2 + frac{1}{2}(1.0)(2.1)^2
$$
$$
E_i = 6.6 text{J}
$$
$$
begin{equation} tag{3}
E_f = frac{1}{2}m_2v_{2f}^2
end{equation}
$$
$$
m_1v_{1i} + m_2v_{2i} = m_1v_{1f} + m_2v_{2f}
$$
$$
begin{equation} tag{4}
v_{2f} = frac{m_1v_{1i} + m_2v_{2i} – m_1v_{1f}}{m_2}
end{equation}
$$
$$
v_{2f} = frac{(2.0) cdot (2.1) + (1.0) cdot (2.1) + (2.01) cdot (0)}{(1.0)}
$$
$$
v_{2f} = 6.3 frac{text{m}}{text{s}}
$$
$$
E_f = frac{1}{2}(1.0)(6.3)^2
$$
$$
E_f = 20 text{J}
$$
$$
Delta E = 20 – 6.6
$$
$$
boxed{Delta E = 13 text{J}}
$$
Delta E = 13 text{J}
$$
=1/2(2+1)(2.1m/s)^2
=6.6J
=(2+1)(2.1m/s)
=6.3m/s=pf=1(vf)
vf=6.3m/s
=0.5*1*6.3^2=19.83j
13J was added by the spring
textbf{Given:} \
$m_1 = 55.0 text{kg}$ \
$h_1 = 12.0 text{m}$ \
$m_2 = 21.0 text{kg}$ \
We can write the conservation of momentum of this system as follows
$$
begin{equation}
m_1v_1 = (m_1 + m_2)v_2
end{equation}
$$
where, $v_1$ is the velocity of the scientist before grabbing the antelope and $v_2$ is the velocity of the scientist and the antelope
Since the total mechanical energy of the scientist is conserved, the potential energy of the scientist at the top of the hill must be equal to its kinetic energy before grabbing the antelope
$$
PE_text{max} = KE_text{max}
$$
$$
m_1gh_1 = frac{1}{2}m_1v_1^2
$$
Isolating $v_1$ on one side of the equation, we have
begin{equation} tag{2}
v_1 = sqrt{2gh_1}
end{equation}
Since the total mechanical energy of the scientist and the antelope is conserved, the kinetic energy of the scientist after grabbing the antelope must be equal to their potential energy as they reach the tree limb
$$
KE_text{max} = PE_text{max}
$$
$$
frac{1}{2}(m_1 + m_2)v_2^2 = (m_1 + m_2)gh_2
$$
Isolating $v_2$ on one side of the equation
begin{equation} tag{3}
v_2 = sqrt{2gh_2}
end{equation}
Plugging in Equation (2) and (3) to Equation (1)
$$
m_1sqrt{2gh_1} = (m_1 + m_2)sqrt{2gh_2}
$$
$$
m_1^2(2gh_1) = (m_1 + m_2)(2gh_2)
$$
Isolating $h_2$ on one side of the equation, we have
$$
h_2 = left( frac{m_1}{m_1 + m_2} right)^2h_1
$$
Plugging in the given values
$$
h_2 = left( frac{55.0}{55.0 + 21.0} right)^2 cdot(12.0)
$$
$$
boxed{h_2 = 6.28 text{m}}
$$
h_2 = 6.28 text{m}
$$
textbf{Given:} \
$m = 0.80 text{kg}$ \
$theta = 30^circ$ \
$h = 0.50 text{m}$ \
$F_f = 5.0 text{N}$\
The total mechanical energy of system is equal to the potential energy of the cart at the top of the hill. We can express this using the equation below
$$
begin{equation}
ME_text{total} = PE
end{equation}
$$
$$
PE = mgh
$$
Thus, we can express Equation (1) as follows
$$
begin{equation} tag{2}
ME_text{total} = mgh
end{equation}
$$
$$
begin{equation} tag{3}
W = F_fd cos{(theta)}
end{equation}
$$
$$
W = ME_text{total}
$$
Plugging in Equation (2) and (3)
$$
F_fd cos{(theta)} = mgh
$$
$$
begin{equation} tag{4}
d = frac{mgh}{F_f cos{(theta)}}
end{equation}
$$
$$
d = frac{(0.80) cdot (9.8) cdot (0.50)}{(5.0) cdot cos{(30)}}
$$
$$
d = 0.91 text{m}
$$
Since the calculated $d$ is less than $l$, the cart will not reach the bottom of the hill so $boxed{text{No}}$
$$
m_Av_i = m_A(-v_f) + m_Bv_f
$$
$$
m_Av_i = (-m_A + m_B)v_f
$$
$$
begin{equation}
frac{v_i}{v_f} = frac{m_B – m_A}{m_A}
end{equation}
$$
$$
frac{1}{2}m_Av_i^2 = frac{1}{2}m_A(-v_f)^2 + frac{1}{2}m_Bv_f^2
$$
$$
m_Av_i^2 = m_Av_f^2 + m_Bv_f^2
$$
$$
m_Av_i^2 = (m_A + m_B)v_f^2
$$
$$
begin{equation} tag{2}
m_Aleft(frac{v_i}{v_f}right)^2 = m_A + m_B
end{equation}
$$
$$
m_Aleft(frac{m_B – m_A}{m_A}right)^2 = m_A + m_B
$$
$$
m_Aleft(frac{m_B^2 – 2m_Am_B + m_A^2}{m_A^2}right) = m_A + m_B
$$
$$
frac{m_B^2 – 2m_Am_B + m_A^2}{m_A} = m_A + m_B
$$
$$
m_B^2 – 2m_Am_B + m_A^2 = m_A^2 + m_Am_B
$$
$$
m_B^2 = 3m_Am_B
$$
$$
begin{equation} tag{3}
m_A = frac{m_B}{3}
end{equation}
$$
$$
m_A = frac{2.0}{3}
$$
$$
begin{equation} tag{4}
m_A = 0.67 text{kg}
end{equation}
$$
The mass of Object A is found to be $boxed{m_A = 0.67 text{kg}}$
m_A = 0.67 text{kg}
$$
$$
E_{lost}=E_{ki}-E_{kf}
$$
Where inital kinetic energy consists of a sum of kinetic energies of each player:
$$
E_{ki}=frac{m_1v_1^2}{2}+frac{m_2v_2^2}{2}
$$
And final kinetic energy also,but this time with their common speed:
$$
E_{kf}=frac{(m_1+m_2)v^2}{2}
$$
$$
E_{lost}=frac{m_1v_1^2}{2}+frac{m_2v_2^2}{2}-frac{(m_1+m_2)v^2}{2}
$$
Inserting values we get:
$$
E_{lost}=frac{90cdot 5^2}{2}+frac{110cdot 3^2}{2}-frac{(90+110)cdot 1^2}{2}
$$
$$
boxed{E_{lost}=1520,,rm{J}}
$$
E_{lost}=1520,,rm{J}
$$
textbf{Given:} \
$m_1 = 0.046 text{kg}$ \
$m_2 = 0.220 text{kg}$ \
$u_2 = 44 frac{text{m}}{text{s}}$ \
textbf{Calculation:}\
Since the collision is elastic, the kinetic energy of the system must be conserved. We can express this using the equation below.
$$
frac{1}{2}m_2u_2^2 = frac{1}{2}m_1v_1^2 + frac{1}{2}m_2v_2^2
$$
where, $v_1$ and $v_2$ are the velocity of the golf ball and the golf club after the collision
$$
frac{1}{2}m_2u_2^2 = frac{1}{2}m_1v_1^2 + frac{1}{2}m_2v_2^2
$$
$$
begin{equation}
v_2 = frac{m_2u_2 – m_1v_1}{m_2}
end{equation}
$$
Since the momentum of the system is also conserved, we can write the momentum of the ball and the club before and after the collision as follows
$$
m_2u_2 = m_1v_1 + m_2v_2
$$
Plugging in Equation (1), we have
$$
m_2u_2 = m_1v_1 + m_2 left( frac{m_2u_2 – m_1v_1}{m_2} right)
$$
Isolating $v_1$ on one side of the equation
$$
m_2^2u_2^2 = m_1m_2v_1^2 + (m_2^2u_2^2 – 2m_1m_2v_1u_2 + m_1^2v_1^2)
$$
$$
2m_1m_2v_1u_2 = m_1m_2v_1^2 + m_1^2v_1^2
$$
$$
2m_2u_2 = v_1(m_1 + m_2)
$$
$$
v_1 = frac{2m_2}{(m_1 + m_2)}u_2
$$
Plugging in the given values, we have
$$
v_1 = frac{2 cdot (0.220)}{(0.046 + 0.220)} cdot (44)
$$
$$
boxed{v_f = 73 frac{text{m}}{text{s}}}
$$
v_1 = 73 frac{text{m}}{text{s}}
$$
We know that the energy of the system is purely kinetic thus we can express it as follows:
$$
begin{equation}
E = KE = frac{1}{2}mv^2
end{equation}
$$
Using Equation (1), we can express the initial energy of the system as
$$
E_i = frac{1}{2}m_1v_1^2
$$
$$
m_1v_1 = m_1v_3 + m_2v_4
$$
Since $m_1 = m_2$,
$$
v_1 = v_3 + v_4
$$
$$
begin{equation} tag{2}
v_3 = v_1 – v_4
end{equation}
$$
$$
frac{1}{2}m_1v_1^2 = frac{1}{2}m_1v_3^2 + frac{1}{2}m_2v_4^2
$$
Since $m_1 = m_2$,
$$
begin{equation} tag{3}
v_1^2 = v_3^2 + v_4^2
end{equation}
$$
$$
v_1^2 = (v_1 – v_4 )^2 + v_4^2
$$
$$
v_1 = v_1^2 – 2v_1v_4 + v_4^2 + v_4^2
$$
$$
2v_1v_4 = 2v_4^2
$$
$$
begin{equation} tag{4}
v_1 = v_4
end{equation}
$$
$$
E_{2f} = frac{1}{2}m_2v_4^2
$$
Plugging in Equation (4)
$$
E_{2f} = frac{1}{2}m_2v_1^2
$$
$$
frac{E_{2f}}{E_i} = frac{frac{1}{2}m_2v_1^2}{frac{1}{2}m_2v_1^2}
$$
$$
boxed{frac{E_{2f}}{E_i} = 1}
$$
From part (a), we know that the conservation of momentum of the system can be expressed as follows
$$
m_1v_1 = m_1v_3 + m_2v_4
$$
Isolating $v_3$ on one side of the equation
$$
begin{equation} tag{5}
v_3 = frac{m_1v_1 – m_2v_2}{m_1}
end{equation}
$$
$$
frac{1}{2}m_1v_1^2 = frac{1}{2}m_1v_3^2 + frac{1}{2}m_2v_4^2
$$
$$
m_1v_1^2 = m_1v_3^2 + m_2v_4^2
$$
$$
m_1v_1^2 = m_1(frac{m_1v_1 – m_2v_2}{m_1})^2 + m_2v_4^2
$$
$$
m_1^2v_1^2 = (m_1^2v_1^2 – 2m_1m_2v_1v_4 + m_2^2v_4^2) + m_2^2v_4^2
$$
$$
m_2^2v_4^2 + m_1m_2v_4^2 = 2m_1m_2v_1v_4
$$
Isolating $v_4$ on one side of the equation
$$
v_4^2 (m_2^2 + m_1m_2) = 2m_1m_2v_1v_4
$$
$$
begin{equation} tag{6}
v_4 = frac{2m_1}{m_1 + m_2}v_1
end{equation}
$$
$$
v_4 = frac{2m_1}{m_1}v_1
$$
$$
v_4 = 2v_1
$$
$$
E_{2f} = frac{1}{2}m_2v_4^2
$$
Plugging in $v_4$ we calculated earlier
$$
E_{2f} = frac{1}{2}m_2(2v_1)^2
$$
$$
E_{2f} = 2m_2v_1^2
$$
$$
frac{E_{2f}}{E_i} = frac{2m_2v_1^2}{frac{1}{2}m_1v_1^2}
$$
$$
boxed{frac{E_{2f}}{E_i} = 4frac{m_2}{m_1}}
$$
Hydrogen is the most desirable to use because it can slow down neutrons but not too much unlike more massive atoms.
(b) $frac{E_{2f}}{E_i} = 4frac{m_2}{m_1}$
(c) See the explanation
$$
begin{equation}
m_A v_A + m_Bv_B = m_A u_A + m_Bu_B
end{equation}
$$
$$
m_A v_A – m_A u_A = m_B u_B – m_Bv_B
$$
$$
begin{equation}
m_A(v_A – u_A) = m_B(u_B – v_B)
end{equation}
$$
$$
frac{1}{2}m_Av_A^2 + frac{1}{2}m_Bv_B^2 = frac{1}{2}m_Au_A^2 + frac{1}{2}m_Bu_B^2
$$
$$
m_Av_A^2 – m_Au_A^2 = m_Bu_B^2 – m_Bv_B^2
$$
$$
m_A(v_A^2 – u_A^2) = m_B(u_B^2 – v_B^2)
$$
$$
begin{equation} tag{3}
m_A(v_A – u_A)(v_A + u_A) = m_B(v_B – u_B)(v_B + u_B)
end{equation}
$$
$$
m_B(v_B – u_B)(v_A + u_A) = m_B(v_B – u_B)(v_B + u_B)
$$
$$
v_A + u_A = v_B + u_B
$$
We can now get expressions for both $u_A$ and $u_B$
$$
begin{equation} tag{4}
u_A = v_B + u_B – v_A
end{equation}
$$
$$
begin{equation} tag{5}
u_B = v_A + u_A – v_B
end{equation}
$$
$$
m_Av_A + m_Bv_B = m_Au_A + m_B(v_A + u_A – v_B)
$$
$$
m_Av_A + m_Bv_B = m_Au_A + m_Bv_A + m_Bu_A – m_Bv_B
$$
Isolating $u_A$ on one side of the equation
$$
u_A(m_A + m_B) = 2m_Bv_B + m_Av_A – m_Bv_A
$$
$$
begin{equation} tag{6}
boxed{u_A = left( frac{m_A – m_B}{m_A + m_B} right)v_A + left( frac{2m_Bv_B}{m_A + m_B} right)v_B}
end{equation}
$$
$$
m_Av_A + m_Bv_B = m_A(v_B + u_B – v_A) + m_Bu_B
$$
$$
m_Av_A + m_Bv_B = m_Av_B + m_Au_B – m_Av_A + m_Bu_B
$$
Isolating $u_B$ on one side of the equation
$$
u_B(m_A + m_B) = 2m_Av_A + m_Bv_B – m_Av_B
$$
$$
begin{equation} tag{7}
boxed{u_B = left( frac{2m_A}{m_A + m_B} right)v_A + left( frac{m_B – m_A}{m_A + m_B} right)v_B}
end{equation}
$$
$$
u_B = left( frac{2m_A}{m_A + m_B} right)v_A + left( frac{m_B – m_A}{m_A + m_B} right)v_B
$$
$textbf{(1)}$ Solar energy can be transformed into electrical energy using solar panel. The generated electrical energy can be used by humans to operate machineries by converting it to mechanical energy or to be stored in batteries by converting it to chemical energy.
$textbf{(2)}$ Solar energy can also be transformed into chemical energy by plants. This energy be used by animals and humans when they consume the plants.
textbf{Given:} \
$r = 1.0 times 10^7 text{m}$ \
$T = 9.9 times 10^3 text{s}$ \
$G = 6.67 times 10^{-11} frac{text{m}^3}{text{kg} cdot text{s}^2}$
textbf{Calculation:}\
We start with Newton’s Second Law to get an expression for the net force acting on the satellite (We use $m_s$ for the mass of the satellite)
$$
F_text{net} = m_s a
$$
Since the gravtiational force is the net force acting on the satellite, we can express the equation above as follows (We use $m_e$ for the mass of the Earth)
begin{equation}
Gfrac{m_s m_e}{r^2} = m_sa
end{equation}
$$
a = frac{4pi^2 r}{T^2}
$$
Plugging this into Equation (1), we have
$$
Gfrac{m_s m_e}{r^2} = m_sfrac{4pi^2 r}{T^2}
$$
Isolating $m_e$ on one side of the equation
$$
m_e = frac{4pi^2r^3}{GT^2}
$$
Plugging in the given values, we have
$$
m_e = frac{4pi^2(1.0 times 10^7)^3}{(6.67 times 10^{-11})(9.9 times 10^3)^2}
$$
$$
boxed{m_e = 6.04 times 10^{-24} text{kg}}
$$
m_e = 6.04 times 10^{-24} text{kg}
$$
$9.9e3 = (2)*(3.14)*sqrt{dfrac{(1.0e7)y3}{(6.67e-11)*(M)}}$
$$
M = 6.04 times 10^{24} Kg
$$
6.04 times 10^{24} Kg
$$
textbf{Given:} \
$m_1 = 5.00 times 10^{-3} text{g}$ \
$m_2 = 10.00 text{kg}$ \
$u_1 = 100.0 frac{text{m}}{text{s}}$ \
$u_2 = 0 frac{text{m}}{text{s}}$
$v_1 = -99 frac{text{m}}{text{s}}$ for Part (b) \
textbf{Calculation:}\
We calculate the change in momentum of the bullet using the equation below
begin{equation}
Delta p_1 = m_1v_1 – m_1u_1
end{equation}
To solve for $u_1$, we can express the conservation of momentum of the system as follows
$$
m_1u_1 + m_2u_2 = (m_1 + m_2)v_1
$$
Isolating $u_1$ on one side of the equation
$$
v_1 = frac{m_1u_1 + m_2u_2}{m_1 + m_2}
$$
Plugging in the given values, we have
$$
v_1 = frac{(5.00 times 10^{-3}) cdot (100.0) + (10.0) cdot (0)}{(5.00 times 10^{-3}) + ((10.0))}
$$
$$
v_1 = -0.0500 frac{text{m}}{text{s}}
$$
Plugging in the given values and the calculated $v_1$ into Equation (1)
$$
Delta p_1 = (5.00 times 10^{-3})(-0.0500) – (5.00 times 10^{-3})(100.0)
$$
$$
boxed{Delta p_1 = -0.500 text{kg} cdot frac{text{m}}{text{s}}}
$$
textbf{(b)} \
Plugging in the given values to Equation (1)
$$
Delta p_1 = (5.00 times 10^{-3})(-99) – (5.00 times 10^{-3})(100.0)
$$
$$
boxed{Delta p_1 = -0.995 text{kg} cdot frac{text{m}}{text{s}}}
$$
The block end up with a greater speed in $boxed{text{Case (b)}}$. Since the loss of momentum to the bullet is larger in Case (b) than in Case (a), the momentum transferred to the block is also larger. Since momentum is directly proportional to velocity, the velocity of the block in Case (b) is also larger than in Case (a)
(b) $Delta p_1 = -0.995 text{kg} cdot frac{text{m}}{text{s}}$
(c) See the explanation
textbf{Given:} \
$F_r = 15 text{kN}$ \
$F_e = 0.10 text{kN}$ \
$d_r = 0.33 text{cm}$ \
$e = 75 %$ \
textbf{(a)} \
From Chapter 10, we know that the mechanical advantage is given by the equation below
$$
MA = frac{F_r}{F_e}
$$
Plugging in the the given values, we have
$$
MA = frac{15}{0.10}
$$
$$
boxed{MA = 150}
$$
textbf{(b)} \
From Chapter 10, we know that efficiency is given by the equation below
$$
e = frac{W_o}{W_i} times 100
$$
$$
e = frac{F_rd_r}{F_ed_e} times 100
$$
Isolating $d_e$ on one side of the equation, we have
$$
d_e = frac{F_rd_r}{eF_e} x 100
$$
Plugging in the given values
$$
d_e = frac{(15) cdot (0.33)}{(75) cdot (0.10)} x 100
$$
$$
boxed{d_e = 66 text{cm}}
$$
(b) $d_e = 66 text{cm}$

