Rider and a bike have a combined mass of $m=85,,rm{kg}$ and are travelling with a velocity of $v=8.5,,rm{m/s}$. We need to calculate their final height if they decide to climb the frictionless hill using only inertia.

During the first part of the driving, they have zero potential energy as all of their energy is in the form of kinetic energy. As they climb the hill, kinetic energy transfers into potential energy. At the highest point, all of the kinetic energy will convert to the potential energy. We can write this down as an equation:

$$
E_p+E_{kf}=E_k+E_{p0}
$$

Where $E_p$ and $E_{kf}$ are potential and kinetic energy at the final, highest point and $E_k$ and $E_{p0}$ are kinetic and potential energy at the lowest point:
Since we know that:

$$
E_{kf}=E_{p0}=0
$$

We can get:

$$
E_p=E_k
$$

Since $E_p$ can be calculated as:

$$
E_p=mgh
$$

And kinetic energy as:

$$
E_k=0.5cdot mv^2
$$
we can combine the three equations and get:

$$
0.5cdot mv^2=mgh
$$

We can cancel out $m$ on both sides and get

$$
0.5cdot v^2=gh
$$

From that we can express height and get:

$$
h=frac{v^2}{2g}
$$

Inserting values we get:

$$
h=frac{8.5^2}{2cdot 9.8}
$$

$$
boxed{h=3.69,,rm{m}}
$$

$$
h=3.69,,rm{m}
$$

The greater system that consists of $textbf{bicycle and rider}$ will always $textbf{remain equal}$ in energy. It will only change forms, as in transfer from one particular form of energy into another. In the previous problem we have noticed that the system will transfer energy from kinetic into potential. It can also do opposite.

In this particular case, the energy needed for the climb will be provided from the body of the rider, meaning it will transform from $textbf{chemichal energy}$ found in the food sources into $textbf{mechanical energy }$needed to propell the bicycle uphill.

Starting from a hill at height of $h_1=45,,,rm{m}$, a skier skis down an incline of $theta=30,,^{o}$ through the valley and continues up another hill at height of $h_2=40,,rm{m}$.

When need to determine its velocity at the bottom of the valley floor, speed at the top of the next hill and determine whether or not angles affect the results.

The hills are frictionless.

Since the hills are frictionless, we can use an energy equation that states that there are no energy losses, only energy converting from one form to another. In this case, it is converting from potential to kinetic, and the amount that converted is total potential energy because the skier reached bottom.

$$
E_{kv}=E_{p1}
$$

Inserting equations for potential and kinetic energy respectively:

$$
mgh_1=0.5cdot mv_v^2
$$

We can cancel out $m$ on both sides:

$$
gh_1=0.5cdot v_v^2
$$

From this we can get speed at the bottom of the valley:

$$
v_v=sqrt{2cdot g cdot h_1}
$$

Inserting values we get:

$$
v_v=sqrt{2cdot 9.8cdot 45}
$$

$$
boxed{v_v=29.7,,rm{m/s}}
$$

Similarly we can calculate the velocity at the top of the second hill, with the only difference that the part of the potential energy that transformed into kinetic is only due to the height difference between $h_2$ and $h_1$:

$$
mgcdot (h_1-h_2)=0.5cdot mv_2^2
$$

We can cancel out $m$ on both sides:

$$
gcdot (h_1-h_2)=0.5cdot v_2^2
$$

From this we can get speed at the bottom of the valley:

$$
v_2=sqrt{2cdot g cdot (h_1-h_2)}
$$

Inserting values we get:

$$
v_2=sqrt{2cdot 9.8cdot (45-40)}
$$

$$
boxed{v_2=9.9,,rm{m/s}}
$$

Angles don’t affect the results because energy is a $textbf{system property}$ which means it only depends on the final state of the system, which in this case is final height.

$$
v_v=29.7,,rm{m/s}
$$

$$
v_2=9.9,,rm{m/s}
$$

Angles don’t affect result.

noindent
textbf{Given:} \
$m_1 = 136 text{kg}$ \
$m_2 = 102 text{kg}$ \
$h_1 = 3.00 text{m}$ \
$g = 9.8 frac{text{m}}{text{s}^2}$\

noindent
textbf{Calculation:} \
For the second diver to have a competetive splash, his potential energy should at least be equal to the potential energy of the first diver

$$
PE_1 = PE_2
$$

$$
m_1gh_1 = m_2gh_2
$$

$$
h_2 = frac{m_1gh_1}{m_2g}
$$

Plugging in the given values

$$
h_2 = frac{(136)(9.8)(3.00)}{(102)(9.8)}
$$

$$
h_2 = 4.00 text{m}
$$

noindent
However, since the diving board is already $3.00 text{m}$ high, the second diver only need to leap by boxed{$1.00 text{m}$} high

$$
1.00 text{m}
$$

Bullet with a mass of $m=8,,rm{g}$ is horizontally fired into a block with a mass of $m_b=9,,rm{kg}$. After the collision the slide the frictionless surface together with velocity of $v_2=10,,rm{cm/s}$. We need to determine original speed of the bullet.

In order to solve this problem, we must apply conservation of momentum. It means that momentum before and after collision needs to be equal:

$$
mv_{1i}+m_bv_{2i}=mv_2+m_bv_2
$$

From this we can get:

$$
v_{1i}=frac{(m+m_b)cdot v_2-m_bcdot v_{2i}}{m}
$$

Inserting values we get:

$$
v_{1i}=frac{(0.008+9)cdot 0.1-9cdot 0}{0.008}
$$

Finally we get:

$$
boxed{v_{1i}=113,,rm{m/s}}
$$

$$
v_{1i}=113,,rm{m/s}
$$

noindent
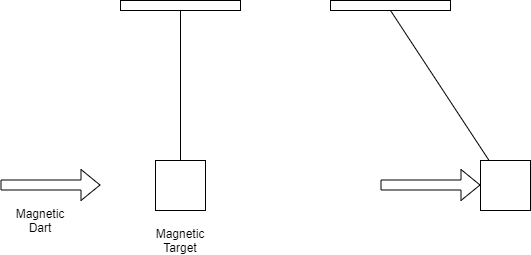
(b)\
The mechanical energy of the system is conserved because there are no external forces acting on the system.\

noindent
(c)\
textbf{Given: }\
$m_text{dart} = 0.025 text{kg}$ \
$m_text{target} = 0.73 text{kg}$ \
$h = 0.012 text{m}$
$g = 9.8 frac{text{m}}{text{s}^2}$\

noindent
textbf{Calculation:}\
Since the mechanical energy of the system is conserved, we can express it as follows

$$
ME_text{initial} = ME_text{final}
$$

$$
KE_text{initial} + PE_text{initial} = KE_text{final} + PE_text{final}
$$

$$
frac{1}{2}m_text{dart}v_i^2 + 0 = 0 + (m_text{dart} + m_text{target})gh
$$

noindent
Plugging in the given values

$$
v_i = sqrt{frac{2(m_text{dart} + m_text{target})gh}{m_text{dart}}}
$$

$$
v_i = sqrt{frac{2(0.025 + 0.73)(9.8)(0.12)}{0.025}}
$$

$$
boxed{v_i = 8.43 frac{text{m}}{text{s}}}
$$

(a) The system that we will use is the magnetic dart and the magnetic target attached to a string. We will use the initial height of the magnetic target as our reference height.

(b) The mechanical energy of the system is conserved because there are no external forces acting on the system.

(c) $v_i = 8.43 frac{text{m}}{text{s}}$

A hockey player with a mass of $m=91,,rm{kg}$ slide on ice with velocity of $v_{1i}=5.5,,rm{m/s}$. Another hockey player with velocity of $v_{2i}=8.1,,rm{m/s}$ and equal mass hits him from behind and they keep sliding together. We need to determine total energy and momentum in the system before the collision, their velocity after collision and the energy that was lost in the collision.

We can calculate the total energy in the system in the system by summing up kinetic energy of both players:

$$
E_{ki}=0.5cdot mv_{1i}^2 + mv_{2i}^2
$$

Inserting values we get.

$$
E_{ki}=0.5cdot 91cdot 5.5^2+0.5cdot 91cdot 8.1^2
$$

$$
boxed{E_{ki}=4360,,rm{J}}
$$

We can calculate the momentum in the system before by summing up the momentum of both players:

$$
p_i=mv_{1i}+mv_{2i}
$$

Inserting values we get:

$$
p_i=91cdot 5.5 + 91cdot 8.1
$$

$$
boxed{p_i=1240,,rm{kgm/s}}
$$

We can determine their velocity after the collision by using an equation of conservation of momentum that states that the moment will remain equal before and after collision:

$$
p_i=p_f
$$

And equation that connects momenntum after collision and velocity of the players:

$$
p_f=2cdot mv_f
$$

From these equations we can get their velocity:

$$
v_f=frac{p_i}{2cdot m}
$$

Inserting values we get.

$$
v_f=frac{1240}{2cdot 91}
$$

$$
boxed{v_f=6.8,,rm{m/s}}
$$

In order to calculate energy that was lost in the collision, we have to calculate the kinetic energy post collision and compare it with the initial kinetic energy:

$$
Delta E_k=E_{ki}-E_{kf}
$$

$$
Delta E_k=E_{ki}-0.5cdot (2cdot m)cdot v_f^2
$$

inserting values we get:

$$
Delta E_k=4360 – 0.5cdot (2cdot 91)cdot 6.8^2
$$

$$
boxed{Delta E_k=150,,rm{J}}
$$

$$
p_i=1240,,rm{kgm/s}
$$

$$
E_{ki}=4360,,rm{J}
$$

$$
v_f=6.8,,rm{m/s}
$$

$$
Delta E_k=150,,rm{J}
$$