All Solutions
Page 292: Section Review
(a) Compressed spring stores purely potential energy\
noindent
(b) Stored potential energy of the string is converted mostly to kinetic energy. \
noindent
(c) As the height of the dart increases, the kinetic energy from the spring potential energy is converted to gravitational potential energy. Thus, at the peak of the dart trajectory, all of the kinetic energy is converted to gravitational energy.\
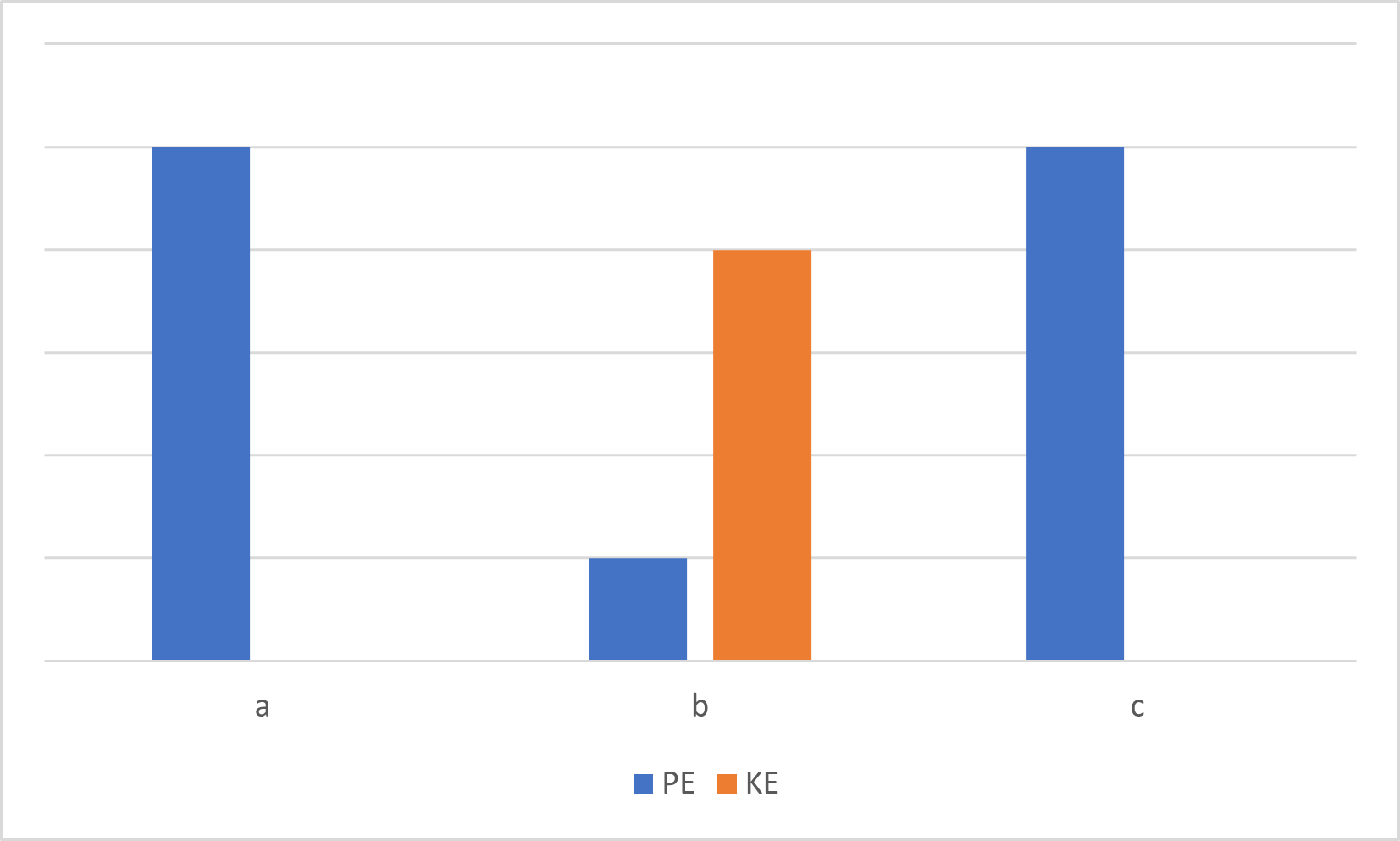
(b) Mostly kinetic energy with some potential energy
(c) Purely gravitational potential energy
We can calculate potential energy at height $h_1$ using the next equation:
$$
E_1=mgh_1
$$
Inserting values we get:
$$
E_1=25cdot 9.8cdot 425
$$
$$
boxed{E_1=1.04cdot 10^5,,rm{J}}
$$
$$
Delta E=mgcdot (h_2-h_1)
$$
Inserting values we get.
$$
Delta E=25cdot 9.8 cdot (225-425)
$$
$$
boxed{Delta E=-4.9cdot 10^4,,rm{J}}
$$
Notice negative result, it makes sense because potential energy decreases with lower height.
E_1=1.04cdot 10^5,,rm{J}
$$
$$
Delta E=-4.9cdot 10^4,,rm{J}
$$
$PE = m g h = (25.0) * (9.80) * (425) = 1.04 times 10^5 J$
the change in potential energy when the shell falls to a height of 225 m:
$Delta PE = m g (h_f – h_i) = (25.0) * (9.80) * (225 – 425) = -4.9 times 10^4 J$
$$
-4.9 times 10^4 J
$$
The angular momentum is given by
$$
L = Iomega
$$
noindent
If the angular speed of the merry-go-round is doubled, its angular momentum will also double.
$$
I(2omega) = 2Iomega = 2L
$$
noindent
The rotational kinetic energy is given by
$$
KE_text{rot} = frac{1}{2}Iomega^2
$$
noindent
If the angular speed of the merry-go-round is doubled, its rotational kinetic energy will quadruple.
$$
frac{1}{2}I(2omega)^2 = frac{1}{2}I(4omega^2) = 4frac{1}{2}Iomega^2 = 4KE_text{rot}
$$
A bowling bowl sitting on a rack will only have potential energy equivalent to the height of the storage rack. In order to lift the bowling ball from the storage rack to your shoulder, it will require work equivalent to the difference between the potential energy of those two location. Thus, the potential energy of the bowling ball on your shoulder is equal to the sum of the potential energy of the bowling ball on the storage rack and the work done by lifting the bowling ball from the storage rack to your shoulder.
$$
PE_text{storage rack} + W = PE_text{shoulder}
$$
textbf{Given:} \
$m = 90.0 text{kg}$\
$h_1 = 45.0 text{m}$\
$h_2 = 85.0 text{m}$\
$g = 9.8 frac{text{m}}{text{s}^2}$\
noindent
textbf{Calculation:} \
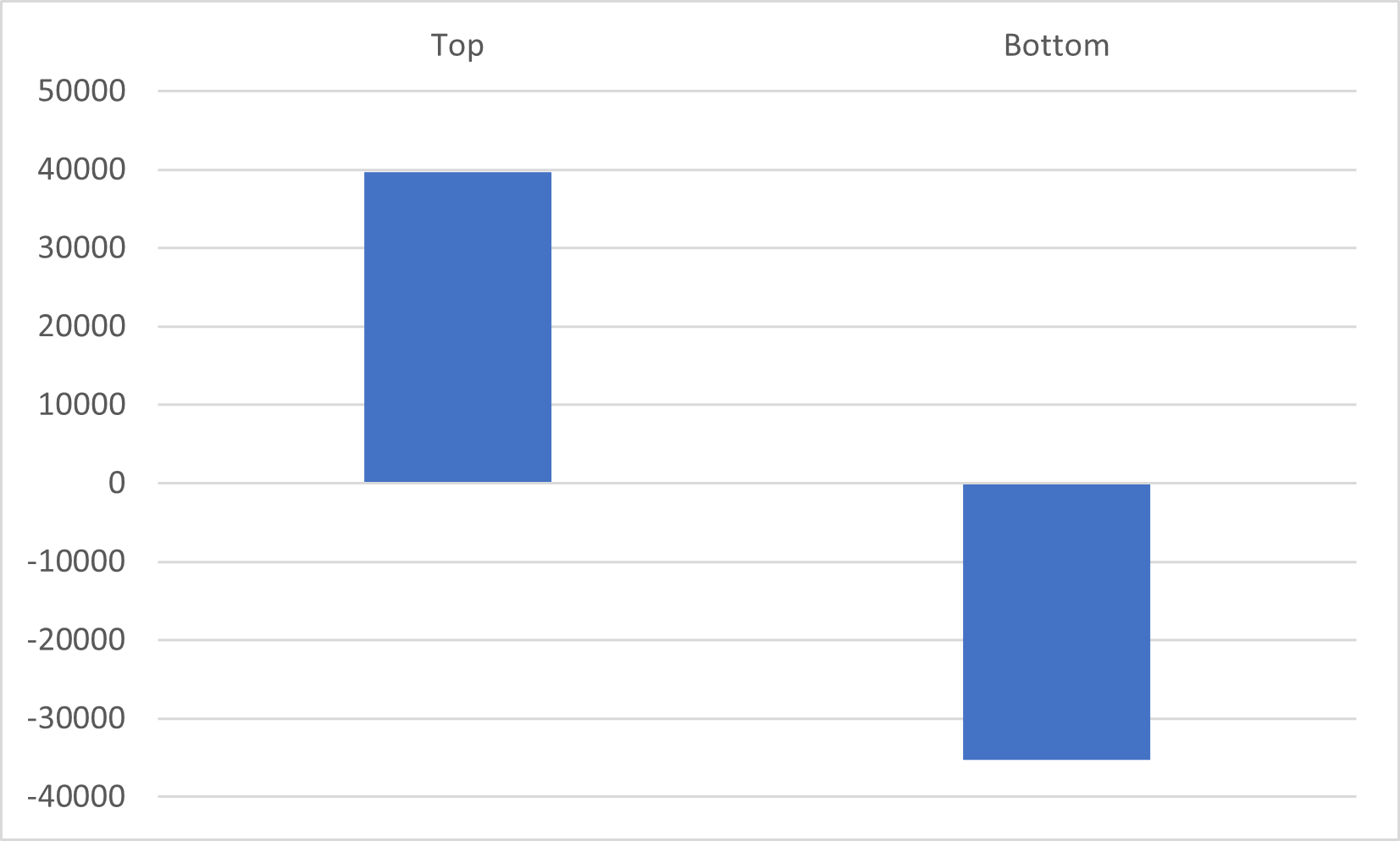
At the top of the quarry, the potential energy is calculated as follows
$$
PE_text{top} = mgh_1
$$
$$
PE_text{top} = (90.0)(9.8)(45.0)
$$
$$
boxed{PE_text{top} = 3.97 times 10^{4} text{J}}
$$
noindent
At the bottom of the quarry, the potential energy is calculated as follows
$$
PE_text{bottom} = mg(h_1-h_2)
$$
$$
PE_text{bottom} = (90.0)(9.8)(45.0-85.0)
$$
$$
boxed{PE_text{bottom} = -3.53 times 10^{4} text{J}}
$$
$$
PE_text{bottom} = -3.53 times 10^{4} text{J}
$$
(a) The puck is initially at rest thus it has no kinetic energy. Work is applied to the puck by the horizontal force exerted by an air hose. This, in turn, increases the kinetic energy of the puck equivalent to the work done by the air hose.\
noindent
(b) \
Kinetic energy is given by
$$
KE = frac{1}{2}mv^2
$$
noindent
If the mass of the puck decreases by a factor of $frac{1}{2}$, its kinetic energy will also decrease by a factor of $frac{1}{2}$.
$$
frac{1}{2}left(frac{1}{2}mright)v^2 = frac{1}{2}left(frac{1}{2}mv^2right) = frac{1}{2}KE
$$
noindent
Work is given by
$$
W = mgh
$$
noindent
If the mass of the puck decreases by a factor of $frac{1}{2}$, the work applied by the air hose on it will also decrease by a factor of $frac{1}{2}$.
$$
left(frac{1}{2}mright)gh = frac{1}{2}mgh = frac{1}{2}W
$$
noindent
(c) \
In part (a), the horizontal force exerted by the air hose causes an impulse that changes the momentum of the puck.\
noindent
In part (b), decreasing the mass of the puck by a factor of $frac{1}{2}$ causes decrease in the impulse and momentum of the puck by a factor of $frac{1}{2}$.
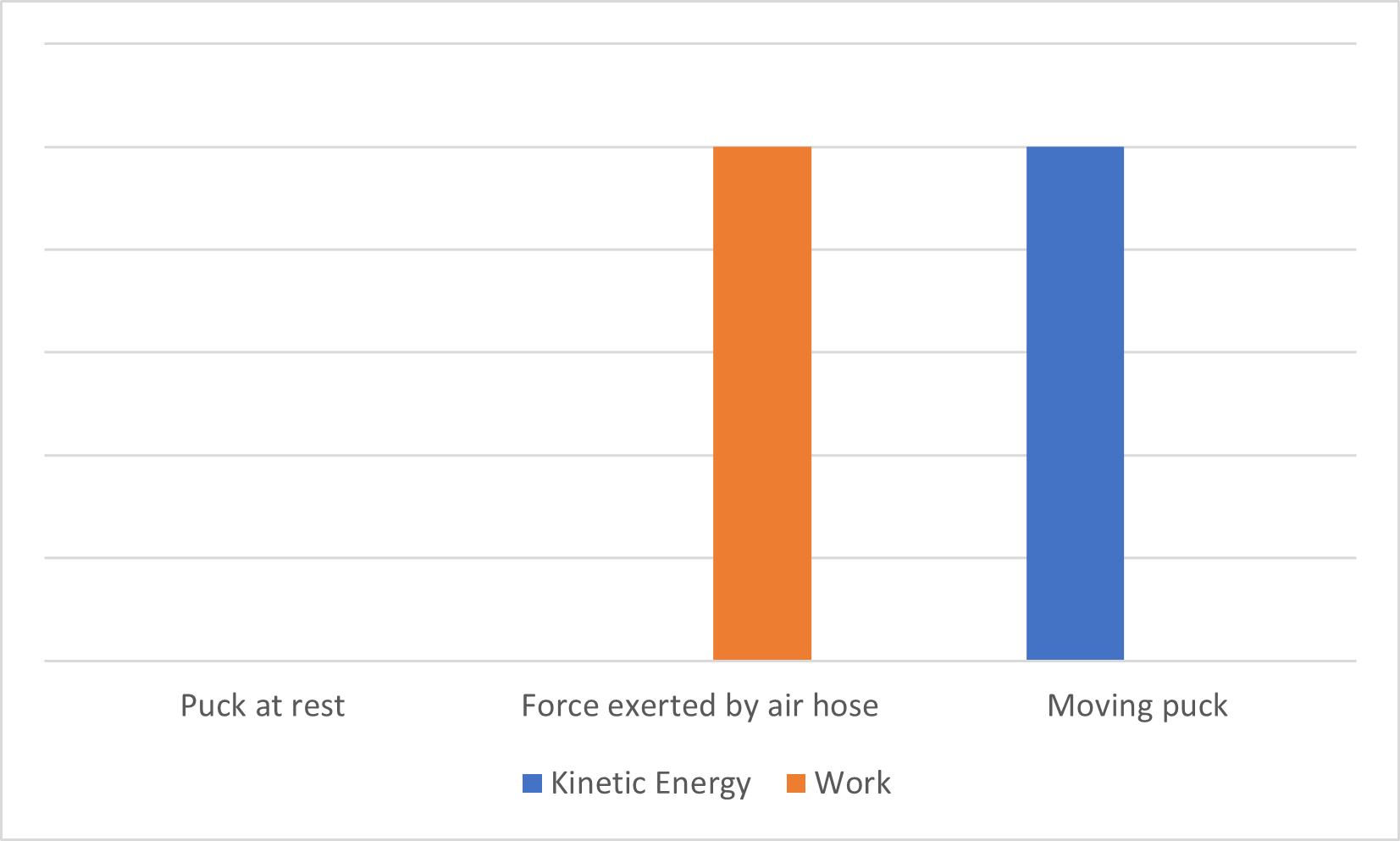
(b) Decrease in mass by a factor of $frac{1}{2}$ causes decrease in kinetic energy and work by also a factor of $frac{1}{2}$
(c) In part (a), impulse causes change in the momentum of the puck. In part (b), the decrease in mass also causes decrease in impulse and momentum.
Haven't found what you were looking for?
Search for samples, answers to your questions and flashcards

