A player exerts a constant $F=9,,rm{N}$ force on a puck weighing $m=105,,rm{g}$ over a distance of $d=0.15,,rm{m}$. What is the puck’s change in kinetic energy compared to using half as much force?

If the same force was applied over only a half of that distance $d_2=0.075,,rm{m}$ what would the change in kinetic energy be then?

Kinetic energy absorbed by the puck is equal to the work done by the force exerted by the player. This work can be expressed as:

$$
E=W=Fd
$$

Inserting values we get:

$$
E=9cdot 0.15
$$

$$
boxed{E=1.35,,rm{J}}
$$

When compared with the half as great force, we can see that kinetic energy is twice as greater.

The same principle works for this scenario as well, only difference is we will be using smaller distance:

$$
E_2=W_2=Fd_2
$$

Inserting values we get:

$$
E_2=9cdot 0.075
$$

$$
boxed{E_2=0.675,,rm{J}}
$$

$$
E=1.35,,rm{J}
$$

$$
E_2=0.675,,rm{J}
$$

Two students are pushing a car with force of 825 N at distance of 35 m. In part $textbf{a}$ we have to calculate how much work do the students do and in part $textbf{b}$ we have to calculate if the force was doubled, how much work would they do pushing the car the same distance.

a)

Work is equal to force times distance:

$$
W=Fs
$$

When we put numbers in we get:

$$
W=825cdot35
$$

$$
boxed{W=28875,,rm J}
$$

b)

We can calculate this with the same equation as in part $textbf{a}$ but we put force that is doubled.

$$
W=2Fs
$$

When we put numbers is we get:

$$
W=2cdot825cdot35
$$

$$
boxed{W=57750,,rm J}
$$

a) $W=28875,,rm$

b) $W=57750,,rm$

A rock climber with backpack is scaling a cliff. In 30 min she is 8.2 m above the starting point. In part $textbf{a}$ we have to calculate how much work does the climber do on the backpack, in part $textbf{b}$ we have to calculate how much work does she do lifting herself and the backpack and in part $textbf{c}$ we have to calculate what is the average power developed by the climber. It is also given that weight of the climber is 645 N.

a)

Work is equal to force times distance. In this case force is equal to weight if the backpack.

$$
W=Fs=mgs
$$

When we put numbers in we get:

$$
W=7.5cdot9.81cdot8.2
$$

$$
boxed{W=603,,rm J}
$$

b)

We can use the same equation as in part $textbf{a}$ but the force is different:

$$
W=Fs=(mg+F_g)s
$$

When we put numbers in we get:

$$
W=(7.5cdot9.81+645)cdot8.2
$$

$$
boxed{W=5892,,rm J}
$$

c)

We can calculate average power with equation:

$$
P=frac{W}{t}
$$

In this case we have to use total work.

When we put numbers we get:

$$
P=frac{5892}{30cdot60}
$$

$$
boxed{P=3.27,,rm W}
$$

a) $W=603,,rm J$

b) $W=5892,,rm J$

c) $P=3.27,,rm W$

A sailor pulls a boat a distance of 30 m along a dock using a rope that makes a 50$rm^o$ with horizontal. We have to calculate how much work would he do. It is also given that force is equal to 255 N.

Work can be calculated as force times distance, but we have to include only component of the force that is in the same direction as path, we can do that by adding $cosphi$ in equation:

$$
W=Fscosphi
$$

When we put numbers in we get:

$$
W=250cdot30cdotcos50^o
$$

$$
boxed{W=4821,,rm J}
$$

$$
W=4821,,rm J
$$

Two people lift a box with ropes and each rope makes an angle of 15$^o$ with vertical. It is given that distance is 15 m and each person exerts an force of 225 N. We have to calculate how much work do they do.

To calculate work we can use force times distance, but we have to use only component of the force that is on the same path.

$$
W=2cdot Fscosphi
$$

When we put numbers in we get:

$$
W=2cdot225cdot15cdotcos15^o
$$

$$
boxed{W=6520,,rm J}
$$

$$
W=6520,,rm J
$$

A passenger carries a suitcase up the stairs. It is given that vertical distance is 4.2 m and horizontal distance is 4.6 m and weight of the suitcase is 215 N. In part $textbf{a}$ we have to calculate how much work does the passenger do and in part $textbf{b}$ how much does it do going back down.

a)

We can use force times distance to calculate work, for distance we will use vertical distance because the force is in that direction.

$$
W=Fs
$$

When we put numbers in we get:

$$
W=215cdot4.2
$$

$$
boxed{W=903,,rm J}
$$

b)

We can calculate this in the same way but because the force is in the opposite orientation as path we have to put minus sign:

$$
W=Fs
$$

When we put numbers we in we get:

$$
W=-215cdot4.2
$$

$$
boxed{W=-903,,rm J}
$$

a) $W=903,,rm J$

b) $W=-903,,rm J$

Metal box is puled with rope at distance of 15 m. The rope is at angle of 46$^o$. It is given that force is 628 N. We have to calculate how much work does the force on the rope do.

We can calculate work with force times distance, but have to include only component of the force that is on the same path.

$$
W=Fscosphi
$$

When we put numbers in we get:

$$
W=628cdot15cdotcos46^o
$$

$$
boxed{W=6544,,rm J}
$$

$$
W=6544,,rm J
$$

A bicycle rider pushes a bicycle up the hill. It is given that mass of the bicycle is 13 kg, the incline is 25$^o$, the road is 275 m long and the rider pushes the bike parallel to the road with a force of 25 N. In part $textbf{a}$ we have to calculate how much work does the rider do on the bike, and i part $textbf{b}$ we have to calculate how much work is done by the force of gravity on the bike.

a)

We can find work using this equation:

$$
W=Fs
$$

When we put numbers in we get:

$$
W=25cdot275
$$

$$
boxed{W=6875,,rm J}
$$

b)

In this case we can use the same equation as in part $textbf{a}$ but we will use weight of the bike as force and height of the hill as distance, and because the gravity is in opposite direction as the path we have to put minus sign.

$$
W_g=-mgssin25^o
$$

When we put numbers in we get that:

$$
W_g=-13cdot9.81cdot275sin25^o
$$

$$
boxed{W_g=-14822,,rm J}
$$

When we evaluate the answer we can conclude that this problem is not possible because amount of work we put on the bike is smaller then work needed to push all the way up.

a) $W=6875,,rm J$

b) $W_g=-14822,,rm J$

In this problem we need to calculate the power $P$ developed by the motor in the given process from the given weight $w=575,text{N}$, height $h=20,text{m}$ and time $t=10,text{s}$.

We will start by calculating the work $W$ done by the motor. The work is given as a product of the force applied $w$ (weight) and the distance traveled $h$ (height).

$$
W=w cdot h hspace{1cm}(1)\
$$

Then the power $P$ developed is calculated by dividing the work $W$ by the time $t$ required for the work to be done. \

$$
P=frac{W}{t} hspace{1cm}(2)\
$$

We will now use the equation (1) to calculate the work done $W$. For the calculation we will use the given weight $w$ and height $h$

$begin{aligned}hspace{3cm}
W&=w cdot h \
W&=575,text{N} cdot 20,text{m} \
W&=11500,text{J} \
end{aligned}$

We can then use the calculated work $W$ and given time $t$ in the equation (2) to calculate the power $P$ developed by the motor.

$begin{aligned}hspace{3cm}
P&=frac{W}{t} \
P&=frac{11500,text{J}}{10,text{s}} \
P&=boxed{color{#c34632}1150,text{W} }\
end{aligned}$

The problem also requires us to express the power in kW units. To do that we need to divide the calculated power expressed in W by $1000$.

$begin{aligned}hspace{3cm}
P&=1150,text{W} cdot frac{1,text{kW}}{1000,text{W}} \
P&=boxed{color{#c34632}1.15,text{kW}}
end{aligned}$

$$
P=1150,text{W}=1.15,text{kW}
$$

In this problem you push a wheelbarrow. It is given distance of 60 m for 25 s, force is 145 N and speed is constant. In part $textbf{a}$ we have to calculate what power do you develop and in part $textbf{b}$ we have to calculate power if you move the wheelbarrow twice as fast.

a)

First we have to find total work and we can do that with equation:

$$
W=Fs
$$

now we can get power from equation:

$$
P=frac{W}{t}
$$

when we connect those equations we get:

$$
P=frac{Fs}{t}
$$

When we put numbers in we get:

$$
P=frac{145cdot60}{25}
$$

$$
boxed{P=348,,rm W}
$$

b)
In this case the speed is doubled and that means that time is two times shorter. We can use the same equation as in part $textbf{a}$.

$$
P=frac{Fs}{t}
$$

When we put numbers in we get:

$$
P=frac{145cdot60}{frac{25}{2}}
$$

$$
boxed{P=696,,rm W}
$$

a) $P=348,,rm W$

b) $P=696,,rm W$

To calculate this we have to get work needed to lift water, we can do that with equation:

$$
W=Fs=mgs
$$

now we can calculate power:

$$
P=frac{W}{t}
$$

When we connect those equations we get:

$$
P=frac{mgs}{t}
$$

When we put numbers in we get:

$$
P=frac{35cdot9.81cdot110}{60}
$$

$$
boxed{P=629,,rm W}
$$

$$
P=629,,rm W
$$

We can use definition of power to get work:

$$
P=frac{W}{t}rightarrow W=Pt
$$

when we have work we can get force if we have distance:

$$
W=Fsrightarrow F=frac{W}{s}
$$

When we connect those equations we get:

$$
F=frac{Pt}{s}
$$

When we put numbers in we get:

$$
F=frac{65cdot10^{3}cdot35}{17.5}
$$

$$
F=130000,,rm N
$$

$$
F=130000,,rm N
$$

We have to calculate how long would to take the truck and the winch to pull an object 15 m. It is also given that force is $6.8cdot10^3,,rm N$, and power is 0.3 kW.

First we have to get work, we can do that with equation:

$$
W=Fs
$$

Now to calculate time we can use equation for power:

$$
P=frac{W}{t}rightarrow t=frac{W}{P}
$$

when we put the first equation in we get:

$$
t=frac{Fs}{P}
$$

When we put numbers in we get:

$$
t=frac{6.8cdot10^{3}cdot15}{0.3cdot10^{3}}
$$

$$
boxed{t=340,,rm s}
$$

$$
t=340,,rm s
$$

Because the fore is not constant and it decrease by constant rate we can use equation:

$$
W=frac{1}{2}(F_1+F_2)d
$$

When we put numbers in we get:

$$
W=frac{1}{2}(210+40)cdot15
$$

$$
boxed{W=1875,,rm J}
$$

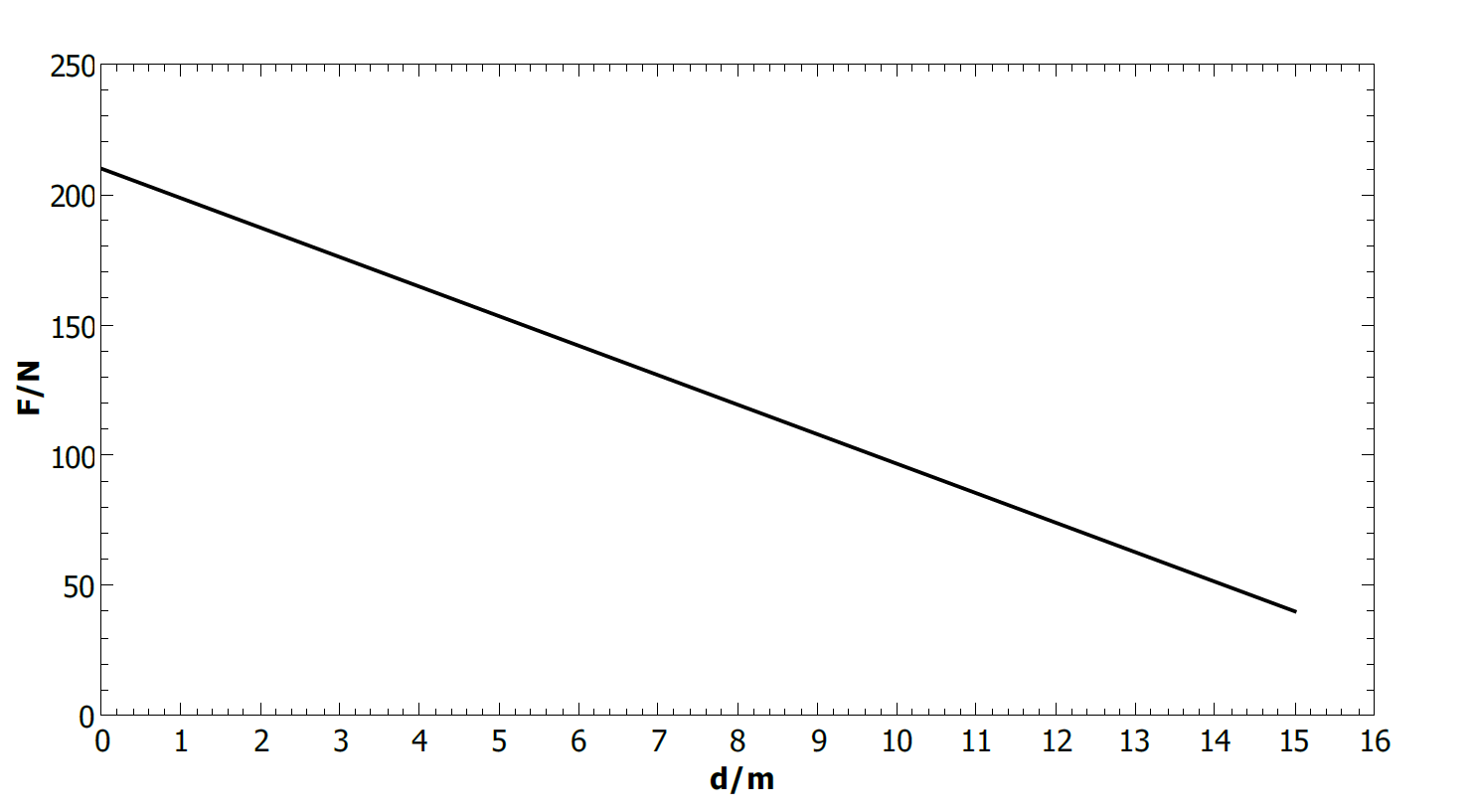
$$
W=1875,,rm J
$$