All Solutions
Page 250: Assessment
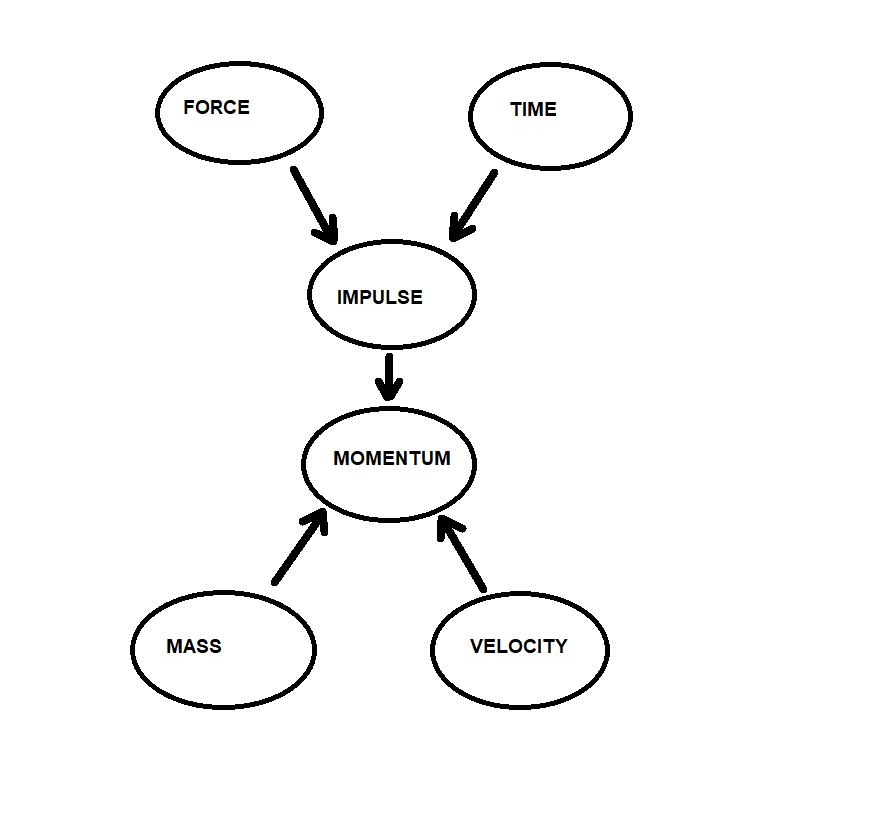
$$
p=mv
$$
The answer is $textbf{yes}$, because it has smaller mass its velocity has to be bigger.
They both exert the same magnitude of the impulse on the ball because there is the same change in magnitude of momentum.
b)
Catcher while caching the ball applies the force in shorter time, to have the same impulse the force has to be larger.
b) catcher
$$
text{color{#c34632}Remember that : Linear momentum = Mass $times$ Velocity}
$$
Notice that this is true only about linear momentum, angular momentum can change even if the net force on the system is 0
text{color{#4257b2}No change in Linear momentum can occur if net force is 0}
$$
b) The skater can decrease his inertia, and that would result in increasing angular velocity. He can do that by joining his hand with his body.
b) decreasing inertia
b) The momentum is conserved when we have in system earth and the ball.
b) Earth and ball.
b) We have to include basketball and the floor in the system.
b) Basketball and the floor
$$
impulse=Ft
$$
$$
Delta p=Ft
$$
After impulse A an object has an change in momentum:
$$
Delta p=Ft=2cdot2=4,,rm kgm/s
$$
during that time an object accelerate.
B)
After impulse A an object has an change in momentum:
$$
Delta p=Ft=-2cdot2=-4,,rm kgm/s
$$
during that time an object deaccelerate.
C)
After impulse A an object has an change in momentum:
$$
Delta p=Ft=-2cdot=-2,,rm kgm/s
$$
during that time an object accelerate but in opposite direction.
B) deaccelerate
C) accelerate in opposite direction.
$$
mv=2mv’rightarrow v’=frac{v}{2}
$$
But they are moving more than half the speed of the moving truck and that means that moving truck must have bigger mass.
$$
begin{align*}
Ft&=Delta p\
Ft&=mv\
t&=frac{mv}{F}\
&=frac{0.058cdot62}{272}
end{align*}
$$
$$
boxed{t=0.013,,rm s}
$$
t=0.013,,rm s
$$
Change in momentum is equal to:
$$
begin{align*}
Delta p&=mv’-mv\
&=0.145cdot(-58)-0.145cdot42
end{align*}
$$
$$
boxed{Delta p=-14.5,,rm kgm/s}
$$
b)
Impulse is equal to the change in momentum:
$$
begin{align*}
Ft&=Delta p\
F&=frac{Delta p}{t}\
&=frac{-14.5}{4.6cdot10^{-4}}
end{align*}
$$
$$
boxed{F=-31522,,rm N}
$$
b) $F=-31522,,rm N$
$$
begin{align*}
F &= 186 ,mathrm{N}\
m &= 7.3 ,mathrm{kg} \
Delta{t} &= 0.40 ,mathrm{s}
end{align*}
$$
Given the formula such that $Delta{p}$ is the change in momentum, $F$ is the force acting upon the object, and time $t$ is the duration in which the force is acting upon the same object.
$$
begin{equation}
Delta{p} = FDelta{t}
end{equation}
$$
We can solve for the momentum by plugging in the given values.
$$
begin{align*}
Delta{p} &= FDelta{t}\
&= (186,mathrm{N})(0.40,mathrm{s})\
&= 74 N cdot s\
&= boxed{74 ,mathrm{kg}cdot mathrm{frac{m}{s}}}
end{align*}
$$
textbf{Change in Velocity.}
$$
Given the formula where $Delta{v}$ is the change in velocity, $Delta{p}$ is the change in momentum, and $m$ is the mass.
$$
begin{equation}
Delta{v} = frac{Delta{p}}{m}
end{equation}
$$
We can solve for the momentum by using $Delta{p}$ acquired from the previous solution and the mass($m$) in the given values.
$$
begin{align*}
Delta{v} &= frac{Delta{p}}{m}\
&= frac{74 ,mathrm{kg}cdot mathrm{frac{m}{s}}}{7.3,mathrm{kg}}\
&= boxed{10 ,mathrm{frac{m}{s}}}
end{align*}
$$
a)
We can calculate change in momentum:
$$
Delta p=mv_2-mv_1=5500cdot7.8-5500cdot4.2
$$
$$
boxed{Delta p=19800,,rm kgm/s}
$$
b)
Impulse is equal to change in momentum:
$$
begin{align*}
Ft&=Delta p\
F&=frac{Delta p}{t}\
&=frac{19800}{15}
end{align*}
$$
$$
boxed{F=1320,,rm N}
$$
b) $F=1320,,rm N$
Impulse is equal to change in momentum:
$$
begin{align*}
Ft&=mv\
F&=frac{mv}{t}\
&=frac{6cdot10^{-3}cdot350}{1.8cdot10^{-3}}
end{align*}
$$
$$
boxed{F=1167,,rm N}
$$
F=1167,,rm N
$$
Impulse is equal to change in momentum:
$$
begin{align*}
Ft&=mv_2-mv_1\
F&=frac{mv_2-mv_1}{t}\
&=frac{0.24cdot(-2.4)-0.24cdot3.8}{0.025}
end{align*}
$$
$$
boxed{F=59.5,,rm N}
$$
F=59.5,,rm N
$$
$$
I = Delta p = F Delta t = (30.0) (0.16) = 4.8 Kg.m/s
$$
4.8 Kg.m/s
$$
Combined momentum is equal to:
$$
begin{align*}
p&=(m_1+m_2)v\
&=(35.6+1.3)cdot9.5
end{align*}
$$
$$
boxed{p=350.6,,rm kgm/s}
$$
p=350.6,,rm kgm/s
$$
$p = F t = (30.0) (0.16) = 4.8 Kg.m/s$
Its speed is:
$$
v = dfrac{p}{m} = dfrac{4.8}{0.115} = 42 m/s
$$
42 m/s
$$
a)
Impulse is equal to change in momentum:
$$
begin{align*}
Ft&=mv_a-mv_1\
&=25cdot8-25cdot12\
end{align*}
$$
$$
boxed{Ft=-100,,rm kgm/s}
$$
b)
Impulse is equal to change in momentum:
$$
begin{align*}
Ft&=mv_a-mv_1\
&=25cdot(-8)-25cdot12\
end{align*}
$$
$$
boxed{Ft=-500,,rm kgm/s}
$$
b) $Ft=-500,,rm kgm/s$
Area under the graph is change in momentum:
$$
begin{align*}
Delta p&=2cdotleft(frac{2cdot1}{2}right)\
Delta p&=2,,rm kgm/s
end{align*}
$$
now we can calculate speed:
$$
mv_1+Delta p=mvrightarrow v=frac{mv_1+Delta p}{m}=frac{0.15cdot12+2}{0.15}
$$
$$
boxed{v=25,,rm m/s}
$$
v=25,,rm m/s
$$
a)
Change in momentum is equal to:
$$
Delta p=mv=0.145cdot35
$$
$$
boxed{Delta p=5.075,,rm kgm/s}
$$
b)
Impulse is equal o change in momentum:
$$
begin{align*}
Ft&=Delta p\
F&=frac{Delta p}{t}\
&=frac{5.075}{0.05}
end{align*}
$$
$$
boxed{F=101.5,,rm N}
$$
b)
Impulse is equal o change in momentum:
$$
begin{align*}
Ft&=Delta p\
F&=frac{Delta p}{t}\
&=frac{5.075}{5}
end{align*}
$$
$$
boxed{F=10.15,,rm N}
$$
b) $F=101.5,,rm N$
c) $F=10.15,,rm N$
a)
Impulse is equal to change in momentum:
$$
begin{align*}
Ft&=mv_2-mv_1\
&=0.115cdot(-25)-0.115cdot37
end{align*}
$$
$$
boxed{Ft=-7.13,,rm kgm/s}
$$
b)
Average force is equal to:
$$
F=frac{Ft}{t}=frac{-7.13}{5cdot10^{-4}}
$$
$$
boxed{F=-14260,,rm N}
$$
b) $F=-14260,,rm N$
To calculate impulse we can use difference in momentum:
$$
begin{align*}
Ft&=p_2-p_1\
&=mv_2-mv_1\
&=4.7cdot10^{-26}cdot(-550)-4.7cdot10^{-26}cdot550
end{align*}
$$
$$
boxed{Ft=-5.17cdot10^{-23},,rm kgm/s}
$$
We put minus sign on $v_2$ because it is in opposite direction.
b)
We can calculate average force by using the definition of impulse, for time duration we will put one second and for number of collisions we will put the number of collisions in one second:
$$
begin{align*}
F&=nfrac{Ft}{t}\
&=1.5cdot10^{23}frac{-5.17cdot10^{-23}}{1}
end{align*}
$$
$$
boxed{F=-7.76,,rm N}
$$
b) $F=F=-7.76,,rm N$
$$
begin{align*}
Ft&=mv\
t&=frac{mv}{F}\
&=frac{72000cdot63cdot10^{-2}}{35}
end{align*}
$$
$$
boxed{t=1296,,rm s}
$$
t=1296,,rm s
$$
$$
begin{align*}
mgh&=frac{mv_v^2}{2}\
v_v&=sqrt{2gh}\
v_v&=sqrt{2cdot9.81cdot60}\
v_v&=34.3,,rm m/s
end{align*}
$$
We can get mass of hey from weight:
$$
begin{align*}
F_g&=mg\
m&=frac{F_g}{g}\
m&=frac{175}{9.81}\
m&=17.85,,rm kg
end{align*}
$$
Now we can calculate magnitude of the momentum in vertical direction:
$$
begin{align*}
p_v&=mv_v\
p_v&=17.85cdot1177.2\
p_v&=612.4,,rm kgm/s
end{align*}
$$
Horizontal velocity is the same as planes:
$$
v_h=36,,rm m/s
$$
And magnitude of momentum in horizontal direction is:
$$
begin{align*}
p_h&=mv_v\
p_h&=17.85cdot36\
p_h&=642.2,,rm kgm/s
end{align*}
$$
Now we can calculate magnitude of total momentum:
$$
begin{align*}
p&=sqrt{p_v^2+p_h^2}\
p&=sqrt{612.4^2+642.2^2}
end{align*}
$$
$$
boxed{p=887.4,,rm kgm/s}
$$
$$
begin{align*}
tanphi=frac{p_v}{p_h}\
tanphi=frac{612.4}{642.2}
end{align*}
$$
$$
boxed{phi=44rm^o,,, towards,, the,, center,, of,, the,, earth}
$$
p=887.4,,rm kgm/s
$$
$$
phi=44rm^o
$$
Impulse is equal to change in momentum:
$$
begin{align*}
Ft&=mv\
Ft&=20cdot10
end{align*}
$$
$$
boxed{Ft=200,,rm kgm/s}
$$
b)
Now when we have impulse we can get average force because impulse is equal to force times time:
$$
begin{align*}
F=frac{Ft}{t}\
F=frac{200}{0.05}
end{align*}
$$
$$
boxed{F=4000,,rm N}
$$
We can calculate mass of an object whose weight equals the force with equation:
$$
begin{align*}
F_g&=mg\
m&=frac{F_g}{g}\
m&=frac{4000}{9.81}
end{align*}
$$
$$
boxed{m=408,,rm kg}
$$
d)
World record in lifting weight is 501 kg in deadlift, in that movement human uses almost every muscle, we can conclude that using just arm human $textbf{can not lift that weight}$.
e)
Because restraining seat is build to $textbf{prolongs the time}$ in which force acts on the child, hence the average force is smaller.
b) $F=4000,,rm N$
c) $m=408,,rm kg$
d) No
e) prolongs the time
begin{align*}
m_1v_1+m_2v_2=m_1v_1’+m_2v_2’\
end{align*}
$$
$$
begin{align*}
5cdot0+2cdot0&=5cdot0.12-2v_2’\
v_2’&=frac{5cdot0.12}{2}
end{align*}
$$
$$
boxed{v_2’=0.3,,rm m/s}
$$
v_2’=0.3,,rm m/s
$$
begin{align*}
m_1v_1+m_2v_2=m_1v_1’+m_2v_2’\
end{align*}
$$
$$
begin{align*}
4.65cdot2+50cdot10^{-3}cdot2&=4.65v_1’+50cdot10^{-3}cdot647\
v_1’&=frac{4.65cdot2+50cdot10^{-3}cdot2-50cdot10^{-3}cdot647}{4.65}
end{align*}
$$
$$
boxed{v_1’=-4.9,,rm m/s}
$$
v_1’=-4.9,,rm m/s
$$
begin{align*}
m_1v_1+m_2v_2=m_1v_1’+m_2v_2’\
end{align*}
$$
begin{align*}
8.5cdot 0+12cdot10^{-3}cdot150&=8.5v_1′-12cdot10^{-3}cdot10^{2}\
v_2’&=frac{12cdot10^{-3}cdot150+12cdot10^{-3}cdot10^{2}}{8.5}
end{align*}
$$
$$
boxed{v_1’=0.35,,rm m/s}
$$
v_1’=0.35,,rm m/s
$$
begin{align*}
m_1v_1+m_2v_2=m_1v_1’+m_2v_2’\
end{align*}
$$
$$
begin{align*}
42cdot1.2+2cdot1.2&=42v_1′-2cdot0\
v_1’&=frac{42cdot1.2+2cdot1.2}{42}
end{align*}
$$
$$
boxed{v_1’=1.26,,rm m/s}
$$
The sign of velocity that we got is plus, that means that he jumped in the same direction as he was moving before.
v_1’=1.26,,rm m/s
$$
$$
begin{align*}
m_1v_{x1}+m_2v_{x2}=m_1v_{x1}’+m_2v_{x2}’\
end{align*}
$$
2.
$$
begin{align*}
m_1v_{y1}+m_2v_{y2}=m_1v_{y1}’+m_2v_{y2}’\
end{align*}
$$
1.
$$
begin{align*}
m_1v_{x1}+m_2cdot0&=m_1v_{x1}’+m_2v_{x2}’\
end{align*}
$$
2.
$$
begin{align*}
m_1v_{y1}’&=m_2v_{y2}’\
m_1v_{x1}’&=m_2v_{x2}’\
end{align*}
$$
$$
begin{align*}
m_1v_{x1}&=m_2v_{x2}’+m_2v_{x2}’\
v_{x2}’&=frac{m_1v_{x1}}{2m_2}\
v_{x2}’&=frac{0.16cdot4}{2cdot0.16}\
v_{x2}’&=2,,rm m/s
end{align*}
$$
$$
begin{align*}
m_1v_{x1}&=m_1v_{x1}’+m_1v_{x1}’\
v_{x1}’&=frac{m_1v_{x1}}{2m_1}\
v_{x1}’&=frac{0.16cdot4}{2cdot0.16}\
v_{x1}’&=2,,rm m/s
end{align*}
$$
begin{align*}
sin{45mathrm{^o}}&=frac{v_{x1}’}{v_1′}\
v_1’&=frac{v_{x1}’}{sin{45mathrm{^o}}}
end{align*}
$$
$$
boxed{v_1’=2.8,,rm m/s}
$$
$$
begin{align*}
sin{45mathrm{^o}}&=frac{v_{x2}’}{v_2′}\
v_2’&=frac{v_{x2}’}{sin{45mathrm{^o}}}
end{align*}
$$
$$
boxed{v_2’=2.8,,rm m/s}
$$
v_1’=2.8,,rm m/s
$$
$$
v_2’=2.8,,rm m/s
$$
begin{align*}
m_1v_1+m_2v_2=m_1v_1’+m_2v_2’\
end{align*}
$$
$$
begin{align*}
2575v_1+825cdot0&=2575cdot8.5+825cdot8.5\
v_1&=frac{2575cdot8.5+825cdot8.5}{2575}
end{align*}
$$
$$
boxed{v_1=11.2,,rm m/s}
$$
v_1=11.2,,rm m/s
$$
begin{align*}
m_1v_1+m_2v_2=m_1v_1’+m_2v_2’\
end{align*}
$$
begin{align*}
0.2cdot0.3+0.1cdot0.1&=0.2v_1’+0.1cdot0.26\
v_2’&=frac{0.2cdot0.3+0.1cdot0.1-0.1cdot0.26}{0.2}
end{align*}
$$
$$
boxed{v_1’=0.22,,rm m/s}
$$
v_1’=0.22,,rm m/s
$$
$$
begin{align*}
Ft&=Delta p\
end{align*}
$$
$$
begin{align*}
Delta p=6cdot10\
end{align*}
$$
$$
boxed{Delta p=60,,rm kgm/s}
$$
$$
begin{align*}
Delta p&=p_2-p_1\
Delta p&=mv_2-mv_1\
Delta p&=m(v_2-v_1)\
Delta p&=mDelta v\
Delta v&=frac{Delta p}{m}
end{align*}
$$
$$
begin{align*}
Delta v=frac{60}{3}
end{align*}
$$
$$
boxed{Delta v=20,,rm m/s}
$$
Delta p=60,,rm kgm/s
$$
$$
Delta v=20,,rm m/s
$$
Momentum is defined as mass times velocity, so we can get change in momentum if we know the change in velocity.
$$
begin{align*}
Delta p&=p_2-p_1\
Delta p&=mv_2-mv_1\
Delta p&=m(v_2-v_1)\
end{align*}
$$
$$
Delta p=625cdot(44-10)
$$
$$
boxed{Delta p=21250,,rm kgm/s}
$$
Change in momentum is equal to impulse generated by constant force.
$$
begin{align*}
Ft&=Delta p\
F&=frac{Delta p}{t}
end{align*}
$$
$$
begin{align*}
F=frac{21250}{68}\
end{align*}
$$
$$
boxed{F=312.5,,rm N}
$$
b) $F=312.5,,rm N$
Momentum is defined as mass times velocity.
$$
begin{align*}
Delta p&=p_2-p_1\
Delta p&=mv_2-mv_1\
Delta p&=m(v_2-v_1)\
end{align*}
$$
$$
Delta p=845cdot(27.78-0)
$$
$$
boxed{Delta p=23474,,rm kgm/s}
$$
Change in momentum is equal to impulse generated by force.
$$
begin{align*}
Ft&=Delta p\
F&=frac{Delta p}{t}
end{align*}
$$
$$
F=frac{23474}{0.9}
$$
$$
boxed{F=26082,,rm N}
$$
That force is exerted by the race track. Because that force is friction between dragster and race track.
b) $F=26082,,rm N$
c) race track
$$
begin{align*}
m_1v_1+m_2v_2=m_1v_1’+m_2v_2’\
end{align*}
$$
$$
begin{align*}
0.115cdot35+0.365cdot0&=0.115v’+0.365v’\
v’&=frac{0.115cdot35}{0.115+0.365}
end{align*}
$$
$$
boxed{v’=8.39,,rm m/s}
$$
v’=8.39,,rm m/s
$$
Gymnast spins around axis that goes through its center of mass and it is parallel to the bar, because in free rotation body tends to speed around center of mass and in this case when gymnast lets go of the bar she had angular velocity that was pointing in the same direction as the bar and because there is no external torque when she is in the air the direction of the angular velocity is the same.
Moment of inertia can be calculated with equation:
$$
I=sum_i^nm_ir_i^2
$$
we can see from this equation that moment of inertia is larger the farther mass is from the center of rotation.
$$
boxed{rm first>third>second}
$$
To solve this we have to use conservation of angular momentum, and we know that angular momentum is given by equation:
$$
L=Iomega
$$
We can see form equation that if the angular momentum is conserved, larger the moment of inertia smaller the angular velocity.
$$
boxed{rm second>third>first}
$$
b) $rm first>third>second$
c) $rm second>third>first$
To calculate momentum we have to get velocity in that moment, we can do that with equation for conservation of energy:
$$
mgh=frac{mv^2}{2}rightarrow v=sqrt{2gh}
$$
Now when we can get momentum with equation:
$$
p=mv
$$
$$
v=sqrt{2cdot9.81cdot0.32}=2.5,,rm m/s
$$
Now we can get calculate momentum:
$$
p=60cdot2.5
$$
$$
boxed{p=150,,rm kgm/s}
$$
Impulse is equal to change in momentum, in this case we have that starting momentum is that momentum form part $textbf{a}$ and at the end is zero:
$$
Ft=Delta p
$$
$$
boxed{Ft=150,,rm kgm/s}
$$
Impulse is equal to force time time, we know from part $textbf{b}$ impulse and the time is given:
$$
F=frac{Ft}{t}
$$
$$
F=frac{150}{0.05}
$$
$$
boxed{F=3006,,rm N}
$$
Weight of the dancer can be calculated with equation:
$$
F_g=mg
$$
We can compare the stopping force with his weight by dividing them:
$$
x=frac{F}{F_g}
$$
$$
F_g=60cdot9.81=589,,rm N
$$
and finally we get:
$$
x=frac{3006}{589}
$$
$$
boxed{x=5.1}
$$
The stopping force on the body is 5.1 times bigger then weight.
b) $Ft=150,,rm kgm/s$
c) $F=3006,,rm N$
d) $x=5.1$
$$
F_{cp}=frac{mv^2}{r}
$$
And centripetal force in this case on the top of the ball’s motion is equal to tension plus weight:
$$
T+mg=frac{mv^2}{r}rightarrow T=frac{mv^2}{r}-mg
$$
$$
T=frac{0.72cdot3.3^2}{0.6}-0.72cdot9.81
$$
$$
boxed{T=6,,rm N}
$$
T=6,,rm N
$$
$$
frac{T^2}{T_M^2}=frac{r^3}{r_M^3}rightarrow r=r_Mleft(frac{T^2}{T_M^2}right)^{frac{1}{3}}
$$
$$
r=3.9cdot10^8cdotleft(frac{1^2}{27.33^2}right)^{frac{1}{3}}
$$
$$
boxed{r=4.3cdot10^{7},,rm m}
$$
r=4.3cdot10^{7},,rm m
$$
$$
x=frac{1}{2}at^2rightarrow a=frac{2x}{t^2}
$$
Now when we have linear acceleration we can get angular acceleration:
$$
alpha=frac{a}{r}
$$
To calculate angular velocity we have to get linear velocity first, we can di that with equation:
$$
v=at
$$
Now it is easy to get angular velocity:
$$
omega=frac{v}{r}
$$
And finally to calculate moment of inertia we have to find torque first:
$$
tau=Fr
$$
now we can get moment of inertia:
$$
tau=Ialpharightarrow I=frac{tau}{alpha}
$$
$$
a=frac{2cdot5}{2^2}=2.5,,rm m/s^2
$$
Angular acceleration is:
$$
alpha=frac{2.5}{0.3}
$$
$$
boxed{alpha=8.33,,rm rad/s^2}
$$
Now lets calculate linear velocity:
$$
v=2.5cdot2=5,,rm m/s
$$
Angular velocity is:
$$
omega=frac{5}{0.3}
$$
$$
boxed{omega=16.67,,rm rad/s}
$$
Lets calculate torque:
$$
tau=40cdot0.3=12,,rm N
$$
Moment of inertia is:
$$
I=frac{12}{8.33}
$$
$$
boxed{I=1.44,,rm kgm^2}
$$
alpha=8.33,,rm rad/s^2
$$
$$
omega=16.67,,rm rad/s
$$
$$
I=1.44,,rm kgm^2
$$

