Following Kepler’s law, the conclusion is given in a figure $7-3$, the planet moves fastest when it is close to the Sun, and slowest when it is farther from the Sun.

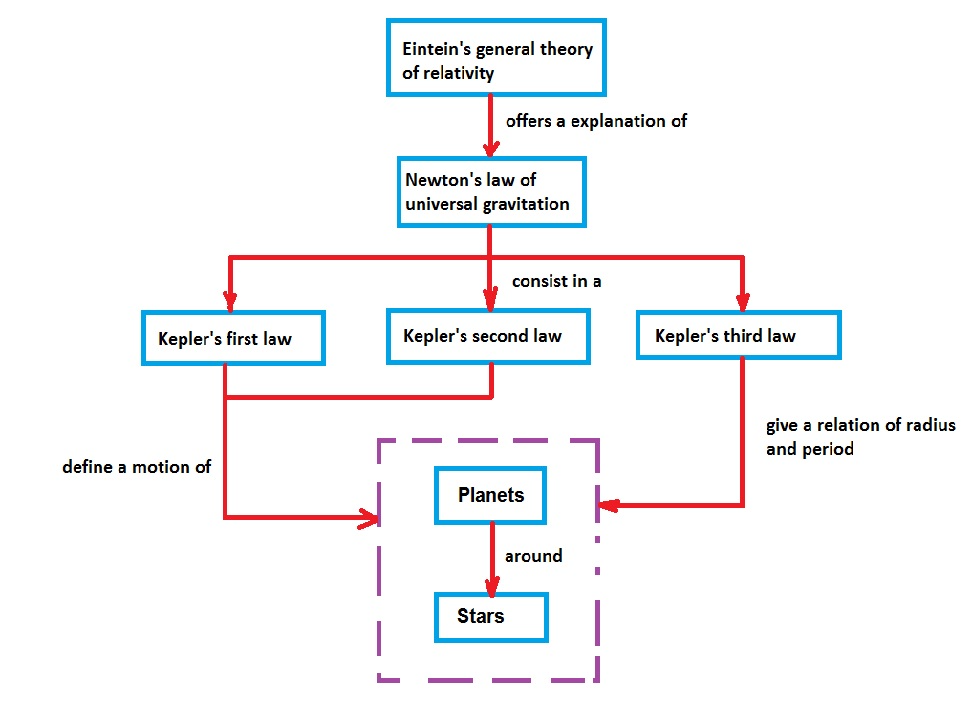
As the Earth moves slower during the summer, the Earth is farther from the Sun during the summer.

$$
boxed{text{The Earth is closer to the Sun during winter and farther during the summer.}}
$$

Kepler’s second law states that an imaginary line from the Sun to a planet sweeps equal area in equal time intervals. But, the area that is defined by a Mars trajectory around the Sun is bigger than the area defined by the Earth trajectory.
$$
boxed{text{The areas sweep out by time interval are not the same for Mars and Earth.}}
$$

Cavendish make a experiments with a device that had horizontal road with two small lead spheres attached to each end. The rod is suspended at midpoint by a thin wire, so it could rotate. Because the rod was suspended by a thin wire, the rod and the spheres were very sensitive to horizontal forces. To measure $G$, Cavendish placed two large lead spheres in fixed positions, close to a small sphere. The force of attraction between the small and the large sphere makes the rod rotate. By measuring the angle through which the rod turned, Cavendish was able to calculate the force of attraction between the objects.

Newton states that force (F) is proportional to $dfrac{1}{r^{2}}$

In accordance of Newton’s interpretation of Kepler’s third law, the ratio $frac{T^2}{r^3}$, where $T$ denotes the period the planet revolves around the Sun and $r$ is their distance from the Sun, will be textbf{halved} if the Sun’s mass was doubled because $frac{T^2}{r^3} = frac{4pi^2}{Gm_{s}}$ such that $m_s$ is the Sun’s mass.
In mathematical terms, given the equation
$$frac{T^2}{r^3} = frac{4pi^2}{Gm_{s}}$$
Since the mass of the Sun is doubled, $m_s = 2m_s$, thus
begin{align*}
&=frac{4pi^2}{2m_{s}cdot G}\
&=frac{1}{2}left( frac{4pi^2}{Gm_{s}} right)\
intertext{Since,}
&=frac{T^2}{r^3} = frac{4pi^2}{Gm_{s}}\
intertext{Therefore,}
&=frac{4pi^2}{2m_{s}cdot G}\
&=frac{1}{2}left( frac{4pi^2}{Gm_{s}} right)\
intertext{Since,}
&=frac{T^2}{r^3} = frac{4pi^2}{Gm_{s}}\
intertext{Therefore,}
&=boxed{frac{1}{2}left( frac{T^2}{r^3} right)}\
intertext{if the Sun’s mass is doubled.}
end{align*}

The ratio, $frac{T^2}{r^3}$, will be $textbf{halved}$.

The speed of a satellite that orbits around the Earth is defined by the equation:

$$
begin{align*}
v&=sqrt{Gcdotfrac{m_e}{r}}
end{align*}
$$

Where the $G$ represents the universal gravitational constant, $m_e$ is the mass of the Earth, and $r$ stands for the radius of the satellite orbit.

So the correct answer is:

$$
boxed{text{Mass of the Earth and distance from the Earth.}}
$$

By Newton’s third law, every force that acts on a body has the same reaction force. So the centripetal force must have the same cause of action. As the satellite orbits around the planet, there must be a gravitational force that acts in an opposite direction.

$$
boxed{text{The gravitational force crate a reaction force that acts as a centripetal force.}}
$$

The force of $5g$ on an astronaut’s body means that the force that acts on an astronaut’s body is $5$ times higher than a gravitational force that acts on his body on Earth. This means that the weight of the astronaut’s body is $5$ times bigger than on Earth.

The force of $5g$ that acts on a astronaut body in space means that the force on his body is $5$ times bigger than the gravitational force on Earth.

The units for $g= dfrac{F}{g}$ are $dfrac{N}{kg}$.

A newton (N) is equal to $dfrac{kgm}{s^{2}}$

Therefore, $g = dfrac{N}{kg} = dfrac{dfrac{kgm}{s^{2}}}{kg} = dfrac{m}{s^{2}}$

The attraction between the object occurs because of the gravitational field that persists around the objects. If the object is inserted in a gravitational field of the other object the gravitational force will act on it. The gravitation force also creates a gravitation acceleration that is given by:

$$
begin{align*}
g&=Gcdotfrac{m_e}{r^2}
end{align*}
$$

where the $G$ stands for universal gravitation constant, $m_e$ is mass of earth and the $r$ is a distance from the Earth center in which we compute gravitational field.

So, if the mass of Earth is doubled but the radius stays the same:

$$
begin{align*}
g_2&=Gcdotfrac{2cdot{m_e}}{r^2}\
g_2&=2cdot{G}cdotfrac{{m_e}}{r^2}\
g_2&=2cdot{g}
end{align*}
$$

$$
boxed{text{If the mass of the Earth is doubled, the gravitational field will double also.}}
$$

The gravitational acceleration, g, is independent of the ball’s mass ans it is:

$g = dfrac{G m_E}{R_E^2}$

Where G is universal constant, $m_E$ is the mass of Earth an $r_E$ is the radius of Earth.

As we know, there is a lot of satellite around the Jupiter, so we can implement Kepler’s Third law on a motion of a satellite around the Jupiter. The time period of Jupiter satellite rotation is given by:

$$
begin{align*}
T&=2cdotpisqrtfrac{r^3}{Gcdot{m_J}}
end{align*}
$$

Where the $r$ stands for the radius of orbit of Jupiter satellite, $G$ is universal gravitational constant and $m_J$ is the mass of Jupiter.

Let’s express the mass of Jupiter from the upper equation:

$$
begin{align*}
sqrtfrac{r^3}{Gcdot{m_J}}&=frac{T}{2cdotpi}\
frac{r^3}{Gcdot{m_J}}&=frac{T^2}{4cdotpi^2}\
Gcdot{m_J}&=frac{r^3cdot{4cdotpi^2}}{T^2}\
m_j&=frac{4cdotpi^2cdot{r^3}}{Gcdot{T^2}}
end{align*}
$$

As the $G$ is the constant, we need to know the radius of Jupiter’s satellite orbit and the period of orbits.

The mass of the planets can be calculated by using the Kepler’s Third Law:

$$
begin{align*}
T&=2cdotpisqrtfrac{r^3}{Gcdot{m}}
end{align*}
$$

Where the $r$ stands for the radius of orbit of planet satellite, $G$ is universal gravitational constant and $m$ is the mass of planet.

Let’s express the mass of planet from the upper equation:

$$
begin{align*}
sqrtfrac{r^3}{Gcdot{m}}&=frac{T}{2cdotpi}\
frac{r^3}{Gcdot{m}}&=frac{T^2}{4cdotpi^2}\
Gcdot{m}&=frac{r^3cdot{4cdotpi^2}}{T^2}\
m&=frac{4cdotpi^2cdot{r^3}}{Gcdot{T^2}}
end{align*}
$$

So there is no other way to get the mass of Pluto before discovering its satellite because we can’t implement the equation.

The gravitational force between two massive objects is defined by the equation:

$$
begin{align*}
F&=Gcdotfrac{m_1cdot{m_2}}{r^2}
end{align*}
$$

So we can conclude that the magnitude of the gravitational force between the Moon and Earth is the same. But the forces act in opposite directions.

$$
boxed{overrightarrow{F_E}=-overrightarrow{F_M}}
$$

$$
overrightarrow{F_E}=-overrightarrow{F_M}
$$

The $G$ is the universal gravitational constant and the value is get by a Cavendish experiment in order to make a relation between the force of attraction, masses of the objects, and the square of the distance between them.

$$
begin{align*}
F&=Gcdotfrac{m_1cdot{m_2}}{r^2}
end{align*}
$$

So, as the $G$ represents the constant value, it stays unchanged if we change any parameter in the equation.

$$
G=text{const.}
$$

According to the equation $v=sqrt{dfrac{G m_E}{r}}$, the orbiting speed is inversely proportional to $sqrt{r}$, thus a satellite with a smaller orbital radius have the greater velocity.

According to the equation $T = 2 pi sqrt{dfrac{r^3}{G m_E}}$, a shuttle with a higher orbit, have a longer period.

According to the equation $T = 2 pi sqrt{dfrac{r^3}{G m}}$, orbiting around a planet with a greater mass, Earth, has a smaller period.

The gravitational acceleration is:

$g = dfrac{G m}{r^2}$

The ratio of the gravitational accelerations is:

$dfrac{g_J}{g_E} = (dfrac{m_J}{m_E}) (dfrac{r_E}{r_J})^2$

$dfrac{g_J}{g_E} = (dfrac{300}{1}) (dfrac{1}{10})^2$

$dfrac{g_J}{g_E} = 3.0$

Thus:

$$
g_J = 3.00 g_E = (3.00) (9.80) = 29.4 m/s^2
$$

$$
29.4 m/s^2
$$

The gravitational acceleration is:

$g = dfrac{G m}{r^2}$

The ratio of the gravitational accelerations is:

$dfrac{g_r}{g_E} = (dfrac{r_E}{r})^2$

(Where $g_r$ is the gravitational acceleration at one Earth radius above the surface of Earth)

$dfrac{g_r}{g_E} = (dfrac{1}{2})^2$

$dfrac{g_r}{g_E} = 0.25$

Thus:

$$
g_r = (0.25) (9.8) = 2.45 m/s^2
$$

$$
2.45 m/s^2
$$

The force is proportional to the mass:

$F = m g$

Thus the force will be doubled.

By Kepler’s Third Law, the velocity of the satellite has to be:

$$
begin{align*}
v&=sqrt{Gcdotfrac{m_e}{r}}
end{align*}
$$

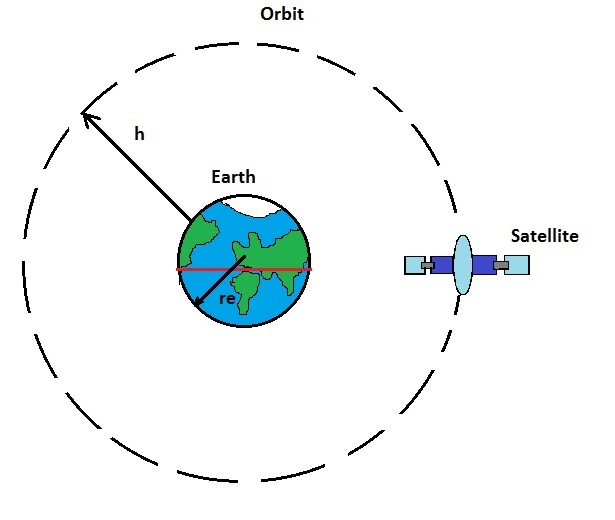
Where the $r$ is the radius of the orbit, from the center of the Earth.
From the equation, we can see that if the satellite moves closer to the Earth, the velocity of the satellite has to be increased to have the satellite in the same position every day.

If the height of the satellite is increased, the speed of the satellite has to be decreased in order to keep the same position.

The orbital period of Earth is $1 text{year}$ and it’s given by the equation:

$$
begin{align*}
T_E&=2cdotpicdotsqrt{frac{r^3_E}{Gcdot{m_S}}}
end{align*}
$$

In case of Jupiter the relation will be:

$$
begin{align*}
T_J&=2cdotpicdotsqrt{frac{r^3_J}{Gcdot{m_S}}}\
T_J&=2cdotpicdotsqrt{frac{left(5.2cdot{r_E}right)^3}{Gcdot{m_S}}}\
T_J&=2cdotpicdotsqrt{frac{left(5.2right)^3cdot{r_E^3}}{Gcdot{m_S}}}\
T_J&=sqrt{(5.2)^3}cdot{2}cdotpicdotsqrt{frac{{r_E^3}}{Gcdot{m_S}}}\
T_J&=sqrt{(5.2)^3}cdot{T_E}\
T_J&=sqrt{(5.2)^3}cdot{1 text{ year}}
end{align*}
$$

$$
boxed{T_J=11.86text{ year}}
$$

$$
T_J=11.86text{ year}
$$

$F = dfrac{G m_1 m_2}{r^2}$

$F = dfrac{(6.67e-11)*(5.9)*(0.047)}{(0.055)^2}$

$$
F = 6.11 times 10^{-9} N
$$

$$
6.11 times 10^{-9} N
$$

The force of attraction between the Sun and Jupiter can be computed, by the equation:

$$
begin{align*}
F&=Gcdotfrac{m_Scdot{m_J}}{r^2}
end{align*}
$$

Where the $G$ stands for the universal gravitational constant, $m_S$ and $m_J$ are the mass of the Sun and Jupiter and $r$ is the distance between them. So let’s take this data from the table and substitute it.

$$
begin{align*}
m_S&=1.99cdot{10^{30}}text{ kg}\
m_J&=1.9cdot{10^{27}}text{ kg}\
r&=7.78cdot{10^{11}}text{ m}\
F&=6.67cdot{10^{-11}} frac{text{N}cdottext{m}^2}{text{kg}^2}cdotfrac{1.99cdot{10^{30}}text{ kg}cdot{1.9cdot{10^{27}}text{ kg}}}{left(7.78cdot{10^{11}}text{ m}right)^2}
end{align*}
$$

$$
boxed{F=4.17cdot{10^{23}}text{ N}}
$$

$$
F=4.17cdot{10^{23}}text{ N}
$$

The force of attraction between Tom and Sally can be computed, by the equation:

$$
begin{align*}
F&=Gcdotfrac{m_Scdot{m_T}}{r^2}
end{align*}
$$

Where the $G$ stands for the universal gravitational constant, $m_S$ and $m_T$ are the mass of the Sally and Tom and $r$ is the distance between them. So let’s substitute given data.

$$
begin{align*}
m_S&=50text{ kg}\
m_T&=70text{ kg}\
r&=20text{ m}\
F&=6.67cdot{10^{-11}} frac{text{N}cdottext{m}^2}{text{kg}^2}cdotfrac{50text{ kg}cdot{70text{ kg}}}{left(20text{ m}right)^2}
end{align*}
$$

$$
boxed{F=5.84cdot{10^{-10}}text{ N}}
$$

$$
F=5.84cdot{10^{-10}}text{ N}
$$

The force of attraction between the two balls can be computed, by the equation:

$$
begin{align*}
F&=Gcdotfrac{m_1cdot{m_2}}{r^2}
end{align*}
$$

Where the $G$ stands for the universal gravitational constant, $m_1$ and $m_2$ are the mass of two balls and $r$ is the distance between them. So let’s substitute given data.

$$
begin{align*}
m_1&=8text{ kg}\
m_2&=6text{ kg}\
r&=2text{ m}\
F&=6.67cdot{10^{-11}} frac{text{N}cdottext{m}^2}{text{kg}^2}cdotfrac{8text{ kg}cdot{6text{ kg}}}{left(2text{ m}right)^2}
end{align*}
$$

$$
boxed{F=8cdot{10^{-10}}text{ N}}
$$

$$
F=8cdot{10^{-10}}text{ N}
$$

The force of attraction between the two bowling balls can be computed, by the equation:

$$
begin{align*}
F&=Gcdotfrac{m_1cdot{m_2}}{r^2}
end{align*}
$$

Where the $G$ stands for the universal gravitational constant, $m_1$ and $m_2$ are the mass of two balls and $r$ is the distance between them. So let’s substitute given data.

$$
begin{align*}
m_1&=6.8text{ kg}\
m_2&=6.8text{ kg}\
r&=0.218text{ m}\
F&=6.67cdot{10^{-11}} frac{text{N}cdottext{m}^2}{text{kg}^2}cdotfrac{6.8text{ kg}cdot{6.8text{ kg}}}{left(0.218text{ m}right)^2}
end{align*}
$$

$$
boxed{F=6.49cdot{10^{-8}}text{ N}}
$$

$$
F=6.49cdot{10^{-8}}text{ N}
$$

$bold{a)}$

The force of attraction between us and the Earth can be computed, by the equation:

$$
begin{align*}
F&=Gcdotfrac{mcdot{m_E}}{r^2}
end{align*}
$$

Where the $G$ stands for the universal gravitational constant, $m$ and $m_E$ are the mass of us and the Earth and $r$ is the distance between them. So let’s substitute given data.

$$
begin{align*}
m&=50text{ kg}\
m_2&=5.97cdot{10^{24}}text{ kg}\
r&=6.38cdot{10^6}text{ m}\
F&=6.67cdot{10^{-11}} frac{text{N}cdottext{m}^2}{text{kg}^2}cdotfrac{50text{ kg}cdot{5.97cdot{10^{24}}text{ kg}}}{left(6.38cdot{10^6}text{ m}right)^2}
end{align*}
$$

$$
boxed{F=489text{ N}}
$$

$bold{b)}$

The weight of us at the surface of the Earth is given by:

$$
begin{align*}
W&=mcdot{g}
end{align*}
$$

where the $g$ stands for the gravitational acceleration on the Earth’s surface. Let’s compute the weight:

$$
begin{align*}
W&=50text{ kg}cdot{9.81 frac{text{ m}}{text{s}^2}}
end{align*}
$$

$$
boxed{W=490.5text{ N}}
$$

a) $F=489text{ N}$

b) $W=490.5text{ N}$

The force of attraction between two electrons can be computed, by the equation:

$$
begin{align*}
F&=Gcdotfrac{m_ecdot{m_e}}{r^2}\
F&=Gcdotfrac{m^2_e}{r^2}
end{align*}
$$

Where the $G$ stands for the universal gravitational constant, $m_e$ is the mass of electron and $r$ is the distance between them. Let’s express the mass of electron from the equation:

$$
begin{align*}
Gcdot{m^2_e}&=Fcdot{r^2}\
m^2_e&=frac{Fcdot{r^2}}{G}\
m_e&=sqrt{frac{Fcdot{r^2}}{G}}
end{align*}
$$

Let’s substitute the given data and compute the mass of electron:

$$
begin{align*}
F&=5.54cdot{10^{-71}}text{ N}\
r&=1text{ m}\
m_e&=sqrt{frac{5.54cdot{10^{-71}}text{ N}cdot{(1text{ m})^2}}{6.67cdot{10^{-11}} frac{text{ N}cdottext{m}^2}{text{ kg}^2}}}
end{align*}
$$

$$
boxed{m_e=9.11cdot{10^{-31}}text{ kg}}
$$

$$
m_e=9.11cdot{10^{-31}}text{ kg}
$$

$bold{a)}$

The force of attraction by the Earth to a body is given by the equation:

$$
begin{align*}
F&=Gcdotfrac{mcdot{m_E}}{r^2}
end{align*}
$$

Where the $G$ stands for the universal gravitational constant, $m_E$ is the mass of the Earth, $m$ is the mass of the body and $r$ is the distance between them. Let’s express the mass of Earth from the equation:

$$
begin{align*}
Gcdot{mcdot{m_E}}&=Fcdot{r^2}\
m_E&=frac{Fcdot{r^2}}{Gcdot{m}}
end{align*}
$$

Let’s substitute the given data and compute the mass of electron:

$$
begin{align*}
F&=9.8text{ N}\
r&=6.4cdot{10^6}text{ m}\
m&=1text{ kg}\
m_E&=frac{9.8text{ N}cdot{left(6.4cdot{10^6}text{ m}right)^2}}{6.67cdot{10^{-11}} frac{text{N}cdottext{m}^2}{text{kg}^2}cdot{1text{ kg}}}
end{align*}
$$

$$
boxed{m_E=60.18cdot{10^{23}}text{ kg}}
$$

$bold{b)}$

The density of the Earth is given by the equation:

$$
begin{align*}
rho&=frac{m_E}{V_E}
end{align*}
$$

The Earth is a ball, so the Earth volume is:

$$
begin{align*}
V_E&=frac{4}{3}cdot{r^3}cdotpi
end{align*}
$$

Let’s substitute and compute:

$$
begin{align*}
rho&=frac{m_E}{frac{4}{3}cdot{r^3}cdotpi}\
rho&=frac{3cdot{m_E}}{4cdot{r^3}cdotpi}\
rho&=frac{3cdot{60.18cdot{10^{23}}text{ kg}}}{4cdot{left(6.4cdot{10^6}text{ m}right)^3}cdotpi}
end{align*}
$$

$$
boxed{rho=5480 frac{text{kg}}{text{m}^3}}
$$

a) $m_E=60.18cdot{10^{23}}text{ kg}$

b) $rho=5480 frac{text{kg}}{text{m}^3}$

The Kepler Third law gives a relation between the radius of orbit and the period of orbiting of two planets that orbit around the same star. It’s given by the equation:

$$
begin{align*}
left(frac{r_A}{r_B}right)^3&=left(frac{T_A}{T_B}right)^2
end{align*}
$$

If we implement this Law to Earth and Uranus, we get:

$$
begin{align*}
left(frac{r_e}{r_u}right)^3&=left(frac{T_e}{T_u}right)^2\
frac{r^3_e}{r^3_u}&=frac{T^2_e}{T^2_u}
end{align*}
$$

We have to compute Uranus orbital radius so let’s express it:

$$
begin{align*}
r^3_u&=r^3_ecdotfrac{T^2_u}{T^2_e}\
r_u&=r_ecdotsqrtfrac{T^2_u}{T^2_e}
end{align*}
$$

Uranus needs an $84text{ year}$ to circle the Sun, the period of orbit for the Earth is $1text{ year}$. Let’s substitute:

$$
begin{align*}
r_u&=r_ecdotsqrt[3]{frac{left(84text{ year}right)^2}{left(1text{ year}right)^2}}
end{align*}
$$

$$
boxed{r_u=19.2cdot{r_e}}
$$

$$
r_u=19.2cdot{r_e}
$$

The Kepler Third law gives a relation between the radius of orbit and the period of orbiting of two planets that orbit around the same star. It’s given by the equation:

$$
begin{align*}
left(frac{r_A}{r_B}right)^3&=left(frac{T_A}{T_B}right)^2
end{align*}
$$

If we implement this Law to Earth and Venus, we get:

$$
begin{align*}
left(frac{r_e}{r_v}right)^3&=left(frac{T_e}{T_v}right)^2\
frac{r^3_e}{r^3_v}&=frac{T^2_e}{T^2_v}
end{align*}
$$

We have to compute Venus orbital radius so let’s express it:

$$
begin{align*}
r^3_v&=r^3_ecdotfrac{T^2_v}{T^2_e}\
r_v&=r_ecdotsqrtfrac{T^2_v}{T^2_e}
end{align*}
$$

Venus needs an $225text{ days}$ to circle the Sun, the period of orbit for the Earth is $365text{ days}$. Let’s substitute:

$$
begin{align*}
r_v&=r_ecdotsqrt[3]{frac{left(225text{ days}right)^2}{left(365text{ days}right)^2}}
end{align*}
$$

$$
boxed{r_v=0.724cdot{r_e}}
$$

$$
r_v=0.724cdot{r_e}
$$

The Kepler Third law gives a relation between the radius of orbit and the period of orbiting of two planets that orbit around the same star. It’s given by the equation:

$$
begin{align*}
left(frac{r_A}{r_B}right)^3&=left(frac{T_A}{T_B}right)^2
end{align*}
$$

If we implement this Law to Earth and planet D, we get:

$$
begin{align*}
left(frac{r_E}{r_D}right)^3&=left(frac{T_E}{T_Dv}right)^2\
frac{r^3_E}{r^3_D}&=frac{T^2_E}{T^2_D}
end{align*}
$$

We have to compute planet D orbital period so let’s express it:

$$
begin{align*}
T^2_D&=T^2_Ecdotfrac{r^3_D}{r^3_E}\
T_D&=T_Ecdotsqrt{frac{r^3_D}{r^3_E}}
end{align*}
$$

We have given that $r_D=8cdot{r_E}$, lets substitute:

$$
begin{align*}
T_D&=1text{ year}cdotsqrt{left(frac{8cdot{r_E}}{r_E}right)^3}\
T_D&=1text{ year}cdotsqrt{8^3}
end{align*}
$$

$$
boxed{T_D=22.63text{ years}}
$$

$$
T_D=22.63text{ years}
$$

The force of attraction between two spheres is given by the equation:

$$
begin{align*}
F&=Gcdotfrac{m_1cdot{m_2}}{r^2}
end{align*}
$$

Where the $G$ stands for the universal gravitational constant, $m_1$ and $m_2$ is the mass of the spheres,$r$ is the distance between them.
Also, we have given relation:

$$
begin{align*}
m_1&=2cdot{m_2}
end{align*}
$$

Let’s substitute and express the mass of sphere $m_2$ from the equation:

$$
begin{align*}
Gcdot{2cdot{m_2}cdot{m_2}}&=Fcdot{r^2}\
(m_2)^2&=frac{Fcdot{r^2}}{2cdot{G}}\
m_2&=sqrt{frac{Fcdot{r^2}}{2cdot{G}}}
end{align*}
$$

Let’s substitute the given data and compute the mass of sphere $m_2$:

$$
begin{align*}
F&=2.75cdot{10^{-12}}text{ N}\
r&=2.6text{ m}\
m_2&=sqrtfrac{2.75cdot{10^{-12}}text{ N}cdot{left(2.6text{ m}right)^2}}{2cdot{6.67}cdot{10^{-11}} frac{text{N}cdottext{m}^2}{text{kg}^2}}
end{align*}
$$

$$
boxed{m_2=0.375text{ kg}}
$$

Let’s return for $m_1$:

$$
begin{align*}
m_1&=2cdot{m_2}\
m_1&=2cdot{0.375text{ kg}}
end{align*}
$$

$$
boxed{m_1=0.750text{ kg}}
$$

$m_1=0.750text{ kg}$ and $m_2=0.375text{ kg}$.

We have given the distance between the Moon center toward the Sun center $r_S=1.5cdot{10^8}text{ km}$, and the distance from the Moon to the Earth $r_E=3.9cdot{10^5}text{ km}$. And we have given the masses of the Earth, the Sun, and the Moon. Our target is to compute the ratio of the gravitational force exerted to the Moon by the Earth and the Sun.

To find the ratio, we have to compute the individual gravitational force between the Moon and the Earth and the Moon and the Sun and divide values.

By the universal gravitational law, we know:

$$
begin{align*}
F_g&=Gcdotfrac{m_1cdot{m_2}}{r^2}
end{align*}
$$

Where $G$ stands for the universal gravitational constant, $m_1$ is the mass of the one object, $m_2$ the mass of the second object, and $r$ represents the distance between them.

Let’s implement the universal gravitational law, and compute the gravitational force between the Earth and the Moon.

$$
begin{align*}
F_{EM}&=Gcdotfrac{m_Ecdot{m_M}}{r_{EM}^2}
end{align*}
$$

Here we have given the universal gravitational constant is:

$$
begin{align*}
G&=6.67cdot{10^{-11}} frac{text{N}cdottext{m}^2}{text{kg}}
end{align*}
$$

Masses of the Earth and the Moon are:

$$
begin{align*}
m_E&=6cdot{10^{24}} text{kg}\
m_M&=7.3cdot{10^{22}} text{kg}
end{align*}
$$

And the distance between them is:

$$
begin{align*}
r_{EM}&=3.9cdot{10^5} text{ km}
end{align*}
$$

Let’s substitute and compute:

$$
begin{align*}
F_{EM}&=Gcdotfrac{m_Ecdot{m_M}}{r_{EM}^2}\
F_{EM}&=6.67cdot{10^{-11}} frac{text{N}cdottext{m}^2}{text{kg}}cdotfrac{6cdot{10^{24}} text{kg}cdot{7.3cdot{10^{22}} text{kg}}}{left(3.9cdot{10^5}cdot{10^3} text{ m}right)^2}\
F_{EM}&=1.92cdot{10^{20}}text{ N}
end{align*}
$$

In the same way we can compute the gravitational force between the Moon and the Sun.

$$
begin{align*}
F_{SM}&=Gcdotfrac{m_Scdot{m_M}}{r_{SM}^2}\
F_{SM}&=6.67cdot{10^{-11}} frac{text{N}cdottext{m}^2}{text{kg}}cdotfrac{2cdot{10^{30}} text{kg}cdot{7.3cdot{10^{22}} text{kg}}}{left(1.5cdot{10^8}cdot{10^3} text{ m}right)^2}\
F_{SM}&=4.33cdot{10^{20}}text{ N}
end{align*}
$$

To find the ratio between the force on the Moon exerted by the Earth and the Sun, we have to divide the magnitudes of the forces:

$$
begin{align*}
frac{F_{EM}}{F_{SM}}&=frac{1.92cdot{10^{20}}text{ N}}{4.33cdot{10^{20}}text{ N}}
end{align*}
$$

$$
boxed{frac{F_{EM}}{F_{SM}}=0.44}
$$

$$
frac{F_{EM}}{F_{SM}}=0.44
$$

The boat moves with the constant speed when the external force of $F=40text{ N}$ was exerted. This means that the frictional force between the boat and the surface and the external force of $F=40text{ N}$ on the Earth is the same magnitude. The magnitude of the friction force and the externally applied force on Jupiter have to be also the same magnitude in order to have a constant velocity.

The force of friction between the boat and the glass surface is given by the equation:

$$
begin{align*}
F=f=mucdot{F_N}
end{align*}
$$

where the $mu$ represents the constant of friction, $m_b$ is the mass of a boat, and the $g$ is gravitational constant that is different on an Earth and the Jupiter.

The normal component of gravitational force is explained by Newton’s universal gravitational law:

$$
begin{align*}
F_N&=Gcdotfrac{{m_p}cdot{m_b}}{r_p^2}
end{align*}
$$

Where the $G$ is universal gravitational constant, $m_p$ and $m_b$ stands for the mass of the planet and the boat, and $r_p$ is the distance between the boat center of mass and the planet center of mass, in that case, this is the radius of the planet.

The externally applied force $F$ on the boat at the Earth, can be written as:

$$
begin{align*}
F&=mucdot{F_N}\
F&=mucdot{G}cdotfrac{m_ecdot{m_b}}{r_e^2}
end{align*}
$$

And the force that has to be applied on the boat at Jupiter will be:

$$
begin{align*}
F_j&=mucdot{G}cdotfrac{m_jcdot{m_b}}{r_j^2}
end{align*}
$$

In this equation, all the data can be found as table values except the coefficient of friction, but it can be expressed from the equation from the upper equation.

$$
begin{align*}
mu&=frac{F}{{G}cdotfrac{m_ecdot{m_b}}{r_e^2}}\
mu&=frac{Fcdot{r_e^2}}{Gcdot{m_ecdot{m_b}}}
end{align*}
$$

And now can be substituted in an equation for the force needed on Jupiter.

$$
begin{align*}
F_j&=frac{Fcdot{r_e^2}}{Gcdot{m_ecdot{m_b}}}cdot{G}cdotfrac{m_jcdot{m_b}}{r_j^2}\
F_j&=frac{Fcdot{r_e^2}}{{m_e}}cdotfrac{m_j}{r_j^2}\
F_j&=Fcdotfrac{r_e^2cdot{m_j}}{r_j^2cdot{m_e}}
end{align*}
$$

From the table $7-1$ we can found all needed data:

$$
begin{align*}
m_e&=5.98cdot{10^{24}}text{ kg}\
m_j&=1.9cdot{10^{27}}text{ kg}\
r_e&=6.38cdot{10^6}text{ m}\
r_j&=7.15cdot{10^7}text{ m}
end{align*}
$$

So let’s compute the force needed:

$$
begin{align*}
F_j&=Fcdotfrac{r_e^2cdot{m_j}}{r_j^2cdot{m_e}}\
F_j&=40text{ N}cdotfrac{left(6.38cdot{10^6}text{ m}right)^2cdot{1.9cdot{10^{27}}text{ kg}}}{left(7.15cdot{10^7}text{ m}right)^2cdot{5.98cdot{10^{24}}text{ kg}}}
end{align*}
$$

$$
boxed{F_j=101.2text{ N}}
$$

$$
F_j=101.2text{ N}
$$

Kepler’s Third Law gives us a relation between the satellite period of orbit around a planet, the radius of the orbit, and the mass of the planet. The relation is given as:

$$
begin{align*}
T&=2cdotpicdotsqrt{frac{r^3}{Gcdot{m}}}
end{align*}
$$

Where $T$ stands for the period of the orbit, $r$ is the radius of the satellite orbit, $G$ is the universal gravitational constant, and $m$ is the mass of the planet (in our case mass of the Saturn).

We have given:

$$
begin{align*}
r&=1.87cdot{10^8}text{ m}\
T&=23text{ days}=23text{ days}cdot{3600} frac{text{s}}{text{h}}=8.28cdot{10^4}text{ s}
end{align*}
$$

Let fix the upper equation in order to express the mass of the Saturn.

$$
begin{align*}
T&=2cdotpicdotsqrt{frac{r^3}{Gcdot{m}}}\
T^2&=4cdotpi^2cdotfrac{r^3}{Gcdot{m}}\
m&=frac{4cdotpi^2cdot{r}^3}{Gcdot{T^2}}
end{align*}
$$

Let’s substitute data and compute the result:

$$
begin{align*}
m&=frac{4cdotpi^2cdot{r}^3}{Gcdot{T^2}}\
m&=frac{4cdotpi^2cdot{left(1.87cdot{10^8}text{ m}right)}^3}{6.67cdot{10^{-11}} frac{text{ N}cdottext{m}^2}{text{kg}}cdot{left(8.28cdot{10^4}text{ s}right)^2}}
end{align*}
$$

$$
boxed{m=5.65cdot{10^{26}}text{ kg}}
$$

$$
m=5.65cdot{10^{26}}text{ kg}
$$

Kepler’s Third Law gives us a relation between the Moon period of orbit around a planet, the radius of the orbit, and the mass of the planet. The relation is given as:

$$
begin{align*}
T&=2cdotpicdotsqrt{frac{r^3}{Gcdot{m}}}
end{align*}
$$

Where $T$ stands for the period of the orbit, $r$ is the radius of the Moon orbit, $G$ is the universal gravitational constant, and $m$ is the mass of the planet (in our case mass of the Earth).

We have given:

$$
begin{align*}
r&=3.9cdot{10^8}text{ m}\
T&=27.33text{ days}=27.33text{ days}cdot{24 frac{text{h}}{text{days}}}cdot{3600} frac{text{s}}{text{h}}=2.36cdot{10^6}text{ s}
end{align*}
$$

Let fix the upper equation in order to express the mass of the Earth.

$$
begin{align*}
T&=2cdotpicdotsqrt{frac{r^3}{Gcdot{m}}}\
T^2&=4cdotpi^2cdotfrac{r^3}{Gcdot{m}}\
m&=frac{4cdotpi^2cdot{r}^3}{Gcdot{T^2}}
end{align*}
$$

Let’s substitute data and compute the result:

$$
begin{align*}
m&=frac{4cdotpi^2cdot{r}^3}{Gcdot{T^2}}\
m&=frac{4cdotpi^2cdot{left(3.9cdot{10^8}text{ m}right)}^3}{6.67cdot{10^{-11}} frac{text{ N}cdottext{m}^2}{text{kg}}cdot{left(2.36cdot{10^6}text{ s}right)^2}}
end{align*}
$$

$$
boxed{m=6.3cdot{10^{24}}text{ kg}}
$$

In the problem $60$ we compute that the mass of the Earth is $m_2=6.02cdot{10^{24}}text{ kg}$, so let’s compare results:

$$
begin{align*}
delta&=frac{m-m_1}{m}cdot{100%}\
delta&=frac{6.3cdot{10^{24}}text{ kg}-6.02cdot{10^{24}}text{ kg}}{6.3cdot{10^{24}}text{ kg}}cdot{100%}\
delta&=4.44%
end{align*}
$$

The difference in results is $4.44%$.

$$
m=6.3cdot{10^{24}}text{ kg}
$$

$textbf{Given.}$ We know that for Earth, the average distance $r$ is $1 ,mathrm{AU}$ which will be denoted as $r_b$ and its period of revolution is $T = 1.0 ,mathrm{y}$ which will be denoted as $T_b$. For Halley’s Comet, its period $T = 74,mathrm{y}$ which will be denoted as $T_a$
Given the equation:

$$
begin{equation}
left(frac{r_a}{r_b} right)^3 = left(frac{T_a}{T_b} right)^2
end{equation}
$$

We isolate $r_a$ to get the average distance of Halley’s Comet.

$$
begin{align*}
r_{a}^{3} &= r_{b}^3 left(frac{T_a}{T_b} right)^2\
r_a &= sqrt[3]{r_{b}^3 left(frac{T_a}{T_b} right)^2}
end{align*}
$$

After isolating $r_a$, we can plug-in the given values and obtain the value for $r_a$.

$$
begin{align*}
r_a &= sqrt[3]{(1.0,mathrm{AU})^3 left(frac{74 ,mathrm{y}}{1.0,mathrm{y}} right)^2}\
&= boxed{18,mathrm{AU}}
end{align*}
$$

$$
r_a = 18 ,mathrm{AU}
$$

$bold{a)}$
We know that the Earth’s revolution orbit is elliptical, but let’s assume that it has a circular trajectory. So, for one complete rotation, the Earth swept out the area that is equal to an area of a circle with the radius that represents the distance between the Sun and the Earth.

Let’s mark the speed of area swept out by the letter $x$. The speed of swept out will be:

$$
begin{align*}
x&=frac{A}{T}
end{align*}
$$

where the $A$ represents the area swept out by the Earth in one revolution around the Sun, and $T$ stands for the period of rotation around the Sun.

From the table $7-1$ we have that the distance between the Sun and the Earth that represent the radius of a circle described during the Earth rotation is:

$$
begin{align*}
r&=1.5cdot{10^{11}}text{ m}
end{align*}
$$

And the period of rotation is equal to:

$$
begin{align*}
T&=365.25text{ days}cdot{24 frac{text{h}}{text{days}}}cdot{3600 frac{text{s}}{text{h}}}=3.156cdot{10^7}text{ s}
end{align*}
$$

As we know the area of the circle is:

$$
begin{align*}
A&=r^2cdotpi
end{align*}
$$

Let’s substitute and compute:

$$
begin{align*}
x&=frac{A}{T}\
x&=frac{r^2cdotpi}{T}\
x&=frac{left(1.5cdot{10^{11}}text{ m}right)^2cdotpi}{3.156cdot{10^7}text{ s}}
end{align*}
$$

$$
boxed{x=2.24cdot{10^{15}} frac{text{m}^2}{text{s}}}
$$

$bold{b)}$

The speed of area swept out by the Moon during the rotation around the Earth has to be computed in the same way.

We have given:

$$
begin{align*}
r&=3.9cdot{10^8}text{ m}\
T&=27.33text{ days}cdot{24 frac{text{h}}{text{days}}}cdot{3600 frac{text{s}}{text{h}}}=2.36cdot{10^6}text{ s}
end{align*}
$$

Let’s substitute and compute the speed of area swept out by the Moon:

$$
begin{align*}
x&=frac{A}{T}\
x&=frac{r^2cdotpi}{T}\
x&=frac{left(3.9cdot{10^{8}}text{ m}right)^2cdotpi}{2.36cdot{10^6}text{ s}}
end{align*}
$$

$$
boxed{x=20.25cdot{10^{10}} frac{text{m}^2}{text{s}}}
$$

a) $x=2.24cdot{10^{15}} frac{text{m}^2}{text{s}}$.

b) $x=20.25cdot{10^{10}} frac{text{m}^2}{text{s}}$.

$bold{a)}$ The satellite orbiting the Earth over a circular trajectory with a constant velocity witch depends of the orbit radius and it is given by the equation:

$$
begin{align*}
v&=sqrtfrac{Gcdot{m_e}}{r}
end{align*}
$$

Where the $G$ stands for the universal gravitational constant, $m_e$ is the mass of the Earth, and $r$ stands for the radius of the orbit.

From the table $7-1$ we can find the mass of the Earth
$m_e=5.98cdot{10^{24}}text{ kg}$.

In our question, we also have given the radius of the orbit $r=4.23cdot{10^7}text{ kg}$.

So let’s substitute and compute the velocity of the satellite:

$$
begin{align*}
v&=sqrtfrac{Gcdot{m_e}}{r}\
v&=sqrtfrac{6.67cdot{10^{-11}} frac{text{N}cdottext{m}^2}{text{kg}^2}cdot{5.98cdot{10^{24}}text{ kg}}}{4.23cdot{10^7}text{ m}}
end{align*}
$$

$$
boxed{v=3070 frac{text{m}}{text{s}}}
$$

$bold{b)}$ The period of the satellite that orbiting the Earth is given with the equation:

$$
begin{align*}
T&=2cdotpicdotsqrtfrac{r^3}{Gcdot{m_e}}
end{align*}
$$

The $r$ stands for the radius of the orbit, $G$ is the universal gravitational constant, and $m_e$ represents the mass of the Earth.

We have all known, so let’s substitute and compute the period of orbit.

$$
begin{align*}
T&=2cdotpicdotsqrtfrac{r^3}{Gcdot{m_e}}\
T&=2cdotpicdotsqrtfrac{left(4.23cdot{10^{7}}text{ m}right)^3}{6.67cdot{10^{-11}} frac{text{N}cdottext{m}^2}{text{kg}^2}cdot{5.98cdot{10^{24}}text{ kg}}}
end{align*}
$$

$$
boxed{T=8.66cdot{10^4}text{ s}}
$$

a) $v=3070 frac{text{m}}{text{s}}$

b) $T=8.66cdot{10^4}text{ s}$

$bold{a)}$ We have given:

$$
begin{align*}
r&=500text{ km}=5cdot{10^2}cdot{10^3}text{ m}=5cdot{10^5}text{ m}\
m_c&=7cdot{10^{20}}text{ kg}
end{align*}
$$

The acceleration due to gravity is given by the universal gravitational law and described by the equation:

$$
begin{align*}
g&=frac{Gcdot{m}}{r^2}
end{align*}
$$

where the $G$ stands for the universal gravitational constant, $m$ is the mass of the object that is the reason for the gravitation and $r$ is the distance from the object center of mass.

Let’s substitute and compute the acceleration due to a gravity:

$$
begin{align*}
g&=frac{Gcdot{m_c}}{r^2}\
g&=frac{6.67cdot{10^{-11}} frac{text{N}cdottext{m}^2}{text{kg}^2}cdot{7cdot{10^{20}}text{ kg}}}{left(5cdot{10^5}text{ m}right)^2}
end{align*}
$$

$$
boxed{g=0.187 frac{text{m}}{text{s}^2}}
$$

$bold{b)}$ The weight of the astronaut is equal to the magnitude of gravitational force that acting on an astronaut on the asteroid Ceres.

The magnitude of the gravitational force is equal to a product of the gravitational field and the mass of the object.

$$
begin{align*}
W&=mcdot{g}
end{align*}
$$

Let’s substiutute and compute:

$$
begin{align*}
W&=mcdot{g}\
W&=90text{ kg}cdot{0.187 frac{text{m}}{text{s}^2}}
end{align*}
$$

$$
boxed{W=16.83text{ N}}
$$

a) $g=0.187 frac{text{m}}{text{s}^2}$

b) $W=16.83text{ N}$

The weight of an object is equal to a product of gravitational field and object mass. Given by the equation, we have:

$$
begin{align*}
W&=gcdot{m}
end{align*}
$$

Where the $g$ stands for the acceleration due to a gravitational field, and $m$ is the mass of the object. Let’s express the gravitational field from the upper equation:

$$
begin{align*}
g&=frac{W}{m}
end{align*}
$$

Let’s substitute and compute the magnitude of gravitational field:

$$
begin{align*}
g&=frac{W}{m}\
g&=frac{8.35text{ N}}{1.25text{ kg}}
end{align*}
$$

$$
boxed{g=6.68 frac{text{m}}{text{s}^2}}
$$

$$
g=6.68 frac{text{m}}{text{s}^2}
$$

$bold{a)}$ We have given:

$$
begin{align*}
m_M&=7.34cdot{10^{22}}text{ kg}\
m_E&=5.97cdot{10^{24}}text{ kg}\
r&=3.8cdot{10^8}text{ m}
end{align*}
$$

By the law of universal gravitation, the attraction force between two objects is directly proportional to a product of their masses and universal gravitational constant, and reversible proportional to a square of the distance between them. Given by the equation:

$$
begin{align*}
F&=Gcdotfrac{m_1cdot{m_2}}{r^2}
end{align*}
$$

Where the $m_1$ and $m_2$ stand for the object masses, $G$ is the universal gravitational constant, and $r$ represents the distance between objects center of mass.

If we implement this equation to our problem, we get the next equation:

$$
begin{align*}
F&=Gcdotfrac{m_Ecdot{m_M}}{r^2}
end{align*}
$$

Let’s substitute and compute:

$$
begin{align*}
F&=6.67cdot{10^{-11}} frac{text{N}cdottext{m}^2}{text{kg}^2}cdotfrac{5.97cdot{10^{24}}text{ kg}cdot{7.34cdot{10^{22}}text{ kg}}}{left(3.8cdot{10^8}text{ m}right)^2}
end{align*}
$$

$$
boxed{F=20.24cdot{10^{19}}text{ N}}
$$

$bold{b)}$ The gravitational field at any point from the massive object is given by the equation:

$$
begin{align*}
g&=Gcdotfrac{m}{r^2}
end{align*}
$$

where the $G$ stands for the universal gravitational constant, $m$ is the mass of the object and $r$ represents the distance from the object.

So in our case, the gravitational field of Earth at the Moon will be:

$$
begin{align*}
g&=Gcdotfrac{m_E}{r^2}\
g&=6.67cdot{10^{-11}} frac{text{N}cdottext{m}^2}{text{kg}^2}cdotfrac{5.97cdot{10^{24}}text{ kg}}{left(3.8cdot{10^8}text{ m}right)^2}
end{align*}
$$

$$
boxed{g=2.76cdot{10^{-3}} frac{text{m}}{text{s}^2}}
$$

a) $F=20.24cdot{10^{19}}text{ N}$

b) $g=2.76cdot{10^{-3}} frac{text{m}}{text{s}^2}$

We have given:

$$
begin{align*}
m_1&=m_2=1text{ kg}\
r&=1text{ m}
end{align*}
$$

By the law of universal gravitation, the attraction force between two objects is directly proportional to a product of their masses and universal gravitational constant, and reversible proportional to a square of the distance between them. Given by the equation:

$$
begin{align*}
F&=Gcdotfrac{m_1cdot{m_2}}{r^2}
end{align*}
$$

Where the $m_1$ and $m_2$ stand for the object masses, $G$ is the universal gravitational constant, and $r$ represents the distance between objects center of mass.

Let’s substitute and compute the attraction force between objects:

$$
begin{align*}
F&=Gcdotfrac{m_1cdot{m_2}}{r^2}\
F&=6.67cdot{10^{-11}} frac{text{N}cdottext{m}^2}{text{kg}}cdotfrac{1text{kg}cdot{1text{kg}}}{left(1text{m}right)^2}
end{align*}
$$

$$
boxed{F=6.67cdot{10^{-11}}text{ N}}
$$

$$
F=6.67cdot{10^{-11}}text{ N}
$$

By the universal gravitational law, the weight of an object at some distance from the massive object is given as a product of the gravitational field at that point and the mass of the object.

$$
begin{align*}
W&=gcdot{m}
end{align*}
$$

Also, we have the equation for the gravitational field of the Earth at some point given by the relation:

$$
begin{align*}
g&=Gcdotfrac{m_E}{r^2}
end{align*}
$$

where the $G$ stands for the universal gravitational constant, $m_E$ is the mass of the Earth, and $r$ represents the distance from the Earth center.

As we know the weight of the spacecraft at the Earth’s surface, we can compute the mass of the spacecraft. Let’s substitute the second equation into the first one:

$$
begin{align*}
W&=gcdot{m}\
W&=Gcdotfrac{m_E}{r_E}cdot{m}\
W&=Gcdotfrac{m_Ecdot{m}}{r_E^2}
end{align*}
$$

Where the $G$ stands for the universal gravitational constant, $m_E$ and $m$ are the mass of the Earth and spacecraft, and the $r_E$ represents the radius of the Earth because this is the distance of the spacecraft from the Earth center.

The weight of the object distance from the Earth can be computed as:

$$
begin{align}
W&=Gcdotfrac{m_Ecdot{m}}{r^2}
end{align}
$$

Where the $r$ represents the distance from the Earth center.

Let’s express the mass of the spacecraft:

$$
begin{align*}
m&=frac{Wcdot{r_E^2}}{Gcdot{m_E}}
end{align*}
$$

Now, let’s substitute and compute the mass of the spacecraft:

$$
begin{align*}
m&=frac{Wcdot{r_E^2}}{Gcdot{m_E}}\
m&=frac{7.2cdot{10^3}text{ N}cdot{left(6.38cdot{10^6}text{ m}right)^2}}{6.67cdot{10^{-11}} frac{text{N}cdot{text{m}^2}}{text{kg}^2}cdot{5.98cdot{10^{24}}text{ kg}}}\
m&=734.8text{ kg}
end{align*}
$$

$bold{a)}$ We have given the height of the spacecraft from the Earth surface, but be aware this is not the distance from the Earth center of mass. The distance from the Earth center will be:

$$
begin{align*}
r&=r_E+h
end{align*}
$$

Let’s substitute all given into the first equation and compute the weight of spacecraft at height $h=6.38cdot{10^6}text{ m}$ from the Earth surface.

$$
begin{align*}
W&=Gcdotfrac{m_Ecdot{m}}{left(r_e+hright)^2}\
W&=6.67cdot{10^{-11}} frac{text{N}cdottext{m}^2}{text{kg}^2}cdotfrac{5.98cdot{10^{24}}text{ kg}cdot{734.8text{ kg}}}{left(6.38cdot{10^6}text{ m}+6.38cdot{10^6}text{ m}right)^2}
end{align*}
$$

$$
boxed{W=1800text{ N}}
$$

$$
bold{b)}
$$

Let’s do the same for the height of $h=1.28cdot{10^7}text{ m}$ above the Earth surface. Let’s substitute:

$$
begin{align*}
W&=Gcdotfrac{m_Ecdot{m}}{left(r_e+hright)^2}\
W&=6.67cdot{10^{-11}} frac{text{N}cdottext{m}^2}{text{kg}^2}cdotfrac{5.98cdot{10^{24}}text{ kg}cdot{734.8text{ kg}}}{left(6.38cdot{10^6}text{ m}+1.28cdot{10^7}text{ m}right)^2}
end{align*}
$$

$$
boxed{W=796.7text{ N}}
$$

a) $W=1800text{ N}$

b) $W=796.7text{ N}$

By the universal gravitational law, the weight of an object at some distance from the massive object is given as a product of the gravitational field at that point and the mass of the object.

$$
begin{align}
W&=gcdot{m}
end{align}
$$

Also, we have the equation for the gravitational field of the Earth at some point given by the relation:

$$
begin{align}
g&=Gcdotfrac{m_E}{r^2}
end{align}
$$

where the $G$ stands for the universal gravitational constant, $m_E$ is the mass of the Earth, and $r$ represents the distance from the Earth center.

If we substitute the second equation into the first one, we get:

$$
begin{align*}
W&=Gcdotfrac{m_Ecdot{m}}{r^2}
end{align*}
$$

Let’s find the height at which we have half of the initial weight.

At some height the distance from the Earth center will be:

$$
begin{align*}
r&=r_E+h
end{align*}
$$

where the $r_E$ represents the Earth radius.

$$
begin{align*}
W&=frac{1}{2}cdot{W_E}\
Gcdotfrac{m_Ecdot{m}}{r^2}&=frac{1}{2}cdot{Gcdotfrac{m_Ecdot{m}}{r_E^2}}\
frac{1}{r^2}&=frac{1}{2}cdotfrac{1}{r_E^2}
end{align*}
$$

We get the relation that have to be true:

$$
begin{align*}
r^2&=2cdot{r_E}^2\
left(r_E+hright)^2&=2cdot{r_E}^2\
0&=r_E^2+2cdot{r_E}cdot{h}+h^2-2cdot{r_E^2}
end{align*}
$$

We get the quadratic equation that we have to solve:

$$
begin{align*}
h^2+2cdot{r_E}cdot{h}-r_E^2=0
end{align*}
$$

The solution of this equation will be:

$$
begin{align*}
h_{12}&=frac{-2cdot{r_E}pmsqrt{4cdot{r_E^2}+4cdot{r_E^2}}}{2}\
h_{12}&=frac{-2cdot{r_E}pmsqrt{8cdot{r_E^2}}}{2}\
h_{12}&=frac{-2cdot{r_E}pm{2cdotsqrt{2}cdot{r_E}}}{2}\
h_{12}&=left(-1pmsqrt{2}right)cdot{r_E}
end{align*}
$$

The second solution is not possible because the height cant be an negative value, so we have just one possible solution:

$$
begin{align*}
h&=left(-1+sqrt{2}right)cdot{r_E}\
h&=0.414cdot{r_E}
end{align*}
$$

If we substitute the radius of the Earth we get the needed height above the surface:

$$
begin{align*}
h&=0.414cdot{6.38cdot{10^3}text{ km}}
end{align*}
$$

$$
boxed{h=2.64cdot{10^3}text{ km}}
$$

$$
h=2.64cdot{10^3}text{ km}
$$

We have given:

$$
begin{align*}
m_1&=m_2\
r&=30text{ m}\
F&=2cdot{10^{-7}}text{ N}
end{align*}
$$

And we have to compute the mass of the objects and the initial acceleration of the object as a result of attraction force.

$bold{a)}$ By the law of universal gravitation, the attraction force between two objects is directly proportional to a product of their masses and universal gravitational constant, and reversible proportional to a square of the distance between them. Given by the equation:

$$
begin{align*}
F&=Gcdotfrac{m_1cdot{m_2}}{r^2}
end{align*}
$$

Where the $m_1$ and $m_2$ stand for the object masses, $G$ is the universal gravitational constant, and $r$ represents the distance between objects center of mass.

We know that the object masses are equal, so our equation becomes:

$$
begin{align*}
F&=Gcdotfrac{m^2}{r^2}
end{align*}
$$

Let’s express the mass from this equation:

$$
begin{align*}
m^2&=frac{Fcdot{r^2}}{G}\
m&=sqrt{frac{Fcdot{r^2}}{G}}
end{align*}
$$

Let’s substitute and compute the masses of the objects:

$$
begin{align*}
m&=sqrt{frac{2cdot{10^{-7}text{ N}}cdot{left(30text{ m}right)^2}}{6.67cdot{10^{-11}}frac{text{N}cdot{text{m}^2}}{text{kg}}}}
end{align*}
$$

$$
boxed{m=1642.76text{ kg}}
$$

$bold{b)}$ To find the initial acceleration of the object we have to implement Newton’s second law of motion. The magnitude of the acceleration of the object that is the result of a force is equal to a magnitude of force divided by the mass of the object.

$$
begin{align*}
a&=frac{F}{m}
end{align*}
$$

We have just to substitute and compute the acceleration:

$$
begin{align*}
a&=frac{F}{m}\
a&=frac{2cdot{10^{-7}}text{ N}}{1642.76text{ kg}}
end{align*}
$$

$$
boxed{a=1.22cdot{10^{-10}}frac{text{m}}{text{s}^2}}
$$

a) $m=1642.67text{ kg}$

b) $a=1.22cdot{10^{-10}}frac{text{m}}{text{s}^2}$

The force of attraction between two spheres is given by the universal gravitational law. The magnitude of attraction force between two massive objects is equal to universal gravitational constant times the mass of one object, times the mass of the second object divided by the square of the distance between the object’s center of mass.

$$
begin{align*}
F&=Gcdotfrac{m_1cdot{m_2}}{r^2}
end{align*}
$$

Where the $G$ stands for the universal gravitational constant, $m_1$ and $m_2$ stands for the mass of the first and the second object, and $r$ is the distance between its center of mass.

We don’t have given the mass of the objects, but we have given it its weight, and we know that the weight is a product of mass and gravitational acceleration. So let’s compute the mass of the first sphere:

$$
begin{align*}
W_1&=m_1cdot{g}\
m_1&=frac{W_1}{g}\
m_1&=frac{9.8cdot{10^2}text{ N}}{9.8 frac{text{m}}{text{s}^2}}\
m_1&=100text{ kg}
end{align*}
$$

And let’s repeat calculation for the second sphere:

$$
begin{align*}
W_2&=m_2cdot{g}\
m_2&=frac{W_2}{g}\
m_2&=frac{1.96cdot{10^2}text{ N}}{9.8 frac{text{m}}{text{s}^2}}\
m_2&=20text{ kg}
end{align*}
$$

We have all necessary to substitute into the first equation and compute the attraction force between two spheres.

$$
begin{align*}
F&=Gcdotfrac{m_1cdot{m_2}}{r^2}\
F&=6.67cdot{10^{-11}} frac{text{N}cdottext{m}^2}{text{kg}}cdotfrac{100text{ kg}cdot{20text{ kg}}}{left(4text{ m}right)^2}
end{align*}
$$

$$
boxed{F=83.375cdot{10^{-10}}text{ N}}
$$

$$
F=83.375cdot{10^{-10}}text{ N}
$$

The force of attraction between two objects is given by the universal gravitational law. The magnitude of attraction force between two massive objects is equal to universal gravitational constant times the mass of one object, times the mass of the second object divided by the square of the distance between the object’s center of mass.

$$
begin{align}
F&=Gcdotfrac{m_1cdot{m_2}}{r^2}
end{align}
$$

Where the $G$ stands for the universal gravitational constant, $m_1$ and $m_2$ stands for the mass of the first and the second object, and $r$ is the distance between its center of mass.

If we mark the mass of the Earth with $m_E$ and the mass of the Moon with $m_M$, our equation becomes:

$$
begin{align*}
F&=Gcdotfrac{m_Ecdot{m_M}}{r^2}
end{align*}
$$

Let’s fix the equation to express the mass of the Moon. First, let’s multiply both sides by $r^2$:

$$
begin{align*}
Fcdot{r^2}&=Gcdot{m_Ecdot{m_M}}
end{align*}
$$

Now, we can express the mass of the Moon as:

$$
begin{align*}
m_M&=frac{Fcdot{r^2}}{Gcdot{m_E}}
end{align*}
$$

Let’s substitute all given and look into a table $7-1$ to find the mass of the Earth and compute:

$$
begin{align*}
m_M&=frac{1.9cdot{10^{20}}text{ N}cdot{left(3.9cdot{10^8}right)^2}}{6.67cdot{10^{-11}} frac{text{N}cdottext{m}^2}{text{kg}}cdot{5.97cdot{10^{24}}text{ kg}}}
end{align*}
$$

$$
boxed{m_M=7.26cdot{10^{22}}text{ kg}}
$$

$$
m_M=7.26cdot{10^{22}}text{ kg}
$$

The weight of an object is equal to a product of object mass and the gravitational field.

$$
begin{align*}
W&=mcdot{g}
end{align*}
$$

where the $m$ stands for the mass of an object, and $g$ represents the gravitational field.

If we express the gravitational field at the Moon surface from the upper equation, we get the relation:

$$
begin{align*}
g&=frac{W}{m}
end{align*}
$$

let’s substitute and compute the result.

$$
begin{align*}
g&=frac{145.6text{ N}}{91text{ kg}}
end{align*}
$$

$$
boxed{g=1.6 frac{text{m}}{text{s}^2}}
$$

$$
g=1.6 frac{text{m}}{text{s}^2}
$$

The force of attraction between electron and the proton are defined by the universal gravitational law. The magnitude of attraction force between two objects is equal to the universal gravitational constant times the mass of one object, times the mass of the second object divided by the square of the distance between the object’s center of mass.

$$
begin{align*}
F&=Gcdotfrac{m_1cdot{m_2}}{r^2}
end{align*}
$$

Where the $G$ stands for the universal gravitational constant, $m_1$ and $m_2$ stands for the mass of the first and the second object, and $r$ is the distance between its center of mass.

If we marks the mass of the electron with $m_e$ and the mass of the proton with $m_p$, our relation will become:

$$
begin{align*}
F&=Gcdotfrac{m_ecdot{m_p}}{r^2}
end{align*}
$$

Let’s substitute all given data:

$$
begin{align*}
F&=6.67cdot{10^{-11}} frac{text{N}cdottext{m}^2}{text{kg}^2}cdotfrac{9.1cdot{10^{-31}}text{ kg}cdot{1.7cdot{10^{-27}}text{ kg}}}{left(0.59cdot{10^{-10}}text{ m}right)^2}
end{align*}
$$

The attraction force between electron and proton is:

$$
boxed{F=2.96cdot{10^{-47}}text{ N}}
$$

$$
F=2.96cdot{10^{-47}}text{ N}
$$

The force of attraction between two objects is defined by the universal gravitational law. The magnitude of attraction force between two objects is equal to the universal gravitational constant times the mass of one object, times the mass of the second object divided by the square of the distance between the object’s center of mass.

$$
begin{align*}
F&=Gcdotfrac{m_1cdot{m_2}}{r^2}
end{align*}
$$

Where the $G$ stands for the universal gravitational constant, $m_1$ and $m_2$ stands for the mass of the first and the second object, and $r$ is the distance between its center of mass.

As we have the two objects of the same mass, our equation becomes:

$$
begin{align*}
F&=Gcdotfrac{m^2}{r^2}
end{align*}
$$

$bold{a)}$ We have given:

$$
begin{align*}
m&=8text{ kg}\
r&=5text{ m}
end{align*}
$$

Let’s substitute and compute the gravitational force between the spheres:

$$
begin{align*}
F&=6.67cdot{10^{-11}} frac{text{ N}cdottext{ m}^2}{text{ kg}^2}cdotfrac{left(8text{ kg}right)^2}{left(5text{ m}right)^2}
end{align*}
$$

$$
boxed{F=17.08cdot{10^{-11}}text{ N}}
$$

$bold{b)}$ We have given:

$$
begin{align*}
m&=8text{ kg}\
r&=50text{ m}
end{align*}
$$

Let’s substitute and compute the gravitational force between the spheres:

$$
begin{align*}
F&=6.67cdot{10^{-11}} frac{text{ N}cdottext{ m}^2}{text{ kg}^2}cdotfrac{left(8text{ kg}right)^2}{left(50text{ m}right)^2}
end{align*}
$$

$$
boxed{F=17.08cdot{10^{-13}}text{ N}}
$$

a) $F=17.08cdot{10^{-11}}text{ N}$

b) $F=17.08cdot{10^{-13}}text{ N}$

The weight of an object is equal to a product of its mass and the gravitational field around them.

$$
begin{align}
W&=mcdot{g}
end{align}
$$

The magnitude of the gravitational field at some distance from the object center of mass is defined by the universal gravitational law and described by the equation:

$$
begin{align}
g&=frac{Gcdot{m}}{r^2}
end{align}
$$

where the $G$ stands for the universal gravitational constant, $m$ is the mass of the object, and $r$ is the distance from the point center of mass.

The mass of the body is the same on Earth and Mars, so we can compute the mass of the body from the information of body weight and gravitational field on Earth. Let’s express and compute the mass of the body from the first equation:

$$
begin{align*}
m&=frac{W}{g}\
m&=frac{637text{ N}}{9.8 frac{text{m}}{text{s}^2}}\
m&=65text{ kg}
end{align*}
$$

When we stand at the Mars surface, the distance from the Mars center of mass is equal to the radius of Mars. So we have all needed and we can substitute into the second equation:

$$
begin{align*}
g&=frac{6.67cdot{10^{-11}} frac{text{N}cdottext{m}^2}{text{kg}^2}cdot{6.24cdot{10^{23}}text{ kg}}}{left(3.4cdot{10^6}text{ m}right)^2}
end{align*}
$$

Now, we have to compute the gravitational field at Mars:

$$
begin{align*}
g_m=3.6 frac{text{m}}{text{s}^2}
end{align*}
$$

Now, we can substitute into the first equation and compute the weight of the body on Mars:

$$
begin{align*}
W_m&=mcdot{g_m}\
W_m&=65text{ kg}cdot{3.6 frac{text{m}}{text{s}^2}}
end{align*}
$$

$$
boxed{W_m=234text{ N}}
$$

$$
W_m=234text{ N}
$$

The Satellite period by Kepler’s Third law, rearranged by Newton, is given by the equation:

$$
begin{align*}
T&=2cdotpicdotsqrt{frac{r^3}{Gcdot{m_p}}}
end{align*}
$$

where the $r$ represents orbital radius, $G$ is universal gravitational constant, and $m_p$ is it the mass of the planet.

From the table $7-1$ we can find the mass of the Earth as $m_p=5.98cdot{10^{24}}text{ kg}$.
We have to compute the orbital period if the orbital radius is twice the original, be aware of this. Let’s substitute all:

$$
begin{align*}
T&=2cdotpicdotsqrt{frac{left(2cdot{3.9cdot{10^8}text{ m}}right)^3}{6.67cdot{10^{-11}} frac{text{N}cdottext{m}^2}{text{kg}^2}cdot{5.98cdot{10^{24}}text{ kg}}}}
end{align*}
$$

Fix the math in order to get result:

$$
boxed{T=6.85cdot{10^6}text{ s}}
$$

$$
T=6.85cdot{10^6}text{ s}
$$

The acceleration due to gravity is given by the universal gravitational Law as a:

$$
begin{align}
g&=frac{Gcdot{m}}{r^2}
end{align}
$$

Where the $G$ stands for the universal gravitational constant, $m$ is the mass of the Earth, and the $r$ represents the distance from the Earth’s center of mass.

From the table $7-1$ we can find the original mass of the Earth and it’s radius:

$$
begin{align*}
m&=5.98cdot{10^{24}}text{ kg}\
r&=6.38cdot{10^6}text{ m}
end{align*}
$$

$bold{a)}$ We have the situation that the Earth mass is tripled and it’s mass remain the same $m_1=3cdot{m}$.

Let’s substitute into the first equation and compute the acceleration due to gravity:

$$
begin{align*}
g_1&=frac{Gcdot{m_1}}{r^2}\
g_1&=frac{Gcdot{3cdot{m}}}{r^2}\
g_1&=frac{6.67cdot{10^{-11}} frac{text{N}cdottext{m}^2}{text{kg}^2}cdot{3cdot{5.98cdot{10^{24}}text{ kg}}}}{left(6.38cdot{10^6}text{ m}right)^2}
end{align*}
$$

$$
boxed{g_1=29.4 frac{text{m}}{text{s}^2}}
$$

$bold{b)}$ We have the situation that the Earth mass is the same, but it’s radius is tripled $r_2=3cdot{r}$.

Let’s substitute into the first equation and compute the acceleration due to gravity:

$$
begin{align*}
g_2&=frac{Gcdot{m}}{(r_2)^2}\
g_2&=frac{Gcdot{{m}}}{left(3cdot{r}right)^2}\
g_2&=frac{6.67cdot{10^{-11}} frac{text{N}cdottext{m}^2}{text{kg}^2}cdot{{5.98cdot{10^{24}}text{ kg}}}}{left(3cdot{6.38}cdot{10^6}text{ m}right)^2}
end{align*}
$$

$$
boxed{g_2=1.09 frac{text{m}}{text{s}^2}}
$$

$bold{c)}$ We have the situation that the Earth mass is doubled $m_3=2cdot{m}$, and it’s radius is doubled also $r_3=2cdot{r}$.

Let’s substitute into the first equation and compute the acceleration due to gravity:

$$
begin{align*}
g_3&=frac{Gcdot{m_3}}{(r_3)^2}\
g_3&=frac{Gcdot{2cdot{m}}}{left(2cdot{r}right)^2}\
g_3&=frac{6.67cdot{10^{-11}} frac{text{N}cdottext{m}^2}{text{kg}^2}cdot{2cdot{5.98cdot{10^{24}}text{ kg}}}}{left(2cdot{6.38}cdot{10^6}text{ m}right)^2}
end{align*}
$$

$$
boxed{g_3=4.9 frac{text{m}}{text{s}^2}}
$$

a) $g_1=29.4 frac{text{m}}{text{s}^2}$

b) $g_2=1.09 frac{text{m}}{text{s}^2}$

c) $g_3=4.9 frac{text{m}}{text{s}^2}$

The gravitational field at some point is the same as the acceleration due to gravity at this point. As we know the mass of an object is constant. The weight at any point is equal to a product of gravitational field and the object mass:
$$
begin{align*}
W&=mcdot{g}
end{align*}
$$

If the weight of the body is reduced by $25%$, the remaining weight will be $75%$ of the original weight.

$$
begin{align*}
W_2&=mcdot{g_2}\
0.75cdot{W}&=mcdot{g_2}
end{align*}
$$

Let’s substitute the original weight from the first equation and express new gravitational field:

$$
begin{align*}
0.75cdot{mcdot{g}}&=mcdot{g_2}\
g_2&=0.75cdot{g}\
g_2&=0.75cdot{9.8frac{text{m}}{text{s}^2}}
end{align*}
$$

$$
boxed{g=7.35frac{text{m}}{text{s}^2}}
$$

$$
g=7.35frac{text{m}}{text{s}^2}
$$

In this problem, we need to find the mass of the Sun. To do this, we are going to use Newton’s version of Kepler’s third law. This law is the combination of Universal Gravitation and Kepler’s Third Law. We can write this law as
$$
begin{aligned}
T=2 pi sqrt{frac{r^{3}}{G m_{S}}}
end{aligned}
$$
where $T$ is a period of a planet, $r$ is a radius of orbit of a planet, $G$ is the gravitational constant, and $m_{S}$ is the mass of the Sun.

In Table 7-1, we can see information about the radius, and the period of planets from the solar system. We can take any of these planets. Also, in table, we can see the mass of the Sun, so our result should be $1.99 cdot 10^{30} hspace{0.5mm} mathrm{kg}$. First, we are going to find the expression for the mass of the Sun from the equation above.
$$
begin{aligned}
T&=2 pi sqrt{frac{r^{3}}{G m_{S}}} /^{2}\
T^{2}&=4 pi^{2}frac{r^{3}}{G m_{S}}\
m_{S}&=4 pi^{2}frac{r^{3}}{G T^{2}}
end{aligned}
$$

We are going to choose Earth, and with radius $r_{E}=1.50 cdot 10^{11} hspace{0.5mm} mathrm{m}$, and with the mass $m_{E}=5.98 cdot 10^{24} hspace{0.5mm} mathrm{kg}$. Also, we know the gravitational constant is $G=6.67 cdot 10^{-11}hspace{0.5mm} mathrm{frac{m^{3}}{kg s^{2}}}$, and the period of Earth is one year, or $T_{E}=31536000 hspace{0.5mm} mathrm{s}$.

Now, we can calculate the mass of the Sun
$$
begin{aligned}
m_{S}&=4 pi^{2}frac{r_{E}^{3}}{GT_{E}^{2}}\
m_{S}&=4 pi^{2}frac{left( 1.50 cdot 10^{11} hspace{0.5mm} mathrm{m} right)^{3}}{6.67 cdot 10^{-11}hspace{0.5mm} mathrm{frac{m^{3}}{kg s^{2}}} cdot left( 31536000 hspace{0.5mm} mathrm{s} right)^{2}}\
m_{S}&=2.00cdot 10^{30} hspace{0.5mm} mathrm{kg}
end{aligned}
$$

$m_{S}=2.00cdot 10^{30} hspace{0.5mm} mathrm{kg}$

In this problem, we want to find the force of attraction between a student with a mass of $m=45.0 hspace{0.5mm} mathrm{kg}$ and Earth. We know that the gravitational acceleration for this case is $g=7.83 hspace{0.5mm} mathrm{N/kg}$. To find the force of attraction, we are going to use the equation
$$
begin{aligned}
F=m g
end{aligned}
$$

First, we are going to substitute the values in the equation above
$$
begin{aligned}
F=45.0 hspace{0.5mm} mathrm{kg} cdot 7.83 hspace{0.5mm} mathrm{N/kg}
end{aligned}
$$

Now, we calculate the force of attraction
$$
begin{aligned}
F&=352.35 hspace{0.5mm} mathrm{N}\
F&approx 352 hspace{0.5mm} mathrm{N}
end{aligned}
$$

$F=352.35 hspace{0.5mm} mathrm{N}$

In this problem, we want to find the period and speed of Mars’s satellite. To find the period of the satellite, we are going to use Newton’s version of Kepler’s third law
We can write this law as
$$
begin{aligned}
T_{s}=2 pi sqrt{frac{left(r_{s}+r_{M}right)^{3}}{G m_{M}}}
end{aligned}
$$
where $T_{s}$ is a period of the satellite, $r_{s}$ is a radius of orbit of the satellite, $r_{M}$ is a radius of Mars, $G$ is the gravitational constant, and $m_{M}$ is the mass of the Mars.
To find the speed of the satellite, we are going to use Universal Gravitational Law in combination with the centripetal force
$$
begin{aligned}
frac{m_{s}v_{s}^{2}}{r_{s}+r_{M}}=Gfrac{m_{M} m_{s}}{left(r_{s}+r_{M}right)^{2}}
end{aligned}
$$
where we use the mass of Mars because the satellite is in Mars’s gravitational field.

First, we are going to find the period of the satellite. The path radius of the satellite is $r_{s}=1.75 cdot 10^{5} hspace{0.5mm} mathrm{m}$, the radius of Mars is $r_{s}=3.40 cdot 10^{6} hspace{0.5mm} mathrm{m}$,the mass of Mars is $m_{M}=6.42 cdot 10^{23} hspace{0.5mm} mathrm{kg}$ , and the gravitational constant is $G=6.67 cdot 10^{-11}hspace{0.5mm} mathrm{frac{m^{3}}{kg s^{2}}}$.

Now, we substitute the values and calculate the period
$$
begin{aligned}
T_{s}&=2 pi sqrt{frac{left(r_{s}+r_{M}right)^{3}}{G m_{M}}}\
T_{s}&=2 pi sqrt{frac{left( 3.58 cdot 10^{6} hspace{0.5mm} mathrm{m} right)^{3}}{6.67 cdot 10^{-11}hspace{0.5mm} mathrm{frac{m^{3}}{kg s^{2}}} cdot 6.42 cdot 10^{23} hspace{0.5mm} mathrm{kg}}}\
T_{s}&=6.50cdot 10^{3} hspace{0.5mm} mathrm{s}
end{aligned}
$$

Now, we are going to calculate the speed of the satellite. First, we divide everything with $m_{s}/left(r_{s}+r_{M}right)$
$$
begin{aligned}
frac{m_{s}v_{s}^{2}}{r_{s}+r_{M}}&=Gfrac{m_{M} m_{s}}{left(r_{s}+r_{M}right)^{2}}/: m_{s}/left(r_{s}+r_{M}right)\
v_{s}^{2}&=Gfrac{m_{M} }{r_{s}+r_{M}}
end{aligned}
$$

In this step, we are going to find the square root of everything, then we are going to calculate the speed
$$
begin{aligned}
v_{s}^{2}&=Gfrac{m_{M} }{r_{s}+r_{M}}\
v_{s}&=sqrt{Gfrac{m_{M} }{r_{s}+r_{M}}}\
v_{s}&=sqrt{6.67 cdot 10^{-11}hspace{0.5mm} mathrm{frac{m^{3}}{kg s^{2}}} frac{6.42 cdot 10^{23} hspace{0.5mm} mathrm{kg} }{3.58 cdot 10^{6} hspace{0.5mm} mathrm{m}}}\
v_{s}&=3.46 cdot 10^{3}hspace{0.5mm} mathrm{frac{m}{s}}
end{aligned}
$$

$T_{s}=6.50cdot 10^{3} hspace{0.5mm} mathrm{s}$
$v_{s}=3.46 cdot 10^{3}hspace{0.5mm} mathrm{frac{m}{s}}$

In this problem, we need to find the period of the satellite. To do this, we are going to use Kepler’s third law, and we can write it as
$$
begin{aligned}
left( frac{T_{s}}{T_{M}} right)^{2}=left( frac{r_{s}}{r_{M}}right)^{3}
end{aligned}
$$
where $T_{s}$ is a period of the satellite, $T_{M}$ is a period of the Moon, $r_{s}$ is a radius of the satellite’s orbit, and $r_{M}$ is a radius of the Moon’s orbit.

We know that a mean orbital radius of the satellite is half the radius of the Moon’s orbit, so we can write
$$
begin{aligned}
r_{s}=0.5r_{M}
end{aligned}
$$

If we combine these relations, we get
$$
begin{aligned}
left( frac{T_{s}}{T_{M}} right)^{2}&=left( frac{0.5r_{M}}{r_{M}}right)^{3}\
left( frac{T_{s}}{T_{M}} right)^{2}&=left( frac{1}{2}right)^{3}\
left( frac{T_{s}}{T_{m}} right)^{2}&=frac{1}{8}\
end{aligned}
$$

Now, we want to find the relation between Moon’s and satellite’s periods. We are going to find the square root of the expression
$$
begin{aligned}
left( frac{T_{s}}{T_{m}} right)^{2}&=frac{1}{8}\
sqrt{left( frac{T_{s}}{T_{m}} right)^{2}}&= sqrt{frac{1}{8}}\
frac{T_{s}}{T_{m}}&=0.35\
T_{s}&=0.35T_{M}
end{aligned}
$$

$T_{s}=0.35T_{M}$

In this problem, we want to find the speed and the period of the cannonball, that is shot from the Moon. To find the period of the satellite, we are going to use Newton’s version of Kepler’s third law
We can write this law as
$$
begin{aligned}
T_{c}=2 pi sqrt{frac{r_{M}^{3}}{G m_{M}}}
end{aligned}
$$
where $T_{c}$ is a period of the cannonball, $r_{M}$ is a radius of the Moon’s orbit, $G$ is the gravitational constant, and $m_{M}$ is the mass of the Moon.
To find the speed of the cannonball, we are going to use Universal Gravitational Law in combination with the centripetal force
$$
begin{aligned}
frac{m_{c}v_{c}^{2}}{r_{M}}=Gfrac{m_{M} m_{c}}{r_{M}^{2}}
end{aligned}
$$
where we use the mass of the Moon because the satellite is in the Moon’s gravitational field.

The radius ofthe Moon’s orbit is $r_{M}=1.785 cdot 10^{6} hspace{0.5mm} mathrm{m}$,the mass of the Moon is $m_{M}=7.3 cdot 10^{22} hspace{0.5mm} mathrm{kg}$ , and the gravitational constant is $G=6.67 cdot 10^{-11}hspace{0.5mm} mathrm{frac{m^{3}}{kg s^{2}}}$.

First, we are going to calculate the speed of the cannonball. First, we divide everything with $m_{c}/r_{M}$
$$
begin{aligned}
frac{m_{c}v_{c}^{2}}{r_{M}}&=Gfrac{m_{M} m_{c}}{r_{M}^{2}}/: m_{c}/r_{M}\
v_{c}^{2}&=Gfrac{m_{M} }{r_{M}}
end{aligned}
$$

In this step, we are going to find the square root of everything, then we are going to calculate the speed
$$
begin{aligned}
v_{c}^{2}&=Gfrac{m_{M} }{r_{M}}\
v_{c}&=sqrt{Gfrac{m_{M} }{r_{M}}}\
v_{c}&=sqrt{6.67 cdot 10^{-11}hspace{0.5mm} mathrm{m^{3}/kg s^{2}} frac{7.3 cdot 10^{22} hspace{0.5mm} mathrm{kg} }{1.785 cdot 10^{6} hspace{0.5mm} mathrm{m}}}\
v_{c}&=1.65 cdot 10^{3}hspace{0.5mm} mathrm{frac{m}{s}}
end{aligned}
$$

Now, we are going to find the period of the cannonball
$$
begin{aligned}
T_{c}&=2 pi sqrt{frac{r_{M}^{3}}{G m_{M}}}\
T_{c}&=2 pi sqrt{frac{left( 1.785 cdot 10^{6} hspace{0.5mm} mathrm{m} right)^{3}}{6.67 cdot 10^{-11}hspace{0.5mm} mathrm{frac{m^{3}}{kg s^{2}}} cdot 7.3 cdot 10^{22} hspace{0.5mm} mathrm{kg}}}\
T_{c}&=6.79 cdot 10^{3} hspace{0.5mm} mathrm{s}
end{aligned}
$$

$v_{c}=1.65 cdot 10^{3}hspace{0.5mm} mathrm{frac{m}{s}}$
$T_{c}=6.79 cdot 10^{3} hspace{0.5mm} mathrm{s}$

In this problem, we are observing a case where Earth has double mass, $m_{E}’=2m_{E}$

$a)$ We can find the period of the Moon by using the equation
$$
begin{aligned}
T_{M}=2 pi sqrt{frac{r_{M}^{3}}{G m_{E}}}
end{aligned}
$$
where $T_{M}$ is a period of the Moon, $r_{M}$ is a radius of the Moon’s orbit, and $m_{E}$ is a mass of Earth.

For this Earth’s mass, the Moon has a period of one month. But if the mass of Earth is doubled, then the period could be calculated as
$$
begin{aligned}
T_{M}’&=2 pi sqrt{frac{r_{M}^{3}}{G m_{E}’}}
end{aligned}
$$

Now, we are going to divide these equations, and then get the relation between the periods
$$
begin{aligned}
frac{T_{M}’}{T_{M}}&=frac{2 pi sqrt{frac{r_{M}^{3}}{G m_{E}’}}}{2 pi sqrt{frac{r_{M}^{3}}{G m_{E}}}}\
frac{T_{M}’}{T_{M}}&=frac{ sqrt{frac{1}{m_{E}’}}}{ sqrt{frac{1}{m_{E}}}}\
frac{T_{M}’}{T_{M}}&=frac{ sqrt{frac{1}{2m_{E}}}}{ sqrt{frac{1}{m_{E}}}}\
frac{T_{M}’}{T_{M}}&=sqrt{frac{1}{2}}\
T_{M}’&=0.707T_{M}\
T_{M}’&=0.707 hspace{0.5mm} mathrm{months}\
end{aligned}
$$

$b)$ To find the radius of an orbit of satellite with the period of one month, we use Kepler’s third law, and we can write it as
$$
begin{aligned}
left( frac{T_{s}}{T_{M}’} right)^{2}=left( frac{r_{s}}{r_{M}}right)^{3}
end{aligned}
$$
where $T_{s}$ is a period of the satellite, $T_{M}’$ is a period of the Moon, $r_{s}$ is a radius of the satellite’s orbit, and $r_{M}$ is a radius of the Moon’s orbit.

First, we are going to find the expression of the radius of the satellite’s orbit
$$
begin{aligned}
left( frac{T_{s}}{T_{M}’} right)^{2}&=left( frac{r_{s}}{r_{M}}right)^{3}\
frac{r_{s}}{r_{M}}&=left( frac{T_{s}}{T_{M}’} right)^{2/3}\
r_{s}&=r_{M}left( frac{T_{s}}{T_{M}’} right)^{2/3}\
end{aligned}
$$

The period of the satellite is one month and the period of the Moon is $0.707 hspace{0.5mm} mathrm{months}$, so we can calculate
$$
begin{aligned}
r_{s}&=r_{M}left( frac{T_{s}}{T_{M}’} right)^{2/3}\
r_{s}&=r_{M}left( frac{1hspace{0.5mm} mathrm{months}}{0.707 hspace{0.5mm} mathrm{months}} right)^{2/3}\
r_{s}&=1.26 r_{M}
end{aligned}
$$

$c)$ We know that the period of Earth can be found from the equation
$$
begin{aligned}
T_{E}&=2 pi sqrt{frac{r_{E}^{3}}{G m_{S}}}
end{aligned}
$$
where $m_{S}$ is the mass of the Sun. We can see there is no mass of Earth in this equation, so the period of Earth will remain the same.

In this problem, we need to find how fast the planet should be spinning, so the object in the equator be weightless. The condition for an object to be weightless is the gravity force and the centripetal force be equal
$$
begin{aligned}
frac{mv_{p}^{2}}{r_{p}}=Gfrac{m_{p} m}{r_{p}^{2}}
end{aligned}
$$
where $m$ is a mass of an object, $m_{p}$ is a mass of a planet, $v_{p}$ is a speed of a planet, and $r_{p}$ is a radius of a planet.

First, we divide everything with $m/r_{p}$
$$
begin{aligned}
frac{mv_{p}^{2}}{r_{p}}&=Gfrac{m_{p} m}{r_{p}^{2}}/: m/r_{p}\
v_{p}^{2}&=Gfrac{m_{p} }{r_{p}}\
v_{p}&=sqrt{Gfrac{m_{p} }{r_{p}}}\
end{aligned}
$$

Now, we are going to find the period of the planet as
$$
begin{aligned}
2 pi r_{p}&=T_{p}v_{p}\
T_{p}&=frac{2 pi r_{p}}{v_{p}}\
T_{p}&=frac{2 pi r_{p}}{sqrt{Gfrac{m_{p} }{r_{p}}}}\
T_{p}&=2 pi sqrt {frac{ r_{p}^{3}}{G m_{p}}}\
end{aligned}
$$

This planet has the same mass and radius as Earth, so we can write
$$
begin{aligned}
T_{p}&=2 pi sqrt{frac{ left( 6.38 cdot 10^{6} hspace{0.5mm} mathrm{m} right)^{3}}{6.67 cdot 10^{-11} hspace{0.5mm} mathrm{frac{m^{3}}{kg s^{2}}} cdot 5.98 cdot 10^{24} hspace{0.5mm} mathrm{kg}}}\
T_{p}&=50.66 cdot 10^{2} hspace{0.5mm} mathrm{s}\
T_{p}&=84.43 hspace{0.5mm} mathrm{min}
end{aligned}
$$

$T_{p}=84.43 hspace{0.5mm} mathrm{min}$.

In this problem, we want to find the smallest radius of a track. To solve this problem, we are going to use two equations
$$
begin{aligned}
F_{fr}&leq mu m g_{M}\
F_{c}&=frac{mv^{2}}{r^{2}}
end{aligned}
$$
where $m$ is the mass of the car, $g_{M}$ is the gravitational acceleration on Mars, $r$ is a radius of a track, and $v$ is a speed of a car.

We are going to combine these equations to find the expression for the radius of a track. We are going to observe the extremal case when the radius of the track is minimal, so we use “$=$”
$$
begin{aligned}
frac{mv^{2}}{r}&= mu m g_{M} / :m\
frac{v^{2}}{r}&= mu g_{M}\
r&=frac{v^{2}}{mu g_{M}}
end{aligned}
$$

We know the speed of the car $v=12 hspace{0.5mm} mathrm{m/s}$ and the coefficient of friction $mu=0.50$, but we do not know the gravitational acceleration on Mars. We can find it by using Universal Gravitational Law
$$
begin{aligned}
mg_{M}&=G frac{m hspace{0.5mm} m_{M}}{r_{M}^{2}}/:m\
g_{M}&=G frac{ m_{M}}{r_{M}^{2}}
end{aligned}
$$
where $m_{M}$ is the mass of Mars, and $r_{M}$ is the radius of Mars. We can find these infromation in Table 7-1. Mass of Mars is $m_{M}=6.37 cdot 10^{23}hspace{0.5mm} mathrm{kg}$, the radius of Mars is $r_{M}=3.43cdot 10^{6}hspace{0.5mm} mathrm{m}$ , and the gravitational constant is $G=6.67 cdot 10^{-11}hspace{0.5mm} mathrm{frac{m^{3}}{kg s^{2}}}$.

First, we are going to find the gravitational acceleration on Mars
$$
begin{aligned}
g_{M}&=G frac{ m_{M}}{r_{M}^{2}}\
g_{M}&=6.67 cdot 10^{-11}hspace{0.5mm} mathrm{m^{3}/kg s^{2}}frac{ 6.37 cdot 10^{23}hspace{0.5mm} mathrm{kg}}{left( 3.43cdot 10^{6}hspace{0.5mm} mathrm{m} right)^{2}}\
g_{M}&=3.61hspace{0.5mm} mathrm{frac{m}{s^{2}}}
end{aligned}
$$

Now, we can find the radius of a track
$$
begin{aligned}
r&=frac{v^{2}}{mu g_{M}}\
r&=frac{left(12 hspace{0.5mm} mathrm{m/s}right)^{2}}{0.50 cdot 3.61hspace{0.5mm} mathrm{frac{m}{s^{2}}}}\
r&=79.78 hspace{0.5mm} mathrm{m}
end{aligned}
$$

$r=79.78 hspace{0.5mm} mathrm{m}$

The radius of the Moon is $r_{M}=1.785 cdot 10^{6} hspace{0.5mm} mathrm{m}$,the mass of the Moon is $m_{M}=7.3 cdot 10^{22} hspace{0.5mm} mathrm{kg}$, also the radius of Apollo’s orbit is $r_{A}=1.11 cdot 10^{5} hspace{0.5mm} mathrm{m}+1.785 cdot 10^{6} hspace{0.5mm} mathrm{m}=1.896 cdot 10^{6} hspace{0.5mm} mathrm{m}$.

$a)$ In this problem, we want to find the period of Apollo II around the Moon. We are going to use the equation
$$
begin{aligned}
T_{A}=2 pi sqrt{frac{r_{A}^{3}}{G m_{M}}}
end{aligned}
$$
where $T_{A}$ is a period of Apollo II, $r_{A}$ is a radius of Apollo’s orbit, $m_{M}$ is a mass of the Moon, and the gravitational constant is $G=6.67 cdot 10^{-11}hspace{0.5mm} mathrm{frac{m^{3}}{kg s^{2}}}$.

Now, we need to substitute the values and find the period of Apollo
$$
begin{aligned}
T_{A}&=2 pi sqrt{frac{r_{A}^{3}}{G m_{M}}}\
T_{A}&=2 pi sqrt{frac{left( 1.896 cdot 10^{6} hspace{0.5mm} mathrm{m} right)^{3}}{6.67 cdot 10^{-11}hspace{0.5mm} mathrm{frac{m^{3}}{kg s^{2}}} cdot 7.3 cdot 10^{22} hspace{0.5mm} mathrm{kg}}}\
T_{A}&= 7.43cdot 10^{3} hspace{0.5mm} mathrm{s}\
T_{A}&=123 hspace{0.5mm} mathrm{min}
end{aligned}
$$

$b)$ Now, we need to find the speed of Apollo. We are going to use the equation
$$
begin{aligned}
v_{A}&=frac{2 pi r_{A}}{T_{A}}
end{aligned}
$$

We already know these values, so we are going to substitute them, and calculate the speed
$$
begin{aligned}
v_{A}&=frac{2 pi r_{A}}{T_{A}}\
v_{A}&=frac{2 pi cdot 1.896 cdot 10^{6} hspace{0.5mm} mathrm{m}}{7.43cdot 10^{3} hspace{0.5mm} mathrm{s}}\
v_{A}&=1.60 cdot 10^{3} hspace{0.5mm} mathrm{m/s}
end{aligned}
$$

$a)$ $T_{A}=123 hspace{0.5mm} mathrm{min}$
$b)$ $v_{A}=1.60 cdot 10^{3} hspace{0.5mm} mathrm{m/s}$

$a)$ We are going to find two forces, one between the Sun and the water mass on Earth, and the other one between the Moon and the water mass on Earth. That water mass has the mass $m$, and from Table 7-1 we read others parameters, as the mass of the Sun and the Moon, and the distances between objects. Also, we know the gravitational constant is $G=6.67 cdot 10^{-11}hspace{0.5mm} mathrm{frac{m^{3}}{kg s^{2}}}$.

We are going to use the gravitational force
$$
begin{aligned}
F=Gfrac{m’m}{r^{2}}
end{aligned}
$$

The gravitational force between the Sun and the water mass is
$$
begin{aligned}
F_{Sun}&=Gfrac{m_{S}m}{r_{S}^{2}}\
F_{Sun}&=m cdot6.67 cdot 10^{-11}hspace{0.5mm} mathrm{frac{m^{3}}{kg s^{2}}}frac{1.99 cdot 10^{30}hspace{0.5mm} mathrm{kg}}{(1.50 cdot 10^{11} hspace{0.5mm} mathrm{m})^{2}}\
F_{Sun}&=m cdot 5.90 cdot 10^{-3}hspace{0.5mm} mathrm{N} end{aligned}
$$
In the previous result, we have the term $m$, which is the water mass, and not the unit of meters.

Now, we are going to find the gravitational force between the Moon and the water mass
$$
begin{aligned}
F_{Moon}&=Gfrac{m_{M}m}{r_{M}^{2}}\
F_{Moon}&=m cdot 6.67 cdot 10^{-11}hspace{0.5mm} mathrm{frac{m^{3}}{kg s^{2}}}frac{7.36 cdot 10^{22}hspace{0.5mm} mathrm{kg}}{(3.80 cdot 10^{8} hspace{0.5mm} mathrm{m})^{2}}\
F_{Moon}&=m cdot 0.034 cdot 10^{-3}hspace{0.5mm} mathrm{N}
end{aligned}
$$
Same as before, the term $m$ is the water mass and not the unit of meters.

$b)$ From the previous part, we can see that the Sun has a greater pull on the waters of Earth.

$c)$ In part $a)$ the distance was between the center of Earth to the center of another object, but now, we need to find the forces at the near-surface and the water at the far surface. In Figure 7-27, we can see that this surface is $pm$ radius of Earth from the center. So we can calculate the force exerted by the Moon on the water at the near-surface and the water at the far surface.

We can calculate
$$
begin{aligned}
F&=Gfrac{m_{M}m}{(r_{M}-r_{E})^{2}}-Gfrac{m_{M}m}{(r_{M}+r_{E})^{2}}\
F&=m cdot 6.67 cdot 10^{-11}hspace{0.5mm} mathrm{frac{m^{3}}{kg s^{2}}}frac{7.36 cdot 10^{22}hspace{0.5mm} mathrm{kg}}{(3.80 cdot 10^{8} hspace{0.5mm} mathrm{m}-0.064 cdot 10^{8} hspace{0.5mm} mathrm{m})^{2}}-\
&hspace{2.5mm}-m cdot 6.67 cdot 10^{-11}hspace{0.5mm} mathrm{frac{m^{3}}{kg s^{2}}}frac{7.36 cdot 10^{22}hspace{0.5mm} mathrm{kg}}{(3.80 cdot 10^{8} hspace{0.5mm} mathrm{m}+0.064 cdot 10^{8} hspace{0.5mm} mathrm{m})^{2}}\
F&=m cdot 2.28 cdot 10^{-6}hspace{0.5mm} mathrm{N}
end{aligned}
$$

$d)$ In the same way as before, we are going to find the difference in force exerted by the Sun on the water at the near-surface and on the water at the far surface.

We can calculate
$$
begin{aligned}
F&=Gfrac{m_{S}m}{(r_{S}-r_{E})^{2}}-Gfrac{m_{S}m}{(r_{S}+r_{E})^{2}}\
F&=m cdot 6.67 cdot 10^{-11}hspace{0.5mm} mathrm{frac{m^{3}}{kg s^{2}}}frac{1.99 cdot 10^{30}hspace{0.5mm} mathrm{kg}}{(1.50 cdot 10^{11} hspace{0.5mm} mathrm{m}-6.37 cdot 10^{6} hspace{0.5mm} mathrm{m})^{2}}-\
&hspace{2.5mm}-m cdot6.67 cdot 10^{-11}hspace{0.5mm} mathrm{frac{m^{3}}{kg s^{2}}}frac{1.99 cdot 10^{30}hspace{0.5mm} mathrm{kg}}{(1.50 cdot 10^{11} hspace{0.5mm} mathrm{m}+6.37 cdot 10^{6} hspace{0.5mm} mathrm{m})^{2}}\
F&=m cdot 1.00cdot 10^{-6}hspace{0.5mm} mathrm{N}
end{aligned}
$$

$e)$ From parts $c)$ and $d)$ we can see that the Moon has a greater difference than the Sun.

$f)$ The start statement is not correct because the tides do not depend only on the gravitational force. They depend on the difference between the far and the near-surface.

In this problem, we need to read the gravity acceleration from the graph. To draw the graph we use the equation
$$
begin{aligned}
mg&=Gfrac{mcdot m_{E}}{r^{2}}\
g&=Gfrac{m_{E}}{r^{2}}
end{aligned}
$$
where $m_{E}$ is the mass of Earth.
So the factor, $Gm_{E}$ is our constant $c=4.0 cdot 10^{8} hspace{0.5mm} mathrm{frac{m}{s^{2}m^{2}}}$.

$a)$ At sea level, $r=6400 hspace{0.5mm} mathrm{km}$, the gravity acceleration is $g=9.76hspace{0.5mm} mathrm{frac{m}{s^{2}}}$

$b)$ On top of Mt. Everest, $r=6410 hspace{0.5mm} mathrm{km}$, the gravity acceleration is $g=9.72hspace{0.5mm} mathrm{frac{m}{s^{2}}}$

$c)$ In a typical satellite orbit, $r=6500 hspace{0.5mm} mathrm{km}$, the gravity acceleration is $g=9.46hspace{0.5mm} mathrm{frac{m}{s^{2}}}$

$d)$ In a much higher orbit, $r=6600 hspace{0.5mm} mathrm{km}$, the gravity acceleration is $g=9.18hspace{0.5mm} mathrm{frac{m}{s^{2}}}$

Nowadays, we know that the Astronomical Unit, or AU, is roughly $AU=150 cdot 10^{6} hspace{0.5mm}mathrm{km}$.

In this problem, we need to find the distance between the cities. We know how much time the plane needs to travel that distance, and we know the average speed of the plane, so we are going to use the equation
$$
begin{aligned}
Delta d=v Delta t
end{aligned}
$$
where $Delta d$ is the distance between the cities, $v$ is an average speed, and $Delta t$ is the time.

The time of taking off is 2.20 p.m., and the time of landing down is 3.15 p.m., so the time difference between these actions is $Delta t=55hspace{0.5mm} mathrm{min}=$. The average speed is $v=441.0hspace{0.5mm} mathrm{km/h}=122.5hspace{0.5mm} mathrm{m/s}$.

Now, we can write
$$
begin{aligned}
Delta d&=v Delta t\
Delta d&=122.5hspace{0.5mm} mathrm{m/s} cdot 3300 hspace{0.5mm} mathrm{s}\
Delta d&=404250 hspace{0.5mm} mathrm{m}\
Delta d&=404.25 hspace{0.5mm} mathrm{km}\
end{aligned}
$$

$Delta d=404.25 hspace{0.5mm} mathrm{km}$

In this problem, we need to find Jared’s usual weight on Earth. We know his weight, when he is in an elevator that goes upward at $1.75 hspace{0.5mm} mathrm{m/ s^{2}}$. So, the reaction force $F_{r}$ from the scale is directed upward, while the gravity force $F_{g}$ is directed downward. So, we are going to use Newton’s second law
$$
begin{aligned}
ma&= sum F\
ma&=F_{r}-F_{g}
end{aligned}
$$
where $m$ is Jared’s mass, and $a$ is an acceleration of the system.

The mass of Jared can be written as $m=frac{F_{g}}{g}$, so we can combine these relations, and get the expression for the weight
$$
begin{aligned}
ma&=F_{r}-F_{g}\
frac{F_{g}}{g}a&=F_{r}-F_{g}\
frac{F_{g}}{g}a+F_{g}&=F_{r}\
F_{g}left(1+frac{a}{g} right)&=F_{r}\
F_{g}&=F_{r} frac{1}{1+frac{a}{g}}
end{aligned}
$$

Now, we can substitute the values and find the usual weight on Earth
$$
begin{aligned}
F_{g}&=F_{r} frac{1}{1+frac{a}{g}}\
F_{g}&=716 hspace{0.5mm} mathrm{N} frac{1}{1+frac{1.75 hspace{0.5mm} mathrm{m/ s^{2}}}{9.81 hspace{0.5mm} mathrm{m/ s^{2}}}}\
F_{g}&=607.6 hspace{0.5mm} mathrm{N}
end{aligned}
$$

$F_{g}=607.6 hspace{0.5mm} mathrm{N}$

In this problem, the bug is walking on the outer rim of the flying disk. That bug has the mass of $m=10^{-3} hspace{0.5mm} mathrm{kg}$, and it moves at rate of $v=0.63 hspace{0.5mm} mathrm{cm/s}=0.63 cdot 10^{-2} hspace{0.5mm} mathrm{m/s}$. The radius of that flying disk is $r=frac{17.2}{2} hspace{0.5mm} mathrm{cm}=8.6 cdot 10^{-2} hspace{0.5mm} mathrm{m}$.

Now, we can find the centripetal force substituting the values in the equation
$$
begin{aligned}
F_{cp}&=frac{m v^{2}}{r}\
F_{cp}&=frac{10^{-3} hspace{0.5mm} mathrm{kg} cdot left( 0.63 cdot 10^{-2} hspace{0.5mm} mathrm{m/s}right)^{2}}{8.6 cdot 10^{-2} hspace{0.5mm} mathrm{m}}\
F_{cp}&=4.6 cdot 10^{-7} hspace{0.5mm} mathrm{N}
end{aligned}
$$

$F_{cp}=4.6 cdot 10^{-7} hspace{0.5mm} mathrm{N}$