All Solutions
Page 164: Assessment
intertext{Plane and crate would have the same horizontal velocities, so when crate hits the ground, airplane will be directly above it. For person who is looking from the ground path of crate would look like on picture below. Path of crate is combination of horizontal and vertical motion.}
end{align*}

intertext{Airplane will be directly above crate. Path of crate is combination of horizontal and vertical motion.}
end{align*}
intertext{Vertical motion is accelerated because there is gravity force acting in direction of y axis, which is vertical axis, so it can accelerate or decelerate body in vertical direction, and in horizontal direction we don’t have force like that.}
intertext{When air resistance is is taken into consideration, it would affect on both directions, and it would be opposite to those directions.}
end{align*}\
intertext{Vertical motion is accelerated because there is gravity force , and in horizontal direction we don’t have force like that.}
intertext{Air resistance will act in direction opposite to direction of motion.}
end{align*}
intertext{Ball is caught at the same height as it was thrown. So maximum height it reaches is at $frac{1}{2}$ of a range ball has, which means that ball need the same time to get to maximum height, and from that height to initial height, so for total range, ball would need:}
&t=2cdot 3=6hspace{1mm}s
end{align*}
begin{align*}
&t=6hspace{1mm}s
end{align*}
$$
intertext{We can find tension using Newton’s second law of motion that says that force is:}
&F_t=ma_c
intertext{$F_t$ is tension force, $m$ is mass and $a_c$ is centripetal acceleration}
intertext{As we can see tension force is directly proportional to mass, so if mass is doubled, like in this case, tension force is doubled as well}
end{align*}
intertext{Tension force is doubled.}
end{align*}
intertext{Data known:}
&v_x=8hspace{1mm}frac{m}{s}\
&y=-64hspace{1mm}mhspace{2mm}text{- because it is opposite to y axis, it is falling}
intertext{We are looking for how far do keys go, so we are looking for x, which is actually a range.}
intertext{We can find time needed for that, we know that:}
&y=v_{iy}t-frac{1}{2}gt^2\
intertext{In problem is said that there is only horizontal velocity at initial moment, so initial velocity $v_{iy}$ is equal to zero.}
&y=v_{iy}t-frac{1}{2}gt^2\
&t=sqrt{frac{2y}{-g}}\
&t=sqrt{frac{2(-64)}{-9.8}}\
&t=3.6hspace{1mm}s\
intertext{We know that horizontal velocity in this case remains constant, so we can find x using formula: }
&v_x=frac{x}{t}\
&x=v_xt\
&x=8cdot 3.6\
&x=28.8hspace{1mm}m
end{align*}
begin{align*}
&x=28.8hspace{1mm}m
end{align*}
$$
$$
begin{align*}
v_x &= 8.0 ,mathrm{frac{m}{s}}\
y&= 64 ,mathrm{m}
end{align*}
$$
where $v_x$ is the horizontal velocity and $y$ is the height in which the keys were launched.
$$
begin{align}
x = v_{x}t
end{align}
$$
we can obtain distance $x$.
$$
begin{align}
y = v_{y}t – frac{1}{2}gt^2
end{align}
$$
such that $v_y$ is the initial vertical velocity and $g$ is the acceleration due to gravity.
begin{align*}
y &= v_{y}t – frac{1}{2}gt^2
intertext{Since we know that the initial vertical velocity is zero,}
y &= -frac{1}{2}gt^2\
-2y &= gt^2\
frac{-2y}{g} &= t^2\
sqrt{frac{-2y}{g}} &= t
end{align*}
begin{align*}
x &= v_{x}t\
&= v_{x}sqrt{frac{-2y}{g}}
intertext{We can start plugging in the given values.}
x &= v_{x}sqrt{frac{-2y}{g}}\
&= left(8.0 ,mathrm{frac{m}{s}}right)sqrt{frac{-2(-64 ,mathrm{m})}{9.8,mathrm{frac{m}{s^2}}}}\
&= boxed{29.0 ,mathrm{m}}
end{align*}
x = 29.0 ,mathrm{m}
$$
intertext{Data known:}
&y=-1.225hspace{1mm}mhspace{2mm}text{- because it is opposite to y axis, it is falling}\
&x=0.4hspace{1mm}m
intertext{Part a:}
intertext{We are looking for time car needs to fall to the ground.}
intertext{We know that:}
&y=v_{iy}t-frac{1}{2}gt^2\
intertext{In problem’s figure is shown that there is only horizontal velocity at initial moment, so initial velocity $v_{iy}$ is equal to zero.}
&y=v_{iy}t-frac{1}{2}gt^2\
&t=sqrt{frac{2y}{-g}}\
&t=sqrt{frac{2(-1.225)}{-9.8}}\
&t=0.5hspace{1mm}s\
intertext{Part b:}
intertext{We are looking for car’s initial velocity. In problem’s figure is shown that there is only horizontal velocity. }
intertext{We know that horizontal velocity in this case remains constant, so we can find x using formula: }
&v=v_x=frac{x}{t}\
&v=frac{0.4}{0.5}\
&v=0.8hspace{1mm}frac{m}{s}
end{align*}
Part b: $v=0.8hspace{1mm}dfrac{m}{s}$
$$
begin{align*}
y &= 1.225 ,mathrm{m}\
x &= 0.400 ,mathrm{m}
end{align*}
$$
where $y$ is the height of the table and $x$ is the distance from the base of the table to the point where the car lands.
Using the equation
$$
begin{align}
y = v_{y0} – frac{1}{2}gt^2
end{align}
$$
such that $v_{y0}$ is the initial velocity in the $y$-axis and $g$ is the acceleration due to gravity.
begin{align*}
y &= v_{y}t – frac{1}{2}gt^2
intertext{Since we know that the initial vertical velocity is zero,}
y &= -frac{1}{2}gt^2\
-2y &= gt^2\
frac{-2y}{g} &= t^2\
sqrt{frac{-2y}{g}} &= t
end{align*}
$$
begin{align*}
t &= sqrt{frac{-2y}{g}}\
&= sqrt{frac{-2(-1.225 ,mathrm{m})}{9.8 ,mathrm{frac{m}{s^2}}}}\
&= boxed{0.500 ,mathrm{s}}
end{align*}
$$
Using the equation
$$
begin{align}
x = v_{x}t
end{align}
$$
$$
begin{align*}
x &= v_{x}t\
frac{x}{t} &= v_x
end{align*}
$$
$$
begin{align*}
v_x &= frac{x}{t}\
&= frac{0.400 ,mathrm{m}}{0.500 ,mathrm{s}}\
&= boxed{0.800 ,mathrm{frac{m}{s}}}
end{align*}
$$
$textbf{b.)}$ $v_x = 0.800 ,mathrm{frac{m}{s}}$
$$
begin{align*}
v_x &= 12.4 ,mathrm{frac{m}{s}}\
y&= 0.32 ,mathrm{m}
end{align*}
$$
where $v_x$ is the horizontal velocity and $y$ the distance where the dart hits the board.
$$
begin{align}
x = v_{x}t
end{align}
$$
we can obtain distance $x$.
$$
begin{align}
y = v_{y}t – frac{1}{2}gt^2
end{align}
$$
such that $v_y$ is the initial vertical velocity and $g$ is the acceleration due to gravity.
begin{align*}
y &= v_{y}t – frac{1}{2}gt^2
intertext{Since the initial vertical velocity is zero,}
y &= -frac{1}{2}gt^2\
-2y &= gt^2\
frac{-2y}{g} &= t^2\
sqrt{frac{-2y}{g}} &= t
end{align*}
begin{align*}
x &= v_{x}t\
&= v_{x}sqrt{frac{-2y}{g}}
intertext{Then, plugging in the given}
x &= v_{x}sqrt{frac{-2y}{g}}\
&= left(12.4 ,mathrm{frac{m}{s}}right)sqrt{frac{-2(-0.32 ,mathrm{m})}{9.8,mathrm{frac{m}{s^2}}}}\
&= boxed{3.2,mathrm{m}}
end{align*}
x = 3.2 ,mathrm{m}
$$
intertext{Data known:}
&v_x=12.4hspace{1mm}frac{m}{s}\
&y=-0.32hspace{1mm}mhspace{2mm}text{- because it is opposite to y axis, it is falling}
intertext{We are looking for how far do keys go, so we are looking for x, which is actually a range.}
intertext{We can find time needed for that, we know that:}
&y=v_{iy}t-frac{1}{2}gt^2\
intertext{In problem is said that there is only horizontal velocity at initial moment, so initial velocity $v_{iy}$ is equal to zero.}
&y=v_{iy}t-frac{1}{2}gt^2\
&t=sqrt{frac{2y}{-g}}\
&t=sqrt{frac{2(-0.32)}{-9.8}}\
&t=0.26hspace{1mm}s\
intertext{We know that horizontal velocity in this case remains constant, so we can find x using formula: }
&v_x=frac{x}{t}\
&x=v_xt\
&x=12.4cdot 0.26\
&x=3.2hspace{1mm}m
end{align*}
begin{align*}
&x=3.2hspace{1mm}m
end{align*}
$$
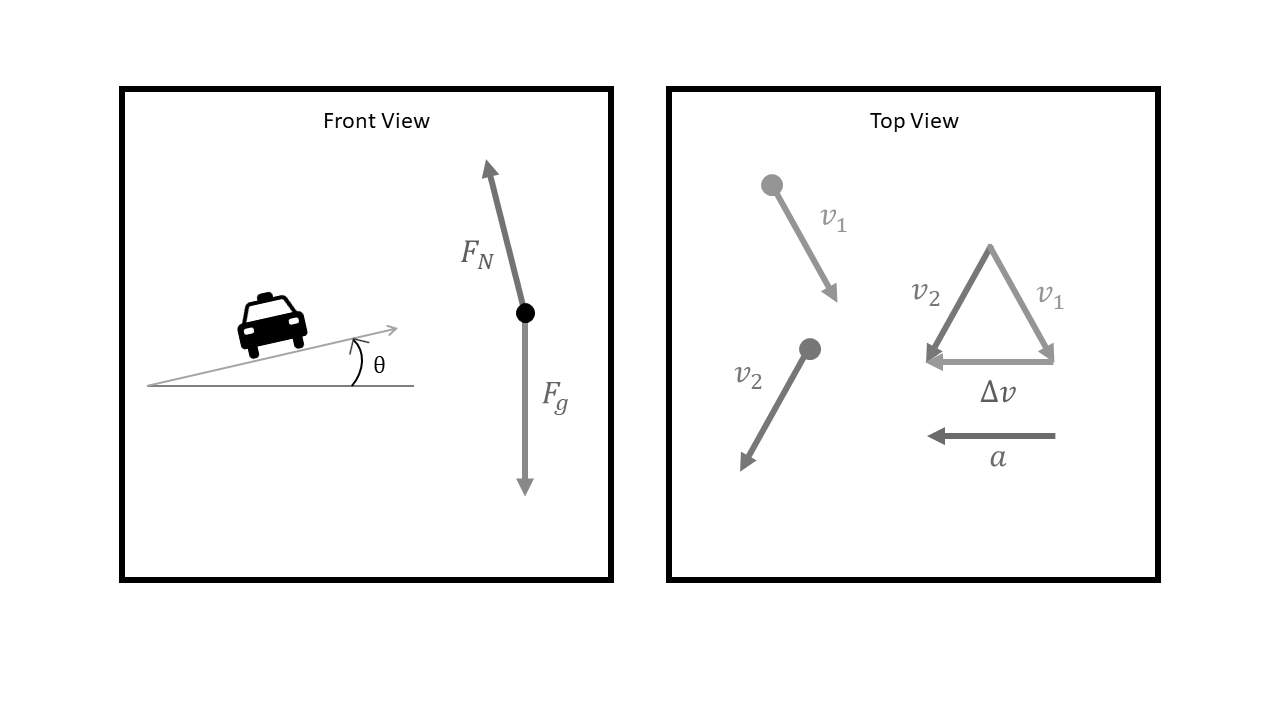
intertext{Case A:}
intertext{We need to draw x various t, and y various t graph. Data known:}
&v=25hspace{1mm}frac{m}{s}\
&theta=60^{circ}
intertext{Horizontal velocity remains constant, during motion, so we can find x using that information:}
&v_x=frac{x}{t}\
intertext{We can find $v_x$ using $v$ and $theta$:}
&v_x=vcos theta\
&v_x=25 cos 60\
&v_x=25cdot 0.5\
&v_x=12.5hspace{1mm}frac{m}{s}\
rightarrow\
&x=v_xt\
&x=12.5t\
intertext{As we can see, x is linear function of t, where $v_x=12.5hspace{1mm}frac{m}{s}$ is slope of a graph.}
end{align*}
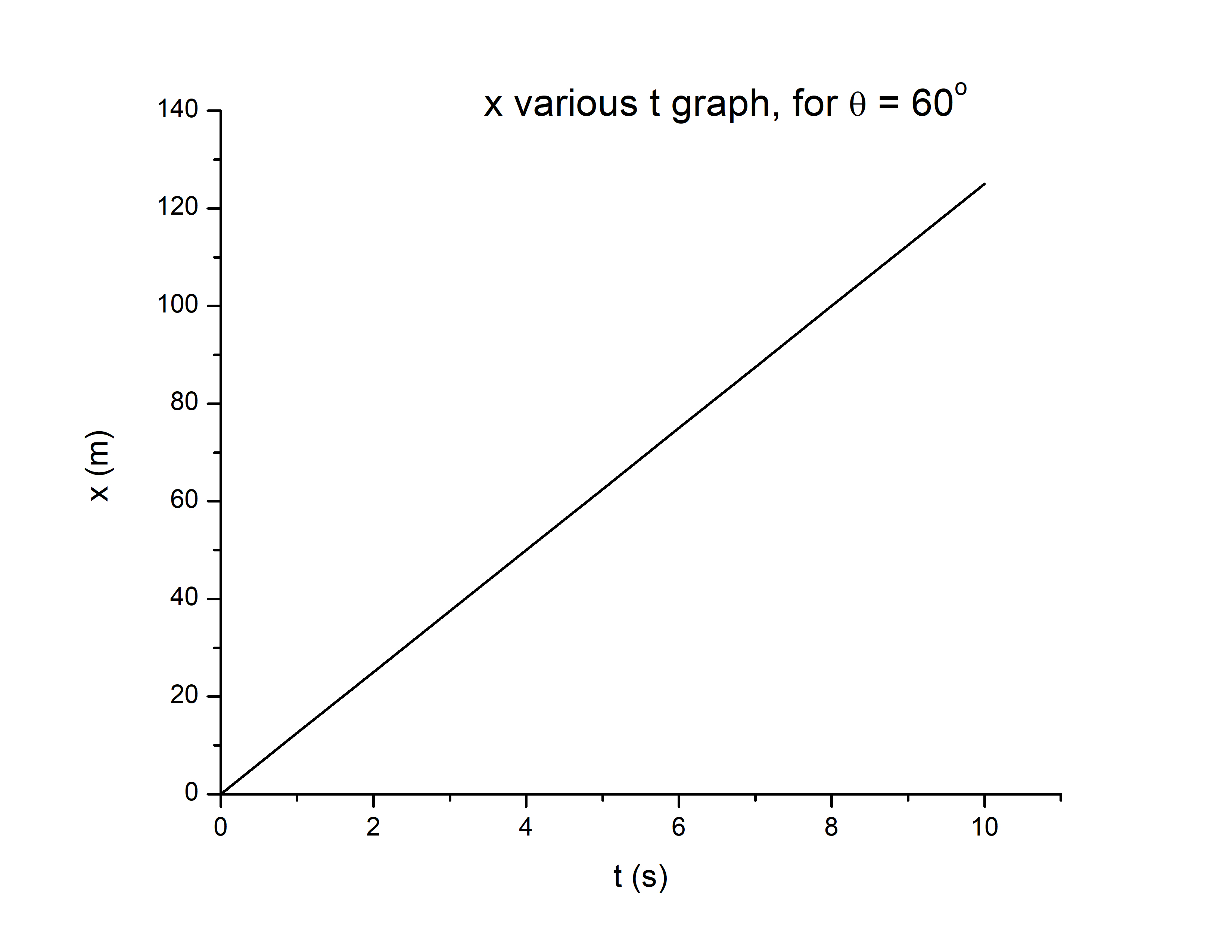
intertext{We know that y is:}
&y=v_{yi}t-frac{1}{2}gt^2\
intertext{We can find $v_{yi}$ using $v$ and $theta$:}
&v_{yi}=vsin theta\
&v_{yi}=25 sin 60\
&v_{yi}=25cdot 0.866\
&v_{yi}=21.65hspace{1mm}frac{m}{s}\
rightarrow\
&y=21.65t-frac{1}{2}9.8t^2\
intertext{As we can see, y is a quadratic function of t, so graph is a parabola. }
end{align*}
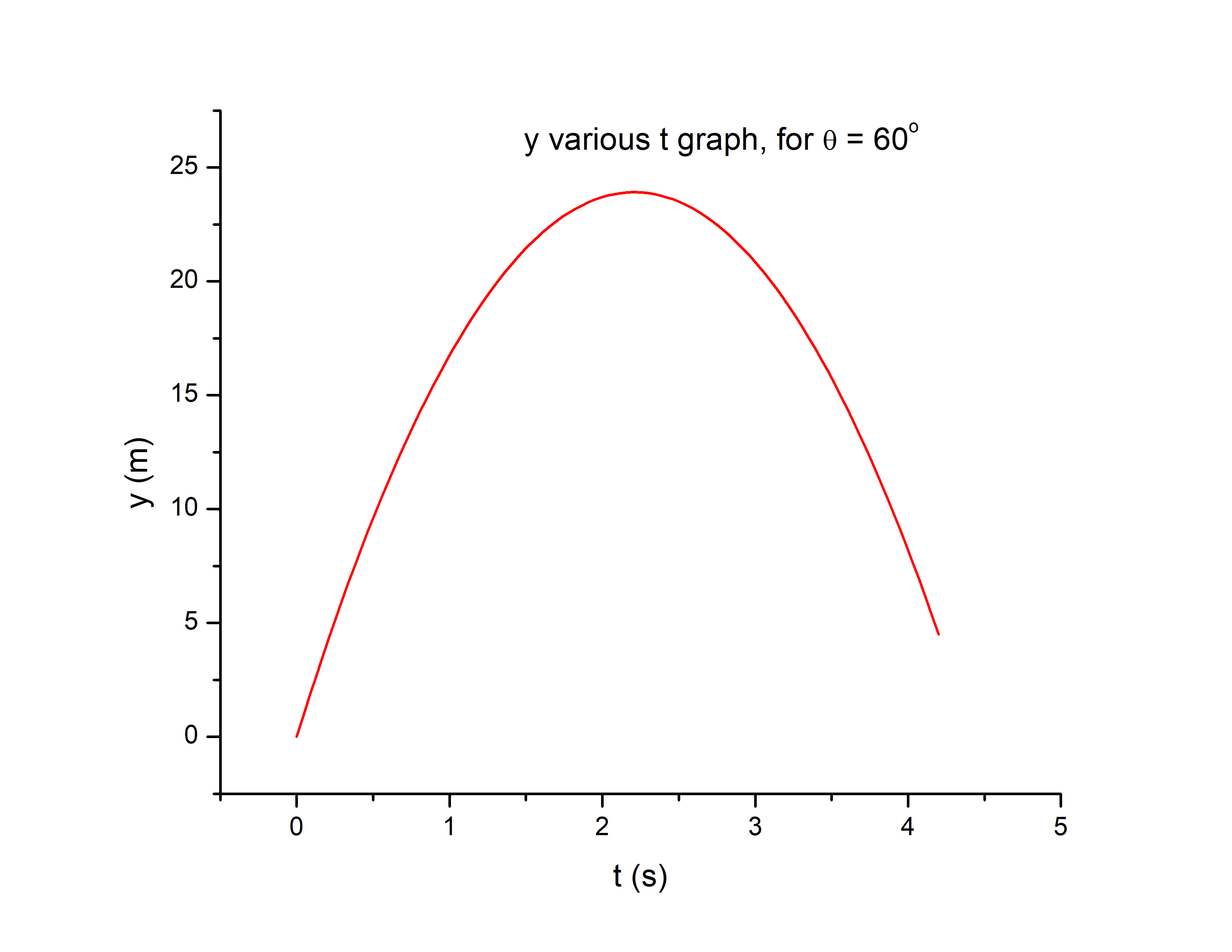
intertext{Case B:}
intertext{We need to draw x various t, and y various t graph. Data known:}
&v=25hspace{1mm}frac{m}{s}\
&theta=30^{circ}
intertext{Horizontal velocity remains constant, during motion, so we can find x using that information:}
&v_x=frac{x}{t}\
intertext{We can find $v_x$ using $v$ and $theta$:}
&v_x=vcos theta\
&v_x=25 cos 30\
&v_x=25cdot 0.866\
&v_x=21.65hspace{1mm}frac{m}{s}\
rightarrow\
&x=v_xt\
&x=21.65t\
intertext{As we can see, x is linear function of t, where $v_x=21.65hspace{1mm}frac{m}{s}$ is slope of a graph.}
end{align*}
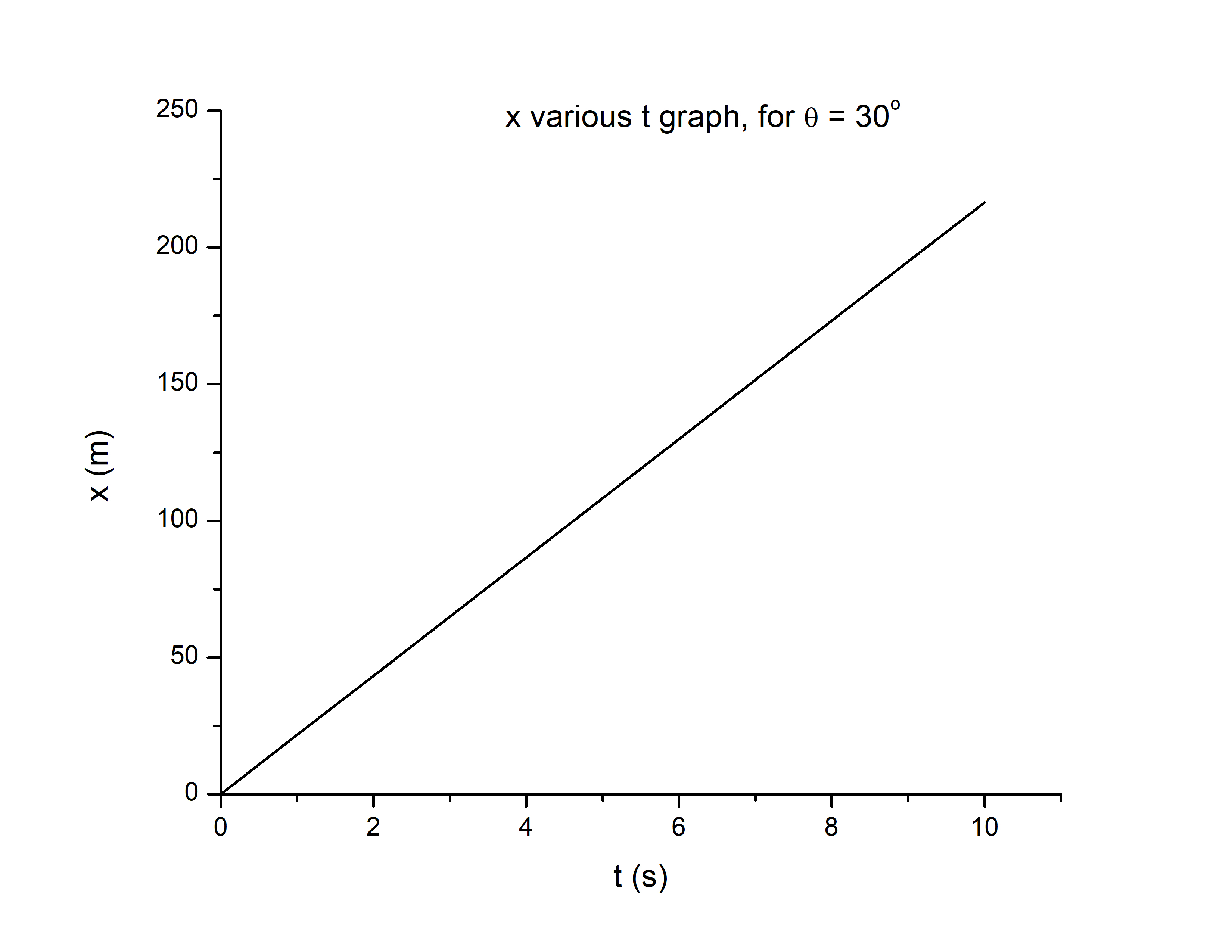
intertext{We know that y is:}
&y=v_{yi}t-frac{1}{2}gt^2\
intertext{We can find $v_{yi}$ using $v$ and $theta$:}
&v_{yi}=vsin theta\
&v_{yi}=25 sin 30\
&v_{yi}=25cdot 0.5\
&v_{yi}=12.5hspace{1mm}frac{m}{s}\
rightarrow\
&y=12.5t-frac{1}{2}9.8t^2\
intertext{As we can see, y is a quadratic function of t, so graph is a parabola. }
end{align*}
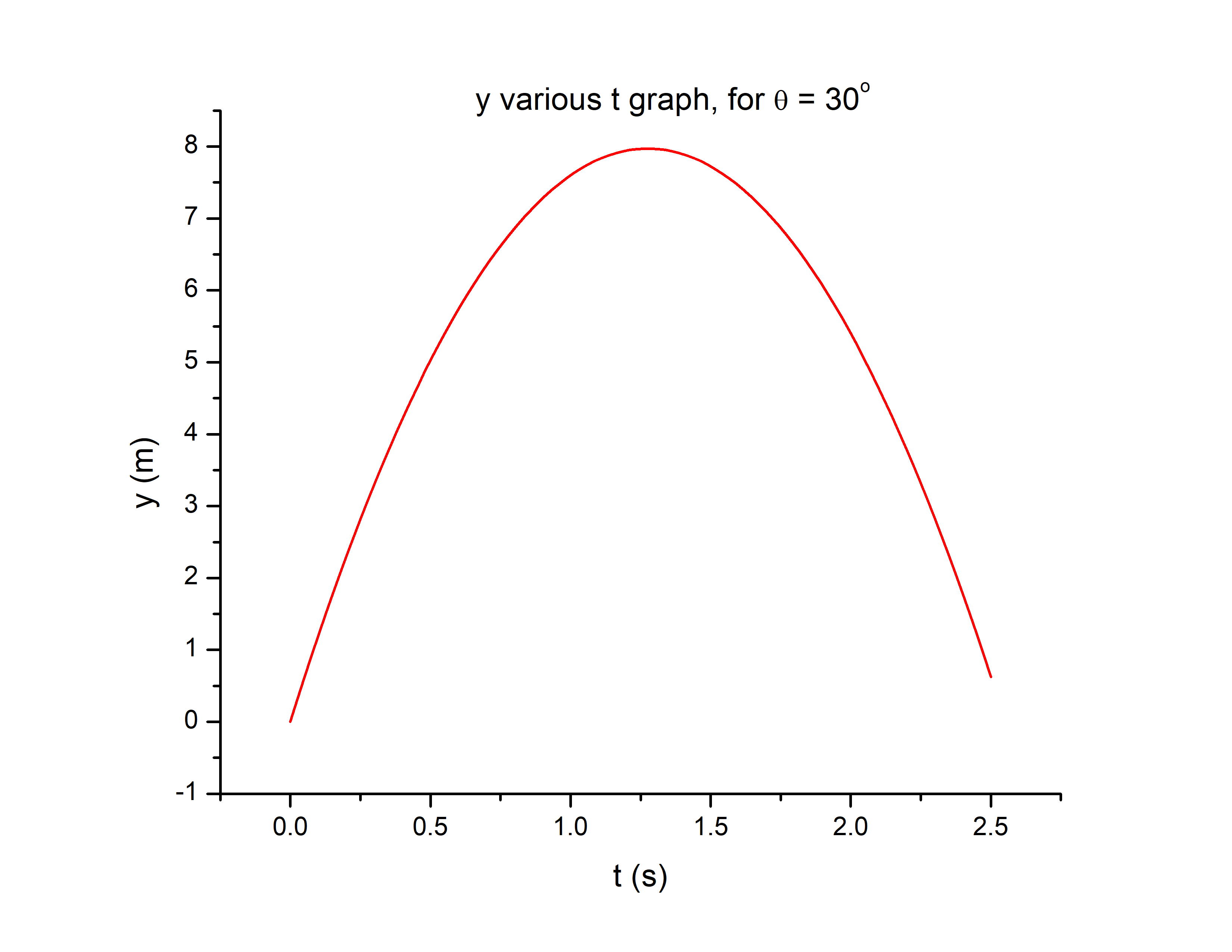
intertext{Case A:}
&x=12.5t\
intertext{As we can see, x is linear function of t, where $v_x=12.5hspace{1mm}frac{m}{s}$ is slope of a graph.}
&y=21.65t-frac{1}{2}9.8t^2\
intertext{As we can see, y is a quadratic function of t, so graph is a parabola. }
intertext{Case B:}
&x=21.65t\
intertext{As we can see, x is linear function of t, where $v_x=21.65hspace{1mm}frac{m}{s}$ is slope of a graph.}
&y=12.5t-frac{1}{2}9.8t^2\
intertext{As we can see, y is a quadratic function of t, so graph is a parabola. }
end{align*}
$$
begin{align*}
v_x &= 2.8 ,mathrm{frac{m}{s}}\
t &= 2.6 ,mathrm{s}
end{align*}
$$
$$
begin{align*}
v_x &= 12.4 ,mathrm{frac{m}{s}}\
y&= 0.32 ,mathrm{m}
end{align*}
$$
where $v_x$ is the horizontal velocity and $y$ the distance where the dart hits the board.
$$
begin{align}
y = v_{yi}t – frac{1}{2}gt^2
end{align}
$$
such that $v_{yi}$ is the initial velocity with respect to the $y$-axis and $g$ is the gravitational acceleration.
begin{align*}
y &= v_{yi}t – frac{1}{2}gt^2
intertext{Since, the initial velocity in the $y$-axis, $v_{yi}$, is zero, we can remove the term from the equation.}
y &= -frac{1}{2}gt^2\
&= -frac{1}{2}left(9.8 ,mathrm{frac{m}{s^2}}right)(2.6 ,mathrm{s})^2\
&= -33 ,mathrm{m} text{, so the height of the platform is } boxed{33 ,mathrm{m}}
end{align*}
We will use the equation
$$
begin{align}
x = v_{x}t
end{align}
$$
such that $v_x$ is the horizontal velocity and $t$ is time which you hit the water.
$$
begin{align*}
x &= v_{x}t\
&= left(2.8 ,mathrm{frac{m}{s}} right)(2.6 ,mathrm{s})\
&= boxed{7.3 ,mathrm{m}}
end{align*}
$$
$$
x = 7.3 ,mathrm{m}
$$
$y = (-1/2) (9.80) (2.6)^2$
$y = 33 m$
The horizontal distance is:
$$
x = v_x t = 2.8 times 2.6 = 7.3 m
$$
$$
begin{align*}
theta &= 30/0^{circ}\
v_i &= 49 ,mathrm{frac{m}{s}}
end{align*}
$$
such that $theta$ is the angle in which the arrow is fired, and $v$ is the velocity of the arrow.
$$
begin{align}
v_{y}^2 = v_{yi}^2 -2gy
end{align}
$$
such that $v_{yi}$ is the initial velocity in the $y$-axis, $v_y$ is the velocity in the $y$-axis and $g$ is the acceleration due to gravity.
$$
begin{align}
v_{yi} = v_i sin{theta}
end{align}
$$
begin{align*}
v_{y}^2 &= v_{yi}^2 -2gy
intertext{since we know that the final velocity of the arrow is emph{zero}.}
v_{yi}^2 &= 2gy\
frac{v_{yi}^2}{2g} &= y\
frac{(v_i sin{theta})^2}{2g} &= y
end{align*}
$$
begin{align*}
y &= frac{(v_i sin{theta})^2}{2g}\
&= frac{left(left(49 ,mathrm{frac{m}{s}}right)sin{(30.0^{circ})}right)^2}{2 left(9.8,mathrm{frac{m}{s^2}}right)}\
&= boxed{31 ,mathrm{m}}
end{align*}
$$
$$
begin{align}
x = v_{x}t
end{align}
$$
such that $v_{x}$ is the velocity of the arrow with respect to the $x$-axis and time $t$ is the flight time of the arrow.
$$
begin{align}
v_x = v_i cos{theta}
end{align}
$$
and for time $t$, we can derive it from the equation
$$
begin{align}
y = v_{yi}t + frac{1}{2}gt^2
end{align}
$$
$$
begin{align*}
0 &= (v_{yi} = v_i sin{theta})t – frac{1}{2}gt^2\
frac{1}{2}gt^2 &= (v_i sin{theta})t\
frac{1}{2}gt &= (v_i sin{theta})\
t &= frac{2(v_i sin{theta})}{g}
end{align*}
$$
$$
begin{align*}
x &= v_{x}t\
&= (v_i cos{theta})(frac{2(v_i sin{theta})}{g})\
&= left(left(49 ,mathrm{frac{m}{s}}right)cos{}{(30.0^{circ})}right) left(frac{2left(left(49 ,mathrm{frac{m}{s}}right)sin{(30.0^{circ})}right)}{9.8 ,mathrm{frac{m}{s^2}}}right)\
&= boxed{2.1 times 10^2 mathrm{m}}
end{align*}
$$
$x = 2.1 times 10^2 mathrm{m}$
intertext{Data known:}
&theta=45^{circ}\
&x=98hspace{1mm}m
intertext{We are looking for initial velocity. }
intertext{We know that y is equal to zero, because the fence is at the same height
as the pitch, and we know
that :}
&y=v_{yi}t-frac{1}{2}gt^2\
&0=v_{yi}t-frac{1}{2}gt^2\
intertext{We can transform expression:}
&0=t(v_{yi}-frac{1}{2}gt)\
intertext{If this expression is true, we have two options, either is $t=0$, or $v_{yi}-frac{1}{2}gt=0$. Time is not zero, ball needed some time for movement, so:}
&v_{yi}-frac{1}{2}gt=0&(1)
intertext{We know that: }
&v_{yi}=v_i sin theta
intertext{We need to rewrite t, using some expression. We can use:}
&v_x=frac{x}{t}\
rightarrow\
&t=frac{x}{v_x}\
\
&v_{xi}=v_i cos theta\
rightarrow\
&t=frac{x}{v_i cos theta}\
end{align*}
intertext{Now we can put expressions for t and $v_{yi}$ into equastion (1)}
&v_{yi}-frac{1}{2}gt=0&(1)\
&v_i sin theta-frac{1}{2}gfrac{x}{v_i cos theta}=0\
&v_i sin theta=frac{1}{2}gfrac{x}{v_i cos theta}\
intertext{We are looking for initial velocity:}
&v_i^2=frac{gx}{2sin theta cos theta}\
\
&v_i^2=frac{9.8cdot 98}{2cdot 0.707 cdot 0.707}\
&v_i^2=960\
&v_i=sqrt{960}\
&v_i=31hspace{1mm}frac{m}{s}
intertext{Velocity is vector, it has magnitude and direction, so velocity is $v_i=31hspace{1mm}frac{m}{s}$ at $45^{circ}$.}
end{align*}
intertext{ $v_i=31hspace{1mm}frac{m}{s}$ at $45^{circ}$.}
end{align*}
$$
begin{align*}
theta &= 45^{circ}\
x &= 98 ,mathrm{m}
end{align*}
$$
such that $theta$ is the angle in which the ball is launched, and $x$ is the distance it travels.
begin{align}
v_{x} &= v_i cos{theta}\
v_{iy} &= v_i sin{theta}
intertext{Since we know that the angle is $45^{circ}$, we can say that}
v_{x} &= v_{iy}
end{align}
such that $v_x$ is the velocity with respect to the $x$-axis and $v_{iy}$ is the initial velocity with respect to the $y$-axis.
$$
begin{align}
y = v_{iy}t – frac{1}{2}gt^2
end{align}
$$
such that $y$ change in height with respect to the launching point, and time $t$ which is the duration of the ball’s flight.
$$
begin{align}
x &= v_{x}t
end{align}
$$
such that $t$ is the duration of the ball’s flight to distance $x$, and $v_x$ is the velocity with respect to the $x$-axis.
$$
begin{align*}
x &= v_{x}t\
frac{x}{v_i cos{theta}} &= t
end{align*}
$$
begin{align*}
y &= v_{iy}t – frac{1}{2}gt^2
intertext{Since the change in height of the ball is emph{zero},}
0 &= (v_{iy} – frac{1}{2}gt)t\
0 &= v_{iy} – frac{1}{2}gt
intertext{We know that $v_{iy} = v_x$, so we can use the equation for $v_x$.}
0 &= v_i cos{theta} – frac{1}{2}g left(frac{x}{v_i cos{theta}}right)\
0 &= (v_i cos{theta})^2 – frac{1}{2}gx\
frac{1}{2}gx &= (v_i cos{theta})^2 \
frac{1}{2(cos{theta})^2}gx &= (v_i)^2 \
sqrt{frac{1}{2(cos{theta})^2}gx} &= v_i
end{align*}
$$
begin{align*}
v_i &= sqrt{frac{1}{2(cos{theta})^2}gx}\
&= sqrt{frac{1}{2(cos{(45^{circ})^2}} left(9.8,mathrm{frac{m}{s^2}}right)(98 ,mathrm{m})}\
&= boxed{31 ,mathrm{frac{m}{s}}}
end{align*}
$$
v_i = 31 ,mathrm{frac{m}{s}} text{ at } 45^{circ}
$$
$$
begin{align*}
y &= 1001,mathrm{m}\
v_x &= 125 ,mathrm{frac{km}{h}}
end{align*}
$$
such that $y$ is the height of the plane above the ocean, and $v_x$ is the plane’s velocity with respect to the $x$-axis.
$$
begin{align}
y = v_{iy}t – frac{1}{2}gt^2
end{align}
$$
such that $y$ is the distance of the plane from the sea, $v_{iy}$ is the initial velocity of the plane with respect to the $y$-axis.
begin{align*}
y &= v_{iy}t – frac{1}{2}gt^2
intertext{since $v_{iy} = 0$,}
y &= -frac{1}{2}gt^2\
-frac{2y}{g} &= t^2\
sqrt{-frac{2y}{g}} &= t
end{align*}
$$
begin{align*}
t &= sqrt{-frac{2y}{g}}\
&= sqrt{-frac{2(-1001 ,mathrm{m}}{left(9.8 frac{m}{s^2}right)}}\
&= boxed{14.3 ,mathrm{s}}
end{align*}
$$
$$
begin{align}
x = v_{x}t
end{align}
$$
$$
begin{align*}
x &= v_{x}t\
&= left(125 ,mathrm{frac{km}{h}} cdot frac{1 ,mathrm{h}}{3600 ,mathrm{s}} cdot frac{1000 ,mathrm{m}}{1 ,mathrm{km}}right)(14.3 ,mathrm{s})\
&= boxed{497 ,mathrm{m}}
end{align*}
$$
$$
x = 497 ,mathrm{m}
$$
intertext{Data known from the problem:}
&y=1001hspace{1mm}m\
&v=125hspace{1mm}frac{m}{s}
intertext{Part a:}
intertext{We can find time using formula: }
&y=v_{yi}-frac{1}{2}gt^2
intertext{Airplane, as well as a box, does not have initial vertical velocity $v_{yi}=0$.}
&y=-frac{1}{2}gt^2\
&t=sqrt{frac{2y}{g}}\
&t=sqrt{2(-1001)}{9.8}\
&t=14.3hspace{1mm}s\
end{align*}
intertext{Part b:}
intertext{We are looking for horizontal distance when box is dropped.}
intertext{Horizontal velocity remains the same during motion}
&v_x=frac{x}{t}\
&x=v_xt\
\
&v_x=v_{xi}=const
intertext{Airplane only has horizontal velocity, so horizontal velocity is equal to total initial velocity}
&v_x=v_i=125hspace{1mm}frac{m}{s}\
intertext{We need to convert this into $frac{m}{s}$, because t is in seconds:}
&v_x=125frac{1000}{3600}\
&v_x=34.72hspace{1mm}frac{m}{s}\
\
&x=34.72cdot 14.3\
&x=496.5hspace{1mm}m
end{align*}
intertext{Part a:}
&t=14.3hspace{1mm}s
intertext{Part b:}
&x=496.5hspace{1mm}m
end{align*}
$$
begin{align*}
y &= 61 ,mathrm{m}\
x &= 23 ,mathrm{m}
end{align*}
$$
such that $y$ is the height of the cliff from the ocean and $x$ is the extension of rocks below the cliff.
$$
begin{align}
v_x= frac{x}{t}
end{align}
$$
$$
begin{align}
y = v_{iy}t – frac{1}{2}gt^2
end{align}
$$
begin{align*}
y &= v_{iy}t – frac{1}{2}gt^2
intertext{since $v_{iy} = 0$,}
y &= -frac{1}{2}gt^2\
-frac{2y}{g} &= t^2\
sqrt{-frac{2y}{g}} &= t
end{align*}
begin{align*}
v_x &= frac{x}{t}\
&= frac{x}{sqrt{-frac{2y}{g}}}\
intertext{Now, plugging in the given values and solving for $v_x$.}
v_x &= frac{x}{sqrt{-frac{2y}{g}}}\
&= frac{(23 ,mathrm{m})}{sqrt{-frac{2(-61 ,mathrm{m})}{9.8 ,mathrm{frac{m}{s^2}}}}}\
&= boxed{6.4 ,mathrm{frac{m}{s}}}
end{align*}
v_x = 6.4 ,mathrm{frac{m}{s}}
$$
$y = (-1/2) g t^2$
$==> t = sqrt{dfrac{-2y}{g}} = sqrt{dfrac{(-2) (-61)}{9.8}} = 3.528 s$
In the x direction:
$$
v_x = dfrac{x}{t} = dfrac{23}{3.528} = 6.5 m/s
$$
6.5 m/s
$$
intertext{Data known:}
&theta=51^{circ}\
&x=14hspace{1mm}m
intertext{We are looking for initial speed. }
intertext{We know that y is equal to zero:}
&y=v_{yi}t-frac{1}{2}gt^2\
&0=v_{yi}t-frac{1}{2}gt^2\
intertext{We can transform expression:}
&0=t(v_{yi}-frac{1}{2}gt)\
intertext{If this expression is true, we have two options, either is $t=0$, or $v_{yi}-frac{1}{2}gt=0$. Time is not zero, ball needed some time for movement, so:}
&v_{yi}-frac{1}{2}gt=0&(1)
intertext{We know that: }
&v_{yi}=v_i sin theta
intertext{We need to rewrite t, using some expression. We can use:}
&v_x=frac{x}{t}\
rightarrow\
&t=frac{x}{v_x}\
\
&v_{xi}=v_i cos theta\
rightarrow\
&t=frac{x}{v_i cos theta}\
end{align*}
intertext{Now we can put expressions for t and $v_{yi}$ into equastion (1)}
&v_{yi}-frac{1}{2}gt=0&(1)\
&v_i sin theta-frac{1}{2}gfrac{x}{v_i cos theta}=0\
&v_i sin theta=frac{1}{2}gfrac{x}{v_i cos theta}\
intertext{We are looking for initial speed:}
&v_i^2=frac{gx}{2sin theta cos theta}\
\
&v_i^2=frac{9.8cdot 14}{2cdot 0.777 cdot 0.629}\
&v_i^2=140\
&v_i=sqrt{140}\
&v_i=11.83hspace{1mm}frac{m}{s}
end{align*}
begin{align*}
&v_i=11.83hspace{1mm}frac{m}{s}
end{align*}
$$
$$
begin{align*}
theta &= 51^{circ}\
x &= 14.0 ,mathrm{m}
end{align*}
$$
such that $theta$ is the angle in which the ball is thrown, and $x$ is the distance it travels to the basket.
$$
begin{align}
v_{ix} &= v_i cos{theta}\
v_{iy} &= v_i sin{theta}
end{align}
$$
such that $v_{ix}$ is the initial velocity with respect to the $x$-axis and $v_{iy}$ is the initial velocity with respect to the $y$-axis.
$$
begin{align}
y = v_{iy}t – frac{1}{2}gt^2
end{align}
$$
such that $y$ change in height with respect to the launching point, and time $t$ which is the duration of the ball’s flight.
$$
begin{align}
x &= v_{x}t
end{align}
$$
such that $t$ is the duration of the ball’s flight to distance $x$, and $v_{ix}$ is the velocity with respect to the $x$-axis.
$$
begin{align*}
x &= v_{ix}t\
frac{x}{v_i cos{theta}} &= t
end{align*}
$$
begin{align*}
y &= v_{iy}t – frac{1}{2}gt^2
intertext{Since the change in height of the ball is emph{zero},}
0 &= (v_{iy} – frac{1}{2}gt)t\
0 &= v_{iy} – frac{1}{2}gt\
0 &= v_{i} sin{theta} – frac{1}{2}g left(frac{x}{v_i cos{theta}}right)\
0 &= v_{i}^{2} (sin{theta})(cos{theta}) – frac{1}{2}gx\
frac{1}{2}gx &= v_{i}^{2} (cos{theta})(sin{theta}) \
frac{1}{2(cos{theta})(sin{theta})}gx &= (v_i)^2 \
sqrt{frac{gx}{2(cos{theta})(sin{theta})}} &= v_i
end{align*}
$$
begin{align*}
v_i &= sqrt{frac{gx}{2(cos{theta})(sin{theta})}}\
&= sqrt{frac{left(9.8,mathrm{frac{m}{s^2}}right)(14.0 ,mathrm{m})}{2(cos{(51^{circ})})(sin{(51^{circ})})}}\
&= boxed{11.8 ,mathrm{frac{m}{s}}}
end{align*}
$$
v_i = 11.8 ,mathrm{frac{m}{s}} text{ at } 51^{circ}
$$
$a_c = dfrac{4 pi^2 r}{T^2} = dfrac{(4)*(3.1416)^2*(50.0)}{(14.3)^2} = 9.65 m/s^2$
b)
$$
F = m a = (615)*(9.65) = 5940 N
$$
b) $5940 N$
$$
begin{align*}
m &= 615 ,mathrm{kg}\
T &= 14.3 ,mathrm{s}\
r &= 50.0 ,mathrm{m}
end{align*}
$$
such that $m$ is the mass of the racing car, $T$ is the period it takes for a lap to be completed, and lastly, $r$ is the radius of the track.
$$
begin{align}
a_c = frac{4pi^{2}r}{T^2}
end{align}
$$
where $a_c$ is the centripetal acceleration of the racing car.
$$
begin{align*}
a_c &= frac{4pi^{2}r}{T^2}\
&= frac{4pi^{2}(50.0 ,mathrm{m})}{(14.3 ,mathrm{s})^2}\
&= boxed{9.59 ,mathrm{frac{m}{s^2}}}
end{align*}
$$
$$
begin{align}
F_c = ma_c
end{align}
$$
where $F_c$ is the centripetal force and $m$ is the mass of the racing car.
$$
begin{align*}
F_c &= ma_c\
&= (615 ,mathrm{kg})(9.59 ,mathrm{frac{m}{s^2}})\
&= boxed{5.90 times 10^3 ,mathrm{N}}
end{align*}
$$
$$
F_c = 5.90 times 10^3 ,mathrm{N}
$$
$$
begin{align*}
m &= 7.00 ,mathrm{kg}\
r &= 1.8 ,mathrm{m}\
T &= 1.0 ,mathrm{s}
end{align*}
$$
where $m$ is the mass of the hammer, $r$ is the distance of the hammer from the axis of rotation, and $T$ is the time it takes for one revolution.
$$
begin{align}
a_c = frac{4pi^{2}r}{T^2}
end{align}
$$
where $r$ is the radius and $T$ is the period.
$$
begin{align*}
a_c &= frac{4pi^{2}r}{T^2}\
&= frac{4pi^{2}(1.8,mathrm{m})}{(1.0,mathrm{s})^2}\
&= boxed{71 ,mathrm{frac{m}{s^2}}}
end{align*}
$$
$$
begin{align}
F_c = ma_c
end{align}
$$
$$
begin{align*}
F_c &= ma_c\
&= (7.00 ,mathrm{kg})left(71 ,mathrm{frac{m}{s^2}}right)\
&= boxed{5.0 times 10^2 ,mathrm{N}}
end{align*}
$$
$$
F_c = 5.0 times 10^2 ,mathrm{N}
$$
$$
begin{align*}
m&= 7 mathrm{kg} \
R&= 1.8 mathrm{m} \
T&=1 mathrm{s}
end{align*}
$$
Unknown:
$$
begin{align*}
a_{cp}&=? \
F_t&=?
end{align*}
$$
$a_{cp}$ centripetal aceleration
$F_t$ tension force
$$
begin{align*}
v&=dfrac{s}{t}\
&=dfrac{2pi R}{T}\
v^2&=dfrac{4{pi}^2 R^2}{T^2}
end{align*}
$$
We then compute centripetal acceleration from an expression derived a few pages earlier. Notice that $R ^ 2$ in the numerator is canceld out by $R$ in the denominator.
$$
begin{align*}
a_{cp}&=dfrac{v^2}{R}\
&=dfrac{4pi ^2R}{T^2}\
&=dfrac{4pi^2 1.8 mathrm{m} }{1 mathrm{s^2}}\
&=boxed{71 mathrm{ dfrac{m}{s^2}}}
end{align*}
$$
$$
begin{align*}
F_t=F_{cp}&=ma_{cp}\
&=7 mathrm{kg} cdot 71 mathrm{m/s^2}\
&=boxed{497 mathrm{N}}
end{align*}
$$
a_{cp}=71 mathrm{dfrac{m}{s^2}}
$$
$$
F_t = 497 mathrm{N}
$$
$a_c = dfrac{4 pi^2 r}{T^2} = dfrac{(4)*(3.1416)^2*(1.8)}{(1.0)^2} = 71 m/s^2$
The tension in the chain is:
$$
F = m a = (7.0)*(71) = 500 N
$$
intertext{Data known from the problem:}
&f=33frac{1}{3}hspace{1mm}frac{rev}{min}\
&r_1=5hspace{1mm}cm=0.05hspace{1mm}m\
&r_2=10hspace{1mm}cm=0.1hspace{1mm}m\
&r_1=15hspace{1mm}cm=0.15hspace{1mm}m\
end{align*}
intertext{Case A:}
intertext{The turntable on which vinyl sits is rotating with constant angular velocity, therefore the coin is in uniform circular motion. That means the coin has centripetal acceleration which is directed toward the center of the vinyl.}
end{align*}
intertext{Case B:}
intertext{In this part we have to find acceleration of coin at 3 different positions}
intertext{To do that first we have to find period of rotation T using the given frequency of rotation f}
&f=33.33hspace{1mm}frac{rev}{min}\
&T=frac{1}{f}=frac{1}{33.33frac{rev}{min}}=0.03hspace{1mm}min\
intertext{For calculating acceleration it is more convenient to have T in seconds, so we multiply this expression with 60 as every minute has 60 seconds.}
&T=0.03cdot 60=1.8hspace{1mm}s\
intertext{To calculate acceleration we use expression for centripetal acceleration :}
&a_c=frac{4pi ^2 r}{T^2}
end{align*}
intertext{For $r_1=5hspace{1mm}m$:}
&a_1=frac{4pi ^2 hspace{1mm}0.05}{(1.8)^2}\
&a_1=frac{4cdot 9.87cdot 0.05hspace{1mm}}{3.24}\
&a_1=0.61hspace{1mm}frac{m}{s^2}\
intertext{In the same way we calculate $a_2$ and $a_3$:}
intertext{For $r_2=10hspace{1mm}m$:}
&a_2=frac{4cdot 9.87cdot 0.1hspace{1mm}}{3.24}\
&a_2=1.21hspace{1mm}frac{m}{s^2}\
intertext{For $r_3=15hspace{1mm}m$:}
&a_3=frac{4cdot 9.87cdot 0.15hspace{1mm}}{3.24}\
&a_3=1.83hspace{1mm}frac{m}{s^2}\
end{align*}
intertext{Case C:}
intertext{Frictional force between coin and vinyl accelerates the coin}
end{align*}
intertext{Case D:}
intertext{Frictional force needed to keep the coin on the turntable is dependent of the centripetal acceleration $F_f=ma_c$, so the coin is most likely to fly of the table at 15cm since there is the greatest acceleration, and with that the greatest friction needed to keep it on the vinyl}
end{align*}
intertext{Case A: Toward the center of the vinyl}
intertext{Case B:}
&a_1=0.61hspace{1mm}frac{m}{s^2}\
&a_2=1.21hspace{1mm}frac{m}{s^2}\
&a_3=1.83hspace{1mm}frac{m}{s^2}\
intertext{Case C: Frictional force }
intertext{Case D: At 15cm.}
end{align*}
$a_c = dfrac{v^2}{r} = dfrac{(2010)^2}{0.153} = 2.64 times 10^7 m/s^2$
b)
$$
F = m a = (0.001)*(2.64 times 10^7) = 2.64 times 10^4 N
$$
b) $2.64 times 10^4 N$
– Length: $l = 15.3 mathrm{~cm}$;
– Speed: $v = 2010 ,frac{text{m}}{text{s}}$;
– Mass: $m = 1 mathrm{~g}$;
**Required:**
a) The acceleration $a_text c$;
b) The force on the object $F$;
$$begin{align*}
a_text c = frac{v^2}{r} &&(1) \
F &= ma &&(2)
end{align*}$$
$$begin{align*}
a_text c &= frac{v^2}{l} \
&= dfrac{ left( 2010 ,frac{text{m}}{text{s}} right)^2}{15.3 mathrm{~cm}} \
&= dfrac{ left( 2010 ,frac{text{m}}{text{s}} right)^2}{0.153 mathrm{~m}} \
&= 2.64 times 10^7 ,frac{text{m}}{text{s}^2}
end{align*}$$
$$boxed{ a_text c = 2.64 times 10^7 ,frac{text{m}}{text{s}^2} }$$
$$begin{align*}
F &= m a_text c \
&= 1 mathrm{~g} cdot 2.64 times 10^7 ,frac{text{m}}{text{s}^2} \
&= 0.001 mathrm{~kg} cdot 2.64 times 10^7 ,frac{text{m}}{text{s}^2} \
&= 2.64 times 10^4 mathrm{~N}
end{align*}$$
$$boxed{ F = 2.64 times 10^4 mathrm{~N}}$$
&text{a) } a_text c = 2.64 times 10^7 ,frac{text{m}}{text{s}^2} \
&text{b) }F = 2.64 times 10^4 mathrm{~N}
end{align*}$$
intertext{Data known from the problem:}
&r=80.0hspace{1mm}m\
&mu =0.40\
end{align*}
intertext{Frictional force is needed for car to turn. It provides centripetal acceleration.}
intertext{In our problem car travels around flat circular race track, so at the maximum speed of the car around this track we have that centripetal force and frictional force are equal. From that relation we can find the maximum speed.}
&F_c=frac{mv^2}{r}\
&F_f=mu F_N=mu mg\
intertext{As we said for maximum speed these two forces need to be equal.}
&F_c=F_f\
&frac{mv^2}{r}=mu mg\
&v^2=mu gr\
&v=sqrt{mu gr}\
&v=sqrt{0.40cdot 9.80cdot 80.0}\
&v=17.7hspace{1mm}frac{m}{s}\
end{align*}
begin{align*}
&v=17.7hspace{1mm}frac{m}{s}\
end{align*}
$$
intertext{Data known from the problem:}
&r=18m\
end{align*}
intertext{At the slowest speed of the motorcycle, centripetal force and gravitational force acting on the motorcycle (i.e. it’s weight) are equal.}
&F_c=frac{mv^2}{r}\
&F_g=mg\
&F_c=F_g\
&frac{mv^2}{r}=mg\
&v^2=rg\
&v=sqrt{rg}\
&sqrt{18cdot 9.80}\
&v=13.28hspace{1mm}frac{m}{s}\
end{align*}
begin{align*}
&v=13.28hspace{1mm}frac{m}{s}\
end{align*}
$$
intertext{Data known from the problem:}
&m=75hspace{1mm}kg\
&v=120hspace{1mm}frac{m}{s}\
end{align*}
intertext{Since pilot does not push against the belt, but hang freely in the seat that means that the centripetal force $F_c$ and gravitational force acting on him (i.e. his weight) $F_g$ are equal.}
&F_c=ma_c=frac{mv^2}{r}\
&F_g=mg\
intertext{Now we equal out these two forces:}
&F_c=F_g\
&frac{mv^2}{r}=mg\
&r=frac{v^2}{g}\
&r=frac{(120)^2}{9.80}\
&r=1469.39hspace{1mm}mapprox 1.5hspace{1mm}km\
end{align*}
begin{align*}
&r=1469.39hspace{1mm}mapprox 1.5hspace{1mm}km\
end{align*}
$$
$v_{a/air}$ aircraft velocity relative to air
$v_{tw}$ velocity of tailwind relative to ground
$v_{hw}$ velocity of headwind relative to ground
$v_{a/g}$ velocity of aircraft relative to ground
Assuming that the plane is moving in a positive direction then the signs of velocity will be as follows:
$$
v_{a/air} > 0, v_{tw} > 0, v_{hw} <0
$$
Note that the sign of the velocity refers to its direction.
Known:
$$
begin{align*}
v_{a/air}&=200 mathrm{km/h}\
v_{tw}&=50 mathrm{km/h}\
v_{hw}&=-50 mathrm{km/h}
end{align*}
$$
Unknown:
$$
v_{a/g}=?
$$
$$
v_{a/c}=v_{a/b}+v_{b/c}
$$
The relative velocity of object a to object c is the $textbf{vector sum}$ of object a’s
velocity relative to object b and object b’s velocity relative to object c. In this case object a is aircraft, object b is air and object c is ground. Because it is a $textbf{vector sum}$, we must pay close attention to the $textbf{sign of velocity}$.
$$
begin{align*}
v_{a/g}&=v_{a/air}+v_{tw}\
&=200 mathrm{km/h}+50 mathrm{km/h}\
&=250 mathrm{km/h}
end{align*}
$$
$$
begin{align*}
v_{a/g}&=v_{a/air}-v_{hw}\
&=200 mathrm{km/h}-50 mathrm{km/h}\
&=150 mathrm{km/h}
end{align*}
$$
b) $v_{a/g}=150 mathrm{km/h}$
200.0 km/h + 50.0 km/h = 250.0 km/h
$$
200.0 km/h – 50.0 km/h = 150.0 km/h
$$
$$
begin{align*}
v_r=4 mathrm{m/s} \
v_{river}=2 mathrm{m/s} \
l=1.5 mathrm{km}=1500 mathrm{m}
end{align*}
$$
Unknown: winner
$v_r$ running/rowing speed
$$
begin{align*}
v&=dfrac{s}{t}\
t&=dfrac{s}{v}
end{align*}
$$
When calculating Odina’s time, we divide the total path by the velocity.
$$
begin{align*}
t_{Odina}&=dfrac{2l}{v}\
&=dfrac{2cdot1500 mathrm{m}}{4 mathrm{m/s}}\
&= 750 mathrm { s}
end{align*}
$$
When calculating LaToya’s time we have to be careful because half the way the river velocity has the same direction as LaToya and the other half the opposite.
$$
begin{align*}
t_{Latoya}&=dfrac{l}{v_r+v_{river}}+dfrac{l}{v_r-v_{river}}\
&=dfrac{1500 mathrm{m} }{6 mathrm{m/s}}+dfrac{1500 mathrm{m}}{2 mathrm{m/s}}\
&=1000 mathrm{ s}\
t_{Odina}&<t_{LaToya}
end{align*}
$$
The winner is Odina because it took her less time.
intertext{Data known from the problem:}
&v_w=3hspace{1mm}frac{m}{s}\
&v_b=4hspace{1mm}frac{m}{s}\
end{align*}
intertext{Case A:}
intertext{Velocity of the boat relative to shore is sum of vectors $v_b$ and $v_w$}
intertext{We can calculate intensity of vector of velocity as:}
&v_{rel}^2=v_b^2+v_w^2\
&v_{rel}=sqrt{v_b^2+v_w^2}\
&v_{rel}=sqrt{4^2+3^2}\
&v_{rel}=5hspace{1mm}frac{m}{s}\
intertext{Direction of velocity is determined by angle $alpha$ relative to shore. We can calculate that angle as:}
&tanalpha=frac{v_b}{v_w}\
&alpha=tan^{-1}(frac{v_b}{v_w})\
&alpha=tan^{-1}(frac{4}{3})\
&alpha=53^o\
end{align*}
intertext{Case B:}
intertext{Parallel component of velocity to the shore is:}
&v_w=3hspace{1mm}frac{m}{s}\
intertext{Perpendicular component of velocity to the shore is:}
&v_b=4hspace{1mm}frac{m}{s}\
end{align*}
intertext{a: $v_{rel}=5hspace{1mm}frac{m}{s}$; $alpha=53^o$}
intertext{b: $parallel=v_w=3hspace{1mm}frac{m}{s}$; $perpendicular=v_b=4hspace{1mm}frac{m}{s}$}
end{align*}
intertext{Data known from the problem:}
&v_{ba}=15hspace{1mm}frac{m}{s}\
&v_a=6.5hspace{1mm}frac{m}{s}\
end{align*}\
intertext{Velocity of balloon is sum of vectors $v_b$ and $v_{ba}$}
intertext{We can calculate intensity of vector of velocity as:}
&v_b^2=v_a^2+v_{ba}^2\
&v_b=sqrt{v_a^2+v_{ba}^2}\
&v_b=sqrt{15^2+6.5^2}\
&v_b=16.35hspace{1mm}frac{m}{s}\
intertext{Direction of velocity is determined by angle $alpha$. We can calculate that angle as:}
&tanalpha=frac{v_{ba}}{v_a}\
&alpha=tan^{-1}(frac{v_{ba}}{v_a})\
&alpha=tan^{-1}(frac{15}{6.5})\
&alpha=67^ohspace{1mm}text{west of vertical}\
end{align*}
begin{align*}
&v_b=16.35hspace{1mm}frac{m}{s}\
&alpha=67^ohspace{1mm}text{west of vertical}\
end{align*}
$$
begin{align*}
&theta=53^ohspace{1mm}text{west of north}\
&v_b=6hspace{1mm}frac{m}{s}hspace{1mm}text{due north}
end{align*}
$$
intertext{Case A:}
intertext{We are looking for velocity of current. We can fi.nd it using angle given in the problem.}
intertext{We can use tan, because we know that tan is The length of the side opposite the angle divided by the length of the adjacent side}
&tan theta=frac{v_c}{v_b}
intertext{$v_c$ is velocity of a current, and $v_b$ is velocity of boat, relative to the shore.}
&v_c=tan theta v_b\
&v_c=tan(53) 6\
&v_c=8hspace{1mm}frac{m}{s}
intertext{Velocity has magnitude and direction, direction is given in the problem: to east.}
end{align*}
intertext{Case B:}
intertext{We are looking for speed of a boat, relative to the water.. We can find it using angle given in the problem.}
intertext{We can use cos, because we know that cosine is the length of the adjacent side divided by the length of the hypotenuse.}
&cos theta=frac{v_b}{v_{bw}}
intertext{$v_{bw}$ is velocity of a boat relative to the river, and $v_b$ is velocity of boat, relative to the shore.}
&v_{bw}=frac{v_b}{cos theta}\
&v_{bw}=frac{6}{cos 53}\
&v_{bw}=10hspace{1mm}frac{m}{s}
intertext{Speed only has magnitude, so that is the answer.}
end{align*}
intertext{Case A:}
&v_c=8hspace{1mm}frac{m}{s}hspace{1mm}text{to east}\
intertext{Case B:}
&v_{bw}=10hspace{1mm}frac{m}{s}
end{align*}
intertext{Data known from the problem:}
&y=450hspace{1mm}kmhspace{1mm}text{Distance you want to reach, to south}\
&t=3hspace{1mm}hhspace{1mm}text{time you have for that}\
&v_w=50hspace{1mm}frac{km}{h}hspace{1mm}text{Velocity of wind,directed from the west}
end{align*}
intertext{We are looking for velocity of airplane you need, velocity is a vector, so we are looking for magnitude and direction}
intertext{We want that airplane is flying to south, and wind is blowing from west, so velocity of airplane has two components, south component and component that has same magnitude as wind, but opposite direction, which means from east. $v_a$ is velocity of airplane, $v_{as}$ is south component of it, and $v_{ae}$ is component from the east:}
&v_a=sqrt{v_{as}^2+v_{ae}^2}
intertext{As we already said, $v_{ae}$ has the same magnitude as wind so it is equal to $50hspace{1mm}frac{km}{h}$. Now we should find south component. It remains constant, so we cam find it using given data:}
&v_{as}=frac{y}{t}\
&v_{as}=frac{450}{3}\
&v_{as}=150hspace{1mm}frac{km}{h}\
end{align*}
intertext{Now we can find velocity of airplane:}
&v_a=sqrt{v_{as}^2+v_{ae}^2}\
&v_a=sqrt{150^2+50^2}\
&v_a=158hspace{1mm}frac{km}{h}
end{align*}
intertext{Now we have to find direction. We can use tan function, because we know that tan is The length of the side opposite the angle divided by the length of the adjacent side}
&tan theta=frac{v_{ae}}{v_{as}}\
&tan theta=frac{50}{150}\
&tan theta=0.33\
&theta=tan^{-1}(0.33)\
&theta=18.26^o
end{align*}
begin{align*}
&v_a=158hspace{1mm}frac{km}{h}hspace{1mm}text{$18.26^o$ west of south}
end{align*}
$$
intertext{Given data:}
&r=6.38cdot10^3hspace{1mm}km\
&m=97hspace{1mm}kg
end{align*}
intertext{Part A:}
intertext{We are looking for speed of person who has 97 kg, at the equator.Formula for speed:}
&v=frac{d}{t}
intertext{In this case t is period of earth rotation which is 24 h, and d is circumference }
&v=frac{2rpi}{24}\
&v=frac{2cdot6.38 cdot 10^3 cdot3.14}{24}\
&v=1669.43hspace{1mm}frac{km}{h}
intertext{Let’s convert this into $frac{m}{s}$}
&v=1669.43 frac{1000}{3600}frac{m}{s}\
&v=463.7hspace{1mm}frac{m}{s}
end{align*}
intertext{Part B:}
intertext{We are looking for force needed to accelerate person in case A. And it’s path should be circle, so that is centripetal force. Formula for centripetal force is: }
&F_c=mfrac{v^2}{r}\
&F_c=97frac{463.7^2}{6.38cdot10^6}
intertext{We converted km to m, because speed has units $frac{m}{s}$}
&F_c=3.27hspace{1mm}N
end{align*}
intertext{Part C:}
intertext{We are looking for weight of a person. It is actually force that is equal to mass multiplied by gravity acceleration.}
&W=mg\
&W=97cdot9.8\
&W=950.6hspace{1mm}N
end{align*}
intertext{Part D:}
intertext{Person’s apparent weight in this case is difference between weight and centripetal force:}
&F_N=W-F_c\
&F_N=950.6-3.27\
&F_N=947.33hspace{1mm}N
end{align*}
intertext{Part A:}
&v=463.7hspace{1mm}frac{m}{s}\
intertext{Part B:}
&F_c=3.27hspace{1mm}N\
intertext{Part C:}
&W=950.6hspace{1mm}N\
intertext{Part D:}
&F_N=947.33hspace{1mm}N
end{align*}
$$
v = 375 + 782 = 1160 m/s
$$
1160 m/s
$$
$$
v = 2.75 – 1.25 = 1.50 km/s
$$
1.50 km/s
$$
– Speed: $v_{text{r/o}} = 1.25 ,frac{text{km}}{text{s}}$;
– Speed: $v_{text{g/r}} = 2.75 ,frac{text{km}}{text{s}}$;
**Required:**
– The relative speed $v_{text{g/o}}$;
$$begin{align*}
v_{text{g/o}} &= v_{text{r/o}} + v_{text{g/r}} \
&= 1.25 ,frac{text{km}}{text{s}} + left( -2.75 ,frac{text{km}}{text{s}} right) \
&= – 1.5 ,frac{text{km}}{text{s}} \
&= – 1500 ,frac{text{m}}{text{s}} \
end{align*}$$
intertext{Data known from the problem:}
&x=500hspace{1mm}m\
&v_{dog}=2.5hspace{1mm}frac{m}{s}\
&v_{dragonfly}=3hspace{1mm}frac{m}{s}\
intertext{We are looking for total distance a dragonfly passed, when dogs run
into each other.}
intertext{First we will find how much time dogs need to run
into each other}
intertext{Dogs are moving with the same speed, but opposite direction, so they will run
into each other in half of total distance between them, so we can find time needed for that using formula:}
&v_{dog}=frac{frac{x}{2}}{t}\
&t=frac{frac{x}{2}}{v_{dog}}\
&t=frac{frac{500}{2}}{2.5}\
&t=100hspace{1mm}s
intertext{Now we can find total distance a dragonfly passed, when dogs run
into each other, using formula: }
&v_{dragonfly}=frac{d}{t}\
&d=v_{dragonfly}t\
&d=3cdot100\
&d=3hspace{1mm}m
end{align*}
begin{align*}
&d=3hspace{1mm}m
end{align*}
$$
intertext{Data known from the problem:}
&m=1.13hspace{1mm}kg\
&r=0.5hspace{1mm}m\
&v=2.4hspace{1mm}frac{m}{s}\
intertext{We are looking for tension in the cord at the
bottom of the ball’s motion}
intertext{In this case we have gravity force that is applied on a ball, direction of that force is downwards, and centripetal force. Tension is sum of those forces. Let’s find those forces first. }
&F_g=mg\
&F_g=1.13cdot9.8\
&F_g=11.074approx 11.08hspace{1mm}N\
\
&F_c=mfrac{v^2}{r}\
&F_c=1.13frac{2.4^2}{0.5}\
&F_c=13.0176approx 13.02hspace{1mm}N
intertext{Tension force:}
&F_t=F_g+F_c\
&F_t=11.08+13.02\
&F_t=24.1hspace{1mm}N
end{align*}
begin{align*}
&F_t=24.1hspace{1mm}N
end{align*}
$$
$textbf{a.)}$ For 35mph: $v = 15.7 ,mathrm{frac{m}{s}}$
$textbf{b.)}$ For 45mph: $v = 20.1 ,mathrm{frac{m}{s}}$
such that $r$ is the radius, and $v$ is the velocity of the car.
intertext{Using the equation,}
F_c &= F_g\
intertext{Such that $F_c$ is the centripetal force and $F_g$ is the gravitational force, }
F_c &= frac{mv^2}{r} cos{theta}\
intertext{where for the centripetal force, $m$ is the mass of the car, $v$ is its velocity, and $r$ is its radius, and}
F_g &= mg sin{theta}
intertext{such that $m$ is also the mass of the car and $g$ is the gravitational acceleration}
end{align*}
intertext{We can then equate these two equations and find $theta$.}
F_c &= F_g\
frac{mv^2}{r} cos{theta} &= mg sin{theta}\
frac{v^2}{r} &= g left( frac{sin{theta}}{cos{theta}} right)\
intertext{Since $frac{cos{theta}}{sin{theta}} = tan{theta}$, thus}
frac{v^2}{r} &= g tan{theta}\
theta &= tan^{-1} left(frac{v^2}{gr} right)
end{align*}
$$
textbf{a.)}v = 15.7,mathrm{frac{m}{s}}
$$
$$
begin{align*}
theta &= tan^{-1} left(frac{v^2}{gr} right)\
&= tan^{-1} left(frac{(15.7,mathrm{frac{m}{s}})^2}{(9.8,mathrm{frac{m}{s^2}})(36.0,mathrm{m})} right)\
&= boxed{34.9^{circ}}
end{align*}
$$
$$
textbf{b.)}v = 15.7,mathrm{frac{m}{s}}
$$
$$
begin{align*}
theta &= tan^{-1} left(frac{v^2}{gr} right)\
&=tan^{-1} left(frac{(20.1,mathrm{frac{m}{s}})^2}{(9.8,mathrm{frac{m}{s^2}})(36.0,mathrm{m})} right)\
&= boxed{48.9^{circ}}
end{align*}
$$
intertext{Data known from the problem:}
&r=36hspace{1mm}m\
&v_1=15.7hspace{1mm}frac{m}{s}\
&v_2=20.1hspace{1mm}frac{m}{s}\
intertext{We are looking for at what angle
should the road be banked.}
intertext{In order to find that angle, we should first see what forces are applied on car. There is centripetal force and gravity force. Because road is not flat, there is angle, Object’s gravity force, as well as centripetal force has components. And one component is in direction of motion, and the other one is at $90^o$ from that. If we want car to stay on circle, those components of centripetal force and gravity force that are in direction of movement, have to be equal. }
&F_c costheta = F_g sin theta\
end{align*}
begin{align*}
&frac{F_c }{F_g }=frac{sin theta}{cos theta}\
&frac{F_c }{F_g }=tan theta\
&frac{mfrac{v_1^2}{r}}{mg}=tan theta\
&frac{v_1^2}{gr}=tan theta\
& tan theta=frac{15.7^2}{9.8cdot 36}\
&tan theta=0.698\
&theta=tan^{-1}(0.698)\
&theta=34.9^o
end{align*}
$$
intertext{For $v_2$:}
&frac{v_2^2}{gr}=tan theta\
& tan theta=frac{20.1^2}{9.8cdot 36}\
&tan theta=1.145\
&theta=tan^{-1}(1.145)\
&theta=48.9^o
end{align*}
intertext{For $v_1$:}
&theta=34.9^o\
intertext{For $v_2$:}
&theta=48.9^o
end{align*}
$$
begin{align*}
m &= 1.45 ,mathrm{kg}\
r &= 0.80 ,mathrm{m}\
theta &= 14.0^{circ}
end{align*}
$$
such that $m$ is the mass of the ball, $r$ is the length of the string, $theta$ is the angle, from the vertical, in which the ball is spinning.
$$
begin{align}
F_c = F_{T}cos{theta} = mg
end{align}
$$
where $F_{T}$ is the tension acting on the string, $m$ is the mass, $g$ is the acceleration due to gravity, and $theta$ is the angle in which the tension is acting on the string with respect to the vertical.
begin{align*}
F_{T}cos{theta} &= mg\
F_{T} &= frac{mg}{cos{theta}}
intertext{To solve for the tension $F_{T}$, we can know plug in the corresponding values.}
F_{T} &= frac{mg}{cos{theta}}\
&= frac{(1.45 ,mathrm{kg})(9.8,mathrm{frac{m}{s^2}})}{cos{(14.0^{circ}})}\
&= boxed{14.6 ,mathrm{N}}
end{align*}
$$
begin{align}
F_c = F_{T}sin{theta} = mg = F_{T}cos{theta} = ma_c
end{align}
$$
{}
such that these are the possible values for the centripetal force $F_c$.
We also know that
$$
begin{align}
a_c = frac{v^2}{r}
end{align}
$$
such that $a_c$ is the centripetal acceleration.
$$
begin{align*}
F_{T}sin{theta} &= mg = F_{T}cos{theta} = ma_c \
frac{F_{T}sin{theta}}{F_{T}cos{theta}} &= frac{ma_c}{mg}\
tan{theta} &= frac{a_c}{g}\
tan{theta} &= frac{v^2}{r}cdotfrac{1}{g}\
rg tan{theta} &= v^2\
sqrt{rg tan{theta}} &= v
end{align*}
$$
$$
begin{align*}
v &= sqrt{rg tan{theta}}\
&= sqrt{(0.80 ,mathrm{m})left(9.8,mathrm{frac{m}{s^2}}right)cdot tan{(14.0^{circ})}}\
&= boxed{1.40 ,mathrm{frac{m}{s}}}
end{align*}
$$
F_{T} = 14.6 ,mathrm{N} text{ and } v = 1.40 ,mathrm{frac{m}{s}}
$$
intertext{Data given in the problem:}
&theta=35^o\
&v_b=22hspace{1mm}frac{m}{s}\
&v_o=2.5hspace{1mm}frac{m}{s}\
intertext{We are looking for initial distance between the hitter and outfielder, and we know that the the ball is caught at the same height
at which it was hit.Also there is a hint in problem that there are 2 solutions.}
end{align*}
intertext{First we are looking for time before ball is caught. }
intertext{We can find it using formula:}
&y=v_{yb}t-frac{1}{2}gt^2\
intertext{y is equal to zero, because he ball is caught at the same height
at which it was hit.}
&0=v_{yb}t-frac{1}{2}gt^2\
&v_{yb}t=frac{1}{2}gt^2\
&v_{yb}=frac{1}{2}gt\
&t=frac{2v_{yb}}{g}\
&t=frac{2v_b sin theta}{g}\
&t=frac{2cdot 22 sin 35}{9.8}\
&t=2.56hspace{1mm}s
end{align*}
intertext{To find distance x, we need to find horizontal component of it’s velocity:}
&v_{xb}=v_b cos 35\
&v_{xb}=22 cos 35\
&v_{xb}=18.04hspace{1mm}frac{m}{s}
intertext{Now we can find distance:}
intertext{It can be sum or difference between distance that ball passed and distance that outfielder passed.}
&x_1=x_b+x_o\
&x_2=x_b-x_0\
\
&x_1=v_{xb}t+v_ot\
&x_1=18.04cdot 2.56+2.5 cdot2.56\
&x_1=52.58hspace{1mm}m\
\
&x_2=v_{xb}t+v_ot\
&x_2=18.04cdot 2.56-2.5 cdot2.56\
&x_2=39.78hspace{1mm}m\
end{align*}
begin{align*}
&x_1=52.58hspace{1mm}m\
&x_2=39.78hspace{1mm}m\
end{align*}
$$
intertext{Data known from the problem:}
&y=60hspace{1mm}m\
&x=20hspace{1mm}m\
&v_{bj}=7.3hspace{1mm}frac{m}{s}hspace{1mm}text{
speed of a bag of jewels}\
intertext{We are looking for velocity of the balloon, if we want Shifty to easily catch the bag}
intertext{We can find that speed using formula bellow, because it is said in the problem that speed of a balloon is constant:}
&v_b=frac{y_b}{t}\
intertext{$y_b$ is height of balloon, and t is time needed for bag of jewels to get into balloon.}
end{align*}\
intertext{We can find that time using speed of the bag of jewels. We have initial speed of that beg and it is said in the problem that it is a horizontal speed, and horizontal component of speed remains constant,so:}
&v_{bj}=frac{x}{t}\
rightarrow\
&t=frac{x}{v_{bj}}\
&t=frac{20}{7.3}\
&t=2.74hspace{1mm}s\
intertext{Now we should find $y_b$. Balloon is going upward, and bag is going downward from the building that has height 60 m. So height of balloon, when bag gets inside it, is:}
&y_b=y-y_{bj}\
&y_b=60-y_{bj}\
end{align*}
intertext{Now we should find height of bag $y_{bj}$, we can use formula:}
&y_{bj}=v_{iybj}t-frac{1}{2}gt^2\
intertext{Bag only has horizontal initial velocity, so $v_{iybj}=0$.}
&y_{bj}=-frac{1}{2}gt^2\
&y_{bj}=-frac{1}{2}(-9.8)cdot 2.74^2\
intertext{We put time we calculated because we are looking for height at thre moment when a bag falls into the balloon. }
&y_{bj}=36.79hspace{1mm}m\
intertext{Now we can calculate $y_b$:}
&y_b=60-y_{bj}\
&y_b=60-36.79\
&y_b=23.21hspace{1mm}m\
intertext{Now we can calculate velocity:}
&v_b=frac{y_b}{t}\
&v_b=frac{23.21}{2.74}\
&v_b=8.47hspace{1mm}frac{m}{s}
intertext{Direction is direction of y axis.}
end{align*}
&v_b=8.47hspace{1mm}frac{m}{s}
intertext{Direction is direction of y axis.}
end{align*}
intertext{Data known from the problem:}
&x=6.02hspace{1mm}m\
&y_f=3.05hspace{1mm}m\
&y_i=2.2hspace{1mm}m\
&theta_1=30^o\
&theta_2=60^o\
intertext{We are looking for speed the
ball needs if we want that ball to make the basket, it is initial speed.}
end{align*}\
intertext{We know y and x, so we can start from those expressions:}
&y_f-y_i=v_{yi}t-frac{1}{2}gt^2\
intertext{We can write $v_{yi}$ using velocity that we are looking for, and angle:}
&v_{yi}=v_i sin theta\
&y_f-y_i=v_i sin theta t-frac{1}{2}gt^2&(1)\
intertext{We can rewrite t, using:}
&v_{xi}=frac{x}{t}\
&t=frac{x}{v_{xi}}\
&v_{xi}=v_i cos theta\
rightarrow\
&t=frac{x}{v_i cos theta}\
intertext{Now let’s put this expression in expression (1)}
&y_f-y_i=v_i sin theta frac{x}{v_i cos theta}-frac{1}{2}g(frac{x}{v_i cos theta})^2\
end{align*}
&y_f-y_i= x tan theta -frac{1}{2}g(frac{x^2}{v_i^2 cos^2 theta})\
&2(y_f-y_i)v_i^2 cos^2 theta=2 x tan theta v_i^2 cos^2 theta-gx^2
intertext{We can find $v_i$:}
&v_i^2(2 x tan theta cos^2 theta-2(y_f-y_i)cos^2)=gx^2\
\
&v_i^2=frac{gx^2}{(2 x tan theta cos^2 theta-2(y_f-y_i)cos^2)}\
\
&v_i=sqrt{frac{gx^2}{(2 x tan theta cos^2 theta-2(y_f-y_i)cos^2)}}\
\
&v_i=frac{x}{cos theta}sqrt{frac{g}{(2 x tan theta -2(y_f-y_i))}}
end{align*}
intertext{For $theta_1=30^o$:}
&v_i=frac{x}{cos 30}sqrt{frac{g}{(2 x tan 30 -2(y_f-y_i))}}\
&v_i=frac{6.02}{0.866}sqrt{frac{9.8}{(2 cdot6.02 cdot0.577 -2(3.05-2.2))}}\
&v_i=9.5hspace{1mm}frac{m}{s}\
end{align*}
intertext{For $theta_2=60^o$:}
&v_i=frac{x}{cos 60}sqrt{frac{g}{(2 x tan 60 -2(y_f-y_i))}}\
&v_i=frac{6.02}{0.5}sqrt{frac{9.8}{(2 cdot6.02 cdot1.73 -2(3.05-2.2))}}\
&v_i=8.6hspace{1mm}frac{m}{s}\
end{align*}
intertext{For $theta_1=30^o$:}
&v_i=9.5hspace{1mm}frac{m}{s}\
intertext{For $theta_2=60^o$:}
&v_i=8.6hspace{1mm}frac{m}{s}\
end{align*}
intertext{We need to vary the speed at each angle
by 5 percent:}
intertext{For $theta=30^o$}
&v=9.5hspace{1mm}frac{m}{s}\
&0.95cdot v=9.025\
&y_f-y_i= x tan theta -frac{1}{2}g(frac{x^2}{v_i^2 cos^2 theta})\
&3.02-2.2=x tan 30 -frac{1}{2}9.8(frac{x^2}{9.025^2 cos^2 30})\
&0.85=0.577x -4.9(frac{x^2}{81.45cdot 0.749})\
&0.85=0.577x -0.08x^2\
intertext{This is quadratic equation, and after we solve it and use larger value for x, we have:}
&x=5.15hspace{1mm}m
intertext{x was 6.02, so change in range is 0.9 m}
&1.05cdot v=9.975\
&y_f-y_i= x tan theta -frac{1}{2}g(frac{x^2}{v_i^2 cos^2 theta})\
&3.02-2.2=x tan 30 -frac{1}{2}9.8(frac{x^2}{9.975^2 cos^2 30})\
&0.85=0.577x -4.9(frac{x^2}{96.5cdot 0.749})\
&0.85=0.577x -0.068x^2\
intertext{This is quadratic equation, and after we solve it and use larger value for x, we have:}
&x=6.89hspace{1mm}m
intertext{x was 6.02, so change in range is 0.9 m}
end{align*}
intertext{We need to vary the speed at each angle
by 5 percent:}
intertext{For $theta=60^o$}
&v=8.6hspace{1mm}frac{m}{s}\
&0.95cdot v=8.17\
&y_f-y_i= x tan theta -frac{1}{2}g(frac{x^2}{v_i^2 cos^2 theta})\
&3.02-2.2=x tan 60 -frac{1}{2}9.8(frac{x^2}{8.17^2 cos^2 60})\
&0.85=1.73 x -4.9(frac{x^2}{66.75cdot 0.25})\
&0.85=1.73x -0.29x^2\
intertext{This is quadratic equation, and after we solve it and use larger value for x, we have:}
&x=5.37hspace{1mm}m
intertext{x was 6.02, so change in range is 0.6 m}
&1.05cdot v=9.03\
&3.02-2.2=x tan 60 -frac{1}{2}9.8(frac{x^2}{9.03^2 cos^2 60})\
&0.85=1.73 x -4.9(frac{x^2}{81.54cdot 0.25})\
&0.85=1.73x -0.24x^2\
intertext{This is quadratic equation, and after we solve it and use larger value for x, we have:}
&x=6.66hspace{1mm}m
intertext{x was 6.02, so change in range is around 0.65 m}
end{align*}
intertext{From this we can conclude that if launch angle is higher, it is less sensitive to speed variation. }
end{align*}\
intertext{ Higher the angle, lower the sensitivity to speed variation. }
end{align*}
intertext{Let’s find y as a
function of its distance from home plate, which is x:
}
intertext{We can start from expressions for x and $Delta y=y_f-y_i$:}
&y_f-y_i=v_{yi}t-frac{1}{2}gt^2\
intertext{We can write $v_{yi}$ using initial velocity, and angle:}
&v_{yi}=v_i sin theta\
&y_f-y_i=v_i sin theta t-frac{1}{2}gt^2&(1)\
intertext{We can rewrite t, using:}
&v_{xi}=frac{x}{t}\
&t=frac{x}{v_{xi}}\
&v_{xi}=v_i cos theta\
rightarrow\
&t=frac{x}{v_i cos theta}\
intertext{Now let’s put this expression in expression (1)}
&y_f-y_i=v_i sin theta frac{x}{v_i cos theta}-frac{1}{2}g(frac{x}{v_i cos theta})^2\
&y_f-y_i= x tan theta -frac{1}{2}g(frac{x^2}{v_i^2 cos^2 theta})\
end{align*}\
intertext{Let’s put values for $v_i$ and $theta$ into equation, we know them from text of the problem, and let’s put value for g. We can also put value for $y_i$}
&theta=26^o\
&v_i=42hspace{1mm}frac{m}{s}\
&y_i=1hspace{1mm}m
\
&y_f-1= x tan 26 -frac{1}{2}9.8(frac{x^2}{42^2 cos^2 26})\
&y_f-1= x tan 26 -frac{1}{2}9.8(frac{x^2}{42^2 cos^2 26})\
&y_f=1+ 0.49x -frac{1}{2}9.8(frac{x^2}{1764cdot 0.8})\
&y_f=1+ 0.49x -frac{1}{2}9.8(frac{x^2}{1411})\
&y_f=1+ 0.49x -0.0035x^2\
intertext{Let’s plot this function:}
end{align*}
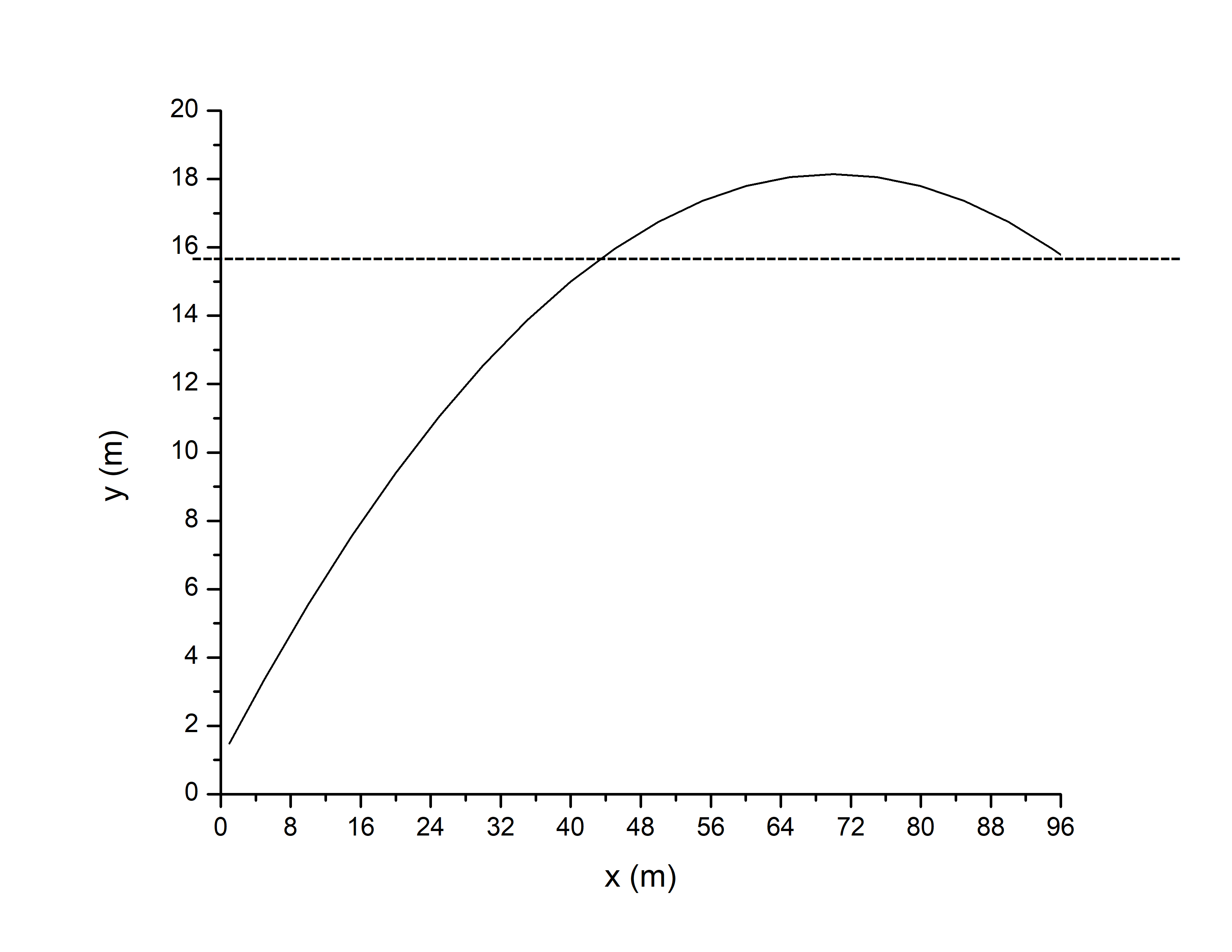
intertext{As we can see from the graph, when a ball is at the wall, which is $x=96$ m, ball is at the height around 15.7 m, we can see that at the graph. We can also calculate correct value, if we put $x=96$ m, into equation we used to plot the graph:}
&y_f=1+ 0.49x -0.0035x^2\
&y_f=1+ 0.49cdot 96 -0.0035cdot 96^2\
&y_f=15.784hspace{1mm}m\
intertext{Part a:}
intertext{We have to say if the hit is a home run.}
intertext{It is, ball gets on the wall. }
end{align*}
intertext{Part b:}
intertext{We are looking for minimal speed needed. We can find it from upper formula}
&y_f-y_i= x tan theta -frac{1}{2}g(frac{x^2}{v_i^2 cos^2 theta})\
&2(y_f-y_i)v_i^2 cos^2 theta=2 x tan theta v_i^2 cos^2 theta-gx^2
intertext{We can find $v_i$:}
&v_i^2(2 x tan theta cos^2 theta-2(y_f-y_i)cos^2)=gx^2\
\
&v_i^2=frac{gx^2}{(2 x tan theta cos^2 theta-2(y_f-y_i)cos^2)}\
\
&v_i=sqrt{frac{gx^2}{(2 x tan theta cos^2 theta-2(y_f-y_i)cos^2)}}\
\
&v_i=frac{x}{cos theta}sqrt{frac{g}{(2 x tan theta -2(y_f-y_i))}}
intertext{Let’s put values:}
&v_i=frac{96}{cos 26}sqrt{frac{9.8}{(2 cdot96 tan 26 -2(14-1))}}\
&v_i=41hspace{1mm}frac{m}{s}\
intertext{Part c:}
intertext{We are looking for range of angles if the ball goes over the wall, we conclude that is between $25^o$ and $70^o$}
end{align*}
intertext{Part a:}
intertext{Hit is a home run.}
intertext{Part b:}
&v_i=41hspace{1mm}frac{m}{s}\
intertext{Part c:}
intertext{ between $25^o$ and $70^o$}
end{align*}
intertext{Data known:}
intertext{$v_A$ is velocity of a rocket, $v_B$ is velocity of missile relative to rocket, and $v$ is velocity of missile relative to the fixed observer. Formula for $v$ is given in problem as well:}
&v=frac{v_A+v_B}{1+frac{v_Av_B}{c^2}}
intertext{c is speed of light, and it has value: $c=3cdot10^8hspace{1mm}frac{m}{s}$}
end{align*}\
intertext{First part}
intertext{Given data:}
&v_A=11hspace{1mm}frac{km}{s}\
&v_B=3cdot10^8hspace{1mm}frac{m}{s}
intertext{This value is $3cdot10^8hspace{1mm}frac{m}{s}$ because laser emits light. We have to convert units for $v_A$ into $frac{m}{s}$:}
&v_A=11hspace{1mm}frac{1000}{1}frac{m}{s}\
&v_A=11cdot10^3 hspace{1mm}frac{m}{s}
intertext{We are looking for speed of laser, relative to fixed observer, which is $v$, and we will call it $v_1$:}
&v_1=frac{v_A+v_B}{1+frac{v_Av_B}{c^2}}\
&v_1=frac{11cdot10 ^3+3cdot10^8}{1+frac{(11cdot10 ^3)cdot ( 3cdot10^8)}{(3cdot10^8)^2}}\
&v_1=3cdot10^8hspace{1mm}frac{m}{s}\
end{align*}
intertext{Second part}
intertext{Given data:}
&v_A=frac{c}{2}\
&v_B=frac{c}{2}
intertext{We are looking for speed of missle, relative to fixed observer, which is $v$, and we will call it $v_2$:}
&v_2=frac{v_A+v_B}{1+frac{v_Av_B}{c^2}}\
&v_2=frac{frac{c}{2}+frac{c}{2}}{1+frac{(frac{c}{2})(frac{c}{2})}{(c)^2}}\
&v_2=frac{c}{1+frac{frac{1}{4}}{1}}\
&v_2=frac{c}{1+frac{1}{4}}\
&v_2=frac{c}{frac{5}{4}}\
&v_2=frac{4}{5}c\
end{align*}
intertext{First part}
&v_1=3cdot10^8hspace{1mm}frac{m}{s}\
intertext{Second part}
&v_2=frac{4}{5}c\
end{align*}
intertext{We are talking about circular motion when a ball is going higher and lower in the air, it is not rotating around horizontal surface.}
intertext{We have to forces that are acting on a ball, it is a gravity force, which direction is always downward, and tension. Tension is pulling ball.Rope is pulling a ball, and that is the tension. In order to analyse motion of a ball, We have to imagine 2 cases:}
end{align*}
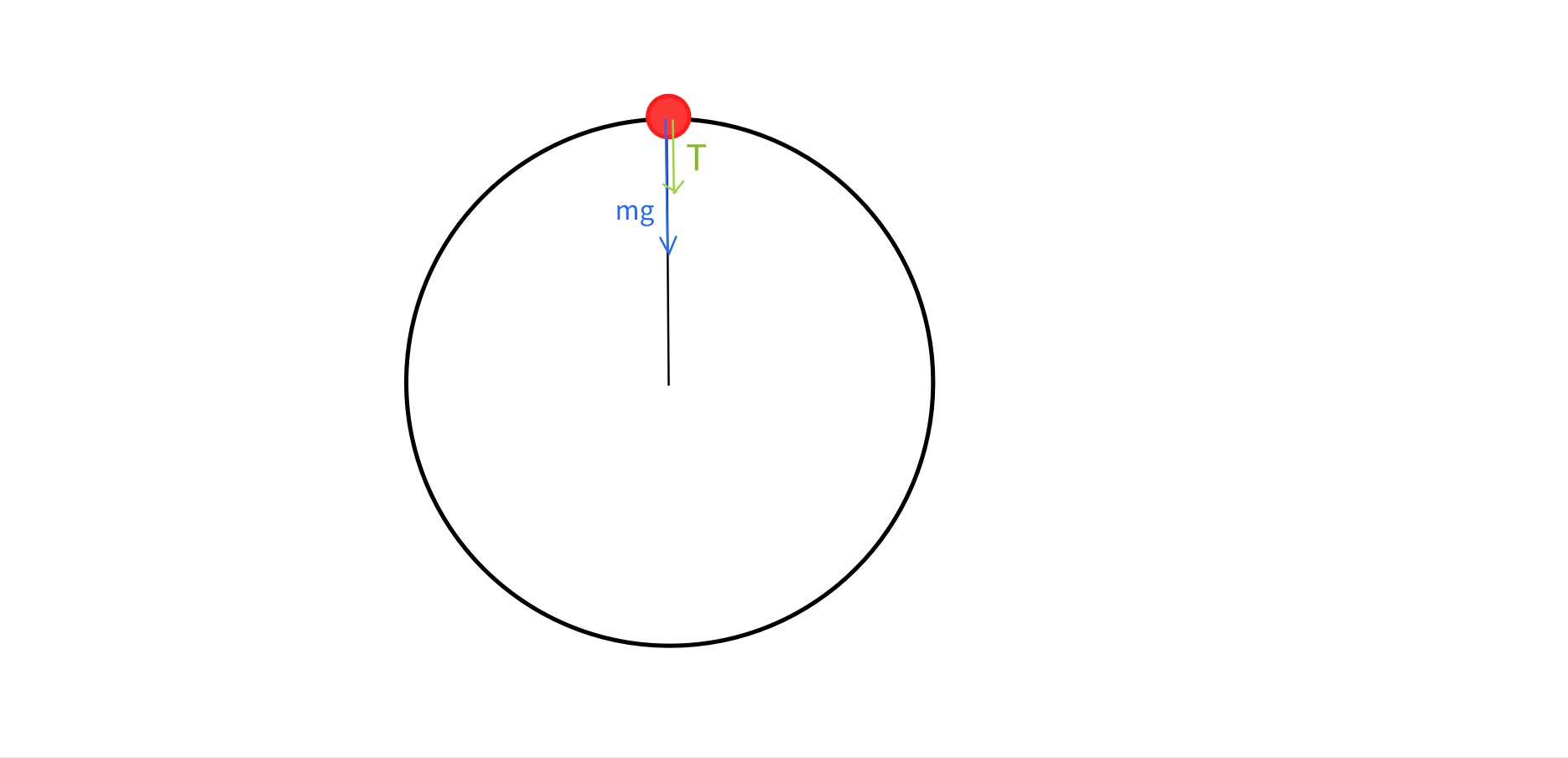
intertext{First case: When ball is at the highest possible height.}
intertext{So, gravity force is acting downward, as we already said, and tension is pulling a ball, rope is pulling a ball, so in this case it is also acting downward, like in picture below. Centripetal force, that keeps the ball in a circle, in this case is:}
&F_c=T+F_g\
&F_c=T+mg\
intertext{Because centripetal force has direction to the center of circle, those two forces have sign + before them.}
intertext{We know that centripetal force is:}
&F_c=mfrac{v^2}{r}
intertext{Where v is velocity of a ball, and r is radius of a circle, so:}
&mfrac{v^2}{r}=T+mg\
rightarrow\
&T=mfrac{v^2}{r}-mg\
end{align*}
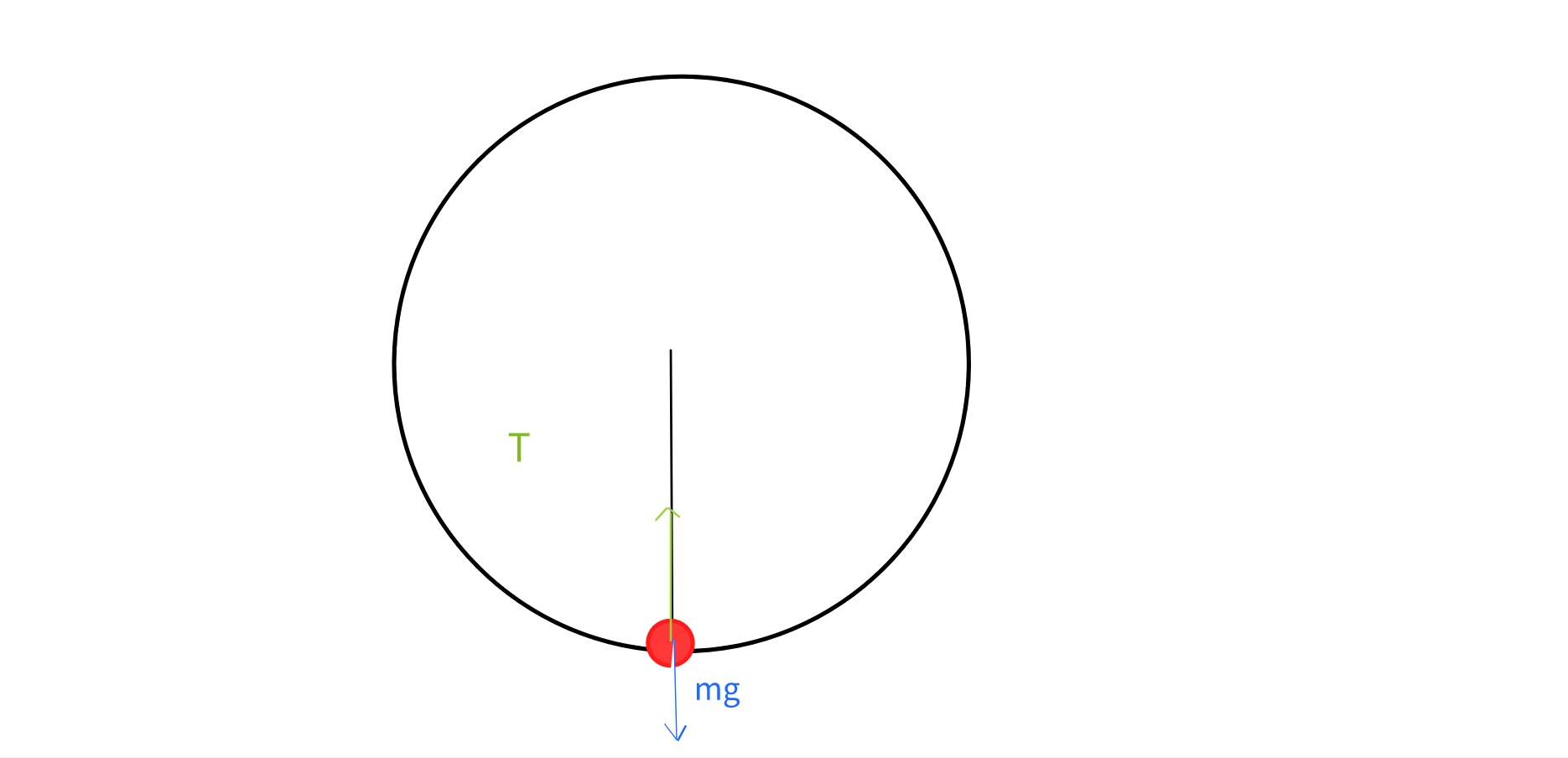
intertext{Second case: When ball is at the lowest possible height.}
intertext{So, gravity force is acting downward, as we already said, and tension is pulling a ball, rope is pulling a ball, so in this case it is acting upward, like in picture below. Centripetal force, that keeps the ball in a circle, in this case is:}
&F_c=T-F_g\
&F_c=T-mg\
intertext{Because centripetal force has direction to the center of circle, those two forces have signs + before tension, and – before gravity.}
intertext{We know that centripetal force is:}
&F_c=mfrac{v^2}{r}
intertext{Where v is velocity of a ball, and r is radius of a circle, so:}
&mfrac{v^2}{r}=T-mg\
rightarrow\
&T=mfrac{v^2}{r}+mg\
end{align*}
intertext{As we can see, gravity force in a first case has the same direction as tension and centripetal force, and opposite direction from them in second case. That means that because of that gravity increases the speed of a ball in first case, and decreases it in the second case, and also it is the same for acceleration. If we want to keep acceleration at constant value, tension must be higher in second case, in order to keep the centripetal force that keeps the ball on circle. We can see that from formulas, so this is not uniform circular motion,}
end{align*}
intertext{This is not uniform circular motion, we need to analyze two cases in order to see what is happening, when ball is at highest height, and at the lowest.}
end{align*}
Bumper cars are a great place to see Sir Isaac Newton’s three laws of motion in action. Here’s how:
Newton’s First Law: Every object in motion continues in motion and every object at rest continues to be at rest unless an outside force acts upon it. This is because all objects have inertia – the property of matter that resists changes to the object’s motion. Newton found that if a ball is sitting on a table, it will stay sitting there because that is what it ‘wants’ to do. If the ball is set in motion, it will keep traveling in a straight path because, again, that is what it ‘wants’ to do. An object in motion will not stop, slow down, or change its direction unless an outside force acts on it (such as gravity, friction, and air resistance). When you are riding in a bumper car and end up in a collision with another bumper car, you feel a jolt. This is because your body’s inertia wants it to keep traveling in the direction it was moving with the car even though your bumper car has now suddenly stopped.
Newton’s Second Law: The greater the mass of an object, the harder it is to change its speed. (More force is needed to move it.) You already know this law and practice it in your everyday life. Something that is small, such as a pebble, is much easier to pick up and throw than something that is large and heavy, such as a boulder. When riding in the bumper cars, you may have noticed that people who weigh less tend to get pushed around more than people who weigh more. The more mass (weight) an object has, the more force it takes to move it. And since all the bumper cars usually have the same top velocity, the cars carrying more mass will never travel as far as the cars carrying less mass after a collision.
Newton’s Third Law: For every action, there is an equal and opposite reaction. If two bumper cars traveling at the same speed and carrying the same amount of weight run into each other, they will bounce off and move an equal distance away from each other. And based on the second law, if there is a difference in the amount of weight being carried in the two cars, the car with less weight will travel farther away from the point of impact than the car carrying more weight.
showing centripetal force
Imagine spinning a ball on a string around you. The ball is traveling in a circular path. But Newton’s first law states that an object in motion stays in motion and that motion is in a straight path, not a circular path. Since the ball is traveling in a circular path, an outside force must be acting on the ball – that force is the string. The string is pulling the ball back toward you, acting as the centripetal force.
forces and inertia diagram
Centripetal means ‘center-seeking’ and is the force that is acting on the carousel. The platform upon which the horses and people are riding is the centripetal force that keeps them traveling in a circular motion just as the string was the centripetal force for the ball. As long as the ride is moving slowly enough, the centripetal force of the platform can keep everyone and everything on board. In theory, if the carousel starts moving really fast, centrifugal force* (‘center-fearing’) takes over and breaks the hold the platform (centripetal force) had on the riders and the riders would fly off.
*Centrifugal force is actually not a real force. If the centripetal force that pulls an object into the center stops working (e.g. the string breaks), then it is the object’s inertia that takes over and sends the object traveling in a straight path. You can test this outside by spinning a ball around you and letting go of the string. If centrifugal force was a real force, the ball would move straight away from the center at the point where the string was let go. But it doesn’t. Instead, the ball follows its path of inertia and moves in a straight path that is tangent to the circular path.
intertext{a:}
&(5cdot 10^8 hspace{1mm}m)(4.2cdot 10^7hspace{1mm} m)=2cdot 10^{16}hspace{1mm} m^2\
intertext{b:}
&(1.67cdot 10^{-2} hspace{1mm}km)(8.5cdot 10^{-6}hspace{1mm}km)=1.4cdot 10^{-7}hspace{1mm} km^2\
intertext{c:}
&(2.6cdot 10^4 hspace{1mm}kg)/(9.4cdot 10^3hspace{1mm} m^3)=2.8hspace{1mm} frac{kg}{m^3}\
intertext{d:}
&(6.3cdot 10^{-1} hspace{1mm}m)/(3.8cdot 10^2hspace{1mm} m)=1.7cdot 10^{-3}hspace{1mm} frac{m}{s}\
end{align*}
intertext{a:}
&2cdot 10^{16}hspace{1mm} m^2\
intertext{b:}
&1.4cdot 10^{-7}hspace{1mm} km^2\
intertext{c:}
&2.8hspace{1mm} frac{kg}{m^3}\
intertext{d:}
&1.7cdot 10^{-3}hspace{1mm} frac{m}{s}\
end{align*}
$$
begin{align*}
m_{carlos} &= 17.0,mathrm{kg}\
m_{cart} &= 12.4,mathrm{kg}\
a & = 0.20 ,mathrm{frac{m}{s^2}}
end{align*}
$$
$$
begin{align}
F = m_{T}a
end{align}
$$
where the force $F$ is equal to the total mass of the system $m_{T}$ and its acceleration $a$.
$$
begin{align*}
F &= m_{T}cdot a\
&= (m_{carlos} + m_{cart})a\
&= (17.0 ,mathrm{kg} + 12.4,mathrm{kg})left(0.20 ,mathrm{frac{m}{s^2}}right)\
&= boxed{5.88 ,mathrm{N}}
end{align*}
$$
begin{align}
sum F_{net} &= sqrt{F_{x}^2 + F_{y}^2} = 0\
F_{x}^2 + F_{y}^2 &= 0\
intertext{such that}
F_x &= 0 text{ since Carlos is not moving horizontally}\
F_y = -F_g &= F_{N} text{ such that $F_{N}$ is force on Carlos by cart}
end{align}
$$
begin{align*}
F_{N} &= F_g\
&= m_{carlos}cdot g\
&= (17.0,mathrm{kg})left(9.8,mathrm{frac{m}{s^2}}right)\
&= boxed{167 ,mathrm{N}}
end{align*}
$$
$$
F_N = 167 ,mathrm{N}
$$

