All Solutions
Page 145: Standardized Test Practice
From the force diagram, shown on picture below, we can see that the total force exerted on the log is equal to twice the amount of the component, parallel to the direction of traction, of the force of one tractor.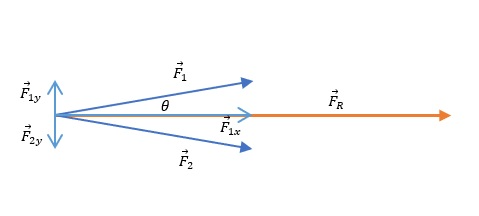
Known:
$$
begin{align*}
F_1&=800 mathrm{N} \
theta&=9text{textdegree}
end{align*}
$$
Unknown:
$$
begin{align*}
F_R&=? \
\
F_R&=2cdot F_{1x} \
&=2cdot F_1 cdot cos(theta) \
&=2cdot 800 mathrm{N} cdot cos(9text{textdegree}) \
&=boxed{1580 mathrm{N}}
end{align*}
$$
boxed{mathrm{C}} F_R=1.58cdot 10^3 mathrm{N}
$$
Known:
$$
begin{align*}
v_W&=80 mathrm{km/h} \
theta &=45text{textdegree}
end{align*}
$$
Unknown:
$$
begin{align*}
v_{We}&=? \
v_{Wn} &= ? \
\
V_{Wn}&=v_Wcdot cos(theta) \
&=80 mathrm{km/h} cdot cos(45text{textdegree}) \
&=56.57 mathrm{km/h} \
\
V_{We}&=v_Wcdot sin(theta) \
&=80 mathrm{km/h} cdot sin(45text{textdegree}) \
&=56.57 mathrm{km/h} \
end{align*}
$$
Component representation of crosswind velocity.
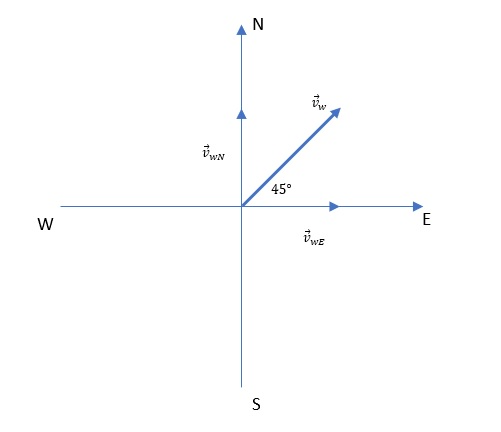
Known:
$$
begin{align*}
v_{Wn}&=56.57 mathrm{km/h} \
v_{We}&=56.57 mathrm{km/h} \
v_{p}&=800 mathrm{km/h}
end{align*}
$$
Unknown:
$$
begin{align*}
v_R&=? \
\
V_{Rn}&=v_{Wn} \
&=56.57 mathrm{km/h} \
\
V_{Re}&=v_p+v_{We} \
&=800 mathrm{km/h} +56.57 mathrm{km/h} \
&=856.57 mathrm{km/h} \
\
v^2_R&=v^2_{Rn}+v^2_{Re} \
&=56.57^2 mathrm{km^2/h^2} +856.57^2 mathrm{km^2/h^2} \
&=7.369cdot 10^5 mathrm{km^2/h^2} \
&=boxed{858.4 mathrm{km/h}}
end{align*}
$$
$$
begin{align*}
v_{Rn}&=56.57 mathrm{km/h} \
v_{Re}&=856.57 mathrm{km/h}
end{align*}
$$
Unknown:
$$
begin{align*}
theta_R&=? \
\
tan(theta)&=dfrac{v_{Rn}}{v_{Re}} \
theta&=tan^{-1}(dfrac{v_{Rn}}{v_{Re}}) \
&=tan^{-1}(dfrac{56.57 mathrm{km/h}}{856.57 mathrm{km/h}} ) \
&=boxed{3.8text{textdegree} mathrm{N of E} }
end{align*}
$$
The resulting speed is shown in the diagram below.
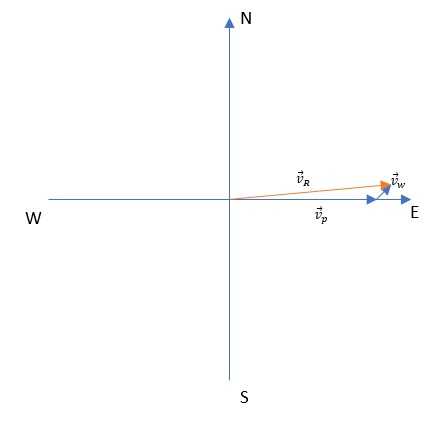
boxed{B} v_R=858 mathrm{km/h}, theta_R=3.8text{textdegree} mathrm{N of E}
$$
Known:
$$
begin{align*}
m_p&=90 mathrm{kg} tag{mass of one passenger}\
m_c&=30 mathrm{kg} tag{mass of cart}
end{align*}
$$
Unknown:
$$
begin{align*}
F_g&=? \
\
F_g&=Mcdot g tag{M: total mass} \
&=(2cdot m_p +m_c)cdot g \
&=(2cdot 90 mathrm{kg} +30 mathrm{kg}) cdot 9.8 mathrm{m/s^2} \
&=2058 mathrm{N}
end{align*}
$$
Known:
$$
begin{align*}
F_g&=2058 mathrm{N} \
mu &=0.15
end{align*}
$$
Unknown:
$$
begin{align*}
F&=? \
\
F&=F_{fric} \
&=mu cdot F_g \
&=0.15cdot 2058 mathrm{N} \
&=boxed{308.7 mathrm{N}}
end{align*}
$$
boxed{B} 3.1cdot10^2 mathrm{N}
$$
Known:
$$
begin{align*}
m&=50 mathrm{kg} \
g&=9.8 mathrm{m/s^2}
end{align*}
$$
Unknown:
$$
begin{align*}
F_g&=? \
\
F_g&=mcdot g \
&=50 mathrm{kg} cdot 9.8 mathrm{m/s^2} \
&=490 mathrm{N}
end{align*}
$$
Known:
$$
begin{align*}
F_g&=490 mathrm{N} \
F_{min}&=280 mathrm{N}
end{align*}
$$
Unknown:
$$
begin{align*}
mu_{max}&=? \
\
F_{fric}&=F_{min} \
mu_{max}cdot F_g&=F_{min} \
mu_{max}&=dfrac{F_{min}}{F_g} \
&=dfrac{280 mathrm{N}}{490 mathrm{N}} \
&=boxed{0.57}
end{align*}
$$
boxed{mathrm{B}} mu_{max}=0.57
$$
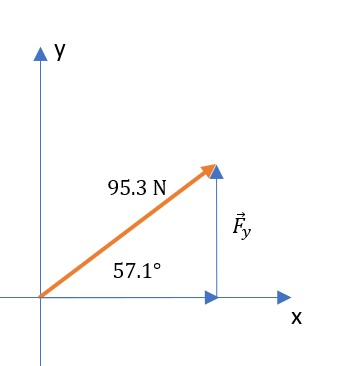
Known:
$$
begin{align*}
F&=95.3 mathrm{N} \
theta&=57.1text{textdegree}
end{align*}
$$
Unknown:
$$
begin{align*}
F_y&= ? \
\
F_y&=Fcdot sin(theta) \
&=95.3 mathrm{N} cdot sin(57.1text{textdegree}) \
&=boxed{80.0 mathrm{N}}
end{align*}
$$
mathrm{B} F_y=80.0 mathrm{N}
$$
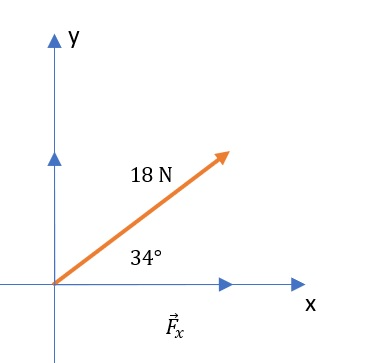
Known:
$$
begin{align*}
F&=18 mathrm{N} \
theta&=34text{textdegree}
end{align*}
$$
Unknown:
$$
begin{align*}
F_x&=? \
\
F_x&=Fcdot cos(theta) \
&=18 mathrm{N}cdot 34text{textdegree} \
&=boxed{15 mathrm{N}}
end{align*}
$$
mathrm{B} F_x=15 mathrm{N}
$$
$$
F = F_ {fric}
$$
We can use Newton’s second law and replace the force on the left side of the expression with $m cdot a$. The force of friction can be replaced by the product of the friction factor and the normal force, which in this case is weight. So it is valid:
$$
m cdot a = mu cdot F_g
$$
Acceleration can be obtained from the expression $v^2 = 2 cdot a cdot s$. We can also extend the weight as $F_g = m cdot g$. that is how we come to the expression
$$
m cdot dfrac {v^2} {2 cdot s} = mu cdot m cdot g
$$
When we cancel out the mass on both sides of the equation and express the path we come to the expression:
$$
v^2=2cdot mu cdot g cdot s
$$
$$
s = dfrac {v^2} {2 cdot mu cdot g}
$$
Known:
$$
begin{align*}
v&=50 mathrm{km/h}=13.89 mathrm{m/s} \
mu&=0.36 \
g&=9.8 mathrm{m/s^2}
end{align*}
$$
Unknown:
$$
begin{align*}
s&=? \
\
s&=dfrac{v^2}{2cdot mu cdot g} \
&=dfrac{13.89^2 mathrm{m^2/s^2}}{2cdot 0.36cdot9.8 mathrm{m/s^2}} \
&=boxed{27.34 mathrm{m}}
end{align*}
$$
mathrm{D} s=27.3 mathrm{m}
$$
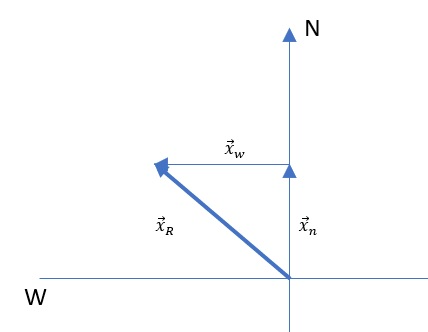
Known:
$$
begin{align*}
v&=10 mathrm{km/h}=2.78 mathrm{m/s} \
t&=2.7 mathrm{min}=162 mathrm{s}
end{align*}
$$
Unknown:
$$
begin{align*}
x_w&=? \
\
x_w&=vcdot t \
&=2.78 mathrm{m/s} cdot 162 mathrm{s} \
&=450 mathrm{m}
end{align*}
$$
Known:
$$
begin{align*}
x_n&=310 mathrm{m} \
x_w&=450 mathrm{m}
end{align*}
$$
Unknown:
$$
begin{align*}
x_R&=? \
\
x^2_R&=x^2_n+x^2_w \
&=310^2 mathrm{m^2} +450^2 mathrm{m^2} \
&=2.989cdot 10^5 mathrm{m^2} \
x_R&=boxed{547 mathrm{m}}
end{align*}
$$
x_R=547 mathrm{m}
$$
$$
F_f = mu cdot F_N
$$
where $F_N$ is the normal force.
On a slope it is a force perpendicular to the surface of the slope.
If we look at the diagram in the figure below we can see that the normal force on a slope is a vertical component of the gravitational force.
From the diagram we can easily see that this component is an adjoining leg with a given angle, and we can easily calculate the same with the function $cos (theta)$.
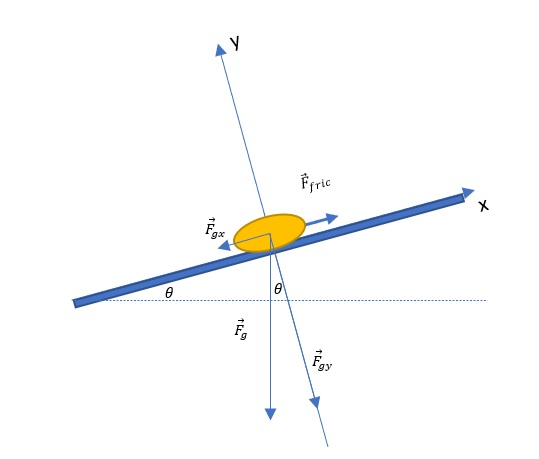
Known:
$$
begin{align*}
m&=41.2 mathrm{kg} \
mu&=0.72 \
g&=9.8 mathrm{m/s^2} \
theta &= 52.4text{textdegree}
end{align*}
$$
Unknown:
$$
begin{align*}
F_{fric}&=? \
\
F_{fric}&= mu cdot F_{gx} \
&=mu cdot F_G cdot cos(theta) \
&=mu cdot m cdot g cdot cos(theta) \
&=0.72 cdot 41.2 mathrm{kg} cdot 9.8 mathrm{m/s^2} cdot cos(52.4text{textdegree}) \
&=boxed{177.4 mathrm{N}}
end{align*}
$$
F_{fric}=177.4 mathrm{N}
$$

