All Solutions
Page 140: Assessment
We will first recall how the functions sine cosine and tangent are defined. Then we will look at them on a unit circle and finally we will fill in the map.
The sine function is defined as the ratio of the leg to the selected angle and the hypotenuse.
The cosine function is defined as the ratio of the adjacent leg to the selected angle.
The tangent function is defined as the ratio of the previous two functions.
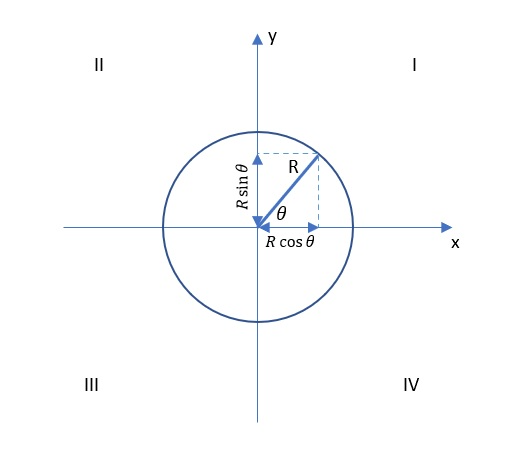
First Quadrant:
$$
begin{align*}
sin(theta)&>0 \
cos(theta)&>0 \
tan(theta)&>0
end{align*}
$$
Second quadrant:
$$
begin{align*}
sin(theta)&>0 \
cos(theta)&<0 \
tan(theta)&<0
end{align*}
$$
Third quadrant:
$$
begin{align*}
sin(theta)&<0 \
cos(theta)&0
end{align*}
$$
Fourth quadrant:
$$
begin{align*}
sin(theta)&0 \
tan(theta)&<0
end{align*}
$$
The completed concept map is shown in the figure below.

First we draw a graphical representation of the vectors we want to sum, let them be the vectors $vec {A}, vec {B}$. Graphical representation are arrows whose length represents the amount of a vector and also have a direction. $textbf {It is important that the vectors are drawn on a scale.}$
When we have arrows representing vectors we have to draw them in such a position that the end of the first and the beginning of the second vector are at the same point.
Finally, we draw the sum of the vectors by drawing an arrow connecting the beginning of the first and the end of the second vector.
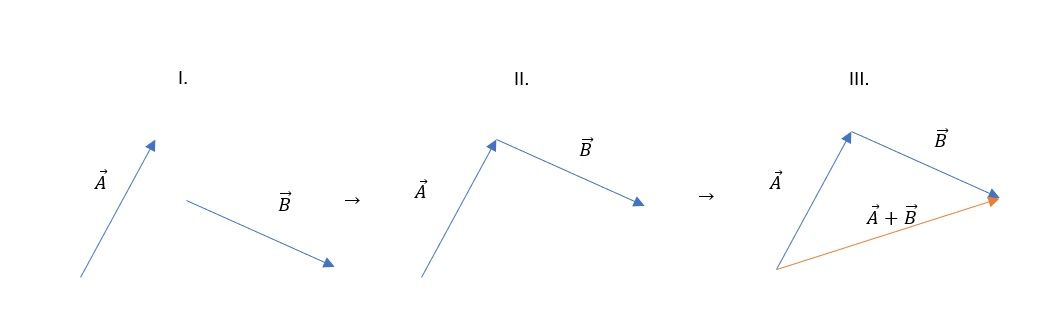
The reason is that the other two actions change the amount (change in length) or direction (rotation) of the vector.
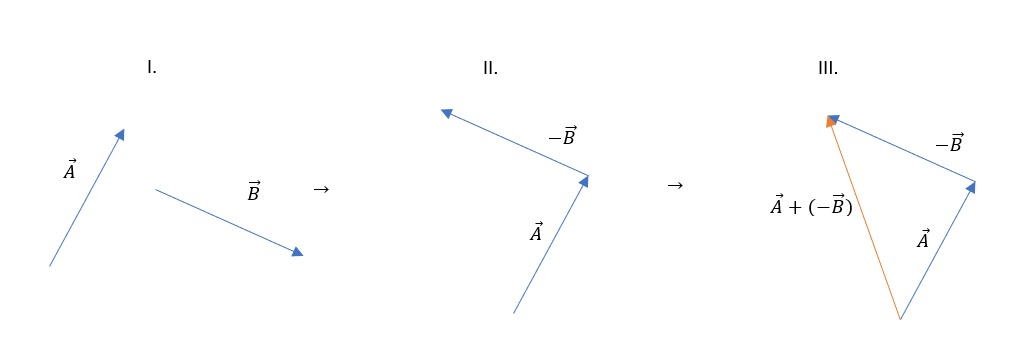
The graphical vector subtraction method consists of several steps:
begin{enumerate}
item{Make a graphical representation of the vector (draw arrows).}
item{Reverse the direction of the vector we are subtracting and place the end of the first and the beginning of the second vector at the same point.}
item{Draw the result vector by dragging the arrow from the beginning of the first to the end of the second vector.}
end{enumerate}
$$
vec{A}-vec{B} = vec{A}+(-vec{B})
$$
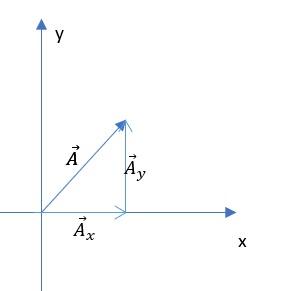
The notation $A$ represents a scalar quantity such as distance. The notation $textit{textbf {A}}$ represents the same as $vec {A}$ and is a vector quantity such as velocity.
The reason for writing vector sizes in bold style is simplicity. Also such a notation has been used in most physical textbooks.
So you could say that equality is valid:
$$
begin{align*}
a&=A_x \
b&=A_y \
c&=A
end{align*}
$$
Remember that the Pythagorean theorem is valid only for a right triangle and that this relation can only be used for summing the vectors that make up a right triangle.
Demonstration of determining the direction of a vector in a coordinate system.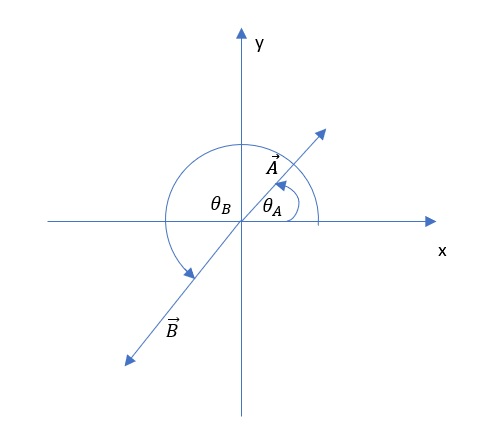
So when the friction factor $mu > 1.0$ it means that the ratio of friction force and normal force is greater than one $dfrac {F_ {frition}}{F_ {normal}} > 1$ which means that the friction force is greater than the force with which the body acts on the surface.
When we have measured the forces we simply calculate the ratio which is actually the friction factor.
$$
mu = dfrac {F_{fri}} {F_{norm}}
$$
$$
F_f = mu cdot F_n
$$
By changing the width of the tire (assuming that the weight of the tire and the factor between the tire and the surface do not change) only the contact surface changes. Since the friction force does not depend on the contact surface it remains the same.
In other words, the most favorable coordinate system for this case would be the 2D Cartesian system. Most often, time is recorded on the x axis and the magnitude of interest is the displacement (height), speed or acceleration.
It is often useful to have all three graphs $x-t, v-t$ and $a-t$.
Common to all three is that all 2D Cartesian diagrams with time are on the x-axis.
To set the coordinate system means to rotate it in some direction, but the axes are always perpendicular to each other if we use the Cartesian system.
When moving on a hill, gravity acts downwards, friction force, if it is considerable, acts parallel to the surface of the hill in the opposite direction to the direction of movement. Another possible force is the force that most often acts parallel to the surface in the direction of motion.
Let us recall what Newton’s first law tells us.
Newton’s first law reads:
$textbf {The body remains at rest or in uniform motion along the straight line until force begins to act on it}$
In other words, the body in equilibrium is at rest because the total force on it is equal to zero.
$textbf{A body is in equilibrium when no force acts on it or if the sum of all forces acting on the body is equal to zero.}$
Let us recall Newton’s first law of motion. It reads:
$textbf{The body rests or remains in a state of uniform motion in a straight line until a force begins to act on it.}$
In other words, if the $textbf{resultant forces}$ acting on the body are $textbf{equal to zero}$, the body is at rest or $textbf{moving uniformly in a direction.}$
It should be remembered that $textbf{force is not needed to move a body but to change its velocity}$, either its amount or its direction.
First example of the motion of a body in equilibrium is the motion of a comet in deep space at a constant speed where all forces are negligible but it is still moving.
Another example is the movement of a car at a constant speed on a long straight road where, although several forces act on it, they cancel each other out and the car is in equilibrium and is still moving.
If we have three vectors that are arranged in such a way to form a triangle, we can easily see that the beginning of the first and the end of the last are at the same point. So $textbf{the sum is a zero vector.}$
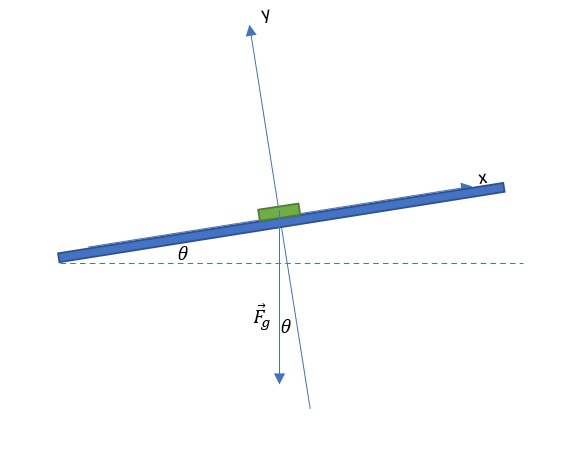
Before choosing, let us consider what forces act on the book.
If we ignore the force of friction the only force on the book is weight. The direction of gravity is perpendicular downwards. The force that causes the book to move down the table is a component of gravity parallel to the table surface.
The best way to place the coordinate system is to place the x-axis parallel to the table surface.
In a coordinate system set up in this way, gravity is deflected from the vertical by the angle of inclination of the table $theta$ and its components are easily obtained using basic trigonometric functions.
A graphical representation of the setting of the coordinate system is shown in the figure.

The components of the gravitational force are directed parallel to the surface and perpendicular to the surface. As we have already said, we can easily express the dependence of the components using the trigonometric functions $sin(theta), cos(theta)$.
$$vec{F}_g tag*{gravitiy force} $$
$$vec{F}_{g(p)} tag*{ parallel component} $$
$$vec{F}_{g(v)} tag*{vertical component} $$
$$vec{F}_{g(p)} = vec{F}_g cdot sin(theta) $$
$$vec{F}_{g(v)} = vec{F}_g cdot cos(theta) $$
The component representation is shown in the figure.
The parallel component of gravity $vec {F}_{g (p)}$ has the following dependence on the angle of inclination
$$
vec {F} _ {g (p)} = vec {F} _g cdot sin (theta)
$$
What is the expression for the force of friction?
The output for the friction force is $vec {F} _ {f} = mu vec {F} _N$ where $vec {F} _N$ is the normal force. On a slope, the normal force arises from the vertical component of gravity, which has the following dependence on the angle of inclination:
$$
vec {F} _ {g (v)} = vec {F} _g cdot cos{ theta}
$$
So the expression for the friction force would be:
$$
vec {F}_{fric} = mu cdot vec {F} _g cdot cos (theta)
$$
Graphical representation of component form of gravitiy force is shown on picture:
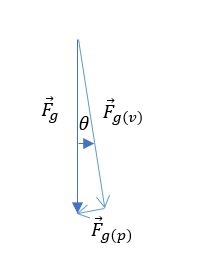
$$
begin{align*}
vec{F}_{g(p)}&=vec{F}_g cdot sin(theta) \
vec{F}_{fric}&=vec{F}_g cdot cos(theta) \
end{align*}
$$
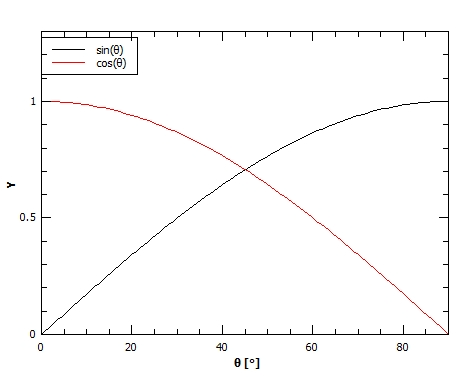
To answer the question we need to actually see what happens to the sine and cosine functions with the angle change, because first part of expressions is constant.
The following graph will help us with this:
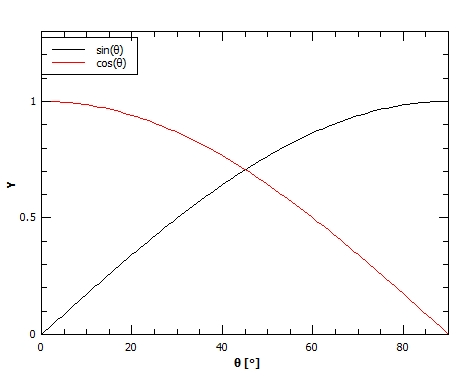
As the $textbf{angle}$ of inclination of the table $textbf{increases}$:
the $textbf{parallel component of gravity increases}$ as the vertical decreases which means that the $textbf{friction force also decreases.}$
$textbf{Decrease of inclination angle}$:
the parallel $textbf{component of gravity decreases}$ as the vertical increases which means that the $textbf{friction force also increases.}$
The ratio of the offset length to the vector length must be the same regardless of the vector length. In order to calculate the displacement of a vector of length 3 cm, we must determine the ratio of the length of the vector and the actual distance and multiply it by the lenght of the second vector.
Known:
$$
begin{align*}
x&=1 mathrm{cm} tag{vector lenght}\
x’&=5 mathrm{km} tag{displacement represented by vector}\
y&=3 mathrm{cm}
end{align*}
$$
Unknown:
$$
begin{align*}
y’&=? \
\
dfrac{y’}{y}&=dfrac{x’}{x} \
y’&=ycdot dfrac{x’}{x} \
&=3 mathrm{cm} cdot dfrac{5 mathrm{km}}{1 mathrm{cm}} \
&=boxed{15 mathrm{km}}
end{align*}
$$

$$
vec{F}_y=vec{F}cdot cos(theta)
$$
If we look at the above expression, the only way to increase the amount $vec {F} _y$ without changing $vec {F}$ is to increase $cos (theta)$ we can do this by decreasing the angle $theta$, because remember that the function $cos (theta)$ grows when the angle decreases.
The ratio of the length of the vector that represents velocity and the velocity itself must remain the same, which means that in order to calculate the length of a vector, we must multiply the velocity that vector represents by the ratio of the length of the vector and the velocity.
Known:
$$
begin{align*}
x&=15 mathrm{mm} tag{lenght of vector} \
v_x&=30 mathrm{m/s} tag{velocity represented by vector} \
v_y&=20 mathrm{m/s}
end{align*}
$$
Unknown:
$$
begin{align*}
y&=? \
\
dfrac{y}{v_y}&=dfrac{x}{v_x} \
y&=v_ycdot dfrac{x}{v_x} \
&=20 mathrm{m/s} cdot dfrac{15 mathrm{mm}}{30 mathrm{m/s}} \
&=boxed{10 mathrm{mm}}
end{align*}
$$
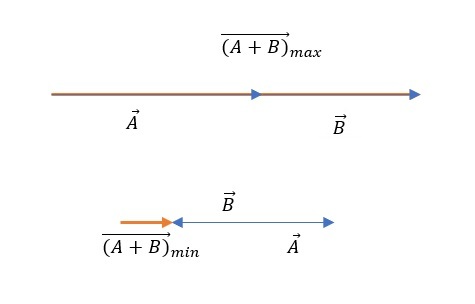
When adding, we have to place the end of the first and the beginning of the second at the same point, and we combine the beginning of the first and the end of the second vector to get the resultant vector.
So for the maximum result vector the vectors must be in the same direction and their sums are summed.
To obtain the minimum resultant, the vectors must be in the same direction but opposite orientation. In that case, their amounts are simply subtract
Known:
$$
begin{align*}
|vec{A}|&=4 mathrm{m} \
|vec{B}|&=3 mathrm{m}
end{align*}
$$
Unknown:
$$
begin{align*}
|vec{A}+vec{B}|_{max}&=? \
|vec{A}+vec{B}|_{min}&=? \
\
|vec{A}+vec{B}|_{max}&=|vec{A}|+|vec{B}| \
&=4 mathrm{m}+3 mathrm{m} \
&=boxed{7 mathrm{m}} \
\
|vec{A}+vec{B}|_{min}&=|vec{A}|-|vec{B}| \
&=4 mathrm{m}-3 mathrm{m} \
&=boxed{1 mathrm{m}}
end{align*}
$$
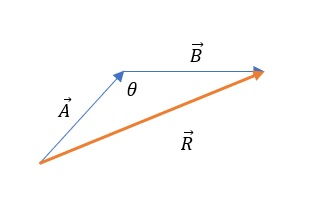
$$
R^2=A^2+B^2+2cdot Acdot B cdot cos(theta)
$$
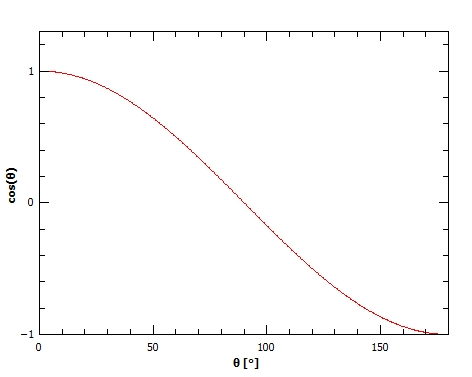
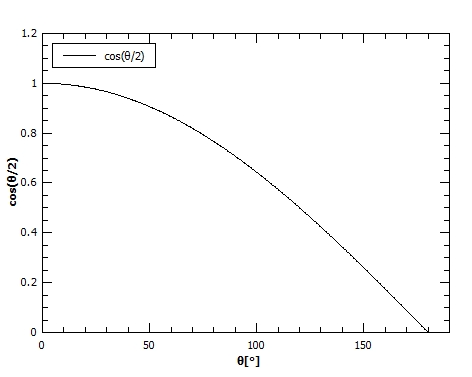
The diagram of the change of the function $cos (theta)$ with the change of the angle $theta$ in the range $[ 0 text{textdegree}, 180 text{textdegree}]$ can be seen in the diagram below.
$$
begin{align*}
R^2&=A^2+B^2+2cdot Acdot Bcdot cos(theta) \
\
{R^2}_{theta =0text{textdegree}}&=A^2+B^2+2cdot Acdot B \
&={(A+B)}^{2}\
R_{theta =0text{textdegree}}&=A+B \
\
{R^2}_{theta =180text{textdegree}}&=A^2+B^2-2cdot Acdot B \
&={(A-B)}^{2} \
R_{theta=180text{textdegree}}&=A-B \
end{align*}
$$
Thus, the amount of the resulting vector varies from $R = A + B$ to $R = A-B$ or in other words from its minimum to maximum possible amount.
$$
R_{theta =0text{textdegree}} = A + B
$$
to
$$
R_{theta =180text{textdegree}} = A – B
$$
$$
begin{align*}
&a) \
&tan(theta)>1 \
&dfrac{A}{B} >1 \
&boxed{A>B} \
\
&b) \
&tan(theta)<1 \
&dfrac{A}{B} <1 \
&boxed{A<B} \
\
&c)\
&tan(theta)=1 \
&dfrac{A}{B} =1 \
&boxed{A=B}
end{align*}
$$
begin{align*}
a) & A \
b) & B \
c) & A=B
end{align*}
$$
$$
begin{align*}
v&=50 mathrm{km/h} \
theta&=60text{textdegree}
end{align*}
$$
Unknown:
$$
begin{align*}
dfrac{v_N}{v_E} &=? \
\
v_N&=vcdot sin(theta) \
&=50 mathrm{km/h} cdot sin(60text{textdegree}) \
&=43.3 mathrm{km/h} \
\
v_E&=vcdot cos(theta) \
&=50 mathrm{km/h} cdot cos(60text{textdegree}) \
&=25 mathrm{km/h} \
\
dfrac{v_N}{v_E}&=dfrac{43.3 mathrm{km/h}}{25 mathrm{km/h}} \
&=1.73 \
\
dfrac{v_N}{v_E}&>1 rightarrow \
rightarrow &boxed{v_N>v_E}
end{align*}
$$
v_N>v_E
$$
The cosine law is given by expression:
$$
C^2=A^2+B^2+2cdot Acdot Bcdot cos(theta)
$$
While the Pythagorean theorem reads:
$$
C^2=A^2+B^2
$$
In which case are the above two expressions equal?
$$
begin{align*}
2 cdot A cdot B cdot cos (theta)&=0 \
cos(theta)&=0 \
&boxed{theta=90text{textdegree}}
end{align*}
$$
We see that the two expressions are equal when the angle between the vectors is $theta = 90 text{textdegree}$ which is logical since we know that the Pythagorean theorem is valid only for right triangles.
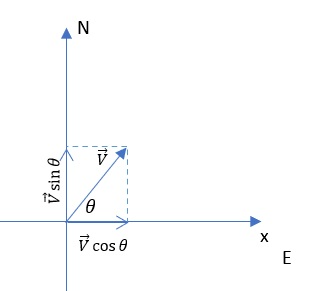
Coordinate system display: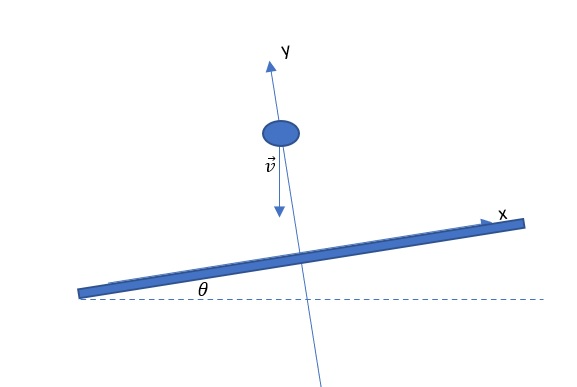
The figure below shows the component representation of the velocity vector. With the help of this image we can easily express the dependence on the angle:
$$
begin{align*}
v_x&=v cdot sin(theta) \
v_y&=vcdot cos(theta)
end{align*}
$$
Where is the problem in reasoning?
In addition to the carriage acting on it, the ground also exerts force. Why?
In order to pull the carriage he must lean against the ground which means that he is acting on it by force. According to Newton’s third law, the ground acts on it with a force of equal amount but in the opposite direction, which creates an imbalance of forces and the system manages to move forward.
Although the weight of the network is relatively small in relation to the voltage force, it is still greater than zero, which means that there must be a component of the voltage force greater than zero.
So the grid will never be horizontal but will always be at some angle no matter how small it may be.
Let us now consider how the vertical component of the tension force depends on the angle.
Note that there are two tension forces on the diagram. The reason for this is that the net is fixed to two pillars. Also note that we have described the horizontality of the grid with the angle $theta$ between the tension forces that can take values in the interval $(0 text{textdegree}, 180 text{textdegree})$.
Let’s write an expression that connects the weight and the vertical component of the tension force:
$$
begin{align*}
F_g& tag{weight} \
F_{t(x)} & tag{vertical component of tension force} \
\
F_{t(x)}&=F_t cdot cos(theta/2) \
\
F_g&=2cdot F_{t(x)} \
&=2cdot F_{t} cdot cos(theta/2)
end{align*}
$$
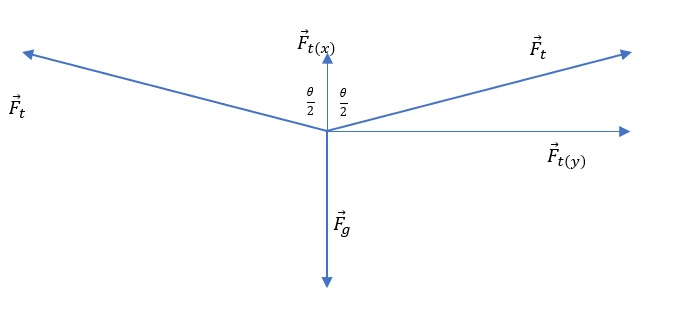
To conclude: the closer the grid is to the horizontal angle $theta$ the heavier the value $180 text{textdegree}$ and thus the cosine function tends to zero. For the weight to continue to be nullified the force of tension must rise greatly.

$$
begin{align*}
F_g & tag{weight} \
F_{g(x)}& tag{component parallel to surface}\
F_{g(y)} &tag{component perpendicular to surface}\
\
F_{g(x)}&=F_g cdot sin(theta) \
F_{g(y)}&=F_g cdot cos(theta)
end{align*}
$$
Using the above expressions we can answer the question.
$$
begin{align*}
F_{g(x)}&=F_g cdot sin(theta) \
F_{g(y)}&=F_g cdot cos(theta)
\
\
a)& \
F_{g(x)}&=F_{g(y)} \
F_g cdot sin(theta)&=F_g cdot cos(theta) \
sin(theta)&=cos(theta) \
theta&=boxed{45text{textdegree}} \
\
b)& \
F_{g(x)}&=0 \
F_g cdot sin(theta)&=0 \
sin(theta)&=0 \
theta&=boxed{0text{textdegree}}\
\
c)&\
F_{g(x)}&=F_g \
F_g cdot sin(theta)&=F_g \
sin(theta)&=1 \
theta&=boxed{90text{textdegree}}
end{align*}
$$
begin{align*}
a)& theta=45text{textdegree} \
b)& theta=0text{textdegree} \
c)& theta=90text{textdegree}
end{align*}
$$
Consider how the expressions for the components of the force of tension would read. The graphical representation of the component representation of the tension force shown in the figure below will help us in this:
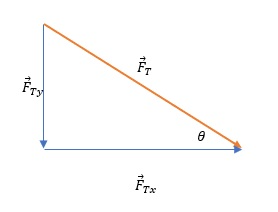
$$
begin{align*}
F_T& tag{tension force} \
F_{Tx}& tag{vertical component} \
F_{Ty}& tag{horizontal component} \
\
F_{Tx}&=F_T cdot cos(theta) \
F_{Ty}&=F_T cdot sin (theta)
end{align*}
$$
Known:
$$
begin{align*}
x_E&=65 mathrm{km} \
x_W&=- 45 mathrm{km}
end{align*}
$$
Unknown:
$$
begin{align*}
x_{tot}&=? \
\
x_{tot}&=x_E+x_W \
&=65 mathrm{km}+(-45 mathrm{km}) \
&=boxed{20 mathrm{km}}
end{align*}
$$
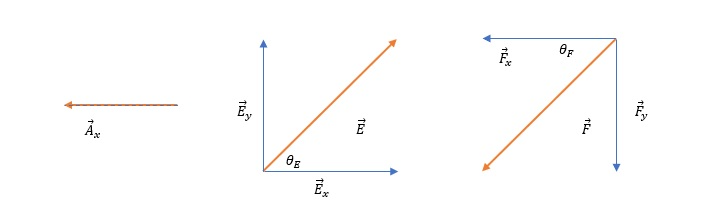
Known:
$$
begin{align*}
|vec{A}|&=3 \
|vec{E}|&=5 \
|vec{F}|&=5 \
theta_E& \
theta_F&
end{align*}
$$
Unknown:
$$
begin{align*}
A_x&, A_y, E_x, E_y, F_x, F_y\
\
E_x&=Ecdot cos(theta_E) \
&=boxed{5cdot cos(theta_E)} \
E_y&=Ecdot sin(theta_E) \
&=boxed{5cdot sin(theta_E)} \
\
F_x&=-Fcdot cos(theta_F) \
&=boxed{-5cdot cos(theta_F)} \
F_y&=-Fcdot sin(theta_F) \
&=boxed{-5cdot sin(theta_F)} \
\
A_x&=-A \
&=boxed{-3} \
A_y&=boxed{0 }
end{align*}
$$
begin{align*}
a) & \
E_x&=5cdot cos(theta_E) \
E_y&=5cdot sin(theta_E) \
\
b) & \
F_x&=-5cdot cos(theta_F) \
F_y&=-5cdot sin(theta_F) \
\
c) & \
A_x&=-3 \
A_y&=0
end{align*}
$$
The default vectors are shown in the figure below: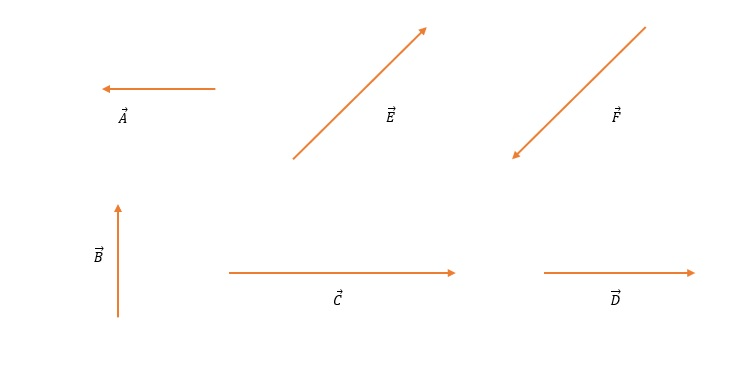
a)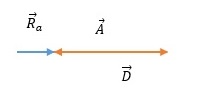
b)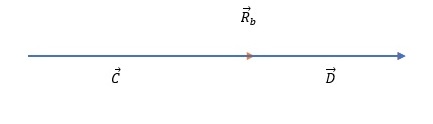
c)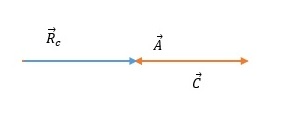
d)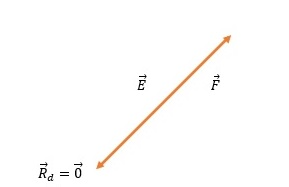
The default vectors are shown in the figure below: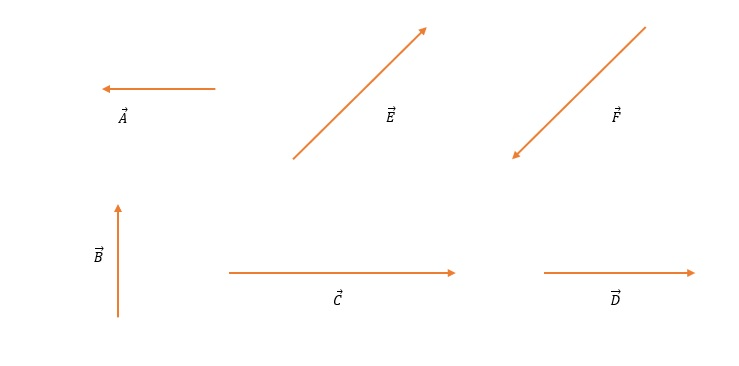
a)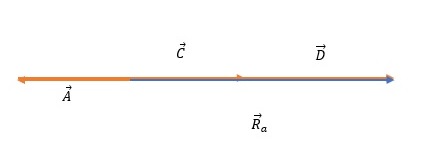
b)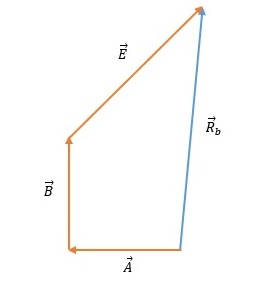
c)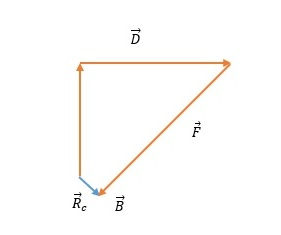
method.
Known:
$$
begin{align*}
x_S&=30 mathrm{m} \
x_E&=30 mathrm{m}
end{align*}
$$
Unknown:
$$
begin{align*}
x_{tot}&=? \
\
x^2_{tot}&=x^2_S+x^2_E \
&=30^2 mathrm{m^2}+30^2 mathrm{m^2} \
&=1800 mathrm{m^2} \
x_{tot}&=boxed{42.43 mathrm{m}}
end{align*}
$$
Once we have determined the amount and direction of the total shift, the result can be written in vector form:
$$
vec{x}_{tot}=42.43 mathrm{m} SE
$$
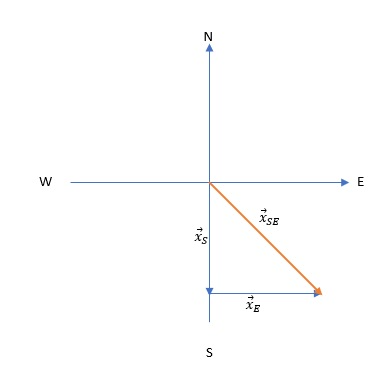
vec{x}_{tot}=42.43 mathrm{m} SE
$$
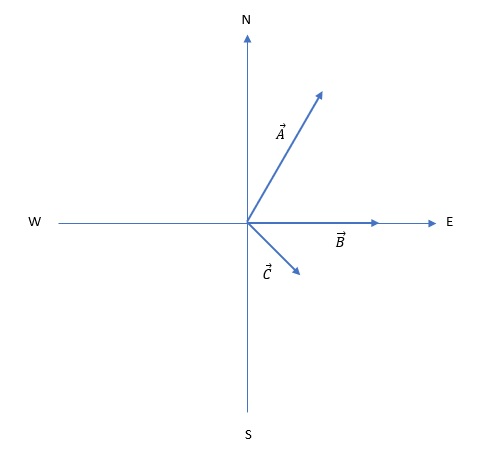
The three segments have the following amounts and directions:
$$
begin{align*}
vec{A}&=8 mathrm{km}, theta_A=30text{textdegree} \
vec{B}&=7 mathrm{km}, theta_B=90text{textdegree} \
vec{C}&=4 mathrm{km}, theta_C=135text{textdegree}
end{align*}
$$
A graphical representation of the segment vector is shown in the figure:
The amounts are shown in the figure below:
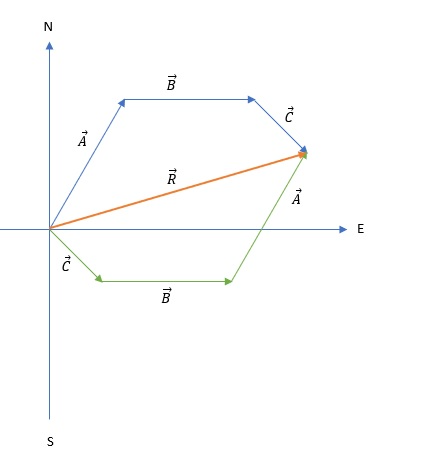
From the figure we can see that in both cases we obtained the same resultant vector therefore we can conclude that the order of summation of the vectors does not affect the final result.
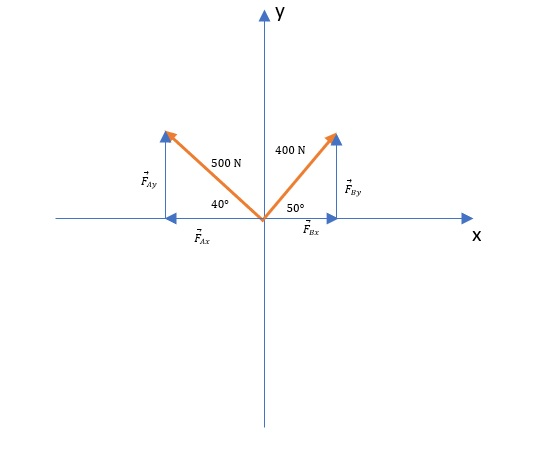
Known:
$$
begin{align*}
F_A&=500 mathrm{N} \
theta_A&=40text{textdegree} \
F_B&=400 mathrm{N} \
theta_B&=50text{textdegree}
end{align*}
$$
Unknown:
$$
begin{align*}
F_R&=? \
theta_R&=? \
\
F_{Ax}&=F_Acdot cos(theta_A) \
&=-500 mathrm{N}cdot cos(40text{textdegree}) \
&=-383 mathrm{N} \
F_{Ay}&=F_Acdot sin(theta_A) \
&=500 mathrm{N}cdot sin(40text{textdegree}) \
&=321.4 mathrm{N} \
\
F_{Bx}&=F_Bcdot cos(theta_B) \
&=400 mathrm{N}cdot cos(50text{textdegree}) \
&=257.1 mathrm{N} \
F_{By}&=F_Bcdot sin(theta_B) \
&=400 mathrm{N}cdot sin(50text{textdegree}) \
&=306.4 mathrm{N}
end{align*}
$$
$$
begin{align*}
F_{Rx}&=F_{Ax}+F_{Bx} \
&=-383 mathrm{N}+257.1 mathrm{N} \
&=-125.9 mathrm{N} \
\
F_{Ry}&=F_{Ay}+F_{By} \
&=321.4 mathrm{N}+306.4 mathrm{N} \
&=627.8 mathrm{N} \
\
F^2_R&=F^2_{Rx}+F^2_{Ry} \
&=125.9^2 mathrm{N^2}+627.8^2 mathrm{N^2} \
&=4.1cdot 10^5 mathrm{N^2} \
F_R&=boxed{640.3 mathrm{N}}
end{align*}
$$
$$
begin{align*}
tan{(theta’)}&= dfrac{F_{Rx}}{F_{Ry}}\
theta’ &= arctan{(dfrac{F_{Rx}}{F_{Ry}})} \
&=arctan{(dfrac{-125.9 mathrm{N}}{627.8 mathrm{N}})} \
&=11text{textdegree}
end{align*}
$$
Then we add 90 degrees to that angle to get an angle of positive x axis.
$$
begin{align*}
theta_R&=theta’ +90text{textdegree} \
&=11text{textdegree} + 90text{textdegree} \
&=boxed{101text{textdegree}}
end{align*}
$$
F_R=640.3 mathrm{N}, theta_R=101text{textdegree}
$$
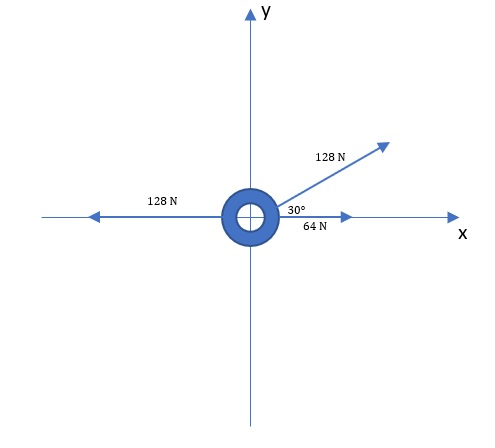
Known:
$$
begin{align*}
vec{F}_1&= -128 mathrm{N} hat{x} \
vec{F}_2&= 64 mathrm{N} hat{x} \
F_3&= 128 mathrm{N} \
theta&=30text{textdegree}
end{align*}
$$
Note that the first two forces are written in vector form while the third force is written only by the amount.
Unknown:
$$
begin{align*}
F_{tot}&=? \
theta_{tot}&=? \
\
vec{F_{3x}}&=F_3cdot cos(theta) hat{x} \
&=128 mathrm{N}cdot cos(30text{textdegree}) hat{x} \
&=110.9mathrm{N} hat{x} \
vec{F_{3y}}&=F_3cdot sin(theta) hat{y} \
&=128 mathrm{N}cdot sin(30text{textdegree}) hat{y} \
&=64mathrm{N} hat{y}
end{align*}
$$
$$
begin{align*}
vec{F}_{toty}&=F_{3y} hat{y} \
&=64 mathrm{N} hat{y} \
\
vec{F}_{totx}&=vec{F}_{1}+vec{F}_{2}+vec{F}_{3x} \
&=-128 mathrm{N} hat{x}+64 mathrm{N} hat{x}+110.9 mathrm{N} hat{x} \
&=46.9 mathrm{N} hat{x} \
\
F_{tot}&=sqrt{F^2_{totx}+F^2_{toty}} \
&=sqrt{46.9^2 mathrm{N^2}+64^2 mathrm{N^2}} \
&=boxed{79.34 mathrm{N}}
end{align*}
$$
$$
begin{align*}
tan(theta’)&=dfrac{F_{totx}}{F_{toty}} \
&=dfrac{46.9 mathrm{N}}{64 mathrm{N}} \
theta’&=36text{textdegree}
end{align*}
$$
To get angle from x axis we subtract the upper angle of 90 degrees:
$$
begin{align*}
theta_{tot}&=90text{textdegree}-theta’ \
&=90text{textdegree}-36text{textdegree} \
&=boxed{54text{textdegree}}
end{align*}
$$
F_{tot}=120.4 mathrm{N}, theta_{tot}=54text{textdegree}
$$
The total distance can be calculated using the Pythagorean instruction because the displacements are at right angles. We will calculate the direction of movement from the ratio of individual displacements.
Known:
$$
begin{align*}
vec{x}_o&=500 mathrm{km} hat{S} tag{original distance to port} \
vec{x}_s&=100 mathrm{km} hat{W} tag{extra distance due to storm}
end{align*}
$$
Unknown:
$$
begin{align*}
vec{x}_{tot}&=? \
\
x^2_{tot}&=x^2_o+x^2_s \
&=500^2 mathrm{km^2}+100^2 mathrm{km^2} \
&=2.6cdot 10^5 mathrm{km^2} \
x_{tot}&=boxed{509.9 mathrm{km}} \
\
tan({theta}_{tot})&=dfrac{x_o}{x_s} \
&=dfrac{500 mathrm{km}}{100 mathrm{km}} \
theta&=boxed{78.7text{textdegree}} mathrm{souht of the west}
end{align*}
$$
begin{align*}
x_{tot}&=509.9 mathrm{km} \
theta &=78.7text{textdegree} mathrm{souht of west}
end{align*}
$$
The angle at which the spacecraft lands can be easily determined if we remember that the ratio of the components is equal to the tangent of the angle.
Let us orient the coordinate system so that the positive y axis is perpendicular to the surface and directed upwards.
Known:
$$
begin{align*}
v_y&=-5.5 mathrm{m/s} \
v_x&=3.5 mathrm{m/s}
end{align*}
$$
Unknown:
$$
begin{align*}
v&=? \
\
v^2&=v^2_x+v^2_y \
&=5.5^2 mathrm{(m/s)^2}+3.5^2 mathrm{(m/s)^2} \
&=42.5 mathrm{(m/s)^2} \
v&=boxed{6.5 mathrm{m/s}}
end{align*}
$$
Known:
$$
begin{align*}
v_y&=-5.5 mathrm{m/s} \
v_x&=3.5 mathrm{m/s}
end{align*}
$$
Unknown:
$$
begin{align*}
theta&=? \
\
tan(theta)&=dfrac{v_x}{v_y} \
&=dfrac{3.5}{5.5} \
&=0.636 \
theta&=boxed{32.5text{textdegree} }
end{align*}
$$
begin{align*}
v&=6.5 mathrm{m/s} \
theta&=32.5text{textdegree}
end{align*}
$$
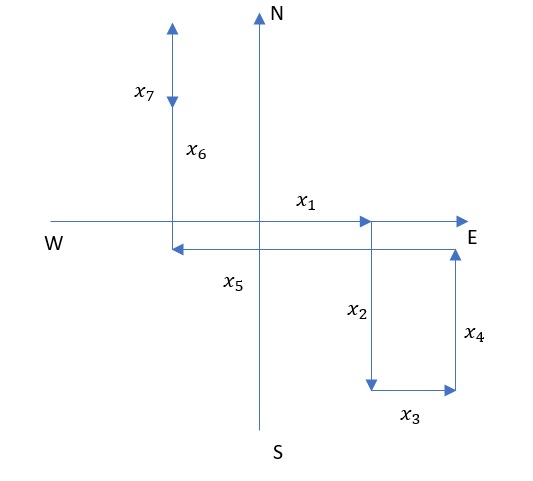
Known:
$$
begin{align*}
x_1&=4 mathrm{km} hat{x}\
x_2&=-6 mathrm{km} hat{y}\
x_3&=3 mathrm{km} hat{x}\
x_4&=5 mathrm{km} hat{y}\
x_5&=-10 mathrm{km} hat{x}\
x_6&=8 mathrm{km} hat{y}\
x_7&=-3 mathrm{km} hat{y}
end{align*}
$$
Unknown:
$$
begin{align*}
x_R&=? \
\
x_{Rx}&=x_1+x_3+x_5 \
&=4 mathrm{km}+3 mathrm{km}-10 mathrm{km} \
&=-3 mathrm{km}
\ \
x_{Ry}&=x_2+x_4+x_6+x_7 \
&=-6 mathrm{km}+5 mathrm{km}+8 mathrm{km}-3 mathrm{km} \
&=4 mathrm{km}\
\
x^2_R&=x^2_{Rx}+x^2_{Ry} \
&=3^2mathrm{km^2}+4^2 mathrm{km^2} \
&=25 mathrm{km^2} \
x_R&=boxed{5 mathrm{km}}
end{align*}
$$
$$
begin{align*}
x_{Rx}&=-3 mathrm{km} \
x_{Ry}&=4 mathrm{km} \
theta&=? \
\
tan(theta)&=dfrac{x_{Ry}}{x_{Rx}} \
&=1.333 \
theta&=53.1text{textdegree} mathrm{south of the west}
end{align*}
$$
To get the direction from the north we have to add $90 text{textdegree}$ to the angle $theta$.
$$
begin{align*}
theta_R&=90text{textdegree}+theta \
&=boxed{143.1text{textdegree}}
end{align*}
$$
the coordinate system with all displacements including return are shown in the figure below.
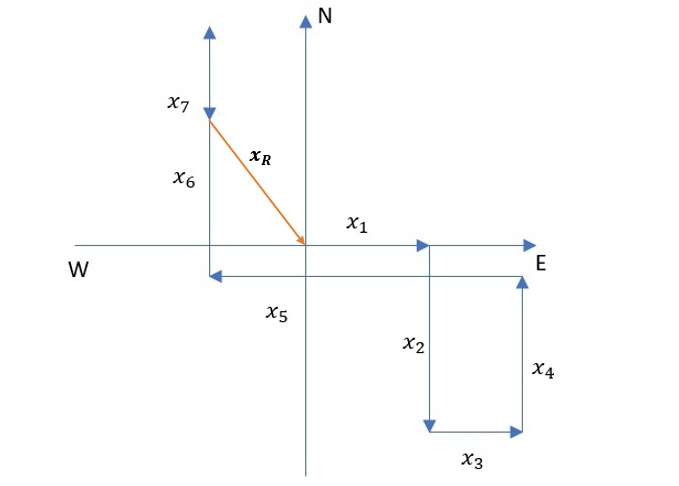
begin{align*}
x_R&=5 mathrm{km} \
theta_R&=143.1text{textdegree} mathrm{from north}
end{align*}
$$
What forces act on the crate?
In the vertical direction, these are gravity and the reaction force of the substrate.
In the horizontal direction, these are the pulling force and the friction force.
Since the body is in equilibrium it means that the total force on it is equal to zero. So the reaction force of the substrate is equal in amount and the opposite in sign is the force of gravity and the pulling force is equal to the friction force is only the opposite sign.
Let us recall the expression for the force of friction.
$$
F_f = mu cdot F_N
$$
In our case, the normal force is weight.
Known:
$$
begin{align*}
m&=12 mathrm{kg} \
F_p&=30 mathrm{N}
end{align*}
$$
Unknown:
$$
begin{align*}
mu&=? \
\
F_N&=mcdot g \
&=12 mathrm{kg} cdot 9.8 mathrm{m/s^2} \
&=11.76 mathrm{N} \
\
F_f&=mu cdot F_N \
mu&=dfrac{F_f}{F_N} \
&=dfrac{30 mathrm{N}}{11.76 mathrm{N}} \
&=boxed{0.26}
end{align*}
$$
mu=0.26
$$
In the horizontal direction on the crate gravitational force. The gravitational force in this situation plays the role of the normal force with which the crate presses the floor. The floor, according to Newton’s third law, acts on the crate upwards, so the forces in the vertical direction are annulled.
In the horizontal direction, the push force acts on the crate, causing it to move. The friction force acts in the direction opposite to the direction of movement.
We will calculate the acceleration of the crate using Newton’s second law.
Known:
$$
begin{align*}
m&=225 mathrm{kg} \
F_p&=710 mathrm{N} \
mu&=0.2
end{align*}
$$
Unknown:
$$
begin{align*}
a&=? \
\
F_N&=F_g \
&=mcdot g \
&=225 mathrm{kg} cdot 9.8 mathrm{m/s^2} \
&=2205 mathrm{N}
end{align*}
$$
$$
begin{align*}
F_f&=mu cdot F_N \
&=0.2cdot 2205 mathrm{N} \
&=441 mathrm{N}
end{align*}
$$
$$
begin{align*}
F_{net}&=F_p-F_f \
&=710 mathrm{N}-441 mathrm{N} \
&=269 mathrm{N}
end{align*}
$$
$$
begin{align*}
F_{net}&=mcdot a \
a&=dfrac{F_{net}}{m} \
&=dfrac{269 mathrm{N}}{225 mathrm{kg}} \
&=boxed{1.20 mathrm{m/s^2}}
end{align*}
$$
a=1.20 mathrm{m/s^2}
$$
Known:
$$
begin{align*}
F&=40 mathrm{N} \
m&=5 mathrm{kg} \
a&=6 mathrm{m/s^2}
end{align*}
$$
Unknown:
$$
begin{align*}
F_f&=? \
\
a_0 tag{acceleration without friction force} \
\
F&=mcdot a_0\
a_0&=dfrac{F}{m} \
&=dfrac{40 mathrm{N}}{5 mathrm{kg} } \
&=8 mathrm{m/s^2} \
\
F_f&=mcdot (a_0-a) \
&=5 mathrm{kg}cdot (8 mathrm{m/s^2}-6 mathrm{m/s^2}) \
&=boxed{10 mathrm{N}}
end{align*}
$$
Known:
$$
begin{align*}
F_f&=10 mathrm{N} \
m&=5 mathrm{kg}
end{align*}
$$
Unknown:
$$
begin{align*}
mu&=? \
\
F_N&=F_g \
&=mcdot g \
&=5 mathrm{kg} cdot 9.8 mathrm{m/s^2} \
&=49 mathrm{N} \
\
F_f&=mu cdot F_N \
mu&=dfrac{F_f}{F_N} \
&=dfrac{10 mathrm{N}}{49 mathrm{N}} \
&=boxed{0.20}
end{align*}
$$
begin{align*}
a) & F_f=10 mathrm{N} \
b) & mu=0.20
end{align*}
$$
These two factors need to be distinguished. While the body is at rest, a static factor should be used, and in the case of movement, kinetic.
In the vast majority of cases, the static factor is slightly higher than the kinetic factor.
The question is how hard the refrigerator needs to be pushed to start.
In order to start the refrigerator, a force greater than the static friction force must be applied, so the normal force (weight) must be multiplied by the static friction factor.
Known:
$$
begin{align*}
m&=180 mathrm{kg} \
mu_{static}&=0.21
end{align*}
$$
Unknown:
$$
begin{align*}
F&=? \
\
F&=mu_{static} cdot F_N \
&=mu_{static} cdot mcdot g \
&=0.21cdot 180 mathrm{kg} cdot 9.8 mathrm{m/s^2} \
&=boxed{370.4 mathrm{N}}
end{align*}
$$
F=370.4 mathrm{N}
$$
$$
begin{align*}
m&=2500 mathrm{kg} \
v&=14 mathrm{m/s} \
s&=25 mathrm{m} \
F_f&=? \
\
v^2&=2cdot acdot s \
a&=dfrac{v^2}{2cdot s} \
\
F_f&=mcdot a \
&=mcdot dfrac{v^2}{2cdot s} \
&=2500 mathrm{kg}cdot dfrac{14^2 mathrm{m^2/s^2}}{2cdot 25 mathrm{m}} \
&=9800 mathrm{N}
end{align*}
$$
$$
begin{align*}
m&=2500 mathrm{kg} \
F_N&=? \
\
F_N&=F_g \
&=mcdot g \
&=2500 mathrm{kg}cdot 9.8 mathrm{m/s^2} \
&=24 500 mathrm{N}
end{align*}
$$
$$
begin{align*}
F_N &=24500 mathrm{N} \
F_f &=9800 mathrm{N} \
mu &=? \
\
F_f &=mu cdot F_N \
mu &=dfrac{F_f}{F_N} \
&=dfrac{9800 mathrm{N}}{24500 mathrm{N}} \
&=boxed{0.4}
end{align*}
$$
mu = 0.4
$$
$$
begin{align*}
F_1&=33 mathrm{N } \
F_2&=44 mathrm{N } \
theta_2&=60text{textdegree} \
F_{2x}&=? \
F_{2y}&=? \
\
F_{2x}&=F_2cdot cos(theta_2) \
&=44 mathrm{N} cdot cos(60text{textdegree})\
&=22 mathrm{N} \
\
F_{2y}&=F_2cdot sin(theta_2) \
&=44 mathrm{N} cdot sin(60text{textdegree})\
&=38.11 mathrm{N}
end{align*}
$$
$$
begin{align*}
F_{1y}&=33 mathrm{N} \
F_{2x}&=22 mathrm{N} \
F_{2y}&=38.11 mathrm{N} \
F_{3x}&=? \
F_{3y}&=? \
\
F_{3x}&=-F_{2x} \
&=-22 mathrm{N} \
\
F_{1y}&=-(F_{1y}+F_{2y}) \
&=-(33 mathrm{N}+38.11 mathrm{N}) \
&=-71.11 mathrm{N} \
\
F^2_3&=F^2_{3x}+F^2_{3y} \
&=-22^2 mathrm{N^2} + (-71.11)^2 mathrm{N^2} \
&=5540 mathrm{N^2} \
F_3&=boxed{74.43 mathrm{N}}
end{align*}
$$
$$
begin{align*}
F_{3x}&=-22 mathrm{N} \
F_{3y}&=-71.11 mathrm{N} \
{theta}_3&=? \
\
tan(theta ‘)&=dfrac{F_{3y}}{F_{3x}} \
&=dfrac{-71.11 mathrm{N}}{-22 mathrm{N}} \
&=3.23 \
theta ‘&=72.8text{textdegree} \
\
{theta}_3&=theta ‘+180text{textdegree} \
&=72.8text{textdegree} +180text{textdegree} \
&=boxed{252.8text{textdegree}}
end{align*}
$$
begin{align*}
F_3&=74.43 mathrm{N} \
theta_3 &=252.8text{textdegree}
end{align*}
$$
The given forces and corresponding directions are:
$$
begin{align*}
F_1&=60 mathrm{N}, theta_1=90text{textdegree} \
F_2&=40 mathrm{N}, theta_2=0text{textdegree} \
F_3&=80 mathrm{N}, theta_3=270text{textdegree} \
F_4&=40 mathrm{N}, theta_4=180text{textdegree} \
F_5&=50 mathrm{N}, theta_5=60text{textdegree}
end{align*}
$$
Note that the force $F_2$ and the force $F_4$ are canceled because they are of the same amount and opposite direction.
Also the force $F_1$ is in the opposite direction from the force $F_3$ which means that only for the force $F_5$ we have to calculate the amounts of the components.
$$
begin{align*}
vec{F}_1&=60 mathrm{N} hat{y} \
vec{F}_3&=-80 mathrm{N} hat{y} \
F_5&=50 mathrm{N} \
theta_5&=60text{textdegree} \
F_{6x}&=? \
F_{6y} &=? \
\
F_{6x}&=-F_5cdot cos(theta_5) \
&=-50 mathrm{N}cdot cos(60text{textdegree}) \
&=-25 mathrm{N} \
\
F_{6y}&=-(F_1+F_3+F_5cdot sin(theta_5)) \
&=-(60 mathrm{N}-80 mathrm{N}+50 mathrm{N}cdot sin(60)) \
&=-23.3 mathrm{N}
\
end{align*}
$$
$$
begin{align*}
F_{6x}&=-25 mathrm{N} \
F_{6y}&=-23.3 mathrm{N} \
F_6&=? \
theta_6 &=? \
\
F^2_6&=F^2_{6x}+F^2_{6y} \
&=-25^2 mathrm{N^2} +(-23.3^2 mathrm{N^2}) \
&=1168 mathrm{N^2} \
F_6&=boxed{34.18 mathrm{N}}
end{align*}
$$
$$
begin{align*}
tan({theta}’_6)&=dfrac{F_{6x}}{F_{6y}} \
&=dfrac{-25 mathrm{N}}{-23.3 mathrm{N}}\
&=1.087 \
{theta}’_6&= 47.4text{textdegree} \
\
{theta}_6&={theta}’_6+180text{textdegree} \
&=47.4text{textdegree}+180text{textdegree} \
&=boxed{227.4text{textdegree}}
end{align*}
$$
F_6=34.18 mathrm{N}, theta_6=227.4text{textdegree}
$$
The data given are the sign weight and the angles of the tension forces. In order to calculate the tension force in a cabel B, we must first calculate the tension force of the cabel A. The tension force $F_B$ must be equal to the horizontal component of the the tension force $F_A$, in order for the sign to be at rest.
Known:
$$
begin{align*}
F_g&=750 mathrm{N} \
{theta}_A&=30text{textdegree}
end{align*}
$$
Unknown:
$$
begin{align*}
F_A&=? \
\
F_g&=F_A cdot cos({theta}_A) \
F_A&=dfrac{F_g}{cos({theta}_A)} \
&=dfrac{750 mathrm{N}}{cos(30text{textdegree})} \
&=866 mathrm{N}
end{align*}
$$
Known:
$$
begin{align*}
F_A&=866 mathrm{N} \
{theta}_A&=30text{textdegree}
end{align*}
$$
Unknown:
$$
begin{align*}
F_B &=? \
\
F_B&=F_A cdot sin ({theta}_A) \
&=866 mathrm{N}cdot sin(30text{textdegree}) \
&=boxed{433 mathrm{N}}
end{align*}
$$
F_B=433 mathrm{N}
$$
To make it easier to visualize the problem, let’s look at the free body diagram shown in the image below.
It is easy to see from the figure that the y component cancels the gravitational force, and we calculate this component using the function $cos (theta/2)$. It should also be noted that the amount of gravity is equal to twice the y component due to the two forces of tension.
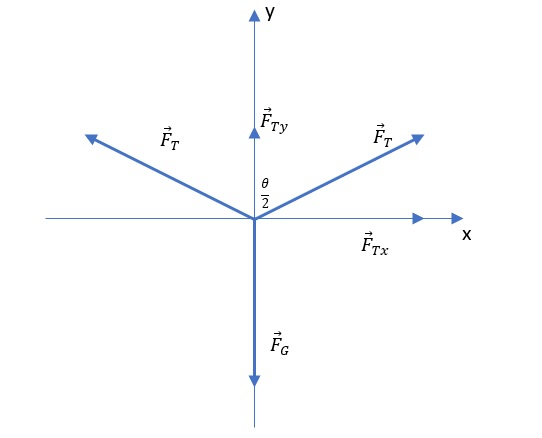
Known:
$$
begin{align*}
F_G&=150 mathrm{N} \
theta_a&=120text{textdegree}
end{align*}
$$
Unknown:
$$
begin{align*}
F_T&=? \
\
F_G&=2cdot F_T cdot cos(theta_a /2) \
F_T&=dfrac{F_G}{2cdot cos(theta_a /2)} \
&=dfrac{150 mathrm{N}}{2cdot cos(60text{textdegree})} \
&=boxed{150 mathrm{N}}
end{align*}
$$
Known:
$$
begin{align*}
F_G&=150 mathrm{N} \
theta_b&=90text{textdegree}
end{align*}
$$
Unknown:
$$
begin{align*}
F_T&=? \
\
F_G&=2cdot F_T cdot cos(theta_b/2) \
F_T&=dfrac{F_G}{2cdot cos(theta_b/2)} \
&=dfrac{150 mathrm{N}}{2cdot cos(45text{textdegree})} \
&=boxed{106.1 mathrm{N}}
end{align*}
$$
begin{align*}
a) F_{Ta}&= 150 mathrm{N} \
b) F_{Tb}&= 106.1 mathrm{N}
end{align*}
$$
Notice that the coordinate system is rotated by the angle of inclination counterclockwise.
The gravitational force in the rotated coordinate system is deflected by the angle of inclination of the negative y axis.
The parallel component of weight in our coordinate system lies on the negative x axis, so we calculate this component using the function $sin (theta)$
For easier visualization, observe the coordinate system shown in the figure below.
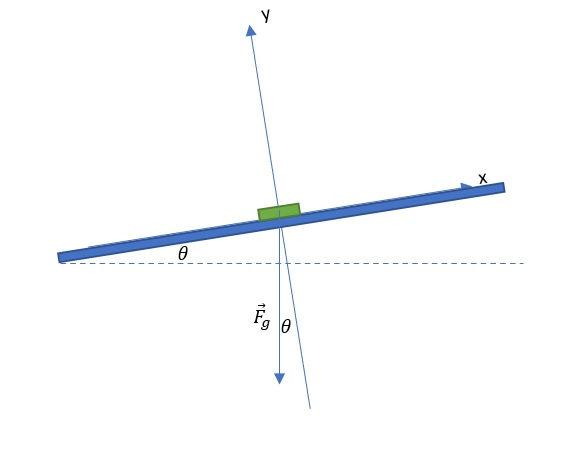
Calculation:
Known:
$$
begin{align*}
F_G&=-215 mathrm{N} \
theta&=35text{textdegree}
end{align*}
$$
Unknown:
$$
begin{align*}
F_{Gx}&=? \
\
F_{Gx}&=F_Gcdot sin (theta) \
&=-215cdot sin (35text{textdegree}) \
&=boxed{-123.3 mathrm{N} hat x}
end{align*}
$$
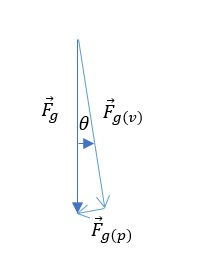
vec{F}_{Gx}=-123.3 mathrm{N} hat x
$$
When the patient is lying in bed he must rest. So he is in equilibrium. When the bed is tilted, the patient is acted upon by gravity acting down the slope and a friction force acting along the slope and resisting gravity.
Since this is a static situation, the friction force is determined by the static coefficient of friction.
The friction force is equal to the amount of the parallel component of gravity but of the opposite direction.
Recall the friction force is given by the expression $F_f = mu cdot F_N$. On a slope, the role of the normal force is played by the vertical component of gravity, therefore,textbf{changing the angle changes the amount of gravity components, which indirectly changes the amount of friction force.}
For a body on a slope in equilibrium, it must be true that the parallel component of gravity and the friction force are of equal amount, which means that a given angle of inclination can determine the friction factor.
Known:
$$
begin{align*}
theta&=32°
end{align*}
$$
Unknown:
$$
begin{align*}
mu_{static}&=? \
\
F_Gcdot sin(theta)&=F_f \
F_Gcdot sin(theta)&=mu_{static}cdot F_N \
F_Gcdot sin(theta)&=mu_{static} cdot F_G cdot cos(theta) \
mu_{static}&=dfrac{sin(theta)}{cos(theta)} \
&=tan (theta) \
&=tan (32°) \
&=boxed{0.62}
end{align*}
begin{align*}
a)& F_G rightarrow F_f \
b)& mu_{static}=0.62
end{align*}
$$
Let’s start by recognizing the forces.
The force $F_A$ acts on block A, which is actually a component of weight parallel to the slope. The force of friction and the force of tension are two more forces that act on block A .
Block B is affected by the force $F_B$ which is a weight acting downwards and the tension force upwards.
Assume that the system will move so that block A will go along the slope and block B down. If we made a mistake, it will only affect the sign of acceleration.
We will calculate the acceleration of the system using Newton’s second law.
To determine the total force that causes motion, we must determine which forces act in the direction of motion and which in the opposite.
By choosing the direction, we also determined the directions of the forces. Forces that act in the direction of motion have a positive sign and those otherwise, a negative one.
Then we have to calculate all the forces and finally calculate the resultant force which we include in Newton’s second law.
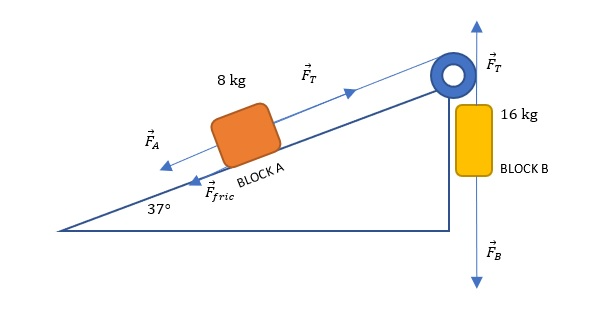
Known:
$$
begin{align*}
F_A& 0 \
F_{fric}&<0 \
m_A&=8 mathrm{kg} \
m_B&=16 mathrm{kg} \
theta&=37text{textdegree} \
mu &=0.23
end{align*}
$$
Unknown:
$$
begin{align*}
F_A&=? \
F_B&=?\
F_{fric}&=? \
\
F_A&=-(F_{GA}cdot sin(theta)) \
&=-(m_A cdot gcdot sin(theta))\
&=-(8 mathrm{kg} cdot 9.8 mathrm{m/s^2} cdot sin(37text{textdegree})) \
&=-47.2 mathrm{N} \
\
F_B&=F_{GB} \
&=m_B cdot g \
&=16 mathrm{kg} cdot 9.8 mathrm{m/s^2}\
&=156.8 mathrm{N} \
\
F_{fric}&=-(mu cdot F_{GA}cdot cos(theta)) \
&=-(mu cdot m_Acdot gcdot cos(theta)) \
&=-0.23cdot 8 mathrm{kg}cdot 9.8 mathrm{m/s^2}cdot cos(37text{textdegree}) \
&=-14.4 mathrm{N}
end{align*}
$$
Calculation:
Known:
$$
begin{align*}
F_A&=-47.2 mathrm{N} \
F_B&=156.8 mathrm{N} \
F_{fric}&=-14.4 mathrm{N}
end{align*}
$$
Unknown:
$$
begin{align*}
a&=? \
\
F_{net}&=F_A+F_B+F_{fric} \
\
F_{net}&=Mcdot a tag{M: mass of system} \
a&=dfrac{F_{net}}{M} \
&=dfrac{F_A+F_B+F_{fric}}{m_A+m_B} \
&=dfrac{-47.2 mathrm{N}+156.8 mathrm{N}-14.4 mathrm{N}}{8 mathrm{kg}+16 mathrm{kg}} \
&=boxed{3.97 mathrm{m/s^2}}
end{align*}
$$
calculation is with block B. Block B must move with the acceleration of the whole system. The force of tension in this case slows down block B so that it does not accelerate by accelerating g, which it would move if only gravity acted on it.
Thus, the tension force $F_T$ is calculated using Newton’s second law with a small change, which is that instead of acceleration we include the difference between the acceleration of gravity and the acceleration of the system.
Known:
$$
begin{align*}
g&=9.8 mathrm{m/s^2} \
m&=16 mathrm{kg}
end{align*}
$$
Unknown:
$$
begin{align*}
F_T&= ?\
\
\
F_T&=mcdot(g-a) \
&=16 mathrm{kg}cdot (9.8 mathrm{m/s^2}-3.97 mathrm{m/s^2}) \
&=boxed{93.28 mathrm{N}}
end{align*}
$$
begin{align*}
a)& a=3.97 mathrm{m/s^2} \
b)& F_T=93.28 mathrm{N}
end{align*}
$$
The two blocks form a system that we accelerate by some force F. The acceleration of the system is simply obtained from Newton’s second law.
$$
F = (M + m) cdot a
$$
Let’s look at what’s going on inside the system. When we act on a large block, it accelerates and acts with some force on a smaller block, and it also accelerates with acceleration of the system.
According to Newton’s third law, a small block also acts on a large block by a force of equal amount and opposite direction
Because the surfaces are not perfectly smooth there is a friction force that prevents the smaller block from falling.
$$
F_{fric} = {mu}_s cdot F_N
$$
The normal force in this case is equal in amount to the force with which a small block acts on a large one, and this is exactly the amount of force required for a small block to move by accelerating the system.
$$
F_N =mcdot a
$$
If the force of friction prevents a small block from falling down, it must be of the same amount as its weight.
$$
begin{align*}
F_{fric}&=F_G tag{smaller block dosen’t fall down}\
mu_s cdot F_N&=mcdot g tag{$F_N$ accelerate smaller block }\
mu_s cdot mcdot a&=mcdot g\
a&=dfrac{g}{mu_s} \
\
F&=(M+m)cdot a tag{2. Newton’s law} \
F&=(M+m)cdot dfrac{g}{mu_s} \
&=boxed{dfrac{(M+m)cdot g}{mu_s}}
end{align*}
$$
F=dfrac{(M+m)cdot g}{mu_s}
$$
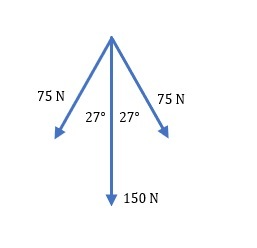
Known:
$$
begin{align*}
F_1&=F_2=75 mathrm{N} \
F_3&=150 mathrm{N} \
theta&=27text{textdegree}
end{align*}
$$
Unknown:
$$
begin{align*}
F_{net}&=? \
\
F_{net} &=F_1 cdot cos(theta)+F_2cdot cos(theta)+F_3 \
&=75 mathrm{N} cdot cos(27text{textdegree})+75 mathrm{N} cdot cos(27text{textdegree})+150 mathrm{N}\
&=boxed{283.7 mathrm{N}}
end{align*}
$$
F_{net}=283.7 mathrm{N}
$$
Known:
$$
begin{align*}
m&=50 mathrm{kg} \
g&=9.8 mathrm{m/s^2}
end{align*}
$$
Unknown:
$$
begin{align*}
F_G&=? \
\
F_G&=mcdot g \
&=50 mathrm{kg} cdot 9.8 mathrm{m/s^2} \
&=boxed{490 mathrm{N}}
end{align*}
$$
Known:
$$
begin{align*}
F_G&=490 mathrm{N} \
mu_s &=0.3
end{align*}
$$
Unknown:
$$
begin{align*}
F_B&=? \
\
F_B&=F_{fric} \
&=mu_s cdot F_G \
&=0.3cdot 490 mathrm{N} \
&=boxed{147 mathrm{N}}
end{align*}
$$
Known:
$$
begin{align*}
F_G&=490 mathrm{kg} \
mu_k&=0.1
end{align*}
$$
Unknown:
$$
begin{align*}
F_C&=? \
\
F_C&=F_{fric} \
&=mu_k cdot F_G \
&=0.1cdot 490 mathrm{N}\
&=boxed{49 mathrm{N}}
end{align*}
$$
Known:
$$
begin{align*}
F_G&=490 mathrm{kg} \
mu_k&=0.1 \
a&=3 mathrm{m/s^2}
end{align*}
$$
Unknown:
$$
begin{align*}
F_D&=? \
\
F_D&=F_i+F_{fric} \
&=mcdot a + mu_k cdot F_G \
&=50 mathrm{kg} cdot 3 mathrm{m/s^2}+0.1cdot 490 mathrm{N} \
&=boxed{ 199mathrm{N}}
end{align*}
$$
begin{align*}
a) F_g&=490 mathrm{N} \
b) F_B&=147 mathrm{N} \
c) F_C&=49 mathrm{N} \
d) F_D&=199 mathrm{N} \
end{align*}
$$
Known:
$$
begin{align*}
m&=20 mathrm{kg} \
theta&=30text{textdegree} \
mu &=0.4
end{align*}
$$
Unknown:
$$
begin{align*}
F&=? \
\
F&=F_Gcdot sin(theta) +F_{fric} \
&=mcdot gcdot sin(theta) + mu cdot F_G cdot cos(theta) \
&=20 mathrm{kg}cdot 9.8 mathrm{m/s^2}cdot sin(30text{textdegree})+0.4cdot 20 mathrm{kg}cdot 9.8 mathrm{m/s^2}cdot cos (30text{textdegree}) \
&=boxed{165.9 mathrm{N}}
end{align*}
$$
Known:
$$
begin{align*}
v&=0.25 mathrm{m/s} \
t&=8 mathrm{h}=2.88cdot 10^4 mathrm{s} \
theta&=30text{textdegree}
end{align*}
$$
Unknown:
$$
begin{align*}
h&=? \
\
sin(theta)&=dfrac{h}{s} tag{$s$: path along the side of the mountain } \
h&=scdot sin(theta) \
&=vcdot t cdot sin(theta) \
&=0.25 mathrm{m/s} cdot 2.88cdot10^4 mathrm{s} cdot sin(30text{textdegree}) \
&=boxed{3600 mathrm{m }}
end{align*}
$$
begin{align*}
a) F&=165.9 mathrm{N} \
b) h&=3600 mathrm{m}
end{align*}
$$
In order to calculate the minimum stopping distance we must first express the acceleration.
Known:
$$
begin{align*}
mu&=0.5
end{align*}
$$
Unknown:
$$
begin{align*}
a&=? \
\
F&=F_{fric} \
mcdot a&=mu cdot mcdot g \
a&=mu cdot g \
&=0.5cdot 9.8 mathrm{m/s^2} \
&=4.9 mathrm{m/s^2}
end{align*}
$$
Calculation:
Known:
$$
begin{align*}
a&=4.9 mathrm{m/s^2} \
v&=55 mathrm{km/h}=15.28 mathrm{m/s}
end{align*}
$$
Unknown:
$$
begin{align*}
s&=? \
\
v^2&=a cdot s \
s&=dfrac{v^2}{2cdot a } \
&=dfrac{15.28^2 mathrm{m^2/s^2}}{2cdot 4.9 mathrm{m/s^2}} \
&=boxed{23.82 mathrm{m} }
end{align*}
$$
s_{min}=23.82 mathrm{m}
$$
$$
F_ {fric} = mu cdot F_N
$$
The normal force that presses a car against the ground is its weight which means
$$
F_ {fric} = mu cdot m cdot g
$$
If we include the force of friction in Newton’s second law, we come to the expression for friction force
$$
F_ {fric} = m cdot a
$$
From that we can obtain the expression for acceleration:
$$
a=mu cdot g
$$
To reach the final expression that connects the friction force and the stopping distance, we need the following kinematic expression
$$
v ^ 2 = 2 cdot a cdot s
$$
The final expression needed for the calculation is obtained when we connect the above two and it reads
$$
s =dfrac{v^2}{2cdot mucdot g}
$$
A sketch of the force problem is shown in the figure below.
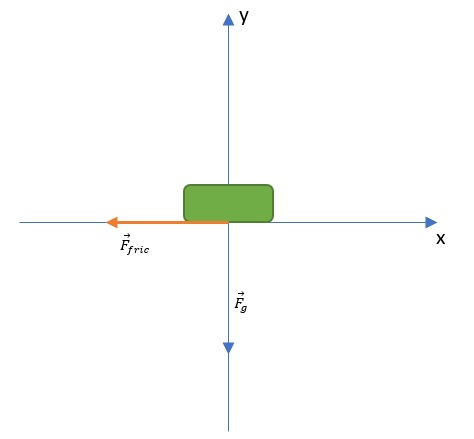
Known:
$$
begin{align*}
v&=25 mathrm{m/s} \
m&=975 mathrm{kg} \
mu_k &=0.65 tag{from Tabel 5-1(pg. 129.)}
end{align*}
$$
Unknown:
$$
begin{align*}
s_{min}&=? \
\
s_{min}&=dfrac{v^2}{2cdot mu cdot g} \
&=dfrac{25^2 mathrm{m^2/s^2}}{2cdot 0.65 cdot 9.8 mathrm{m/s^2}} \
&=boxed{49.06 mathrm{m}}
end{align*}
$$
So, when driving at higher speeds, one should be careful and watch what is happening far enough in front of the current position to stop.
s_{min}=49.06 mathrm{m}
$$
The force of gravity $F_G=mcdot g$ acts downwards but its component parallel to the slide $F_{Gx}$ is responsible for the movement.
The force of friction slows down the movement. The expression for determining the force of friction is
$$
F_F = mu cdot F_N
$$
In this case, the role of the normal force $F_N$ is played by the gravitational component perpendicular to the slide $F_ {Gy}$.
The force diagram is shown in the figure below. From the image we can easily determine the expressions for the components.
$$
begin{align*}
F_{Gx}&=F_Gcdot sin(theta) \
F_{Gy}&=F_Gcdot cos(theta) \
\
F_{Gx}&=mcdot g cdot sin(theta) \
F_{Gy}&=mcdot g cdot cos(theta) \
end{align*}
$$
Let’s write down the expressions of forces acting parallel to the slope.
$$
begin{align*}
F_{Gx}&=mcdot g cdot sin(theta) \
F_{fri}&=mcdot g cdot cos(theta) \
end{align*}
$$
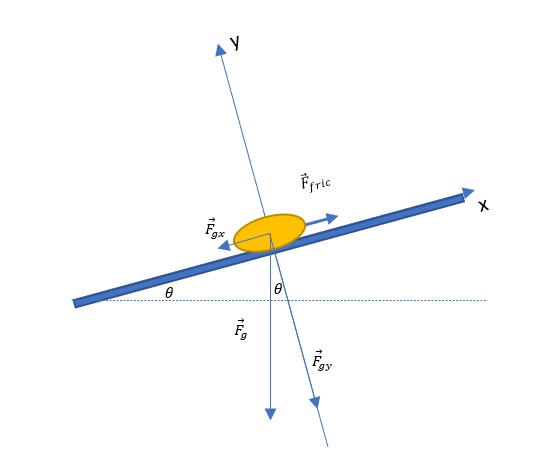
$$
begin{align*}
F_{net}&=F_{Gx}-F_{fric} \
&=mcdot g cdot sin(theta)-mucdot mcdot g cdot cos(theta) \
&=mcdot g cdot (sin(theta)-mu cdot cos(theta)) \
\
F_{net}&=mcdot a \
mcdot g cdot (sin(theta)-mucdot cos(theta)) &=mcdot a \
a&=g cdot (sin(theta)-mucdot cos(theta))
end{align*}
$$
$textbf {The conclusion is that Kako was right.}$
The most common form of friction is sliding friction. It is of the simplest form and depends on only two factors, the friction factor and the normal force that presses the body against the surface on which it is located.
$$
F_ {friction} = mu cdot F_N
$$
We can reduce the friction force by reducing the Friction coefficient $mu$ or normal force $F_N$ .
In addition to sliding friction, another form of friction force is the resistance of the medium, for example air resistance. This form of friction depends on many factors such as speed of movement density of medium or body shape. The easiest way to reduce this type of friction is by changing the shape of the body.
Let us consider how these procedures are applied in industry.
Another way to reduce friction factors, widely used in industry, is the use of lubricants. In some cases we cannot change the materials of the body and the surface then we use lubricants that create a thin layer between the body and the surface, smooth the surface and thus reduce the friction force.
One way to reduce the effect of gravity is to tilt the surface by some angle. thus we reduce the weight component perpendicular to the surface, i.e. the normal force and thus the friction force.
In some cases we cannot tilt the surface but we can act with some force in the opposite direction and thus reduce the normal force. One example of such a way to reduce the friction force is in the glass industry where large glass surfaces are lifted by air currents that act opposite to weight and thus reduce friction.
The easiest way to reduce it is to adjust the shape of the body, in this case the body of the car so that the cross section of the vehicle in the direction of movement is as small as possible.
If we look at the clothes of sprinters 50 years ago and today we can see that they are very different. Previously, runners ’clothing was the most common linen T-shirt and shorts. Most often, the clothing was loose and provided extra resistance when running. Today’s clothing is thin and elastic in order to adhere better to the body and thus reduce the cross-section of the runners and air resistance.
But it’s not all about reducing friction. In footwear, the opposite is true. Today’s footwear has a much higher coefficient of friction with the base than before. The reason for this is that the runner must act on the floor in order to move forward. According to Newton’s third law, the ground pushes the runner away with equal force. The higher the friction force, the more force acts back on the runner and he has a higher acceleration.
To add or subtract measurements, first perform the operation, then
round off the result to correspond to the least-precise value involved.
$$
begin{align*}
& a) m=85.26 mathrm{g} +4.7 mathrm{g}=90 mathrm{g} \
& b) s=1.07 mathrm{km} +0.608 mathrm{km}=1.68 mathrm{km} \
& c) m=186.4 mathrm{kg} – 57.83 mathrm{kg}=128.6 mathrm{kg} \
& d) t=60.08 mathrm{s} – 12.2 mathrm{s}=47.9 mathrm{s}
end{align*}
$$
Known:
$$
begin{align*}
v_1&=10 mathrm{km/h} \
v_2&=15 mathrm{km/h} \
t_1&=1.5 mathrm{h} \
t_2&=0.5 mathrm{h}
end{align*}
$$
Unknown:
$$
begin{align*}
s_1&=?\
s_2&=? \
\
s_1&=v_1cdot t_1 \
&=10 mathrm{km/h} cdot 1.5 mathrm{h} \
&=15 mathrm{km} \
\
s_2&=v_2cdot t_2 \
&=15 mathrm{km/h} cdot 0.5 mathrm{h} \
&=7.5 mathrm{km}
end{align*}
$$
Known:
$$
begin{align*}
s_1&=15 mathrm{km} \
s_2&=7.5 mathrm{km} \
t_1&=1.5 mathrm{h} \
t_2&=0.5 mathrm{h}
end{align*}
$$
Unknown:
$$
begin{align*}
s&=?\
t&=?\
v_{avg}&=? \
\
s&=s_1+s_2 \
&=15 mathrm{km} +7.5 mathrm{km}\
&=22.5 mathrm{km} \
\
t&=t_1+t_2 \
&=1.5 mathrm{h} +0.5 mathrm{h}\
&=2 mathrm{h} \
\
v_{avg}&=dfrac{s}{t} \
&=dfrac{22.5 mathrm{km}}{2 mathrm{h}} \
&=boxed{11.25 mathrm{km/h}}
end{align*}
$$
v_{avg}=11.25 mathrm{km/h}
$$
Known:
$$
begin{align*}
m &=2 mathrm{kg} \
g &=-9.8 mathrm{m/s^2}
end{align*}
$$
Unknown:
$$
begin{align*}
F_G &=? \
\
F_G &=mcdot g \
&=2 mathrm{kg} cdot – 9.8 mathrm{m/s^2} \
&=-19.6 mathrm{N}
end{align*}
$$
Known:
$$
begin{align*}
F_G&=-19.6 mathrm{N} \
F&=45 mathrm{N}
end{align*}
$$
Unknown:
$$
begin{align*}
F_{net} &=? \
\
F_{net}&=F+F_G \
&=45 mathrm{N} – 19.6 mathrm{N} \
&=25.4 mathrm{N}
end{align*}
$$
Known:
$$
begin{align*}
F_{net}&=25.4 mathrm{N} \
m&=2 mathrm{kg}
end{align*}
$$
Unknown:
$$
begin{align*}
a &=? \
\
F_{net}&=mcdot a \
a&=dfrac{25.4 mathrm{N}}{2 mathrm{kg}} \
&=boxed{12.7 mathrm{m/s^2}}
end{align*}
$$
a=12.7 mathrm{m/s^2}
$$

