Home Page Textbooks Physics: Principles and Problems Page 121: Practice Problems

Physics: Principles and Problems

9th Edition

Elliott, Haase, Harper, Herzog, Margaret Zorn, Nelson, Schuler, Zitzewitz

ISBN: 9780078458132

Textbook solutions

All Solutions

Page 121: Practice Problems

Exercise 1

Step 1

1 of 3

In this task we will calculate the total offset.

Known:

$$
begin{align*}
A&=125 mathrm{km} W \
B&=65 mathrm{km} S \
end{align*}
$$

Unknown:

$$
begin{align*}
R&=? \
\
R^2&=A^2+B^2 \
R&=sqrt{A^2+B^2} \
&=sqrt{125^2 mathrm{km^2}+65^2 mathrm{km^2}} \
&=boxed{140.9 mathrm{km}}
end{align*}
$$

Step 2

2 of 3

Graphic solution:

The figure shows a graphical representation of the vector sum.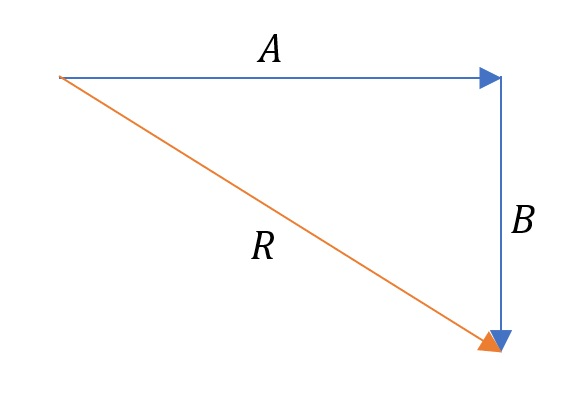 Exercise scan

Result

3 of 3

$R=140.9 mathrm{km}$, graphic solution in the explanation.

Exercise 2

Step 1

1 of 3

In this task we will calculate the total offset.

Known:

$$
begin{align*}
A&=250 mathrm{m} \
B&=60 mathrm{m} \
end{align*}
$$

Unknown:

$$
begin{align*}
R&=? \
\
R^2&=A^2+B^2 \
R&=sqrt{A^2+B^2} \
&=sqrt{250^2 mathrm{m^2}+60^2 mathrm{m^2}} \
&=boxed{257.1 mathrm{m}}
end{align*}
$$

Step 2

2 of 3

Graphic solution:

The figure shows a graphical representation of the vector sum.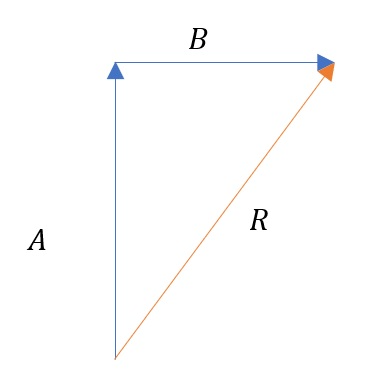 Exercise scan

Result

3 of 3

$R=257.1 mathrm{m}$.

Exercise 3

Step 1

1 of 4

After walking $a=4.5,,rm{km}$ in one direction, hiker turns at an angle of $theta=45,,^{o}$ and walks for another $b=6.4,,rm{km}$. We need to determine the magnitude of her displacement.

Step 2

2 of 4

Total displacement can be calculated as:
$$R^2=a^2+b^2+2cdot a dot b cdot cos (theta )$$
From this we can get:
$$R=sqrt{a^2+b^2+2cdot a cdot b cdot cos (theta )}$$

Step 3

3 of 4

Inserting values we get:
$$R=sqrt{4.5^2+6.4^2+2cdot 4.5cdot 6.4cdot cos (45)}$$
Finally we get:
$$boxed{R=10.19,,rm{km}}$$

Result

4 of 4

$$R=10.19,,rm{km}$$

Exercise 4

Solution 1

Solution 2

Solution 3

Step 1

1 of 4

Ant moves $a=5,, rm{mm}$ south and then $b=4,,rm{ mm}$ southwest. We need to calculate total displacement of the ant.

Step 2

2 of 4

The angle between directions is $theta = 45,,^{o}$.
Total displacement can be calculated as:
$$R^2=a^2+b^2+2cdot a cdot b cdot cos (theta)$$
From the previous equation we can get:
$$R=sqrt{a^2+b^2+2cdot a cdot b cdot cos (theta)}$$

Step 3

3 of 4

Inserting values we get:
$$R=sqrt{5^2+4^2+2cdot 5cdot 4 cdot cos (45)}$$
$$boxed{R=8.324,,rm{mm}}$$

Result

4 of 4

$$R=8.324,,rm{mm}$$

Step 1

1 of 2

In this task we will calculate the total offset.

Known:

$$
begin{align*}
A&=5 mathrm{mm} \
B&=4 mathrm{mm} \
theta&=45text{textdegree} \
end{align*}
$$

Unknown:

$$
begin{align*}
R&=? \
\
R^2&=A^2+B^2+2cdot Acdot Bcdot cos(theta) \
R&=sqrt{A^2+B^2+2cdot Acdot Bcdot cos(theta)} \
&=sqrt{5^2 mathrm{mm^2}+4^2 mathrm{mm^2}+2cdot 5 mathrm{mm}cdot 4 mathrm{mm}cdot cos(45text{textdegree}) } \
&=boxed{8.324 mathrm{mm}}
end{align*}
$$

Result

2 of 2

$$
R=8.324 mathrm{mm}
$$

Step 1

1 of 3

R^2 = A^2 + B^2 – 2AB cos (theta)

Since there is not a 90 degree angle, we must use the law of cosines.

Step 2

2 of 3

R = √(5^2 + 4^2 – 2(5 x 4) cos 135)

Plug in the values of the problem into the law of cosines.

Result

3 of 3

8.3 mm (remember significant digits)

Exercise 5

Step 1

1 of 3

In this task we will calculate the total offset.

The figure shows the vector sum of the displacements.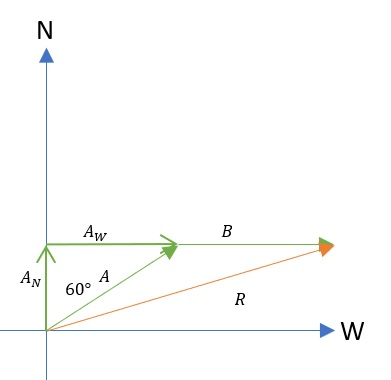 Exercise scan

Step 2

2 of 3

To calculate $R$ we need to break $A$ into components. After that, R is calculated according to Pythagoras’ teaching, the components of R are included in the formula.

Known:

$$
begin{align*}
A&=0.4 mathrm{km} \
B&=0.5 mathrm{km} \
theta &=60text{textdegree} \
end{align*}
$$

Unknown:

$$
begin{align*}
R&=? \
\
A_N&=Acdot cos(theta) \
&=0.4 mathrm{km}cdot cos(60text{textdegree}) \
&=0.2 mathrm{km} \
\
A_W&=Acdot sin(theta) \
&=0.4 mathrm{km}cdot sin(60text{textdegree}) \
&=0.3464 mathrm{km} \
\
R_N&=A_N \
&=0.2 mathrm{km} \
R_W&=A_W+B \
&=0.3464 mathrm{km}+0.5 mathrm{km} \
&=0.8464 mathrm{km}
\
R^2&=R_W^2+R_N^2 \
R&=sqrt{R_W^2+R_N^2} \
&=sqrt{0.2^2 mathrm{km^2}+0.8464^2 mathrm{km^2}} \
&=boxed{ 0.8697 mathrm{km} }
end{align*}
$$

Result

3 of 3

$$
R=0.8697 mathrm{km}
$$

Exercise 6

Step 1

1 of 4

In this task we will calculate the net force for the given data.

The figure shows a force diagram.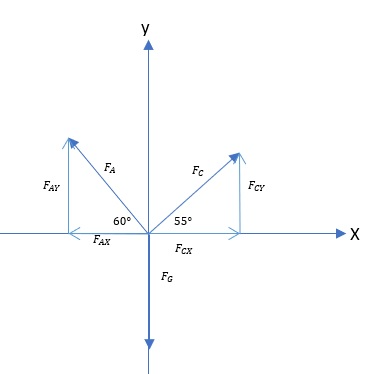 Exercise scan

Step 2

2 of 4

In order to calculate the net force we have to disassemble the individual forces into their components. Pay attention when choosing the angle for calculating the components $F_A$. In the figure, we marked the angle $60 text{textdegree}$ for clarity but $theta_A = 120 text{textdegree}$.

Known:

$$
begin{align*}
F_A&=20.4 mathrm{N} \
F_B&=17.7 mathrm{N} \
theta_A&=120text{textdegree} \
theta_B&=55text{textdegree} \
m&=3.2 mathrm{kg} \
end{align*}
$$

Unknown:

$$
begin{align*}
F_{net}&=? \
\
F_{AX}&=F_Acdot cos{theta_A} \
&=20.4 mathrm{N}cdot cos(120text{textdegree}) \
&=-10.2 mathrm{N}\
\
F_{BX}&=F_Bcdot cos{theta_B} \
&=17.7 mathrm{N}cdot cos(55text{textdegree}) \
&=10.15 mathrm{N}\
\
F_{AY}&=F_Acdot sin{theta_A} \
&=20.4 mathrm{N}cdot sin(120text{textdegree}) \
&=17.67 mathrm{N}\
\
F_{BY}&=F_Bcdot sin{theta_B} \
&=17.7 mathrm{N}cdot sin(55text{textdegree}) \
&=14.5 mathrm{N}\
end{align*}
$$

Step 3

3 of 4

$$
begin{align*}
F_{netX}&=F_{AX}+F_{BX} \
&=-10.2 mathrm{N}+10.15 mathrm{N} \
&=-0.05 mathrm{N} \
\
F_{netY}&=F_{AY}+F_{BY}-F_g \
&=17.67 mathrm{N}+14.5 mathrm{N}-3.2 mathrm{kg}cdot 9.8 mathrm{m/s^2} \
&=0.81 mathrm{N} \
\
F^2_{net}&=F^2_{netX}+F^2_{netY} \
F_{net}&=sqrt{F^2_{netX}+F^2_{netY}} \
&=sqrt{0.05^2 mathrm{N^2}+0.81^2 mathrm{N^2}} \
&=boxed{0.8115 mathrm{N}}
end{align*}
$$

Result

4 of 4

$$
F_{net}=0.8115 mathrm{N}
$$

Exercise 7

Step 1

1 of 3

In this task we will calculate the total offset.

The figure shows the vector sum of the individual offsets.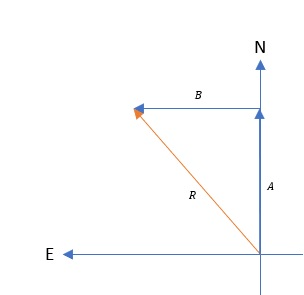 Exercise scan

Step 2

2 of 3

Calculation:

Known:

$$
begin{align*}
A&=8 mathrm{km} \
R&=10 mathrm{km} \
end{align*}
$$

Unknown:

$$
begin{align*}
B&=? \
\
R^2&=A^2+B^2 \
B^2&=R^2-A^2 \
B&=sqrt{R^2-A^2} \
&=sqrt{10^2mathrm{km^2}-8^2 mathrm{km^2}} \
&=boxed{6 mathrm{km}}
end{align*}
$$

Result

3 of 3

$$
B=6 mathrm{km}
$$

Exercise 8

Step 1

1 of 3

In this problem we will calculate the net force.

The figure shows a force diagram.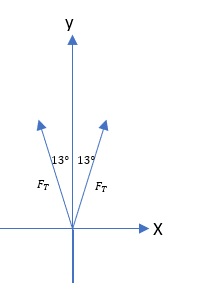 Exercise scan

Step 2

2 of 3

Calculation:

Known:

$$
begin{align*}
F_T&=2.28 mathrm{N} \
theta &=13text{textdegree} \
end{align*}
$$

Unknown:

$$
begin{align*}
F_{Tnet}&=?\
\
F_{Tnet}&=2cdot F_Tcdot cos(theta) \
&=2cdot 2.28 mathrm{N} cos(13text{textdegree}) \
&=boxed{4.443 mathrm{N}}
end{align*}
$$

Result

3 of 3

Combined force is $F_{Tnet}=4.443 mathrm{N}$ in $+y$ direction.

Exercise 9

Step 1

1 of 2

The vector will never be shorter than the components, for the same reason that the hypotenuse is never shorter than the leg of a right triangle.

$$
begin{align*}
R^2&=R^2_X+R^2_Y \
R&=sqrt{R^2_X+R^2_Y}
end{align*}
$$

The vector will never be shorter than the components, for the same reason that the hypotenuse is never shorter than the leg of a right triangle.

Result

2 of 2

No.

Exercise 10

Step 1

1 of 2

In the coordinate system, the positive direction of the $x$ axis would be east.

$x$ has a positive sign when $theta$ ranges from $270text{textdegree}$ to $90text{textdegree}$.

$x$ has a negative sign when $theta$ ranges from $90text{textdegree}$ to $270text{textdegree}$.

Result

2 of 2

$East Rightarrow x>0$

$theta in (270text{textdegree}, 360text{textdegree})cup (0text{textdegree}, 90text{textdegree}) Rightarrow x>0$

$theta in (90text{textdegree}, 270text{textdegree}) Rightarrow x>0$

unlock

All Solutions

Page 121: Practice Problems

Haven't found what you were looking for?

Search for samples, answers to your questions and flashcards