All Solutions
Page 112: Assessment
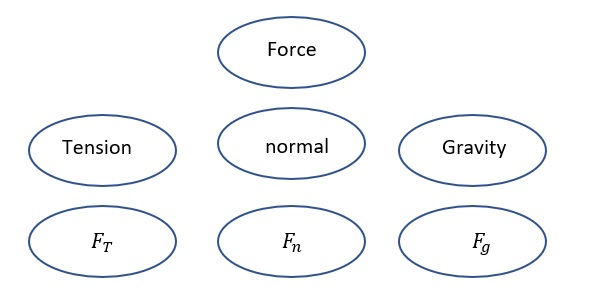
A properly completed concept map is shown in the figure.
b) The force with which the hand acts on it is greater than the force of friction and the total force is different from zero and the result is the acceleration of the book. (Newton’s 2nd law)
c) The book will move if the force of the hand is equal to the force of friction, ie if the total force on the book is equal to 0. (1st Newton’s law.)
b) $F_{net}ne 0 rightarrow F_{net}=mcdot a$ (2nd Newton’s law)
c) $F_{friction}=F_{push} rightarrow F_{net}= 0 rightarrow v=const$ (1st Newton’s law)
F_{start}=mcdot a + F_{friction}> F_{drive}=F_{friction}
$$
We know that when riding a bike we have to press the pedals to maintain a constant speed which means we act with force while the acceleration is $a = 0$. Of course, we know that the force of air resistance and friction acts in the opposite direction, and that we actually overcome these two forces, that is, we maintain the sum of forces equal to 0.
b) Assuming that the air density is constant with height the parachute will fall at a constant speed due to equalizing the force of air resistance and the force of gravity. The speed at which it descends is small enough to land safely on the ground.
b) It moves at a constant speed until it hits the ground when it slows down abruptly.
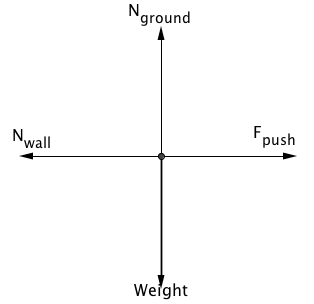
N_ground: The normal force the ground applies on the bed (Up)
Weight: The force of gravity that the earth pulls down on the bed (Down)
F_push: The force the person applies on the bed (Right)
N_wall: The normal force the wall applies on the bed (Left)
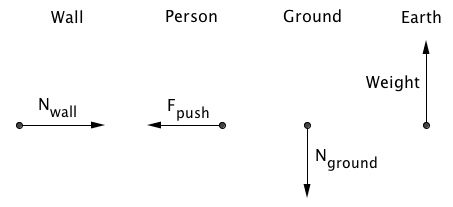
The reaction force of N_ground is the force the bed applies on the ground. (Down)
The reaction force of Weight is the force of gravity the bed pulls up on the earth (Up)
The reaction force of of F_push is the force the bed applies on the bed (Left)
The reaction force of N_wall is the normal force the bed applies on the wall (Right)
$$
4<1<3<2
$$
A possible solution is also:
$$
4 <1 = 3 <2
$$
if the rope tension on block no. 2 is $F_T = 0$. And another possible solution would be:
$$
4 <1 <3 = 2
$$
If the rope tension on block no. 3 were equal to weight of blue block: $F_T = F_g$.
But this is not the case in a massless rope as there is no weight of the rope to affect the tension, hence it is constant throughout the rope.
$$
begin{align*}
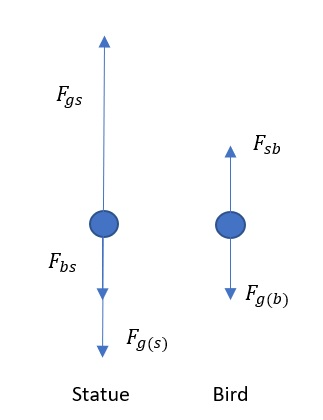
& F_{g(b)} tag{weight of bird} \
& F_{sb} tag{normal force exerted by statue on bird} \
& F_{bs} tag{ force exerted by bird on statue} \
& F_{g(s)} tag{ weight of statue} \
& F_{gs} tag{ force exerted by ground on statue}
end{align*}
$$
Interaction pair is: $F_{sb}$ and $F_{bs}$.
Note that the weight of the bird and the weight of the statue are not in a realistic ratio but this is for the purpose of clarity.
$$
F=ma
$$
We can therefore calculate the force of the man
$F_{Man}=75(10)=750$ N
And the force fo the Lion
$F_{Lion}=170(10)=1700$
To calculate the difference in forces we simply subtract the force of the man from the force of the lion
$$
F=F_{Lion}-F_{Man}=1700-750=boxed{950text{ N}}
$$
$$
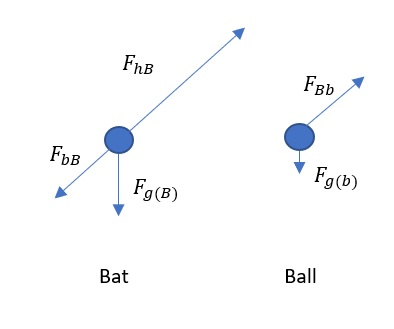
begin{align*}
& F_{g(b)} tag{weight of ball} \
& F_{Bb} tag{normal force exerted by bat on ball} \
& F_{bB} tag{ force exerted by ball on bat} \
& F_{g(B)} tag{ weight of Bat} \
& F_{hB} tag{force exerted by hand on bat}
end{align*}
$$
Interaction pair is: $F_{bB}$ and $F_{Bb}$.
The role of the headrest is to speed up the head by applying force to the bones of the skull, which are much stronger and more resistant, thus preventing neck injuries.
b) The role of the headrest: it accelerates the head instead of the neck and thus reduces the force on it.
$$
begin{align*}
& 2 mathrm{OZ} \
& 340 mathrm{g}
end{align*}
$$
During a free fall in a vacuum, the only force acting on the body is the gravitational force $F_g = m cdot g$ if we include this force in Newton’s second law, we can calculate the acceleration.
$$
begin{align*}
F&=mcdot g \
mcdot a&= mcdot g \
a&=g
end{align*}
$$
$textbf{Air force is also included}$ in this task. The key thing is that objects are of equal surface area, volume and have equal acceleration. It is also crucial that the force of air resistance does not depend on the mass of the object but on its volume, area and speed. As a result, the balls will fall with an acceleration of less than $9.8 mathrm {m / s^2}$ until they reach the terminal velocity. $textbf{The difference occurs after reaching the terminal speed.}$ The terminal velocity is the one at which the force of gravity $F_g$ equals the force of air resistance $F_ {ar}$. A $textbf{heavier ball}$ is subjected to a $textbf{higher gravitational force}$, which means that a $textbf{higher force of air resistance}$ will be required, which ultimately means that the heavier ball will have a $textbf{higher terminal velocity.}$
So while it will $textbf{accelerate equally}$, the $textbf{lighter ball will reach its terminal speed earlier}$ and will continue to move constantly while the heavier one will continue to accelerate to its terminal speed and continue to continue constantly but faster, which tells us that the $textbf{heavier ball will fall sooner.}$
A correct comparison is one and only that between two equal physical quantities, i.e. mass can be compared only with mass and weight with weight.
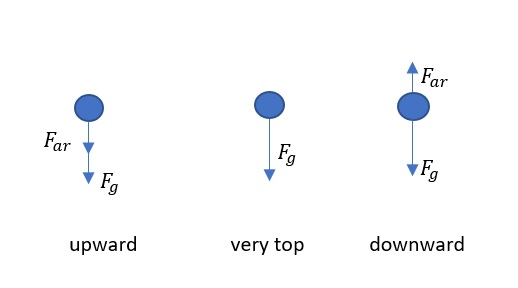
b) $v_{ball}=0 mathrm{m/s}$
c) $a=g=9.8 mathrm{m/s^2}$
$$
begin{align*}
m&=1 mathrm{kg} \
g&=9.8 mathrm{m/s^2} \
F_{net}&=? \
\
F_{net}&=F_g \
&=mcdot g \
&=1 mathrm{kg} cdot 9.8 mathrm{m/s^2} \
&=9.8 mathrm{N}
end{align*}
$$
F_{net}=9.8 mathrm{N}
$$
Known:
$$
begin{align*}
F&=5 mathrm{N} \
m&=40 mathrm{kg}
end{align*}
$$
Unknown:
$$
begin{align*}
a&=? \
\
F&=mcdot a \
a&=dfrac{F}{m} \
&=dfrac{5 mathrm{N}}{40 mathrm{kg}} \
&=boxed{0.125 mathrm{m/s^2}}
end{align*}
$$
a=0.125 mathrm{m/s^2}
$$
Known:
$$
begin{align*}
a&=3 mathrm{m/s^2} \
m&=2300 mathrm{kg}
end{align*}
$$
Unknown:
$$
begin{align*}
F&=? \
\
F&=mcdot a \
&=2300 mathrm{kg}cdot 3 mathrm{m/s^2} \
&=boxed{6900 mathrm{N}}
end{align*}
$$
F=6900 mathrm{N}
$$
Known:
$$
begin{align*}
F{net}&=0.17 mathrm{N} \
m&=13 mathrm{g}=1.3*10^{-2} mathrm{kg}
end{align*}
$$
Unknown:
$$
begin{align*}
a&=? \
\
F&=mcdot a tag{Newton’s second law} \
\
a&=dfrac{F}{m} \
&=dfrac{0.17 mathrm{N}}{1.3*10^{-2} mathrm{kg}} \
&=boxed{13.08 mathrm{m/s^2}}
end{align*}
$$
a=13.08 mathrm{m/s^2}
$$
$$
F = m g = (70) times (9.8) = 686 N
$$
Known:
$$
begin{align*}
F_g&=2450 mathrm{N} \
g&=9.8 mathrm{m/s^2}
end{align*}
$$
Unknown:
$$
begin{align*}
m&=?\
\
F_G&=mcdot g \
m&=dfrac{F_G}{g} \
&=dfrac{2450 mathrm{N}}{9.8 mathrm{m/s^2}} \
&=boxed{250 mathrm{kg}}
end{align*}
$$
m=250 mathrm{kg}
$$
b) shot put, basketball, balloon
c) they are in reverse order.
1 newton = 0.224808943 pounds force
$$
==> 100.0 N = 22.5 pounds
$$
Known:
$$
begin{align*}
m&= 7.5 mathrm{kg} \
F&=78.4 mathrm{N} \
end{align*}
$$
Unknown:
$$
begin{align*}
g&=?\
\
F_G&=mcdot g \
g&=dfrac{F_G}{m} \
&=dfrac{F}{m} \
&=dfrac{78.4 mathrm{N}}{7.5 mathrm{kg}} \
&=boxed{10.45 mathrm{m/s^2}}
end{align*}
$$
g=10.45 mathrm{m/s^2}
$$
Known:
$$
begin{align*}
m&=873 mathrm{kg} \
v_f&=26.3 mathrm{m/s} \
t_f&=0.59 mathrm{s} \
m_D&=68 mathrm{kg}
end{align*}
$$
Unknown:
$$
begin{align*}
a&=? \
F_C&=? tag{force on car}\
F_{sd}&=? tag{force of seat on driver}
end{align*}
$$
$$
begin{align*}
a&=dfrac{v_f-v_i}{t_f-t_i} \
&=dfrac{26.3 mathrm{m/s}}{0.59 mathrm{s}} \
&=boxed{44.58 mathrm{m/s^2}}
end{align*}
$$
$$
begin{align*}
F_{sd}&=mcdot a \
&=873 mathrm{kg}cdot 44.58 mathrm{m/s^2} \
&=boxed{3.892cdot 10^{4} mathrm{N}}
end{align*}
$$
$$
begin{align*}
F_C&=mcdot a \
&=68 mathrm{kg}cdot 44.58 mathrm{m/s^2} \
&=boxed{3031 mathrm{N}}
end{align*}
$$
b) $F_C=3.892*10^4 mathrm{N}$
c) $F_{sd}=3031 mathrm{N}$
$$
begin{align*}
m&=53 mathrm{kg} \
g&=9.8 mathrm{m/s^2} \
a_A&=0 mathrm{m/s^2} \
a_B&=-2 mathrm{m/s^2} \
a_C&=-2 mathrm{m/s^2} \
a_D&=0 mathrm{m/s^2} \
a_E&=a \
F_s&=?
\
F_s&=F_g+ma \
&=mcdot (g+a) \
\
F_{s(A)}&=mcdot (g+0) \
&=53 mathrm{kg}cdot 9.8 mathrm{m/s^2} \
&=519.4 mathrm{N} \
\
F_{s(B)}&=mcdot (g-2) \
&=53 mathrm{kg}cdot 7.8 mathrm{m/s^2} \
&=413.4 mathrm{N} \
\
F_{s(C)}&=mcdot (g-2) \
&=53 mathrm{kg}cdot 7.8 mathrm{m/s^2} \
&=413.4 mathrm{N} \
\
F_{s(D)}&=mcdot (g+0) \
&=53 mathrm{kg}cdot 9.8 mathrm{m/s^2} \
&=519.4 mathrm{N} \
\
F_{s(E)}&=mcdot (g+a)
end{align*}
$$
begin{align*}
F_{s(A)}&=519.4 mathrm{N} \
F_{s(B)}&=413.4 mathrm{N} \
F_{s(C)}&=413.4 mathrm{N} \
F_{s(D)}&=519.4 mathrm{N} \
F_{s(E)}&=mcdot (g+a)
end{align*}
$$
No, it can not hold.
– Bag threshold: $F_b=230mathrm{~N}$
– Groceries mass: $m_g=15mathrm{~kg}$
– Acceleration: $a=7.0mathrm{~dfrac{m}{s^2}}$
**Objective**
– Find if the bag can endure the force.
In order to solve this problem, we will need to consider Newton’s third law: A body that is acting with a certain force on another body will experience the force of the same intensity in the opposite direction.
Let’s take upward direction to be positive. There are two forces that are acting on the bag by Newton’s second law, the gravitational force of the groceries $F_g=m_gcdot g$ and a force due to upward acceleration of groceries $F_{a}=m_gcdot a$.
The gravitational force is acting downwards on the groceries, but the groceries are, by Newton’s third law, acting on the bag with the same intensity in opposite direction – meaning upwards.
The force due to upward acceleration $F_a$ is pulling both the bag and the groceries upwards, so it also acting on the bag in the upward direction.
$$begin{aligned}
F_{sum}&=F_g+F_a
\&=m_gcdot g + m_gcdot a
\&= 15cdot 9.81 + 15cdot 7
\&=boxed{252mathrm{~N}}
end{aligned}$$
Since the total force acting on the bag $F_{sum}$ is bigger than the bag threshold $F_b$, the bag cannot stand the force.
$$
F = W = m g = (0.50)*(9.8) = 4.9 N
$$
$$
begin{align*}
g_M&=0.38cdot g_E \
g_E&=9.8 mathrm{m/s^2} \
m_A&=6 mathrm{kg} \
g_P&=0.08cdot g_M \
m_B&=7 mathrm{kg}
end{align*}
$$
$$
begin{align*}
F_{g(A)}&=? \
F_{g(B)}&=?
end{align*}
$$
$$
begin{align*}
F_g&=mcdot g
end{align*}
$$
$$
begin{align*}
F_{g(A)}&=m_Acdot g_M \
&=m_Acdot 0.38cdot g_E \
&=6 mathrm{kg}cdot 0.38cdot 9.8 mathrm{m/s^2} \
&=boxed{22.34 mathrm{N}}
end{align*}
$$
$$
begin{align*}
F_{g(B)}&=m_Bcdot g_P \
&=m_Bcdot 0.08cdot 0.38cdot g_E \
&=7 mathrm{kg}cdot 0.08cdot 0.38cdot 9.8 mathrm{m/s^2} \
&=boxed{2.085 mathrm{N}}
end{align*}
$$
begin{align*}
F_{g(A)}&=22.34 mathrm{N} \
F_{g(B)}&=2.085 mathrm{N}
end{align*}
$$
Known:
$$
begin{align*}
m&=65 mathrm{kg} \
h&=10 mathrm{m} \
d&=2 mathrm{m} \
end{align*}
$$
Unknown:
$$
begin{align*}
a&=?\
F_w&=? tag{stopping force of water}
end{align*}
$$
In order to calculate the speed at which a diver strikes the surface of the water we must consider its motion. When he jumps from the tower he accelerates with an initial speed of zero. If we ignore the resistance of the air, the only force acting on it and which accelerates it is the gravitational force. if we incorporate this force into Newton’s second law we get:
$$
begin{align*}
F&=mg \
ma&=mg\
a&=g=9.8 mathrm{m/s^2}
end{align*}
$$
The velocity at uniformly accelerated motion is calculated as follows:
$$
begin{align*}
v^2&=2cdot acdot s \
v^2&=2cdot gcdot h \
&=2cdot 9.8 mathrm{m/s^2}cdot 10 mathrm{m} \
v^2&=196 mathrm{m^2/s^2} \
v&=boxed{14 mathrm{m/s}}
end{align*}
$$
$$
begin{align*}
v^2 &=2cdot acdot s \
a&=dfrac{v^2}{2cdot s} \
a&=dfrac{v^2}{2cdot d} \
&=dfrac{196 mathrm{m^2/s^2}}{2cdot 2 mathrm{m}} \
&=-49 mathrm{m/s^2} tag{we must add negative signe because of direction}\
\
F_w&=mcdot a \
&=65 mathrm{kg}cdot -49 mathrm{m/s^2} \
&=boxed{-3185 mathrm{N}}
end{align*}
$$
begin{align*}
v&=14 mathrm{m/s} \
F_w&=- 3185 mathrm{N}
end{align*}
$$
Where x is the displacement, a is the acceleration, t is the time duration, $v_0$ is the initial velocity.
$x = (1/2) a t^2 + v_0 t$
$40.0 = (1/2) a (3.0)^2 + (0.0) (3.0)$
$==> a = 8.889 m/s^2$
The net force:
$$
F_{net} = m a = (710)*(8.8889) = 6300 N
$$
6300 N
$$
Known:
$$
begin{align*}
m_1&=6 mathrm{kg} \
m_2&=7 mathrm{kg} \
end{align*}
$$
Unknown:
$$
begin{align*}
F_{12}&=? tag{force exerted by upper block on the lower block} \
F_{21}&=? tag{force with which the lower block acts on the upper} \
\
F_{12}&=m_cdot g \
&=6 mathrm{kg}cdot -9.8 mathrm{m/s^2} \
&=boxed{-58.8 mathrm{N}} \
\
F_{21}=-F_{12} \
&=boxed{58.8 mathrm{N}}
end{align*}
$$
Positive direction: upward
b) $F_{12}=-58.8 mathrm{N}$
Known:
$$
begin{align*}
m&=2.45 mathrm{mg}=2.45cdot 10^{-6} mathrm{kg} \
g&=9.8 mathrm{m/s^2}
end{align*}
$$
Unknown:
$$
begin{align*}
F_{rE}&=? tag{force of rain drop exerted on Earth}
end{align*}
$$
$$
F_g=mcdot g
$$
We also know if the Earth acts by force on a droplet then the droplet also acts by force on the Earth due to Newton’s third law.
$$
begin{align*}
F_{21}&=-F_{12} tag{third Newton’s law} \
F_{rE}&=-F_{Er} tag{$F_{Er} $force of Earth exerted on rain drop}
end{align*}
$$
$$
begin{align*}
F_{Er}&=mcdot g \
&=2.45cdot 10^{-6} mathrm{kg}cdot 9.8 mathrm{m/s^2} \
&=2.401cdot 10^{-5} mathrm{N} \
\
F_{rE}&=-F_{Er} \
&=boxed{-2.401cdot 10^{-5} mathrm{N}}
end{align*}
$$
Notice that force of gravity $F_{Er}$ is positive meaning that positive direction is toward the Earth, ie. downward.
F_{rE}=-2.401cdot 10^{-5} mathrm{N}
$$
$F_{55} = m g = (55)*(0.025) = 1.4 N$
The force on the 90 Kg man is equal to the force on the 55 Kg man:
$$
F_{90} = F_{55} = 1.4 N
$$
1.4 N
$$
$$
begin{align*}
m_H&=75 mathrm{kg} \
m_L&=170 mathrm{kg} \
a&=10 mathrm{m/s^2}
end{align*}
$$
Unknown:
$$
begin{align*}
F_L/F_H&=?
end{align*}
$$
$$
begin{align*}
F&=mcdot a
end{align*}
$$
Then to get the ratio we simply divide the two forces.
$$
begin{align*}
F_L&=m_Lcdot a \
&=170 mathrm{kg}cdot 9.8 mathrm{m/s^2} \
&=1666 mathrm{N}
end{align*}
$$
$$
begin{align*}
F_H&=m_Hcdot a \
&=75 mathrm{kg}cdot 9.8 mathrm{m/s^2} \
&=735 mathrm{N}
end{align*}
$$
$$
begin{align*}
F_L/F_H&=dfrac{F_L}{F_H} \
&=dfrac{1666 mathrm{N}}{735 mathrm{N}} \
&=boxed{2.267}
end{align*}
$$
To have the same acceleration as a human sprinter, a lion must use approximately twice as much force because of its approximately twice as much mass.
dfrac{F_L}{F_H}=2.267
$$
$F_{grav}$ = (4500)(9.8)
$F_{grav}$ = 44100 N
Let’s look at the first part: What’s the gravitational force on that helicopter? We know it’s mass and the acceleration due to gravity (9.8 m/$s^{2}$).
$F_{motion}$ = (4500)(2.0)
$F_{motion}$ = 9000 N
$F_{lift}$ = (44100) + (9000)
$F_{lift}$ = 53100 N
Known:
$$
begin{align*}
m_U&=4.6 mathrm{kg} \
m_M&=1.2 mathrm{kg} \
m_D&=3.7 mathrm{kg} \
end{align*}
$$
Unknown:
$$
begin{align*}
F_n? tag{all normal forces in the task}
end{align*}
$$
In this task, 6 normal forces act, three in the downward direction and three in the upward direction. It is enough to calculate the forces in only one direction. We will calculate the forces in the second using Newton’s third law. Let’s choose the direction down. Here we actually calculate the weights of the blocks because the forces with which the upper blocks act on the lower ones are their weights. We have to make sure that the second and third blocks have a block above them so we have to add their weight as well.
begin{align*}
F_{UM}& tag{force of upper block on the middle } \
F_{ML}& tag{force of middle block on the lower } \
F_{LG}& tag{force of lower block on the ground} \
\
F_{UM}&=m_Ug \
&=4.6 mathrm{kg}9.8 mathrm{m/s^2} \
&=boxed{45.08 mathrm{N}} \
\
F_{ML}&=m_Ug+m_Mg \
&=4.6 mathrm{kg}9.8 mathrm{m/s^2} + 1.2 mathrm{kg}9.8 mathrm{m/s^2} \
&=boxed{56.84 mathrm{N}} \
\
F_{LG}&=m_Ug+m_Mg+m_Lg \
&=4.6 mathrm{kg}9.8 mathrm{m/s^2} + 1.2 mathrm{kg}9.8 mathrm{m/s^2}+3.7 mathrm{kg}9.8 mathrm{m/s^2} \
&=boxed{93.1 mathrm{N}} \
\
F_{MU}& tag{force of middle block on the upper } \
F_{LM}& tag{force of lower block on the middle } \
F_{GM}& tag{force of ground on the lower block} \
\
F_{12}&=-F_{21} tag{third Newton’s law} \
F_{MU}&=-F_{UM} \
&=boxed{-45.08 mathrm{N}} \
\
F_{LM}&=-F_{ML}\
&=boxed{-56.84 mathrm{N}} \
\
F_{GL}&=-F_{LG} \
&=boxed{-93.1 mathrm{N}}
end{align*}
$$
Notice that the positive direction is downward.
begin{align*}
F_{UM}&=45.08 mathrm{N} \
F_{ML}&=56.84 mathrm{N} \
F_{LG}&=93.1 mathrm{N} \
F_{MU}&=-45.08 mathrm{N} \
F_{LM}&=-56.84 mathrm{N} \
F_{GL}&=-93.1 mathrm{N}
end{align*}
$$
Positive direction: downward.
Known:
$$
begin{align*}
s&=402.3 mathrm{m} \
t&=4.936 mathrm{s} \
end{align*}
$$
Unknown:
$$
begin{align*}
a&=? \
v_f&=? \
\
s&=dfrac{1}{2} acdot t^2 \
a&=dfrac{2s}{t^2} \
&=dfrac{2cdot 402.3 mathrm{m}}{4.936^2 mathrm{s^2}} \
&=boxed{33.02 mathrm{m/s^2}} \
\
v&=at \
\
v_f&=at \
&=33.02 mathrm{m/s^2}cdot 4.936 mathrm{s}\
&=boxed{163 mathrm{m/s^2}}
end{align*}
$$
begin{align*}
a&=33.02 mathrm{m/s^2}\
v_f&=163 mathrm{m/s^2}
end{align*}
$$
Known:
$$
begin{align*}
F_g&=2.75cdot 10^6 mathrm{N} tag{weight of jet} \
F_t&=6.35cdot 10^6 mathrm{N} tag{thrust force}\
v_f&=285 mathrm{km/h}=79.17 mathrm{m/s} \
end{align*}
$$
Unknown:
$$
begin{align*}
s&=? tag{required runway length}\
\
F_g&=mg \
m&=dfrac{F_g}{g} tag{mass of jet} \
&=dfrac{2.75cdot 10^6 mathrm{N}}{9.8 mathrm{m/s^2}} \
&=2.806cdot 10^5 mathrm{kg} \
\
F_t&=mcdot a \
a&=dfrac{F_t}{m} \
&=dfrac{6.35cdot 10^6 mathrm{N}}{2.806cdot 10^5 mathrm{kg}} \
&=22.63 mathrm{m/s^2} \
\
v^2&=2cdot a cdot s \
s&=dfrac{v^2}{2cdot a} \
&=dfrac{v_F^2}{2cdot a} \
&=dfrac{79.17 mathrm{m/s}^2}{2cdot 22.63 mathrm{m/s^2}}\
&=boxed{138.5 mathrm{m}}
end{align*}
$$
s=138.5 mathrm{m}
$$
$$
begin{align*}
m&=873 mathrm{kg} \
Delta v&=26.3 mathrm{m/s} \
Delta t&=0.59 mathrm{s} \
v_f&=126.6 mathrm{m/s} \
s&=402.3 mathrm{m} tag{assumed race lenght} \
\
a_1&=dfrac{Delta v}{Delta t } tag{acceleration from task 68} \
&=dfrac{26.3 mathrm{m/s}}{0.59 mathrm{s}} \
&=44.58 mathrm{m/s^2} \
\
v^2&=2cdot acdot s \
a&=dfrac{v^2}{2s} \
a_2&=dfrac{v_f^2}{2s} tag{average acceleration of whole race} \
&=dfrac{126.6^2 mathrm{m^2/s^2}}{2cdot 402.3 mathrm{m}} \
&=19.92 mathrm{m/s^2}
end{align*}
$$
We can see that the average acceleration $a_2$ is less than the acceleration at the beginning of $a_1$ which means that the acceleration is certainly not constant throughout the race. Another way to determine whether the acceleration is constant is to measure the time in several places, measure the distances from the start to the measurement site and display the data in a $s-t^2$ diagram, if the direction cannot be drawn through the data, ie if the dependence is not linear. acceleration is not constant.
$$
begin{align*}
m_B&=65 mathrm{kg} \
m_G&=45 mathrm{kg} \
a_G&=-3 mathrm{m/s^2} \
a_B&=? \
\
F_{12}&=-F_{21} tag{Third Newton’s law} \
F_{BG}&=-F_{GB} tag{ the force with which the boy acts on the girl through the force of tension and vice versa} \
m_Bcdot a_B&=-(m_Gcdot a_G) \
a_B&=dfrac{-(m_Gcdot a_G)}{m_B} \
&=dfrac{-(45 mathrm{kg}cdot -3 mathrm{m/s^2})}{65 mathrm{kg}} \
&=2.077 mathrm{m/s^2}
end{align*}
$$
$$
begin{align*}
F_g&=588 mathrm{N} \
a&=3 mathrm{m/s^2} \
F_{wP}&=? tag{force with which wall acts on Pratish}
end{align*}
$$
We must first calculate Pratisha’s mass from the weight. When we calculate the mass we can calculate the force required for a given acceleration.
$$
begin{align*}
F_g&=mg \
m&=dfrac{F_g}{g} \
&=dfrac{588 mathrm{N}}{9.8 mathrm{m/s^2}} \
&=60 mathrm{kg} \
\
F&=mcdot a \
F_{wP}&=mcdot a \
&=60 mathrm{kg}cdot 3 mathrm{m/s^2} \
&=180 mathrm{N}
end{align*}
$$
F_{wP}=180 mathrm{N}
$$
Known:
$$
begin{align*}
v_i&=30 mathrm{m/s} \
v_f&=0 mathrm{m/s} \
Delta t&=0.005 mathrm{s} \
m&=0.145 mathrm{kg} \
end{align*}
$$
Unknown:
$$
begin{align*}
a&=? \
F_{PB}&=? tag{force with which player acts on ball} \
F_{BP}&=? tag{force with which ball acts on player}
end{align*}
$$
Suppose the positive direction is in the direction of motion of the ball before it is caught. Acceleration is calculated from the data on the change in speed.
$$
begin{align*}
a&=dfrac{v_f-v_i}{Delta t} \
&=dfrac{0 mathrm{m/s}-30 mathrm{m/s}}{0.005 mathrm{s}} \
&=boxed{-6000 mathrm{m/s^2}}
end{align*}
$$
The force exerted on the ball required to stop it is calculated according to Newton’s second law:
$$
begin{align*}
F&=mcdot a \
F_{PB}&=mcdot a\
&=0.145 mathrm{kg}cdot -6000 mathrm{m/s^2} \
&=boxed{-870 mathrm{N}}
end{align*}
$$
The force acting on the player is calculated using Newton’s third law:
$$
begin{align*}
F_{BP}&=-F_{PB} \
&=boxed{870 mathrm{N}}
end{align*}
$$
b) $F_{PB}=-870 mathrm{N}$
c) $F_{BP}=870 mathrm{N}$
Known:
$$
begin{align*}
m&=0.25 mathrm{kg} \
F&=12 mathrm{N} \
Delta t&=9 mathrm{s} \
end{align*}
$$
Unknown:
$$
begin{align*}
a&=? \
v_f&=?
end{align*}
$$
Friction can be ignored, gravity is reversed by the force with which air acts upwards. The only force we are interested in is the one with which he was pushed. Acceleration is then calculated from Newton’s second law. When we calculate the acceleration, we can easily calculate the final speed of the puck.
$$
begin{align*}
F&=mcdot a \
a&=dfrac{F}{m} \
&=dfrac{12 mathrm{N}}{0.25 mathrm{kg}} \
&=boxed{48 mathrm{m/s^2}} \
\
v&=acdot t \
v_f&=acdot t \
&=48 mathrm{m/s^2}cdot 9 mathrm{s} \
&=boxed{432 mathrm{m/s}}
end{align*}
$$
By calculation, the final speed turns out to be very high, even unrealistically high. Although the force is not large the time of action is relatively large. Anyone who has played air hockey knows that the force on the puck acts only for a fraction of a second because the puck is started by hitting.
b) $v_f=432 mathrm{m/s}$
Known:
$$
begin{align*}
F_{s(v=0)}&=836 mathrm{N} tag{the force shown by the scale} \
F_{s(A)}&=936 mathrm{N} \
F{s(B)}&=782 mathrm{N} \
end{align*}
$$
Unknown:
$$
begin{align*}
a_A&=? \
a_B&=?
end{align*}
$$
At rest the scale shows the amount of student weight. When the elevator accelerates, the scale shows the net force of the student’s weight and the inertial force that we will calculate using Newton’s second law.
begin{align*}
F_{s(v=0)}&=F_g \
&=mcdot g \
m&=dfrac{F_{s(v=0)} }{g} \
&=dfrac{836 mathrm{N}}{9.8 mathrm{m/s^2}} \
&=85.31 mathrm{kg} \
\
F_s&=F_{s(v=0)}+F \
F_s&=F_{s(v=0)}+ma \
\
F_{s(A)}&=F_{s(v=0)}+ma_A \
a_A&=dfrac{F_{s(A)}-F_{s(v=0)}}{m} \
&=dfrac{936 mathrm{N}-836 mathrm{N}}{85.31 mathrm{kg}}\
&=boxed{1.172 mathrm{m/s^2}} \
\
F_{s(B)}&=F_{s(v=0)}+ma_B \
a_B&=dfrac{F_{s(B)}-F_{s(v=0)}}{m} \
&=dfrac{782 mathrm{N}-836 mathrm{N}}{85.31 mathrm{kg}}\
&=boxed{-0.633 mathrm{m/s^2}} \
\
a_A/a_B&=dfrac{|a_A|}{|a_B|} \
&=dfrac{1.172 mathrm{m/s^2}}{0.633 mathrm{m/s^2}} \
&=boxed{1.852}
end{align*}
$$
b) $a_B=0.633 mathrm{m/s^2}$
c) More time is needed to stop
Known:
$$
begin{align*}
m&=5 mathrm{kg} \
F_{up}&=98 mathrm{N} \
t&=10 mathrm{s} \
end{align*}
$$
Unknown:
$$
begin{align*}
a&=? \
v_f&=?
end{align*}
$$
We must first calculate the net force on the instruments which is actually the difference between the upward force and the gravitational force. After that, we get the acceleration using Newton’s second law.
$$
begin{align*}
F_{net}&=F_{up}-F_g \
&=98 mathrm{N}-5 mathrm{kg}cdot 9.8 mathrm{m/s^2} \
&=49 mathrm{N}
end{align*}
$$
$$
begin{align*}
F&=mcdot a \
a&=dfrac {F}{m} \
\
a&=dfrac{F_{up}}{m} \
&=dfrac{49 mathrm{N}}{5 mathrm{kg}} \
&=boxed{9.8 mathrm{m/s^2}} \
\
v&=acdot t \
v_f&=acdot t \
&=9.8 mathrm{m/s^2}cdot 10 mathrm{s} \
&=boxed{98 mathrm{m/s}}
end{align*}
$$
After releasing the instruments, $textbf{only gravity}$ acts on them and they start to slow down.
$$
begin{align*}
v&=acdot t \
t&=dfrac{v}{a} \
\
t&=dfrac{v}{g} \
&=dfrac{98 mathrm{m/s}}{9.8 mathrm{m/s^2}} \
&=boxed{10 mathrm{s}}
end{align*}
$$
We see that the deceleration time is equal to the acceleration time.
b) $v=98 mathrm{m/s}$
c) Force of gravity
d) The instruments will change direction after $10 mathrm {s}$
Known:
$$
begin{align*}
F&=4.5 mathrm{N} \
a_1&=2.5 mathrm{m/s^2} \
m_2&=4 mathrm{kg} \
end{align*}
$$
Unknown:
$$
begin{align*}
a_2&=? tag{acceleration of combination}
end{align*}
$$
To calculate the acceleration of a combination of blocks we need to know the total mass which means we need to calculate the mass of the first block. We will calculate this using Newton’s 2nd law, then only the total mass and the total force are included in the same law.
$$
begin{align*}
F&=mcdot a \
m&=dfrac{F}{a} \
\
m_1&=dfrac{F}{a_1} \
&=dfrac{4.5 mathrm{N}}{2.5 mathrm{m/s^2}} \
&=1.8 mathrm{kg} \
\
a&=dfrac{F}{m} \
a_2&=dfrac{F}{m_1+m_2} \
&=dfrac{4.5 mathrm{N}}{1.8 mathrm{kg}+4 mathrm{kg}} \
&=boxed{0.7759 mathrm{m/s^2}}
end{align*}
$$
a_2=0.7759 mathrm{m/s^2}
$$
Known:
$$
begin{align*}
m_1&=4.3 mathrm{kg} \
m_2&=5.4 mathrm{kg} \
F&=22.5 mathrm{N} \
end{align*}
$$
Unknown:
$$
begin{align*}
F_{12}&=? tag {force of $4.3 mathrm{kg}$ block on $5.4 mathrm{kg}$ block} \
F_{21}&=? tag {force of $5.4 mathrm{kg} $ block on $4.3 mathrm{kg}$ block }
end{align*}
$$
It is first necessary to calculate the acceleration of the system, which we will do using Newton’s second law.
$$
begin{align*}
F&=mcdot a \
a&=dfrac{F}{m} \
\
a&=dfrac{F}{m_1+m_2} \
&=dfrac{22.5 mathrm{N}}{4.3 mathrm{kg}+5.4 mathrm{kg}} \
&=boxed{2.32 mathrm{m/s^2}}
end{align*}
$$
$$
begin{align*}
F&=mcdot a \
\
F_{12}&=m_2cdot a \
&=5.4 mathrm{kg}cdot 2.32 mathrm{m/s^2} \
&=boxed{12.53 mathrm{N}} \
\
F_{21}&=-F_{12} \
&=boxed{-12.53 mathrm{N}}
end{align*}
$$
b) $F_{12}=12.53 mathrm{N}$
c) $F_{21}=-12.53 mathrm{N}$
Known:
$$
begin{align*}
m_1&=3 mathrm{kg} \
m_2&=5 mathrm{kg} \
end{align*}
$$
Unknown:
$$
begin{align*}
F_T&=? \
a&=?
end{align*}
$$
To solve this problem, consider which forces act on a particular block. The forces acting on the block are the gravitational force and the tension force of the rope. The force of gravity varies from block to block because they are not of equal mass but the tension have to be the same.
To calculate the rope tension force we will have to solve the equations for both blocks at the same time.
$$
begin{align*}
F_T&=F_{G1}+F \
&=F_{G1}+m_1cdot a \
F_T&=F_{G2}+F \
&=F_{G2}+m_2cdot -a\
\
a&=dfrac{F_T-F_{G1}}{m_1} \
a&=dfrac{F_{G2}-F_T}{m_2}
end{align*}
$$
Pay attention to the sign of acceleration in individual blocks.
$$
begin{align*}
dfrac{F_T-F_{G1}}{m_1}&=dfrac{F_{G2}-F_T}{m_2} \
dfrac{F_T-m_1g}{m_1}&=dfrac{m_2g-F_T}{m_2} \
m_2F_T-m_1m_2g&=m_1m_2g-m_1F_T tag{crosswise multiplication} \
(m_1+m_2)F_T&=2m_1m_2g \
F_T&=dfrac{2m_1m_2g}{(m_1+m_2)}
end{align*}
$$
begin{align*}
F_T&=dfrac{2m_1m_2g}{(m_1+m_2)} \
&=dfrac{2cdot 3 mathrm{kg}cdot 5 mathrm{kg}cdot 9.8 mathrm{m/s^2}}{3 mathrm{kg}+5 mathrm{kg}} \
&=boxed{36.75 mathrm{N}}
end{align*}
$$
$$
begin{align*}
a&=dfrac{F_T-F_{G1}}{m_1} \
&=dfrac{F_T-m_1g}{m_1} \
&=dfrac{36.75 mathrm{N}-3 mathrm{kg}cdot 9.8 mathrm{m/s^2}}{3 mathrm{kg}} \
&=boxed{2.45 mathrm{m/s^2}}
end{align*}
$$
b) $a=2.45 mathrm{m/s^2}$
The figure shows a sketch of the system and free body diagrams for both weights.
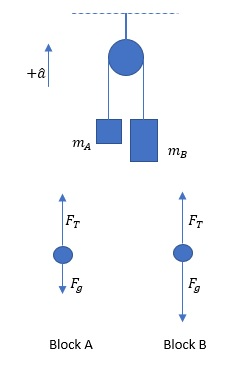
$$
begin{align*}
m_A&=2 mathrm{kg} \
m_B&=3 mathrm{kg} \
end{align*}
$$
Unknown:
$$
begin{align*}
a&=? \
\
F_{net}&=mcdot a \
\
F_{net(A)}&=F_T-F_{gA} \
F_{net(B)}&=F_{GB}-F_T \
\
F_T&=m_Acdot a+F_{gA} \
F_T&=F_{GB}-m_Bcdot a\
\
m_A cdot a+F_{gA}&=F_{GB}-m_B cdot a\
a(m_A+m_B)&=F_{GB}-F_{GA} \
a&=dfrac{F_{GB}-F_{GA}}{(m_A+m_B)}\
&=dfrac{m_Bg-m_Ag}{m_A+m_B} \
&=dfrac{3 mathrm{kg}cdot 9.8 mathrm{m/s^2}-2 mathrm{kg}cdot 9.8 mathrm{m/s^2}}{3 mathrm{kg}+2 mathrm{kg}} \
&=boxed{1.96 mathrm{m/s^2}}
end{align*}
$$
$$
a=1.96 mathrm{m/s^2}
$$
$$
begin{align*}
m_A&=1 mathrm{kg} \
m_B&=4 mathrm{kg}
end{align*}
$$
Unknown:
$$
begin{align*}
a&=?
end{align*}
$$
$$
begin{align*}
F_{net(A)}&=F_{T(A)}-F_{GA} \
F_{net(B)}&=F_{GB}-F_{T(B)}
end{align*}
$$
We know that this difference of forces causes motion so we can replace the net force by another Newton’s law, and express the force of tension for a particular block.
$$
begin{align*}
F_{net}&=mcdot a \
\
F_{T(A)}&=m_Acdot a+F_{GA} \
F_{T(B)}&=F_{GB}-m_Bcdot a\
end{align*}
$$
$$
begin{align*}
F_{T(A)}&=F_{T(B)} \
m_A cdot a+F_{gA}&=F_{GB}-m_B cdot a\
a(m_A+m_B)&=F_{GB}-F_{GA} \
a&=dfrac{F_{GB}-F_{GA}}{(m_A+m_B)}
end{align*}
$$
$$
begin{align*}
a&=dfrac{m_Bg-m_Ag}{m_A+m_B} \
&=dfrac{4 mathrm{kg}cdot 9.8 mathrm{m/s^2}-1 mathrm{kg}cdot 9.8 mathrm{m/s^2}}{4 mathrm{kg}+1 mathrm{kg}} \
&=boxed{5.88 mathrm{m/s^2} }
end{align*}
$$
$$
begin{align*}
F_{t=0}&=0 mathrm{N} \
F_{t=0.001}&=10^4 mathrm{N} \
F_{t=0.002}&=0 mathrm{N}
end{align*}
$$
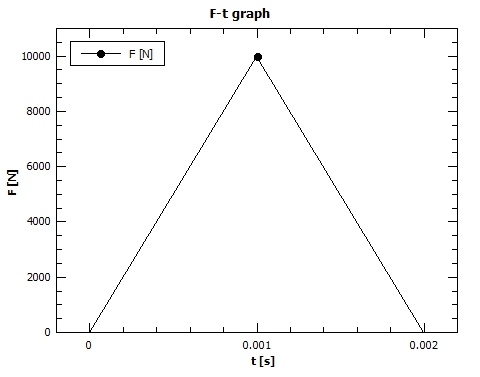
$$
begin{align*}
F_{avg}&=dfrac{F_{t=0}+F_{t=0.001}}{2} \
&=dfrac{0 mathrm{N}+10^4 mathrm{N}}{2} \
&=boxed{5000 mathrm{N}}
end{align*}
$$
Known values:
$$
begin{align*}
F_{avg}&=5000 mathrm{N}\
m&=0.145 mathrm{kg}
end{align*}
$$
Unknown:
$$
begin{align*}
a_{avg}&=? \
\
F&=mcdot a tag{Newton’s second law} \
a&=dfrac{F}{m} \
\
a_{avg}&=dfrac{F_{avg}}{m} \
&=dfrac{5000 mathrm{N}}{0.145 mathrm{kg}} \
&=boxed{3.448cdot 10^4 mathrm{m/s^2}}
end{align*}
$$
Positive direction: opposite to the speed of the ball before impact
$$
begin{align*}
a_{avg}&=3.448cdot 10^4 mathrm{m/s^2} \
v_i&=-25 mathrm{m/s} \
t&=0.002 mathrm{s} \
v_f&=? \
\
v_f&=v_i+acdot t \
&=-25 mathrm{m/s}+3.448cdot10^4 mathrm{m/s^2}cdot 0.002 mathrm{s} \
&=boxed{43.97 mathrm{m/s}}
end{align*}
$$
b) $a_{avg}=3.448cdot 10^4 mathrm{m/s^2}$
c) $v_f=43.97 mathrm{m/s}$
Known:
$$
begin{align*}
m_1&=2 mathrm{kg} \
m_2&=4 mathrm{kg} \
m_3&=6 mathrm{kg} \
F&=36 mathrm{N} \
end{align*}
$$
Unknown:
$$
begin{align*}
a&=? \
F_{T1}&=? \
F_{T2}&=?
end{align*}
$$
$$
begin{align*}
F=&mcdot a\
a&=dfrac{F}{m} \
\
a&=dfrac{F}{(m_1+m_2+m_3)} \
&=dfrac{36 mathrm{N}}{2 mathrm{kg}+4 mathrm{kg}+6 mathrm{kg}} \
&=boxed{3 mathrm{m/s^2}}
end{align*}
$$
$$
begin{align*}
F_{T1}&=F_1 \
&=m_1cdot a \
&=2 mathrm{kg}cdot 3 mathrm{m/s^2} \
&=boxed{6 mathrm{N}} \
\
F_{T2}&=F_2+F_{T1} \
&=m_2cdot a+F{T1} \
&=4 mathrm{kg}cdot 3 mathrm{m/s^2} +6 mathrm{N} \
&=boxed{18 mathrm{N}}
end{align*}
$$
b) $F_{T1}=6 mathrm{N}, F_{T2}=18 mathrm{N}$
Known:
$$
begin{align*}
m&=3.46 mathrm{kg}\
g&=9.8 mathrm{m/s^2} \
end{align*}
$$
Unknown:
$$
begin{align*}
F_T&=?
end{align*}
$$
$$
begin{align*}
2cdot F_T&=F_G \
F_T&=dfrac{F_G}{2} \
&=dfrac{mcdot g}{2} \
&=dfrac{3.46 mathrm{kg}cdot 9.8 mathrm{m/s^2}}{2} \
&=boxed{16.95 mathrm{N}}
end{align*}
$$
F_T=16.95 mathrm{N}
$$
The experiment would be carried out very quickly and very easily. The device would simply be placed on the ground and the spring extension would be read. On the planet Pluto where $g_P=0.3 mathrm {m/ s^2}$ our spring would extend by $l=3 mathrm {mm}$ On a scale we would read this as $0.3 mathrm{m/s^2}$. The same procedure would apply to Mercury but due to $g_M =3.7 mathrm{m/s^2}$ the spring would be extended by $l =3.7 mathrm{cm}$.
In that book, Newton expounds his laws of motion, giving rise to classical mechanics. He is also considered the founder of dynamics and was the first to introduce the concept of force. \
His three laws of motion have long been considered the fundamental laws of physics. in the 20th century this role was taken over by the laws of quantum mechanics and the theory of relativity. \
The magnitude of these laws is reflected in their wide applicability. The fact that they apply to small bodies like raindrops to planetary bodies and allow them to predict their movements with great precision is amazing. \
The precision of his laws is the result of his expertise in the field of mathematics. His great contribution is the development of mathematical language and mathematical methods \
In addition to mechanics, Newton laid the foundations in astronomy by discovering the law of gravity by which he determined the masses of the planets and the sun. Also, his discoveries and brop laws such as the separation of light into rainbow colors, the law of refraction make the basic discoveries in optics. His theory of the particle nature of light was so far ahead of his time that it took several hundred years to prove it. \
All his discoveries undoubtedly had a great impact on physics but his contribution that changed science in general was the introduction of the scientific method. \
Before Newton, scientific research was based on observation and religious mysticism, a methodology that rarely yielded any significant results. \
The scientific method is based on three key points
begin{enumerate}
item observation
item generalization
item experimentation
end{enumerate}
Using this method allowed the facts to speak for themselves.
The introduction of the scientific method has revolutionized science in general and that is why I believe that this is precisely its greatest contribution.
$textbf {A body at rest or moving at a constant speed will remain in that state until a non-zero force begins to act on it}$
From this law we can read the following:
Force is needed to start moving or to change direction but not to move the body.
Care should be taken when claiming that no force is required to maintain speed. It is valid only when no force acts on the body. In the real world we know very well from experience that it takes some force to move at a certain speed. The reason for this is that in the real world a force of friction acts, which means that a force of equal amount and opposite direction should be applied.
Newton’s first law is closely related to the principle of relativity. Let us think in a different way, a different form of the law of motion. One very intuitive form of the law of motion is:
A body at rest in a frame of reference will remain at rest until a force acts on it. But this law must obey the principles of relativity which say that another observer from his frame of reference, moving at a constant speed must observe the same law. In this frame of reference, the body moves at a constant speed along a straight line.
Therefore, in order for Newton’s law to be in accordance with the principles of relativity, it must be supplemented, which brings us to the original form of Newton’s First Law.
Electromagnetic force was described and mathematically formulated somewhat later, in the 19th century by J. C. Maxwell.
Weak and strong nuclear power were discovered only in the 20th century when scientists were able to analyze the nucleus of atoms and subatomic particles.
Weak nuclear power is even smaller.
In contrast, gravitational and electromagnetic forces are extremely large in range, or more precisely infinite.
Gravitational force controls planetary motions while electromagnetic force can be seen as electromagnetic waves such as light and various forms of radiation.
Known:
$$
begin{align*}
t_i&=8:25 mathrm{A.M.} \
v_{avg}&=8 mathrm{km/h} \
s&=5.2 mathrm{km} \
end{align*}
$$
Unknown:
$$
begin{align*}
t_f&=? \
\
s&=vcdot t \
t&=dfrac{s}{v}\
\
t&=dfrac{s}{v_{avg}} \
&=dfrac{5.2 mathrm{km}}{8 mathrm{km/h}} \
&=0.65mathrm{h} \
&=39 mathrm{min}
\
t_f&=t_i+t \
&=8:25 mathrm{A.M.}+39 mathrm{min} \
&=boxed{9:04 mathrm{A.M.}}
end{align*}
$$
A faster car is one with a higher speed. If we know that in the $s-t$ graph the speed is actually the slope of the curve then we can easily compare the speeds of the car. At $t =7 mathrm {s}$ the car A has a higher speed.
As we have already said, velocity is the slope of the graph. The velocities A and B are equal to $t = 5 mathrm {s}$.
If we look at the curve showing the motion of the B car, we can see that the slope never increases but on the contrary falls all the time.
b) Car A
c) $t=5 mathrm{s}$
d) Never
e) Through out the movement, From $t=3 mathrm{s}$ to $t=8 mathrm{s}$.
Since we have no data for car B at the moment $t = 2 mathrm {s}$ we cannot determine the speed, we can say that it did not move because it did not cross any road and time passed so we can say that its speed was $v = 0 mathrm {m / s}$.
At the moment $t = 9 mathrm {s}$ the curve describing the motion of car B is almost parallel to the x axis which means that the distance traveled is constant over time which means that its velocity $v=0 mathrm{m / s}$.
At the moment $t= 2 mathrm{s}$ on the curve describing the motion of car A we can draw a tangent passing through the points $(2,0)$ and $4,4)$ which means that its slope ie speed is $v= 2 mathrm{m/s}$.
b) $v_{B,t=9 mathrm{s}}=0 mathrm{m/s}$
c) $v_{A,t=2 mathrm{s}}=2 mathrm{m/s}$

