a.)
(i) We need to draw the diagram containing 5 payments of $$650$ each and its corresponding present value as shown below.

(ii) The present value is therefore

$PV=650(1.037)^{-1}+650(1.037)^{-2}+650(1.037)^{-3}+…+650(1.037)^{-5}$

(iii) Using the formula for the present value of annuity

$PV=Rcdot dfrac{1-(1+i)^m}{i}=650times dfrac{1-1.037^{-5}}{0.037}=$2918.24$

(iv) The interest is the difference between the present value and the total amount paid.

$$
I=650(5)-2918.24=$331.77
$$

b.)

(i) We need to draw the diagram containing 18 payments of $$1200$ each and its corresponding present value as shown below.

(ii) The present value is therefore

$PV=1200(1.047)^{-1}+1200(1.047)^{-2}+1200(1.047)^{-3}+…+1200(1.047)^{-18}$

(iii) Using the formula for the present value of annuity

$PV=Rcdot dfrac{1-(1+i)^m}{i}=1200times dfrac{1-1.047^{-18}}{0.047}=$14,362.17$

(iv) The interest is the difference between the present value and the total amount paid.

$$
I=18(1200)-14,362.17=$7237.83
$$

c.)

(i) We need to draw the diagram containing $4times 3.5=14$ payments of $$84.73$ each and its corresponding present value as shown below.

(ii) The present value is therefore

$PV=84.73(1.009)^{-1}+84.73(1.009)^{-2}+84.73(1.009)^{-3}+…+84.73(1.009)^{-14}$

(iii) Using the formula for the present value of annuity

$PV=Rcdot dfrac{1-(1+i)^m}{i}=84.73times dfrac{1-1.009^{-14}}{0.009}=$1109.85$

(iv) The interest is the difference between the present value and the total amount paid.

$$
I=14(84.73)-1109.85=$76.37
$$

d.)

(i) We need to draw the diagram containing $12times 10=120$ payments of $$183.17$ each and its corresponding present value as shown below.

(ii) The present value is therefore

$PV=183.17(1.0055)^{-1}+183.17(1.0055)^{-2}+183.17(1.0055)^{-3}+…+183.17(1.0055)^{-120}$

(iii) Using the formula for the present value of annuity

$PV=Rcdot dfrac{1-(1+i)^m}{i}=183.17times dfrac{1-1.0055^{-120}}{0.0055}=$16,059.45$

(iv) The interest is the difference between the present value and the total amount paid.

$$
I=120(183.17)-16059.45=$5920.95
$$

The present value of the $m^{th}$ payment denoted as $PV_m$ is

$PV_m=R(1+i)^{-m}$

where

$R$ = regular payment

$i$ = interest rate per compounding period

$m$ = number of compounding periods

The sum of the series $PV_1+PV_2+PV_3+…+PV_m$ is the present value of the annuity which is calculated as

$$
PV=Rcdot dfrac{1-(1+i)^{-m}}{i}
$$

a.)

(i) We shall calculate the present value of each payment
$(R=8000,; i=0.09,; m=7)$

$PV_n=R(1+i)^{-m}$

$PV_1=8000(1.09)^{-1}=$7339.45$

$PV_2=8000(1.09)^{-2}=$6733.44$

$PV_3=8000(1.09)^{-3}=$6177.47$

$PV_4=8000(1.09)^{-4}=$5667.40$

$PV_5=8000(1.09)^{-5}=$5199.45$

$PV_6=8000(1.09)^{-6}=$4770.14$

$PV_7=8000(1.09)^{-7}=$4376.27$

(ii) $PV = 8000(1.09)^{-1}+8000(1.09)^{-2}+8000(1.09)^{-3}+…+8000(1.09)^{-7}$

(iii) $PV=Rcdot dfrac{1-(1+i)^-m}{i}=8000cdot dfrac{1-1.09^{-7}}{0.09}=$40;263.62$

b.)

(i) We shall calculate the present value of each payment
$(R=300,; i=0.04,; m=7)$

$PV_n=R(1+i)^{-m}$

$PV_1=300(1.04)^{-1}=$288.46$

$PV_2=300(1.04)^{-2}=$277.37$

$PV_3=300(1.04)^{-3}=$266.70$

$PV_4=300(1.04)^{-4}=$256.44$

$PV_5=300(1.04)^{-5}=$246.58$

$PV_6=300(1.04)^{-6}=$237.09$

$PV_7=300(1.04)^{-7}=$227.98$

(ii) $PV = 300(1.04)^{-1}+300(1.04)^{-2}+300(1.04)^{-4}+…+300(1.04^{-7}$

(iii) $PV=Rcdot dfrac{1-(1+i)^-m}{i}=300cdot dfrac{1-1.04^{-7}}{0.04}=$1800.62$

c.)

(i) We shall calculate the present value of each payment
$(R=750,; i=0.02,; m=8)$

$PV_n=R(1+i)^{-m}$

$PV_1=750(1.02)^{-1}=$735.29$

$PV_2=750(1.02)^{-2}=$720.88$

$PV_3=750(1.02)^{-3}=$706.74$

$PV_4=750(1.02)^{-4}=$692.88$

$PV_5=750(1.02)^{-5}=$679.30$

$PV_6=750(1.02)^{-6}=$665.98$

$PV_7=750(1.02)^{-7}=$652.92$

$PV_8=750(1.02)^{-8}=$640.12$

(ii) $PV = 750(1.02)^{-1}+750(1.02)^{-2}+750(1.02)^{-3}+…+750(1.04)^{-8}$

(iii) $PV=Rcdot dfrac{1-(1+i)^-m}{i}=750cdot dfrac{1-1.02^{-7}}{0.02}=$5494.11$

a.) $$40263.62$

b.) $$1800.62$

c.) $$5494.11$

The present value of an annuity is

$PV=Rcdot dfrac{1-(1+i)^{-m}}{i}$

where

$R$ = regular payment

$i$ = interest rate per compounding period

$m$ = number of compounding periods

If the annual interest rate $r$, payment mode, and the number of years $t$ is given,

$i=dfrac{r}{n}$

$m=ntimes t$

$n$ = number of payment per year

a.)

We shall calculate the present value of the annuity
$(R=5000,; i=0.072,; m=5)$

$$
PV=Rcdot dfrac{1-(1+i)^{-m}}{i}=8000cdot dfrac{1-1.072^{-5}}{0.072}=$20;391.67
$$

b.)

We shall calculate the present value of the annuity
$(R=250,; i=0.024,; m=24)$

$$
PV=Rcdot dfrac{1-(1+i)^{-m}}{i}=8000cdot dfrac{1-1.024^{-24}}{0.024}=$4521.04
$$

c.)

We shall calculate the present value of the annuity
$(R=2550,; i=0.001,; m=100)$

$$
PV=Rcdot dfrac{1-(1+i)^{-m}}{i}=8000cdot dfrac{1-1.001^{-100}}{0.001}=$2425.49
$$

d.)

We shall calculate the present value of the annuity
$(R=48.50,; i=0.0195,; m=30)$

$$
PV=Rcdot dfrac{1-(1+i)^{-m}}{i}=48.50cdot dfrac{1-1.0195^{-24}}{0.0195}=$1093.73
$$

a.) $$20;391.67$

b.) $$4521.04$

c.) $$2425.49$

d.) $$1093.73$

The present value of an annuity is

$PV=Rcdot dfrac{1-(1+i)^{-m}}{i}$

where

$R$ = regular payment

$i$ = interest rate per compounding period

$m$ = number of compounding periods

If the annual interest rate $r$, payment mode, and the number of years $t$ is given,

$i=dfrac{r}{n}$

$m=ntimes t$

$n$ = number of payment per year

We are given with present value $PV=1300$, $i=0.015$, $m=24$, and we shall calculate the regular payments.

$PV=Rcdot dfrac{1-(1+i)^{-m}}{i}$

$$
R=dfrac{PVcdot i }{1-(1+i)^{-m}}=dfrac{1300(0.015)}{1-1.015^{-24}}=$64.90
$$

$$
$64.90
$$

The present value of an annuity is

$PV=Rcdot dfrac{1-(1+i)^{-m}}{i}$

where

$R$ = regular payment

$i$ = interest rate per compounding period

$m$ = number of compounding periods

If the annual interest rate $r$, payment mode, and the number of years $t$ is given,

$i=dfrac{r}{n}$

$m=ntimes t$

$n$ = number of payment per year

$r=10%implies i=dfrac{0.1}{4}=0.025$

$t=4$ years, quarterly compounding $implies m=4times 4=16$

a.) The diagram is sketched below.

b.) The present value of each R is $dfrac{R}{(1+i)^m}$

$7500=R(1.025)^{-1}+R(1.025)^{-2}+R(1.025)^{-3}+…+R(1.025)^{-16}$

c.) Using the formula for the present value of annuity

$PV=Rcdot dfrac{1-(1+i)^{-m}}{i}$

$$
R=dfrac{PVcdot i}{1-(1+i)^{-m}}=dfrac{7500(0.025)}{1-1.025^{-16}}=$574.49
$$

a.) see diagram

b.) $7500=R(1.025)^{-1}+R(1.025)^{-2}+R(1.025)^{-3}+…+R(1.025)^{-16}$

c.) $R=$574.49$

The present value of an annuity is

$PV=Rcdot dfrac{1-(1+i)^{-m}}{i}$

where

$R$ = regular payment

$i$ = interest rate per compounding period

$m$ = number of compounding periods

If the annual interest rate $r$, payment mode, and the number of years $t$ is given,

$i=dfrac{r}{n}$

$m=ntimes t$

$n$ = number of payment per year

a.) In this case,

$R=40$ , $i=0.015$, $m=10$

The present value of the loaned amount is

$PV=Rcdot dfrac{1-(1+i)^{-m}}{i}=40cdot dfrac{1-1.015^{-10}}{0.015}=$368.89$

Since Rocco made an initial down payment of $$50$, the total present value is

$$
368.89+50=boxed{bf{$418.89}}
$$

b.) The interest paid is the difference between the present value of the annuity and the actual amount paid.

Since there are 10 payments of $$40$ each, the interest is

$$
I=10(40)-368.89=boxed{bf{$31.11}}
$$

a.) $$418.89$

b.) $$31.11$

The present value of an annuity is

$PV=Rcdot dfrac{1-(1+i)^{-m}}{i}$

where

$R$ = regular payment

$i$ = interest rate per compounding period

$m$ = number of compounding periods

If the annual interest rate $r$, payment mode, and the number of years $t$ is given,

$i=dfrac{r}{n}$

$m=ntimes t$

$n$ = number of payment per year

a.) In this case,

$PV=128,000$

$i=0.0065$

$m=300$

The regular payments can be calculated as

$PV=Rcdot dfrac{1-(1+i)^{-m}}{i}implies R=dfrac{PVcdot i}{1-(1+i)^{-m}}$

$$
R=dfrac{128,000(0.0065)}{1-1.0065^{-300}}=boxed{bf{$971.03}}
$$

$$
R=$971.03
$$

The present value of an annuity is

$PV=Rcdot dfrac{1-(1+i)^{-m}}{i}$

where

$R$ = regular payment

$i$ = interest rate per compounding period

$m$ = number of compounding periods

If the annual interest rate $r$, payment mode, and the number of years $t$ is given,

$i=dfrac{r}{n}$

$m=ntimes t$

$n$ = number of payment per year

a.) We need to find the monthly payment for the 7-year loan.

$m=12cdot 7=84$

$i=0.12/12=0.01$

$PV=Rcdot dfrac{1-(1+i)^{-m}}{i}$

$R_7=dfrac{PVcdot i}{1-(1+i)^{-m}}=dfrac{64,000(0.01)}{1-1.01^{-84}}=boxed{bf{$1029.70}}$

For the 10-year loan, $m=10times 12=120$

$$
R_{10}=dfrac{64,000(0.01)}{1-1.01^{-120}}=boxed{bf{$810.72}}
$$

b.) We shall calculate the interest which is the difference between PV and $mcdot R$

7-year loan: $I_7=mcdot R_7-PV=1029.70(84)-64000=$22,494.80$

10-year loan: $I_{10}=mcdot R_{10}-PV=$810.72(120)-64000=$33,286.40$

Thus, the 7-year loan would save her $33286.40-22294.80=boxed{bf{$10,791.60}}$

a.) $R_7=$1029.70$ , $R_{10}=$810.72$

b.) 7-year loan would save her $$10,791.60$

The present value of an annuity is

$PV=Rcdot dfrac{1-(1+i)^{-m}}{i}$

where

$R$ = regular payment

$i$ = interest rate per compounding period

$m$ = number of compounding periods

If the annual interest rate $r$, payment mode, and the number of years $t$ is given,

$i=dfrac{r}{n}$

$m=ntimes t$

$n$ = number of payment per year

We shall evaluate which of the two options is better. We shall compare the $R$ for both cases.

Option 1: Borrow $29000$ from the bank to pay the car in cash.

$PV=29000$ , $i=0.0045$ , $m=60$

$R_1=dfrac{PVcdot i}{1-(1+i)^{-m}}=dfrac{29000(0.0045)}{1-1.0045^{-60}}=$552.60$

Option 2: Finance at the dealership

$PV=32000$, $i=0.0020$ , $m=60$

$R_2=dfrac{32,000(0.002)}{1-1.002^{-60}}=$566.51$

Therefore, Option 1 is better since it requires lesser amount per month for the same period of 60 months.

Borrow $$29000$ from the bank to pay the car in cash

The present value of an annuity is

$PV=Rcdot dfrac{1-(1+i)^{-m}}{i}$

where

$R$ = regular payment

$i$ = interest rate per compounding period

$m$ = number of compounding periods

If the annual interest rate $r$, payment mode, and the number of years $t$ is given,

$i=dfrac{r}{n}$

$m=ntimes t$

$n$ = number of payment per year

a.) We need to find $R$ for each payment plan with different $m$

$PV=Rcdot dfrac{1-(1+i)^{-m}}{i}implies R=dfrac{PVcdot i}{1-(1+i)^{-m}}$

5-year plan: $m=5times 12=60 implies R=dfrac{35,000cdot 0.007}{1-1.007^{-60}}=$716.39$

10-year plan: $m=10times 12=120implies R=dfrac{35,000cdot 0.007}{1-1.007^{-120}}=$432.08$

15-year plan: $m=15times12=180implies R=dfrac{35,000cdot 0.007}{1-1.007^{-180}}=$342.61$

b.) We shall calculate the interest

$I=Rcdot m – PV$

5-year plan: $I=(716.39)(60)-35000=$7983.40$

10-year plan: $I=432.08(120)-35000=$16849.60$

15-year plan: $I=342.61(180)-35000=$26669.80$

a.) $R_5=$716.39$ , $R_{10}=$432.08$ , $R_{15}=$342.61$

b.) $I_5=$7983.40$ , $I_{10}=$16849.60$ , $I_{15}=$26669.80$

The present value of an annuity is

$PV=Rcdot dfrac{1-(1+i)^{-m}}{i}$

where

$R$ = regular payment

$i$ = interest rate per compounding period

$m$ = number of compounding periods

If the annual interest rate $r$, payment mode, and the number of years $t$ is given,

$i=dfrac{r}{n}$

$m=ntimes t$

$n$ = number of payment per year

a.) Here, $R=25$ , $i=0.0155$ , $m=12$

$PV=Rcdot dfrac{1-(1+i)^{-m}}{i}=25cdot dfrac{1-1.0155^{-12}}{0.0155}=$271.84$

Since $$45$ down payment is required, the price of the stereo is

$$
271.84+45=boxed{bf{$316.74}}
$$

b.) The interest is calculated as

$$
I=Rcdot m – PV=25(12)-371.84=boxed{bf{$28.16}}
$$

a.) $$271.84$

b.) $$28.16$

The present value of an annuity is

$PV=Rcdot dfrac{1-(1+i)^{-m}}{i}$

where

$R$ = regular payment

$i$ = interest rate per compounding period

$m$ = number of compounding periods

If the annual interest rate $r$, payment mode, and the number of years $t$ is given,

$i=dfrac{r}{n}$

$m=ntimes t$

$n$ = number of payment per year

We’re given with

$PV=1800$ , $R=75.84$ and $m=30$, $n=12$, and we shall find $r$

$1800=75.84cdot dfrac{1-(1+r/12)^{-30}}{r/12}$

We shall solve this graphically.

Therefore, $r=19%$

$$
r=19%
$$

The present value of an annuity is

$PV=Rcdot dfrac{1-(1+i)^{-m}}{i}$

where

$R$ = regular payment

$i$ = interest rate per compounding period

$m$ = number of compounding periods

If the annual interest rate $r$, payment mode, and the number of years $t$ is given,

$i=dfrac{r}{n}$

$m=ntimes t$

$n$ = number of payment per year

With $P=50,000$, quarterly compounding (n=4), and
$r=11.2%implies i=dfrac{0.112}{4}=0.028$, the account value after 20 years is

$A=P(1+i)^m=50,000(1+0.028)^{4(20)}=$455,427.52$

Now, we shall calculate how much quarterly withdrawals can it support for 10 years after retirement.

$m=10(4)=40$ , $i=0.028$

$R=dfrac{PVcdot i}{1-(1+i)^{-m}}=dfrac{455,427.42(0.028)}{1-(1.028)^{-40}}=boxed{bf{$19,070.96}}$

Therefore, Leo shall receive $$19,070.96$ every 3 months after retirement.

$$
$19,070.96
$$

The present value of an annuity is

$PV=Rcdot dfrac{1-(1+i)^{-m}}{i}$

where

$R$ = regular payment

$i$ = interest rate per compounding period

$m$ = number of compounding periods

If the annual interest rate $r$, payment mode, and the number of years $t$ is given,

$i=dfrac{r}{n}$

$m=ntimes t$

$n$ = number of payment per year

Charmaine plans on retiring 25 years from now and wants to have $R=$2500$ per month from her retirement account for 180 months.

$R=2500$

$i=0.0075$

$m=180$

The present value of such retirement plan is

$PV=Rcdot dfrac{1-(1+i)^{-m}}{i}=2500cdot dfrac{1-1.0075^{-180}}{0.0075}=$246,483.52$

We shall then find how much should she save every month over the next 25 years to reach her goal.

This time, $m=25times12=300$

$R=dfrac{PVcdot i}{1-(1+i)^{-m}}=dfrac{246,483.52cdot (0.0075)}{1-1.0075^{300}}=boxed{bf{$219.75}}$

Therefore, Charmaine needs to save $$219.75$ per month for 25 years.

$$
$219.75
$$

The present value of an annuity is

$PV=Rcdot dfrac{1-(1+i)^{-m}}{i}$

where

$R$ = regular payment

$i$ = interest rate per compounding period

$m$ = number of compounding periods

If the annual interest rate $r$, payment mode, and the number of years $t$ is given,

$i=dfrac{r}{n}$

$m=ntimes t$

$n$ = number of payment per year

a.) Here, we want to find $R$ such that $PV=660,000$ at $r=6.604%$ and $t=25$ years,

For weekly payment, $n=52$

$i=dfrac{0.06604}{52}=0.00127$

$m=52times 25=1300$

$R=dfrac{PVcdot i}{1-(1+i)^{-m}}=dfrac{660,000(0.00127)}{1-1.00127^{-1300}}=boxed{bf{$1037.45}}$

Thus, option B suits people who expects to live more than 25 years.

b.) If $R=$1000$, we shall find the number of weeks can it support

$660,000=1000cdot dfrac{1-1.00127^{-m}}{0.00127}$

$1.00127^{-n}=0.1618$

Option A can support 1435 weeks or $dfrac{1435}{52}=27.6$ years. Thus, option A suits for those who expect to live more than 27.6 years.

a.) Option B: $$1037.45$ per week for 25 years

b.) Option A: $$1000.00$ per week for 27.6 years

The present value of an annuity is

$PV=Rcdot dfrac{1-(1+i)^{-m}}{i}$

where

$R$ = regular payment

$i$ = interest rate per compounding period

$m$ = number of compounding periods

If the annual interest rate $r$, payment mode, and the number of years $t$ is given,

$i=dfrac{r}{n}$

$m=ntimes t$

$n$ = number of payment per year

a.) We’re given with

$R=500$

$i=0.0083$

$m=10$

$$
PV=Rcdot dfrac{1-(1+i)^{-m}}{i}=500cdot dfrac{1-(1.083)^{-10}}{0.083}=boxed{bf{$3310.11}}
$$

b.) $r=5.6%=0.056$ , $n=4$ (quarterly), $R=$500$, $t=6$ years

$i=r/n=0.056/4=0.014$

$m=ntimes t=4cdot 6=24$

$$
PV=Rcdot dfrac{1-(1+i)^{-m}}{i}=500cdot dfrac{1-1.014^{-24}}{0.014}=boxed{bf{$10,132.49}}
$$

c.) You can simply substitute $A$ in the present value formula with the future value.

a.) $$3310.11$

b.) $$10,132.49$

The present value of an annuity is

$PV=Rcdot dfrac{1-(1+i)^{-m}}{i}$

where

$R$ = regular payment

$i$ = interest rate per compounding period

$m$ = number of compounding periods

If the annual interest rate $r$, payment mode, and the number of years $t$ is given,

$i=dfrac{r}{n}$

$m=ntimes t$

$n$ = number of payment per year

a.) We are given with

$R=325$

$PV=17000$

$i=0.006$

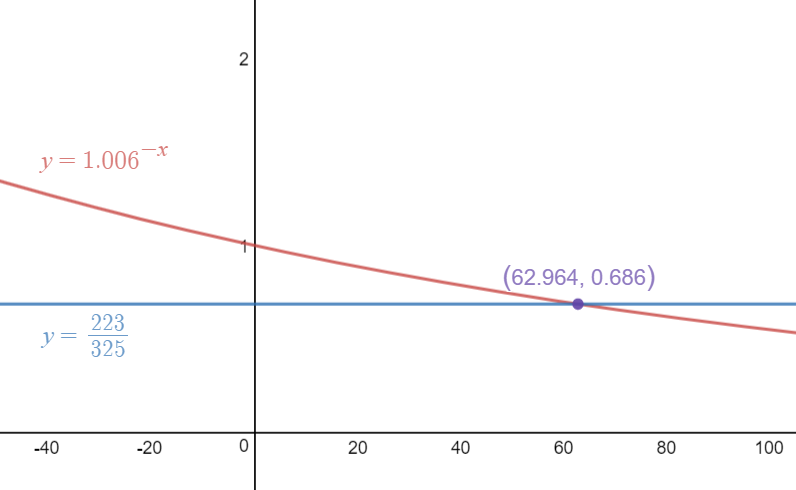
We shall find $m$

$PV=Rcdot dfrac{1-(1+i)^{-m}}{i}$

$17000=325cdot dfrac{1-1.006^{-m}}{0.006}$

$1.006^{-m}=1-dfrac{17000(0.006)}{325}$

$1.006^{-m}=dfrac{223}{325}$

$63$ months

The present value of an annuity is

$PV=Rcdot dfrac{1-(1+i)^{-m}}{i}$

where

$R$ = regular payment

$i$ = interest rate per compounding period

$m$ = number of compounding periods

If the annual interest rate $r$, payment mode, and the number of years $t$ is given,

$i=dfrac{r}{n}$

$m=ntimes t$

$n$ = number of payment per year

Let $Q$ be the regular payment done $q$ times while $Y$ is the regular payment done $y$ times.

We shall find the relationship between $Q$ and $Y$ such that the future value of $Q$ payments is equivalent to the present value of $Y$ payments for the same value of $i$.

$Qcdot dfrac{(1+i)^q-1}{i}=Ycdot dfrac{1-(1+i)^{-y}}{i}$

$Q=Ycdot dfrac{1-(1+i)^{-y}}{i} cdot dfrac{i}{(1+i)^q-1}$

$$
Q=Ycdot dfrac{1-(1+i)^{-y}}{(1+i)^q-1}
$$

$$
Q=Ycdot dfrac{1-(1+i)^{-y}}{(1+i)^q-1}
$$