We can simplify this using the rules of radical. In this case,

$sqrt{a^{2} cdot b}=asqrt{b}$

To apply this, factor the expression under the radical sign such that one factor is a perfect square.

a) $sqrt{27}=sqrt{9cdot 3}=sqrt{3^2cdot 3}=3sqrt{3}$

b) $sqrt{50}=sqrt{25cdot 2}=sqrt{5^2cdot 2}=5sqrt{2}$

c) $sqrt{98}=sqrt{49cdot 2}=sqrt{7^2cdot 2}=7sqrt{2}$

d) $sqrt{32}=sqrt{16cdot 2}=sqrt{4^2cdot 2}=4sqrt{2}$

a) $3sqrt{3}$

b) $5sqrt{2}$

c) $7sqrt{2}$

d) $4sqrt{2}$

We can simplify this using the rules of radical. In this case,

$asqrt{b}times csqrt{d}=(acdot c)sqrt{(bcdot d)}$

a) $sqrt{5}times sqrt{7}=sqrt{5times 7}=sqrt{35}$

b) $sqrt{11}timessqrt{6}=sqrt{11times 6}=sqrt{66}$

c) $2sqrt{3}times 5sqrt{2}=(2cdot 5)sqrt{3cdot 2}=10sqrt{6}$

d) $-4sqrt{3}times 8sqrt{13}=(-4cdot 8)sqrt{3cdot 13}=-32sqrt{39}$

a) $sqrt{35}$

b) $sqrt{66}$

c) $10sqrt{6}$

d) $-32sqrt{39}$

We can simplify this using the rules of radical. In this case,

$$
asqrt{m} + bsqrt{m}+ csqrt{n}+dsqrt{n}=(a+b)sqrt{m}+(c+d)sqrt{n}
$$

$bold{a)}$ $4sqrt{5}+3sqrt{5}$

$=(4+3)sqrt{5}$

$=7sqrt{5}$

$bold{b)}$ $9sqrt{7}-4sqrt{7}$

$=(9-4)sqrt{7}$

$=5sqrt{7}$

$bold{c)}$ $3sqrt{3}+8sqrt{2}-4sqrt{3}+11sqrt{2}$

$=(3-4)sqrt{8}+(8+11)sqrt{2}$

$=-sqrt{8}+19sqrt{2}$

$bold{d)}$ $sqrt{8}-sqrt{18}$

$=sqrt{4cdot 2}-sqrt{9cdot 2}$

$=sqrt{2^2cdot 2}-sqrt{3^2cdot 2}$

$=2sqrt{2}-3sqrt{2}$

$=(2-3)sqrt{2}$

$=-sqrt{2}$

a) $7sqrt{5}$

b) $5sqrt{7}$

c) $-sqrt{8} +19sqrt{2}$

d) $-sqrt{2}$

We can simplify this using the rules of radical. In this case,

$sqrt{a^{2} cdot b}=asqrt{b}$

To apply this, factor the expression under the radical sign such that one factor is a perfect square.

a) $3sqrt{12}$

$=3sqrt{4cdot 3}$

$=3sqrt{2^2cdot 3}$

$=3cdot (2sqrt{3})$

$$
=6sqrt{3}
$$

b) $-5sqrt{125}$

$=-5sqrt{25cdot 5}$

$=-5sqrt{5^2cdot 5}$

$=-5cdot (5sqrt{5})$

$$
=-25sqrt{5}
$$

c) $10sqrt{40}$

$=10sqrt{4cdot 10}$

$=10sqrt{2^2cdot 10}$

$=10(2sqrt{10})$

$=20sqrt{10}$

d) $=-dfrac{1}{2}sqrt{60}$

$=-dfrac{1}{2}sqrt{4cdot 15}$

$=-dfrac{1}{2}sqrt{2^2cdot 15}$

$=-dfrac{1}{2}cdot 2sqrt{15}$

$=-sqrt{15}$

e) $dfrac{2}{3}sqrt{45}$

$=dfrac{2}{3}sqrt{9cdot 5}$

$=dfrac{2}{3}sqrt{3^2cdot 5}$

$=dfrac{2}{3}cdot 3sqrt{5}$

$$
=2sqrt{5}
$$

f) $-dfrac{9}{10}sqrt{400cdot 3}$

$=-dfrac{9}{10}sqrt{20^2cdot 3}$

$=-dfrac{9}{10}cdot 20sqrt{3}$

$$
=-18sqrt{3}
$$

a) $6sqrt{3}$

b) $-25sqrt{5}$

c) $20sqrt{10}$

d) $-sqrt{15}$

e) $2sqrt{5}$

f) $-18sqrt{3}$

a) Using the Distributive Property, the given expression, $sqrt{3}(2-sqrt{5})
,$ is equivalent to

$$
begin{align*}
sqrt{3}(2)-sqrt{3}(sqrt{5})
.end{align*}
$$

Using the properties of radicals, the expression above is equivalent to

$$
begin{align*}
&
2sqrt{3}-sqrt{3(5)}
\&=
2sqrt{3}-sqrt{15}
.end{align*}
$$

b) Using the Distributive Property, the given expression, $2sqrt{2}(sqrt{7}+3sqrt{3})
,$ is equivalent to

$$
begin{align*}
2sqrt{2}(sqrt{7})+2sqrt{2}(3sqrt{3})
.end{align*}
$$

Using the properties of radicals, the expression above is equivalent to

$$
begin{align*}
&
2sqrt{2(7)}+2(3)sqrt{2(3)}
\&=
2sqrt{14}+6sqrt{6}
.end{align*}
$$

c) The given expression, $(4sqrt{2})^2
,$ is equivalent to

$$
begin{align*}
(4sqrt{2})(4sqrt{2})
.end{align*}
$$

Using the properties of radicals, the expression above is equivalent to

$$
begin{align*}
&
4(4)sqrt{2(2)}
\&=
16sqrt{(2)^2}
\&=
16(2)
\&=
32
.end{align*}
$$

d) The given expression, $(-2sqrt{3})^3
,$ is equivalent to

$$
begin{align*}
(-2sqrt{3})(-2sqrt{3})(-2sqrt{3})
.end{align*}
$$

Using the properties of radicals, the expression above is equivalent to

$$
begin{align*}
&
-2(-2)(-2)sqrt{3(3)(3)}
\&=
-8sqrt{27}
.end{align*}
$$

Extracting the factor of the radicand that is a perfect power of the index, the expression above is equivalent to

$$
begin{align*}
&
-8sqrt{9cdot3}
\&=
-8sqrt{(3)^2cdot3}
\&=
-8(3)sqrt{3}
\&=
-24sqrt{3}
.end{align*}
$$

e) Using the properties of radicals, the given expression, $4sqrt{3}times3sqrt{6}
,$ is equivalent to

$$
begin{align*}
&
4(3)sqrt{3(6)}
\&=
12sqrt{18}
.end{align*}
$$

Extracting the factor of the radicand that is a perfect power of the index, the expression above is equivalent to

$$
begin{align*}
&
12sqrt{9cdot2}
\&=
12sqrt{(3)^2cdot2}
\&=
12(3)sqrt{2}
\&=
36sqrt{2}
.end{align*}
$$

f) Using the properties of radicals, the given expression, $-7sqrt{2}times5sqrt{8}
,$ is equivalent to

$$
begin{align*}
&
-7(5)sqrt{2(8)}
\&=
-35sqrt{16}
.end{align*}
$$

Extracting the factor of the radicand that is a perfect power of the index, the expression above is equivalent to

$$
begin{align*}
&
-35sqrt{(4)^2}
\&=
-35(4)
\&=
140
.end{align*}
$$

a) $2sqrt{3}-sqrt{15}$

b) $2sqrt{14}+6sqrt{6}$

c) $32$

d) $-24sqrt{3}$

e) $36sqrt{2}$

f) $140$

a) Extracting the factor of the radicand that is a perfect power of the index, the given expression, $sqrt{8}-sqrt{32}
,$ is equivalent to

$$
begin{align*}
&
sqrt{4cdot2}-sqrt{16cdot2}
\&=
sqrt{(2)^2cdot2}-sqrt{(4)^2cdot2}
\&=
2sqrt{2}-4sqrt{2}
.end{align*}
$$

By combining like radicals, the expression above is equivalent to

$$
begin{align*}
&
(2-4)sqrt{2}
\&=
-2sqrt{2}
.end{align*}
$$

b) Extracting the factor of the radicand that is a perfect power of the index, the given expression, $sqrt{12}+sqrt{18}-sqrt{27}+sqrt{50}
,$ is equivalent to

$$
begin{align*}
&
sqrt{4cdot3}+sqrt{9cdot2}-sqrt{9cdot3}+sqrt{25cdot2}
\&=
sqrt{(2)^2cdot3}+sqrt{(3)^2cdot2}-sqrt{(3)^2cdot3}+sqrt{(5)^2cdot2}
\&=
2sqrt{3}+3sqrt{2}-3sqrt{3}+5sqrt{2}
.end{align*}
$$

By combining like radicals, the expression above is equivalent to

$$
begin{align*}
&
(2sqrt{3}-3sqrt{3})+(3sqrt{2}+5sqrt{2})
\&=
(2-3)sqrt{3}+(3+5)sqrt{2}
\&=
-sqrt{3}+8sqrt{2}
\&=
8sqrt{2}-sqrt{3}
.end{align*}
$$

c) Extracting the factor of the radicand that is a perfect power of the index, the given expression, $3sqrt{98}-5sqrt{72}
,$ is equivalent to

$$
begin{align*}
&
3sqrt{49cdot2}-5sqrt{36cdot2}
\&=
3sqrt{(7)^2cdot2}-5sqrt{(6)^2cdot2}
\&=
3(7)sqrt{2}-5(6)sqrt{2}
\&=
21sqrt{2}-30sqrt{2}
.end{align*}
$$

By combining like radicals, the expression above is equivalent to

$$
begin{align*}
&
(21-30)sqrt{2}
\&=
-9sqrt{2}
.end{align*}
$$

d) Extracting the factor of the radicand that is a perfect power of the index, the given expression, $-4sqrt{200}+5sqrt{242}
,$ is equivalent to

$$
begin{align*}
&
-4sqrt{100cdot2}+5sqrt{121cdot2}
\&=
-4sqrt{(10)^2cdot2}+5sqrt{(11)^2cdot2}
\&=
-4(10)sqrt{2}+5(11)sqrt{2}
\&=
-40sqrt{2}+55sqrt{2}
.end{align*}
$$

By combining like radicals, the expression above is equivalent to

$$
begin{align*}
&
(-40+55)sqrt{2}
\&=
15sqrt{2}
.end{align*}
$$

e) Extracting the factor of the radicand that is a perfect power of the index, the given expression, $-5sqrt{45}+sqrt{52}+3sqrt{125}
,$ is equivalent to

$$
begin{align*}
&
-5sqrt{9cdot5}+sqrt{4cdot13}+3sqrt{25cdot5}
\&=
-5sqrt{(3)^2cdot5}+sqrt{(2)^2cdot13}+3sqrt{(5)^2cdot5}
\&=
-5(3)sqrt{5}+2sqrt{13}+3(5)sqrt{5}
\&=
-15sqrt{5}+2sqrt{13}+15sqrt{5}
.end{align*}
$$

By combining like radicals, the expression above is equivalent to

$$
begin{align*}
&
(-15sqrt{5}+15sqrt{5})+2sqrt{13}
\&=
0+2sqrt{13}
\&=
2sqrt{13}
.end{align*}
$$

f) Extracting the factor of the radicand that is a perfect power of the index, the given expression, $7sqrt{12}-3sqrt{28}+dfrac{1}{2}sqrt{48}+dfrac{2}{3}sqrt{63}
,$ is equivalent to

$$
begin{align*}
&
7sqrt{4cdot3}-3sqrt{4cdot7}+dfrac{1}{2}sqrt{16cdot3}+dfrac{2}{3}sqrt{9cdot7}
\&=
7sqrt{(2)^2cdot3}-3sqrt{(2)^2cdot7}+dfrac{1}{2}sqrt{(4)^2cdot3}+dfrac{2}{3}sqrt{(3)^2cdot7}
\&=
7(2)sqrt{3}-3(2)sqrt{7}+dfrac{1}{2}(4)sqrt{3}+dfrac{2}{3}(3)sqrt{7}
\&=
14sqrt{3}-6sqrt{7}+2sqrt{3}+2sqrt{7}
.end{align*}
$$

By combining like radicals, the expression above is equivalent to

$$
begin{align*}
&
(14sqrt{3}+2sqrt{3})+(-6sqrt{7}+2sqrt{7})
\&=
(14-6)sqrt{3}+(-6+2)sqrt{7}
\&=
8sqrt{3}-4sqrt{7}
.end{align*}
$$

a) $-2sqrt{2}$

b) $8sqrt{2}-sqrt{3}$

c) $-9sqrt{2}$

d) $15sqrt{2}$

e) $2sqrt{13}$

f) $8sqrt{3}-4sqrt{7}$

a) Using the FOIL Method which is given by $(a+b)(c+d)=ac+ad+bc+bd,$ the given expression, $(6-sqrt{5})(3+2sqrt{10})
,$ is equivalent to

$$
begin{align*}
&
6(3)+6(2sqrt{10})-sqrt{5}(3)-sqrt{5}(2sqrt{10})
.end{align*}
$$

Using the properties of radicals, the expression above simplifies to

$$
begin{align*}
&
18+12sqrt{10}-3sqrt{5}-2sqrt{5(10)}
\&=
18+12sqrt{10}-3sqrt{5}-2sqrt{50}
\&=
18+12sqrt{10}-3sqrt{5}-2sqrt{25cdot2}
\&=
18+12sqrt{10}-3sqrt{5}-2sqrt{(5)^2cdot2}
\&=
18+12sqrt{10}-3sqrt{5}-2(5)sqrt{2}
\&=
18+12sqrt{10}-3sqrt{5}-10sqrt{2}
.end{align*}
$$

b) Using the square of a binomial which is given by $(a+b)^2=a^2+2ab+b^2$ or by $(a-b)^2=a^2-2ab+b^2,$ the given expression, $(2+3sqrt{3})^2
,$ is equivalent to

$$
begin{align*}
&
(2)^2+2(2)(3sqrt{3})+(3sqrt{3})^2
\&=
4+12sqrt{3}+9(3)
\&=
4+12sqrt{3}+27
\&=
31+12sqrt{3}
.end{align*}
$$

c) Using the product of the sum and difference of like terms which is given by $(a+b)(a-b)=a^2-b^2,$ the given expression, $(sqrt{2}+sqrt{5})(sqrt{2}-sqrt{5})
,$ is equivalent to

$$
begin{align*}
&
(sqrt{2})^2-(sqrt{5})^2
\&=
2-5
\&=
-3
.end{align*}
$$

d) Using the FOIL Method which is given by $(a+b)(c+d)=ac+ad+bc+bd,$ the given expression, $(3sqrt{3}+4sqrt{2})(sqrt{3}-2sqrt{2})
,$ is equivalent to

$$
begin{align*}
&
3sqrt{3}(sqrt{3})+3sqrt{3}(-2sqrt{2})+4sqrt{2}(sqrt{3})+4sqrt{2}(-2sqrt{2})
.end{align*}
$$

Using the properties of radicals, the expression above simplifies to

$$
begin{align*}
&
3(sqrt{3})^2+3(-2)sqrt{3(2)}+4sqrt{2(3)}+4(-2)(sqrt{2})^2
\&=
3(3)-6sqrt{6}+4sqrt{6}-8(2)
\&=
9-6sqrt{6}+4sqrt{6}-16
.end{align*}
$$

By combining like terms, the expression above is equivalent to

$$
begin{align*}
&
(9-16)+(-6sqrt{6}+4sqrt{6})
\&=
-7-2sqrt{6}
.end{align*}
$$

e) Using the square of a binomial which is given by $(a+b)^2=a^2+2ab+b^2$ or by $(a-b)^2=a^2-2ab+b^2,$ the given expression, $(2sqrt{5}-3sqrt{7})^2
,$ is equivalent to

$$
begin{align*}
&
(2sqrt{5})^2-2(2sqrt{5})(3sqrt{7})+(3sqrt{7})^2
.end{align*}
$$

Using the properties of radicals, the expression above simplifies to

$$
begin{align*}
&
4(5)-2(2)(3)sqrt{5(7)}+9(7)
\&=
20-12sqrt{35}+63
\&=
83-12sqrt{35}
.end{align*}
$$

f) Using the FOIL Method which is given by $(a+b)(c+d)=ac+ad+bc+bd,$ the given expression, $(1-sqrt{3})(2+sqrt{6})(5+sqrt{2})
,$ is equivalent to

$$
begin{align*}
&
[(1-sqrt{3})(2+sqrt{6})](5+sqrt{2})
\&=
[1(2)+1(sqrt{6})-sqrt{3}(2)-sqrt{3}(sqrt{6})](5+sqrt{2})
\&=
[2+sqrt{6}-2sqrt{3}-sqrt{18}](5+sqrt{2})
\&=
[2+sqrt{6}-2sqrt{3}-3sqrt{2}](5+sqrt{2})
.end{align*}
$$

Using the Distributive Property, the expression above simplifies to

$$
begin{align*}
&
2(5)+2(sqrt{2})+sqrt{6}(5)+sqrt{6}(sqrt{2})-2sqrt{3}(5)-2sqrt{3}(sqrt{2})-3sqrt{2}(5)-3sqrt{2}(sqrt{2})
\&=
10+2sqrt{2}+5sqrt{6}+sqrt{12}-10sqrt{3}-2sqrt{6}-15sqrt{2}-3sqrt{4}
\&=
10+2sqrt{2}+5sqrt{6}+2sqrt{3}-10sqrt{3}-2sqrt{6}-15sqrt{2}-6
\&=
(10-6)+(2sqrt{2}-15sqrt{2})+(5sqrt{6}-2sqrt{6})+(2sqrt{3}-10sqrt{3})
\&=
4-13sqrt{2}+3sqrt{6}-8sqrt{3}
.end{align*}
$$

a) $18+12sqrt{10}-3sqrt{5}-10sqrt{2}$

b) $31+12sqrt{3}$

c) $-3$

d) $-7-2sqrt{6}$

e) $83-12sqrt{35}$

f) $4-13sqrt{2}+3sqrt{6}-8sqrt{3}$

Recall the Pythagorean theorem $c^2=a^2+b^2$ where $c$ is the hypotenuse while $a$ and $b$ are legs.

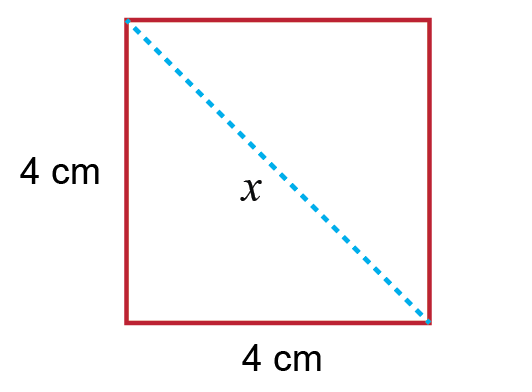
$x^2=4^2+4^2$

$x^2=16+16$

$x^2=32$

$x=pmsqrt{32}$

Since $x$ can not take positive values,

$x=sqrt{32}$

$x=sqrt{16cdot 2}$

$x=sqrt{4^2cdot 2}$

$x=4sqrt{2}$ cm

Therefore, the diagonal is $4sqrt{2}$ cm long.

$4sqrt{2}$ cm

The area $A$ of a square with side $s$ is

$A=s^2$

In this case, we are given $A=450$ $text{cm}^2$ and we shall find $s$

$s^2=450; text{cm}^2$

Take the square root of both sides.

$s=sqrt{450}$ cm

$s=sqrt{225cdot 2}$ cm

$s=sqrt{15^2cdot 2}$ cm

$s=15sqrt{2}$ cm

$s=15sqrt{2}$ cm

Remember the Pythagorean formula $c^2=a^2+b^2$ where $c$ is the hypotenuse and $a$ and $b$ are legs of a right triangle.

In this case, we want to find $c$ given $a$ and $b$

$c^2=a^2+b^2$

$c^2=3^2+9^2$

$c^2=9+81$

$c^2=90$

$c=sqrt{90}$

$c=sqrt{9cdot 10}$

$c=sqrt{3^2cdot 10}$

$c=3sqrt{10}$

Therefore, the diagonal is $3sqrt{10}$ cm long.

$3sqrt{10}$ cm

With the given points, $A(-2,7)$ and $B(4,1)
,$ then

$$
begin{align*}
x_1&=
-2
\x_2&=
4
\y_1&=
7
\y_2&=
1
.end{align*}
$$

Using the Distance Formula which is given by $d=sqrt{(x_1-x_2)^2+(y_1-y_2)^2}
,$ then

$$
begin{align*}
d&=sqrt{(-2-4)^2+(7-1)^2}
\
d&=sqrt{(-6)^2+(6)^2}
\
d&=sqrt{36+36}
\
d&=sqrt{72}
\
d&=sqrt{36cdot2}
\
d&=sqrt{(6)^2cdot2}
\
d&=6sqrt{2}
.end{align*}
$$

Hence, the distance is $6sqrt{2} text{ units}
.$

$$
6sqrt{2} text{ units}
$$

The perimeter $P$ of a triangle is the sum of the lengths of the 3 sides. In this case, we are given all three sides so we just need to add it up.

To simplify, remember the radical rule: $sqrt{a^2cdot b}=asqrt{b}$

$P=2sqrt{2}+3sqrt{8}+sqrt{80}$

$;;;=2sqrt{2}+3sqrt{4cdot 2}+sqrt{16cdot 5}$

$;;;=2sqrt{2}+3cdot 2sqrt{2}+4sqrt{5}$

$;;;=2sqrt{2}+6sqrt{2}+4sqrt{5}$

$;;;=(2+6)sqrt{2}+4sqrt{5}$

$$
P=8sqrt{2}+4sqrt{5}
$$

$$
P=8sqrt{2}+4sqrt{5}
$$

Using the square of a binomial which is given by $(a+b)^2=a^2+2ab+b^2$ or by $(a-b)^2=a^2-2ab+b^2,$ the given expression, $left( sqrt{a}+sqrt{b} right)^2
,$ is equivalent to

$$
begin{align*}
&
left( sqrt{a} right)^2+2left( sqrt{a} right)left(sqrt{b} right)+left(sqrt{b} right)^2
\&=
a+2left( sqrt{ab} right)+b
text{ (Equation 1)}
.end{align*}
$$

With $a>0$ and $b>0,$ the expression, $sqrt{a^2}+sqrt{b^2}
,$ simplifies to

$$
begin{align*}
a+b
text{ (Equation 2)}
.end{align*}
$$

Since Equation $1$ contains an extra term ($2sqrt{ab}$) which is nonzero, then Equation $1$ is greater than Equation $2$.

Equation $1$ is greater than Equation $2$

The radicals given below are equivalent to the given expression $sqrt{200}
:$

$$
begin{align*}
10sqrt{2}Rightarrow&
sqrt{(10)^2cdot2}
\&=
sqrt{100cdot2}
\&=
sqrt{200}
,\\
5sqrt{8}Rightarrow&
sqrt{(5)^2cdot8}
\&=
sqrt{25cdot8}
\&=
sqrt{200}
,\\
2sqrt{50}Rightarrow&
sqrt{(2)^2cdot50}
\&=
sqrt{4cdot50}
\&=
sqrt{200}
.end{align*}
$$

$10sqrt{2},$ $5sqrt{8},$ $2sqrt{50}$

a) Using the properties of radicals, the given expression, $sqrt{a^3}
,$ is equivalent to

$$
begin{align*}
&
sqrt{a^2cdot a}
.end{align*}
$$

Using $sqrt{x^2}=|x|,$ the expression above is equivalent to

$$
begin{align*}
&
|a|sqrt{a}
.end{align*}
$$

b) Using the properties of radicals, the given expression, $sqrt{x^5y^6}
,$ is equivalent to

$$
begin{align*}
&
sqrt{x^4y^6cdot x}
\&=
sqrt{(x^2y^3)^2cdot x}
.end{align*}
$$

Using $sqrt{x^2}=|x|,$ the expression above is equivalent to

$$
begin{align*}
&
|x^2y^3|sqrt{x}
\&=
|x^2y^2|cdot|y|sqrt{x}
\&=
x^2y^2|y|sqrt{x}
.end{align*}
$$

c) Using the properties of radicals, the given expression, $5sqrt{n^7}-2nsqrt{n^5}
,$ is equivalent to

$$
begin{align*}
&
5sqrt{n^6cdot n}-2nsqrt{n^4cdot n}
\&=
5sqrt{(n^3)^2cdot n}-2nsqrt{(n^2)^2cdot n}
.end{align*}
$$

Using $sqrt{x^2}=|x|,$ the expression above is equivalent to

$$
begin{align*}
&
5|n^3|sqrt{n}-2n|n^2|sqrt{n}
\&=
5|n^2|cdot|n|sqrt{n}-2n|n^2|sqrt{n}
\&=
5(n^2)cdot|n|sqrt{n}-2n(n^2)sqrt{n}
\&=
5n^2|n|sqrt{n}-2n^3sqrt{n}
\&=
left( 5n^2|n|-2n^3 right)sqrt{n}
.end{align*}
$$

d) Using the FOIL Method which is given by $(a+b)(c+d)=ac+ad+bc+bd,$ the given expression, $(sqrt{p}+2sqrt{q})(sqrt{q}-sqrt{p})
,$ is equivalent to

$$
begin{align*}
&
sqrt{p}(sqrt{q})-sqrt{p}(sqrt{p})+2sqrt{q}(sqrt{q})+2sqrt{q}(-sqrt{p})
.end{align*}
$$

Using the properties of radicals, the expression above is equivalent to

$$
begin{align*}
&
sqrt{pq}-p+2q-2sqrt{pq}
\&=
-p+2q+(sqrt{pq}-2sqrt{pq})
\&=
-p+2q-sqrt{pq}
.end{align*}
$$

a) $|a|sqrt{a}$

b) $x^2y^2|y|sqrt{x}$

c) $left( 5n^2|n|-2n^3 right)sqrt{n}$

d) $-p+2q-sqrt{pq}$

Start with the innermost radicals and simplify one at a time.

$sqrt{sqrt{(sqrt{4096})}}$

$=sqrt{sqrt{(sqrt{64^2})}}$

$=sqrt{sqrt{64}}$

$=sqrt{sqrt{8^2}}$

$=sqrt{8}$

$=sqrt{4cdot 2}$

$=sqrt{2^2cdot 2}$

$$
=2sqrt{2}
$$

$$
2sqrt{2}
$$

To solve exponential equations, rewrite both sides such that both have the same base, then equate the exponents.

Also, remember that $sqrt{a}=a^{1/2}$

$(sqrt{2})^x=256$

$(2^{1/2})^x=256$

$2^{frac{1}{2}x}=32cdot 8$

$2^{frac{1}{2}x}=2^5cdot 2^3$

$2^{frac{1}{2}x}=2^8$

$dfrac{1}{2}x=8$

$$
x=16
$$

$$
x=16
$$