$bold{Concept:}$ If $f(x)$ is transformed to $f(kx)$, then it is $bold{horizontally ;scaled}$ by a factor of $dfrac{1}{|k|}$

If $f(x)$ contains the point $(a,b)$, then $f(kx)$ must contain $left(dfrac{a}{k},bright)$.

The graph can either be $bold{compressed}$ (if $|k|>1$) or $bold{stretched}$ (if $0<|k|<1$ )

If $k<0$, the graph is not just horizontally scaled but also reflected in the $y$-axis.

$bold{Solution:}$

a) Since the red graph is horizontally compressed by a factor of $dfrac{1}{3}$,
$k=dfrac{1}{1/3}=3$ so the equation of the red graph must be

$$
y=(3x)^2
$$

b) Since the blue graph is stretched by a factor of 2 and also reflected in the $y$-axis, $k=-dfrac{1}{2}$. Thus, the equation of the blue graph must be

$$
y=sqrt{-dfrac{1}{2}x}
$$

a) $y=(3x)^2$

b) $y=sqrt{-dfrac{1}{2}{x}}$

a) Function is $y=|0.5 x|$. The parent function is $y=|x|$.

We know from the absolute value signs that the parent
function is the absolute value function.The horizontal stretch factor is $dfrac{1}{0.5}=2$. The point that
originally was (1, 1) corresponded to the new point $(2,1)$. So we multiplied the x-coordinates of the points on $y=|x|$ by 2 to find point of the new graph.

b) Function is $y=(dfrac{1}{4}x)^{2}$. The parent function is $y=x^{2}$

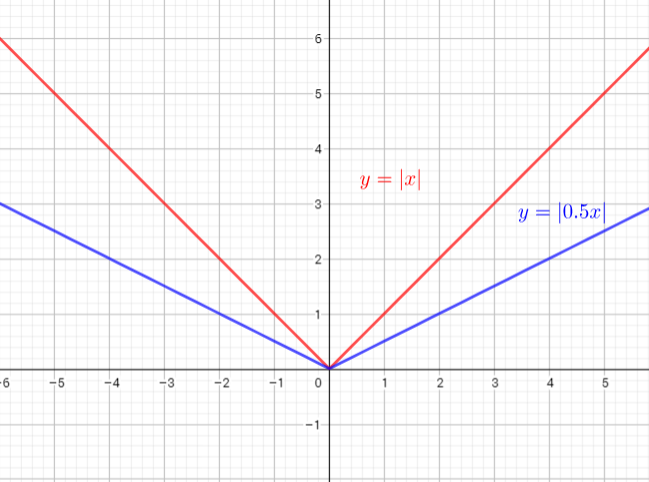
When $x$ is multiplied by a number between 0 and 1, the graph is stretched horizontally

To graph $y=(dfrac{1}{4}x)^{2}$ horizontal stretch the graph of $y=x^{2}$ horizontally by the factor $dfrac{1}{dfrac{1}{4}}=4$.

c) Function is $y=sqrt{-2x}$. The parent function is $y=sqrt{x}$.

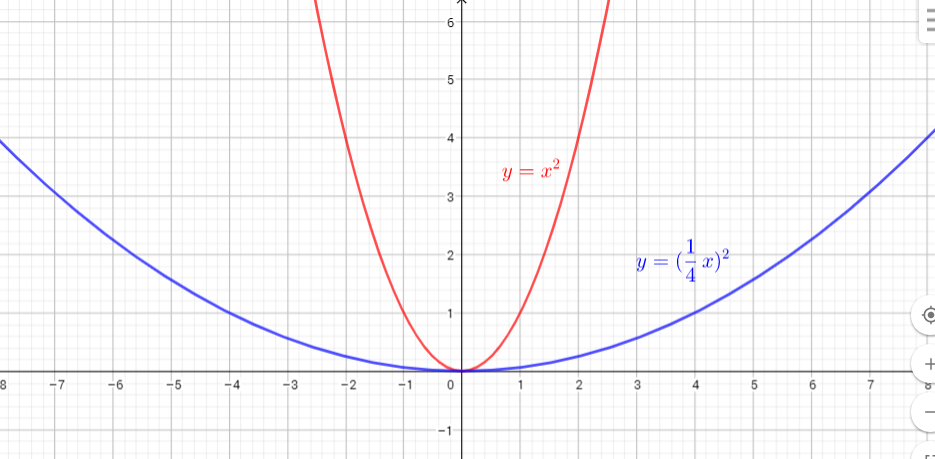
We know, when x is multiply by a number greater than 1, the graph
is compress horizontally, and if we switch the values of x and -x we reflect the graph of $y=x$ in the y-axis.

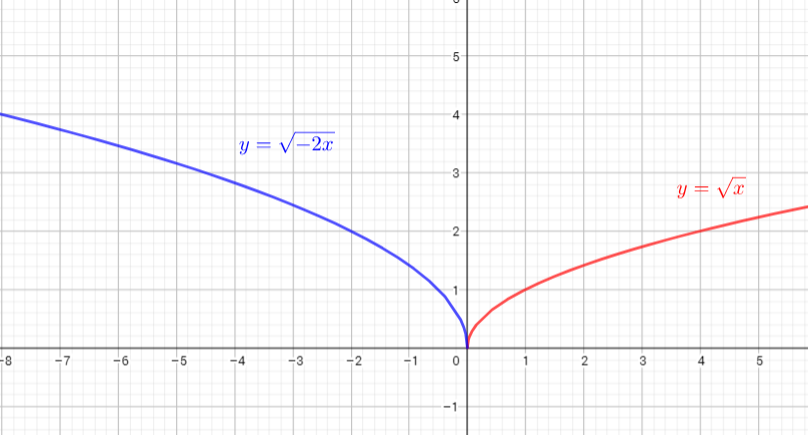
To graph $y=sqrt{-2x}$ horizontal stretch the graph of $y=sqrt{x}$ horizontally by the factor $dfrac{1}{2}$ and reflect the parent function
graph in the y-axis.

d) Function is $y=dfrac{1}{5x}$. The parent function is $y=dfrac{1}{x}$

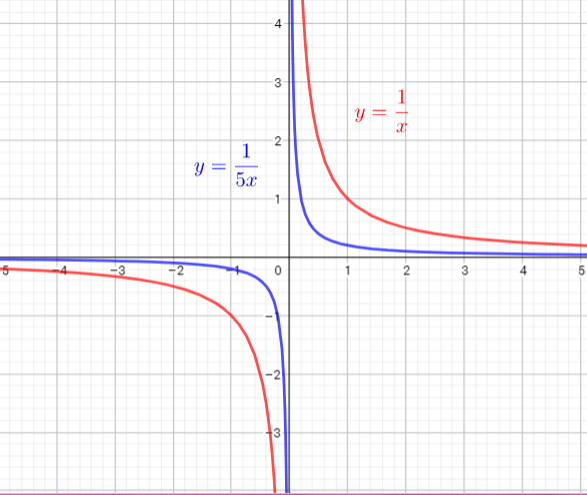
The graph $y=dfrac{1}{x}$ is compressed horizontally by the factor $dfrac{1}{5}$

a) $y=|x|$ ; horizontal stretching by a factor of 2

b) $y=x^2$ ; horizontal stretching by a factor of 4

c) $y=sqrt{x}$ ; horizontal compression by a factor of $dfrac{1}{2}$ and reflection in the $y$-axis

d) $y=dfrac{1}{x}$ ; horizontal compression by a factor of $dfrac{1}{5}$

a) The point (3, 4) is on the graph of $y=f(x)$.

To find the coordinates of the image of this point (3,4) on graph $y=f(2x)$ we need determine x- and y- coordintes on the new graph.
Since $y$ is equal we can equate
$4=f(3)=f(2 cdot x)$,

solve $3=2cdot x$ divide both sides by 2

$dfrac{3}{2}=x$ or $x=1.5$
So, the coordinates of the image of the point is (1.5, 4)

b) The point (3, 4) is on the graph of $y=f(x)$.

To find the coordinates of the image of this point (3,4) on graph $y=f(0.5x)$ we need determine x- and y- coordintes on the new graph.
Since $y$ is equal we can equate
$4=f(3)=f(0.5 cdot x)$,

solve $3=0.5cdot x$ divide both sides by 0.5

$dfrac{3}{0.5}=x$ or $x=6$
So, the coordinates of the image of the point is (6, 4)

c) The point (3, 4) is on the graph of $y=f(x)$.

To find the coordinates of the image of this point (3,4) on graph $y=f(dfrac{1}{3}x)$ we need determine x- and y- coordintes on the new graph.
Since $y$ is equal we can equate
$4=f(3)=f(dfrac{1}{3} cdot x)$,

solve $3=dfrac{1}{3}cdot x$ multiply both sides by 3

$3cdot3=x$ or $x=9$
So, the coordinates of the image is (9, 4)

d) The point (3, 4) is on the graph of $y=f(x)$.

To find the coordinates of the image of this point (3,4) on graph $y=f(-4x)$ we need determine x- and y- coordintes on the new graph.
Since $y$ is equal we can equate
$4=f(3)=f(-4cdot x)$,

solve $3=-4cdot x$ divide both sides by -4

$dfrac{3}{-4}=x$ or $x=-0.75$
So, the coordinates of the image is (-0.75, 4)

a) $(1.5,4)$

b) $(6,4)$

c) $(9,4)$

d) $(-0.75,4)$

We know that, if $0 < |k| 1$ then the graph $y=f(kx)$ is compressed horizontally by the factor $dfrac{1}{|k|}$ and

if $k< 0$ the graph is also reflected in the y-axis.

a) The parent function is $y=x^{2}$

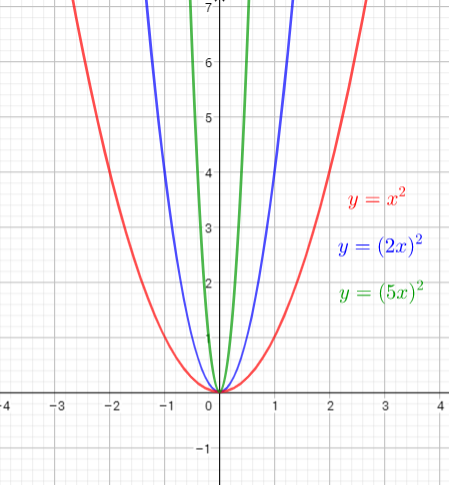
The graph of $y=(2x)^{2}$ is the graph of the parent function $y=x^{2}$ is the graph is compressed horizontally by the factor $dfrac{1}{2}$. There is (0,0) invariant point.

The graph of $y=(5x)^{2}$ is the graph of the parent function $y=x^{2}$ is the graph is compressed horizontally by the factor $dfrac{1}{5}$. There is (0,0) invariant point.

b)
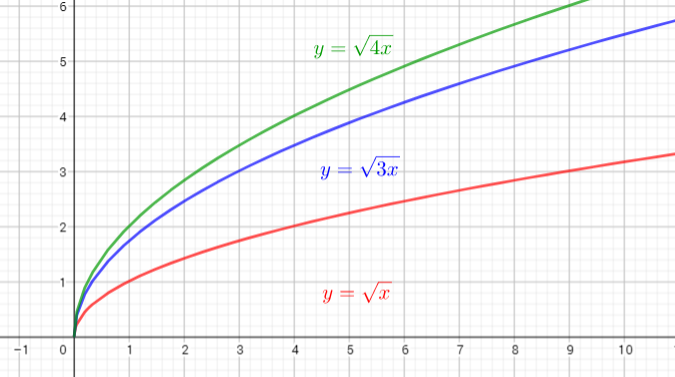
The parent function is $y=sqrt{x}$

The graph of $y=sqrt{3x}$ is the graph of the parent function $y=sqrt{x}$ is the graph is compressed horizontally by the factor $dfrac{1}{3}$. There is (0,0) invariant point.

The graph of $y=sqrt{4x}$ is the graph of the parent function $y=sqrt{x}$ isthe graph is compressed horizontally by the factor $dfrac{1}{4}$. There is (0,0) invariant point.

c)
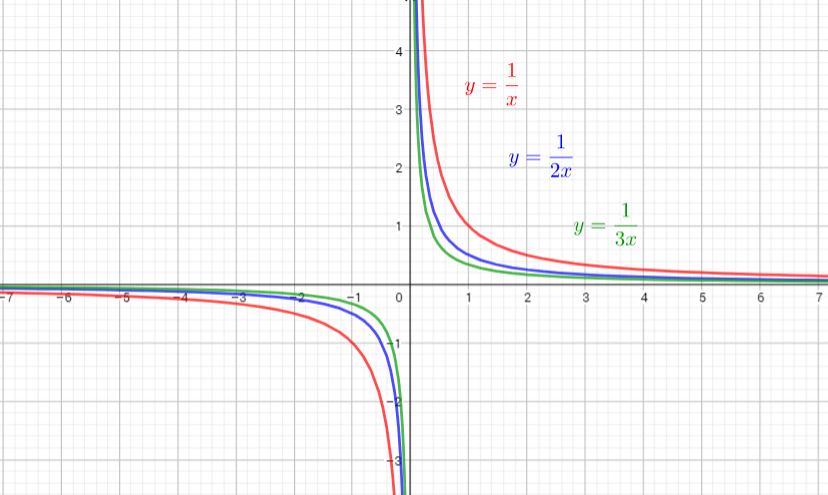
The parent function is $y=dfrac{1}{x}$

The graph of $y=dfrac{1}{2x}$ is the graph of the parent function $y=dfrac{1}{x}$ isthe graph is compressed horizontally by the factor $dfrac{1}{2}$. There is no invariant points.

The graph of $y=dfrac{1}{5x}$ is the graph of the parent function $y=dfrac{1}{x}$ isthe graph is compressed horizontally by the factor $dfrac{1}{5}$. There is no invariant points.

d) The parent function is $y=|x|$

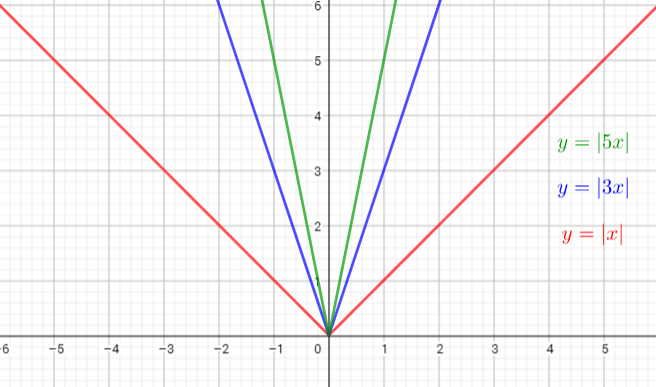
The graph of $y=|3x|$ is the graph of the parent function $y=|x|$ is the graph is compressed horizontally by the factor $dfrac{1}{3}$. There is (0,0) invariant point.

The graph of $y=|5x|$ is the graph of the parent function $y=|x|$ is the graph is compressed horizontally by the factor $dfrac{1}{5}$. There is (0,0) invariant point.

a) horizontal compression by a factor of $dfrac{1}{2}$, $(0,0)$

horizontal compression by a factor of $dfrac{1}{5}$, $(0,0)$

b) horizontal compression by a factor of $dfrac{1}{3}$ , $(0,0)$

horizontal compression by a factor of $dfrac{1}{4}$ , $(0,0)$

c) horizontal compression by a factor of $dfrac{1}{2}$, no invariant points

horizontal compression factor of $dfrac{1}{3}$, no invariant points

d) horizontal compression by a factor of $dfrac{1}{3}$, $(0,0)$

horizontal compression of $dfrac{1}{5}$ , $(0,0)$

We know that:

1) if $0 < |k| 1$ then the graph $y=f(kx)$ is compressed horizontally by the factor $dfrac{1}{|k|}$ and

3) if $k< 0$ the graph is also reflected in the y-axis.

a) The parent function is $y=x^{2}$

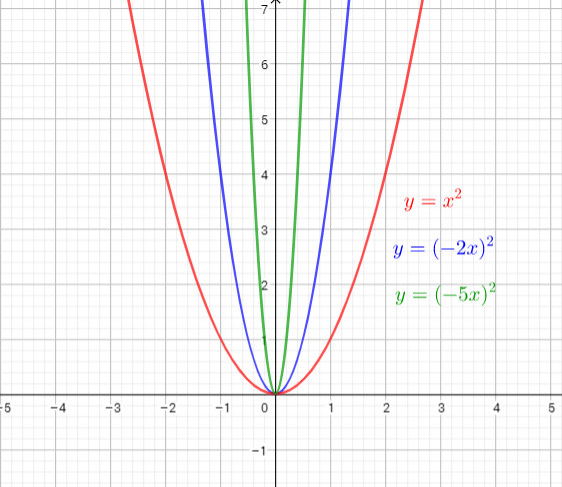
The graph of $y=(-2x)^{2}$ is the graph of the parent function $y=x^{2}$ . The graph is compressed horizontally by the factor $dfrac{1}{2}$ and reflected in the y-axis . There is (0,0) invariant point.

The graph of $y=(-5x)^{2}$ is the graph of the parent function $y=x^{2}$ . The graph is compressed horizontally by the factor $dfrac{1}{5}$ and reflected in the y-axis. There is (0,0) invariant point.

b)
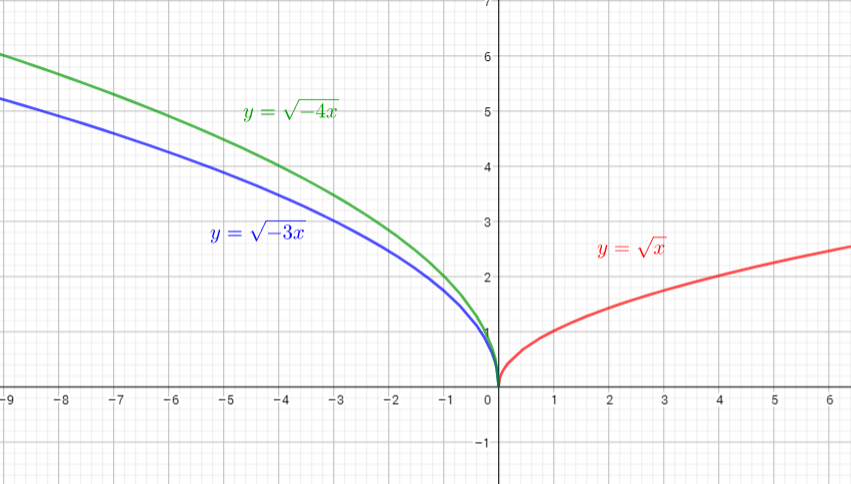
The parent function is $y=sqrt{x}$

The graph of $y=sqrt{-3x}$ is the graph of the parent function $y=sqrt{x}$ . The graph is compressed horizontally by the factor $dfrac{1}{3}$ and reflected in the y-axis. There is (0,0) invariant point.

The graph of $y=sqrt{-4x}$ is the graph of the parent function $y=sqrt{x}$ . The graph is compressed horizontally by the factor $dfrac{1}{4}$ and reflected in the y-axis. There is (0,0) invariant point.

c)
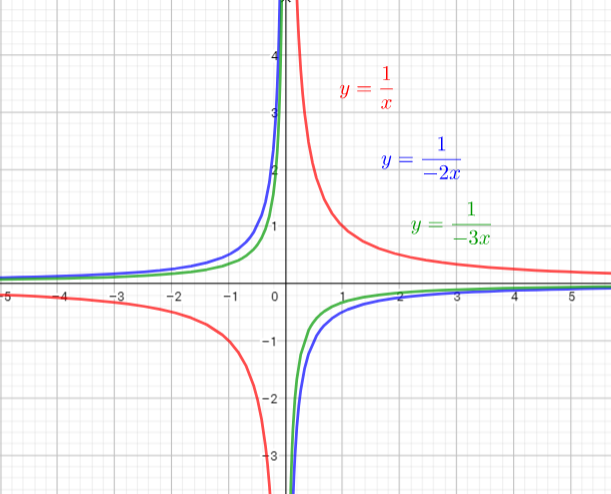
The parent function is $y=dfrac{1}{x}$

The graph of $y=dfrac{1}{-2x}$ is the graph of the parent function $y=dfrac{1}{x}$ . The graph is compressed horizontally by the factor $dfrac{1}{2}$ and reflected in the y-axis. There is no invariant points.

The graph of $y=dfrac{1}{-5x}$ is the graph of the parent function $y=dfrac{1}{x}$ .The graph is compressed horizontally by the factor $dfrac{1}{5}$ and reflected in the y-axis. There is no invariant point

d) The parent function is $y=|x|$

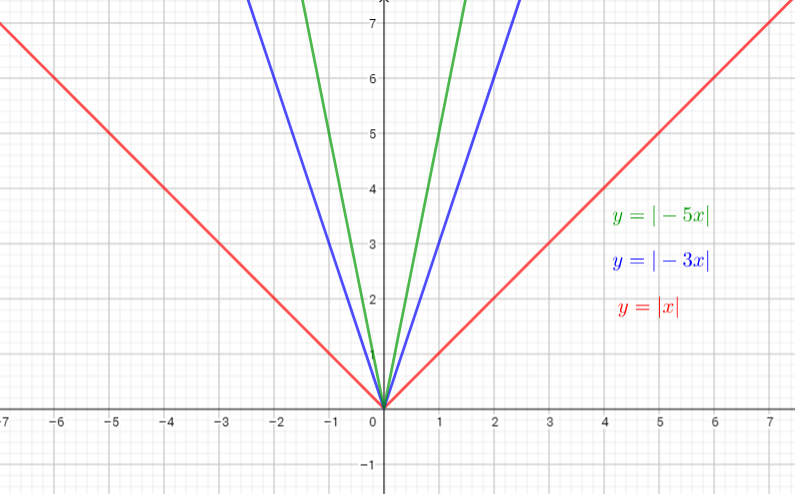
The graph of $y=|-3x|$ is the graph of the parent function $y=|x|$ . The graph is compressed horizontally by the factor $dfrac{1}{3}$ and reflected in the y-axis. There is (0,0) invariant point.

The graph of $y=|-5x|$ is the graph of the parent function $y=|x|$ . The graph iscompressed horizontally by the factor $dfrac{1}{5}$ and reflected in the y-axis. There is (0,0) invariant point.

a) horizontal compression by a factor of $dfrac{1}{2}$ and reflection in $y-axis$, $(0,0)$

horizontal compression by a factor of $dfrac{1}{5}$ and reflection in $y$-axis, $(0,0)$

b) horizontal compression by a factor of $dfrac{1}{3}$ and reflection in $y$-axis , $(0,0)$

horizontal compression by a factor of $dfrac{1}{4}$ and reflection in $y$-axis , $(0,0)$

c) horizontal compression by a factor of $dfrac{1}{2}$ and reflection in $y$-axis, no invariant points

horizontal compression factor of $dfrac{1}{3}$ and reflection in $y$-axis, no invariant points

d) horizontal compression by a factor of $dfrac{1}{3}$ and reflection in the $y$-axis, $(0,0)$

horizontal compression by a factor of $dfrac{1}{5}$ and reflection in the $y$-axis , $(0,0)$

We know that, if $0 < |k| 1$ then the graph $y=f(kx)$ is compressed horizontally by the factor $dfrac{1}{|k|}$ and

if $k< 0$ the graph is also reflected in the y-axis.

a) The parent function is $y=x^{2}$

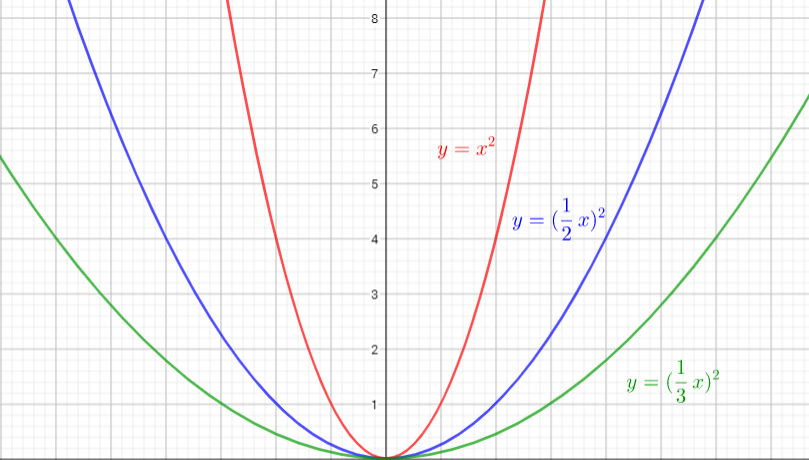
The graph of $y=(dfrac{1}{2}x)^{2}$ is the graph of the parent function $y=x^{2}$. The graph is stretched horizontally by the factor $2$. There is (0,0) invariant point.

The graph of $y=(dfrac{1}{3}x)^{2}$ is the graph of the parent function $y=x^{2}$ The graph is stretched horizontally by the factor $3$. There is (0,0) invariant point.

b)
The parent function is $y=sqrt{x}$

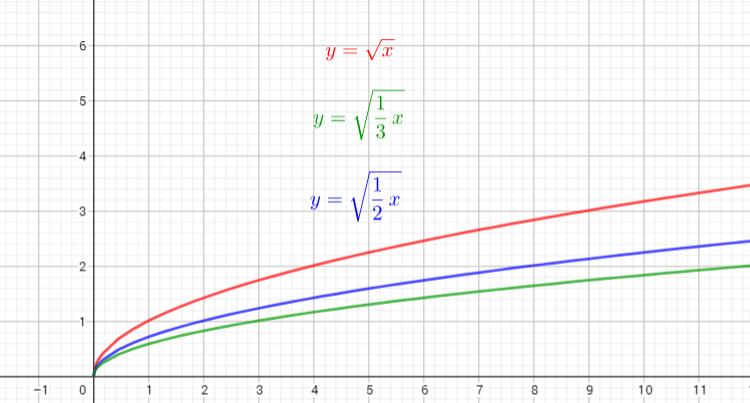
The graph of $y=sqrt{dfrac{1}{2}x}$ is the graph of the parent function $y=sqrt{x}$ .The graph is stretched horizontally by the factor $2$. There is (0,0) invariant point.

The graph of $y=sqrt{dfrac{1}{3}x}$ is the graph of the parent function $y=sqrt{x}$. The graph isstretched horizontally by the factor $3$. There is (0,0) invariant point.

c)
The parent function is $y=dfrac{1}{x}$

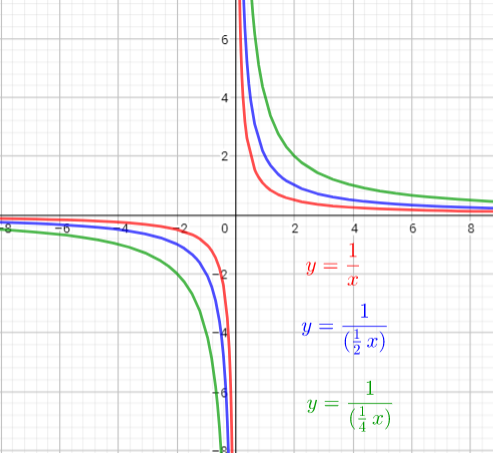
The graph of $y=dfrac{1}{(dfrac{1}{2}x)}$ is the graph of the parent function $y=dfrac{1}{x}$ .The graph is stretched horizontally by the factor $2$. There is no invariant points.

The graph of $y=dfrac{1}{(dfrac{1}{4}x)}$ is the graph of the parent function $y=dfrac{1}{x}$. The graph is stretched horizontally by the factor $4$. There is no invariant points.

d) The parent function is $y=|x|$

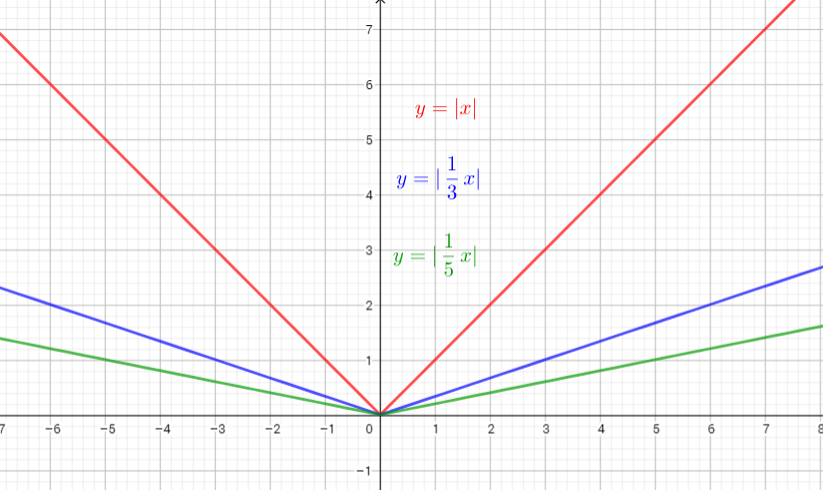
The graph of $y=|dfrac{1}{3}x|$ is the graph of the parent function $y=|x|$ . The graph is stretched horizontally by the factor $3$. There is (0,0) invariant point.

The graph of $y=|dfrac{1}{5}x|$ is the graph of the parent function $y=|x|$ is the graph stretched horizontally by the factor $5$. There is (0,0) invariant point.

a) horizontal stretching by a factor of 2, $(0,0)$

horizontal stretching by a factor of 3, $(0,0)$

b) horizontal stretching by a factor of 2 , $(0,0)$

horizontal stretching by a factor of 3, $(0,0)$

c) horizontal stretching by a factor of 2, no invariant points

horizontal stretching by a factor of 4, no invariant points

d) horizontal stretch by a factor of 3, $(0,0)$

horizontal stretch by a factor of 5 , $(0,0)$

We know that, if $0 < |k| 1$ then the graph $y=f(kx)$ is compressed horizontally by the factor $dfrac{1}{|k|}$ and

if $k< 0$ the graph is also reflected in the y-axis.

a) The parent function is $y=x^{2}$

The graph of $y=(-dfrac{1}{2}x)^{2}$ is the graph of the parent function $y=x^{2}$ . The graph is stretched horizontally by the factor $2$ and reflected in the y-axis. There is (0,0) invariant point.

The graph of $y=(-dfrac{1}{3}x)^{2}$ is the graph of the parent function $y=x^{2}$. The graph is stretched horizontally by the factor $3$ and reflected in the y-axis. There is (0,0) invariant point.

b)
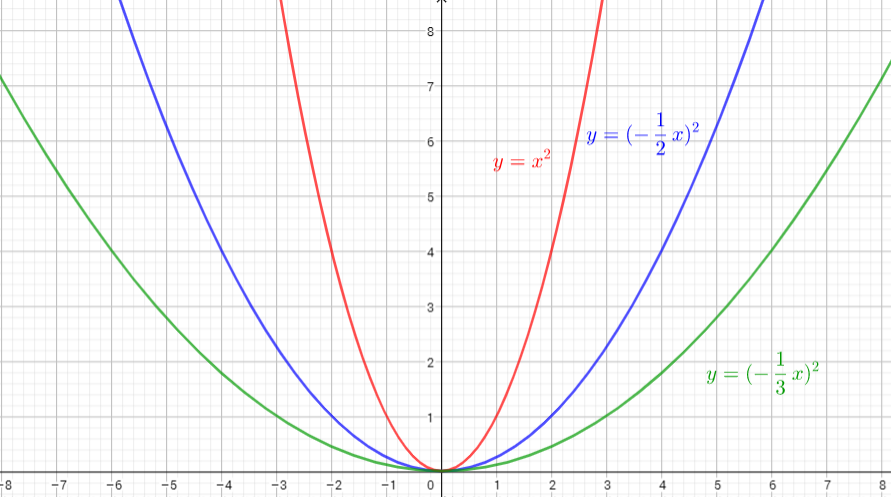
The parent function is $y=sqrt{x}$

The graph of $y=sqrt{-dfrac{1}{2}x}$ is the graph of the parent function $y=sqrt{x}$.The graph is stretched horizontally by the factor $2$ and reflected in the y-axis. There is (0,0) invariant point.

The graph of $y=sqrt{-dfrac{1}{3}x}$ is the graph of the parent function $y=sqrt{x}$ .The graph is stretched horizontally by the factor 3 and reflected in the y-axis. There is (0,0) invariant point.

c)
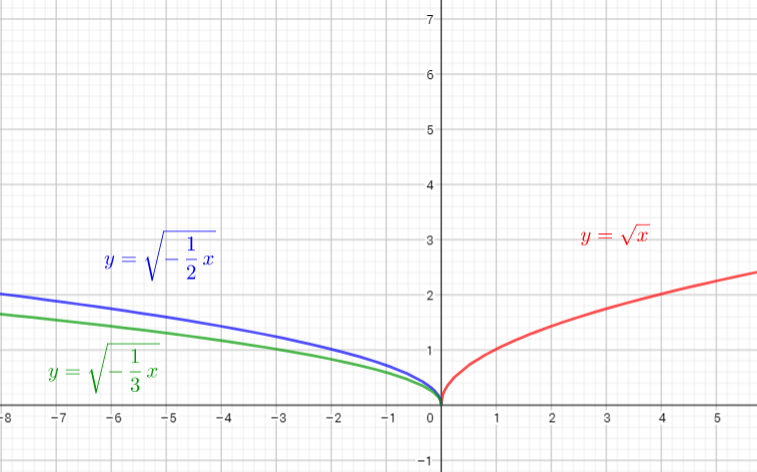
The parent function is $y=dfrac{1}{x}$

The graph of $y=dfrac{1}{(-dfrac{1}{2}x)}$ is the graph of the parent function $y=dfrac{1}{x}$ .The graph is stretched horizontally by the factor $2$ and reflected in the y-axis.. There is no invariant points.

The graph of $y=dfrac{1}{(-dfrac{1}{4}x)}$ is the graph of the parent function $y=dfrac{1}{x}$ The graph is stretched horizontally by the factor $4$ and reflected in the y-axis. There is no invariant points.

d) The parent function is $y=|x|$

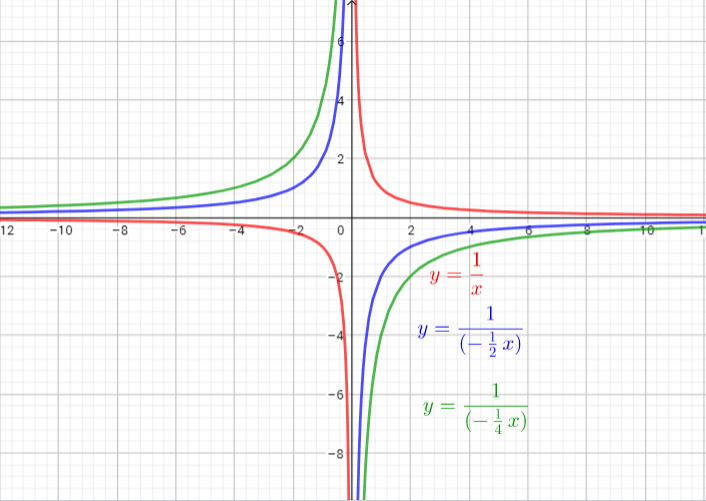
The graph of $y=|-dfrac{1}{3}x|$ is the graph of the parent function $y=|x|$ .The graph is stretched horizontally by the factor 3 and reflected in the y-axis. There is (0,0) invariant point.

The graph of $y=|-dfrac{1}{5}x|$ is the graph of the parent function $y=|x|$ is the graph stretched horizontally by the factor $5$ and reflected in the y-axis. There is (0,0) invariant point.

a) horizontal stretching by a factor of 2 and reflection in $y$-axis, $(0,0)$

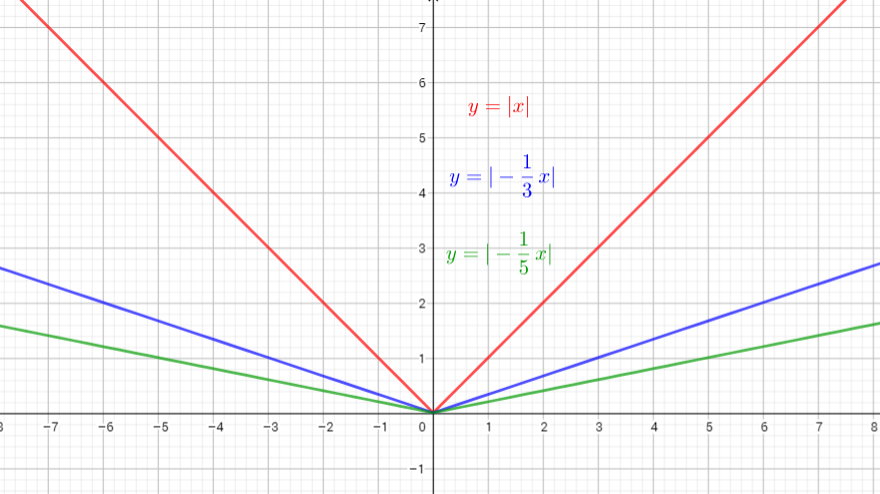
horizontal stretching by a factor of 3 and reflection in $y$-axis, $(0,0)$

b) horizontal stretching by a factor of 2 and reflection in $y$-axis , $(0,0)$

horizontal stretching by a factor of 3 and reflection in $y$-axis, $(0,0)$

c) horizontal stretching by a factor of 2 and reflection in $y$-axis, no invariant points

horizontal stretching by a factor of 4 and reflection in $y$-axis, no invariant points

d) horizontal stretching by a factor of 3 and reflection in $y$-axis, $(0,0)$

horizontal stretching by a factor of 5 and reflection in $y$-axis, $(0,0)$

a) From the graph we can conclude function is $y=|2x|$.

The graph of $y=|2x|$ is the graph of the parent function $y=|x|$. The graph is compressed horizontally by the factor $dfrac{1}{2}$

b)From the graph we can conclude function is $y=-dfrac{1}{2x}$.

The graph of $y=-dfrac{1}{2x}$ is the graph of the parent function $y=dfrac{1}{x}$. The graph is compressed horizontally by the factor 2 and reflected in the y-axis.

c) From the graph we can conclude $y=(dfrac{1}{4}x)^{2}$.

The graph of $y=(dfrac{1}{4}x)^{2}$ is the graph of the parent function $y=x^{2}$. The graph stretched horizontally by the factor $4$ and reflected in the y-axis

d) From the graph we can conclude $y=sqrt{-3x}$

The graph of $y=sqrt{-3x}$ is the graph of the parent function $y=sqrt{x}$. The graph is compressed horizontally by the factor $dfrac{1}{3}$ and reflected in the y-axis.

a) $g(x)=|2x|$

b) $g(x)=-dfrac{1}{2x}$

c) $g(x)=left(dfrac{1}{4}right)^2$

d) $g(x)=sqrt{-3x}$

a) The function is $t(h)=sqrt{dfrac{h}{4.9}}$, where $h$ is in metres and $t$ is in seconds.

The domain is all the values that $h$ is allowed to take on. This function is defined for each $hgeq0$

We know, range is the set of all output values of a function.

In our case, for each $hgeq0$ we get $tgeq0$.

Domain=$left{ hin R| hgeq0right}$

Range=$left{tin R|tgeq0 right}$

a) domain = ${ hinbold{R};|;hgeq0}$

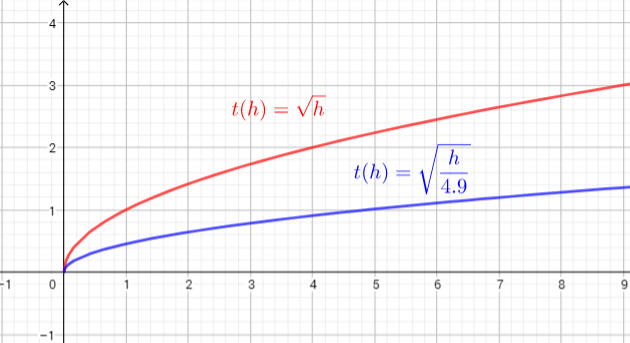
range = ${ tinbold{R};|;tgeq0}$

b) The graph has been plotted in the answers

$bold{Concept:}$

If $f(x)$ is transformed to $f(kx)$, then it is $bold{horizontally ;scaled}$ by a factor of $dfrac{1}{|k|}$

If $f(x)$ contains the point $(a,b)$, then $f(kx)$ must contain $left(dfrac{a}{k},bright)$.

The graph can either be $bold{compressed}$ (if $|k|>1$) or $bold{stretched}$ (if $0<|k|<1$ )

If $k<0$, the graph is not just horizontally scaled but also reflected in the $y$-axis.

a) $f(x)=x^2$

domain: ${ xinbold{R}}$

range : ${ yinbold{R};|;ygeq 0}$

$g(x)=dfrac{1}{4}x^2=left(dfrac{1}{2}xright)^2 implies$ horizontal compression by a factor of $dfrac{1}{1/2}=2$

domain: ${ xinbold{R}}$

range : ${ yinbold{R};|;ygeq 0}$

$h(x)=-4x^2=-(2x)^2 implies$ horizontal stretching by a factor of $dfrac{1}{2}$ and reflection in $x$-axis

domain: ${ xinbold{R}}$

range : ${ yinbold{R};|;yleq 0}$

b) $f(x)=sqrt{x}$

The expression inside a square root must not be negative.

domain: ${ xinbold{R};|;xgeq 0}$

range: ${ yinbold{R};|;ygeq0}$

$g(x)=sqrt{dfrac{1}{5}x}implies$ horizontal compression by a factor of $dfrac{1}{1/5}=5$

domain: ${ xinbold{R};|;xgeq 0}$

range : ${ yinbold{R};|;ygeq0}$

$h(x)=sqrt{-5x}implies$ horizontal stretching by a factor of $dfrac{1}{5}$ and reflection in $y$-axis

domain: ${ xinbold{R};|;xleq 0}$

range : ${ yinbold{R};|;yleq0}$

c) $f(x)=dfrac{1}{x}$

domain = ${ xinbold{R};|;xneq 0}$

range = ${ yinbold{R};|;yneq 0}$

$g(x)=dfrac{1}{4x}implies$ vertical compression by a factor of $dfrac{1}{4}$

domain = ${ xinbold{R};|;xneq 0}$

range = ${ yinbold{R};|;yneq 0}$

$h(x)=dfrac{1}{left(-frac{1}{3}xright)}implies$ vertical stretching by a factor of $dfrac{1}{left|-1/3right|}=3$ and reflection in $y$-axis.

domain = ${ xinbold{R};|;xneq 0}$

range = ${ yinbold{R};|;yneq 0}$

d) $f(x)=|x|$

domain = ${ xinbold{R}}$

range = ${ yinbold{R};|;ygeq0}$

$g(x)=|-2x|implies$ horizontal compression by a factor of $dfrac{1}{2}$ and reflection in $y$-axis

domain = ${ xinbold{R}}$

range = ${ yinbold{R};|;ygeq0}$

$h(x)=left|dfrac{1}{2}xright|implies$ horizontal stretching by a factor of $dfrac{1}{1/2}=2$

domain = ${ xinbold{R}}$

range = ${ yinbold{R};|;ygeq0}$

a) $g(x)$: domain = ${ xinbold{R}}$ , range = ${ yinbold{R};|;ygeq0}$

$h(x):$ domain = ${ xinbold{R}}$ , range = ${ yinbold{R};|;yleq0}$

b) $g(x)$: domain = ${ xinbold{R};|;xgeq 0}$ , range = ${ yinbold{R};|;ygeq0}$

$h(x)$: domain = ${ xinbold{R};|;xleq 0}$ , range = ${ yinbold{R};|;ygeq0}$

c) $g(x)$: domain = ${ xinbold{R};|;xneq 0}$ , range = ${ yinbold{R};|;yneq 0}$

$h(x)$: domain = ${ xinbold{R};|;xneq 0}$ , range = ${ yinbold{R};|;yneq 0}$

d) g(x): domain = ${ xinbold{R}}$ , range = ${ yinbold{R};|;ygeq0}$

h(x): domain = ${ xinbold{R}}$ , range = ${ yinbold{R};|;ygeq0}$

We know that:

1) if $0 < |k| 1$ then the graph $y=f(kx)$ is compressed horizontally by the factor $dfrac{1}{|k|}$ and

3) if $k< 0$ the graph is also reflected in the y-axis.

a) The function $f(x)$ is stretched horizontally by the factor 4, so, $dfrac{1}{k}=4$, or $k=4$

b) The function $f(x)$ is compressed horizontally by the factor $dfrac{1}{2}$, so $dfrac{1}{k}=dfrac{1}{2}$, or $k=2$

c) The function $f(x)$ is reflected in the y-axis , so $k=-1$

d) The function $f(x)$ is compressed horizontally by the factor $dfrac{1}{5}$ so $dfrac{1}{k}=dfrac{1}{5}$, or $k=5$ and reflected in the y-axis so $k=-5.$

a) $dfrac{1}{4}$

b) 2

c) $-1$

d) $-5$

a) A quaratic function is $f(x)=x^{2}-x-6$

The first, to find $f(2x)$, plug in $2x$ wherever $x$ occures in the equation of $f(x)$ and simplify to get $f(2x)$:

$f(2x)=(2x)^{2}-2x-6=4x^{2}-2x-6$.

Now, we need determine the x-intercepts for $f(2x)$.

We need solve quadratic equation $f(2x)=0$ or $4x^{2}-2x-6=0$ use the quadratic formula $x_{1,2}=dfrac{-b pm sqrt{b^{2}-4ac}}{2a}$ where $a, b$, and $c$ are the numerical coefficients of the terms of the quadratic equation

$a=4, b=-2$ and $c=-6$, substitute numerical coefficients in the quadratic formula we get:

$x_{1,2}=dfrac{-(-2) pm sqrt{(-2)^{2}-4cdot 4 cdot(-6)}}{2cdot4}$

$x_{1,2}=dfrac{2pmsqrt{4+96}}{8}=dfrac{2pmsqrt{100}}{8}$

$$
x_{1,2}=dfrac{2pm10}{8}
$$

$x_{1}=dfrac{2+10}{8}=dfrac{12}{8}=dfrac{3}{2}=1.5$ and

$x_{2}=dfrac{2-10}{8}=dfrac{-8}{8}=-1$

Solution is: x-intercepts for function $f(2x)$ are 1.5 and -1

b) A quaratic function is $f(x)=x^{2}-x-6$

The first, to find $f(dfrac{1}{3}x)$, plug in $dfrac{1}{3}x$ wherever $x$ occures in the equation of $f(x)$ and simplify to get $f(dfrac{1}{3}x)$:

$f(dfrac{1}{3}x)=(dfrac{1}{3}x)^{2}-dfrac{1}{3}x-6=dfrac{1}{9}x^{2}-dfrac{1}{3}x-6$.

Now, we need determine the x-intercepts for $f(dfrac{1}{3}x)$.

We need solve quadratic equation $f(dfrac{1}{3}x)=0$ or $dfrac{1}{9}x^{2}-dfrac{1}{3}x-6=0$, or ( multiply equation by 9) $x^{2}-3x-54=0$ use the quadratic formula $x_{1,2}=dfrac{-b pm sqrt{b^{2}-4ac}}{2a}$ where $a, b$, and $c$ are the numerical coefficients of the terms of the quadratic equation

$a=1, b=-3$ and $c=-54$, substitute numerical coefficients in the quadratic formula we get:

$x_{1,2}=dfrac{-(-3) pm sqrt{(-3)^{2}-4cdot 1 cdot(-54)}}{2cdot1}$

$x_{1,2}=dfrac{3pmsqrt{9+216}}{2}=dfrac{3pmsqrt{225}}{2}$

$$
x_{1,2}=dfrac{3pm15}{2}
$$

$x_{1}=dfrac{3+15}{2}=dfrac{18}{2}=9$ and

$x_{2}=dfrac{3-15}{2}=dfrac{-12}{2}=-6$

Solution is: x-intercepts for function $f(dfrac{1}{3}x)$ are 9 and -6

c) A quaratic function is $f(x)=x^{2}-x-6$

The first, to find $f(-3x)$, plug in $-3x$ wherever $x$ occures in the equation of $f(x)$ and simplify to get $f(-3x)$:

$f(-3x)=(-3x)^{2}-(-3x)-6=9x^{2}+3x-6$.

Now, we need determine the x-intercepts for $f(-3x)$.

We need solve quadratic equation $f(-3x)=0$ or $9x^{2}+3x-6=0$ use the quadratic formula $x_{1,2}=dfrac{-b pm sqrt{b^{2}-4ac}}{2a}$ where $a, b$, and $c$ are the numerical coefficients of the terms of the quadratic equation

$a=9, b=3$ and $c=-6$, substitute numerical coefficients in the quadratic formula we get:

$x_{1,2}=dfrac{-3 pm sqrt{3^{2}-4cdot 9 cdot(-6)}}{2cdot9}$

$x_{1,2}=dfrac{-3pmsqrt{9+216}}{8}=dfrac{-3pmsqrt{225}}{18}$

$$
x_{1,2}=dfrac{-3pm15}{18}
$$

$x_{1}=dfrac{-3+15}{18}=dfrac{12}{18}=dfrac{2}{3}$ and

$x_{2}=dfrac{-3-15}{18}=dfrac{-18}{18}=-1$

Solution is: x-intercepts for function $f(2x)$ are $dfrac{2}{3}$ and -1

a) $1.5,-1$

b) $9,-6$

c) $-1,dfrac{2}{3}$

a)

1) if $0 < k 1$ then the graph $y=f(kx)$ is compressed horizontally by the factor $dfrac{1}{k}$ and

3) if $k< 0$ the graph is also reflected in the y-axis.

b)

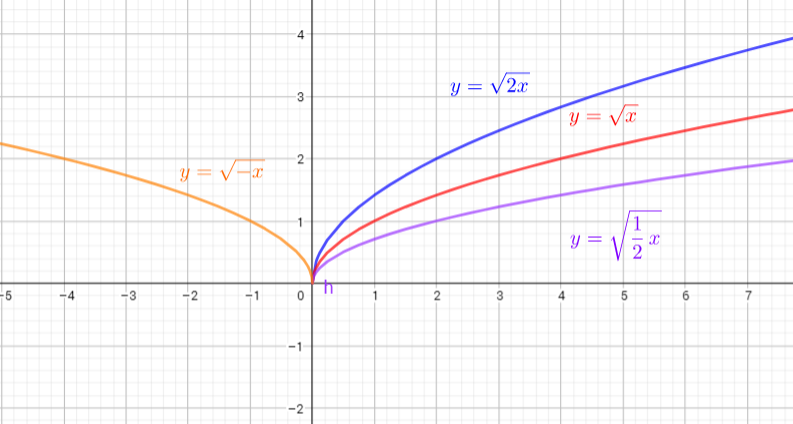
1) if $0 < k 1$ then the graph $y=f(kx)$ is compressed horizontally by the factor $dfrac{1}{k}$ and and the graph of $kf(x)$ is stretched verticaly by the factor $k$

3) if $k< 0$ the graph is reflected in the y-axis and the graph of $kf(x)$ is reflected in the x-axis

a)

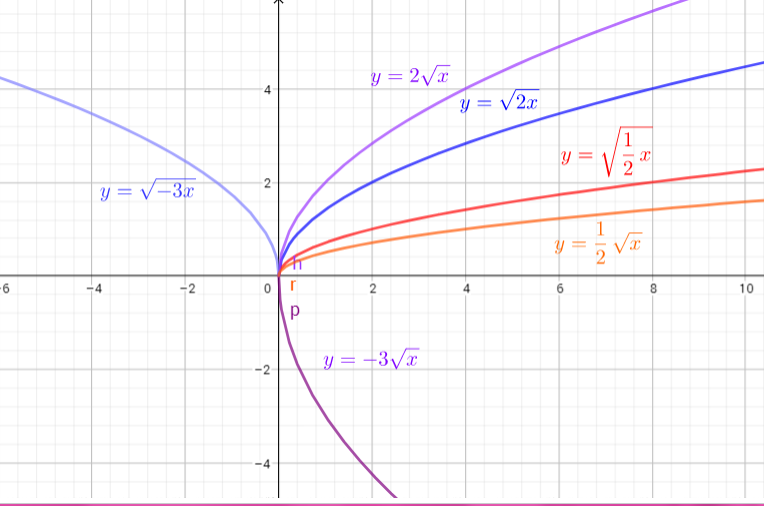
(1) if $0<|k|1$, the graph is horizontally compressed by $dfrac{1}{|k|}$

(3) if $k<0$, the graph is also reflected in the $y$-axis.

b) Horizontal stretching is equivalent to vertical compression and horizontal compression is equivalent to vertical stretching. However, the scale factors may or may not be reciprocal of each other.

a) Graph of the function $f(x)=dfrac{1}{x}$ is on the picture left (red graph)

b)-c) Graph of the function a horizontaly stretched with factor 2 and graph of the function a verticaly stretched with factor 2 are on the picture left (blue liine)

Use the graph, we can conclude that the horizontal and vertical stretches give the same graph.

d) We know that, if $0 < k<1$ then the graph $y=f(kx)$ is stretched horizontally by the factor $dfrac{1}{k}$, so, if factor equal 2, then $dfrac{1}{k}=2$ or $k=dfrac{1}{2}$. That means, a function is $y=f(dfrac{1}{2}x)=dfrac{1}{dfrac{1}{2}x}$

Graph $y=kf(x)$ is a vertical stretch with factor 2 if $k=2$. That means, a function is $y=2f(x)=2cdotdfrac{1}{x}$

Now we can simplify these functions:

$y=dfrac{1}{dfrac{1}{2}x}=dfrac{1}{dfrac{x}{2}}=dfrac{2}{x}$ and

$y=2cdotdfrac{1}{x}=dfrac{2}{x}$

If we compare $y=dfrac{1}{dfrac{1}{2}x}$ and $y=2cdotdfrac{1}{x}$
we can conclude the equations are the same and equal $y=dfrac{2}{x}$

a-c) The graphs have been plotted in the answer.

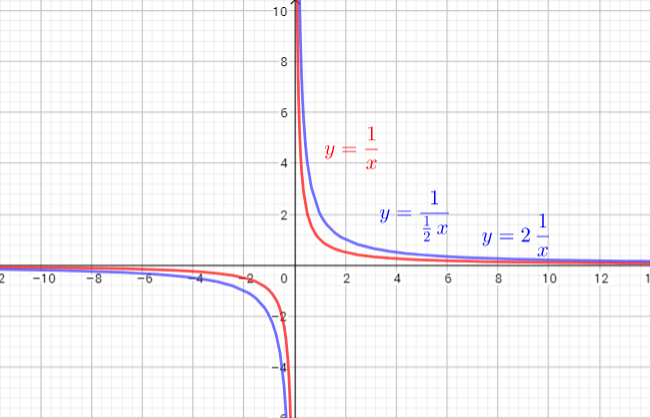
b) The horizontal and vertical stretches result in equivalent graph.

d) $y=dfrac{1}{frac{1}{2}x}$ , $y=2left(dfrac{1}{2}right)$ ; both are equal to $y=dfrac{2}{x}$

begin{table}[]
defarraystretch{1.5}%
begin{tabular}{|l|l|}
hline
Transformation & Description \ hline
$y=f(x)+c$ & begin{tabular}[c]{@{}l@{}}vertical translation of\ $c$ units upwardend{tabular} \ hline
$y=f(x+d)$ & begin{tabular}[c]{@{}l@{}}horizontal translation of $d$ units\ to the leftend{tabular} \ hline
$y=acdot f(x)$ & begin{tabular}[c]{@{}l@{}}vertical stretching by a factor of $a$end{tabular} \ hline
$y=f(kx)$ & begin{tabular}[c]{@{}l@{}}horizontal compression by $dfrac{1}{|k|}$end{tabular} \ hline
$y=-f(x)$ & begin{tabular}[c]{@{}l@{}}reflecting the function in\ the $x$-axisend{tabular} \ hline
$y=f(-x)$ & begin{tabular}[c]{@{}l@{}}reflecting the function in \ the $y$-axisend{tabular} \ hline
end{tabular}
end{table}

We need to find the transformations in $y=f(2x+4)$. We should rewrite this as

$y=f(2(x+2))$

The transformations are:

(1) horizontal compression by a factor of $dfrac{1}{2}implies y=f(2x)$

(2) horizontal translation 2 units to the left $implies y=f(2(x+2))$

If we reverse the order

(1) horizontal translation 2 units to the left $implies y=f(x+2)$

(2) horizontal compression by a factor of $dfrac{1}{2}implies y=f(2x+2)$

Thus, the order does matter here.

For example, if $f(x)=x^2$.

The graph is different when the order is reversed.

(1) horizontal compression by a factor of $dfrac{1}{2}$

(2) horizontal translation 2 units to the left

The order does matter.