$bold{Arithmetic;Series}$ The sum of the first $n$ terms in an arithmetic sequence with first term $t_1$ and common difference $d$ is

$$
S_n=dfrac{n}{2}[;2t_1+(n-1)d;]
$$

a.) In this case, we shall find $S_{10}$ for $t_1=59$ and $d=64-59=5$.

$$
S_{10}=dfrac{10}{2}[2(59)+(10-1)(5)]=815
$$

b.) In this case, we shall find $S_{10}$ for $t_1=31$ and $d=23-31=-8$.

$$
S_{10}=dfrac{10}{2}[2(31)+(10-1)(-8)]=-50
$$

c.) In this case, we shall find $S_{10}$ for $t_1=-103$ and $d=-110-(-103)=-7$

$$
S_{10}=dfrac{10}{2}[2(-103)+(10-1)(-7)]=-1345
$$

d.) In this case, we shall find $S_{10}$ for $t_1=-78$ and $d=-56-(-78)=22$

$$
S_{10}=dfrac{10}{2}[2(-78)+(19-1)(22)]=210
$$

$bold{Arithmetic;Series}$ The sum of the first $n$ terms in an arithmetic sequence with first term $t_1$ and common difference $d$ is

$S_n=dfrac{n}{2}[;2t_1+(n-1)d;]$

In this case, we shall find $S_{20}$ for $t_1=10$ and $d=11$.

$$
S_{10}=dfrac{20}{2}[2(18)+(20-1)(11)]=2450
$$

$$
2450
$$

$bold{Arithmetic;Series}$ The sum of the first $n$ terms in an arithmetic sequence with first term $t_1$, $n^{th}$ term $t_n$, and common difference $d$ is

$S_n=dfrac{n}{2}(t_1+t_n)=dfrac{n}{2}[;2t_1+(n-1)d;]$

Since the number of bricks in each stack increases linearly from the top, we can use an arithmetic series to model the total number of bricks in the $n^{th}$ row from the top.

In this case, $t_1=5$ and $t_n=62$

At the $20^{th}$ row,

$S_{20}=dfrac{20}{2}(5+62)=670$

Therefore, a total of $boxed{bold{670; bricks}}$ is present in the stack with 20 rows.

$670$ bricks

$bold{Identifying;Arithmetic;Series}$ A series containing the terms

$t_1+t_2+t_3+t_4+…$

is arithmetic series if the difference between consecutive terms is constant, that is,

$t_2-t_1=t_3-t_2=t_4-t_3=d$

$bold{Arithmetic;Series}$ The sum of the first $n$ terms in an arithmetic sequence with first term $t_1$, $n^{th}$ term $t_n$, and common difference $d$ is

$S_n=dfrac{n}{2}(t_1+t_n)=dfrac{n}{2}[;2t_1+(n-1)d;]$

a.) This is an arithmetic series with $d=6$ and $t_1=-5$

The sum of the first $25$ terms is

$$
S_{25}=dfrac{25}{2}[2(-5)+(25-1)(6)]=1675
$$

d.) This is an arithmetic series with $d=22-18=4$ and $t_1=18$

The sum of the first $25$ terms is

$$
S_{25}=dfrac{25}{2}[2(18)+(25-1)(4)]=1650
$$

e.) This is an arithmetic series with $d=22-31=-9$ and $t_1=31$

The sum of the first $25$ terms is

$$
S_{25}=dfrac{25}{2}[2(31)+(25-1)(-9)]=-1925
$$

$bold{Identifying;Arithmetic;Series}$ A series containing the terms

$t_1+t_2+t_3+t_4+…$

is arithmetic series if the difference between consecutive terms is constant, that is,

$t_2-t_1=t_3-t_2=t_4-t_3=d$

$bold{Arithmetic;Series}$ The $n^{th}$ term of an arithmetic series $t_n$ with first term $t_1$ and common difference $d$ is

$t_n=t_1+(n-1)d$

The sum of the first $n$ terms is

$S_n=dfrac{n}{2}(t_1+t_n)=dfrac{n}{2}[;2t_1+(n-1)d;]$

a.) This is an arithmetic series with $d=21-17=4$ and $t_1=37$

General term: $t_n=37+(n-1)(4)=4n+33$

12th term: $t_{12}=4(12)+33=81$

The sum of the first $12$ terms is

$$
S_{12}=dfrac{12}{2}[2(37)+(12-1)(4)]=708
$$

b.) This is an arithmetic series with $d=-24-(-13)=-11$ and $t_1=-13$

General term: $t_n=-13+(n-1)(-11)=-2-11n$

12th term: $t_{12}=-2-11(-11)=-134$

The sum of the first $12$ terms is

$$
S_{12}=dfrac{12}{2}[2(-13)+(12-1)(-11)=-882
$$

c.) This is an arithmetic series with $d=-12-(-18)=6$ and $t_1=-18$

General term: $t_n=-18+(n-1)(6)=6n-24$

12th term: $t_{12}=6(12)-24=48$

The sum of the first $12$ terms is

$$
S_{12}=dfrac{12}{2}[2(-18)+(12-1)(6)=180
$$

d.) This is an arithmetic series with $d=dfrac{7}{10}-dfrac{1}{5}=dfrac{1}{2}$ and $t_1=dfrac{1}{5}$

General term: $t_n=dfrac{1}{5}+(n-1)cdot dfrac{1}{2}=dfrac{1}{2}n-dfrac{3}{10}$

12th term: $t_{12}=dfrac{1}{2}(12)-dfrac{3}{10}=5.7$

The sum of the first $12$ terms is

$$
S_{12}=dfrac{12}{2}left[2cdot dfrac{1}{5}+(12-1)left(dfrac{1}{2}right)right]=dfrac{177}{5}=35.4
$$

e.) This is an arithmetic series with $d=4.31-3.19=1.12$ and $t_1=3.19$

General term: $t_n=3.19+(n-1)(1.12)=1.12n+2.07$

12th term: $t_{12}=1.12(12)+2.07=15.51$

The sum of the first $12$ terms is

$$
S_{12}=dfrac{12}{2}[2(3.19)+(12-1)(1.12)]=112.2
$$

f.) This is an arithmetic series with $d=(2p+2q)-p=p+2q$ and $t_1=p$

General term: $t_n=p+(n-1)(p+2q)=(p+2q)n-2q$

The $12^{th}$ term is

$t_{12}=p+(12-1)(p+2q)=12p+22q$

The sum of first 12 terms is

$$
S_{12}=dfrac{12}{2}(p+12p+22q)=78p+132q
$$

a.) 708

b.) $-8$82

c.) 180

d.) 35.4

e.) 112.2

f.) $78p+132q$

$bold{Identifying;Arithmetic;Series}$ A series containing the terms

$t_1+t_2+t_3+t_4+…$

is arithmetic series if the difference between consecutive terms is constant, that is,

$t_2-t_1=t_3-t_2=t_4-t_3=d$

$bold{Arithmetic;Series}$ The $n^{th}$ term of an arithmetic series $t_n$ with first term $t_1$ and common difference $d$ is

$t_n=t_1+(n-1)d$

The sum of the first $n$ terms is

$S_n=dfrac{n}{2}(t_1+t_n)=dfrac{n}{2}[;2t_1+(n-1)d;]$

a.) In this case, $t_1=8$ and $d=5$

The sum of first 20 terms is

$$
S_{20}=dfrac{20}{2}[2(8)+(20-1)(5)]=1110
$$

b.) Here, $t_1=31$ and $_{20}=109$

We can use the equation

$S_n=dfrac{n}{2}(t_1+t_n)$

$$
S_{20}=dfrac{20}{2}(31+109)=1400
$$

c.) In this case, $t_1=53$, $d=37-53=-16$

The sum of first 20 terms is

$$
S_{20}=dfrac{20}{2}[2(53)+(20-1)(-16)]=-1980
$$

d.) Here we are not given $t_1$, instead we have $t_4=18$ and $d=17$

Remember that for arithmetic sequence

$t_j-t_k=(j-k)d$

$implies t_4-t_1=(4-1)(d)implies t_1=18-3(17)=-33$

The sum of first 20 terms is

$$
S_{20}=dfrac{20}{2}[2(-33)+(20-1)(17)]=2570
$$

e.) Here we are not given $t_1$ and $d$, instead we have $t_{15}=107$ and $d=-3$

Remember that for arithmetic sequence

$t_j-t_k=(j-k)d$

$implies t_15-t_1=(15-1)(-3)implies t_1=149$

Thus, the sum of first 20 terms is

$$
S_{20}=dfrac{20}{2}[2(149)+(20-1)(-3)]=2410
$$

f.) Here we are not given $t_1$ and $d$, instead we have $t_7=43$ and $t_{13}=109$

Remember that for arithmetic sequence

$t_j-t_k=(j-k)d$

$implies t_{13}-t_7=(13-7)(d)implies d=11$

To solve for $t_1$

$t_7-t_1=(7-1)dimplies t_1=43-(7-1)(11)=-23$

Thus, the sum of first 20 terms is

$$
S_{20}=dfrac{20}{2}[2(-23)+11(20-1)]=1630
$$

$bold{Identifying;Arithmetic;Series}$ A series containing the terms

$t_1+t_2+t_3+t_4+…$

is arithmetic series if the difference between consecutive terms is constant, that is,

$t_2-t_1=t_3-t_2=t_4-t_3=d$

$bold{Arithmetic;Series}$ The $n^{th}$ term of an arithmetic series $t_n$ with first term $t_1$ and common difference $d$ is

$t_n=t_1+(n-1)d$

The sum of the first $n$ terms is

$S_n=dfrac{n}{2}(t_1+t_n)=dfrac{n}{2}[;2t_1+(n-1)d;]$

a.) In this case, the common difference $d=6-1=5$ and the first term $t_1=1$, thus, the general term is

$t_n=1+(n-1)(5)=5n-4$

We shall determine which value of $n$ does $t_n=96$ correspond to

$96=5n-4implies n = 20$

The sum of the series is therefore

$S_n=dfrac{n}{2}(t_1+t_n)$

$$
S_{20}=dfrac{20}{2}(1+96)=970
$$

b.) This sequence has a common difference of $d=37-24=13$ and $t_1=24$. The general term is

$t_n=24+(n-1)(13)=13n+11$

Since $t_n=349$, we shall find the value of $n$,

$349=13n+11implies n=dfrac{349-11}{13}=26$

The sum of the series is therefore

$$
S_{26}=dfrac{26}{2}(24+349)=4849
$$

c.) This sequence has a common difference of $d=77-85=-8$ and $t_1=85$. The general term is

$t_n=85+(n-1)(-8)=93-8n$

Since $t_n=-99$, we shall find the value of $n$,

$-99=93-8nimplies n =dfrac{93+99}{8}=24$

Thus, the sum of the series is therefore

$$
S_{24}=dfrac{24}{2}(85-99)=-168
$$

d.) This sequence has a common difference of $d=8-5=3$ and $t_1=5$. The general term is

$t_n=5+(n-1)(3)=3n+2$

Since $t_n=2135$, we shall find the value of $n$,

$2135=3n+2implies n =dfrac{2135-2}{3}=711$

Thus, the sum of the series is therefore

$$
S_{711}=dfrac{711}{2}(5+2135)=760;770
$$

d.) This sequence has a common difference of $d=-38-(-31)=-7$ and $t_1=-31$. The general term is

$t_n=-31+(n-1)(-7)=-7n-24$

Since $t_n=136$, we shall find the value of $n$,

$-136=-7n-24implies n =dfrac{136-24}{7}=16$

Thus, the sum of the series is therefore

$$
S_{16}=dfrac{16}{2}(-31-136)=-1336
$$

d.) This sequence has a common difference of $d=-57-(-63)=6$ and $t_1=-63$. The general term is

$t_n=-63+(n-1)(6)=6n-69$

Since $t_n=63$, we shall find the value of $n$,

$63=6n-69implies n =dfrac{69+63}{6}=22$

Thus, the sum of the series is therefore

$$
S_{22}=dfrac{22}{2}(-63+63)=0
$$

a.) 970

b.) 4849

c.) $-$168

d.) 760 770

e.) -1336

f.) 0

$bold{Arithmetic;Series}$ The $n^{th}$ term of an arithmetic series $t_n$ with first term $t_1$ and common difference $d$ is

$t_n=t_1+(n-1)d$

The sum of the first $n$ terms is

$S_n=dfrac{n}{2}(t_1+t_n)=dfrac{n}{2}[;2t_1+(n-1)d;]$

You might want to sketch some regular polygons and count the number of distinct diagonals. Notice that for $n$ sided polygon, we can obtain the following diagonals $d_n$

$d_4=2$

$d_5=5$

$d_6=9$

$$
d_7=14
$$

Observe that the pattern corresponds to

$d_4=2$

$d_5=2+3$

$d_6=2+3+4$

$d_7=2+3+4+5$

which appears to be an arithmetic series with $t_4=2$ and $d=1$.
From the general term

$t_n=t_1+(n-1)(d)$

We can obtain the first term as

$2=t_1+(4-1)(1)implies t_1=-1$

To find the number of diagonals as a function of $n$ sides, we can use the general term for arithmetic series.

$$
S_n=dfrac{n}{2}[2(-1)+(n-1)(1)]=dfrac{n}{2}(n-3)
$$

Therefore, for $n=7$ (regular heptagon), the number of diagonal is

$S_7=dfrac{7}{2}(7-3)=14$

We can confirm this by sketching the figure$.$

a.) $S_n=dfrac{n}{2}(n-3)$

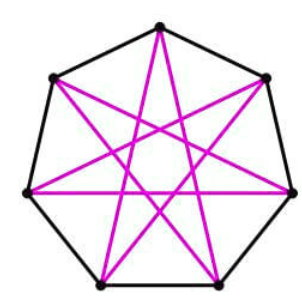
b.) 14 diagonals

$bold{Arithmetic;Series}$ The $n^{th}$ term of an arithmetic series $t_n$ with first term $t_1$ and common difference $d$ is

$t_n=t_1+(n-1)d$

The sum of the first $n$ terms is

$S_n=dfrac{n}{2}(t_1+t_n)=dfrac{n}{2}[;2t_1+(n-1)d;]$

The interest per year is $6.3%$ of the initial amount $$1000$ which is $0.063cdot 1000=$63$

We can model the accumulated investment (with simple annual interest) as an arithmetic series with $t_1=1000$ and $d=63$

At the start of fifth year, the account value shall be

$S_5=dfrac{5}{2}[2(1000)+(5-1)(63)]=$5,630.00$

The account value at the start of $5^{th}$ year is $boxed{bold{$5,630.00}}$

$$
$5,630.00
$$

$bold{Arithmetic;Series}$ The $n^{th}$ term of an arithmetic series $t_n$ with first term $t_1$ and common difference $d$ is

$t_n=t_1+(n-1)d$

The sum of the first $n$ terms is

$S_n=dfrac{n}{2}(t_1+t_n)=dfrac{n}{2}[;2t_1+(n-1)d;]$

In the first second, she fell by $4.9$ and this distance is added by $9.8;m$ for each additional second. Thus, we can model the total distance as an arithmetic series with $t_1=4.9;m$ and $d=9.8$. We are interested in the total distance after $15$ seconds. Using the formula for the sum of arithmetic series,

$S_n=dfrac{n}{2}[2t_1+(n-1)d]$

$S_{15}=dfrac{15}{2}[2(4.9)+(15-1)(9.8)]=1,102.5$ m

Therefore, Chandra covered a total distance of $boxed{bold{1,102.5;m}}$ within 15 seconds before the parachute was released.

$1,102.5$ m

$bold{Arithmetic;Series}$ The $n^{th}$ term of an arithmetic series $t_n$ with first term $t_1$ and common difference $d$ is

$t_n=t_1+(n-1)d$

The sum of the first $n$ terms is

$S_n=dfrac{n}{2}(t_1+t_n)=dfrac{n}{2}[;2t_1+(n-1)d;]$

The number of toys that Jamal can assemble $t_n$ increases by 3 every day and on his 20$^{th}$ day, he was able to complete 137 toys. We can obtain $t_1$ using the general term of arithmetic sequence

$t_n=t_1+(n-1)(d)$

$137=t_1+(20-1)(3)implies t_1=80$

To calculate the total toys that Jamal assembled in his first 20 days, evaluate $S_{20}$

$S_{20}=dfrac{20}{2}[2(80)+(20-1)(3)]=2170$

Therefore, a total of $boxed{bold{2,170 ;toys}}$ was assembled in Jamal’s first 20 days.

$2,170$ toys

$bold{Arithmetic;Series}$ The $n^{th}$ term of an arithmetic series $t_n$ with first term $t_1$ and common difference $d$ is

$t_n=t_1+(n-1)d$

The sum of the first $n$ terms is

$S_n=dfrac{n}{2}(t_1+t_n)=dfrac{n}{2}[;2t_1+(n-1)d;]$

The number of seconds decreases by a constant value with each level. Thus, we can model this is an arithmetic series with $t_1=200$ and $t_{20}=105$.

We need to find the value of $d$

$t_n=t_1+(n-1)d$

$105=200+(20-1)(d)$

$d=-5$

The total time for the first 20 levels is

$S_{20}=dfrac{20}{2}[2(200)+(20-1)(-5)]=boxed{bold{3050;seconds}}$

$3050$ seconds

$bold{Arithmetic;Series}$ The $n^{th}$ term of an arithmetic series $t_n$ with first term $t_1$ and common difference $d$ is

$t_n=t_1+(n-1)d$

The sum of the first $n$ terms is

$S_n=dfrac{n}{2}(t_1+t_n)=dfrac{n}{2}[;2t_1+(n-1)d;]$

Sara runs $5$ times a week and her distance per day is 2 km more than the previous week. This implies that her distance increases by $5times 2=10;km$ every week and initially she ran at $5;km$ per day, that is, $25;km$ per week. We can model this case by an arithmetic series with $t_1=25$ and $d=10$.

To know the total distance that Sara covered in her first 10 weeks, we shall use the formula for the sum of arithmetic series,

$S_n=dfrac{n}{2}[2t_1+(n-1)d]$

$S_{10}=dfrac{10}{2}[2(25)+(10-1)(10)]=700$

Therefore, Sara covered a total of $boxed{bold{700; km}}$ in her $10^{th}$ week.

$700$ km

When the given linking-cube representations is copied and fitted to each other, it forms a full rectangle. The area of a rectangle is length $times$ width and the area corresponds to the total number squares. Since the sum of the series is just half of this area, we can determine the formula of the arithmetic series by determining the product of length and width divided by 2.

In the first representation, the width is $n$ and the length is $t_1+t_n$, therefore

$S_n=dfrac{1}{2}(n)(t_1+t_n)$

In the second representation, the width is $n$ and the length is $2t_1+(n-1)d$. In this example, $n=5$ which results in $2t_1+(5-1)(d)$ which leads to

$$
S_n=dfrac{1}{2}n[2t_1+(n-1)d]
$$

$bold{Arithmetic;Series}$ The $n^{th}$ term of an arithmetic series $t_n$ with first term $t_1$ and common difference $d$ is

$t_n=t_1+(n-1)d$

The sum of the first $n$ terms is

$S_n=dfrac{n}{2}(t_1+t_n)=dfrac{n}{2}[;2t_1+(n-1)d;]$

Here, we are given that the sum of the first 20 terms $S_{20}=710$ and the tenth term $t_{10}=34$.

Using the formula for arithmetic series mentioned above

$34=t_1+(10-1)(d)$

$710=dfrac{20}{2}[2t_1+(20-1)(d)]$

Substitute $t_1=34-9d$ from the first equation to the 2nd equation

$710=10cdot [2(34-9d)+19d]implies 710=20(34-9d)+190d$

$710=680-180d+190dimplies 10d=30implies d=3$

Then, we can find $t_1$ from the first equation

$t_1=34-9(3)=7$

Now we have $t_1=7$ and $d=3$ which we can use to get the general term

$t_n=7+(n-1)(3)=3n+4$

The 25th term can be calculated as

$t_{25}=3(25)+4=79$

Therefore, the 25th term is $boxed{bold{79}}$

$$
t_{25}=79
$$

$bold{Arithmetic;Series}$ The $n^{th}$ term of an arithmetic series $t_n$ with first term $t_1$ and common difference $d$ is

$t_n=t_1+(n-1)d$

The sum of the first $n$ terms is

$S_n=dfrac{n}{2}(t_1+t_n)=dfrac{n}{2}[;2t_1+(n-1)d;]$

We are given that $S_n=1001$, $t_1=1$, and $d=4-1=3$

We need to find $n$ such that $S_n=1001$. Hence, we shall substitute this values to the expression for $S_n$

$S_n=dfrac{n}{2}[2t_1+(n-1)d]$

$1001=dfrac{n}{2}[2(1)+(n-1)(3)]$

$n(3n-1)=1001cdot 2$

$3n^2-n-2002=0$

This is a quadratic equation that we can factor

$(n-26)(3n+77)=0$

$n=26$ or $n=-dfrac{77}{3}$

Since $n$ can only take positive discrete values, we shall consider

$n=26$

Therefore, there are $boxed{bold{26;terms}}$ in the series.

$26$ terms