
All Solutions
Section 5-2: Evaluating Trigonometric Ratios for Special Angles
The greater the measure of an angle, the longer is its opposite side.
Since one side is $30^circ$, the other angle must be $90-30=60^circ$
So the side opposite to $30^circ$ must be the smallest side which is 1.
c) With respect to $60^circ$, the adjacent side is $1$ and the opposite side is $2$
b) adjacent side: 2 ; opposite side: 1
c) adjacent side: 1 ; opposite side: 2
A triangle with equal lengths of legs is called an isosceles right triangle.
b) both opposite and adjacent side are equal to 1
begin{table}[]
defarraystretch{2.4}%
begin{tabular}{llll}
hline
multicolumn{1}{|l|}{begin{tabular}[c]{@{}l@{}}principal angle $theta$end{tabular}} & multicolumn{1}{l|}{Quadrant} & multicolumn{1}{l|}{begin{tabular}[c]{@{}l@{}}sign\ $(cos theta, sin theta)$end{tabular}} & multicolumn{1}{l|}{begin{tabular}[c]{@{}l@{}}reference acute angle $alpha$end{tabular}} \ hline
multicolumn{1}{|l|}{$0leq theta<90^circ$} & multicolumn{1}{l|}{I} & multicolumn{1}{l|}{$(+,+)$} & multicolumn{1}{l|}{$theta$} \ hline
multicolumn{1}{|l|}{$90^circ <theta < 180^circ$} & multicolumn{1}{l|}{II} & multicolumn{1}{l|}{$(-,+)$} & multicolumn{1}{l|}{$180^circ-theta$} \ hline
multicolumn{1}{|l|}{$180^circ <theta < 270^circ$} & multicolumn{1}{l|}{III} & multicolumn{1}{l|}{$(-,-)$} & multicolumn{1}{l|}{$theta-180^circ$} \ hline
multicolumn{1}{|l|}{$270^circ < theta <360^circ$} & multicolumn{1}{l|}{IV} & multicolumn{1}{l|}{$(+,-)$} & multicolumn{1}{l|}{$360^circ-theta$} \ hline
& & & \ cline{1-3}
multicolumn{1}{|l|}{begin{tabular}[c]{@{}l@{}}reference acute angleend{tabular}} & multicolumn{1}{l|}{$cos alpha$} & multicolumn{1}{l|}{$sin alpha$} & \ cline{1-3}
multicolumn{1}{|l|}{30$^circ$} & multicolumn{1}{l|}{$dfrac{sqrt{3}}{2}$} & multicolumn{1}{l|}{$dfrac{1}{2}$} & \ cline{1-3}
multicolumn{1}{|l|}{45$^circ$} & multicolumn{1}{l|}{$dfrac{sqrt{2}}{2}$} & multicolumn{1}{l|}{$dfrac{sqrt{2}}{2}$} & \ cline{1-3}
multicolumn{1}{|l|}{60$^circ$} & multicolumn{1}{l|}{$dfrac{1}{2}$} & multicolumn{1}{l|}{$dfrac{sqrt{3}}{2}$} & \ cline{1-3}
& & &
end{tabular}
end{table}
a) $sin 60^circ =dfrac{sqrt{3}}{2}$
b) $cos 30^circ = dfrac{sqrt{3}}{2}$
c) $tan 45^circ = dfrac{sin 45^circ}{cos 45^circ}=dfrac{sqrt{2}/2}{sqrt{2}/2}=1$
d $cos 45^circ = dfrac{sqrt{2}}{2}$
b) $dfrac{sqrt{3}}{2}$
c) $1$
d) $dfrac{sqrt{2}}{2}$
begin{table}[]
defarraystretch{2.4}%
begin{tabular}{llll}
hline
multicolumn{1}{|l|}{begin{tabular}[c]{@{}l@{}}principal angle $theta$end{tabular}} & multicolumn{1}{l|}{Quadrant} & multicolumn{1}{l|}{begin{tabular}[c]{@{}l@{}}sign\ $(cos theta, sin theta)$end{tabular}} & multicolumn{1}{l|}{begin{tabular}[c]{@{}l@{}}reference acute angle $alpha$end{tabular}} \ hline
multicolumn{1}{|l|}{$0leq theta<90^circ$} & multicolumn{1}{l|}{I} & multicolumn{1}{l|}{$(+,+)$} & multicolumn{1}{l|}{$theta$} \ hline
multicolumn{1}{|l|}{$90^circ <theta < 180^circ$} & multicolumn{1}{l|}{II} & multicolumn{1}{l|}{$(-,+)$} & multicolumn{1}{l|}{$180^circ-theta$} \ hline
multicolumn{1}{|l|}{$180^circ <theta < 270^circ$} & multicolumn{1}{l|}{III} & multicolumn{1}{l|}{$(-,-)$} & multicolumn{1}{l|}{$theta-180^circ$} \ hline
multicolumn{1}{|l|}{$270^circ < theta <360^circ$} & multicolumn{1}{l|}{IV} & multicolumn{1}{l|}{$(+,-)$} & multicolumn{1}{l|}{$360^circ-theta$} \ hline
& & & \ cline{1-3}
multicolumn{1}{|l|}{begin{tabular}[c]{@{}l@{}}reference acute angleend{tabular}} & multicolumn{1}{l|}{$cos alpha$} & multicolumn{1}{l|}{$sin alpha$} & \ cline{1-3}
multicolumn{1}{|l|}{30$^circ$} & multicolumn{1}{l|}{$dfrac{sqrt{3}}{2}$} & multicolumn{1}{l|}{$dfrac{1}{2}$} & \ cline{1-3}
multicolumn{1}{|l|}{45$^circ$} & multicolumn{1}{l|}{$dfrac{sqrt{2}}{2}$} & multicolumn{1}{l|}{$dfrac{sqrt{2}}{2}$} & \ cline{1-3}
multicolumn{1}{|l|}{60$^circ$} & multicolumn{1}{l|}{$dfrac{1}{2}$} & multicolumn{1}{l|}{$dfrac{sqrt{3}}{2}$} & \ cline{1-3}
& & &
end{tabular}
end{table}
Remember that $tan theta = dfrac{sin theta}{cos theta}$
a) $sin 30^circ times tan 60^circ -cos 30^circ=dfrac{1}{2}times dfrac{sqrt{3}/2}{1/2}-dfrac{sqrt{3}}{2}=0$
b) $2cos 45^circ times sin 45^circ=2times dfrac{sqrt{2}}{2}times dfrac{sqrt{2}}{2}=1$
c) $tan^230^circ-cos^245^circ=left(dfrac{1/2}{sqrt{3}/2}right)^2-left(dfrac{sqrt{3}}{2}right)^2=-dfrac{1}{6}$
d) $1-dfrac{sin 45^circ}{cos 45^circ}=1-dfrac{sqrt{2}/2}{sqrt{2}/2}=0$
b) 1
c) $-1/6$
d) 0
begin{table}[]
defarraystretch{2.4}%
begin{tabular}{llll}
hline
multicolumn{1}{|l|}{begin{tabular}[c]{@{}l@{}}principal angle $theta$end{tabular}} & multicolumn{1}{l|}{Quadrant} & multicolumn{1}{l|}{begin{tabular}[c]{@{}l@{}}sign\ $(cos theta, sin theta)$end{tabular}} & multicolumn{1}{l|}{begin{tabular}[c]{@{}l@{}}reference acute angle $alpha$end{tabular}} \ hline
multicolumn{1}{|l|}{$0leq theta<90^circ$} & multicolumn{1}{l|}{I} & multicolumn{1}{l|}{$(+,+)$} & multicolumn{1}{l|}{$theta$} \ hline
multicolumn{1}{|l|}{$90^circ <theta < 180^circ$} & multicolumn{1}{l|}{II} & multicolumn{1}{l|}{$(-,+)$} & multicolumn{1}{l|}{$180^circ-theta$} \ hline
multicolumn{1}{|l|}{$180^circ <theta < 270^circ$} & multicolumn{1}{l|}{III} & multicolumn{1}{l|}{$(-,-)$} & multicolumn{1}{l|}{$theta-180^circ$} \ hline
multicolumn{1}{|l|}{$270^circ < theta <360^circ$} & multicolumn{1}{l|}{IV} & multicolumn{1}{l|}{$(+,-)$} & multicolumn{1}{l|}{$360^circ-theta$} \ hline
& & & \ cline{1-3}
multicolumn{1}{|l|}{begin{tabular}[c]{@{}l@{}}reference acute angleend{tabular}} & multicolumn{1}{l|}{$cos alpha$} & multicolumn{1}{l|}{$sin alpha$} & \ cline{1-3}
multicolumn{1}{|l|}{30$^circ$} & multicolumn{1}{l|}{$dfrac{sqrt{3}}{2}$} & multicolumn{1}{l|}{$dfrac{1}{2}$} & \ cline{1-3}
multicolumn{1}{|l|}{45$^circ$} & multicolumn{1}{l|}{$dfrac{sqrt{2}}{2}$} & multicolumn{1}{l|}{$dfrac{sqrt{2}}{2}$} & \ cline{1-3}
multicolumn{1}{|l|}{60$^circ$} & multicolumn{1}{l|}{$dfrac{1}{2}$} & multicolumn{1}{l|}{$dfrac{sqrt{3}}{2}$} & \ cline{1-3}
& & &
end{tabular}
end{table}
[begin{gathered}
{text{a}}){ ;sin ^2}{30^{text{o}}} + {cos ^2}{30^{text{o}}} = {left( {frac{1}{2}} right)^2} + {left( {frac{{sqrt 3 }}{2}} right)^2} = frac{1}{4} + frac{3}{4} = 1 hfill \
hfill \
{text{b) }}{sin ^2}{45^{text{o}}} + {cos ^2}{45^{text{o}}} = {left( {frac{{sqrt 2 }}{2}} right)^2} + {left( {frac{{sqrt 2 }}{2}} right)^2} = frac{2}{4} + frac{2}{4} = 1 hfill \
hfill \
{text{c) si}}{{text{n}}^2}{60^{text{o}}} + {cos ^2}{60^{text{o}}} = {left( {frac{{sqrt 3 }}{2}} right)^2} + {left( {frac{1}{2}} right)^2} = frac{3}{4} + frac{1}{4} = 1 hfill \
end{gathered} ]
a) $sin 30^circ = dfrac{text{opposite side}}{text{hypotenuse}}=dfrac{1/2}{1}=dfrac{1}{2}$
$cos 30^circ =dfrac{text{adjacent side}}{text{hypotenuse}}=dfrac{sqrt{3}/2}{1}=dfrac{sqrt{3}}{2}$
$tan 30^circ = dfrac{text{opposite side}}{text{adjacent side}}=dfrac{1/2}{sqrt{3}/2}=dfrac{1}{sqrt{3}}$
$dfrac{sin 30^circ}{cos 30^circ}=dfrac{1/2}{sqrt{3}/2}=dfrac{1}{sqrt{3}}$
$therefore dfrac{sin theta}{cos theta}=tan theta$
b) $sin 45^circ = dfrac{text{opposite side}}{text{hypotenuse}}=dfrac{sqrt{2}/2}{1}=dfrac{sqrt{2}}{2}$
$cos 45^circ =dfrac{text{adjacent side}}{text{hypotenuse}}=dfrac{sqrt{2}/2}{1}=dfrac{sqrt{2}}{2}$
$tan45^circ = dfrac{text{opposite side}}{text{adjacent side}}=dfrac{1}{1}=1$
$dfrac{sin 45^circ}{cos 45^circ}=dfrac{sqrt{2}/2}{sqrt{3}/2}=1$
$$
therefore dfrac{sin theta}{cos theta}=tan theta
$$
c) $sin 60^circ = dfrac{text{opposite side}}{text{hypotenuse}}=dfrac{sqrt{3}/2}{1}=dfrac{sqrt{3}}{2}$
$cos 60^circ =dfrac{text{adjacent side}}{text{hypotenuse}}=dfrac{1/2}{1}=dfrac{1}{2}$
$tan60^circ = dfrac{text{opposite side}}{text{adjacent side}}=dfrac{sqrt{3}/2}{1/2}=sqrt{3}$
$dfrac{sin 45^circ}{cos 45^circ}=dfrac{sqrt{3}/2}{1/2}=sqrt{3}$
$$
therefore dfrac{sin theta}{cos theta}=tan theta
$$
a) $sin theta = dfrac{text{opposite side}}{text{hypotenuse}}=dfrac{sqrt{3}/2}{1}implies theta = 60^circ$
$tan theta = dfrac{1}{sqrt{3}}=dfrac{text{opposite side}}{text{adjacent side}}=dfrac{1/2}{sqrt{3}/2}$
This happens when
$$
theta = 30^circ
$$
$cos theta = dfrac{2}{2sqrt{2}}$
$cos theta = dfrac{1}{sqrt{2}}$
$cos theta = dfrac{sqrt{2}}{2}$
This happens when $theta =45^circ$
$cos theta = dfrac{sqrt{3}/2}{1}=dfrac{text{adjacent side}}{text{hypotenuse}}$
This happens when $theta=30^circ$
b) $theta=30^circ$
c) $theta =45^circ$
d) $theta=30^circ$
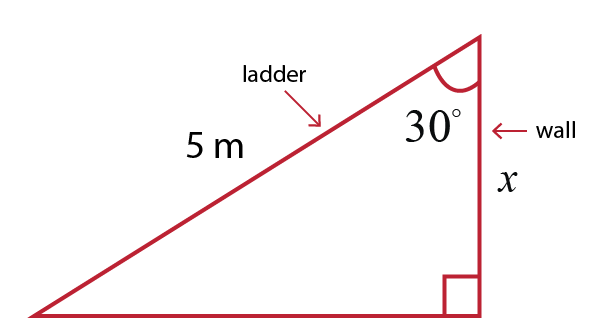
$cos theta = dfrac{text{adjacent side}}{text{hypotenuse}}$
$cos 30^circ = dfrac{x}{5}$
$x=5cos 30=5cdot dfrac{sqrt{3}}{2}=dfrac{5sqrt{3}}{2}$ m
Here, we assumed that the floor is flat (not inclined) and the wall is vertically straight up so that the wall is perpendicular to the floor.
$tan 30^circ = dfrac{text{opposite side}}{text{adjacent side}}=dfrac{1/2}{sqrt{3}/2}=dfrac{1}{sqrt{3}}$
$dfrac{1}{tan 30^circ}=dfrac{1}{1/sqrt{3}}=sqrt{3}$
$sin 30^circ =dfrac{text{opposite side}}{text{hypotenuse}}=dfrac{1/2}{1}$
$cos 30^circ=dfrac{text{adjacent side}}{text{hypotenuse}}=dfrac{sqrt{3}/2}{1}$
Therefore,
$tan 30^circ +dfrac{1}{tan 30^circ}=dfrac{1}{sqrt{3}}+sqrt{3}=dfrac{1+3}{sqrt{3}}=dfrac{4}{sqrt{3}}$
$dfrac{1}{sin 30^circ cdot cos 30^circ}=dfrac{1}{1/2cdot sqrt{3}/2}=dfrac{4}{sqrt{3}}$
$$
implies tan 30^circ+dfrac{1}{tan 30^circ}=dfrac{1}{sin 30^circ cos 30^circ}=dfrac{4}{sqrt{3}}
$$
tan 30^circ+dfrac{1}{tan 30^circ}=dfrac{1}{sin 30^circ cos 30^circ}=dfrac{4}{sqrt{3}}
$$
$x^2=sqrt{27.4^2+27.4^2}=38.75$ m
Therefore, the distance from the home to the second base is $38.75$ m
{text{Refer to the figure in your textbook}}{text{.}} hfill \
hfill \
{text{The area of a triangle is}} hfill \
A = frac{1}{2} cdot left( {{text{base}}} right) cdot left( {{text{altitude}}} right) hfill \
hfill \
{text{The altitude must be perpendicular to the base}}{text{.}} hfill \
hfill \
{text{a) Given that}} hfill \
tan alpha = 1 hfill \
{text{base}} = AC = AB + BC hfill \
{text{height = }}BD = 6 hfill \
hfill \
{text{We shall calculate }}AB{text{ }} hfill \
tan alpha = frac{{{text{opposite side}}}}{{{text{adjacent side}}}} = frac{6}{{AB}} hfill \
AB = frac{6}{{tan alpha }} = frac{6}{1} = 6 hfill \
hfill \
{text{Then calculate }}BC hfill \
hfill \
tan {60^{text{o}}} = frac{{BC}}{{BD}} hfill \
hfill \
BC = 6tan {60^{text{o}}} = 6 cdot frac{{sin {{60}^{text{o}}}}}{{cos {{60}^{text{o}}}}} = left( {frac{{sqrt 3 /2}}{{1/2}}} right) hfill \
BC = 6sqrt 3 hfill \
hfill \
{text{Therefore, }} hfill \
AC = AB + BD = 6 + 6sqrt 3 hfill \
hfill \
{text{Area}} = frac{1}{2}left( {AC} right)left( {BD} right) = frac{1}{2}left( {6 + sqrt 3 } right)left( 6 right) hfill \
{text{Area}} = 3left( {6 + sqrt 3 } right) = 18 + 3sqrt 3 hfill \
hfill \
hfill \
end{gathered} ]
{text{b) Given that}} hfill \
cos beta = frac{{sqrt 3 }}{2} Rightarrow beta = {30^{text{o}}} hfill \
{text{base}} = SQ = SR + RQ hfill \
{text{height = }}PR hfill \
hfill \
{text{We shall calculate }}SR hfill \
sin beta = frac{{{text{opposite side}}}}{{{text{hypotenuse}}}} = frac{{SR}}{{PS}} hfill \
sin {30^{text{o}}} = frac{{SR}}{{13}} Rightarrow SR = 13sin {30^{text{o}}} hfill \
SR = 13left( {frac{1}{2}} right) = frac{{13}}{2} hfill \
hfill \
{text{Then we shall calculate PR}} hfill \
{text{cos}}beta = frac{{{text{adjacent side}}}}{{{text{hypotenuse}}}} hfill \
cos beta = frac{{PR}}{{13}} hfill \
PR = 13left( {frac{{sqrt 3 }}{2}} right) = frac{{13sqrt 3 }}{2} hfill \
{text{Notice that since }}angle Q = {45^{text{o}}}{text{ so the}} hfill \
{text{its corresponding legs are equal, thus}} hfill \
QR = PR = frac{{13sqrt 3 }}{2} hfill \
{text{So now we have}} hfill \
{text{base}} = SR + QR = frac{{13}}{2} + frac{{13sqrt 3 }}{2} = frac{{13}}{2}left( {1 + sqrt 3 } right) hfill \
{text{height = }}PR = frac{{13sqrt 3 }}{2} hfill \
hfill \
{text{Area = }}frac{1}{2}left( {{text{base}}} right)left( {{text{height}}} right) hfill \
{text{Area}} = frac{1}{2}left[ {frac{{13}}{2}left( {1 + sqrt 3 } right)} right] times frac{{13sqrt 3 }}{2} hfill \
{text{Area}} = frac{{168sqrt 3 }}{8}left( {1 + sqrt 3 } right) hfill \
end{gathered} ]
b) $dfrac{168sqrt{3}}{8}(1+sqrt{3})$
a) $2.595$
$sin 45^circ=dfrac{text{opposite side}}{text{hypotenuse}}=dfrac{1}{sqrt{2}}$
$cos 30^circ = dfrac{text{adjacent side}}{text{hypotenuse}}=dfrac{sqrt{3}/2}{1}=dfrac{sqrt{3}}{2}$
$tan 60^circ = dfrac{text{opposite side}}{text{adjacent side}}=dfrac{sqrt{3}/2}{1/2}=sqrt{3}$
$sin 60^circ =dfrac{text{opposite side}}{text{hypotenuse}}=dfrac{sqrt{3}/2}{1}=dfrac{sqrt{3}}{2}$
$$
tan 30^circ = dfrac{text{opposite side}}{text{adjacent side}}=dfrac{1/2}{sqrt{3}/2}=dfrac{1}{sqrt{3}}
$$
sin {45^{text{o}}}left( {1 – cos {{30}^{text{o}}}} right) + 5tan {60^{text{o}}}left( {sin {{60}^{text{o}}} – tan {{30}^{text{o}}}} right) hfill \
= frac{{sqrt 2 }}{2}left( {1 – frac{{sqrt 3 }}{2}} right) + 5left( {sqrt 3 } right)left( {frac{{sqrt 3 }}{2} – frac{{sqrt 3 }}{3}} right) hfill \
= frac{{sqrt 2 }}{2} – frac{{sqrt 6 }}{4} + 5left( {frac{3}{2} – frac{3}{3}} right) hfill \
= frac{{sqrt 2 }}{2} – frac{{sqrt 6 }}{4} + 5left( {frac{1}{2}} right) hfill \
= frac{{sqrt 2 }}{2} – frac{{sqrt 6 }}{4} + frac{5}{2} hfill \
end{gathered} ]
b) $dfrac{sqrt{2}}{2}-dfrac{sqrt{6}}{4}+dfrac{5}{2}$
c) calculator answer is just an approximation
{text{cot}},alpha = sqrt 3 hfill \
Rightarrow tan alpha = frac{1}{{sqrt 3 }} = alpha = {tan ^{ – 1}}left( {frac{1}{{sqrt 3 }}} right) hfill \
alpha = {30^{text{o}}} hfill \
{text{From the special triangles,}} hfill \
{text{}} hfill \
sin {30^{text{o}}} = frac{1}{2} hfill \
cos 3{0^{text{o}}} = frac{{sqrt 3 }}{2} hfill \
hfill \
left( {sin alpha } right)left( {cot alpha } right) – {cos ^2}alpha hfill \
= left( {frac{1}{2}} right)left( {sqrt 3 } right) – {left( {frac{{sqrt 3 }}{2}} right)^2} hfill \
= frac{{sqrt 3 }}{2} – frac{3}{4} hfill \
hfill \
end{gathered} ]
dfrac{sqrt{3}}{2}-dfrac{3}{4}
$$

