Home Page Textbooks Nelson Functions 11 Section 5-1: Trigonometric Ratios of Acute Angles

Nelson Functions 11

1st Edition

Chris Kirkpatrick, Marian Small

ISBN: 9780176332037

Textbook solutions

All Solutions

Section 5-1: Trigonometric Ratios of Acute Angles

Exercise 1

Step 1

1 of 3

Remember the following:

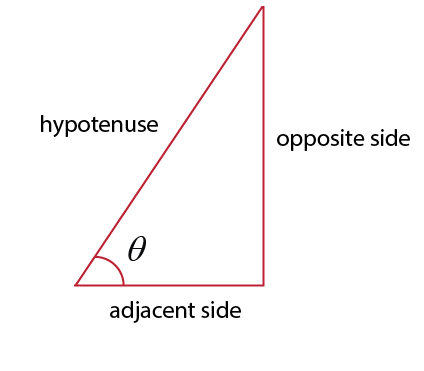
$sin theta = dfrac{text{opposite side}}{text{hypotenuse}}$

$cos theta = dfrac{text{adjacent side}}{text{hypotenuse}}$

$tan theta = dfrac{text{opposite side}}{text{adjacent side}}$

$$
color{white} ddd
$$

Exercise scan

Step 2

2 of 3

Refer to $angle A$

opposite side = 5

adjacent side = 12

hypotenuse = 13

$sin theta = dfrac{5}{13}$

$cos theta = dfrac{12}{13}$

$tan theta = dfrac{5}{12}$

$csc theta =dfrac{1}{sin theta}=dfrac{13}{5}$

$sectheta=dfrac{1}{costheta}=dfrac{13}{12}$

$cot theta=dfrac{1}{tan theta}=dfrac{12}{5}$

Result

3 of 3

[begin{gathered}
{text{sin }}theta = frac{5}{{13}}{text{ ; csc }}theta = frac{{13}}{5} hfill \
cos theta = frac{{12}}{{13}}{text{ ; sec }}theta = frac{{13}}{{12}} hfill \
tan theta = frac{5}{{12}}{text{ ; cot }}theta = frac{{12}}{5} hfill \
end{gathered} ]

Exercise 2

Step 1

1 of 2

Remember the reciprocal identities:

$csc theta=dfrac{1}{sintheta}$

$sectheta=dfrac{1}{costheta}$

$cottheta=dfrac{1}{tan theta}$

Therefore,

$sintheta=dfrac{8}{17}implies csctheta=dfrac{17}{8}$

$costheta=dfrac{15}{17}impliessectheta=dfrac{17}{15}$

$tantheta=dfrac{8}{15}implies cottheta= dfrac{15}{8}$

Result

2 of 2

$csctheta=dfrac{17}{8}$

$sectheta=dfrac{17}{15}$

$cottheta=dfrac{15}{8}$

Exercise 3

Step 1

1 of 3

Remember the reciprocal identities:

$csc theta=dfrac{1}{sintheta}$

$sectheta=dfrac{1}{costheta}$

$cottheta=dfrac{1}{tan theta}$

Step 2

2 of 3

Use the reciprocal identities above to find the corresponding reciprocal ratio.

a) $sin theta=dfrac{1}{2}implies csctheta=dfrac{1}{frac{1}{2}}=2$

b) $costheta=dfrac{3}{4}implies sectheta=dfrac{1}{frac{3}{4}}=dfrac{4}{3}$

c) $tantheta=dfrac{3}{2}implies cottheta=dfrac{1}{frac{3}{2}}=dfrac{2}{3}$

d) $tantheta=dfrac{1}{4}implies cottheta=dfrac{1}{frac{1}{4}}=4$

Result

3 of 3

a) $csctheta=2$

b) $sectheta=dfrac{4}{3}$

c) $cottheta=dfrac{2}{3}$

d) $cottheta=4$

Exercise 4

Step 1

1 of 3

Using our calculator, we shall evaluate the given trigonometric expression to the nearest hundredth (2 digits after decimal point). Be sure to set your calculator to DEGREE mode.

Step 2

2 of 3

a) $cos 34^circapprox 0.83$

b) $sec10^circapproxdfrac{1}{cos 10^circ}=1.02$

c) $cot75^circapproxdfrac{1}{tan 75^circ}=0.27$

d) $csc45^circapproxdfrac{1}{sin 45^circ}=1.41$

Result

3 of 3

a) $0.83$

b) $1.02$

c) $0.27$

d) $1.41$

Exercise 5

Step 1

1 of 5

Refer to the triangles given in your textbook.

i)
opposite side = 6

adjacent side = 8

hypotenuse = 10

$csc theta =dfrac{text{hypotenuse}}{text{opposite side}}=dfrac{10}{6}=dfrac{5}{3}$

$sec theta=dfrac{text{hypotenuse}}{text{adjacent side}}=dfrac{10}{8}=dfrac{5}{4}$

$cot theta =dfrac{text{adjacent side}}{text{opposite side}}=dfrac{8}{6}=dfrac{4}{3}$

$tan theta =dfrac{text{opposite side}}{text{adjacent side}}$

$$
theta = tan^{-1}left(dfrac{6}{8}right)=36.87^circ approx 36^circ
$$

Step 2

2 of 5

ii)
opposite side = 8.5

adjacent side = 8.5

hypotenuse = 12

$csc theta =dfrac{text{hypotenuse}}{text{opposite side}}=dfrac{12}{8.5}=dfrac{24}{17}$

$sec theta=dfrac{text{hypotenuse}}{text{adjacent side}}=dfrac{12}{8.5}=dfrac{24}{17}$

$cot theta =dfrac{text{adjacent side}}{text{opposite side}}=dfrac{8.5}{8.5}=1$

$tan theta =dfrac{text{opposite side}}{text{adjacent side}}$

$$
theta = tan^{-1}left(dfrac{8.5}{8.5}right)=45^circ
$$

Step 3

3 of 5

iii)
opposite side = 3

adjacent side =2

hypotenuse = 3.6

$csc theta =dfrac{text{hypotenuse}}{text{opposite side}}=dfrac{3.6}{3}=dfrac{6}{5}$

$sec theta=dfrac{text{hypotenuse}}{text{adjacent side}}=dfrac{3.6}{2}=dfrac{9}{5}$

$cot theta =dfrac{text{adjacent side}}{text{opposite side}}=dfrac{2}{3}$

$tan theta =dfrac{text{opposite side}}{text{adjacent side}}$

$$
theta = tan^{-1}left(dfrac{3}{2}right )= 56.31^circ approx 56^circ
$$

Step 4

4 of 5

iv)
opposite side = 8

adjacent side =15

hypotenuse = 17

$csc theta =dfrac{text{hypotenuse}}{text{opposite side}}=dfrac{17}{8}$

$sec theta=dfrac{text{hypotenuse}}{text{adjacent side}}=dfrac{17}{15}=dfrac{9}{5}$

$cot theta =dfrac{text{adjacent side}}{text{opposite side}}=dfrac{15}{8}$

$tan theta =dfrac{text{opposite side}}{text{adjacent side}}$

$$
theta = tan^{-1}left(dfrac{8}{15}right)=28.07^circ approx 28^circ
$$

Result

5 of 5

See answers inside.

Exercise 6

Step 1

1 of 5

Use your calculator to evaluate $theta$

a) $cot theta=3.2404implies tan theta = dfrac{1}{3.2404}$

$$
theta = tan^{-1}left(dfrac{1}{3.2404}right)approx 17.15^circ
$$

Step 2

2 of 5

b) $csc theta=1.2711implies sin theta = dfrac{1}{1.2711}$

$$
theta = sin^{-1}left(dfrac{1}{1.2711}right)approx 38.19^circ
$$

Step 3

3 of 5

c) $sec theta=1.4526implies cos theta = dfrac{1}{1.4526}$

$$
theta = cos^{-1}left(dfrac{1}{1.4526}right)approx 34.54^circ
$$

Step 4

4 of 5

d) $cot theta=0.5814implies tan theta = dfrac{1}{0.5814}$

$$
theta = tan^{-1}left(dfrac{1}{0.5814}right)approx 59.83^circ
$$

Result

5 of 5

a) $17^circ$

b) $38^circ$

c) $35^circ$

d) $60^circ$

Exercise 7

Step 1

1 of 3

Remember the following trigonometric ratios:

$sintheta=dfrac{text{opposite side}}{text{hypotenuse}}$

$costheta=dfrac{text{adjacent side}}{text{hypotenuse}}$

$tantheta=dfrac{text{opposite side}}{text{adjacent side}}$

Exercise scan

Step 2

2 of 3

We need to express our answers to the nearest tenth (1 digit after decimal point).

a) We are given the opposite side and we want to find the hypotenuse, so we shall use sine.

$sin 35^circ=dfrac{3.0}{h}implies h=dfrac{3.0}{sin 35^circ}approx 5.2$ m

b) We are given the adjacent side and we want to find the hypotenuse, so we shall use cosine.

$cos 39^circ=dfrac{5.0}{h}implies h=dfrac{5.0}{cos 39^circ}approx 6.4$ m

Result

3 of 3

a) $5.2$ m

b) $6.4$ m

Exercise 8

Step 1

1 of 3

a) We need to use two different methods to solve for $x$.

Method 1: Pythagorean equation

$x=sqrt{1^2+0.7^2}approx 1.22$ cm

Method 2: Use cosine function

$cos 35^circ=dfrac{1}{x}implies x=dfrac{1}{cos 35^circ}approx 1.22$ cm

Step 2

2 of 3

b) We need to use two different methods to solve for $x$.

Method 1: Pythagorean equation

$x=sqrt{8.8^2-3.6^2}approx 8.0$ km

Method 2: Use cosine function

$cos 24^circ=dfrac{x}{8.8}implies x=8.8cos 24^circapprox 8.0$ km

Result

3 of 3

a) $x=1.22$ cm

b) $x=8.0$ km

Exercise 9

Step 1

1 of 3

a) $csc theta = dfrac{text{hypotenuse}}{text{opposite side}}$

From the Pythagorean equation $c^2=a^2+b^2implies c=sqrt{a^2+b^2}$

Since the hypotenuse $c$ is always greater than either of the legs $a$ or $b$,

$csc theta geq 1$ for any acute angle $theta$

Step 2

2 of 3

b) $cos theta = dfrac{text{adjacent side}}{text{hypotenuse}}$

From the Pythagorean equation $c^2=a^2+b^2implies c=sqrt{a^2+b^2}$

Since the hypotenuse $c$ is always greater than either of the legs $a$ or $b$,

$cos theta leq 1$ for any acute angle $theta$

Result

3 of 3

See explanation inside.

Exercise 10

Step 1

1 of 3

Remember that

$tan theta = dfrac{1}{cot theta}$

$tan theta = dfrac{text{opposite side}}{text{adjacent side}}$

So if $tan theta = cot theta$

$dfrac{text{opposite side}}{text{adjacent side}}=dfrac{text{adjacent side}}{text{opposite side}}$

$(text{opposite;side})^2=(text{adjacent side})^2$

$sqrt{(text{opposite;side})^2}=sqrt{(text{adjacent side})^2}$

opposite side = adjacent side

Step 2

2 of 3

If the opposite side and adjacent side is equal, the triangle must be isosceles right triangle. Exercise scan

Result

3 of 3

isosceles right triangle

Exercise 11

Step 1

1 of 4

Sketch the triangle as follows. Exercise scan

Step 2

2 of 4

a) From the sketch, we see that one angle and opposite side are given and we need to find the length of the string which is the hypotenuse. Thus, we shall use sine function.

$sin theta =dfrac{text{opposite side}}{text{hypotenuse}}$

$sin 41^circ = dfrac{8.6}{x}$

$x=dfrac{8.6}{sin 41^circ}approx 13.11$ m

Step 3

3 of 4

b) Here we need to use a reciprocal trigonometric ratio. We shall use $cosecant$ as it is the reciprocal of sine.

$csc theta = dfrac{text{hypotenuse}}{text{opposite side}}$

$csc 41^circ = dfrac{x}{8.6}$

$x=8.6 csc 41^circ approx13.11$ m

Result

4 of 4

a) $x=dfrac{8.6}{sin 41^circ}approx13.11$ m

b) $x=8.6csc 41^circapprox 13.11$ m

Exercise 12

Step 1

1 of 3

Sketch the problem as follows. Exercise scan

Step 2

2 of 3

From the figure,

adjacent side = $7.1$ m

$theta = 15^circ$

The length of the ramp is the hypotenuse, which is what we need to find.

Since adjacent side and hypotenuse are involved, we shall use cosine.

$cos theta =dfrac{text{adjacent side}}{text{hypotenuse}}$

$cos 15^circ = dfrac{7.1}{x}$

$x=dfrac{7.1}{cos 15^circ}approx 7.35$

The length of the ramp is $7.35$ m

Result

3 of 3

$7.35$ m

Exercise 13

Step 1

1 of 7

The area of the right triangle is $A=dfrac{1}{2}times text{base}times text{height}$

In this case,

$A=dfrac{1}{2}bcdot a$

We shall calculate the area for each case.

Exercise scan

Step 2

2 of 7

a) $sec A=dfrac{text{hypotenuse}}{text{adjacent side}}=dfrac{7}{b}=1.7105implies b=4.09$

Use Pythagorean equation to calculate $a$

$a=sqrt{7^2-4.09^2}approx 5.68$

Area = $dfrac{1}{2}(4.09)(5.68)=11.62$

Step 3

3 of 7

b) $cos A=dfrac{text{adjacent side}}{text{hypotenuse}}=dfrac{b}{7}=0.7512 implies b=5.26$

Use Pythagorean equation to calculate $a$

$a=sqrt{7^2-5.26^2}approx 4.62$

Area = $dfrac{1}{2}(5.26)(4.62)=12.15$

Step 4

4 of 7

c) $csc A=dfrac{text{hypotenuse}}{text{opposite side}}=dfrac{7}{a}=2.2703implies a=3.08$

Use Pythagorean equation to calculate $b$

$b=sqrt{7^2-3.08^2}approx 6.29$

Area = $dfrac{1}{2}(6.29)(3.08)=9.69$

Step 5

5 of 7

d) $sin A=dfrac{text{opposite side}}{text{hypotenuse}}=dfrac{a}{7}=0.1515implies a=1.06$

Use Pythagorean equation to calculate $b$

$b=sqrt{7^2-1.06^2}approx 6.92$

Area = $dfrac{1}{2}(1.06)(6.92)=3.67$

Step 6

6 of 7

The highest area is option (b) where $cos A=0.7512$

Result

7 of 7

b) $cos A=0.7512$

Exercise 14

Step 1

1 of 3

The length of the wire is the hypotenuse and the horizontal distance of the guy from the TV antenna is the base of the right triangle. Exercise scan

Step 2

2 of 3

From the triangle, the parts involved are opposite side and hypotenuse so we must use sine.

$sin theta = dfrac{text{opposite side}}{text{hypotenuse}}$

$sin 55^circ = dfrac{3.71}{x}$

$x=dfrac{3.71}{sin 55^circ}approx 4.53$

Here, we are assuming that the ground is flat so that the antenna is perpendicular with the ground.

Result

3 of 3

4.53 m

Exercise 15

Step 1

1 of 3

The situation can be sketched as follows. Exercise scan

Step 2

2 of 3

From the figure, the opposite side of $25^circ$ is the difference between the height of the pole and Julie’s height.

opposite side = $5.35-1.55=3.8$ m

The distance of Julie from the pole is the adjacent side $x$

Since we are asked to use a reciprocal trigonometric ratio, we shall use cotangent.

$cot theta = dfrac{text{adjacent side}}{text{opposite side}}$

$cot 25^circ = dfrac{x}{3.8}$

$x=3.8cot 25^circ=3.8times dfrac{1}{tan 25^circ}approx boxed{8.15 text{ m}}$

Therefore, Julie is 8.15 away from the flag pole.

Result

3 of 3

$8.15$ m

Exercise 16

Step 1

1 of 4

A slope grade of $12%$ means that for every 100 m distance, there is a change of elevation of 12 m.

Exercise scan

Step 2

2 of 4

a) A rough estimate of the angle $theta$ is $approx 10^circ$

b) Since the opposite side and the adjacent side are involved, we shall use tangent.

$tan theta = dfrac{text{opposite side}}{text{adjacent side}}$

$tan theta = dfrac{12}{100}$

$$
theta=tan^{-1}left(dfrac{12}{100}right)approx 7^circ
$$

Step 3

3 of 4

c) We can obtain the hypotenuse using the Pythagorean equation $c^2=a^2+b^2$

hypotenuse = $c=sqrt{12^2+100^2}=100.72$

$sin theta = dfrac{text{opposite side}}{text{hypotenuse}}=dfrac{12}{100.72}approx 0.12$

$cos theta = dfrac{text{adjacent side}}{text{hypotenuse}}=dfrac{100}{100.72}approx 0.99$

$tan theta = dfrac{12}{100}$

$csc theta = dfrac{1}{sin theta}=dfrac{1}{0.12}=8.33$

$sec theta =dfrac{1}{cos theta}=dfrac{1}{0.99}=1.01$

$$
cot theta = dfrac{1}{tan theta}=dfrac{1}{0.12}=8.33
$$

Result

4 of 4

a) $10^circ$

b) $7^circ$

c) $sin theta=0.12$ ; $csc theta=8.33$

$cos theta = 0.99$ ; $sec theta=1.01$

$tan theta=0.12$ ; $cot theta=8.33$

Exercise 17

Step 1

1 of 2

Result

2 of 2

See example of the flowchart inside.

Exercise 18

Step 1

1 of 3

The triangle can be sketched as follows. Exercise scan

Step 2

2 of 3

Given that $tan angle P=0.51$, we can solve $angle P$ as

$angle P = tan^{-1}(0.51)=27^circ$

We can obtain $p$ and $q$ using sine and cosine respectively,

$sin angle P =dfrac{text{opposite side}}{text{hypotenuse}}$

$sin 27 = dfrac{p}{117}implies p=117 sin 27 approx 53$ cm

$cos angle P =dfrac{text{adjacent side}}{text{hypotenuse}}$

$cos 27 =dfrac{q}{117}implies q=117cos 27approx 104$ cm

Since this is right triangle,

$angle R=90^circ$

$angle Q=90-27=63^circ$

Result

3 of 3

$angle P =27^circ$

$p=53$ cm

$q=104$ cm

$angle R=90^circ$

$$
angle Q=63^circ
$$

Exercise 19

Step 1

1 of 2

$sec theta = dfrac{text{hypotenuse}}{text{adjacent side}}$

If the denominator decreases, the value of $sec theta$ increases.

If secant ratio is greater than any other trigonometric ratio, then the adjacent side must be the smaller than the opposite side.

Result

2 of 2

adjacent side $<$ opposite side

Exercise 20

Step 1

1 of 4

A number becomes undefined if the denominator is zero.

$csc theta = dfrac{1}{sin theta}$ is undefined when $sin theta=0implies theta = 0^circ$

Step 2

2 of 4

$sec theta =dfrac{1}{cos theta}$ is undefined when $cos theta=0implies theta =90^circ$

Step 3

3 of 4

$cottheta =dfrac{costheta}{sin theta}$ is undefined when $sin theta=0implies theta=0^circ$

Result

4 of 4

$theta=0^circ$ for cosecant

$theta=90^circ$ for secant

$theta=0^circ$ for cotangent

unlock

All Solutions

Section 5-1: Trigonometric Ratios of Acute Angles

Haven't found what you were looking for?

Search for samples, answers to your questions and flashcards