Part A – To find the inverse simply switch the x and y values. The red dots represent the original values while the blue dots are the inverse.

$$
(x,y)rightarrow (y,x)
$$

Part B – To find the inverse simply switch the x and y values. The red dots represent the original values while the blue dots are the inverse.

$$
(x,y)rightarrow (y,x)
$$

$bold{Concept}$. The inverse of a quadratic equation is obtained by interchanging $x$ and $y$ in vertex form and express $y$ in terms of $x$.

$y=a(x-h)^2+k$

If you replace $y$ with $x$ and $x$ with $y$, this becomes,

$x=a(y-h)^2+k$

$(y-h)^2=dfrac{x-k}{a}$

$y-h=pmsqrt{dfrac{x-k}{a}}$

$y=hpm sqrt{dfrac{x-k}{a}}$

Thus, $y=hpmsqrt{dfrac{x-k}{a}}$ is the inverse of $y=a(x-h)^2+k$

$bold{Solution:}$

We shall find the equation of each quadratic function, find the inverse, and graph the inverse relation.

a) The graph has vertex$(0,0)$ and passes through $(1,1)$

$y=a(x-h)^2+kimplies 1=a(1-0)^2+0implies a=1$

The equation of the parabola is $y=1cdot (x-0)^2+0implies y=x^2$

The inverse relation is $x=y^2implies y=pm sqrt{x}$

b) The graph has a vertex$(h,k)$ at $(-2,3)$ and passes through $(-1,0)$

$y=a(x-h)^2+kimplies 0=a(-1+2)^2+3 implies a=-dfrac{3}{(1)^2}=-3$

The equation is $y=-3(x+2)^2+3$

The inverse relation is obtained as

$x=-3(y+2)^2+3$

$(y+2)^2=dfrac{x-3}{-3}$

$y+2=pmsqrt{dfrac{3-x}{3}}$

$$
y=-2pmsqrt{dfrac{3-x}{3}}
$$

a) $y=pmsqrt{x}$

b) $y=-2pm sqrt{dfrac{3-x}{3}}$

See graph inside.

$bold{Concept}$. The inverse of a quadratic equation is obtained by interchanging $x$ and $y$ in vertex form and express $y$ in terms of $x$.

$y=a(x-h)^2+k$

If you replace $y$ with $x$ and $x$ with $y$, this becomes,

$x=a(y-h)^2+k$

$(y-h)^2=dfrac{x-k}{a}$

$y-h=pmsqrt{dfrac{x-k}{a}}$

$y=hpm sqrt{dfrac{x-k}{a}}$

Thus, $y=hpmsqrt{dfrac{x-k}{a}}$ is the inverse of $y=a(x-h)^2+k$

$bold{Solution:}$

$f(x)=2x^2-1$

$y=2x^2-1$

Replace $y$ with $x$, and replace $x$ with $y$

$x=2y^2-1$

$2y^2=x+1$

$y^2=dfrac{x+1}{2}$

$y=pmsqrt{dfrac{x+1}{2}}$

Therefore, the inverse of $f(x)$ is

$$
f^{-1}(x)=pmsqrt{dfrac{x+1}{2}}
$$

$$
f^{-1}(x)=pmsqrt{dfrac{x+1}{2}}
$$

a) Subtituting $x=3$ in $f(x)=7-2(x-1)^2,$ $xge1,$
results to

$$
begin{align*}
f(3)&=7-2(3-1)^2
\
f(3)&=7-2(2)^2
\
f(3)&=7-2(4)
\
f(3)&=7-8
\
f(3)&=-1
.end{align*}
$$

b) Interchanging the $x$ and $y$ variables and then solving for $y$ in the given function, $f(x)=y=7-2(x-1)^2
,$
results to

$$
begin{align*}
x&=7-2(y-1)^2
\
x-7&=-2(y-1)^2
\
dfrac{x-7}{-2}&=(y-1)^2
\
pmsqrt{dfrac{x-7}{-2}}&=y-1
\
1pmsqrt{dfrac{x-7}{-2}}&=y
\
f^{-1}(x)&=1pmsqrt{dfrac{x-7}{-2}},xge1
.end{align*}
$$

c) Substituting $x=5$ in $f^{-1}(x)=1pmsqrt{dfrac{x-7}{-2}},xge1
,$ results to

$$
begin{align*}
f^{-1}(5)&=1pmsqrt{dfrac{5-7}{-2}}
\
f^{-1}(5)&=1pmsqrt{dfrac{-2}{-2}}
\
f^{-1}(5)&=1pmsqrt{1}
end{align*}
$$

$$
begin{align*}
begin{array}{rcl}
f^{-1}(5)=1+1
& text{ OR } &
f^{-1}(5)=1-1
\
f^{-1}(5)=2
& &
f^{-1}(5)=0
.end{array}
end{align*}
$$

Hence, $f^{-1}(5)=left{ 0,2 right}
.$

d) Substituting $x=2a+7$ in $f^{-1}(x)=1pmsqrt{dfrac{x-7}{-2}},xge1
,$ results to

$$
begin{align*}
f^{-1}(2a+7)&=1pmsqrt{dfrac{2a+7-7}{-2}}
\
f^{-1}(2a+7)&=1pmsqrt{dfrac{2a}{-2}}
\
f^{-1}(2a+7)&=1pmsqrt{-a}
.end{align*}
$$

Since $xge1,$ then

$$
begin{align*}
2a+7&ge1
\
2a&ge1-7
\
2a&ge-6
\
a&ge-dfrac{6}{2}
\
a&ge-3
.end{align*}
$$

Combining the inverse and its restriction, then $f^{-1}(2a+7)=1pmsqrt{-a}, age-3
.$ Since the radicand of an even index should be nonnegative, then the additional restriction, $ale0,$ is needed. Hence, $f^{-1}(2a+7)=1pmsqrt{-a}, -3le ale0
.$

a) $f(3)=-1$

b) $f^{-1}(x)=1pmsqrt{dfrac{x-7}{-2}},xge1$

c) $f^{-1}(5)=left{ 0,2 right}$

d) $f^{-1}(2a+7)=1pmsqrt{-a}, -3le ale0$

$bold{Concept}$. The inverse of a quadratic equation is obtained by interchanging $x$ and $y$ in vertex form and express $y$ in terms of $x$.

$y=a(x-h)^2+k$

If you replace $y$ with $x$ and $x$ with $y$, this becomes,

$x=a(y-h)^2+k$

$(y-h)^2=dfrac{x-k}{a}$

$y-h=pmsqrt{dfrac{x-k}{a}}$

$y=hpm sqrt{dfrac{x-k}{a}}$

Thus, $y=hpmsqrt{dfrac{x-k}{a}}$ is the inverse of $y=a(x-h)^2+k$

$bold{Solution:}$

a) We can sketch the graph of $f(x)=3(x-2)^2-2$ by plotting the vertex $(2,-2)$ (opens upward) with axis of symmetry at $x=2$, and substitute values of $x$ to get another points.

b) Rewrite as $y=3(x-2)^2-2$ and replace $y$ with $x$ and $x$ with $y$

$x=3(y-2)^2-2$

$(y-2)^2=dfrac{x+2}{3}$

$y-2=pmsqrt{dfrac{x+2}{3}}$

$$
y=2pmsqrt{dfrac{x+2}{3}}
$$

$y=2pmsqrt{dfrac{x+2}{3}}$

See graph inside.

a) Using a table of values, the graph of $f(x)=-sqrt{x},xge0
,$ is shown below.

b) Interchanging the $x$ and $y$ coordinates of $g(x),$ the graph of $g^{-1}(x)$ (blue graph) is roughly shown below.

c) The domain is the set of $x$-values that the graph uses, while the range is the set of $y$-values. Based on the graph of $g^{-1}(x)$ above, then

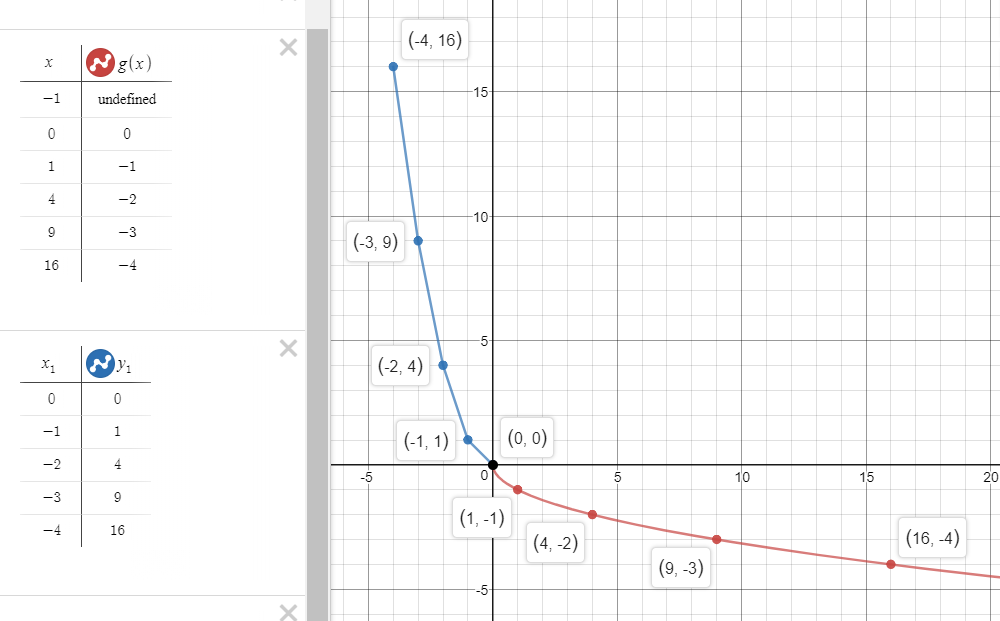
$$
begin{align*}
text{Domain: }&
(-infty,0]
\text{Range: }&
[0,infty)
.end{align*}
$$

d) Replacing $g(x)$ with $y,$ the given function, $g(x)=-sqrt{x},$ is equivalent to $y=-sqrt{x}
.$

Interchanging $x$ and $y$ and then solving for $y,$ then

$$
begin{align*}
x&=-sqrt{y}
\
(x)^2&=(-sqrt{y})^2
\
x^2&=y
\
g^{-1}(x)&=x^2, xle0
.end{align*}
$$

a) see graph

b) see graph

c) Domain: $(-infty,0]$; Range: $[0,infty)$

d) $g^{-1}(x)=x^2, xle0$

$bold{Concept}$. The inverse of a quadratic equation is obtained by interchanging $x$ and $y$ in vertex form and express $y$ in terms of $x$.

$y=a(x-h)^2+k$

If you replace $y$ with $x$ and $x$ with $y$, this becomes,

$x=a(y-h)^2+k$

$(y-h)^2=dfrac{x-k}{a}$

$y-h=pmsqrt{dfrac{x-k}{a}}$

$y=hpm sqrt{dfrac{x-k}{a}}$

Thus, $y=hpmsqrt{dfrac{x-k}{a}}$ is the inverse of $y=a(x-h)^2+k$

$bold{Solution:}$

The graph of $f(x)=-(x+1)^2-3$ has axis of symmetry at $x=-1$, so for $xgeq -1$, we only get the right side from the axis of symmetry.

The inverse is

$x=-(y+1)^2-3implies (y+1)^2=-x-3implies y+1=pm sqrt{-(x+3)}$

$y=-1pmsqrt{-(x+3)}$ for $ygeq -1$

$$
y=-1+sqrt{-(x+3)}
$$

$$
y=-1pmsqrt{-(x-3)}
$$

Using $f(x)=y,$ the given function, $f(x)=dfrac{1}{2}(x-5)^2+3
,$ is equivalent to $y=dfrac{1}{2}(x-5)^2+3
.$

Interchanging $x$ and $y$ and then solving for $y,$ then

$$
begin{align*}
x&=dfrac{1}{2}(y-5)^2+3
\
x-3&=dfrac{1}{2}(y-5)^2
\
2(x-3)&=2cdotdfrac{1}{2}(y-5)^2
\
2(x-3)&=(y-5)^2
\
pmsqrt{2(x-3)}&=y-5
\
5pmsqrt{2(x-3)}&=y
\
f^{-1}(x)&=5pmsqrt{2(x-3)}
.end{align*}
$$

Since $xle5,$ then $f^{-1}(x)=5-sqrt{2(x-3)}
.$

Using a graphing software the graphs of $f(x),xle5$ (red graph) and
$f^{-1}(x)$ (blue graph) are shown below.

$$
f^{-1}(x)=5-sqrt{2(x-3)}
$$

a) In the form $f(x)=a(x-h)^2+k,$ the given function, $f(x)=3x^2-6x
,$ is equivalent to

$$
begin{align*}
f(x)&=3(x^2-2x)
\
f(x)&=3(x^2-2x+1)-3(1)
\
f(x)&=3(x-1)^2-3
.end{align*}
$$

Since $a>0$ ($a=3$) then the graph of the given equation is a parabola that opens up. Its minimum is $-3$ when $x=1$ since the minimum is given by $k$ at $x=h.$

Substituting $x=-2$ and $x=3$ in the given function, $f(x)=3x^2-6x
,$ result to

$$
begin{align*}
x=-2:
\
f(-2)&=3(-2)^2-6(-2)
\
f(-2)&=3(4)-6(-2)
\
f(-2)&=12+12
\
f(-2)&=24
\\
x=3:
\
f(3)&=3(3)^2-6(3)
\
f(3)&=3(9)-6(3)
\
f(3)&=27-18
\
f(3)&=9
.end{align*}
$$

Hence, the highest value of $f(x)$ is $24$ and the lowest value is $-3$ when $-2<x<3.$ Hence,
domain: $(-2,3)$; range: $[-3,24)$.

Substituting $x=1$ and $x=3$ in the given function, $f(x)=3x^2-6x
,$ result to

$$
begin{align*}
x=1:
\
f(1)&=3(1)^2-6(1)
\
f(1)&=3(1)-6(1)
\
f(1)&=3-6
\
f(1)&=-3
\\
x=3:
\
f(3)&=3(3)^2-6(3)
\
f(3)&=3(9)-6(3)
\
f(3)&=27-18
\
f(3)&=9
.end{align*}
$$

Hence, the restrictions for $f^{-1}(x)$ is $-3<x<9.$

Using $f(x)=y,$ the given function, $f(x)=3x^2-6x
,$ is equivalent to

$$
begin{align*}
y=3x^2-6x
.end{align*}
$$

Interchanging the $x$ and $y$ variables and then solving for $y,$ result to

$$
begin{align*}
x&=3y^2-6y
\
x&=3(y^2-2y)
\
x+3(1)&=3(y^2-2y+1)
\
x+3&=3(y-1)^2
\
dfrac{x+3}{3}&=(y-1)^2
\
pmsqrt{dfrac{x+3}{3}}&=y-1
\
1pmsqrt{dfrac{x+3}{3}}&=y
\
f^{-1}(x)&=1pmsqrt{dfrac{x+3}{3}}
.end{align*}
$$

Since $f(x)$ has the restriction, $1<x<3,$ then

$$
begin{align*}
f^{-1}(x)&=1+sqrt{dfrac{x+3}{3}}
text{, }-3<x<9
.end{align*}
$$

a) domain: $(-2,3)$; range: $[-3,24)$

b) $f^{-1}(x)=1+sqrt{dfrac{x+3}{3}}
text{, }-3<x<9$

a) In the form $f(x)=a(x-h)^2+k$ or the Vertex Form of Quadratic Equations, the given function, $h(t)=-5t^2+10t+35
,$ is equivalent to

$$
begin{align*}
h(t)&=(-5t^2+10t)+35
\
h(t)&=-5(t^2-2t)+35
\
h(t)&=-5(t^2-2t+1)+35+5(1)
\
h(t)&=-5(t-1)^2+35+5
\
h(t)&=-5(t-1)^2+40
.end{align*}
$$

b) The value of $t$ in the quadratic equation, $h(t)=-5(t-1)^2+40
,$ can be any real number. Hence its domain is the set of all real numbers. Also, the graph of the given equation is a parabola that opens down. Hence, it has a maximum value. Since the maximum value occurs at $k,$ then the range of the given function is $(-infty,40]
.$

Hence,
domain: all real numbers; range: $-(infty,40]$.

c) Let $h(t)=h.$ Then the given function, $h(t)=-5t^2+10t+35
,$ is equivalent to

$$
begin{align*}
h=-5t^2+10t+35
.end{align*}
$$

Solving for $t$ results to

$$
begin{align*}
h&=(-5t^2+10t)+35
\
h-35&=-5(t^2-2t)
\
h-35-5&=-5(t^2-2t+1)
\
h-40&=-5(t-1)^2
\
dfrac{h-40}{-5}&=(t-1)^2
\
sqrt{dfrac{h-40}{-5}}&=t-1
\
1+sqrt{dfrac{-(h-40)}{5}}&=t
\
t&=1+sqrt{dfrac{-h+40}{5}}
.end{align*}
$$

Hence, the new model, $t(h)=t,$ is $t(h)=1+sqrt{dfrac{-h+40}{5}}
.$

d) The radicand of the new model, $t(h)=1+sqrt{dfrac{-h+40}{5}}
,$ cannot be nonnegative. Hence,

$$
begin{align*}
dfrac{-h+40}{5}&ge0
\\
-h+40&ge0
\\
-h&ge-40
\\
h&le40
text{ (reverse the inequality symbol)}
.end{align*}
$$

Hence, the domain is the set of values of $h$ that are less than or equal to $40.$

Since the lowest value of the radical expression is $0,$ then the lowest value of $t(h)$ is $1.$ This means that the range is greater than or equal to $1.$

Hence,
domain: $(-infty,40];$ range: $[1,infty)$.

a) $h(t)=-5(t-1)^2+40$

b) domain: all real numbers; range: $-(infty,40]$

c) $t(h)=1+sqrt{dfrac{-h+40}{5}}$

d) domain: $(-infty,40];$ range: $[1,infty)$

d) The inverse is a function since using the Vertical Line Test, any vertical line drawn will intersect the graph in at most $1$ point.

a) In the form $f(x)=a(x-h)^2+k$ or the Vertex Form, the given function, $f(x)=-2x^2+3x-1
,$ is equivalent to

$$
begin{align*}
f(x)&=(-2x^2+3x)-1
\&=
-2left( x^2-dfrac{3}{2}x right)-1
\&=
-2left( x^2-dfrac{3}{2}x+dfrac{9}{16} right)-1+2left( dfrac{9}{16} right)
\&=
-2left( x-dfrac{3}{4} right)^2-1+dfrac{9}{8}
\&=
-2left( x-dfrac{3}{4} right)^2-dfrac{8}{8}+dfrac{9}{8}
\&=
-2left( x-dfrac{3}{4} right)^2+dfrac{1}{8}
.end{align*}
$$

Since the vertex is given by $(h,k),$ then the vertex of the given function is $left( dfrac{3}{4},dfrac{1}{8} right)
.$

c) Using $f(x)=y,$ the given function is equivalent to $y=-2x^2+3x-1
.$

Interchanging the $x$ and $y$ variables and then solving for $y,$ then

$$
begin{align*}
x&=-2y^2+3y-1
\
x+1&=-2left(y^2-dfrac{3}{2}y right)
\
x+1-2left(dfrac{9}{16}right)&=-2left(y^2-dfrac{3}{2}y+dfrac{9}{16} right)
\
x+1-dfrac{9}{8}&=-2left(y-dfrac{3}{4} right)^2
\
x-dfrac{1}{8}&=-2left(y-dfrac{3}{4} right)^2
\
dfrac{8x-1}{8}&=-2left(y-dfrac{3}{4} right)^2
\
dfrac{dfrac{8x-1}{8}}{-2}&=left(y-dfrac{3}{4} right)^2
\
dfrac{-8x+1}{16}&=left(y-dfrac{3}{4} right)^2
\
pmsqrt{dfrac{-8x+1}{16}}&=y-dfrac{3}{4}
\
pmdfrac{sqrt{-8x+1}}{4}&=y-dfrac{3}{4}
\
dfrac{3}{4}pmdfrac{sqrt{-8x+1}}{4}&=y
\
y&=dfrac{3pmsqrt{-8x+1}}{4}
.end{align*}
$$

Since it is given that $yge0.75,$ then $f^{-1}(x)=dfrac{3+sqrt{-8x+1}}{4}
.$ The graph of $f^{-1}(x)$ (blue graph) is shown below.

d) With $yge0.75,$ then the domain and range of $f^{-1}(x)=dfrac{9}{4}+sqrt{dfrac{x+1}{-2}}
,$ is
domain: $(-infty,0.125]$; range: $[0.75,infty)$.

e) The values of $x$ were restricted in parts (c) and (d) so that the inverse function will exist. If restrictions were not put, the inverse of $f(x)$ will not be a function.

a) $left( dfrac{3}{4},dfrac{1}{8} right)$

b) see graph

c) $f^{-1}(x)=dfrac{3+sqrt{-8x+1}}{4}$

d) domain: $(-infty,0.125]$; range: $[0.75,infty)$

e) see explanation

a.i) The graph of the given function takes the form $f(x)=a(x-h)^2+k
.$ Since the vertex is at $(4,1),$ then the function takes the form $f(x)=a(x-4)^2+1
.$ Since the graph passes through the point $(3,0),$ then

$$
begin{align*}
f(x)&=a(x-4)^2+1
\
0&=a(3-4)^2+1
\
0&=a(1)+1
\
-1&=a
.end{align*}
$$

Hence, the equation of the given graph is $f(x)=-(x-4)^2+1
.$

a.ii) Reflecting the graph of $f(x)$ (blue graph) about the line $y=x,$ the graph of $f^{-1}(x)$ (red graph) is shown below.

a.iii) The domain of $f(x)$ should be restricted to $xge4$ or $xle4$ so that the inverse is also a function.

a.iv) Using $f(x)=y,$ then the given function, $f(x)=-(x-4)^2+1
,$ is equivalent to $y=-(x-4)^2+1
.$

Interchanging the $x$ and $y$ variables and then solving for $y$ result to

$$
begin{align*}
x&=-(y-4)^2+1
\
x-1&=-(y-4)^2
\
-(x-1)&=(y-4)^2
\
pmsqrt{-x+1}&=y-4
\
4pmsqrt{-x+1}&=y
\
f^{-1}(x)&=4pmsqrt{-x+1}
.end{align*}
$$

Hence, the inverse equations are
$f^{-1}(x)=4+sqrt{-x+1}$ or $f^{-1}(x)=4-sqrt{-x+1}$.

b.i) The graph of the given function takes the form $f(x)=a(x-h)^2+k,xle-3
.$ Since the vertex is at $(1,-3),$ then the function takes the form $f(x)=a(x-1)^2-3
.$ Since the graph passes through the point $(0,-2),$ then

$$
begin{align*}
-2=a(0-1)^2-3
\
-2=a(1)-3
\
-2+3=a(1)
\
1=a
.end{align*}
$$

Hence, the equation of the given graph is $f(x)=(x-1)^2-3
.$

b.ii) Reflecting the graph of $f(x)$ (blue graph) about the line $y=x$ (black graph), the graph of $f^{-1}(x)$ (red graph) is shown below.

The function $f(x)$ should have a restriction of $xge1$ or $xle1$ so that the inverse becomes a function.

b.iv) Using $f(x)=y,$ then the given function, $f(x)=(x-1)^2-3
,$ is equivalent to $y=(x-1)^2-3
.$

Interchanging the $x$ and $y$ variables and then solving for $y$ result to

$$
begin{align*}
x&=(y-1)^2-3
\
x+3&=(y-1)^2
\
pmsqrt{x+3}&=y-1
\
1pmsqrt{x+3}&=y
\
y&=1pmsqrt{x+3}
.end{align*}
$$

Hence, the inverse equations are
$f^{-1}(x)=1-sqrt{x+3}$ or $f^{-1}(x)=1+sqrt{x+3}$.

c.i) The graph of the given function takes the form $f(x)=a(x-h)^2+k,xle-3
.$ Since the vertex is at $(-3,-2),$ then the function takes the form $f(x)=a(x+3)^2-2
.$ Since the graph passes through the point $(-4,-1),$ then

$$
begin{align*}
-1&=a(-4+3)^2-2
\
-1+2&=a(1)
\
1&=a
.end{align*}
$$

Hence, the equation of the given graph is $f(x)=(x+3)^2-2,xle-3
.$

c.ii) Reflecting the graph of $f(x)$ (blue graph) about the line $y=x$ (black graph), the graph of $f^{-1}(x)$ (red graph) is shown below.

c.iii) The domain of $f(x)$ already has the restriction, $xle-3.$ Hence, its inverse is a function.

c.iv) Using $f(x)=y,$ then the given function, $f(x)=(x+3)^2-2,xle-3
,$ is equivalent to $y=(x+3)^2-2,xle-3
.$

Interchanging the $x$ and $y$ variables and then solving for $y$ result to

$$
begin{align*}
x&=(y+3)^2-2
\
x+2&=(y+3)^2
\
pmsqrt{x+2}&=y+3
\
-3pmsqrt{x+2}&=y
.end{align*}
$$

Since $xle-3$ in $f(x),$ then the inverse equation is $f^{-1}(x)=-3-sqrt{x+2}$.

d.i) The graph of the given function takes the form $f(x)=sqrt{-a(x-h)}+k
.$ Since the vertex is at $(2,3),$ then the function takes the form $f(x)=sqrt{-a(x-2)}+3
.$ Since the graph passes through the point $(1,4),$ then

$$
begin{align*}
4=sqrt{-a(1-2)}+3
\
4=sqrt{a}+3
\
4-3=sqrt{a}
\
1=sqrt{a}
\
1=a
.end{align*}
$$

Hence, the equation of the given graph is $f(x)=sqrt{-(x-2)}+3,xle2
.$

d.ii) Reflecting the graph of $f(x)$ (blue graph) about the line $y=x$ (black graph), the graph of $f^{-1}(x)$ (red graph) is shown below.

d.iii) Since $yge3$ in $f(x),$ then $f^{-1}(x)$ has the restriction $xge3$.

d.iv) Using $f(x)=y,$ then the given function, $f(x)=sqrt{-(x-2)}+3,xle2
,$ is equivalent to $y=sqrt{-(x-2)}+3
.$

Interchanging the $x$ and $y$ variables and then solving for $y$ result to

$$
begin{align*}
x&=sqrt{-(y-2)}+3
\
x-3&=sqrt{-y+2}
\
(x-3)^2&=left( sqrt{-y+2} right)^2
\
(x-3)^2&=-y+2
\
(x-3)^2-2&=-y
\
-(x-3)^2+2&=y
\
y&=-(x-3)^2+2
.end{align*}
$$

Since $yge3$ in $f(x),$ then the inverse equation is $f^{-1}(x)=-(x-3)^2+2,xge3$.

a.i) $f(x)=-(x-4)^2+1$;

a.ii) see graph

a.iii) Use $xge4$ or $xle4$ in $f$

a.iv) $f^{-1}(x)=4+sqrt{-x+1}$ or $f^{-1}(x)=4+sqrt{-x+1}$

b.i) $f(x)=(x-1)^2-3$

b.ii) see graph

b.iii) Use $xge1$ or $xle1$ in $f$

b.iv) $f^{-1}(x)=1-sqrt{x+3}$ or $f^{-1}(x)=1+sqrt{x+3}$

c.i) $f(x)=(x+3)^2-2,xle-3$

c.ii) see graph

c.iii) $xle-3$ in $f$

c.iv) $f^{-1}(x)=-3-sqrt{x+2}$

d.i) $f(x)=sqrt{-(x-2)}+3,xle2$

d.ii) see graph

d.iii) $yge3$ in $f$

d.iv) $f^{-1}(x)=-(x-3)^2+2,xge3$

a) To get the inverse, interchange the $x$ and $y$ variables and then solve for $y.$

b) If the domain of the quadratic function is the set of all real numbers, then its graph is a parabola that opens up or down. Reflecting this graph about the line $y=x$ will produce a parabola that opens to the left or right. A parabola that opens to the left or right is not a function since a vertical line drawn anywhere can intersect the parabola opening to the left or right in more than $1$ point. Hence, the inverse cannot be a function.

a) interchange $x$ and $y$ then solve for $y$

b) NO

a) Since profit is the price times number of kilograms less the cost, then the profit, $P(x),$ is

$$
begin{align*}
P(x)&=xcdot m(x)-3.21x
\
P(x)&=x(14700-3040x)-3.21x
\
P(x)&=14700x-3040x^2-3.21x
\
P(x)&=-3040x^2+14696.79x
.end{align*}
$$

Hence, the profit function is $P(x)=-3040x^2+14696.79x
.$

b) Using $P(x)=y,$ the given function, $P(x)=-3040x^2+14696.79x
,$ is equivalent to

$$
begin{align*}
y=-3040x^2+14696.79x
.end{align*}
$$

Interchanging the $x$ and $y$ variables and then solving for $y$ result to

$$
begin{align*}
x&=-3040y^2+14696.79y
\
x-3040(5.83)&=-3040(y^2-4.83y+5.83)
\
x-17723.2&=-3040(y-2.41)^2
\
dfrac{x-17723.2}{-3040}&=(y-2.41)^2
\
pmsqrt{dfrac{17723.2-x}{3040}}&=y-2.41
\
2.41pmsqrt{dfrac{17723.2-x}{3040}}&=y
.end{align*}
$$

Since $y$ is a positive number, then the inverse is $f^{-1}(x)=2.41+sqrt{dfrac{17723.2-x}{3040}}
.$

The inverse gives the amount per kilogram to sell the ground beef for a desired profit, $x.$

c) Substituting $x=1900$ in $f^{-1}(x)=2.41+sqrt{dfrac{17723.2-x}{3040}}
,$ then

$$
begin{align*}
f^{-1}(1900)&=2.41+sqrt{dfrac{17723.2-1900}{3040}}
\\
f^{-1}(1900)&approx2.41+2.28
\\
f^{-1}(1900)&approx4.69
.end{align*}
$$

Hence, the ground beef should sell at
approximately
$$
4.69$/kg
to earn a profit of
$$
1900.$

d) Using $x=-dfrac{b}{2a}$ in $P(x)=-3040x^2+14696.79x
,$ then

$$
begin{align*}
-dfrac{b}{2a}Rightarrow&
-dfrac{14696.79}{2(-3040)}
\\&approx
2.42
.end{align*}
$$

Hence, the price per kilogram that will maximize the profit is $$2.42
.$

e) With the supply cost equal to
$$
3.10$/kg, then the profit function, $P(x),$ is
begin{align*}
P(x)&=xcdot m(x)-3.10x
\
P(x)&=x(14700-3040x)-3.10x
\
P(x)&=14700x-3040x^2-3.10x
\
P(x)&=-3040x^2+14696.9x
.end{align*}

The price, $x,$ is maximize at $x=-dfrac{b}{2a}.$ Hence,
begin{align*}
-dfrac{b}{2a}Rightarrow&
-dfrac{14696.9}{2(-3040)}
\\&approx
2.42
.end{align*}

Hence, the price per kilogram that will maximize the profit is $
$2.42
.$
\

The profit that will be earned is $P(2.42).$ Hence,
begin{align*}
P(2.42)&=-3040(2.42)^2+14696.9(2.42)
\
P(2.42)&=-17803.456+35566.498
\
P(2.42)&=17763.042
\
P(2.42)&approx
17763.04
.end{align*}

The profit is
approximately
$$
17,763.04$.

a) $P(x)=-3040x^2+14696.79x$

b) $f^{-1}(x)=2.41+sqrt{dfrac{17723.2-x}{3040}}$

c) approximately
$$
4.69$/kg
\d)
$$
2.42$\e)$$2.42$/kg; approximately
$$
17,763.04$
$$

a) Using a a table of values, the graph of the given equation, $x=4-4y+y^2
,$ is shown below.

b) The domain is the set of $x$-values used in the graph, while the range is the set of $y$-values. Using the graph of (a), then the
domain is $[0,infty)$ and the range is $(-infty,infty)$.

c) Interchanging the $x$ and $y$ variables and then solving for $y,$ then

$$
begin{align*}
y&=4-4x+x^2
\
y&=x^2-4x+4
\
y&=(x-2)^2
.end{align*}
$$

Hence, the inverse is $f^{-1}(x)=(x-2)^2
.$

d) Reflecting the original graph about the line $y=x$ (black graph), the graph of $f^{-1}(x)$ (blue graph) is shown below. Since a vertical line drawn anywhere on the $xy$-plane will intersect the graph of $f^{-1}(x)$ in at most one point only, then the inverse is a function.

a) see graph

b) domain is $[0,infty)$ and the range is $(-infty,infty)$

c) $f^{-1}(x)=(x-2)^2$

d) YES