
All Solutions
Section 1-6: Exploring Transformations of Parent Functions
Domain= $left{ xin R| xgeq1right}$
Range=$left{ yin R| ygeq0right}$
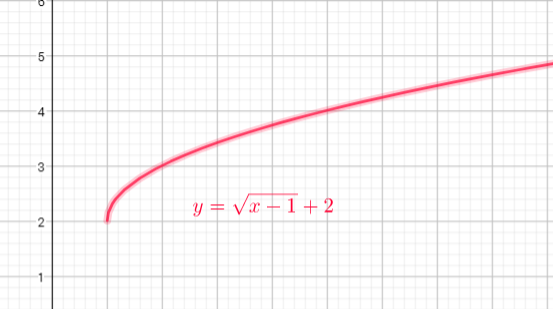
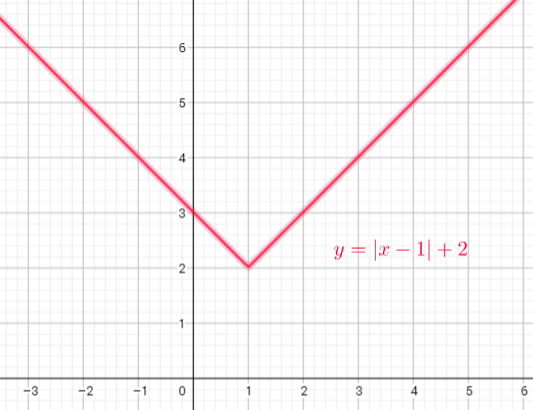
Domain= $left{ xin R right}$
Range=$left{ yin R| ygeq0right}$
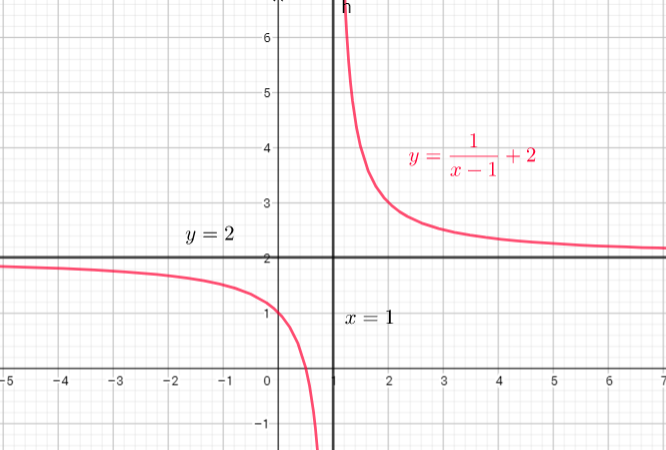
Domain= $left{ xin R| xne1 right}$
Range=$left{ yin R| yne2right}$
b) V-shaped that opens upward with vertex at $(1,2)$
c) Hyperbola with asymptotes at $x=1$ and $y=2$
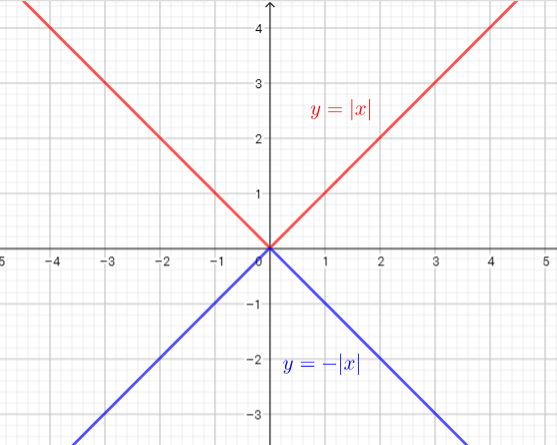
b) The graph of $y=|x|$ opens up and the graph of $y=-|x|$ opens down.
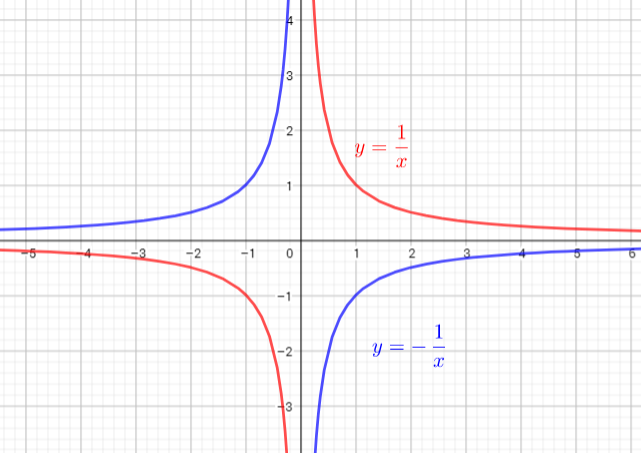
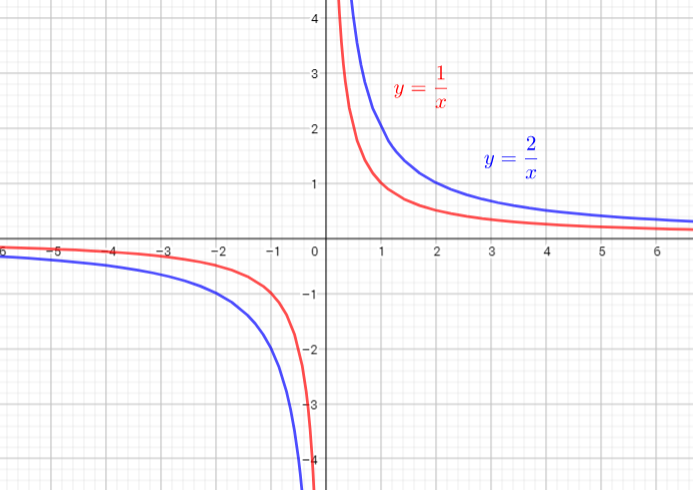
c) The graph of $y=dfrac{1}{x}$ lies to the lower left and upper right of asymptotes $x=0$ and the graph of $y=-dfrac{1}{x}$ lies to the upper left and lower right of asymptotes $x=0$
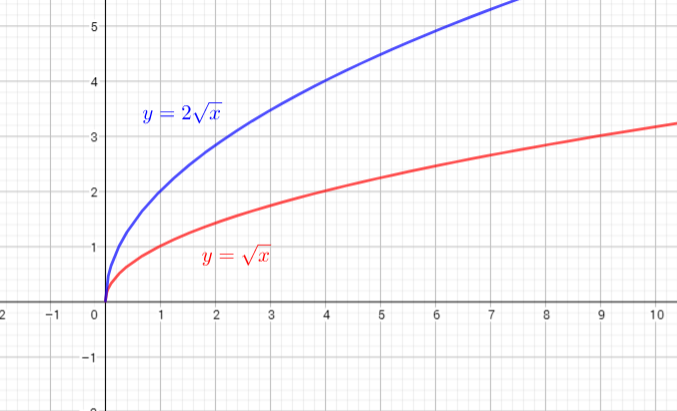
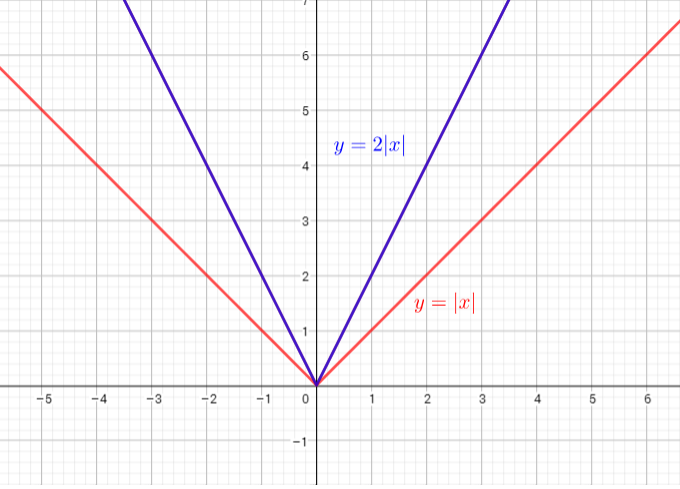
b) The graph of $y=2|x|$ is narrower than the graph of $y=|x|$
c) The graph of $y=dfrac{2}{x}$ is narrower than the graph of $y=dfrac{1}{x}$
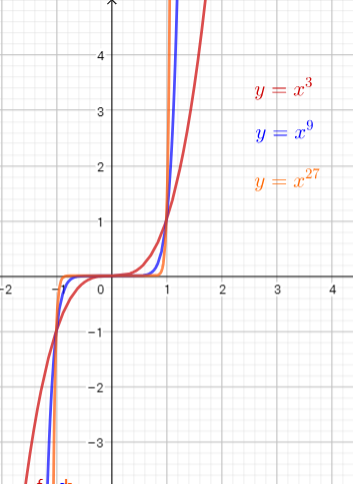
The function $y=x^3$ is a cubic function and is the parent graph for all other cubic functions
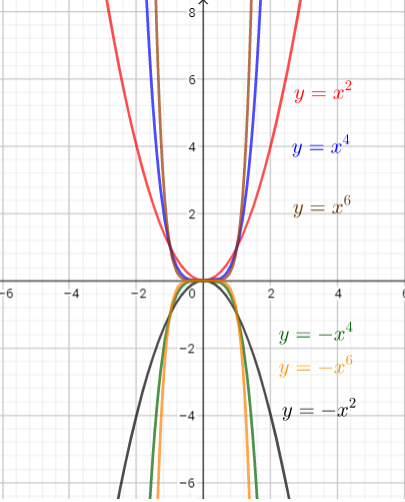
The function $y=x^2$ is a quadratic function and is the parent graph for all other quadratic functions
Haven't found what you were looking for?
Search for samples, answers to your questions and flashcards

