If we switch the x- and y-coordinates
of each point in the graph, we get the inverse relation.

Inverse relation is $left{(3,-2), (4,0), (5,2), (6,4) right}$

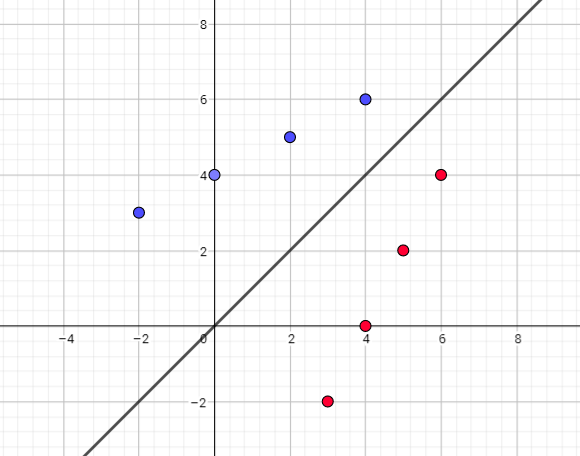
If we switch the x- and y-coordinates
of each point in the graph, we get the inverse relation.

Inverse relation is $left{(5,2), (-1,2), (1,3), (1,5) right}$

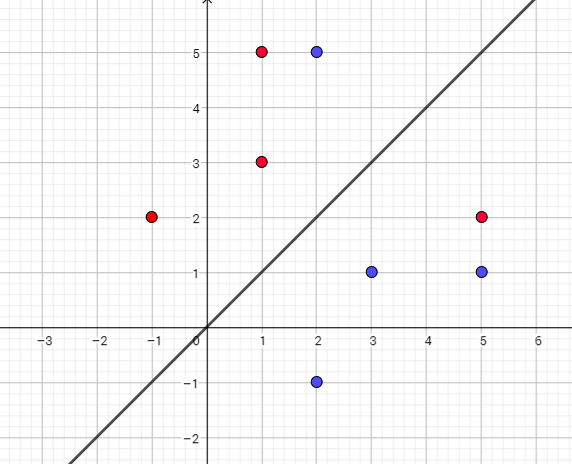
Both are functions.

b) ${(5,2),;(-1,2),;(1,3),;(1,5)}$

Both are NOT functions.

Graphs have been plotted in the answers.

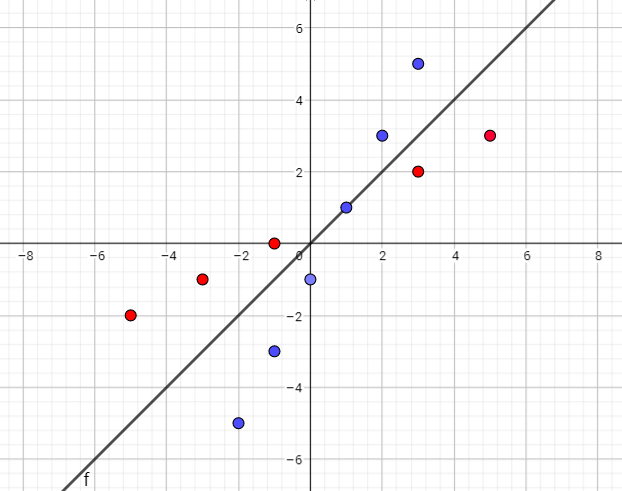
$left{(-2,-5), (-1,-3), (0,-1), (1,1), (2,3), (3,5) right}$
(these points is blue on the graph)

If we switch the x- and y-coordinates
of each point in the graph, we get the inverse relation.

Inverse relation is

$left{(-5,-2), (-3,-1), (-1,0), (1,1), (3,2), (5,3)right}$

(these points is red on the graph )

This relation is a function because each element of the domain has only one corresponding element in the range. Common point is $(1,1)$

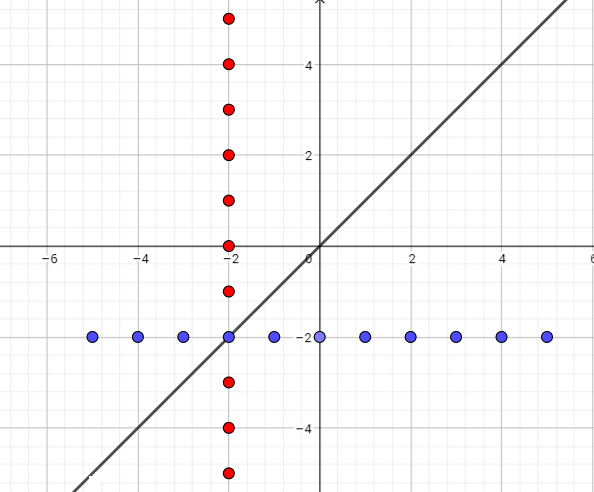
$left{(-5,-2), (-4,-2), (-3,-2), (-2,-2), (-1,-2), (0,-2), (1,-2), (2,-2), (3,-2), (4,-2), (5,-2) right}$

(these points is blue on the graph)

If we switch the x- and y-coordinates
of each point in the graph, we get the inverse relation.

Inverse relation is

$left{(-2,-5), (-2,-4), (-2,-3), (-2,-2), (-2,-1), (-2,0), (-2,1), (-2,2), (-2,3), (-2,4), (-2,5)right}$

(these points is red on the graph )

Inverse relation is not a function because Each element -2 of the domain has the different corresponding elements in the range, so the relation is not a function. Common point is $(-2,-2)$

Now, we need determine inverse function:

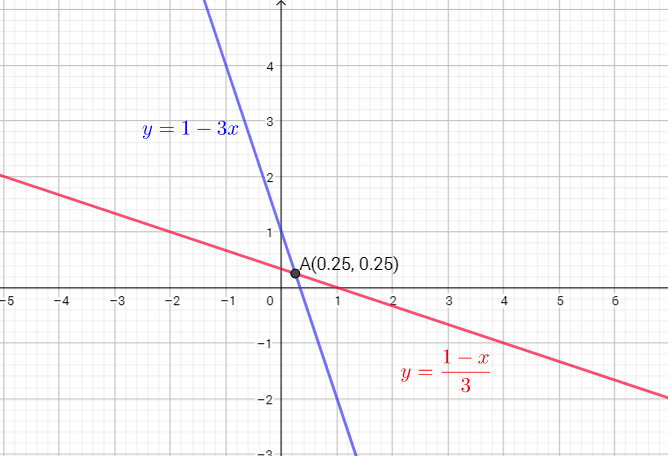
$y=1-3x$ subtract 1 from both sides

$y-1=-3x$ multiply both side by -1

$-1(y-1)=-3x(-1)$

$1-y=3x$ divide both side by 3

$x=dfrac{1-y}{3}$

That means $f^{-1}(x)=dfrac{1-x}{3}$ or $f^{-1}(x)=dfrac{-1}{3}x+dfrac{1}{3}$ is inverse function.

The graph of $f^{-1}(x)=dfrac{1-x}{3}$ is a straight line with slope $-dfrac{1}{3}$. The graph passes the vertical-line test, so, the inverse relation is a function

Common point is A(0.25, 0.25)

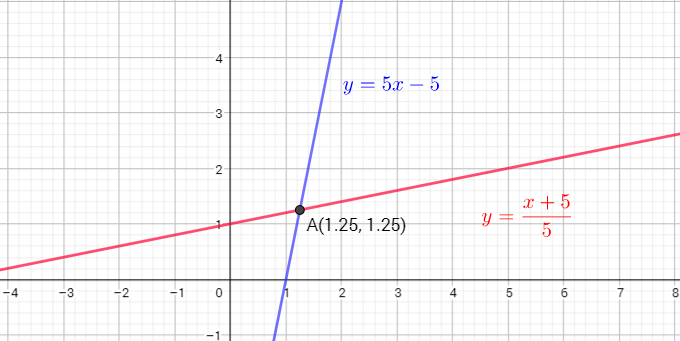
Now, we need determine inverse function:

$y=5x-5$ add 5 to both sides

$y+5=5x$ divide both side by 5

$$
x=dfrac{y+5}{5}
$$

That means $f^{-1}(x)=dfrac{x+5}{5}$ or $f^{-1}(x)=dfrac{1}{5}x+dfrac{1}{5}$ is inverse function.

The graph of $f^{-1}(x)=dfrac{x+5}{5}$ is a straight line with slope $dfrac{1}{5}$. The graph passes the vertical-line test, so, the inverse relation is a function.

Common point is $a(1.25,1.25)$

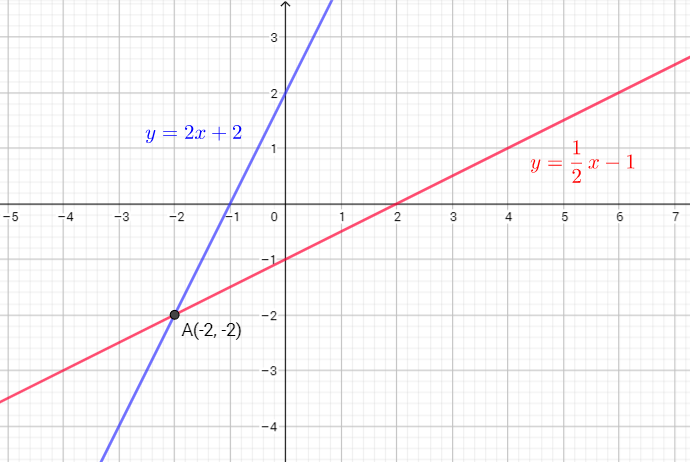
Now, we need determine inverse function:

$y=2x+2$ subtract 2 from both sides

$y-2=2x$ divide both side by 2

$$
x=dfrac{y-2}{2}
$$

That means $f^{-1}(x)=dfrac{x-2}{2}$ or $f^{-1}(x)=dfrac{1}{2}x-1$ is inverse function.

The graph of $f^{-1}(x)=dfrac{x-2}{2}$ is a straight line with slope $dfrac{1}{2}$. The graph passes the vertical-line test, so, the inverse relation is a function.

Common point is $A(-2,-2)$

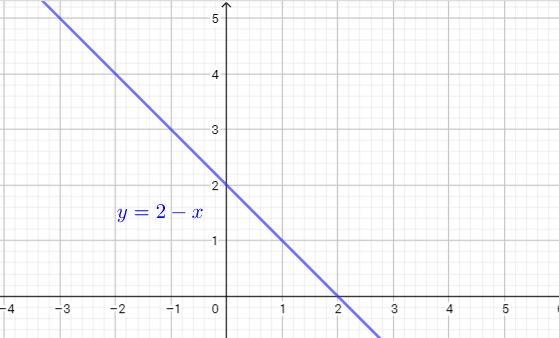
Now, we need determine inverse function:

$y=2-x$ subtract 2 from both sides

$y-2=-x$ multiply both sides by -1

$x=2-y$
That means $f^{-1}(x)=2-x$ is inverse function.

The function $y=2-x$ and its inverse are the same. The graph passes the vertical-line test, so, the inverse relation is a function.

b) NOT a function, point $(-2,-2)$ is common

c) Function, point $(0.25,0.25)$ is common

d) Function, point $(1.25, 1.25)$ is common

e) Function, point $(-2,-2)$ is common

f) Function. All points are common. The function and its inverse have the same graph.

$f(x)=3x+1$ and $g(x)=dfrac{x}{3}-1$

Determine the inverse of linear function $f(x)=3x+1$:

$y=3x+1$ subtract 1 from both sides

$y-1=3x$ divide both side by 3

$x=dfrac{y-1}{3}$

The inverse function of $f(x)=3x+1$ is $f^{-1}(x)=dfrac{x-1}{3}$

Compare the inverse function with $g(x)$ we can conclude $f(x)$ and $g(x)$ ore not pair of inverse function.

Answer is: No

$f(x)=5x-2$ and $g(x)=dfrac{x+2}{5}$

Determine the inverse of linear function $f(x)=5x-2$:

$y=5x-2$ add 2 to both sides

$y+2=5x$ divide both side by 5

$x=dfrac{y+2}{5}$

The inverse function of $f(x)=5x-2$ is
$f^{-1}(x)=dfrac{x+2}{5}$

Compare the inverse function with $g(x)$ we can conclude $f(x)$ and $g(x)$ are pair of inverse function.

Answer is: Yes

Interchange $x$ and $y$

$x=4y-3$

Solve for $y$ in terms of $x$

$4y=x+3$

$$
y=dfrac{x+3}{4}
$$

Interchange $x$ and $y$

$x=2-dfrac{1}{2}y$

Solve for $y$ in terms of $x$

$dfrac{1}{2}y=2-x$

$y=2(2-x)$

$$
y=4-2x
$$

Interchange $x$ and $y$

$3y+4x=6$

Solve for $y$ in terms of $x$

$4y=6-4x$

$y=dfrac{6-4x}{3}$

$$
y=2-dfrac{4}{3}x
$$

$2x-10=5y$

Solve for $y$ in terms of $x$

$y=dfrac{2x-10}{5}$

$$
y=dfrac{2}{5}x-2
$$

b) $y=2(2-x)$

c) $y=2-dfrac{4}{3}x$

d) $y=dfrac{2}{5}x-2$

$x=f(x)+4$

Inverse function is $f^{-1}(x)=x+4$

We used these inverse operations to write the equation of the inverse.

$f(x)-1=3x$ divide both side by 3

$x=dfrac{f(x)-1}{3}$

Inverse function is $f^{-1}(x)=dfrac{x-1}{3}$

$x=dfrac{f(x)}{5}$

Inverse function is $f^{-1}(x)=dfrac{x}{5}$

$f(x)+1=dfrac{1}{2}x$ multiply both side by 2

$x=2(f(x)+1)$

Inverse function is $f^{-1}(x)=2(x+1)$

$f(x)-6=-5x$ multiply both side by -1

$-1(f(x)-6)=-5x(-1)$

$6-f(x)=5x$ divide both side by 5

$x=dfrac{6-f(x)}{5}$

Inverse function is $f^{-1}(x)=dfrac{6-x}{5}$

$f(x)-2=dfrac{3}{4}x$ multiply both side by 4

$4(f(x)-2)=3x$ divide both side by 3

$x=dfrac{4(f(x)-2)}{3}$

$x=dfrac{4}{3(f(x)-2)}$

Inverse function is $f^{-1}(x)=dfrac{4}{3}(x-2)$

b) $f^{-1}(x)=dfrac{x-1}{3}$

c) $f^{-1}(x)=dfrac{1}{5}x$

d) $f^{-1}(x)=2(x+1)$

e) $f^{-1}(x)=dfrac{6-x}{5}$

f) $f^{-1}(x)=dfrac{4}{3}(x-2)$

Write the function in form $y=mx+b$ by putting $y$ in place of $f(x)$

$y=x+7$
switch $x$ and $y$ in the equation and solve for $y$

$x=y+7$ subtract 7 from both sides

$x-7=y$

Write the equation in function notation

$$
f^{-1}(x)=x-7
$$

Write the function in form $y=mx+b$ by putting $y$ in place of $f(x)$

$y=2-x$
switch $x$ and $y$ in the equation and solve for $y$

$x=2-y$ subtract 2 from both sides

$x-2=-y$ multiply both side by -1

$$
2-x=y
$$

Write the equation in function notation

$$
f^{-1}(x)=2-x
$$

Write the function in form $y=mx+b$ by putting $y$ in place of $f(x)$

$y=5$
switch $x$ and $y$ in the equation

$x=5$

Write the equation in function notation

$$
f^{-1}(x)=5
$$

Write the function in form $y=mx+b$ by putting $y$ in place of $f(x)$

$y=-dfrac{1}{5}x-2$
switch $x$ and $y$ in the equation and solve for $y$

$x=-dfrac{1}{5}y-2$ add 2 to both sides

$x+2=-dfrac{1}{5}y$ multiply both sides by -5

$-5(x+2)=y$ simplify

$-5x-10=y$

Write the equation in function notation

$$
f^{-1}(x)=-5x-10
$$

Write the function in form $y=mx+b$ by putting $y$ in place of $f(x)$

$y=x$
switch $x$ and $y$ in the equation

$x=y$

Write the equation in function notation

$$
f^{-1}(x)=x
$$

Write the function in form $y=mx+b$ by putting $y$ in place of $f(x)$

$y=dfrac{x-3}{4}$
switch $x$ and $y$ in the equation and solve for $y$

$x=dfrac{y-3}{4}$ multiply both sides by 4

$4x=y-3$ add 3 to both sides

$$
4x+3=y
$$

Write the equation in function notation

$$
f^{-1}(x)=4x+3
$$

b) $f^{1}(x)=2-x$

c) $x=5$

d) $f^{1}(x)=-5(x+2)$

e) $f^{1}(x)=x$

f) $f^{-1}(x)=4x+3$

Question 5a)

The inverse is linear and a function because it passes the vertical line test.

Domain of this function is the set of x- coordinates, and range is the set of y-coordinates:v

Domain=$left{-1,1,2,3 right}$

Range=$left{2,4,6,8 right}$

Inverse function we can get if switch the x- and y-coordinates
of each points. So, inverse function is:

$left{ (2,-1), (4,1), (6,2), (8,3)right}$

Domain of inverse function is $left{2,4,6,8 right}$

Range of inverse function is $left{-1,1,2,3 right}$

We can conclude that: domain of the function is a range of inverse function and range of function is a domain of inverse function.

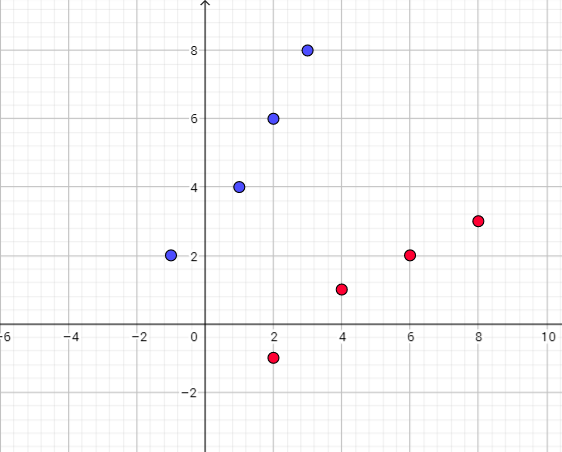
Domain of this function is the set of x- coordinates, and range is the set of y-coordinates:v

Domain=$left{-4,-2,1,5 right}$

Range=$left{6,3,8 right}$

Inverse relation we can get if switch the x- and y-coordinates
of each points. So, inverse relation is:

$left{ (6,-4), (3,-2), (8,1), (8,5)right}$

Inverse relation is not a function because for 8 value of domain we get two values of range 1 and 5.

Domain of inverse relation is $left{6,3,8 right}$

Range of inverse function is $left{-4,-2,1,5 right}$

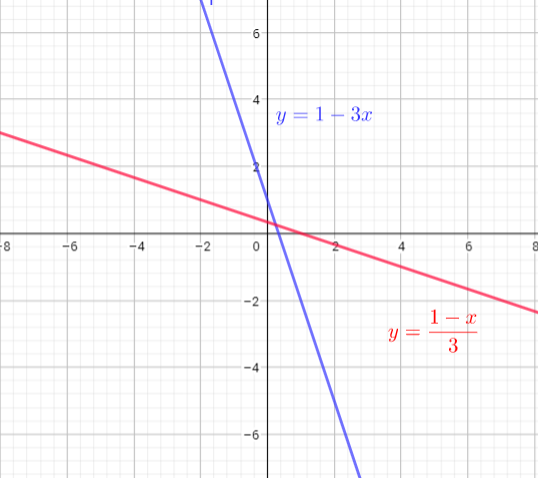
This is a linear function
Domain=$left{xin R right}$

Range=$left{yin R right}$

Inverse function we get on this way:

$y=1-3x$ subtract 1 from both sides

$y-1=-3x$ divide both sides by -3

$dfrac{y-1}{-3}=x$

$x=dfrac{1-y}{3}$

Inverse function is $f^{-1}(x)=dfrac{1-x}{3}$
Domain of inverse function is $left{xin R right}$

Range of inverse function is $left{yin R right}$

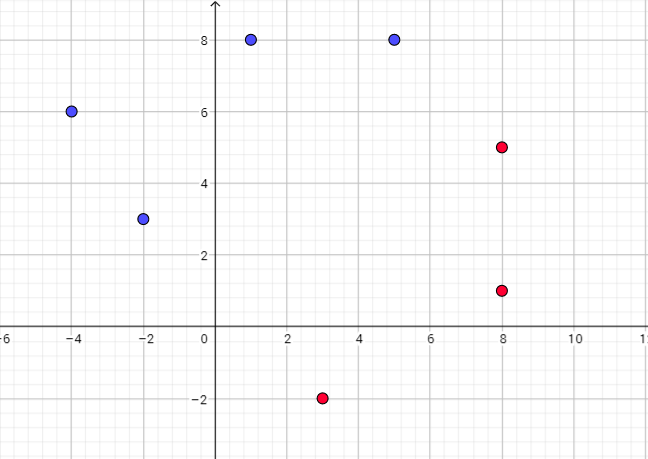
Domain of this function is the set of x- coordinates, and range is the set of y-coordinates:v

Domain=$left{-4,-3,-2,-1,0,1,2,3,4,5right}$

Range=$left{-3,-2,-1,0,1,2,1 right}$

Inverse relation we can get if switch the x- and y-coordinates
of each points. So, inverse relation is:

$left{ (-3,-4),(-2,-3),(-2,-2),(-2,-1),(-1,0),(-1,1),(0,2),(1,3),(2,4),(1,5)right}$

Inverse relation is not a function because for -2 value of domain we get two values of range -1 and -2.

Domain of inverse relation is $left{-3,-2,-1,0,1,2 right}$

Range of inverse function is $left{-4,-3,-2,-1,0,1,2,3,4,5 right}$

function: domain = ${-1,;1,;2,;3}$ , range = ${ 2,;4,;6,;8}$

inverse: domain = ${2,;4,;6,;8}$, range = ${-1,;1,;2,;3}$

The domain and range are interchanged.

b) ${ (6,-4),;(3,-2),;(8,1),;(8,5)}$

Function: domain = ${-4,;-2,;1,;5}$ , range = ${3,;6,;8}$

inverse: domain = ${3,;6,;8}$, range = ${-4,;-2,;1,;5}$

The domain and range are interchanged.

c) $f^{-1}(x)=dfrac{1}{3}(1-x)$

Function: domain = ${xinbold{R}}$ , range = ${yinbold{R}}$

inverse: domain = ${ xinbold{R}}$ , range = ${ yinbold{R}}$

The domain and range are identical for both function and inverse.

d) ${(-3,-4),(-2,-3),(-2,-2),(-2,-1),(-1,0),(-1,1), (0,2),(1,3),(2,4)(1,5)}$

function: domain = ${ 0,pm1,;pm2,;pm3,;pm4,5}$ , range =${0,pm1,;pm2,;-3}$

inverse: domain = ${0,pm1,;pm2,;,-3}$ , range = ${ 0,pm1,;pm2,;pm3,;pm4,;5}$

The domain and range are interchanged.

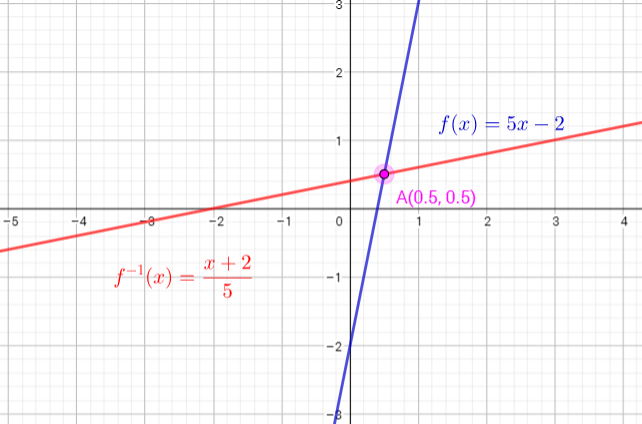
$f(x)=5x-2$ add 2 to a both sides

$f(x)+2=5x$ divide both side by 5

$dfrac{f(x)+2}{5}=x$

Inverse function is $f^{-1}(x)=dfrac{x+2}{5}$ or $f^{-1}(x)=dfrac{1}{5}x+dfrac{2}{5}$

b) see graph on the right side

c) The inverse is a function because any vertical line drawn on the graph intersects the graph at onlyone point. This is the graph of a function. The graph of $f^{-1}(x)=dfrac{1}{5}x+dfrac{2}{5}$ is a straight line with slope $dfrac{1}{5}$ .

d) The common point of the function and it’s inverse is point A(0.5, 0.5) (see graph)

e)

Slope of the function $f(x)=5x-2$ is 5

Slope of the function $f^{-1}(x)=dfrac{1}{5}x+dfrac{2}{5}$ si $dfrac{1}{5}$

We can conclude that: slopes are reciprocals of each other

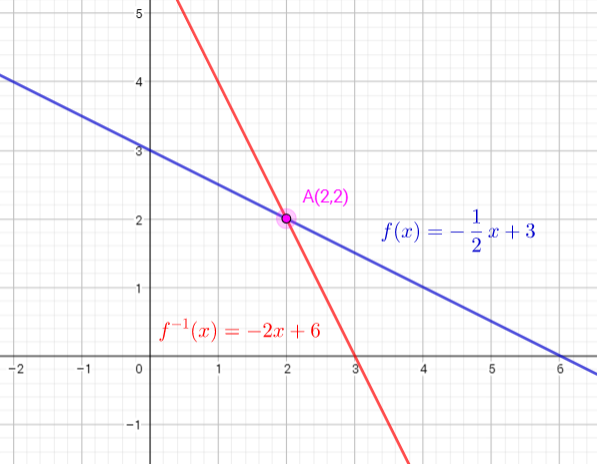
$g(x)=-dfrac{1}{2}x+3$ subtract 3 from the both sides

$g(x)-3=-dfrac{1}{2}x$ multiply both both side by -2

$-2(g(x)-3)=x$ simplify

$-2g(x)+6=x$

Inverse function is $g^{-1}(x)=-2x+6$

b) see graph on the right side

c) The inverse is a function because any vertical line drawn on the graph intersects the graph at onlyone point. This is the graph of a function. The graph of $g^{-1}(x)=-2x+6$ is a straight line with slope $-2$ .

d) The common points of the function and its inverse is point A(2,2) (see graph)

e)

Slope of the function $g(x)=-dfrac{1}{2}x+3$ is $-dfrac{1}{2}$

Slope of the function $g^{-1}(x)=-2x+6$ si $-2$

We can conclude that: slopes are reciprocals of each other

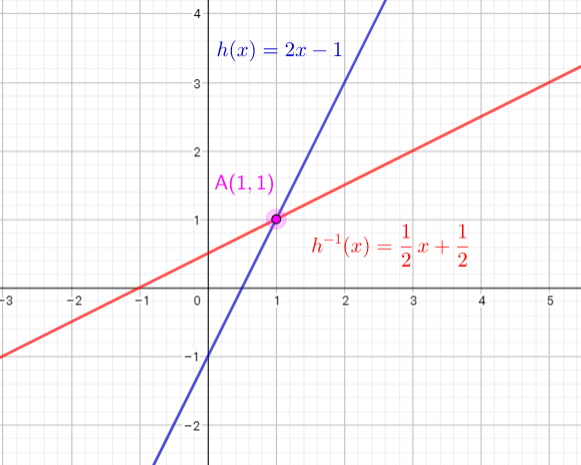
$h(x)=2x-1$ add 1 to a both sides

$h(x)+1=2x$ divide both side by 2

$dfrac{h(x)+1}{2}=x$

Inverse function is $h^{-1}(x)=dfrac{x+1}{2}$ or $h^{-1}(x)=dfrac{1}{2}x+dfrac{1}{2}$

b) see graph on the right side

c) The inverse is a function because any vertical line drawn on the graph intersects the graph at onlyone point. This is the graph of a function. The graph of $h^{-1}(x)=dfrac{1}{2}x+dfrac{1}{2}$ is a straight line with slope $dfrac{1}{2}$ .

d) The common point of the function and it’s inverse is the point A(1,1) (see graph)

e)

Slope of the function $h(x)=2x-1$ is 2

Slope of the function $h^{-1}(x)=dfrac{1}{2}x+dfrac{1}{2}$ si $dfrac{1}{2}$

We can conclude that: slopes are reciprocals of each other

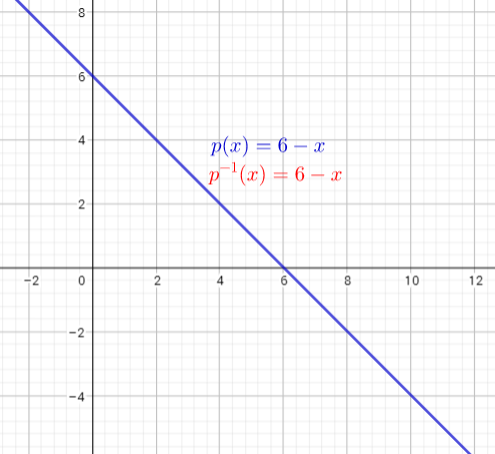
$p(x)=6-x$ subtract 6 from the both sides

$p(x)-6=-x$ multiply both side by -1

$-1(p(x)-6)=x$ simplify

$$
-p(x)+6=x
$$

Inverse function is $p^{-1}(x)=-x+6$

b) see graph on the right side

c) The inverse is a function because any vertical line drawn on the graph intersects the graph at only one point. This is the graph of a function. The graph of $p^{-1}(x)=-x+6$ is a straight line with slope $-1$

d) The common points of the function and its inverse is each points of graphs

Function and it’s inverse are the same

e)

Slope of the function $p(x)=6-x$ is -1

Slope of the function $p^{-1}(x)=-x+6$ is $-1$

We can conclude that: slopes are the same

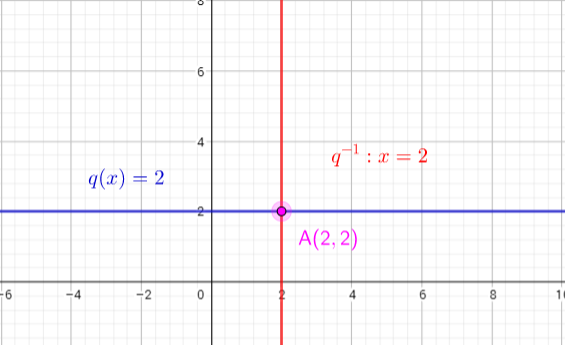
Inverse $q^{-1}$ of this function is relation $x=2$. This is not a function , because for one value $x=2$ we get differente values of $y$. Domain of this relation is $left{xin R| x=2 right}$, and range of this relation is $left{yin R right}$

b) see graph on the right side

c)The graph of $q^{-1}$ is not a function, but it is a straight line.

d)The common points of the function $q(x)=2$ and it’s inverse relation $x=2$ is point A(2,2) (see graph)

e) Slope of the function $q(x)=2$ is 0

Slope of the relation $x=2$ is undefined

b) The graph has been plotted in the answer.

c) The function is linear (straight line) with slope $ne$ 0

d) $left(dfrac{1}{2},dfrac{1}{2}right)$

e) The slopes are reciprocal of each other.

f) Answers are the following

a) $g^{-1}(x)=2(3-x)$

function is linear with slope $ne$ 0

(2,2)

slopes are reciprocals of each other

b) $h^{-1}(x)=dfrac{1}{2}(x+1)$

function is linear with slope $ne$ 0

(1,1) ; slopes are reciprocal of each other.

c) $p^{-1}(x)=6-x$

function is linear with slope $ne$ 0

all points on the graph; slopes are the same.

d) $q^{-1}:x=2$

not a function (slope is zero so the inverse is vertical line)

(2,2) ; slopes are 0 and undefined

a) To find $g(13)$ , plug in 13 wherever $t$ occures in the equation of $g(t)$ and simplify to get $g(t)$

$g(13)=3cdot13-2=39-2=37$

$g(7)=3cdot7-2=21-2=19$

$$
dfrac{g(13)-g(7)}{13-7}=dfrac{37-19}{13-7}=dfrac{18}{6}=3
$$

In the equation $g(t)=3t-2$ the operations on $t$ are as follows: add 2 to both sides and then divide both sides by 3:

$g(t)=3t-2$ add 2 to both sides

$g(t)+2=3t$ divide both sides by 3

$dfrac{g(t)+2}{3}=t$

Inverse function is $g^{-1}(t)=dfrac{t+2}{3}$

Now we can determine $g^{-1}(13)$. plug in 13 wherever $t$ occures in the equation of $g^{-1}(t)$

$g^{-1}(13)=dfrac{13+2}{3}=dfrac{15}{3}=5$

Now we can determine $g^{-1}(7)$. plug in 7 wherever $t$ occures in the equation of $g^{-1}(t)$

$g^{-1}(7)=dfrac{7+2}{3}=dfrac{9}{3}=3$

$$
dfrac{g^{-1}(13)-g^{-1}(7)}{13-7}=dfrac{5-3}{13-7}=dfrac{2}{6}=dfrac{1}{3}
$$

b) 19

c) 3

d) 5

e) 3

f) $dfrac{1}{3}$

$$
m=dfrac{y_2-y_1}{x_2-x_1}=dfrac{f(x_2)-f(x_1)}{x_2-x_1}
$$

$f(x)=2x+30$ subrtact 30 from the both sides

$f(x)-30=2x$ divide both side by 2

$dfrac{f(x)-30}{2}=x$

Inverse function is $f^{-1}(x)=dfrac{x-30}{2}$ or $f^{-1}(x)=dfrac{1}{2}x-15$

This rule use a Canadian visiting the United States

$$
f(14)=2cdot14+30=28+30=58^{o}F
$$

$$
f^{-1}(70)=dfrac{1}{2}cdot70-15=35-15=20^{o}C
$$

b) subtract 30 from both sides and divide by 2 ; a Canadian visiting the United States

c) $f^{-1}(x)=dfrac{x-30}{2}$

d) $f(14)=58^circ$ F

e) $f^{-1}(70)=20^circ$ C

Let $x$ represent centimeters. Then, Ben’s rule is $g(x)=dfrac{4x}{10}$

Let $g^{-1}$ be the method for converting inches to centimeters, according to rule: multiply by 10 and then divide by 4.

$g(x)=dfrac{4x}{10}$ multiply both side by 10

$10g(x)=4x$ divide both side by 4

$dfrac{10g(x)}{4}=x$

So, inverse is $g^{-1}(x)=dfrac{10x}{4}$

Now, we need determine rule $g^{-1}(x)$

$g(x)=dfrac{4x}{10}$ multiply both side by 10

$10g(x)=4x$ divide both side by 4

$dfrac{10g(x)}{4}=x$

So, inverse is $g^{-1}(x)=dfrac{10x}{4}$

$g(x)=dfrac{4x}{10}=dfrac{4cdot15}{10}=dfrac{60}{10}=6$ inches

Using function notation $g^{-1}(x)=dfrac{10x}{4}$ to represent 70 inches in centimeters we get:

$g^{-1}(x)=dfrac{10x}{4}=dfrac{10cdot70}{4}=dfrac{700}{4}=175$ cm

Thus, this is asking for the inverse of $y=2.63x-1.29$

To find the inverse of any function, swap the positions of the variables and solve for $y$

$x=2.63y-1.29$

$2.63y=x+1.29$

$dfrac{2.63y}{2.63}=dfrac{x+1.29}{2.63}$

$y=dfrac{x+1.29}{2.63}$

We need to write it in the form $y=mx+b$

$y=dfrac{1}{2.63}x+dfrac{1.29}{2.63}$

$$
y=0.38x+0.50
$$

payment for hourly work: $8.05(40)$

payment for sales over $$1000$: $0.05(x-1000)$

Thus, the equation describing her weekly earning is

$y=8.05(40)+0.05(x-1000)$

Since number of sales can’t be negative, the domain is $xgeq 0$

$f(x)=322+0.05(x-1000)$ ; $xgeq 0$

c) The inverse relation is obtained by switching the position of the variables then solve for $y$

$x=322+0.05(y-1000)$

$0.05(y-1000)=x-322$

$y-1000=dfrac{x-322}{0.05}$

$y=20(x-322)+1000$

Note that the range of the original function must the domain of its inverse.

The original function has a range of ${ yinbold{R};|;ygeq 278}$ because the minimum salary occurs when she has zero sales ($y$-intercept).

So the domain of the inverse must be ${ xinbold{R};|;xgeq 278}$

$f^{-1}(x)=20(x-322)+1000$ ; $xgeq 278$

e) We must find $x$ such that $f(x)=420$. This is just the value of $f^{-1}(420)$

$f^{-1}(420)=1000+20(420-322)=$2960$

Note that the answer at the back of your book is different because it incorrectly evaluates $8.05(40)=32.2$ instead of 322.

b) $f(x)=32.2+0.05(x-1000)$

c) graph of $y=20(x-32.2)+1000$

d) $f^{-1}(x)=1000+20(x-32.2)$

e) $f^{-1}(420)=1000+20(420-322)=$2960$

Because (2,1) cannot belong to $f^{-1}$

The first, we need find $f^{-1}(x)$.

In the equation $f(x)=k(2+x)$ the operations on $x$ are as follows: divide both sides by $k$, and then subtract 2 from the both sides.

$f(x)=k(2+x)$ divide both sides by $k$

$dfrac{f(x)}{k}=2+x$ subtract 2 from the both sides

$dfrac{f(x)}{k}-2=x$

Inverse function is $f^{-1}(x)=dfrac{x}{k}-2$

To find value $k$ plug in -2 in to $f^{-1}(x)=dfrac{x}{k}-2$ and solve for $k$

$f^{-1}(-2)=dfrac{-2}{k}-2=-3$ add 2 to both sides

$dfrac{-2}{k}=-3+2$

$dfrac{-2}{k}=-1$ multiply both sides by $k$

$-2=-k$, or $k=2$

Solution is $k=2$.

Function is $f(x)=2(2+x)$

Example1: Function $f(x)=dfrac{1}{x}, xne0$ is a self-inverse.

check:

$f(x)=dfrac{1}{x}$ multiply both sides by x

$xcdot f(x)=1$ divide both sides by $f(x)ne0$

$x=dfrac{1}{f(x)}$

Inverse function is $f^{-1}(x)=dfrac{1}{x}$.

We can conclude $f(x)=f^{-1}(x)$, so $f(x)$ is a self-inverse

Example 2: Function $g(x)=3-x$ is a self-inverse.

check:

$g(x)=3-x$ subtract from the both sides 3

$g(x)-3=-x$ multiply both sides by -1

$-1(g(x)-3)=x$ simlify

$$
3-g(x)=x
$$

Inverse function is $g^{-1}(x)=3-x$.

We can conclude $g(x)=g^{-1}(x)$, so $g(x)$ is a self-inverse

Example 3: Function $h(x)=x$, is a self-inverse.

check:

$h(x)=x$

$$
x=h(x)
$$

Inverse function is $h^{-1}(x)=x$.

We can conclude $h(x)=h^{-1}(x)$, so $h(x)$ is a self-inverse

$y=dfrac{1}{x}$ , $y=3-x$, $y=x$

Substitute

$f(x)implies (x)$

$x implies f^{-1}(x)$

Thus,

$x = 3 f^{-1}(x)+4$

If $f^{-1}(x)$ is the inverse of $f(x)$, then

$f(f^{-1}(x))=x$

To find the inverse of a function $f(x)$, do the following substitutions:

$f(x) implies x$

$x implies f^{-1}(x)$

$dfrac{3f^{-1}(x)}{3}=dfrac{x-4}{3}$

$$
f^{-1}(x)=dfrac{x-4}{3}
$$

$f(f^{-1}(x))=x-4+4$

$$
f(f^{-1}(x))=x
$$

$x=dfrac{g^{-1}(x)-4}{3}$

$3x = g^{-1}(x)-4$

$g^{-1}(x)=3x+4$

Thus

$$
f^{-1}[(f^{-1})(x)]=f(x)=3x+4
$$