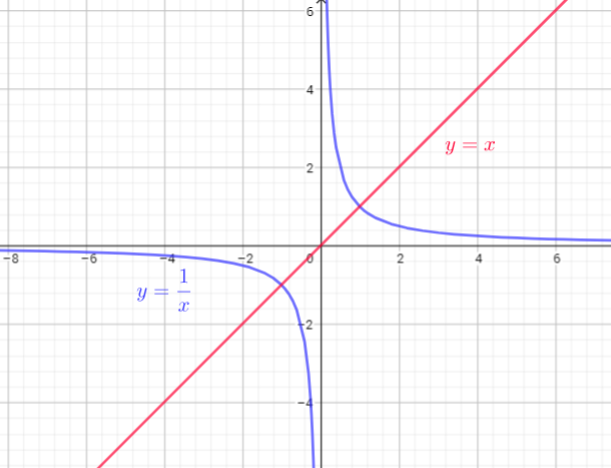
Both functions lie in the first and third quadrants. Function $f(x)=x$ is defined for each $x$, and function $g(x)=dfrac{1}{x}$ is defined for $xne0$. Function $f(x)=x$ is rising and continuous. Function $g(x)$ is rising and decreasing, and has a break in $x=0$

Function $g(x)=dfrac{1}{x}$ has vertical asymptote $x=0$ and horizontal asymptote $g(x)=0$

Similarities: Both lie in quadrant 1 and 3

Differences: $f(x)$ is a straight line passing through the origin while $g(x)$ is a hyperbola and does not touch the $x$ and $y$ axes.

vertical asymptote: $x=0$

horizontal asymptote : $g(x)=0$

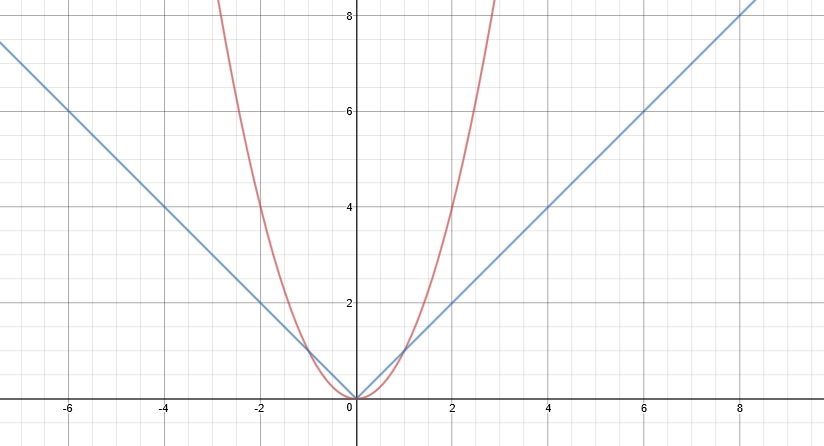
The red graph is $f(x)$ while blue is $g(x)$. They are both similar in that the equations will always result in a positive x-value. However, they are different in the fact that $g(x)$ is linear while $f(x)$ is nonlinear.

Similarities: Both lie in quadrant 1 and 2.

Differences: $f(x)$ is curved while $g(x)$ consists of straight lines.

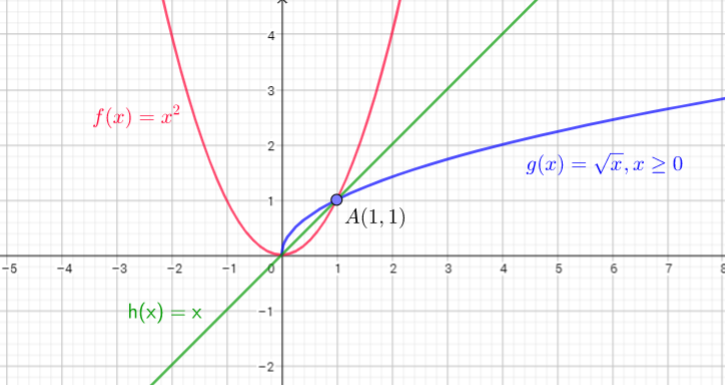
From the graphs we can see: graph of $g(x)=sqrt{x}, xgeq0$ is reflection of graph of $f(x)=x^{2}$ in graph of $h(x)=x$

All three functions pass through a one point $A(1,1)$

$g(x)$ is a reflection of $f(x)$ along the line $h(x)$