
All Solutions
Section 1-1: Relations and Functions
Range is $left{ 1,2,3,2right}$
This relation is a function because each element of the domain corresponds with only one element in the range
Range is $left{ -3,-1,0,2right}$
The value 1 of the independent variable maps
to two different values -3 and 0 of the dependent variable
This relation is not a function.
Range is $left{ 4,5,-2,1right}$
The value 0 of the independent variable maps
to two different values 4 and 1 of the dependent variable
This relation is not a function.
Range is $left{ 1,6right}$
Each element of the domain has only one
corresponding element in the range, so the relation
is a function.
b) not a function ; for $x$=1, $y=0$ and $-3$
c) not a function; for $x=0$ , $y=1$ and 4
d) function ; each $x$-value has a unique $y$-value
If the vertical line touches the graph $bold{only;once}$, then it is a function. If it touches the vertical line $bold{more;than;once}$, it is not a function.
In this case, if you draw a vertical line at $x=1$, it touches the graph at three points. Thus, it is $boxed{not;a;function}$
it would touch the graph at two points. It is therefore $boxed{not;a;function}$
b.) not a function
c.) function
d.) not a function
e.) function
f.) not a function
$$
left{ (Barbara, 10), (Pierre, 12), (Kateri,11), (Mandeep, 11), (Elly,10 )right}
$$
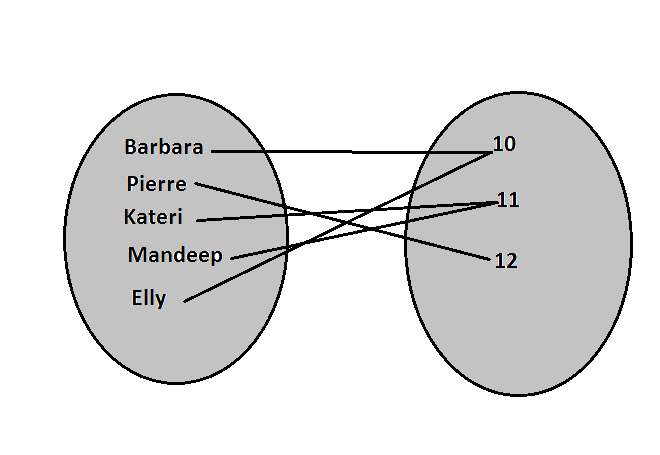
Domain is $left{ Barbara, Pierre, Kateri, Mandeep, Ellyright}$
Range is: $left{10,11,12 right}$
c) Each element of the domain has only one
corresponding element in the range, so the relation student-grade
is a function.
$$
left{ (10,8), (12,25), (11,15), (11,18), (10,16 )right}
$$
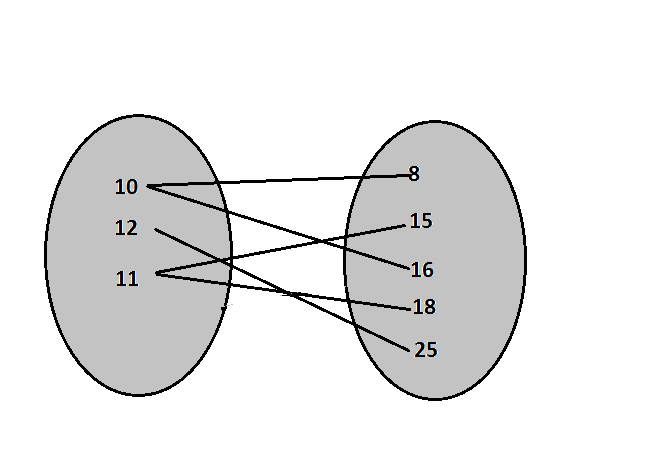
Domain is $left{ 10,11,12right}$
Range is: $left{8, 15, 16, 18, 25 right}$
c) Element 11 of the domain has two
corresponding element in the range 15 and 18,and e lement 10 of the domain has two
corresponding element in the range 8 and 16 so the relation grade-credits is not a function.
$$
left{ (Barbara, 8), (Pierre, 25), (Kateri,15), (Mandeep, 18), (Elly,16 )right}
$$
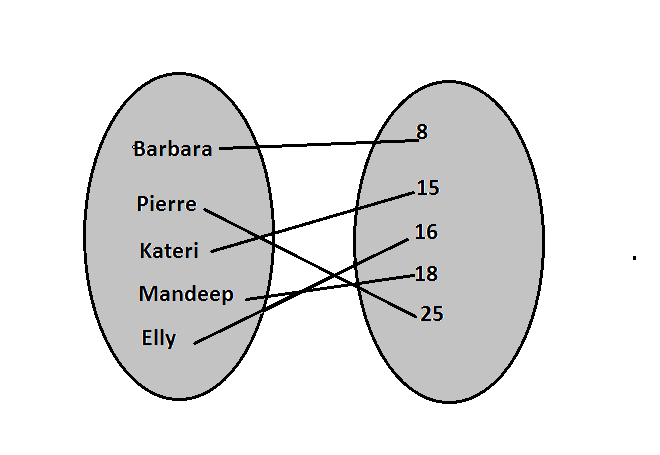
Domain is $left{ Barbara, Pierre, Kateri, Mandeep, Ellyright}$
Range is: $left{8,15,16,18,25 right}$
c)Each element of the domain has only one
corresponding element in the range, so the relation student-credits is a function.
b) students, grades: domain = ${$ Barbara, Pierre, Kateri, Mandeep, Elly $}$
range = ${$ 10, 11, 12 $}$
grades, credits: domain = ${$ 10, 11, 12 $}$
range = ${$ 8, 15, 16, 18, 25 $}$
students, credits: domain = ${$ Barbara, Pierre, Kateri, Mandeep, Elly $}$
range = ${$ 8, 15, 16, 18, 25 $}$
c) The grades-credits relation is NOT a function because 10 in the domain corresponds to 8 and 16 in the range.
Use this data to plot the domain vs range as follows.
a.) students vs grades
b.) grades vs credits
c.) student vs credits
Thus, the grades-credit relation is not a function.
y=3
$$
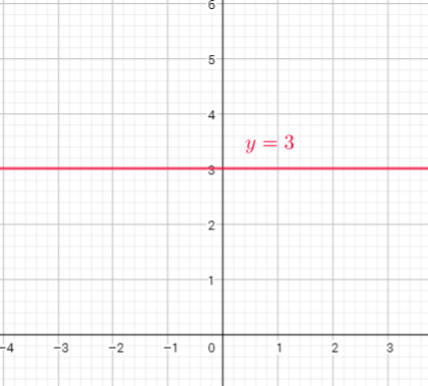
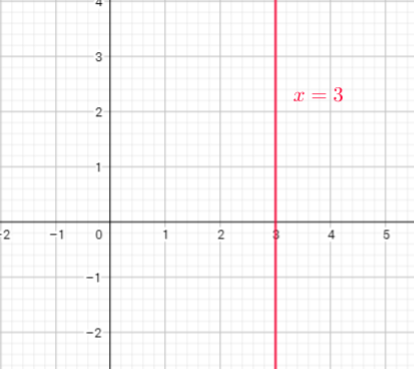
$x=3$ ; vertical line ; NOT a function since it fails vertical line test
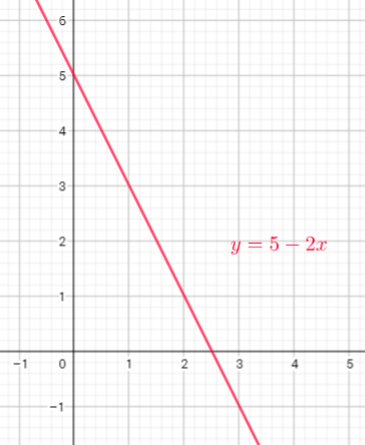
This is the graph of a linear
function
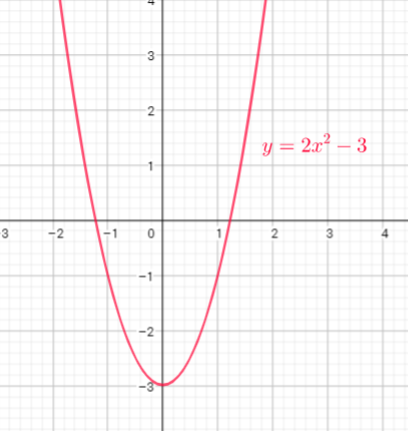
This is the graph of a quadratic function
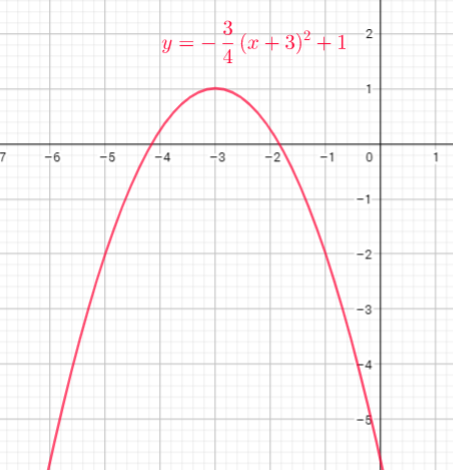
This is the graph of a quadratic function
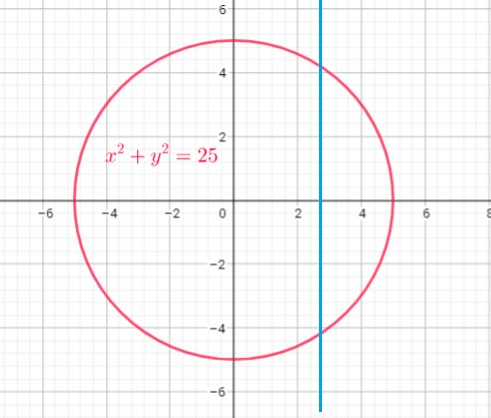
the graph intersects the graph at
two points. This is not the graph of
a function.
This is a circle. It is a not a function
b) quadratic, function
c) quadratic, function
d) circle, NOT a function
see graphs inside
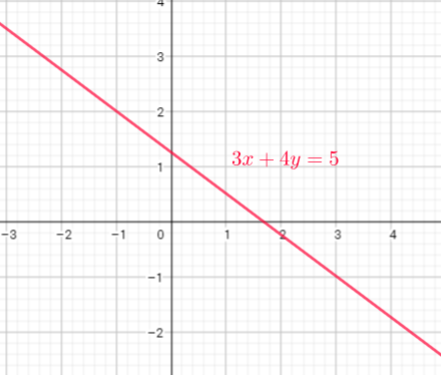
$3cdot0+4y=5$
$0+4y=5$ divide both sides by 4
$y=dfrac{5}{4}$
Substitute $x=-2$ into equation $3x+4y=5$, now we get:
$3cdot(-2)+4y=5$
$-6+4y=5$ add 6 on both sides
$-6+4y+6=5+6$
$4y=11$ divide both sides by 4
$y=dfrac{11}{4}$
This is a function for each $x$ we get only one value $y$
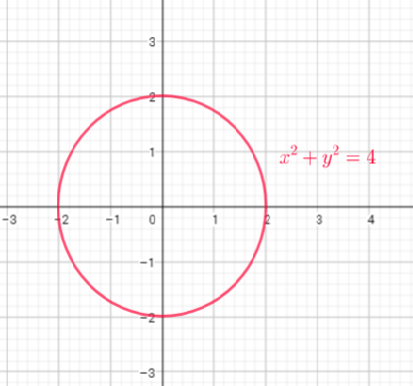
$0^{2}+y^{2}=4$
$y^{2}=4$
$y=pm sqrt{4}$
$y=pm2$
so, if $x=0$, then , $y=-2$ or $y=2$
Substitute $x=-2$ into equation $x^{2}+y^{2}=4$, now we get:
$(-2)^{2}+y^{2}=4$
$4+y^{2}=4$
$y^{2}=0$
$y=0$
This is a not a function because for $x=0$ we get two values of $y$
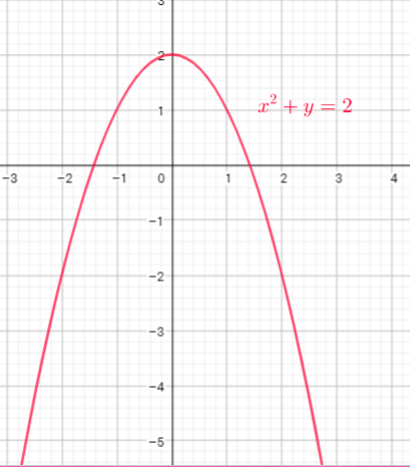
$0^{2}+y=2$
$0+y=2$
$y=2$
Substitute $x=-2$ into equation $x^{2}+y=2$, now we get:
$(-2)^{2}+y=2$
$4+y=2$
$y=2-4$
$y=-2$
This is a function because for each value $x$ we get only one value of $y$.
$x+y^{2}=0$
$0+y^{2}=0$
$y^{2}=0$
$y=0$
iv) Substitute $x=-2$ into equation $x+y^{2}=0$, now we get:
$-2+y^{2}=0$
$y^{2}=2$
$y=pmsqrt{2}$
so, if $x=-2$, then $y=-sqrt{2}$ or $y=sqrt{2}$
This is a not a function because for $x=-2$ we get two values of $y$
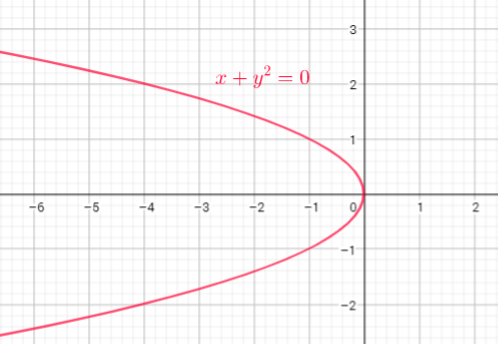
c) We can verify our answer use graph and apply vertical-line test, or solve equation for y
and check for multiple values
b) functions: (i) and (iii)
c) From the graph, apply vertical-line test or solve for $y$ in terms of $x$ then see if there are multiple possible values of $x$.
We know $sqrt{x}$ is defined for $xgeq0$, so, in our case, $y=sqrt{x+2}$ is defined for $x+2geq0$, or $xgeq-2$
For each $xgeq0$ we get only one value of $y$.
We see graph passes the vertical-line test, showing that
for each x-value in the domain there is only one
y-value in the range.
The relation $y=sqrt{x+2}$ is a function.
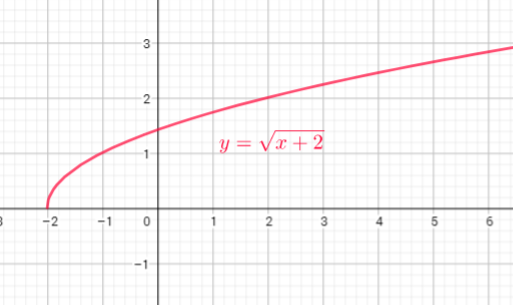
For each $x$ we get only one value of $y$.
We see graph passes the vertical-line test, showing that
for each x-value in the domain there is only one
y-value in the range.
The relation $y=2-x$ is a function.
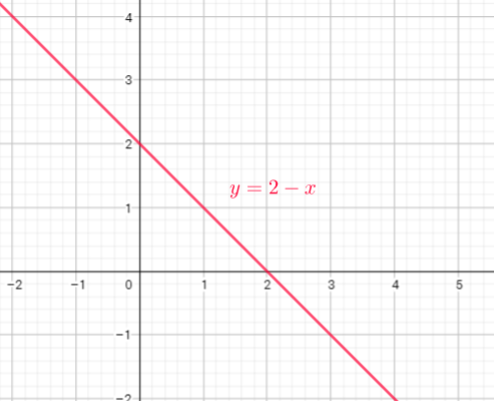
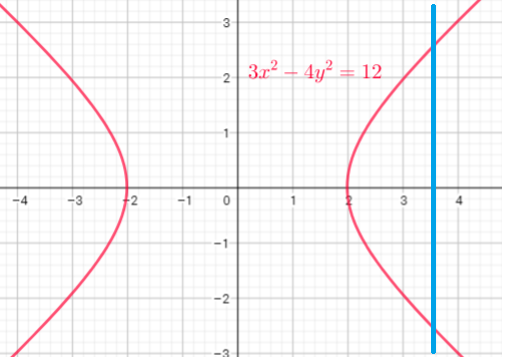
At least one vertical line drawn on
the graph intersects the graph at
two points.
This relation $3x^{2}-4y^{2}=12$ not the graph of
a function.
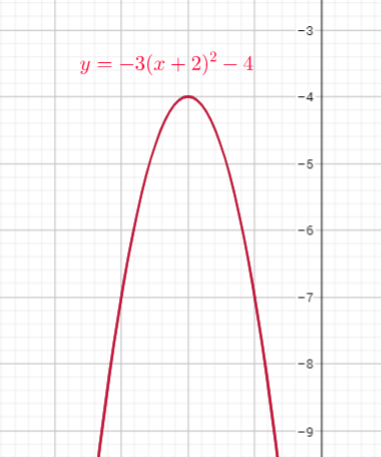
For each $x$ we get only one value of $y$.
We see graph passes the vertical-line test, showing that
for each x-value in the domain there is only one
y-value in the range.
The relation $y=-3(x+2)^{2}-4$ is a function.
$x-y^2=2$
$y^2=x-2$
$y=pmsqrt{x-2}$
For instance if $x=6$
$y=pmsqrt{6-2}=pmsqrt{4}=pm 2$
$y=2$ or $-2$
Each value of $x$ does NOT have a unique value of $y$. Therefore, it is NOT a function.
graphically, it fails vertical line test
numerically, at $x=6$, $y=pm 2$
b) For each given time, there is a unique distance that Bran could walk. Therefore, it is a function.
c) Each age is not uniquely assigned to a certain number of credits so it is possible that two or more students at the same age could take varying numbers of credits. Therefore, it is NOT a function.
The distance traveled by a car cannot be negative so the domain is
${ xinbold{R};|;xgeq 0}$
To find the range, notice that the cost cannot be less than $$44$
$$
{ yinbold{R};|;ygeq 44}
$$
For the range, the cost cannot be lower than the minimum daily rental charge.
c) It passes the vertical line test so it is a function.
b) distance can’t be negative, cost cannot lower than minimum daily rental charge
c) function; passes vertical line test
The point at $x=10$ must be solid while the point at $y=-5$ must be open.
Function is a relation from a set of inputs to a set of possible outputs where each input is related to exactly one output.
1) For each value $x$ , function $y=f(x)$ has only one value $y$
(Each element $x$ of the domain has only one
corresponding element $y$ in the range)
2)If any vertical line drawn on the
graph intersects the graph at only
one point
1) $y=2x-3$ linear function
2) $y=x^2+3x-4$ quadratic function
3) $3x^{2}+2y-1=0$
4) $y=sqrt{2x+1}$
1) $x^{2}+y^{2}=9$
2) $3x^{2}-4y^{2}=24$
3) $x+2y^{2}=0$
4) $y=pmsqrt{x+y}$
domain = ${ xinbold{R};|;xgeq 0}$
The cost can’t also be negative and there are no minimum fees required so the range is
range = ${ yinbold{R};|;ygeq 0}$
c) The graph can be drawn as follows.
A recommended system would be:
For items less than $100$ kg, charge $$4$ per kilogram, for items more than $100$ kg, charge $$400$ plus $$3.5$ per kilogram that exceeds $100$ kg. The graph looks like this.
b) domain = ${ xinbold{R};|;xgeq 0}$ , range = ${ yinbold{R};|;ygeq 0}$
c) see graph inside
d) for $y=4x$ for $x<100$, $y=400+3.5(x-100)$ for $xgeq 100$

