
All Solutions
Page 76: Practice Questions
This relation is not a function,because $x=0$ value of the independent variable corresponds two value of the dependent variable.
Domain of this relation is :$left{ -3,-1,0,4,right}$
Range of this relation is: $left{0,1,5,6 right}$
This relation is a function, because each $x$-value ( independent variable) corresponds with only one $y$-value (dependent variable)
This is a linear function.
Domain of this function is the set of all real numbers, $(-infty,+infty )$
Range of this function is the set of all real numbers, $(-infty, +infty)$
We can identify the domain and range of functions is by using graphs. Because the domain refers to the set of possible input values, the domain of a graph consists of all the input values shown on the x-axis. The range is the set of possible output values, which are shown on the y-axis.
$text{Domain of this relation is: $[-4,+infty)$}$
Range of this relation is: $(-infty, +infty)$
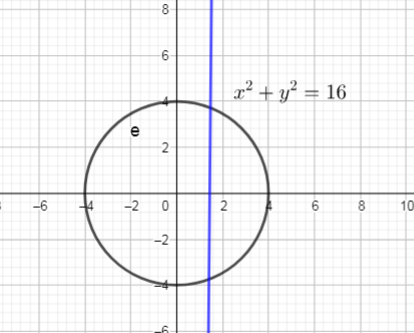
Domain of this relation is interval $(-4,4)$
Range of this relation is interval $(-4,4)$
defarraystretch{1.3}%
begin{tabular}{|l|l|}
hline
a) & begin{tabular}[c]{@{}l@{}}domain = ${ -3,-1,0,4}$\ range = ${ 0,1,5,6}$\ not a function since there are 2 $y$-values for $x=0$end{tabular} \ hline
b) & begin{tabular}[c]{@{}l@{}}domain = ${ xinbold{R}}$\ range = ${ yinbold{R}}$\ function because each $x$-value has only one $y$-valueend{tabular} \ hline
c) & begin{tabular}[c]{@{}l@{}}domain = ${ xinbold{R};|;xgeq-4}$\ range = ${ yinbold{R}}$\ not a function, because at $x>-4$, each has two $y$-valuesend{tabular} \ hline
d) & begin{tabular}[c]{@{}l@{}}domain = ${ xinbold{R};|;-4leq xleq 4}$\ range = ${ yinbold{R};|;-4leq xleq 4}$\ not a function because some $x$-values have two $y$-valuesend{tabular} \ hline
end{tabular}
end{table}
$text{textcolor{#4257b2}{ Vertical line test}}$:,,If any vertical line intersects the graph of a relation more than once, then the relation is not a function”
Use graph, we can conclude that: this relation is not passes Vertical line test, so, this relation is not a function
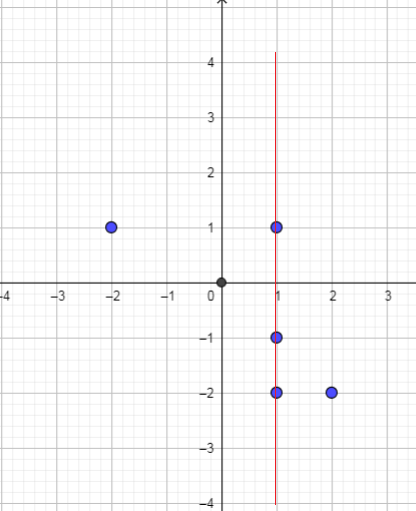
We need use the vertical-line test to see how many points on the graph there were for each value of $x$.
Use graph, the vertical line intersected the graph in only one
place. So, each $x$-value in the domain corresponds with only one
$y$-value in the range.
So, this relation is a function.
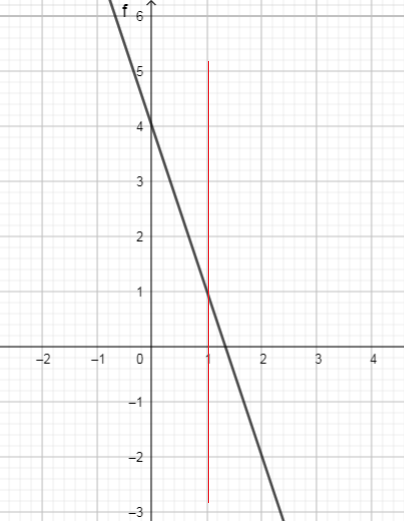
Use graph, we can see the vertical line intersected the graph in only one place. So each $x$-value in the domain corresponds with only one $y$-value in the range.
We can conclude: This relation is a function
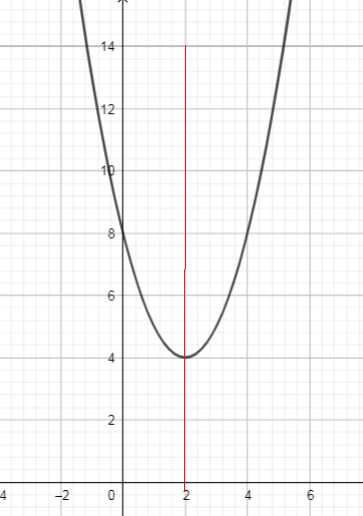
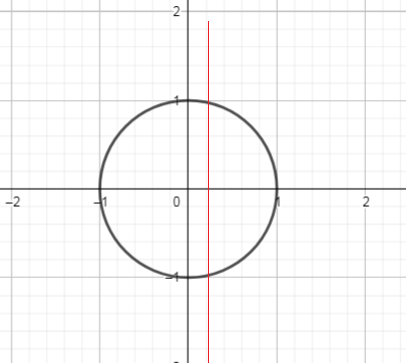
Using the vertical-line test to see how many points on the graph there were for each value of $x$, we can conclude vertical line intersects the graph of a relation in two points, then the relation is not a function
This relation is not a function.
Using vertical line intersects the graph of a relation only once, so the relation is a function.
This relation is a function.
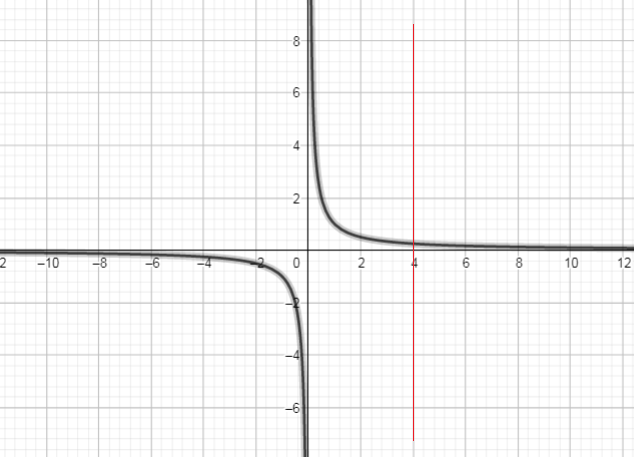
e) $y=dfrac{1}{x}$
Using vertical line intersects the graph in only one point, so the relation is a function.
This relation is a function.
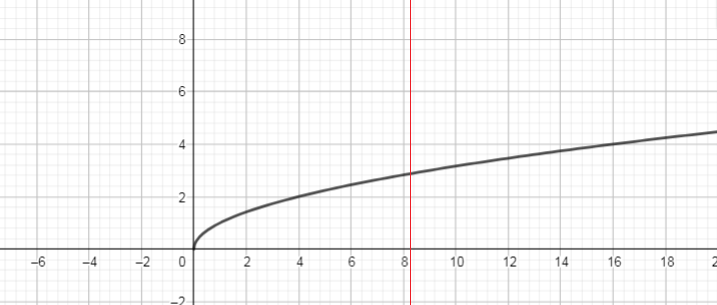
b) Function
c) Function
d) Not a function
e) Function
f) Function
For example,
one of these functions is $y=-x^{2}+3$
We can identify the domain and range of functions is by using graphs. Because the domain refers to the set of possible input values, the domain of a graph consists of all the input values shown on the x-axis. The range is the set of possible output values, which are shown on the y-axis.
Domain of this function is interval $(-infty,+infty)$
Range of this function is interval $(-infty,3]$
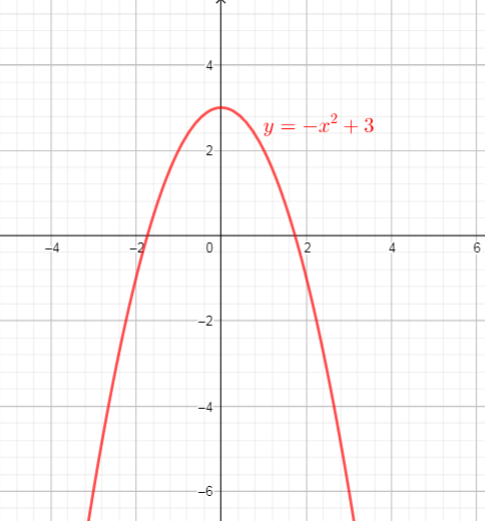
y=-x^{2}+3
$$
$$
begin{align*}
f(x)&=x^{2}+3x-5\
f(-1)&=(-1)^{2}+3(-1)-5\
&=1-3-5\
&=-7\
end{align*}
$$
So, $f(-1)=-7$
$$
begin{align*}
f(x)&=x^{2}+3x-5\
f(0)&=(0)^{2}+3(0)-5\
&=0+0-5\
&=-5\
end{align*}
$$
So, $f(0)=-5$
$$
begin{align*}
g(x)&=2x-3\
g(dfrac{1}{2})&=2cdotdfrac{1}{2}-3\
&=1-3\
&=-2\
end{align*}
$$
So, $g(dfrac{1}{2})=-2$
$$
begin{align*}
f(x)&=x^{2}+3x-5\
f(2b)&=(2b)^{2}+3(2b)-5\
&=4b^{2}+6b-5\
end{align*}
$$
So is, $f(2b)=4b^{2}+6b-5$
$$
begin{align*}
g(x)&=2x-3\
g(1-4a)&=2(1-4a)-3\
&=2-8a-3\
&=-1-8a\
end{align*}
$$
So, $g(1-4a)=-1-8a$
$$
begin{align*}
f(x)&=g(x)\
x^{2}+3x-5&=2x-3 tag{text{subtract 2x-3 from both sides}}\
x^{2}+3x-5-2x+3&=0\
x^{2}+x-2&=0\
x^{2}-x+2x-2&=0 tag{text{solve equation by factoring}}\
x(x-1)+2(x-1)&=0\
(x-1)(x+2)&=0\
x-1=0 &lor x+2=0\
x=1 & lor x=-2
end{align*}
$$
This means, if $x=1$ or $x=-2$, then $f(x)=g(x)$
b) $f(0)=-5$
c) $g(dfrac{1}{2})=-2$
d) $f(2b)=4b^{2}+6b-5$
e) $g(1-4a)=-1-8a$
f) $f(x)=g(x)$ when $x=1$ or $x=-2$
We can identify the domain and range of functions is by using graphs. Because the domain refers to the set of possible input values, the domain of a graph consists of all the input values shown on the x-axis. The range is the set of possible output values, which are shown on the y-axis.
Use graph, we can determine:
Domain of this function is: $(-infty, +infty)$
Range of this function is : $(-infty,4]$
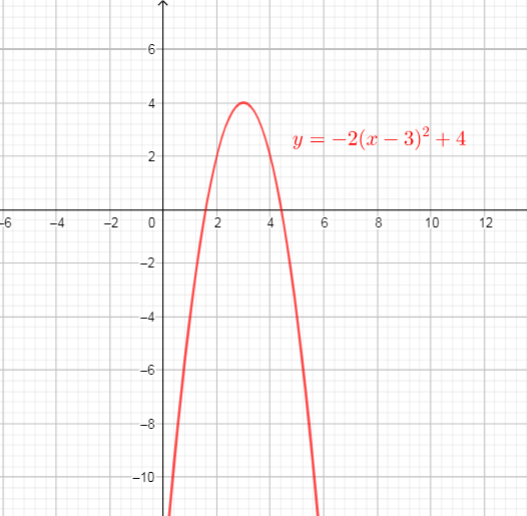
From the graph we can conclude $f(1)$ takes the value -4 at $x=1$,
then $f(1)=-4$ and the point $(1, -4)$ lies on the graph of $f(x)$.
Answer is: $f(1)$ represent $y$-coordinate corresponding to $x=1$.
$text{textcolor{#c34632}{i)}}$ Using the equation of the function we can determine $f(3)-f(2)$
The first we need determine $f(3)$ and $f(2)$:
$$
begin{align*}
f(x)&=-2(x-3)^{2}+4 \
f(3)&=-2(3-3)^{2}+4 tag{text{substitute $3$ for $x$ into function $f(x)$}}\
&=-2cdot0+4\
&=4\
end{align*}
$$
$$
begin{align*}
f(x)&=-2(x-3)^{2}+4 \
f(2)&=-2(2-3)^{2}+4 tag{text{substitute $2$ for $x$ into function $f(x)$}}\
&=-2(-1)^{2}+4\
&=-2+4\
&=2\
end{align*}
$$
Now we can determine $f(3)-f(2)=4-2=2$
$$
begin{align*}
f(x)&=-2(x-3)^{2}+4 \
2f(5)+7&=2cdot(-2(5-3)^{2}+4)+7 tag{text{substitute $5$ for $x$ into function $f(x)$}}\
&=2(-2(2)^{2}+4)+7\
&=2(-8+4)+7\
&=2(-4)+7\
&=-8+7\
&=-1\
end{align*}
$$
$$
begin{align*}
f(x)&=-2(x-3)^{2}+4 \
f(1-x)&=-2(1-x-3)^{2}+4 tag{text{substitute $1-x$ for $x$ into function $f(x)$}}\
&=-2(-2-x)^{2}+4\
end{align*}
$$
b) $f(1)$ corresponds to the $y$-coordinate at $x=1$
c)
text${text{i}}$) 2
ii) $-$1
iii) $-2(-x-2)^2+4$
$$
begin{align*}
f(x)&=8\
&x^{2}-4x+3=8\
&x^{2}-4x+3-8=0 tag{text{subtract 8 from both sides}}\
&x^{2}-4x-5=0\
&x^{2}+x-5x-5=0 tag{text{set $-4x=x-5x$}}\
&x(x+1)-5(x+1)=0tag{text{factor}}\
&(x+1)(x-5)=0 tag{text{factor}}\
&x+1=0 lor x-5=0 tag{text{set factors equal to 0}}\
&x=-1 lor x=5\
end{align*}
$$
So, this means , if $x=-1$ or $x=5$, then $f(x)=8$
text{$x=-1 lor x=5$}
$$
${ tinbold{R};|;0leq tleq 6}$
Since the maximum height is $80$ m and height cannot be negative, the range is
${ hinbold{R};|;0leq hleq 80}$
c) We must find the equation of the parabola containing $(0,60)$, (2,80), and $(6,0)$.
Since the maximum height is at $(2,80)$, the vertex form is
$y=a(x-2)^2+80$
Now, we can find the value of $a$ using any of the two points.
$60=a(0-2)^2+80$
$a=dfrac{60-80}{(0-2)^2}=dfrac{-20}{4}=-5$
Therefore, the equation of the parabola is
$h=-5(t-2)^2+80$
$h=-5(t^2-4t+4)+80$
$h=-5t^2+20t-20+80$
$$
h=-5t^2+20t+60
$$
$60=a(0-h)^2+kimplies 60=ah^2+k$
$80=a(2-h)^2+k$
$0=a(6-h)^2+k$
Subtract 3rd equation from 1st equation
$60-0=a(h^2-(6-h)^2)+(k-k)$
$60=a(h^2-(36-12h+h^2))$
$60=a(h^2-36+12h-h^2)$
$60=a(12h-36)$
$5=a(h-3)$
Subtract 1st equation from 2nd equation
$80-60=a[(2-h)^2-h^2]+(k-k)$
$20=a(4-4h+h^2-h^2)$
$20=a(4-4h)$
$5=a(1-h)$
Thus,
$a(h-3)=a(1-h)$
$h-3=1-h$
$2h=4$
$h=2$
$a=dfrac{5}{1-h}=dfrac{5}{1-2}=-5$
$k=60-ah^2=60-(-5)(2^2)=80$
$$
therefore y=-5(x-2)^2+80
$$
b) domain = ${ tinbold{R};|;0leq tleq 6}$ , range = ${ hinbold{R};|;0leq hleq 80}$
c) $h=-5t^2+20t+60$
b) domain = ${ xinbold{R};|;xgeq -2}$ , range= ${ yinbold{R};|;ygeq 0}$
Use the given section of the rectangular we can determine lenth $l$ as a function of the area $A$ and width $w$:
$$
begin{align*}
&540=3w+2l\
&540-3w=2l
tag{text{subtract 3w from the both sides}}\
&l=dfrac{540-3w}{2} tag{text{divide both sides by 2}}\
end{align*}
$$
We know, the tota area of the rectangular is equal $A=length cdot width$
Substitute equation of the length $l$ into equation of the area $A$ we get:
$$
begin{align*}
A&=lcdot w\
&=dfrac{540-3w}{2}cdot w\
&=dfrac{w(540-3w)}{2}\
end{align*}
$$
$A$ is area of the rectangular, so $A$ must be greater than zero, but if we look a equation of the area $A=dfrac{w(540-3w)}{2}$, we can conclude that A is greater than zero if $540-3w>0$ , so, this means 3w must be less than 540:
$$
begin{align*}
540-3w>0\
3w<540\
w< dfrac{540}{3}\
w<180\
end{align*}
$$
This means, domain of the function $A=dfrac{w(540-3w)}{2}$ is:
$Domain=left{ w in R| 0<w<180 right}$
This is a quadratic function that opens down It has two zeros, at 0 and 180. The vertex lies halfway in between the
zeros, above the x-axis, so the numbers
in the domain have to be between 0
and 180.
The vertex is halfway between $w=0$ and $w=180$, so,the $x$-coordinate of the vertex is: $dfrac{0+180}{2}=90$
Substitute $w=90$ into the area function $A$ we will find the $y$-coordinate of the vertex:
$$
begin{align*}
A(w)&=dfrac{w(540-3w)}{2}\
A(90)&=dfrac{90(540-3cdot90)}{2}\
&=dfrac{90cdot 270}{2}\
&=12150\
end{align*}
$$
So, vertex is $(90,12150)$
This means that: Range od the function is $left{ Ain R| 0<Aleq12150right}$
b) domain = ${ xinbold{R};|;0leq wleq 180}$
range = ${ Ainbold{R};|;0<Aleq 12;150}$
c) $l=270$ m , $w=90$ m
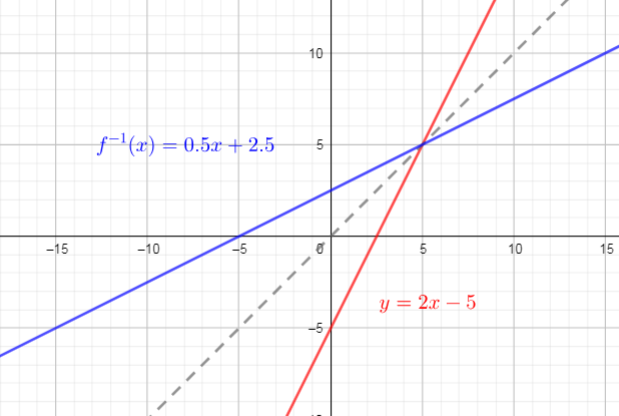
one of the methods for determining the inverse of a linear function is draw a graph of linear function and then determine its reflection in the line $y=x$
Use graph to determine the slope-intercept form of inverse :slope is 0.5 and $y$-intercept is 2.5.
Inverse function is: $f^{-1}(x)=0.5 x +2.5$
Linear function is: $f(x)=dfrac{x+3}{7}$
Use reverse operations we get:
$$
begin{align*}
f(x)&=dfrac{x+3}{7}
7f(x)&=x+3 tag{text{multiply both sides by 7}}\
7f(x)-3&=x tag{text{subtract 3 from both sides}}
end{align*}
$$
The inverse function of $f(x)=dfrac{x+3}{7}$ is
$$
f^{-1}(x)=7x-3
$$
Switch $x$ and $f(x)$, then solve for $f(x)$:
$$
begin{align*}
x&=4-dfrac{1}{2}f(x)\
x-4&=-dfrac{1}{2} tag{text{subtract 4 from both sides}}\
-2(x-4)=f(x) tag{text{multiply both sides by -2}}\
f(x)=-2x+8
end{align*}
$$
So, inverse function of $f(x)=4-dfrac{1}{2}x$ is
$f^{-1}(x)=-2x+8$
b) $f^{-1}(x)=7x-3$
c) $f^{-1}(x)=-2x+8$
$f(x)=30x+15;000$
domain = ${ xinbold{R};|;xgeq 0}$
Regardless of the number of people who would join, the income could not be less than the fixed $$15;000$ from the sponsors.
range = ${ yinbold{R};|;ygeq 15;000}$
To find the inverse, swap the positions of the variable and solve for $y$
$y=30x+15000$
$x=30y+15000$
$30y=x-15000$
$y=f^{-1}(x)=dfrac{x-15000}{30}$
The domain of the inverse is the range of the original function.
domain = ${ xinbold{R};|;xgeq 15000}$
b) domain = ${ xinbold{R}}$ , range = ${ yinbold{R};|;ygeq 15000}$
c) $f^{-1}(x)=dfrac{x-15000}{30}$ , domain = ${ xinbold{R};|;xgeq 15;000}$
If $k<0$, then it is also reflected in the $y$-axis.
Now, the transformed graph (in red) appears to be compressed. Notice that it apparently passes through $(4,4)$. (though not exactly, this might be graphic error)
$y=sqrt{kx}$
$4=sqrt{k(4)}$
$16=4k$
$k=4$
Therefore, the equation is $y=sqrt{4x}$
$y=dfrac{1}{-kx}$
$1=dfrac{1}{-k(5)}$
$k=-dfrac{1}{5}$
Therefore, the equation is $y=dfrac{1}{-frac{1}{5}x}$
b) $y=dfrac{1}{-frac{1}{5}x}$
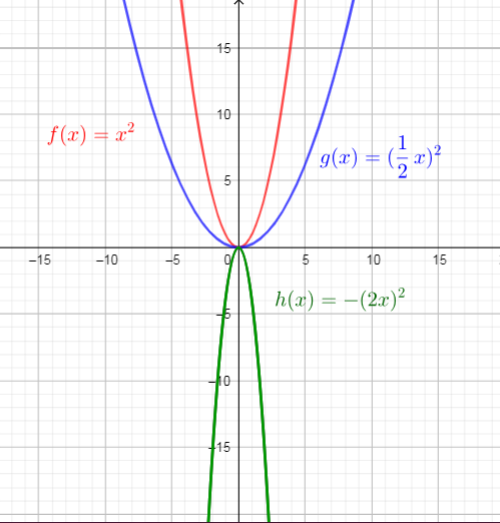
$f(x)=x^{2}$
$g(x)=(dfrac{1}{2}x)^{2}$
$h(x)=-(2x)^{2}$
the function $f(x)$ is a parent function of the functions $g(x)$ and $h(x)$.
We can identify the domain and range of functions is by using graphs. Because the domain refers to the set of possible input values, the domain of a graph consists of all the input values shown on the $x$-axis. The range is the set of possible output values, which are shown on the $y$-axis.
$f(x)$ : Domain=${xin R| -inftyleq xleq +infty}$ , Range=$left{ yin R| 0leq y<+infty right}$
$g(x)$ : Domain=${xin R | -inftyleq xleq +infty}$ , Range=$left{ yin R | 0leq y<+infty right}$
$h(x)$ : Domain=${xin R| -inftyleq xleq +infty}$ , Range=$left{ yin R| -infty<yleq 0 right}$
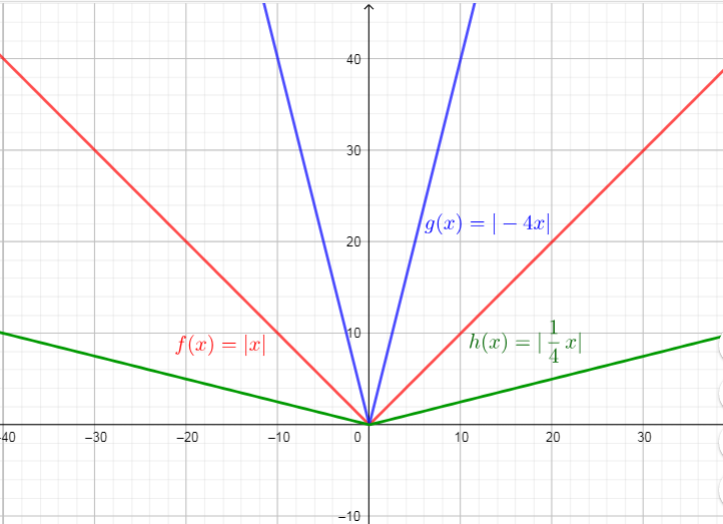
$f(x)=|x|$
$g(x)=|-4x|$
$h(x)=|dfrac{1}{4}x|$
The function $f(x)=|x|$ is a parent function of the functions $g(x)$ and $h(x)$.
We can identify the domain and range of functions is by using graphs. Because the domain refers to the set of possible input values, the domain of a graph consists of all the input values shown on the $x$-axis. The range is the set of possible output values, which are shown on the $y$-axis.
$f(x)$ : Domain=${xin R| -inftyleq xleq +infty}$ , Range=$left{ yin R| 0leq y<+infty right}$
$g(x)$ : Domain=${xin R | -inftyleq xleq +infty}$ , Range=$left{ yin R | 0leq y<+infty right}$
$h(x)$ : Domain=${xin R| -inftyleq xleq +infty}$ , Range=$left{ yin R| 0leq y<+infty right}$
defarraystretch{1.6}%
begin{tabular}{|l|l|}
hline
a) & begin{tabular}[c]{@{}l@{}}$f(x):$ domain = ${ xinbold{R}}$ , range = ${ yinbold{R};|;ygeq 0}$\ $g(x):$ domain = ${ xinbold{R}}$ , range = ${ yinbold{R};|;ygeq 0}$\ $h(x):$ domain = ${ xinbold{R}}$ , range = ${ yinbold{R};|;yleq 0}$end{tabular} \ hline
b) & begin{tabular}[c]{@{}l@{}}$f(x):$ domain = ${ xinbold{R}}$ , range = ${ yinbold{R};|;ygeq 0}$\ $g(x):$ domain = ${ xinbold{R}}$ , range = ${ yinbold{R};|;ygeq 0}$\ $h(x):$ domain = ${ xinbold{R}}$ , range = ${ yinbold{R};|;ygeq0}$end{tabular} \ hline
end{tabular}
end{table}
When combining vertical transformations written in the form $af(x)+k$, first vertically stretch by $a$ and then vertically shift by $k$.
A vertical stretch with factor 2, translation 4 units down, and
translation 3 units right.
b) Yes ; vertical stretching by a factor of 2, translation 4 units downward, and translation 3 units to the right
We shall examine what will happen to this point upon performing the transformations:
(1) reflecting in the $y$-axis $implies$ change $x$ to $-x$
$y=f(-x)implies (-1,4)$
(2) horizontal compression by $dfrac{1}{4}$ $implies$ multiply $x$-values by $frac{1}{4}$
$y=f(-4x)implies left(-dfrac{1}{4},4right)$
(3) vertical stretching by 3 $implies$ multiply $y$-values by 3
$y=3f(-4x) implies left( -dfrac{1}{4}, 12right)$
(4) horizontal translation 1 unit to the left $implies$ subtract $x$-values by 1
$y=3f[-4(x+1)] implies left(-dfrac{5}{4}, 12right)$
(5) vertical translation 2 units down $implies$ subtract $y$-values by $2$
$y=3f[-4(x+1)]-2implies left(-dfrac{5}{4}, 10right)$
We need determine the coordinates of the image of the point $(1,4)$ on the graph $y=3f[-4(x+1)]-2$.
If $-4(x+1)=1$ then we can determine $y=3f[-4(x+1)]-2$.
$$
begin{align*}
&-4(x+1)=1\
&-4x-4=1\
&-4x=1+4 tag{text{add 4 to both sides}}\
&-4x=5\
& x=-dfrac{5}{4} tag{text{divide both sides by -4}}\
end{align*}
$$
So, $x$- coordinate of the point $(1,4)$ is $x=-dfrac{5}{4}$
Now, we can determine $y$-coordinate.
$$
begin{align*}
y&=3f(-4(x+1))-2 \
&=3f(1)-2 tag{text{substitute 1 for -4(x+1)}}\
&=3cdot4-2 tag{text{substitute f(1)=4}}\
&=12-2=10\
end{align*}
$$
Answer is: The coordinates of the image of the point $(1,4)$ is $(-dfrac{5}{4},10)$
(-dfrac{5}{4},10)
$$
The graph of $y=f(x)$ is reflected across the x-axiss $longrightarrow$ $y=-f(x)$
then, stretched vertically by the factor 2 $longrightarrow$ $y=-2f(x)$
then, stretched horizontaly by the factor 3 $longrightarrow$ $y=-2f(dfrac{1}{3}x)$
then translated 4 units left $longrightarrow$ $y=-2f(dfrac{1}{3}x+4)$
then translated 1 unit down $longrightarrow$ $y=-2f(dfrac{1}{3}x+4)-1$
Use these steps, we get function $textcolor{#4257b2}{y=-2f(dfrac{1}{3}x+4)-1}$
$$
begin{align*}\
y&=-2f(dfrac{1}{3}x+4)-1\
&=-2(dfrac{1}{3}x+4)^{2}-1\
end{align*}
$$
Graph of this function is:
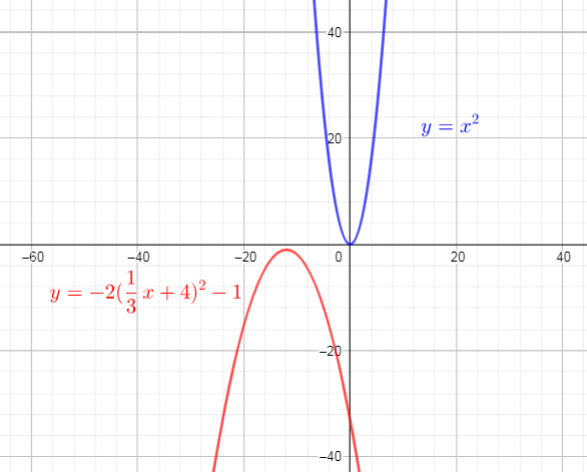
b) The graph has been plotted in the answers.
then, reflected across the y -axiss $longrightarrow$ $y=sqrt{-x2}$
then translated 3 units right $longrightarrow$ $y=sqrt{-2(x-3)}$
then translated 2 units down $longrightarrow$ $y=sqrt{-2(x-3)}-2$
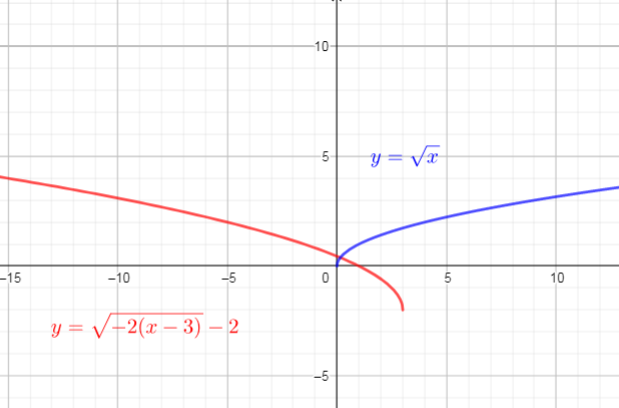
Use these steps, we get function $textcolor{#4257b2}{y=sqrt{-2(x-3)}-2}$
We can identify the domain and range of functions is by using graphs.
Because the domain refers to the set of possible input values, the domain of a graph consists of all the input values shown on the $x$-axis. The range is the set of possible output values, which are shown on the $y$-axis.
Domain$={xin R | xleq3}$
Range$=left{yin R | ygeq-2 right}$
then, reflected across the x-axiss $longrightarrow$ $y=dfrac{-3}{x}$
then translated 4 units left $longrightarrow$ $y=dfrac{-3}{x+4}$
then translated 1 unit up $longrightarrow$ $y=dfrac{-3}{x+4}+1$
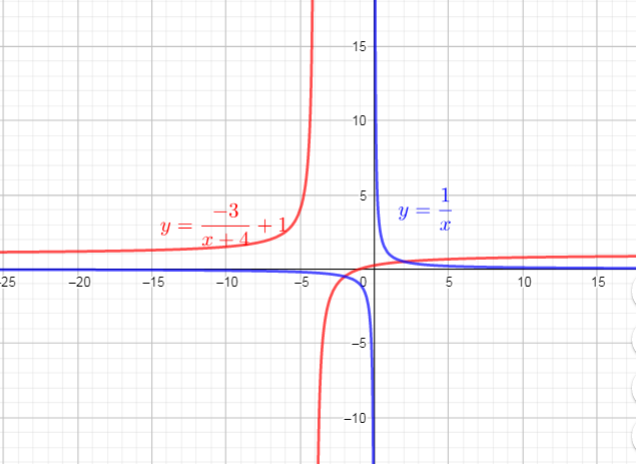
Use these steps, we get a function $textcolor{#4257b2}{y=dfrac{-3}{x+4}+1}$
Use graph, we can determine domain and range of this function:
Domain$={xin R | xne -4}$
Range$={yin R | yne 1}$
defarraystretch{1.9}%
begin{tabular}{|l|l|}
hline
a) & begin{tabular}[c]{@{}l@{}}$y=-sqrt{2(x-3)}-2$\ domain = ${ xinbold{R};|;xgeq 3}$\ range = ${ yinbold{R};|;yleq -2}$end{tabular} \ hline
b) & begin{tabular}[c]{@{}l@{}}$y=dfrac{-3}{x+4}+1$\ domain = ${ xinbold{R};|;xneq 4}$\ range = ${ yinbold{R};|;yneq 1}$end{tabular} \ hline
end{tabular}
end{table}
Algebraic, an x-intercept is a point on the graph where y is zero,
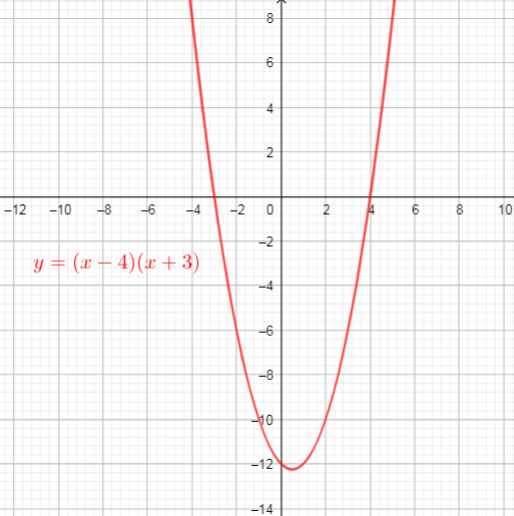
$text{If $f(x)=(x-4)(x+3)$, we need determine x-intercepts}$.
Using the definitions of the intercepts, we will proceed as follows:
$text{$y = 0$ for the x-intercepts, so}$
$$
begin{align*}
y&=0\
(x-4)&(x+3)=0\
x-4=0 &lor x+3=0\
x=4 &lor x=-3\
end{align*}
$$
$text{Then the x-intercepts are the points $(4,0)$ and $(-3,0)$}$
$text{$y = 0$ for the x-intercepts, so}$
$$
begin{align*}
y&=0\
-2(x-4)&(x+3)=0\
x-4=0 &lor x+3=0\
x=4 &lor x=-3\
end{align*}
$$
$text{Then the x-intercepts are the points $(4,0)$ and $(-3,0)$}$
We can conclude that: the x-intercepts are the same as in part a)
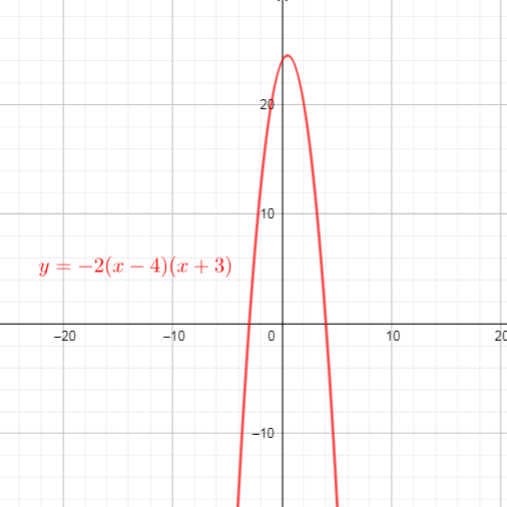
$y=f(-dfrac{1}{2}x)=(-dfrac{1}{2}x-4)(-dfrac{1}{2}x+3)$ ($text{replace $x$ with $-dfrac{1}{2}x$}$)
$text{$y = 0$ for the x-intercepts, so}$
$$
begin{align*}
y&=0\
(-dfrac{1}{2}x-4)&(-dfrac{1}{2}x+3)=0\
-dfrac{1}{3}-4=0 &lor -dfrac{1}{2}x+3=0\
-dfrac{1}{2}x=4 &lor -dfrac{1}{2}x=-3 tag{text{multiply both sides of equation by -2}}\
x=-8 & lor x=6\
end{align*}
$$
$text{Then the x-intercepts are the points $(-8,0)$ and $(6,0)$}$
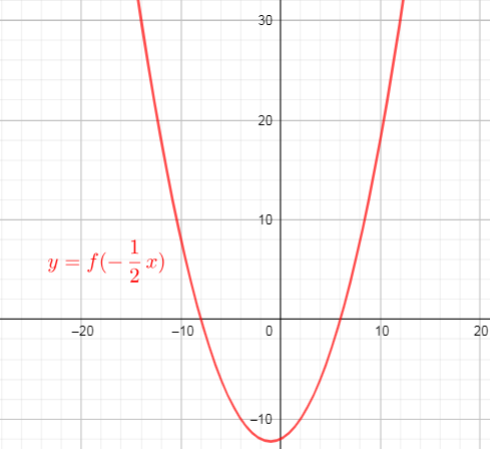
$$
begin{align*}\
y&=f(-(x+1))\
&=(-(x+1)-4)(-(x+1)+3)\ tag{text{replace x with -(x+1)}}\
&=(-x-1-4)(-x-1+3)\
&=(-x-5)(-x+2) \
end{align*}
$$
$text{$y = 0$ for the x-intercepts, so}$
$$
begin{align*}
y&=0\
(-x-5)&(-x+2)=0\
-x-5=0 &lor -x+2=0\
-x=5 &lor -x=-2 tag{text{multiply both sides of equation by -1}}\
x=-5 & lor x=2\
end{align*}
$$
$text{Then the x-intercepts are the points $(-5,0)$ and $(2,0)$}$
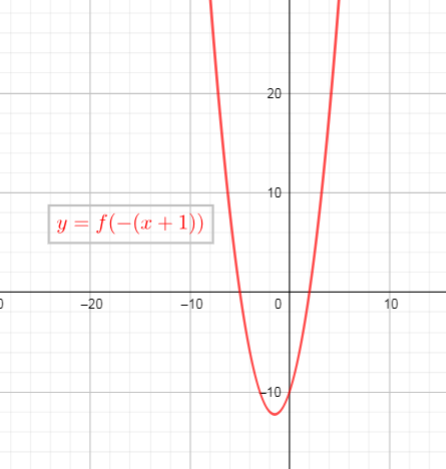
b) $(4,0)$ and $(-,0)$
c) $(-8,0)$ and $(6,0)$
a) $(-5,0)$ and $(2,0)$
domain = ${ xinbold{R};|;xgeq -4}$
range = ${ yinbold{R};|;y<-1}$
a) $y=2f(x)$ means vertical stretching by a factor of 2 $implies$ $y$-values are multiplied by 2
Thus, the domain is unaffected but the range will be multiplied by 2.
domain = ${ xinbold{R};|;xgeq -4}$
range = ${ yinbold{R};|;y<-2}$
domain = ${ xinbold{R};|;xleq 4}$
range = ${ yinbold{R};|;y<-1}$
transformations affecting domain:
horizontal translation 1 unit to the left $implies$ subtract 1 to the $x$-values
domain = ${ xinbold{R};|;xgeq -5}$
transformations affecting range:
vertical stretching by factor 3 and translation 4 units up $implies$ multiply $y$-values by 3 then add 4
$3(-1)+4=1$
range = ${ yinbold{R};|;y< 1}$
transformations affecting the domain:
reflecting the $y$-axis $implies$ multiply $x$ values by $-1$ and reverse inequality symbol
translating 5 units to the right $implies$ add 5 to $x$-values
$-4(-1)+5=9$
domain = ${ xinbold{R};|;xleq 9}$
transformations affecting the range:
reflecting in $x$-axis $implies$ multiply $y$-values by $-1$ and reverse inequality symbol
vertical stretching by factor 2 $implies$ multiply $y$-values by 2
add 1 unit to $y$-values
$(-1)(2)(-1)+1=3$
range = ${ yinbold{R};|;y>3}$
defarraystretch{1.5}%
begin{tabular}{|l|l|}
hline
a) & begin{tabular}[c]{@{}l@{}}domain = ${ xinbold{R};|;xgeq -4}$\ range = ${ yinbold{R};|;y<-2}$end{tabular} \ hline
b) & begin{tabular}[c]{@{}l@{}}domain = ${ xinbold{R};|;xleq 4}$\ range = ${ yinbold{R};|;y<-1}$end{tabular} \ hline
c) & begin{tabular}[c]{@{}l@{}}domain = ${ xinbold{R};|;xgeq -5}$\ range = ${ yinbold{R};|;y3}$end{tabular} \ hline
end{tabular}
end{table}

