
Nelson Functions 11
1st Edition
ISBN: 9780176332037
Textbook solutions
All Solutions
Page 538: Cumulative Review
Exercise 1
Step 1
1 of 2
[begin{gathered}
{text{We shall first determine the type of series}}{text{.}} hfill \
{text{If there’s a common difference between }} hfill \
{text{consecutive terms, then it is arithmetic series}}{text{.}} hfill \
3.2 – 2.8 = 0.4 hfill \
3.6 – 3.2 = 0.4 hfill \
4.0 – 3.6 = 0.4 hfill \
hfill \
{text{Thus, it is an arithmetic series}}{text{. The sum of}} hfill \
{text{an arithmetic series is}} hfill \
hfill \
{S_n} = frac{n}{2} cdot left[ {2{t_1} + left( {n – 1} right)d} right] hfill \
hfill \
{text{In this case,}} hfill \
{t_1} = 2.8 hfill \
d = 0.4 hfill \
n = 21 hfill \
hfill \
{text{Substituting the values to the formula}} hfill \
hfill \
{S_{21}} = frac{{21}}{2}left[ {2left( {2.8} right) + left( {21 – 1} right)left( {0.4} right)} right] hfill \
{S_{21}} = 142.8 hfill \
hfill \
{text{The answer is }}boxed{{mathbf{option;; (a)}}} hfill \
end{gathered} ]
{text{We shall first determine the type of series}}{text{.}} hfill \
{text{If there’s a common difference between }} hfill \
{text{consecutive terms, then it is arithmetic series}}{text{.}} hfill \
3.2 – 2.8 = 0.4 hfill \
3.6 – 3.2 = 0.4 hfill \
4.0 – 3.6 = 0.4 hfill \
hfill \
{text{Thus, it is an arithmetic series}}{text{. The sum of}} hfill \
{text{an arithmetic series is}} hfill \
hfill \
{S_n} = frac{n}{2} cdot left[ {2{t_1} + left( {n – 1} right)d} right] hfill \
hfill \
{text{In this case,}} hfill \
{t_1} = 2.8 hfill \
d = 0.4 hfill \
n = 21 hfill \
hfill \
{text{Substituting the values to the formula}} hfill \
hfill \
{S_{21}} = frac{{21}}{2}left[ {2left( {2.8} right) + left( {21 – 1} right)left( {0.4} right)} right] hfill \
{S_{21}} = 142.8 hfill \
hfill \
{text{The answer is }}boxed{{mathbf{option;; (a)}}} hfill \
end{gathered} ]
Result
2 of 2
a) 142.8
Exercise 2
Step 1
1 of 2
[begin{gathered}
{text{By inspection, we shall determine which series}} hfill \
{text{is NOT geometric}}{text{. Remember that geometric series}} hfill \
{text{should have }}{mathbf{constant ;ratio}}{text{ between consecutive terms}}{text{.}} hfill \
hfill \
{text{a) common ratio is 4}} hfill \
{text{b) common ratio is 0}}{text{.2}} hfill \
{text{c) NO common ratio}} hfill \
{text{d) common ratio is 1}} hfill \
hfill \
{text{Therefore, the sequence that is not geometric is }}boxed{{mathbf{option ;(c)}}} hfill \
hfill \
end{gathered} ]
{text{By inspection, we shall determine which series}} hfill \
{text{is NOT geometric}}{text{. Remember that geometric series}} hfill \
{text{should have }}{mathbf{constant ;ratio}}{text{ between consecutive terms}}{text{.}} hfill \
hfill \
{text{a) common ratio is 4}} hfill \
{text{b) common ratio is 0}}{text{.2}} hfill \
{text{c) NO common ratio}} hfill \
{text{d) common ratio is 1}} hfill \
hfill \
{text{Therefore, the sequence that is not geometric is }}boxed{{mathbf{option ;(c)}}} hfill \
hfill \
end{gathered} ]
Result
2 of 2
c) 2,6,7,21,22, …
Exercise 3
Step 1
1 of 3
[begin{gathered}
{text{We have the sequence}} hfill \
hfill \
{text{1,}} – frac{2}{3},frac{4}{9}, – frac{8}{{27}} hfill \
hfill \
{text{Notice that the sequence has a common ratio of }} hfill \
r = – frac{2}{3}{text{ and }}{t_1} = 1 hfill \
{text{Thus it is a geometric sequence}}{text{. The formula for the}} hfill \
{text{ nth term of geometric sequence is}} hfill \
hfill \
{t_n} = {t_1} cdot {r^{n – 1}} hfill \
{text{ }} hfill \
{text{Therefore, the eighth term }}{t_{8{text{ }}}}{text{is}} hfill \
{t_8} = 1 cdot {left( { – frac{2}{3}} right)^{8 – 1}} = – frac{{128}}{{2187}} hfill \
end{gathered} ]
{text{We have the sequence}} hfill \
hfill \
{text{1,}} – frac{2}{3},frac{4}{9}, – frac{8}{{27}} hfill \
hfill \
{text{Notice that the sequence has a common ratio of }} hfill \
r = – frac{2}{3}{text{ and }}{t_1} = 1 hfill \
{text{Thus it is a geometric sequence}}{text{. The formula for the}} hfill \
{text{ nth term of geometric sequence is}} hfill \
hfill \
{t_n} = {t_1} cdot {r^{n – 1}} hfill \
{text{ }} hfill \
{text{Therefore, the eighth term }}{t_{8{text{ }}}}{text{is}} hfill \
{t_8} = 1 cdot {left( { – frac{2}{3}} right)^{8 – 1}} = – frac{{128}}{{2187}} hfill \
end{gathered} ]
Step 2
2 of 3
The answer is $boxed{bf{option; (c)}}$
Result
3 of 3
c) $-dfrac{128}{2187}$
Exercise 4
Step 1
1 of 2
[begin{gathered}
{text{The first three terms of the sequence}} hfill \
hfill \
8,{text{ }}a,{text{ }}b,{text{ 36}} hfill \
hfill \
{text{form an arithmetic series, so}} hfill \
hfill \
a – 8 = b – a hfill \
{text{The last three terms form a geometric sequence, so}} hfill \
hfill \
frac{b}{a} = frac{{36}}{b} hfill \
hfill \
{text{Let us try each option and see which one satisfies }} hfill \
hfill \
{text{a) }}left( {a,b} right) = left( {1, – 6} right) hfill \
1 – 8 = – 6 – 1,, Rightarrow {text{True}} hfill \
frac{{ – 6}}{1} = frac{{36}}{{ – 6}} Rightarrow {text{ True}} hfill \
therefore ,{text{ option (a) is possible answer}} hfill \
hfill \
{text{b) }}left( {a,b} right) = left( { – 1,6} right) hfill \
– 1 – 8 ne 6 – left( { – 1} right) hfill \
hfill \
{text{c)}},left( {a,b} right) = left( {16,24} right) hfill \
16 – 6 = 24 – 16 Rightarrow {text{True}} hfill \
frac{{24}}{{16}} = frac{{36}}{{24}} Rightarrow {text{ True}} hfill \
{text{option (c) is possible answer}} hfill \
hfill \
{text{d) }}left( {a,b} right) = left( {12,24} right) hfill \
12 – 8 ne 24 – 12 hfill \
hfill \
{text{Therefore, the answers are}} hfill \
boxed{{mathbf{options; (a); and;(c)}}} hfill \
hfill \
hfill \
end{gathered} ]
{text{The first three terms of the sequence}} hfill \
hfill \
8,{text{ }}a,{text{ }}b,{text{ 36}} hfill \
hfill \
{text{form an arithmetic series, so}} hfill \
hfill \
a – 8 = b – a hfill \
{text{The last three terms form a geometric sequence, so}} hfill \
hfill \
frac{b}{a} = frac{{36}}{b} hfill \
hfill \
{text{Let us try each option and see which one satisfies }} hfill \
hfill \
{text{a) }}left( {a,b} right) = left( {1, – 6} right) hfill \
1 – 8 = – 6 – 1,, Rightarrow {text{True}} hfill \
frac{{ – 6}}{1} = frac{{36}}{{ – 6}} Rightarrow {text{ True}} hfill \
therefore ,{text{ option (a) is possible answer}} hfill \
hfill \
{text{b) }}left( {a,b} right) = left( { – 1,6} right) hfill \
– 1 – 8 ne 6 – left( { – 1} right) hfill \
hfill \
{text{c)}},left( {a,b} right) = left( {16,24} right) hfill \
16 – 6 = 24 – 16 Rightarrow {text{True}} hfill \
frac{{24}}{{16}} = frac{{36}}{{24}} Rightarrow {text{ True}} hfill \
{text{option (c) is possible answer}} hfill \
hfill \
{text{d) }}left( {a,b} right) = left( {12,24} right) hfill \
12 – 8 ne 24 – 12 hfill \
hfill \
{text{Therefore, the answers are}} hfill \
boxed{{mathbf{options; (a); and;(c)}}} hfill \
hfill \
hfill \
end{gathered} ]
Result
2 of 2
(a) and (c)
Exercise 5
Step 1
1 of 2
[begin{gathered}
{text{The fifth term of a geometric series is 405}} hfill \
{text{and the sixth term is 1215}}{text{.}} hfill \
{text{Since the ratio of consecutive terms in geometric}} hfill \
{text{series is constant,}} hfill \
r = frac{{1215}}{{405}} = 3 hfill \
hfill \
{text{Using the formula for general term}} hfill \
{t_n} = {t_1} cdot {r^{n – 1}} hfill \
405 = {t_1} cdot {3^{5 – 1}} hfill \
{t_1} = frac{{405}}{{{3^4}}} = 5 hfill \
hfill \
{text{Using the formula for the sum of geometric series}} hfill \
{S_n} = {t_1} cdot frac{{{r^n} – 1}}{{r – 1}} hfill \
{S_9} = 5 cdot frac{{{3^9} – 1}}{{3 – 1}} = 49,205 hfill \
hfill \
{text{The answer is option (c)}} hfill \
end{gathered} ]
{text{The fifth term of a geometric series is 405}} hfill \
{text{and the sixth term is 1215}}{text{.}} hfill \
{text{Since the ratio of consecutive terms in geometric}} hfill \
{text{series is constant,}} hfill \
r = frac{{1215}}{{405}} = 3 hfill \
hfill \
{text{Using the formula for general term}} hfill \
{t_n} = {t_1} cdot {r^{n – 1}} hfill \
405 = {t_1} cdot {3^{5 – 1}} hfill \
{t_1} = frac{{405}}{{{3^4}}} = 5 hfill \
hfill \
{text{Using the formula for the sum of geometric series}} hfill \
{S_n} = {t_1} cdot frac{{{r^n} – 1}}{{r – 1}} hfill \
{S_9} = 5 cdot frac{{{3^9} – 1}}{{3 – 1}} = 49,205 hfill \
hfill \
{text{The answer is option (c)}} hfill \
end{gathered} ]
Result
2 of 2
c) 49 205
Exercise 6
Step 1
1 of 2
[begin{gathered}
{text{The recursive formula is}} hfill \
{t_1} = – 5,{text{ }}{t_n} = – 3{t_{n – 1}} + 8 hfill \
hfill \
{t_1} = – 5 hfill \
{t_2} = – 3left( { – 5} right) + 8 = 23 hfill \
{t_3} = – 3left( {23} right) + 8 = – 61 hfill \
{t_4} = – 3left( { – 61} right) + 8 = 191 hfill \
{t_5} = – 3left( {191} right) + 8 = – 565 hfill \
{t_6} = – 3left( { – 565} right) + 8 = 1703 hfill \
hfill \
{text{Therefore, the answer is option (a)}} hfill \
end{gathered} ]
{text{The recursive formula is}} hfill \
{t_1} = – 5,{text{ }}{t_n} = – 3{t_{n – 1}} + 8 hfill \
hfill \
{t_1} = – 5 hfill \
{t_2} = – 3left( { – 5} right) + 8 = 23 hfill \
{t_3} = – 3left( {23} right) + 8 = – 61 hfill \
{t_4} = – 3left( { – 61} right) + 8 = 191 hfill \
{t_5} = – 3left( {191} right) + 8 = – 565 hfill \
{t_6} = – 3left( { – 565} right) + 8 = 1703 hfill \
hfill \
{text{Therefore, the answer is option (a)}} hfill \
end{gathered} ]
Result
2 of 2
a) $-5$, 23, $-61$, $-565$, 1703
Exercise 7
Step 1
1 of 2
[begin{gathered}
{text{For the binomial expansion}} hfill \
{left( {x – 3} right)^5} hfill \
{text{We can easily see that }} hfill \
{text{first term: }}{x^5} hfill \
{text{last term: }}{left( { – 3} right)^5} = – 243 hfill \
hfill \
{text{Among the options, the one satisfies both}} hfill \
{text{conditions is option (a)}} hfill \
end{gathered} ]
{text{For the binomial expansion}} hfill \
{left( {x – 3} right)^5} hfill \
{text{We can easily see that }} hfill \
{text{first term: }}{x^5} hfill \
{text{last term: }}{left( { – 3} right)^5} = – 243 hfill \
hfill \
{text{Among the options, the one satisfies both}} hfill \
{text{conditions is option (a)}} hfill \
end{gathered} ]
Result
2 of 2
$$
{text{a) }}{x^5} – 15{x^4} + 90{x^3} – 270{x^2} + 405x – 243
$$
{text{a) }}{x^5} – 15{x^4} + 90{x^3} – 270{x^2} + 405x – 243
$$
Exercise 8
Step 1
1 of 4
[begin{gathered}
{text{The amount of radioactive substance after time }}t{text{ }} hfill \
{text{with half-life }}h{text{ is}} hfill \
A = {left( {frac{1}{2}} right)^{frac{t}{h}}} hfill \
hfill \
{text{If }}90% {text{ of the substance has decayed after 15 days, only 10% remained}} hfill \
hfill \
{text{0}}{text{.1 = }}{left( {frac{1}{2}} right)^{frac{{15}}{h}}} hfill \
end{gathered} ]
{text{The amount of radioactive substance after time }}t{text{ }} hfill \
{text{with half-life }}h{text{ is}} hfill \
A = {left( {frac{1}{2}} right)^{frac{t}{h}}} hfill \
hfill \
{text{If }}90% {text{ of the substance has decayed after 15 days, only 10% remained}} hfill \
hfill \
{text{0}}{text{.1 = }}{left( {frac{1}{2}} right)^{frac{{15}}{h}}} hfill \
end{gathered} ]
Step 2
2 of 4
Step 3
3 of 4
Therefore, the half-life is $4.52$ days, the answer is (a).
Result
4 of 4
a) 1.45 days
Exercise 9
Step 1
1 of 3
[begin{gathered}
{text{The future value of a principal investment}}P{text{ }} hfill \
{text{after }}m{text{ compounding periods is with interest rate}} hfill \
{text{per compounding period }}i{text{ is}} hfill \
hfill \
A = P{left( {1 + i} right)^m} hfill \
hfill \
{text{To find }}i{text{ such that }}P = 2A{text{ after 7 years}} hfill \
hfill \
2A = A{left( {1 + i} right)^7} hfill \
2 = {left( {1 + i} right)^7} hfill \
1 + i = {2^{1/7}} hfill \
i = {2^{1/7}} – 1 hfill \
i = 0.104 = 10.4% hfill \
end{gathered} ]
{text{The future value of a principal investment}}P{text{ }} hfill \
{text{after }}m{text{ compounding periods is with interest rate}} hfill \
{text{per compounding period }}i{text{ is}} hfill \
hfill \
A = P{left( {1 + i} right)^m} hfill \
hfill \
{text{To find }}i{text{ such that }}P = 2A{text{ after 7 years}} hfill \
hfill \
2A = A{left( {1 + i} right)^7} hfill \
2 = {left( {1 + i} right)^7} hfill \
1 + i = {2^{1/7}} hfill \
i = {2^{1/7}} – 1 hfill \
i = 0.104 = 10.4% hfill \
end{gathered} ]
Step 2
2 of 3
Therefore, the answer is option (a)
Result
3 of 3
a) $10.4%$
Exercise 10
Step 1
1 of 4
[begin{gathered}
{text{The formula for future value of investment A}} hfill \
{text{starting from the principal }}P,{text{that is compounded}} hfill \
n{text{ times a year at annual interest rate }}r{text{ is}} hfill \
hfill \
A = P{left( {1 + i} right)^m} = P{left( {1 + frac{r}{n}} right)^{nt}} hfill \
{text{In this case,}} hfill \
A = 6546.42 hfill \
P = 5000 hfill \
r = 0.06 hfill \
{text{compounded monthly}} hfill \
i = frac{{0.06}}{{12}} hfill \
m = 12 times t hfill \
hfill \
6546.42 = 5000{left( {1 + frac{{0.06}}{{12}}} right)^{12t}} hfill \
frac{{6546.42}}{{5000}} = {1.005^{12t}} hfill \
hfill \
end{gathered} ]
{text{The formula for future value of investment A}} hfill \
{text{starting from the principal }}P,{text{that is compounded}} hfill \
n{text{ times a year at annual interest rate }}r{text{ is}} hfill \
hfill \
A = P{left( {1 + i} right)^m} = P{left( {1 + frac{r}{n}} right)^{nt}} hfill \
{text{In this case,}} hfill \
A = 6546.42 hfill \
P = 5000 hfill \
r = 0.06 hfill \
{text{compounded monthly}} hfill \
i = frac{{0.06}}{{12}} hfill \
m = 12 times t hfill \
hfill \
6546.42 = 5000{left( {1 + frac{{0.06}}{{12}}} right)^{12t}} hfill \
frac{{6546.42}}{{5000}} = {1.005^{12t}} hfill \
hfill \
end{gathered} ]
Step 2
2 of 4
Step 3
3 of 4
Therefore, it would take 4.5 years. The answer is option (a)
Result
4 of 4
a) 4.5 years
Exercise 11
Step 1
1 of 2
[begin{gathered}
{text{We shall calculate how much is the future value}} hfill \
{text{of an $ 800 quarterly payments for 10 years}} hfill \
{text{compounded quarterly at 8% /a}}{text{.}} hfill \
hfill \
R = 800 hfill \
r = 0.08 hfill \
{text{compounded quarterly}} hfill \
i = frac{{0.08}}{4} = 0.02 hfill \
t = {text{ 10 years}} hfill \
m = 10 times 4 = 40 hfill \
hfill \
{text{Using the formula for present value of annnuity}} hfill \
hfill \
FV = R cdot frac{{{{left( {1 + i} right)}^m} – 1}}{i} hfill \
FV = 800 cdot frac{{{{left( {1 + 0.02} right)}^{40}} – 1}}{{0.02}} hfill \
FV = 48321.59 hfill \
hfill \
{text{The lump-sum payment is $ 50,000}} hfill \
50,000 – 48321.59 = boxed{{mathbf{$ 1678}}{mathbf{.41}}} hfill \
hfill \
{text{Therefore, Marisa will earn $ 1,678}}{text{.41 more}} hfill \
{text{if she would choose the lump-sum payment}}{text{.}} hfill \
hfill \
{text{The answer is option (b)}} hfill \
hfill \
end{gathered} ]
{text{We shall calculate how much is the future value}} hfill \
{text{of an $ 800 quarterly payments for 10 years}} hfill \
{text{compounded quarterly at 8% /a}}{text{.}} hfill \
hfill \
R = 800 hfill \
r = 0.08 hfill \
{text{compounded quarterly}} hfill \
i = frac{{0.08}}{4} = 0.02 hfill \
t = {text{ 10 years}} hfill \
m = 10 times 4 = 40 hfill \
hfill \
{text{Using the formula for present value of annnuity}} hfill \
hfill \
FV = R cdot frac{{{{left( {1 + i} right)}^m} – 1}}{i} hfill \
FV = 800 cdot frac{{{{left( {1 + 0.02} right)}^{40}} – 1}}{{0.02}} hfill \
FV = 48321.59 hfill \
hfill \
{text{The lump-sum payment is $ 50,000}} hfill \
50,000 – 48321.59 = boxed{{mathbf{$ 1678}}{mathbf{.41}}} hfill \
hfill \
{text{Therefore, Marisa will earn $ 1,678}}{text{.41 more}} hfill \
{text{if she would choose the lump-sum payment}}{text{.}} hfill \
hfill \
{text{The answer is option (b)}} hfill \
hfill \
end{gathered} ]
Result
2 of 2
b) $$1,678.41$
Exercise 12
Step 1
1 of 2
[begin{gathered}
{text{Since the common ratio is 1}}{text{.005}} hfill \
{text{for consecutive months, the interest }} hfill \
{text{rate per compounding is}} hfill \
i = 0.005 hfill \
hfill \
{text{For monthly compounding with}} hfill \
{text{annual interest rate }}r{text{ }} hfill \
i = frac{r}{{12}} hfill \
hfill \
r = 12i = 12left( {0.005} right) = 0.06 = 6% hfill \
hfill \
{text{Therefore, the answer is option (d)}} hfill \
hfill \
hfill \
end{gathered} ]
{text{Since the common ratio is 1}}{text{.005}} hfill \
{text{for consecutive months, the interest }} hfill \
{text{rate per compounding is}} hfill \
i = 0.005 hfill \
hfill \
{text{For monthly compounding with}} hfill \
{text{annual interest rate }}r{text{ }} hfill \
i = frac{r}{{12}} hfill \
hfill \
r = 12i = 12left( {0.005} right) = 0.06 = 6% hfill \
hfill \
{text{Therefore, the answer is option (d)}} hfill \
hfill \
hfill \
end{gathered} ]
Result
2 of 2
d) 6%
Exercise 13
Step 1
1 of 4
[begin{gathered}
{text{The selling price of the television is $1894}}{text{. The }} hfill \
{text{finance plan comes with downpayment of $150 }} hfill \
{text{and monthly payment of $113 for 1}}{text{.5 years}}{text{.}} hfill \
{text{We shall calculate the annual interest rate}}{text{.}} hfill \
hfill \
{text{The amount that has to be financed is the difference}} hfill \
{text{between the selling price and the downpayment}} hfill \
{text{1894}} – 150 = 1744 hfill \
hfill \
{text{Thus, 1744 is the present value of the annuity with}} hfill \
{text{regular payments of }}R = 113 hfill \
{text{number of years of }}t = 1.5{text{ years}} hfill \
{text{compounded monthly}} hfill \
{text{number of compounding period of }}m = 1.5 times 12 = 1818 hfill \
{text{interest rate per compounding period of }}i = frac{r}{{12}}{text{ }} hfill \
hfill \
{text{Using the formulfor present value of annuity}} hfill \
PV = R cdot frac{{1 – {{left( {1 + i} right)}^{ – m}}}}{i} hfill \
1744 = 113 cdot frac{{1 – {{left( {1 + frac{r}{{12}}} right)}^{ – 18}}}}{{r/12}} hfill \
frac{{1744}}{{113}} = frac{{1 – {{left( {1 + frac{r}{{12}}} right)}^{ – 18}}}}{{r/12}} hfill \
hfill \
end{gathered} ]
{text{The selling price of the television is $1894}}{text{. The }} hfill \
{text{finance plan comes with downpayment of $150 }} hfill \
{text{and monthly payment of $113 for 1}}{text{.5 years}}{text{.}} hfill \
{text{We shall calculate the annual interest rate}}{text{.}} hfill \
hfill \
{text{The amount that has to be financed is the difference}} hfill \
{text{between the selling price and the downpayment}} hfill \
{text{1894}} – 150 = 1744 hfill \
hfill \
{text{Thus, 1744 is the present value of the annuity with}} hfill \
{text{regular payments of }}R = 113 hfill \
{text{number of years of }}t = 1.5{text{ years}} hfill \
{text{compounded monthly}} hfill \
{text{number of compounding period of }}m = 1.5 times 12 = 1818 hfill \
{text{interest rate per compounding period of }}i = frac{r}{{12}}{text{ }} hfill \
hfill \
{text{Using the formulfor present value of annuity}} hfill \
PV = R cdot frac{{1 – {{left( {1 + i} right)}^{ – m}}}}{i} hfill \
1744 = 113 cdot frac{{1 – {{left( {1 + frac{r}{{12}}} right)}^{ – 18}}}}{{r/12}} hfill \
frac{{1744}}{{113}} = frac{{1 – {{left( {1 + frac{r}{{12}}} right)}^{ – 18}}}}{{r/12}} hfill \
hfill \
end{gathered} ]
Step 2
2 of 4
Step 3
3 of 4
Therefore, the annual interest rate is $20.06%$. The answer is option (c)
Result
4 of 4
c) $20.06%$
Exercise 14
Step 1
1 of 4
[begin{gathered}
{text{First, we shall calculate how much is the downpayment}} hfill \
{text{This is equal to the future value of the annuity with}} hfill \
R = $ 300 hfill \
r = 6% /a hfill \
{text{compounded monthly}} hfill \
t = 4{text{ years}} hfill \
i = frac{{0.06}}{{12}} = 0.005 hfill \
m = 4 times 12 = 48 hfill \
hfill \
{text{Using the formula for the future value of annuity}} hfill \
FV = R cdot frac{{{{left( {1 + i} right)}^m} – 1}}{i} hfill \
FV = 300 cdot frac{{{{left( {1 + 0.005} right)}^{48}} – 1}}{{0.005}} hfill \
FV = 16229.35 hfill \
hfill \
{text{Since the selling price is $56,000, the difference between}} hfill \
{text{this and the downpayment is the amount that has to be financed}} hfill \
56,000 – 16229.35 = 39770.65 hfill \
hfill \
{text{We shall determine how long it takes for his monthly payment}} hfill \
{text{to achieve the present value of 39770}}{text{.65}} hfill \
R = 525 hfill \
r = 8% /a hfill \
{text{compounded monthly}} hfill \
i = frac{{0.08}}{{12}} hfill \
m = 12 times t hfill \
hfill \
{text{The formula for the present value of annuity is}} hfill \
hfill \
PV = R cdot frac{{1 – {{left( {1 + i} right)}^{ – m}}}}{i} hfill \
{text{39770}}{text{.65}} = 525 cdot frac{{1 – {{left( {1 + frac{{0.08}}{{12}}} right)}^{ – m}}}}{{0.08/12}} hfill \
hfill \
end{gathered} ]
{text{First, we shall calculate how much is the downpayment}} hfill \
{text{This is equal to the future value of the annuity with}} hfill \
R = $ 300 hfill \
r = 6% /a hfill \
{text{compounded monthly}} hfill \
t = 4{text{ years}} hfill \
i = frac{{0.06}}{{12}} = 0.005 hfill \
m = 4 times 12 = 48 hfill \
hfill \
{text{Using the formula for the future value of annuity}} hfill \
FV = R cdot frac{{{{left( {1 + i} right)}^m} – 1}}{i} hfill \
FV = 300 cdot frac{{{{left( {1 + 0.005} right)}^{48}} – 1}}{{0.005}} hfill \
FV = 16229.35 hfill \
hfill \
{text{Since the selling price is $56,000, the difference between}} hfill \
{text{this and the downpayment is the amount that has to be financed}} hfill \
56,000 – 16229.35 = 39770.65 hfill \
hfill \
{text{We shall determine how long it takes for his monthly payment}} hfill \
{text{to achieve the present value of 39770}}{text{.65}} hfill \
R = 525 hfill \
r = 8% /a hfill \
{text{compounded monthly}} hfill \
i = frac{{0.08}}{{12}} hfill \
m = 12 times t hfill \
hfill \
{text{The formula for the present value of annuity is}} hfill \
hfill \
PV = R cdot frac{{1 – {{left( {1 + i} right)}^{ – m}}}}{i} hfill \
{text{39770}}{text{.65}} = 525 cdot frac{{1 – {{left( {1 + frac{{0.08}}{{12}}} right)}^{ – m}}}}{{0.08/12}} hfill \
hfill \
end{gathered} ]
Step 2
2 of 4
Step 3
3 of 4
Therefore, it takes around 8.82 years or 8 years and 10 months.
The answer is option (d)
Result
4 of 4
d) 8 years and 10 months
Exercise 15
Step 1
1 of 2
[begin{gathered}
{text{We shall find which option would result in}} hfill \
{text{lesser time to pay a loan}}{text{.}} hfill \
hfill \
{text{a) decrease the regular pament }} hfill \
Rightarrow {text{ more payments is needed and would take longer time}} hfill \
hfill \
{text{b) increase the regular payment and decrease interest rate}} hfill \
Rightarrow ,{text{more amount is paid per period, and the interest paid}} hfill \
{text{will be less, thus, it would take }}{mathbf{shorter}}{text{ }}{mathbf{time}} hfill \
hfill \
{text{c) decrease the regular payment and increase the interest rate}} hfill \
Rightarrow {text{ more payments is needed and the interest paid will be more,}} hfill \
{text{thus it would take longer time}} hfill \
hfill \
{text{d) none of the above}} hfill \
Rightarrow {text{ not the answer because option (b) satisfies the condition}} hfill \
hfill \
{text{Thereofore, the answer is option (b)}} hfill \
end{gathered} ]
{text{We shall find which option would result in}} hfill \
{text{lesser time to pay a loan}}{text{.}} hfill \
hfill \
{text{a) decrease the regular pament }} hfill \
Rightarrow {text{ more payments is needed and would take longer time}} hfill \
hfill \
{text{b) increase the regular payment and decrease interest rate}} hfill \
Rightarrow ,{text{more amount is paid per period, and the interest paid}} hfill \
{text{will be less, thus, it would take }}{mathbf{shorter}}{text{ }}{mathbf{time}} hfill \
hfill \
{text{c) decrease the regular payment and increase the interest rate}} hfill \
Rightarrow {text{ more payments is needed and the interest paid will be more,}} hfill \
{text{thus it would take longer time}} hfill \
hfill \
{text{d) none of the above}} hfill \
Rightarrow {text{ not the answer because option (b) satisfies the condition}} hfill \
hfill \
{text{Thereofore, the answer is option (b)}} hfill \
end{gathered} ]
Result
2 of 2
b) increase the regular payment and decrease the interest rate
Exercise 16
Step 1
1 of 3
We shall find the best statement describing the regular payment in amortized loan. Remember the formula in the amortization spreadsheet.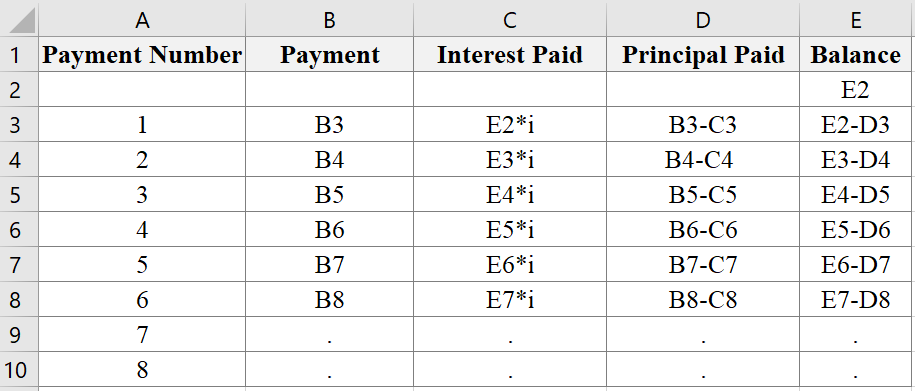
Step 2
2 of 3
Notice that if we add interest paid C3 and the principal paid B3$-$C3, the result is B3 which is the regular payment.
Thus, the regular payment must be the made up of the interest and principal paid.
Therefore, the answer is option (b).
Result
3 of 3
b) the fixed periodic payment made up of interest and principal
Exercise 17
Step 1
1 of 4
[begin{gathered}
{text{The initial dosage is 350 mg and in successive}} hfill \
{text{medication, 350 mg is added but 32% of}} hfill \
{text{the previous one still remains in the body}}{text{.}} hfill \
{text{The recursive formula is therefore,}} hfill \
{text{ }} hfill \
{text{a) }}{t_1} = 350,{text{ }}{t_n} = 350 + 0.32{t_{n – 1}} hfill \
hfill \
{text{b) The amount of medication in his body}} hfill \
{text{will level off at large values of }}n{text{ which we}} hfill \
{text{can obtain by the use of spreadsheets}}{text{.}} hfill \
hfill \
hfill \
end{gathered} ]
{text{The initial dosage is 350 mg and in successive}} hfill \
{text{medication, 350 mg is added but 32% of}} hfill \
{text{the previous one still remains in the body}}{text{.}} hfill \
{text{The recursive formula is therefore,}} hfill \
{text{ }} hfill \
{text{a) }}{t_1} = 350,{text{ }}{t_n} = 350 + 0.32{t_{n – 1}} hfill \
hfill \
{text{b) The amount of medication in his body}} hfill \
{text{will level off at large values of }}n{text{ which we}} hfill \
{text{can obtain by the use of spreadsheets}}{text{.}} hfill \
hfill \
hfill \
end{gathered} ]
Step 2
2 of 4
Step 3
3 of 4
Observe that the amount of drug in the body becomes stable at $514,7059$ mg which is at the 15th dose.
Result
4 of 4
a) $t_1=350$, $t_n=350+0.32t_{n-1}$
b) $514.7059$ mg
c) $15th$ dose
Exercise 18
Step 1
1 of 6
[begin{gathered}
{text{Cowan would like to deposit $ 25 monthly}} hfill \
{text{for 18}} – 4 = 14{text{ years at }}r = 6% /a hfill \
{text{compounded monthly}}{text{.}} hfill \
{text{In this case,}} hfill \
R = 25 hfill \
i = frac{{0.06}}{{12}} = 0.005 hfill \
m = 14 times 12 = 168 hfill \
hfill \
{text{a) We need to show that the monthly payments }}R{text{ }} hfill \
{text{form a geometric series}}{text{. We know that geometric}} hfill \
{text{series must have a constant ratio between consecutive}} hfill \
{text{terms}}{text{. Since the monthly payment is constant, it is}} hfill \
{text{a geometric sequence with common ratio of 1}}{text{.}} hfill \
hfill \
{text{The value of the first deposit increases monthly}} hfill \
{text{with common ratio of 1}}{text{.005}}{text{. Therefore, the }} hfill \
{text{general term }}{t_n}{text{ is }} hfill \
hfill \
{t_n} = {t_1} cdot {r^{n – 1}} hfill \
{t_n} = 25{left( {1.005} right)^{n – 1}} hfill \
end{gathered} ]
{text{Cowan would like to deposit $ 25 monthly}} hfill \
{text{for 18}} – 4 = 14{text{ years at }}r = 6% /a hfill \
{text{compounded monthly}}{text{.}} hfill \
{text{In this case,}} hfill \
R = 25 hfill \
i = frac{{0.06}}{{12}} = 0.005 hfill \
m = 14 times 12 = 168 hfill \
hfill \
{text{a) We need to show that the monthly payments }}R{text{ }} hfill \
{text{form a geometric series}}{text{. We know that geometric}} hfill \
{text{series must have a constant ratio between consecutive}} hfill \
{text{terms}}{text{. Since the monthly payment is constant, it is}} hfill \
{text{a geometric sequence with common ratio of 1}}{text{.}} hfill \
hfill \
{text{The value of the first deposit increases monthly}} hfill \
{text{with common ratio of 1}}{text{.005}}{text{. Therefore, the }} hfill \
{text{general term }}{t_n}{text{ is }} hfill \
hfill \
{t_n} = {t_1} cdot {r^{n – 1}} hfill \
{t_n} = 25{left( {1.005} right)^{n – 1}} hfill \
end{gathered} ]
Step 2
2 of 6
[begin{gathered}
{text{b)}};{text{When Bart turns 18, 14 years have passed}} hfill \
{text{since Mr}}{text{. Cowan started investing}}{text{. Since he}} hfill \
{text{invests monthly, then he would have}} hfill \
m = 14 times 12 = 168{text{ payments}} hfill \
hfill \
{text{The balance in Bart’s fund after 168 payments is}} hfill \
{text{the sum of this geometric series with}} hfill \
{t_1} = 25{text{ and }}r = 1.005 hfill \
hfill \
{S_n} = {t_1} cdot frac{{{r^n} – 1}}{{r – 1}} hfill \
{S_{168}} = 25 cdot frac{{{{1.005}^{168}} – 1}}{{1.005 – 1}} = $ 6557.62 hfill \
end{gathered} ]
{text{b)}};{text{When Bart turns 18, 14 years have passed}} hfill \
{text{since Mr}}{text{. Cowan started investing}}{text{. Since he}} hfill \
{text{invests monthly, then he would have}} hfill \
m = 14 times 12 = 168{text{ payments}} hfill \
hfill \
{text{The balance in Bart’s fund after 168 payments is}} hfill \
{text{the sum of this geometric series with}} hfill \
{t_1} = 25{text{ and }}r = 1.005 hfill \
hfill \
{S_n} = {t_1} cdot frac{{{r^n} – 1}}{{r – 1}} hfill \
{S_{168}} = 25 cdot frac{{{{1.005}^{168}} – 1}}{{1.005 – 1}} = $ 6557.62 hfill \
end{gathered} ]
Step 3
3 of 6
c) We shall create a spreadsheet containing the future value of each payment and them in order to verify our answer i part (b).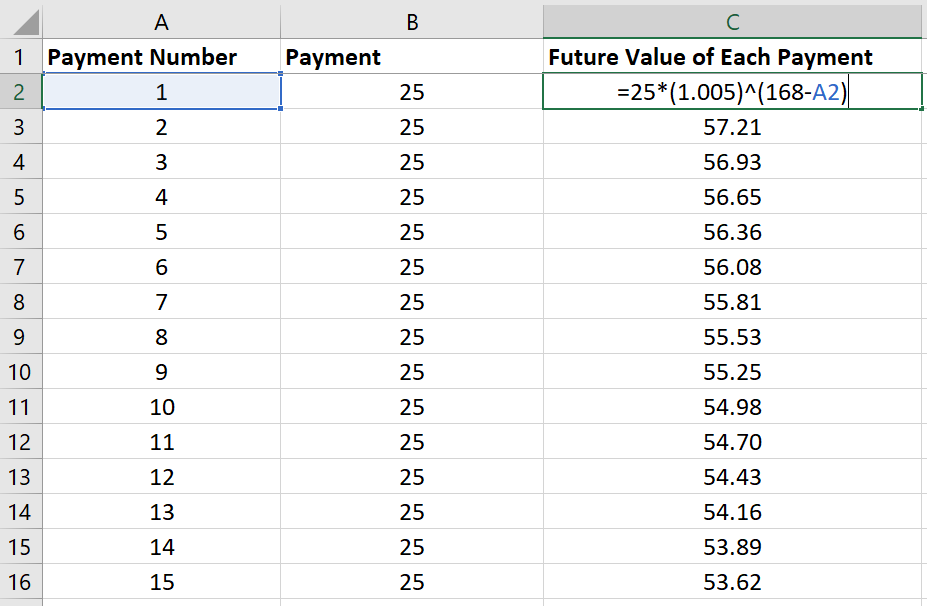
Step 4
4 of 6
Step 5
5 of 6
[begin{gathered}
{text{d) If Mr}}{text{. Cowan, deposited $50 instead of $25}} hfill \
{S_n} = {t_1} cdot frac{{{r^n} – 1}}{{r – 1}} hfill \
{S_{168}} = 50 cdot frac{{{{1.005}^{168}} – 1}}{{1.005 – 1}} = $ 13,115.24 hfill \
end{gathered} ]
{text{d) If Mr}}{text{. Cowan, deposited $50 instead of $25}} hfill \
{S_n} = {t_1} cdot frac{{{r^n} – 1}}{{r – 1}} hfill \
{S_{168}} = 50 cdot frac{{{{1.005}^{168}} – 1}}{{1.005 – 1}} = $ 13,115.24 hfill \
end{gathered} ]
Result
6 of 6
a) $t_n=25(1.005)^{n-1}$
b) $168$ payments, $S_{168}=$6557.62$
c) see spreadsheet
d) $$13,115.24$
unlock

