Domain= $left{ 1900,1920,1940,1960,1980,2000right}$

Range =$left{ 47.3, 54.1, 62.9, 69.7, 73.7, 77.0right}$

Domain=$left{-5,-1,0,3 right}$

Range=$left{9,15,17,23 right}$

Domain=$left{-4,0,3,5 right}$

Range=$left{ -1,0,3,5,7right}$

b) range = ${$ 47.3, 54.1, 62.9, 73.7, 77.0 $}$

c) domain = ${$ -4, 0, 3, 5 $}$

range = ${$ -1, 0, 3, 5, 7 $}$

Domain=$left{pm10,pm8,pm6,pm4,pm2,0 right}$

Range=$left{ -8,-7,-6,-5,-4,-2,0,2,4,8right}$

Domain=$left{ x| xin Rright}$

Range=$left{ y| yin Rright}$

Domain=$left{x| xin R right}$

Range=$left{y| ygeq-8 right}$

Domain=$left{ x|-6leq xleq6right}$

Range=$left{ y|-6leq yleq6right}$

Domain=$left{ x| xleq6right}$

Range=$left{y| ygeq-2 right}$

Domain=$left{x| xgeq-10 right}$

Range=$left{y|y=-6, -2leq ytextless2, ygeq4 right}$

range = ${-8$, $-7$, $-6$, $-5$, $-4$, $-2$, 0, 4, 8 $}$

b) domain = ${ xin bold{R}}$ , range = ${ yinbold{R}}$

c) domain = ${xinbold{R}}$ , range = ${ yinbold{R};|;ygeq-8}$

d) domain = ${ xinbold{R};|;-6leq x leq 6}$

range = ${ yinbold{R};|;-6leq yleq 6}$

e) domain = ${ xin bold{R};|;xleq 6}$
range = ${yinbold{R};|;ygeq -2}$

f) domain = ${ xinbold{R};|;xgeq -10}$
range = ${ yinbold{R};|;y=-6, -2leq y 4}$

domain = ${bold{R}}$

The range is the set of all possible values of $y$. From the graph, notice that $y$ can take values greater than $-3$. Thus, the range is

range = ${ yinbold{R};|;ygeq -3}$

range = ${ yinbold{R};|;ygeq -3}$

b) The domain is the set of all possible values of $x$. From the graph, we see that

domain = ${ xinbold{R};|;0<xleq 500}$

The range is the set of all possible values of $y$. From the graph, we see that

range = ${$ 0.52, 0.93, 1.20, 1.86, 2.55 $}$

b) domain = ${ xinbold{R};|;0<xleq 500}$
range = ${$ 0.52, 0.93, 1.20, 1.86, 2.55 $}$

Table is:

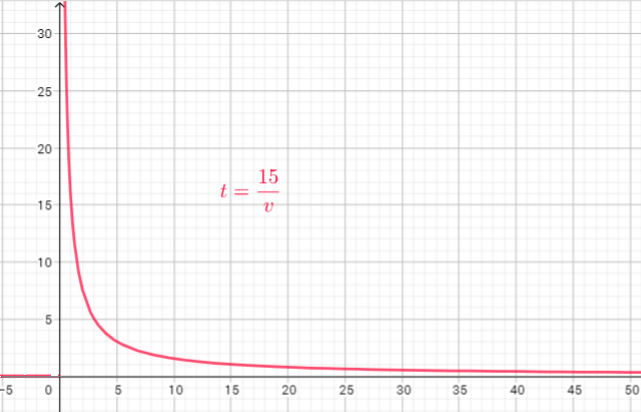
Domain of this function is set of v-coordinates, and range is the set of t-coordinates

Domain=$left { vin R| vtextgreater0 right}$

Range=$left{ tin R| t text{textgreater} 0 right}$

domain = ${ vinbold{R};|;v>0}$

range = ${ tinbold{R};|;t>0}$

domain = ${xinbold{R};|;-6leq xleq 6}$

Range is the set of all possible values of $y$

range = ${yinbold{R};|;-6leq yleq 6}$

b) domain = ${ xinbold{R};|;-6leq xleq 6}$

range = ${ yinbold{R};|;-6leq yleq 6}$

c) not a function; It does not pass vertical line test.

Function which describe coffee dripping into a 10-cup carafe at a rate of
1 mL/s is $V(t)=t$,

Domain=$left{tin R |0leq tleq 2500 right}$

Range=$left{Vin R |0leq Vleq 2500 right}$

domain = ${ tinbold{R};|;leq tleq 2500}$

range = ${Vinbold{R};|;0leq Vleq 2500}$

Domain of this function is the set of x-coordinates , and range of this function is the set of y-coordinates.

Domain=$left{ x| xin R right}$

Range=$left{ y| yin R right}$

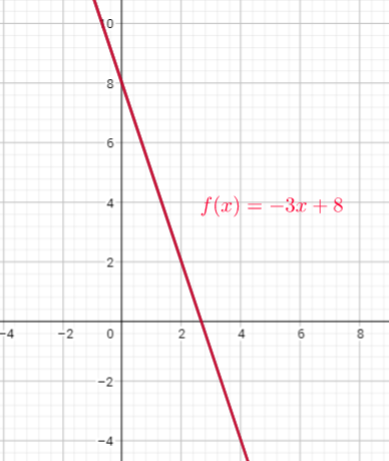
Domain of this function is the set of x-coordinates , and range of this function is the set of y-coordinates.

Domain=$left{ x| xin R right}$

Range=$left{ y| yleq4 right}$

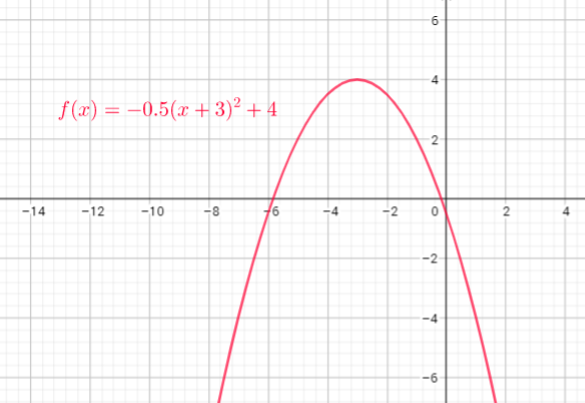
Domain of this function is the set of x-coordinates , and range of this function is the set of y-coordinates.

Domain=$left{ x| xgeq1 right}$

Range=$left{ y| ygeq0 right}$

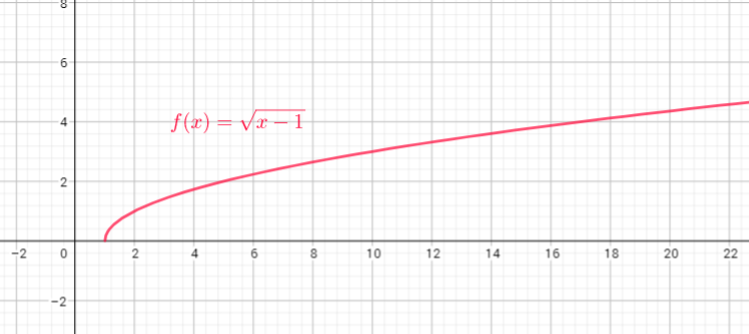
Domain of this function is the set of x-coordinates , and range of this function is the set of y-coordinates.

Domain=$left{ x| xin R right}$

Range=$left{ y| ygeq-5 right}$

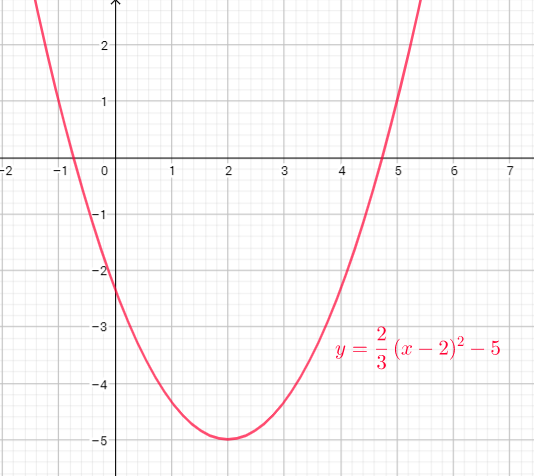
Domain of this function is the set of x-coordinates , and range of this function is the set of y-coordinates.

Domain=$left{ x| xin R right}$

Range=$left{ y| yin R right}$

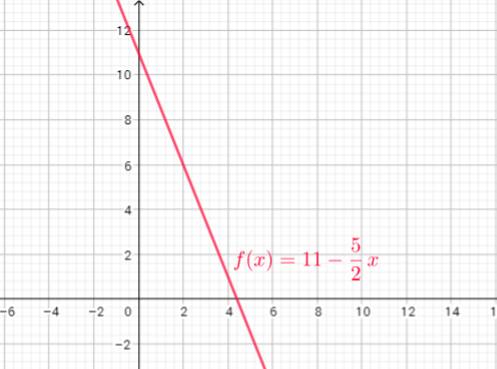
Domain of this function is the set of x-coordinates , and range of this function is the set of y-coordinates.

Domain=$left{ x| xleq5 right}$

Range=$left{ y| ygeq0 right}$

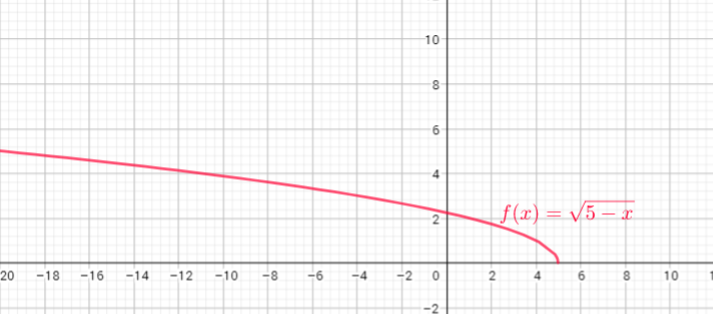
b) domain = ${ xinbold{R}}$ , range = ${yinbold{R};|;yleq 4}$

c) domain = ${ xinbold{R};|;xgeq 1}$ , range = ${ yinbold{R};|;ygeq 0}$

d) domain = ${ xinbold{R}}$ , range = ${ yinbold{R};|;ygeq-5}$

e) domain = ${ xinbold{R}}$, range = ${yinbold{R}}$

f) domain = ${ xinbold{R};|;xleq 5}$ , range = ${ yinbold{R};|;ygeq 0}$

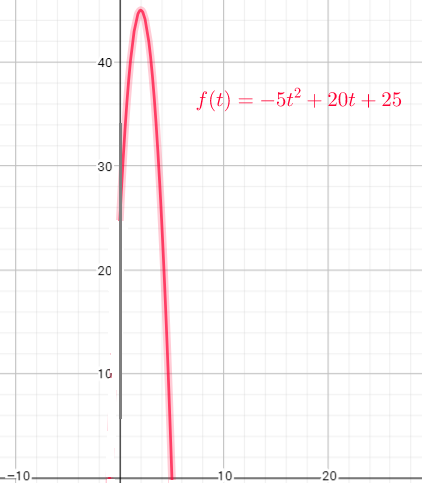
From the graph we can see

Domain=$left{ tin R| 0leq t leq 5right}=left{ 0,1,2,3,4,5right}$

Range=$left{yin R| 0leq y leq 45right}=left{0,1,2,3,4,…,44,45 right}$

$f(t) = at^{2}+bcdot t + f(0)$, where $f(0)$ is the initial height and $b$ is the initial velocity and $t$- time.

Equation is:

$f(t)=at^{2}+bt+f(0)$

if $t=0$, then $f(0)=25$

If $t=2$, then $f(2)=45$, so

$f(2)=45=acdot2^{2}+bcdot2+25$ solve this equation by t

$acdot4+2b=45-25$

$4a+2b=20$ divide both side by 2

$2a+b=10$

If $t=5$, then $f(5)=5$, so

$f(5)=acdot5^{2}+bcdot5+25$

$0=25a+5b+25$

$25a+5b=-25$ divide both side by -5

$-5a-b=5$

Now, we need solve system of two equations:

$-5a-b=5$

$2a+b=10$

add equation 1 and equation 2

$-3a=15$ divide both side by $-3$

$a=-5$ substitute in second (or first ) equation and find $b$

$2cdot(-5)+b=10$

$-10+b=10$ add 10 to both side

$b=10+10$

$b=20$

Now, we have $a=-5, b=20$ and $f(0)=25$, substitute in equation $f(t)=at^{2}+bt+f(0)$ and get:

$f(t)=-5t^{2}+20t+25$

b) domain = ${ tinbold{R};|;0leq tleq 5}$

range = ${ hinbold{R};|;0leq hleq 45}$

c) $h=-5t^2+20t+25$

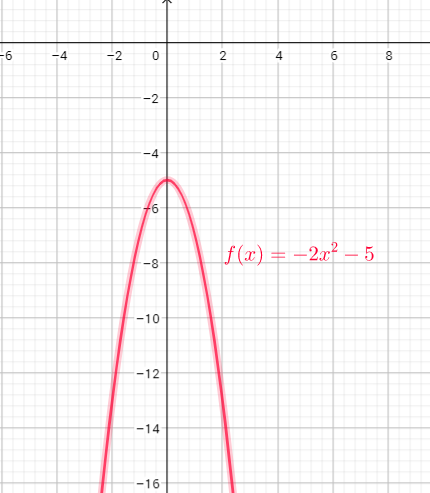
Domain of the function is the set of x-coordinates, and range is the set of y-coordinates.

Domain=$left{ x| xin Rright}$

Range=$left{y|yin R right}$

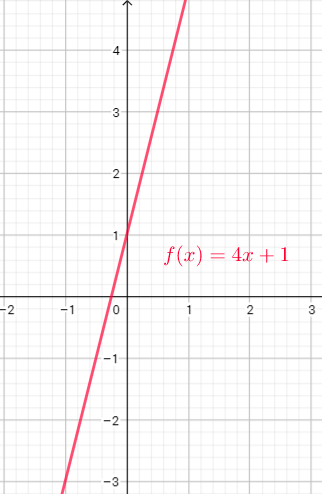
Domain of the function is the set of x-coordinates, and range is the set of y-coordinates.

This function is defined for $x-2geq0$ or $xgeq2$, and range of this function is each $ygeq0$

Domain= $left{ xin R| xgeq2 right}$

Range=$left{yin R | ygeq0 right}$

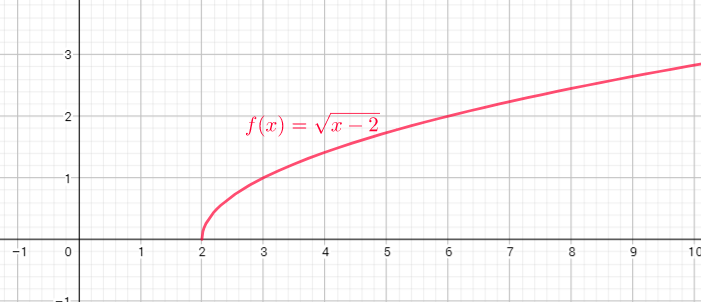
Domain of the function is the set of x-coordinates, and range is the set of y-coordinates.

Domain= $left{ x| xin R right}$

Range=$left{yin R | ygeq-4 right}$

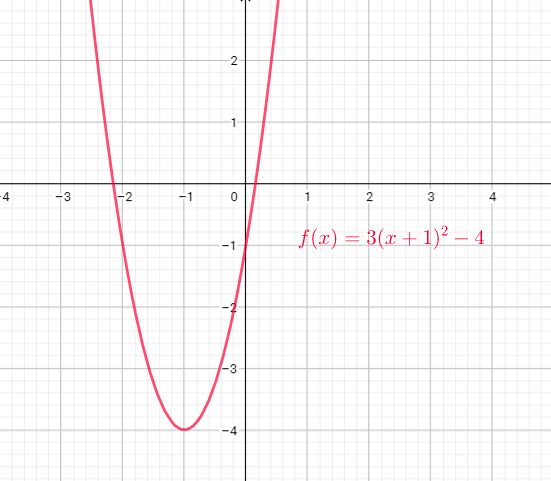
Domain of the function is the set of x-coordinates, and range is the set of y-coordinates.

Domain= $left{ x| xin R right}$

Range=$left{yin R | yleq-5 right}$

b) domain = ${ xinbold{R};|;xgeq 2}$ , range = ${yinbold{R};|;ygeq 0 }$

c) domain = ${ xinbold{R}}$ , range = ${ yinbold{R};|;ygeq -4}$

d) domain = ${ xinbold{R}}$ , range = ${yinbold{R};|;yleq -5}$

Domain of the functin is the set of x-coordinates, and range is the set of y-coorinates

This function is defned for $3-xgeq0$ or $xleq3$

Domain=$left{xin R| xleq3 right}$

Range=$left{ yin R | ygeq2right}$

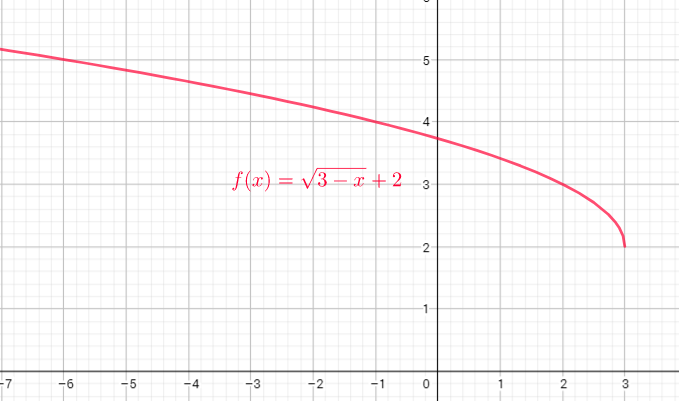
Domain of the function is the set of x-coordinates, and range is the set of y-coorinates

Domain=$left{xin R right}$

Range=$left{ yin R | ygeq-2.25 right}$

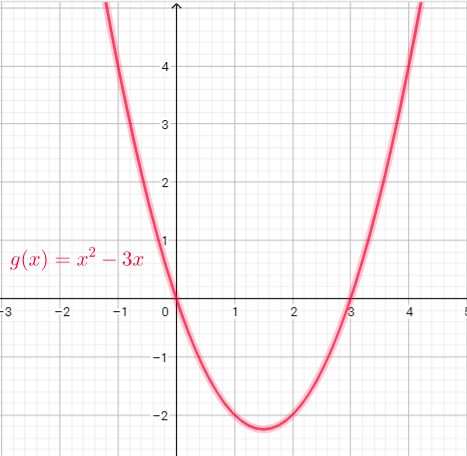
Domain of the functin is the set of x-coordinates, and range is the set of y-coorinates

This function is defned for $x^{2}ne0$ or $x$

Domain=$left{xin R| xne0 right}$

Range=$left{ yin R | ytextgreater0 right}$

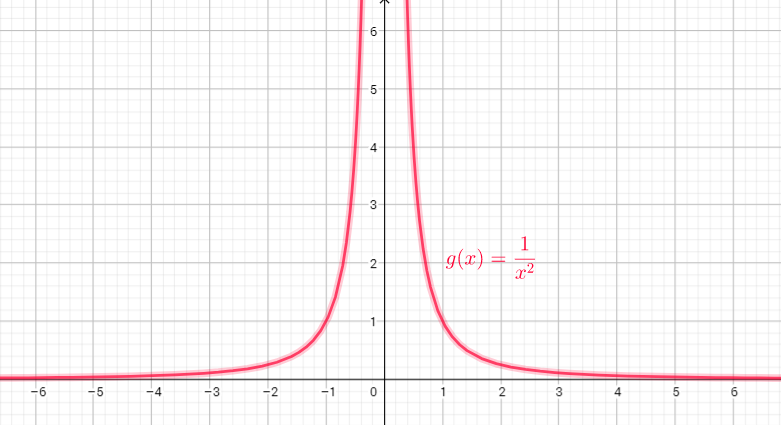
Domain of the functin is the set of x-coordinates, and range is the set of y-coorinates

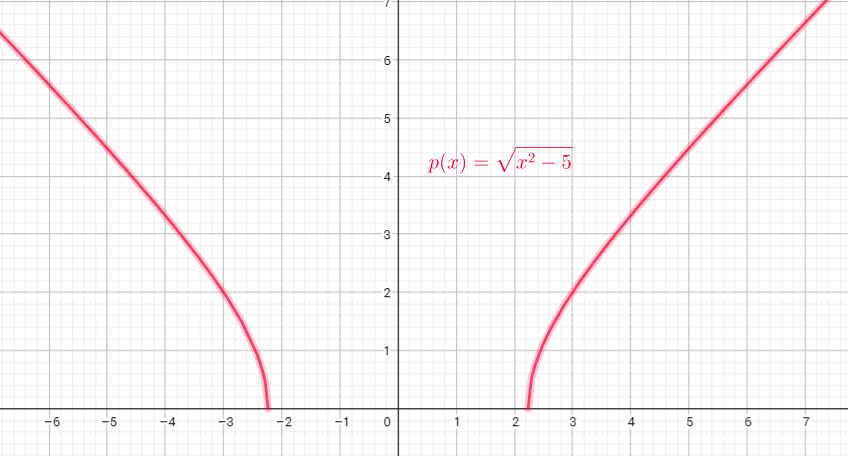
This function is defned for $x^{2}-5geq0$ or $xleq-sqrt{5}$ and $xgeq sqrt{5}$

Domain=$left{xin R| xleq-sqrt{5} and xgeq sqrt{5}
right}$

Range=$left{ yin R | ygeq0 right}$

b) domain = ${ xinbold{R}}$ , range = ${ yinbold{R};|;ygeq-2.25}$

c) domain = ${ xinbold{R};|;xneq 0}$ , range = ${ yinbold{R};|;ygeq 0}$

d) domain = ${ xinbold{R};|;xleq -sqrt{5}, xgeq sqrt{5}}$

range = ${ yinbold{R};|;ygeq 0}$

$3w+2l=450$

Express the length in terms of the width

$l=dfrac{450-3w}{2}$

We need to express the area in terms of the width. The area of a rectangle is product of length and width

$A = ltimes w$

$$
A=left(dfrac{450-3w}{2}right) w
$$

$w>0$

$l>0implies dfrac{450-3w}{2}>0$

$450-3w>0$

$-3w>-450$

When you divide/multiply both sides by negative number, the direction of inequality will change.

$w<dfrac{450}{3}$

$w<150$

Therefore

domain = ${winbold{R};|;0<w0$. To obtain the upper bound, find the value of $A$ at the vertex, that is, halfway between $w=0$ and $w=150$ which is $w=75$

$A=left(dfrac{450-3(75)}{2}right)(75)=8437.5$

Therefore, the range is

range = ${ Ainbold{R};|;0<Aleq 8437.5}$

$l=dfrac{450-3w}{2}=dfrac{450-3(75)}{2}=112.5$

Therefore, the dimensions that maximizes the area is

$l=112.5$ m and $w=75$ m

b) domain = ${ winbold{R};|;0<w<150}$

range = ${ Ainbold{R};|;0<Aleq 8437.5}$

c) $l=112.5$ m , $w=75$ m

Function is $f(x)=4-3x$

If $x=-3$, then $f(x)=4-3(-3)=4+9=13$

If $x=-1$, then $f(x)=4-3(-1)=4+3=7$

If $x=0$, then $f(x)=4-3cdot0=4+0=4$

If $x=2.5$, then $f(x)=4-3cdot2.5=4-7.5=-3.5$

If $x=6$, then $f(x)=4-3cdot6=4-18=-14$

Range of this function is :

Range=$left{ -14,-3.5, 4,7,13right}$

Function is $f(x)=2x^{2}-3x+1$

If $x=-3$, then $f(x)=2(-3)^{2}-3(-3)+1=2cdot9+9+1=18+10=28$

If $x=-1$, then $f(x)=2(-1)^{2}-3(-1)+1=2cdot1+3+1=2+4=6$

If $x=0$, then $f(x)=2cdot0^{2}-3cdot0+1=0+0+1=1$

If $x=2.5$, then $f(x)=2cdot2.5^{2}-3cdot2.5+1=12.5-7.5+1=6$

If $x=6$, then $f(x)=2cdot6^{2}-3cdot6+1=72-18+1=55$

Range of this function is :

Range=$left{ 1,6,28,55right}$

b) ${$ 1, 6, 28, 55 $}$

In table of values, domain are the values in $x$-column while the range are that of $y$-column.

In graphs, domain correspond to the $x$-coordinates while the range are that of $y$-coordinates.

In an equation, domain is the restriction for the value of $x$, for example

$y=x^2$ , $xgeq 0$

Here, the domain is explicitly given. If not stated, we can assume the domain to be ${xinbold{R}}$ except those values of $x$ that could make the denominator of zero. For example,

$y=dfrac{5}{x-1}$

The domain here is all real numbers except $x=1$.

In table of values, domain are the values in $x$-column while the range are that of $y$-column.

In graphs, domain correspond to the $x$-coordinates while the range are that of $y$-coordinates.

In an equation, unless the restriction is explicitly specified, the domain is all real numbers except those $x$-values that make the denominator zero.

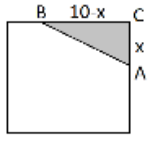
$AB^{2}=BC^{2}+AC^{2}$

$AB^{2}=(10-x)^{2}+x^{2}$

so, area of the inner square is $Area=AB cdot AB=AB^{2}$

now, can conclude area of the inner square is $Area=x^{2}+(10-x)^{2}$ or $Area=2x^{2}-20x+100$

$A(0)=2cdot0^{2}-20cdot0+100=0-0+100=100$

$A(5)=2cdot5^{2}-20cdot5+100=2cdot25-100+100=50$

Now can conclude,

Domain =$left{ xin R| 0leq xleq10right}$

Range=$left{Ain R| 50leq Aleq100 right}$

We calculate n part a) side of the inscribed square is $AB=sqrt{x^{2}+(10-x)^{2}}$. Now can determine perimeter of the inscribed square as a function of $x$:

$$
P=4cdot AB=4cdotsqrt{x^{2}+(10-x)^{2}}
$$

$P(5)=4cdotsqrt{5^{2}+(10-5)^{2}}=4cdotsqrt{25+25}=4cdotsqrt{50}=4cdot5sqrt{2}=20sqrt{2}$

Domain= $left{xin R| 0leq xleq10 right}$

Range=$left{ Pin R|20sqrt{2}leq Pleq40right}$

b) domain = ${ xinbold{R};|;0leq xleq 10}$

range = ${ Ainbold{R};|;50leq Aleq 100}$

c) $P=4sqrt{x^2+(10-x)^2}$

d) domain = ${ xinbold{R};|;0leq xleq 10}$

range = ${ Pinbold{R};|;50sqrt{2}leq Pleq 400}$