begin{table}[]
center
defarraystretch{2.4}%
begin{tabular}{llll}
hline
multicolumn{1}{|l|}{begin{tabular}[c]{@{}l@{}}principal angle;$theta$end{tabular}} & multicolumn{1}{l|}{Quadrant} & multicolumn{1}{l|}{begin{tabular}[c]{@{}l@{}}sign $(cos theta, sin theta)$end{tabular}} & multicolumn{1}{l|}{begin{tabular}[c]{@{}l@{}}reference acute angle $beta$end{tabular}} \ hline
multicolumn{1}{|l|}{$0< theta<90^circ$} & multicolumn{1}{l|}{I} & multicolumn{1}{l|}{$(+,+)$} & multicolumn{1}{l|}{$theta$} \ hline
multicolumn{1}{|l|}{$90^circ <theta < 180^circ$} & multicolumn{1}{l|}{II} & multicolumn{1}{l|}{$(-,+)$} & multicolumn{1}{l|}{$180^circ-theta$} \ hline
multicolumn{1}{|l|}{$180^circ <theta < 270^circ$} & multicolumn{1}{l|}{III} & multicolumn{1}{l|}{$(-,-)$} & multicolumn{1}{l|}{$theta-180^circ$} \ hline
multicolumn{1}{|l|}{$270^circ < theta <360^circ$} & multicolumn{1}{l|}{IV} & multicolumn{1}{l|}{$(+,-)$} & multicolumn{1}{l|}{$360^circ-theta$} \ hline
& & & \ cline{1-3}
multicolumn{1}{|l|}{begin{tabular}[c]{@{}l@{}}reference acute angle $beta$ end{tabular}} & multicolumn{1}{l|}{$cos beta$} & multicolumn{1}{l|}{$sin beta$} & \ cline{1-3}
multicolumn{1}{|l|}{30$^circ$} & multicolumn{1}{l|}{$dfrac{sqrt{3}}{2}$} & multicolumn{1}{l|}{$dfrac{1}{2}$} & \ cline{1-3}
multicolumn{1}{|l|}{45$^circ$} & multicolumn{1}{l|}{$dfrac{sqrt{2}}{2}$} & multicolumn{1}{l|}{$dfrac{sqrt{2}}{2}$} & \ cline{1-3}
multicolumn{1}{|l|}{60$^circ$} & multicolumn{1}{l|}{$dfrac{1}{2}$} & multicolumn{1}{l|}{$dfrac{sqrt{3}}{2}$} & \ cline{1-3}
& & &
end{tabular}
end{table}

a) $315^circ$ is within $270^circ <theta < 360^circ$, so it lies in QIV

reference acute angle $beta =360^circ-315^circ=45^circ$

$sin 315^circ <0$ in QIV

b) $110^circ$ is within $90^circ < theta 0$

$cos 110^circ<0$

Therefore,

$tan 110^circ<0$ in QII

c) $285^circ$ is within $270^circ < theta 0$ in QIV

d) $225^circ$ is within $180^circ < theta 0$ in QIII

a) QIV, $45^circ$, negative

b) QII, $70^circ$, negative

c) QIV, $75^circ$, positive

d) QIII, $45^circ$, positive

i) The sketch is shown as follows.

ii) Use Pythagorean formula: $c^2=a^2+b^2$

$r=sqrt{5^2+11^2}=12.1$

iii) $sin theta =dfrac{text{opposite side}}{text{hypotenuse}}=dfrac{11}{12.1}=0.91$

$cos theta =dfrac{text{adjacent side}}{text{hypotenuse}}=dfrac{5}{12.1}=0.41$

$tan theta=dfrac{text{adjacent side}}{text{opposite side}}=dfrac{11}{5}$

iv) We can calculate $theta$ using inverse tangent function.

$$
theta = tan^{-1}left(dfrac{11}{5}right)=66^circ
$$

b) Do similar approach as in part (a)

(i) sketch is shown below

(ii) $r=sqrt{(-8)^2+3^2}=sqrt{73}=8.5$

(iii) Terminal point of $theta$ is in QII where $sin theta>0$, $cos theta <0$

$sin theta =dfrac{3}{8.5}=0.35$

$cos theta=dfrac{-8}{8.5}=-0.94$

$tan theta=dfrac{3}{-8}=-0.38$

(iv) $beta = tan^{-1}left(dfrac{3}{8}right)=21^circ$

$$
theta=180-beta=180-21=159^circ
$$

c) Do similar approach as in part (a)

(i) sketch is shown below

(ii) $r=sqrt{(-5)^2+8^2}=sqrt{89}=9.4$

(iii) Terminal point of $theta$ is in QIII where $sin theta<0$, $cos theta <0$

$sin theta =-dfrac{8}{9.4}=-0.85$

$cos theta=-dfrac{5}{9.4}=-0.53$

$tan theta=dfrac{-8}{-5}=1.6$

(iv) $beta = tan^{-1}left(1.6right)=58^circ$

$$
theta=180+beta=180-58=238^circ
$$

d) Do similar approach as in part (a)

(i) sketch is shown below

(ii) $r=sqrt{(6)^2+(-8)^2}=10$

(iii) Terminal point of $theta$ is in QIV where $sin theta0$

$sin theta =-dfrac{8}{10}=-0.8$

$cos theta=dfrac{6}{10}=0.6$

$tan theta=dfrac{-8}{6}=-1.33$

(iv) $beta = tan^{-1}left(1.33right)=53^circ$

$$
theta=360-beta=360-53=307^circ
$$

The method in Example 3 can be outlined as follows.

1) Sketch the location of the terminal point that corresponds to the given angle in a unit circle $(r=sqrt{x^2+y^2}=1)$.

2) Determine the coordinates of the terminal point $(x,y)$.

3) Use the following formula to evaluate the primary trigonometric functions.

$cos theta = dfrac{x}{r}$

$sin theta=dfrac{y}{r}$

$$
tan theta=dfrac{y}{x}
$$

a) The terminal point $(x,y)$ that corresponds to $theta=180^circ$ is $(-1,0)$

$cos theta =dfrac{x}{r}=dfrac{-1}{1}=-1$

$sin theta=dfrac{y}{r}=dfrac{0}{1}=0$

$$
tan theta=dfrac{y}{x}=dfrac{0}{-1}=0
$$

b) The terminal point $(x,y)$ that corresponds to $theta=270^circ$ is $(0,-1)$

$cos theta =dfrac{x}{r}=dfrac{0}{1}=0$

$sin theta=dfrac{y}{r}=dfrac{-1}{1}=-1$

$$
tan theta=dfrac{y}{x}=dfrac{-1}{0}=text{undefined}
$$

c) The terminal point $(x,y)$ that corresponds to $theta=360^circ$ is $(1,0)$

$cos theta =dfrac{x}{r}=dfrac{1}{1}=1$

$sin theta=dfrac{y}{r}=dfrac{0}{1}=0$

$$
tan theta=dfrac{y}{x}=dfrac{0}{1}=0
$$

a) $cos 180^circ = -1$ ; $sin 180^circ=0$ ; $tan 180^circ=0$

b) $cos 270^circ=0$ ; $sin 270^circ=-1$ ; $tan 270^circ$ = undefined

c) $cos 360^circ=1$ ; $sin 360^circ=0$ ; $tan 360^circ=0$

${bold{Steps; in; Evaluating; Trigonometric; Functions}}$

1) If $theta$ is within the interval $0leq thetaleq 360^circ$, proceed to step 2. If not, find a coterminal angle $alpha$ within the range using the formula

coterminal angle $alpha=theta+360^circ cdot n$ where $n$ is an integer.

2) Determine which quadrant does the terminal point of $theta$ lie. Based on the quadrant, you can find the reference acute angle $beta$ according to the table below.

3) Evaluate the value of the trigonometric function based on the reference acute angle. You should remember its value for special angles such as $30^circ$, $45^circ$ and $60^circ$.

4) Determine the sign of the trigonometric function based on its quadrant.

begin{table}[]
center
defarraystretch{2.4}%
begin{tabular}{llll}
hline
multicolumn{1}{|l|}{begin{tabular}[c]{@{}l@{}}principal angle;$theta$end{tabular}} & multicolumn{1}{l|}{Quadrant} & multicolumn{1}{l|}{begin{tabular}[c]{@{}l@{}}sign $(cos theta, sin theta)$end{tabular}} & multicolumn{1}{l|}{begin{tabular}[c]{@{}l@{}}reference acute angle $beta$end{tabular}} \ hline
multicolumn{1}{|l|}{$0< theta<90^circ$} & multicolumn{1}{l|}{I} & multicolumn{1}{l|}{$(+,+)$} & multicolumn{1}{l|}{$theta$} \ hline
multicolumn{1}{|l|}{$90^circ <theta < 180^circ$} & multicolumn{1}{l|}{II} & multicolumn{1}{l|}{$(-,+)$} & multicolumn{1}{l|}{$180^circ-theta$} \ hline
multicolumn{1}{|l|}{$180^circ <theta < 270^circ$} & multicolumn{1}{l|}{III} & multicolumn{1}{l|}{$(-,-)$} & multicolumn{1}{l|}{$theta-180^circ$} \ hline
multicolumn{1}{|l|}{$270^circ < theta <360^circ$} & multicolumn{1}{l|}{IV} & multicolumn{1}{l|}{$(+,-)$} & multicolumn{1}{l|}{$360^circ-theta$} \ hline
& & & \ cline{1-3}
multicolumn{1}{|l|}{begin{tabular}[c]{@{}l@{}}reference acute angle $beta$ end{tabular}} & multicolumn{1}{l|}{$cos beta$} & multicolumn{1}{l|}{$sin beta$} & \ cline{1-3}
multicolumn{1}{|l|}{30$^circ$} & multicolumn{1}{l|}{$dfrac{sqrt{3}}{2}$} & multicolumn{1}{l|}{$dfrac{1}{2}$} & \ cline{1-3}
multicolumn{1}{|l|}{45$^circ$} & multicolumn{1}{l|}{$dfrac{sqrt{2}}{2}$} & multicolumn{1}{l|}{$dfrac{sqrt{2}}{2}$} & \ cline{1-3}
multicolumn{1}{|l|}{60$^circ$} & multicolumn{1}{l|}{$dfrac{1}{2}$} & multicolumn{1}{l|}{$dfrac{sqrt{3}}{2}$} & \ cline{1-3}
& & &
end{tabular}
end{table}

a) $160^circ$ is within $90< theta0$, thus, an equivalent expression would be,

$$
sin 160^circ=sin 20^circ
$$

b) $300^circ$ is within $270< theta0$, thus, an equivalent expression would be that in QI

Therefore,

$$
cos300^circ=cos 60^circ
$$

c) $110^circ$ is within $90^circ < theta < 180^circ$ so it lies in QII where the reference angle is

$beta=180^circ-theta=180^circ-110^circ=70^circ$

In QII, $tan theta <0$, thus, an equivalent expression would be

$$
tan 110^circ=-tan 70^circ
$$

d) $350^circ$ is within $270^circ < theta < 360^circ$ so it lies in QIV where the reference angle is

$beta =360^circ-theta=360^circ-350^circ=10^circ$

In QIV, $sin theta<0$, thus an equivalent expression would be.

$$
sin 350^circ=-sin 10^circ
$$

a) $sin 160^circ=sin 20^circ$

b) $cos 300^circ= cos 60^circ$

c) $tan 110^circ=-tan 70^circ$

d) $sin 350^circ=-sin 10^circ$

${bold{Steps; in; Evaluating; Trigonometric; Functions}}$

1) If $theta$ is within the interval $0leq thetaleq 360^circ$, proceed to step 2. If not, find a coterminal angle $alpha$ within the range using the formula

coterminal angle $alpha=theta+360^circ cdot n$ where $n$ is an integer.

2) Determine which quadrant does the terminal point of $theta$ lie. Based on the quadrant, you can find the reference acute angle $beta$ according to the table below.

3) Evaluate the value of the trigonometric function based on the reference acute angle. You should remember its value for special angles such as $30^circ$, $45^circ$ and $60^circ$.

4) Determine the sign of the trigonometric function based on its quadrant.

begin{table}[]
center
defarraystretch{2.4}%
begin{tabular}{llll}
hline
multicolumn{1}{|l|}{begin{tabular}[c]{@{}l@{}}principal angle;$theta$end{tabular}} & multicolumn{1}{l|}{Quadrant} & multicolumn{1}{l|}{begin{tabular}[c]{@{}l@{}}sign $(cos theta, sin theta)$end{tabular}} & multicolumn{1}{l|}{begin{tabular}[c]{@{}l@{}}reference acute angle $beta$end{tabular}} \ hline
multicolumn{1}{|l|}{$0< theta<90^circ$} & multicolumn{1}{l|}{I} & multicolumn{1}{l|}{$(+,+)$} & multicolumn{1}{l|}{$theta$} \ hline
multicolumn{1}{|l|}{$90^circ <theta < 180^circ$} & multicolumn{1}{l|}{II} & multicolumn{1}{l|}{$(-,+)$} & multicolumn{1}{l|}{$180^circ-theta$} \ hline
multicolumn{1}{|l|}{$180^circ <theta < 270^circ$} & multicolumn{1}{l|}{III} & multicolumn{1}{l|}{$(-,-)$} & multicolumn{1}{l|}{$theta-180^circ$} \ hline
multicolumn{1}{|l|}{$270^circ < theta <360^circ$} & multicolumn{1}{l|}{IV} & multicolumn{1}{l|}{$(+,-)$} & multicolumn{1}{l|}{$360^circ-theta$} \ hline
& & & \ cline{1-3}
multicolumn{1}{|l|}{begin{tabular}[c]{@{}l@{}}reference acute angle $beta$ end{tabular}} & multicolumn{1}{l|}{$cos beta$} & multicolumn{1}{l|}{$sin beta$} & \ cline{1-3}
multicolumn{1}{|l|}{30$^circ$} & multicolumn{1}{l|}{$dfrac{sqrt{3}}{2}$} & multicolumn{1}{l|}{$dfrac{1}{2}$} & \ cline{1-3}
multicolumn{1}{|l|}{45$^circ$} & multicolumn{1}{l|}{$dfrac{sqrt{2}}{2}$} & multicolumn{1}{l|}{$dfrac{sqrt{2}}{2}$} & \ cline{1-3}
multicolumn{1}{|l|}{60$^circ$} & multicolumn{1}{l|}{$dfrac{1}{2}$} & multicolumn{1}{l|}{$dfrac{sqrt{3}}{2}$} & \ cline{1-3}
& & &
end{tabular}
end{table}

Refer to the given figures in your textbook.

a)

text${text{i}}$) The terminal point of $theta$ is in QII where the sign of the coordinate is $(-,+)$, thus,

$cos theta implies$ negative

$sin theta implies$ positive

$tan theta implies$ negative

Note that $tan theta$ would only be positive if both $sin theta$ and $cos theta$ have the same sign.

ii) Use your calculator to estimate the ratios to the nearest hundredth

$cos theta=-cos 15^circ=-0.97$

$sin theta=sin 15^circ=0.26$

$$
tantheta=-tan 15^circ=-0.27
$$

b)

text${text{i}}$) The terminal point of $theta$ is in QIII where the sign of the coordinate is $(-,-)$, thus,

$cos theta implies$ negative

$sin theta implies$ negative

$tan theta implies$ positive

ii) Use your calculator to estimate the ratios to the nearest hundredth

$cos theta=-cos 55^circ=-0.57$

$sin theta=-sin 55^circ=-0.82$

$$
tan theta=tan 55^circ=1.43
$$

c)

text${text{i}}$) The terminal point of $theta$ is in QII where the sign of the coordinate is $(-,+)$, thus,

$cos theta implies$ negative

$sin theta implies$ positive

$tan theta implies$ negative

ii) Use your calculator to estimate the ratios to the nearest hundredth

$cos theta=-cos 71^circ=-0.33$

$sin theta=sin 71^circ=0.95$

$$
tan theta=-tan 71^circ=-2.90
$$

d)

text${text{i}}$) The terminal point of $theta$ is in QIV where the sign of the coordinate is $(+,-)$, thus,

$cos theta implies$ positive

$sin theta implies$ negative

$tan theta implies$ negative

ii) Use your calculator to estimate the ratios to the nearest hundredth

$cos theta=cos 28^circ=0.88$

$sin theta=-sin 28^circ=-0.47$

$$
tan theta=-tan 28^circ=-0.53
$$

a) $sin theta>0$ ;$cos theta=-0.97$ ; $sin theta=0.26$ ; $tan theta=-0.27$

b) $tan theta>0$ ; $cos theta=-0.57$ ; $sin theta= -0.82$ ; $tan theta= 1.43$

c) $sin theta>0$ ; $cos theta=-0.33$ ; $sin theta=0.95$ ; $tan theta=-2.90$

d) $cos theta>0$ ; $cos theta=0.88$ ; $sin theta=-0.47$ ; $tan theta=-0.53$

${bold{Steps; in; Evaluating; Trigonometric; Functions}}$

1) If $theta$ is within the interval $0leq thetaleq 360^circ$, proceed to step 2. If not, find a coterminal angle $alpha$ within the range using the formula

coterminal angle $alpha=theta+360^circ cdot n$ where $n$ is an integer.

2) Determine which quadrant does the terminal point of $theta$ lie. Based on the quadrant, you can find the reference acute angle $beta$ according to the table below.

3) Evaluate the value of the trigonometric function based on the reference acute angle. You should remember its value for special angles such as $30^circ$, $45^circ$ and $60^circ$.

4) Determine the sign of the trigonometric function based on its quadrant.

begin{table}[]
center
defarraystretch{2.4}%
begin{tabular}{llll}
hline
multicolumn{1}{|l|}{begin{tabular}[c]{@{}l@{}}principal angle;$theta$end{tabular}} & multicolumn{1}{l|}{Quadrant} & multicolumn{1}{l|}{begin{tabular}[c]{@{}l@{}}sign $(cos theta, sin theta)$end{tabular}} & multicolumn{1}{l|}{begin{tabular}[c]{@{}l@{}}reference acute angle $beta$end{tabular}} \ hline
multicolumn{1}{|l|}{$0< theta<90^circ$} & multicolumn{1}{l|}{I} & multicolumn{1}{l|}{$(+,+)$} & multicolumn{1}{l|}{$theta$} \ hline
multicolumn{1}{|l|}{$90^circ <theta < 180^circ$} & multicolumn{1}{l|}{II} & multicolumn{1}{l|}{$(-,+)$} & multicolumn{1}{l|}{$180^circ-theta$} \ hline
multicolumn{1}{|l|}{$180^circ <theta < 270^circ$} & multicolumn{1}{l|}{III} & multicolumn{1}{l|}{$(-,-)$} & multicolumn{1}{l|}{$theta-180^circ$} \ hline
multicolumn{1}{|l|}{$270^circ < theta <360^circ$} & multicolumn{1}{l|}{IV} & multicolumn{1}{l|}{$(+,-)$} & multicolumn{1}{l|}{$360^circ-theta$} \ hline
& & & \ cline{1-3}
multicolumn{1}{|l|}{begin{tabular}[c]{@{}l@{}}reference acute angle $beta$ end{tabular}} & multicolumn{1}{l|}{$cos beta$} & multicolumn{1}{l|}{$sin beta$} & \ cline{1-3}
multicolumn{1}{|l|}{30$^circ$} & multicolumn{1}{l|}{$dfrac{sqrt{3}}{2}$} & multicolumn{1}{l|}{$dfrac{1}{2}$} & \ cline{1-3}
multicolumn{1}{|l|}{45$^circ$} & multicolumn{1}{l|}{$dfrac{sqrt{2}}{2}$} & multicolumn{1}{l|}{$dfrac{sqrt{2}}{2}$} & \ cline{1-3}
multicolumn{1}{|l|}{60$^circ$} & multicolumn{1}{l|}{$dfrac{1}{2}$} & multicolumn{1}{l|}{$dfrac{sqrt{3}}{2}$} & \ cline{1-3}
& & &
end{tabular}
end{table}

In this exercise, we are given the value of one trigonometric function and we need to work backwards to determine the terminal point, principal angle $theta$ and reference angle $beta$.

We can do this using the following strategy:

1) Assuming a unit circle, $r^2=1$ and we can determine the exact values of $x$ and $y$ using Pythagorean formula $x^2+y^2=1$. Since we are at QII, $x0$.

2) Calculate the corresponding $beta$ using inverse trigonometric function of its absolute value.

3) We are given that each $theta$ lies in QII, so $theta=180^circ-beta$

a)

text${text{i}}$) In QII and $r=1$, $sin theta=dfrac{1}{3}implies y=dfrac{1}{3}$

Using Pythagorean formula,

$x=-sqrt{1-x^2}=-sqrt{1-left(dfrac{1}{3}right)^2}=-sqrt{dfrac{8}{9}}=-dfrac{sqrt{4cdot 2}}{3}=-dfrac{2sqrt{2}}{3}$

Therefore, $x=-dfrac{2sqrt{2}}{3}$, $y=dfrac{1}{3}$, $r=1$

ii) Use the coordinates to sketch $theta$ in standard position.

iii) $beta =sin^{-1}left(dfrac{1}{3}right)=19^circ$

$$
theta=180^circ-beta=180-19=161^circ
$$

b)

text${text{i}}$) In QII and $r=1$, $cot theta=-dfrac{4}{3}=dfrac{cos theta}{sin theta}=dfrac{x}{y}$

Using Pythagorean formula,
$x^2+y^2=1implies left(dfrac{x}{y}right)^2+1=left(dfrac{1}{y}right)^2$

$dfrac{1}{y}=sqrt{left(dfrac{x}{y}right)^2+1}=sqrt{left(-dfrac{4}{3}right)^2+1}=sqrt{dfrac{25}{9}}=dfrac{5}{3}$

which implies that $y=dfrac{3}{5}$

$x=-sqrt{1-y^2}=-sqrt{1-left(dfrac{3}{5}right)^2}=-sqrt{dfrac{16}{25}}=-dfrac{4}{5}$

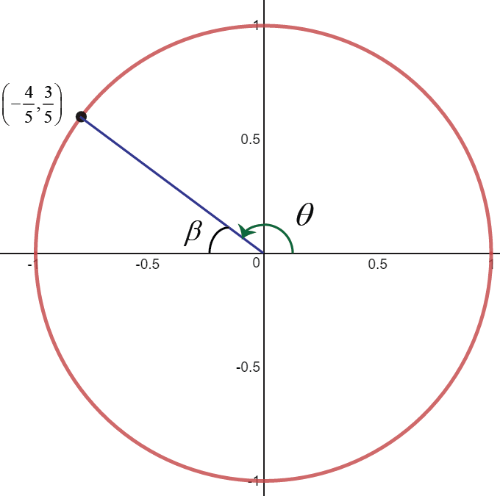
Therefore, $x=-dfrac{4}{5}$ , $y=dfrac{3}{5}$, $r=1$

ii) Using the coordinates, you can sketch the standard position as follows.

iii) $beta=sin^{-1}left(dfrac{3}{5}right)=37^circ$

$$
theta=180^circ-beta=180-37=143^circ
$$

c)

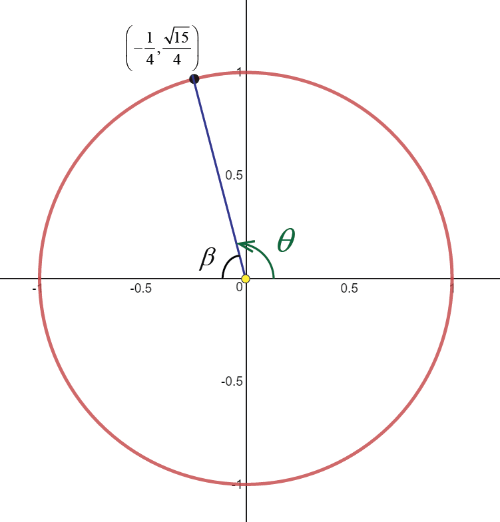
i) $cos theta=-dfrac{1}{4}implies x=-dfrac{1}{4}$

Using Pythagorean formula

$y=pmsqrt{1-x^2}=pmsqrt{1-(-1/4)^2}=pmsqrt{dfrac{15}{16}}=pmdfrac{sqrt{15}}{4}$

Since $sin theta>0$ in QII, $y=dfrac{sqrt{15}}{4}$

Therefore, $x=-dfrac{1}{4}$, $y=dfrac{sqrt{15}}{4}$, $r=1$

ii) Use this coordinate to plot in standard position.

iii) $beta=sin^{-1}left(dfrac{sqrt{15}}{4}right)=76^circ$

$theta=180^circ-76^circ=104^circ$

d)

i) $csc theta=2.5implies sin theta = dfrac{1}{2.5}=dfrac{2}{5}=y$

Using Pythagorean formula

$x=pmsqrt{1-y^2}=pm sqrt{1-(2/5)^2}=pm sqrt{dfrac{21}{25}}=pmdfrac{sqrt{21}}{5}$

Since $cos theta<0$ in QII,

Therefore, $x=-dfrac{sqrt{21}}{5}$, $y=dfrac{2}{5}$, $r=1$

ii) Use this coordinate to plot in standard position.

iii) $beta=sin^{-1}left(dfrac{2}{5}right)=24^circ$

$theta=180^circ-24^circ=156^circ$

e)

text${text{i}}$) In QII and $r=1$, $tan theta=-1.1=dfrac{sin theta}{cos theta}=dfrac{y}{x}$

Using Pythagorean formula,
$x^2+y^2=1implies dfrac{x^2}{x^2}+left(dfrac{y}{x}right)^2=left(dfrac{1}{x}right)^2$

$dfrac{1}{x}=pm sqrt{left(dfrac{y}{x}right)^2+1}=pmsqrt{left(-1.1right)^2+1}=pm sqrt{dfrac{221}{100}}=pm dfrac{sqrt{221}}{10}$

Since in QII, $cos theta<0$

$implies x=-dfrac{10}{sqrt{221}}$

$y=sqrt{1-x^2}=-sqrt{1-left(dfrac{10}{sqrt{221}}right)^2}=sqrt{dfrac{121}{221}}$

Therefore, $x=-dfrac{10}{sqrt{221}}$ , $y=sqrt{dfrac{121}{221}}$, $r=1$

ii) Using the coordinates, you can sketch the standard position as follows.

iii) $beta=sin^{-1}left(sqrt{dfrac{121}{221}}right)=48^circ$

$$
theta=180^circ-beta=180-48=132^circ
$$

d)

i) $sec theta=-3.5implies cos theta = dfrac{1}{-3.5}=-dfrac{2}{7}=x$

Using Pythagorean formula

$y=pmsqrt{1-x^2}=pm sqrt{1-(2/7)^2}=pm sqrt{dfrac{45}{49}}=pmdfrac{sqrt{9cdot 5}}{sqrt{49}}=pmdfrac{3sqrt{5}}{7}$

Since $sin theta>0$ in QII $implies y=dfrac{3sqrt{5}}{7}$

Therefore, $x=-dfrac{2}{7}$, $y=dfrac{3sqrt{5}}{7}$, $r=1$

ii) Use this coordinate to plot in standard position.

iii) $beta=sin^{-1}left(dfrac{3sqrt{5}}{7}right)=73^circ$

$theta=180^circ-73^circ=107^circ$

a) $x=-dfrac{2sqrt{2}}{3}$, $y=dfrac{1}{3}$, $r=1$ , $beta= 19^circ$ , $alpha=161^circ$

b) $x=-dfrac{4}{5}$, $y=dfrac{3}{5}$, $r=1$ , $beta= 37^circ$ , $alpha=143^circ$

c) $x=-dfrac{1}{4}$, $y=dfrac{sqrt{15}}{4}$, $r=1$ , $beta= 76^circ$ , $alpha=104^circ$

d) $x=-dfrac{sqrt{21}}{5}$, $y=dfrac{2}{5}$, $r=1$ , $beta= 24^circ$ , $alpha=156^circ$

e) $x=-dfrac{10}{sqrt{221}}$, $y=sqrt{dfrac{121}{221}}$, $r=1$ , $beta= 48^circ$ , $alpha=132^circ$

f) $x=-dfrac{2}{7}$ , $y=dfrac{3sqrt{5}}{7}$ ; $r=1$ , $beta=73^circ$ , $theta=107^circ$

${bold{Steps; in; Evaluating; Trigonometric; Functions}}$

1) If $theta$ is within the interval $0leq thetaleq 360^circ$, proceed to step 2. If not, find a coterminal angle $alpha$ within the range using the formula

coterminal angle $alpha=theta+360^circ cdot n$ where $n$ is an integer.

2) Determine which quadrant does the terminal point of $theta$ lie. Based on the quadrant, you can find the reference acute angle $beta$ according to the table below.

3) Evaluate the value of the trigonometric function based on the reference acute angle. You should remember its value for special angles such as $30^circ$, $45^circ$ and $60^circ$.

4) Determine the sign of the trigonometric function based on its quadrant.

begin{table}[]
center
defarraystretch{2.4}%
begin{tabular}{llll}
hline
multicolumn{1}{|l|}{begin{tabular}[c]{@{}l@{}}principal angle;$theta$end{tabular}} & multicolumn{1}{l|}{Quadrant} & multicolumn{1}{l|}{begin{tabular}[c]{@{}l@{}}sign $(cos theta, sin theta)$end{tabular}} & multicolumn{1}{l|}{begin{tabular}[c]{@{}l@{}}reference acute angle $beta$end{tabular}} \ hline
multicolumn{1}{|l|}{$0< theta<90^circ$} & multicolumn{1}{l|}{I} & multicolumn{1}{l|}{$(+,+)$} & multicolumn{1}{l|}{$theta$} \ hline
multicolumn{1}{|l|}{$90^circ <theta < 180^circ$} & multicolumn{1}{l|}{II} & multicolumn{1}{l|}{$(-,+)$} & multicolumn{1}{l|}{$180^circ-theta$} \ hline
multicolumn{1}{|l|}{$180^circ <theta < 270^circ$} & multicolumn{1}{l|}{III} & multicolumn{1}{l|}{$(-,-)$} & multicolumn{1}{l|}{$theta-180^circ$} \ hline
multicolumn{1}{|l|}{$270^circ < theta <360^circ$} & multicolumn{1}{l|}{IV} & multicolumn{1}{l|}{$(+,-)$} & multicolumn{1}{l|}{$360^circ-theta$} \ hline
& & & \ cline{1-3}
multicolumn{1}{|l|}{begin{tabular}[c]{@{}l@{}}reference acute angle $beta$ end{tabular}} & multicolumn{1}{l|}{$cos beta$} & multicolumn{1}{l|}{$sin beta$} & \ cline{1-3}
multicolumn{1}{|l|}{30$^circ$} & multicolumn{1}{l|}{$dfrac{sqrt{3}}{2}$} & multicolumn{1}{l|}{$dfrac{1}{2}$} & \ cline{1-3}
multicolumn{1}{|l|}{45$^circ$} & multicolumn{1}{l|}{$dfrac{sqrt{2}}{2}$} & multicolumn{1}{l|}{$dfrac{sqrt{2}}{2}$} & \ cline{1-3}
multicolumn{1}{|l|}{60$^circ$} & multicolumn{1}{l|}{$dfrac{1}{2}$} & multicolumn{1}{l|}{$dfrac{sqrt{3}}{2}$} & \ cline{1-3}
& & &
end{tabular}
end{table}

In this exercise, we are given the value of one trigonometric function and we need to work backwards to determine the terminal point, principal angle $theta$ and reference angle $beta$.

We can do this using the following strategy:

1) Assuming a unit circle, $r^2=1$ and we can determine the exact values of $x$ and $y$ using Pythagorean formula $x^2+y^2=1$. Since we are at QII, $x0$.

2) Calculate the corresponding $beta$ using inverse trigonometric function of its absolute value.

3) We are given that each $theta$ lies in QII, so $theta=180^circ-beta$

Refer to your answers in question 6.

a) $x=-dfrac{2sqrt{2}}{3}$, $y=dfrac{1}{3}$, $r=1$ , $beta= 19^circ$ , $alpha=161^circ$

b) $x=-dfrac{4}{5}$, $y=dfrac{3}{5}$, $r=1$ , $beta= 37^circ$ , $alpha=143^circ$

c) $x=-dfrac{1}{4}$, $y=dfrac{sqrt{15}}{4}$, $r=1$ , $beta= 76^circ$ , $alpha=104^circ$

d) $x=-dfrac{sqrt{21}}{5}$, $y=dfrac{2}{5}$, $r=1$ , $beta= 24^circ$ , $alpha=156^circ$

e) $x=-dfrac{10}{sqrt{221}}$, $y=sqrt{dfrac{121}{221}}$, $r=1$ , $beta= 48^circ$ , $alpha=132^circ$

f) $x=-dfrac{2}{7}$ , $y=dfrac{3sqrt{5}}{7}$ ; $r=1$ , $beta=73^circ$ , $theta=107^circ$

Here, we need to determine a negative angle (clockwise) that has the same ratio.
Remember that the ratio will be the same for any coterminal angle given by

coterminal angle $=theta+360^circ n$

To find the smallest negative angle, we will choose $n=-1$

$implies theta-360^circ$

Therefore,

a) $161^circ-360^circ=-199^circ$

b) $143^circ-360^circ=-217^circ$

c) $104^circ-360^circ=-256^circ$

d) $156^circ-360^circ=-204^circ$

e) $132^circ-360^circ=-228^circ$

f) $107^circ-360^circ=-253^circ$

a) $-199^circ$

b) $-217^circ$

c) $-256^circ$

d) $-204^circ$

e) $-228^circ$

f) $-253^circ$

$bold{Steps;in;Solving;Trigonometric;Equations}$

1) Find the reference acute angle $beta$ using inverse trigonometric function as

$f(theta)=cimplies beta=f^{-1}(|c|)$

2) Based on the sign of $c$, determine the possible quadrants for $theta$ within the given range.

3) Find the principal angle $theta$ on those quadrants that has reference acute angle of $beta$

begin{table}[]
defarraystretch{1.4}%
begin{tabular}{|l|l|l|l|l|}
hline
& QI & QII & QIII & QIV\ hline
sine & $+$ & $+$ & $-$ & $-$ \ hline
cosine & $+$ & $-$ & $-$ & $+$ \ hline
tangent & $+$ & $-$ & $+$ & $-$ \ hline
principal angle $theta$ & $;;;;beta;;;;$ & $180^circ-beta$ & $180^circ+beta$ & $360^circ-beta$ \ hline
end{tabular}

end{table}

a) $sin theta=0.4815 implies beta=sin^{-1}|0.4815|=29^circ$

$sin theta>0$ in the following quadrants

QI: $theta=beta=29^circ$

QII: $theta=180^circ-beta=180^circ-29^circ=151^circ$

b) $tan theta=-0.1623 implies beta=tan^{-1}|-0.1623|=9^circ$

$tan theta<0$ in the following quadrants

QII: $theta=180^circ-beta=180^circ-9^circ=171^circ$

QIV: $theta=360^circ-beta=360^circ-9^circ=351^circ$

c) $cos theta=-0.8722 implies beta=cos^{-1}|-0.8722|=29^circ$

$cos theta<0$ in the following quadrants

QII: $theta=180^circ-beta=180^circ-29^circ=151^circ$

QIII: $theta=180^circ+beta=180^circ+29^circ=209^circ$

d) $cot theta=8.1516 implies tan theta=dfrac{1}{8.1516}implies beta=tan^{-1}|1/8.1516|=7^circ$

$tan theta>0$ in the following quadrants

QI: $theta=beta=7^circ$

QIII: $theta=180^circ+beta=180^circ+7^circ=187^circ$

e) $csc theta=-2.3424 implies sintheta=dfrac{1}{-2.3424}implies beta=sin^{-1}|-1/2.3424|=25^circ$

$sin theta<0$ in the following quadrants

QIII: $theta=180^circ+beta=180+25^circ=205^circ$

QIV: $theta=360^circ-beta=360^circ-25^circ=335^circ$

f) $sec theta=0implies cos theta=dfrac{1}{0}=text{undefined}=dfrac{text{adjacent side}}{text{hypotenuse}}$

This means, $sec theta=0$ only when hypotenuse is zero which is not possible. Hence, the equation has no solution, in other words, no value of $theta$ can satisfy the equation.

a) $29^circ$ , $151^circ$

b) $171^circ$, $351^circ$

c) $151^circ$, $209^circ$

d) $7^circ$, $187^circ$

e) $25^circ$ , $155^circ$

d) $7^circ$ , $187^circ$

e) $205^circ$ , $355^circ$

f) no solution

$bold{Steps;in;Solving;Trigonometric;Equations}$

1) Find the reference acute angle $beta$ using inverse trigonometric function as

$f(theta)=cimplies beta=f^{-1}(|c|)$

2) Based on the sign of $c$, determine the possible quadrants for $theta$ within the given range.

3) Find the principal angle $theta$ on those quadrants that has reference acute angle of $beta$

begin{table}[]
defarraystretch{1.4}%
begin{tabular}{|l|l|l|l|l|}
hline
& QI & QII & QIII & QIV\ hline
sine & $+$ & $+$ & $-$ & $-$ \ hline
cosine & $+$ & $-$ & $-$ & $+$ \ hline
tangent & $+$ & $-$ & $+$ & $-$ \ hline
principal angle $theta$ & $;;;;beta;;;;$ & $180^circ-beta$ & $180^circ+beta$ & $360^circ-beta$ \ hline
end{tabular}

end{table}

a) $cos theta=0.6951 implies beta=cos^{-1}|0.6951|=45.96^circ$

$cos theta>0$ in the following quadrants

QI: $theta=beta=45.96^circ$

QIV: $theta=360^circ-beta=360^circ-45.96^circ=314.04^circ$

b) $tan theta=-0.7571 implies beta=tan^{-1}|-0.7571|=37.12^circ$

$tan theta<0$ in the following quadrants

QII: $theta=180^circ-beta=180^circ-37.12^circ=142.88^circ$

QIV: $theta=360^circ-beta=360^circ-37.12^circ=322.88^circ$

c) $sin theta=0.3154 implies beta=sin^{-1}|0.3154|=18.38^circ$

$sin theta>0$ in the following quadrants

QI: $theta=beta=18.38^circ$

QII: $theta=180^circ-beta=180^circ-18.38^circ=161.62^circ$

d) $cos theta=-0.2882 implies beta=cos^{-1}|-0.2882|=73.25^circ$

$costheta<0$ in the following quadrants

QII: $theta=180^circ-beta=180-73.25=106.75^circ$

QIII: $theta=180^circ+beta=180^circ+73.25^circ=253.25^circ$

e) $tan theta=2.3151 implies beta=tan^{-1}|2.3151|=66.64^circ$

$tan theta>0$ in the following quadrants

QI: $theta=beta=66.64^circ$

QIII: $theta=180^circ+beta=180^circ+66.64^circ=246.64^circ$

f) $sin theta=-0.7503implies beta=sin^{-1}|-0.7503|=48.62^circ$

$sin <0$ in the following quadrants

QIII: $theta=180^circ+beta=180^circ+48.62^circ=228.62^circ$

QIV: $theta=360^circ-beta=360^circ-48.62^circ=311.38^circ$

a) $45.96^circ$ , $314.04^circ$

b) $142.88^circ$, $322.88^circ$

c) $18.38^circ$ ; $161.62^circ$

d) $106.75^circ$ ; $253.25^circ$

e) $66.64^circ$ ; $246.64^circ$

f) $228.62^circ$ ; $311.38^circ$

Draw a unit circle. Remember the convention. For $theta>0$, it’s counterclockwise, for $theta<0$, it's clockwise.

begin{table}[]
defarraystretch{1.4}%
begin{tabular}{|l|l|l|l|l|}
hline
& QI & QII & QIII & QIV\ hline
sine & $+$ & $+$ & $-$ & $-$ \ hline
cosine & $+$ & $-$ & $-$ & $+$ \ hline
tangent & $+$ & $-$ & $+$ & $-$ \ hline
principal angle $theta$ & $;;;;beta;;;;$ & $180^circ-beta$ & $180^circ+beta$ & $360^circ-beta$ \ hline
end{tabular}

end{table}

Given a terminal point $P(x,y)$, you can obtain the primary trigonometric functions using the following formula:

$r=sqrt{x^2+y^2}$

$cos theta=dfrac{x}{r}$

$sin theta=dfrac{y}{r}$

$tan theta = dfrac{y}{x}$

a) $P(-1,-1)$

$r=sqrt{x^2+y^2}=sqrt{(-1)^2+(-1)^2}=sqrt{2}$

$cos theta = dfrac{-1}{sqrt{2}}=-dfrac{sqrt{2}}{2}$

$sin theta=dfrac{-1}{sqrt{2}}=-dfrac{sqrt{2}}{2}$

$tan theta=dfrac{-1}{-1}=1$

The reference angle is $beta=tan^{-1}(1)=45^circ$

The terminal point is in QIII, so

counterclockwise: $theta=180^circ+beta=180^circ+45^circ=225^circ$

clockwise: $theta=-(180-beta)=-(180^circ-45^circ)=-135^circ$

b) $P(0,-1)$

$r=sqrt{x^2+y^2}=sqrt{(0)^2+(-1)^2}=1$

$cos theta = dfrac{0}{1}=0$

$sin theta=dfrac{-1}{1}=-1$

$tan theta=dfrac{-1}{0}$ = undefined

The reference angle is $beta=cos^{-1}(0)=90^circ$

The terminal point is in negative $y$-axis, so

counterclockwise: $theta=180^circ+beta=180^circ+90^circ=270^circ$

clockwise: $theta=-(beta)=-90^circ$

c) $P(-1,0)$

$r=sqrt{x^2+y^2}=sqrt{(-1)^2+0^2}=1$

$cos theta = dfrac{-1}{1}=-1$

$sin theta=dfrac{0}{1}=0$

$tan theta=dfrac{0}{1}$ = 0

The reference angle is $beta=sin^{-1}(0)=0^circ$

The terminal point is in negative $x$-axis, so

counterclockwise: $theta=180^circ-beta=180^circ+0^circ=180^circ$

clockwise: $theta=-180^circ$

d) $P(1,0)$

$r=sqrt{x^2+y^2}=sqrt{(1)^2+0^2}=1$

$cos theta = dfrac{1}{1}=1$

$sin theta=dfrac{0}{1}=0$

$tan theta=dfrac{0}{1}$ = 0

The reference angle is $beta=sin^{-1}(0)=0^circ$

The terminal point is in positive $x$-axis, so

counterclockwise: $theta=0^circ$

clockwise: $theta=-360^circ$

a) $225^circ$ , $-135^circ$ ; $cos theta=-dfrac{sqrt{2}}{2}$ ; $sin theta=-dfrac{sqrt{2}}{2}$ ; $tan theta=1$

b) $270^circ$ , $-90^circ$ ; $cos theta=0$ , $sin theta=-1$ , $tan theta=$ undefined

c) $180^circ$ , $-180^circ$ ; $cos theta=-1$ , $sin theta=0$ , $tan theta=0$

d) $0^circ$ , $-360^circ$ ; $cos theta=1$ , $sin theta=0$ , $tan theta=0$

Trigonometric ratios are calculated from ratio of sides of right angled triangle. When $theta ge 90^circ$, he cannot create right angled triangle so he can only calculate $theta$ for $0le theta < 90$.

Dennis cannot create right angled triangle for $theta ge 90$.

$bold{Steps;in;Solving;Trigonometric;Equations}$

1) Find the reference acute angle $beta$ using inverse trigonometric function as

$f(theta)=cimplies beta=f^{-1}(|c|)$

2) Based on the sign of $c$, determine the possible quadrants for $theta$ within the given range.

3) Find the principal angle $theta$ on those quadrants that has reference acute angle of $beta$

begin{table}[]
defarraystretch{1.4}%
begin{tabular}{|l|l|l|l|l|}
hline
& QI & QII & QIII & QIV\ hline
sine & $+$ & $+$ & $-$ & $-$ \ hline
cosine & $+$ & $-$ & $-$ & $+$ \ hline
tangent & $+$ & $-$ & $+$ & $-$ \ hline
principal angle $theta$ & $;;;;beta;;;;$ & $180^circ-beta$ & $180^circ+beta$ & $360^circ-beta$ \ hline
end{tabular}

end{table}

a) $cos theta <0$ in QII and QIII

b) Using Pythagorean formula with $r=1$,

$x^2+y^2=r^2$

$y=pmsqrt{1-x^2}=pmsqrt{1-left(-dfrac{5}{12}right)^2}=pm sqrt{dfrac{119}{144}}=pmdfrac{sqrt{119}}{12}$

In QII, $x0$, so the other primary trigonometric ratios are

$sin theta=y=dfrac{sqrt{119}}{12}$

$tan theta=dfrac{y}{x}=dfrac{sqrt{119}/12}{-5/12}=-dfrac{sqrt{119}}{5}$

In QIII, $x<0$ and $y<0$,

$sin theta=-dfrac{sqrt{119}}{12}$

$tan theta=dfrac{sqrt{119}}{5}$

c) We shall evaluate all possible values of $theta$ within $0^circ leq thetaleq 360^circ$

$cos theta=-dfrac{5}{12}implies beta=cos^{-1}left( left|dfrac{-5}{12}right|right)=65.38^circ$

QII: $theta=180^circ-beta=180^circ-65.38^circ=115^circ$

QIII: $theta=180^circ+beta=180^circ+65.38^circ=245^circ$

a) QII and QIII

b) QII: $sin theta=dfrac{sqrt{119}}{12}$ , $tan theta=-dfrac{sqrt{119}}{5}$

QIII: $sin theta=-dfrac{sqrt{119}}{12}$ , $tan theta=dfrac{sqrt{119}}{5}$

c) $theta=115^circ,;245^circ$

Within $0leq alpha < 360^circ$, the value of $cos alpha$ is unique when there is $cos alpha$ attains maximum value or minimum value. For example, $alpha=0^circ, ;180^circ$

$cos 0^circ=1$

$$
cos 180^circ =-1
$$

$$
alpha = 0^circ, ;180^circ
$$

If you know the coordinates of the terminal point $P(x,y)$, you can calculate the trigonometric ratios using the following formula:

$r=sqrt{x^2+y^2}$

$cos theta= dfrac{x}{r}$

$sin theta=dfrac{y}{r}$

$tan theta=dfrac{y}{x}$

$sectheta=dfrac{r}{x}$

$csc theta=dfrac{r}{y}$

$$
cot theta=dfrac{x}{y}
$$

For example, if the terminal point is $(-3,-4)$

$r=sqrt{(-3)^2+(-4)^2}=sqrt{25}=5$

$cos theta=dfrac{x}{r}=dfrac{-3}{5}$

$sin theta=dfrac{y}{r}=dfrac{-4}{5}$

$tan theta=dfrac{y}{x}=dfrac{-4}{-3}=dfrac{4}{3}$

$sec theta=dfrac{r}{x}=dfrac{-5}{3}$

$csc theta=dfrac{r}{y}=dfrac{-5}{4}$

$cottheta=dfrac{x}{y}=dfrac{3}{4}$

$bold{Steps;in;Solving;Trigonometric;Equations}$

1) Find the reference acute angle $beta$ using inverse trigonometric function $f^{-1}$ as

$f(g(theta))=cimplies g(beta)=f^{-1}(|c|)$

2) Based on the sign of $c$, determine the possible quadrants for $g(theta)$ within the given range.

3) Find the principal angle $g(theta)$ on those quadrants that has reference acute angle of $g(beta)$ according to the table below.

begin{table}[]
defarraystretch{1.4}%
begin{tabular}{|l|l|l|l|l|}
hline
& QI & QII & QIII & QIV\ hline
sine & $+$ & $+$ & $-$ & $-$ \ hline
cosine & $+$ & $-$ & $-$ & $+$ \ hline
tangent & $+$ & $-$ & $+$ & $-$ \ hline
principal angle $g(theta)$ & $;;;;g(beta)+360^circ n;;;;$ & $(180^circ-g(beta))+360^circ n$ & $(180^circ+g(beta))+360^circ n$ & $(360^circ-g(beta))+360^circ n$ \ hline
end{tabular}

end{table}

Here we shall find $theta$ within $0^circ leq theta leq 360^circ$

a) $cos 2theta=0.6420$,

in this case, $g(theta)=2theta$

$g(beta)=cos^{-1}(|0.6420|)=50^circ$

$cos g(theta)>0$ in QI and QIV

QI: $g(theta)=g(beta)+360^circ n$

$2theta=50^circ+360^circ n$

$theta=25^circ+180^circ n$

for $n=0$ : $theta=25^circ$

for $n=1$ : $theta=25^circ+180^circ=205^circ$

for $n=2$ : $theta=25^circ+180^circ(2)=385^circ$

QIV: $2theta=(360^circ-g(beta))+360^circ n$

$2theta=(360^circ-50^circ)+360^circ n$

$theta=155^circ+180^circ n$

for $n=0$: $theta=155^circ$

for $n=1$: $theta=155^circ+180^circ(1)=335^circ$

Since the required interval is $0^circ leq thetaleq 360^circ$

$$
theta=25^circ,;205^circ, 155^circ, 335^circ
$$

b) $sin (theta+20^circ)=0.2045$

$g(beta)=beta+20^circ$

$g(beta)=sin^{-1}(|0.2045|)$

$g(beta)=11.8^circ$

$sin(g(theta))>0$ in QI and QII

QI: $g(theta)=g(beta)+360^circ n$

$theta+20^circ=11.8^circ+360^circ n$

for $n=0$: $theta=-8.2^circ$

for $n=1$: $theta=-8.2+360=351.8^circ$

QII: $g(theta)=[180^circ-g(beta)]+360^circ n$

for $n=0$: $theta+20^circ=180^circ-(11.8^circ)implies theta=148.2^circ$

for $n=1$: $theta+20^circ=180^circ-(11.8^circ)+360^circimplies theta=508.2^circ$

Since the required interval is $0^circ leq thetaleq 360^circ$

$$
theta=148.2^circ,;351.8^circ
$$

c) $tan (90^circ-2theta)=1.6443$

In this case $g(theta)=90^circ-2theta$

$g(beta)=tan^{-1}(|1.6443|)=59^circ$

$g(beta)>0$ in QI and QIII

QI: $g(theta)=g(beta)+360^circ n$

$90^circ-2theta=59^circ+360^circ n$

$2theta=31-360^circ n$

$theta=15.5-180^circ n$

for $n=0$ : $theta=15.5^circ$

for $n=-1$: $theta=195.5^circ$

for $n=-2$: $theta=375.5^circ$

QIII: $g(theta)=180^circ+g(beta)+360^circ n$

$90^circ- 2theta=180^circ-59^circ+360^circ n$

$2theta=90^circ-180^circ-59^circ-360^circ n$

$theta=-74.5^circ-180^circ n$

for $n=-1$: $theta=105.5^circ$

for $n=-2$: $theta=285.5^circ$

Since the required interval is $0^circ leq thetaleq 360^circ$

$theta=15.5^circ,; 195.5^circ,; 105.5^circ, 285.5^circ$

a) $theta=25^circ,;205^circ, 155^circ, 335^circ$

b) $theta=148^circ,;352^circ$

c) $theta=16^circ,; 196^circ,; 106^circ, 289^circ$

a)The range of $sin^{-1}(x)$ is

${ sin^{-1}(x)in bold{R} ;|;-90^circ leq sin^{-1}(x)leq 90^circ}$

so it cannot find $theta$ in QII and QIII.

$theta=sin^{-1}(-0.8)=-53.13^circ$

The other value of $theta$ could be in QIII where $theta=233.13^circ$

b) The range of $cos^{-1}(x)$ is

${ cos^{-1}(x) in bold{R};|; 0^circ leq cos^{-1}(x)leq 180^circ}$

so it cannot find $theta$ in QIII and QIV

$theta=cos^{-1}(-0.75)=138.59^circ$

The other value of $theta$ could be in QIII where $theta=221.4^circ$

a) Doubling the height of $sin 32^circ$ does not equate to $sin 64^circ$

a) The height corresponding to the sum of $sin 20^circ$ and $sin 40^circ$ is not the same with the height of $sin 60^circ$

c) The ratios of horizontal and vertical lines are not the same for $25^circ$ and $75^circ$