
All Solutions
Page 274: Getting Started
$c^2=a^2+b^2$
a) $c=sqrt{12^2+5^2}implies c=sqrt{169}=13$
b) $11^2=f^2+8^2implies f=sqrt{11^2-8^2}=sqrt{57}$
b) $sqrt{57}$
$sin theta = dfrac{text{opposite side}}{text{hypotenuse}}$
$cos theta = dfrac{text{adjacent side}}{text{hypotenuse}}$
$tan theta = dfrac{text{opposite side}}{text{adjacent side}}$
$$
color{white} ddd
$$
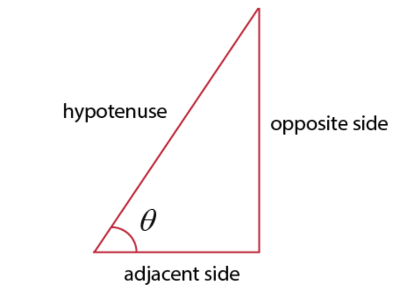
opposite side = 5
adjacent side = 12
hypotenuse = $sqrt{5^2+12^2}=13$
$sin A=dfrac{5}{13}$
$cos A=dfrac{12}{13}$
$tan A=dfrac{5}{12}$
opposite side = 8
hypotenuse = $11$
adjacent side = $sqrt{11^2-8^2}=sqrt{57}$
$sin D=dfrac{8}{11}$
$cos D=dfrac{sqrt{57}}{11}$
$tan D=dfrac{8}{sqrt{57}}$
b) $sin D=dfrac{8}{11}$; $cos D=dfrac{sqrt{57}}{11}$ ; $tan D=dfrac{8}{sqrt{57}}$
$sin theta = dfrac{text{opposite side}}{text{hypotenuse}}$
$cos theta = dfrac{text{adjacent side}}{text{hypotenuse}}$
$tan theta = dfrac{text{opposite side}}{text{adjacent side}}$
$$
color{white} ddd
$$
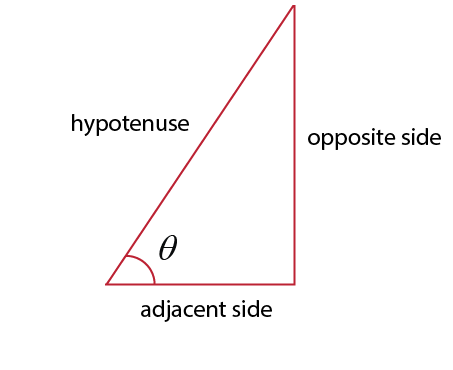
opposite side = 12
adjacent side = 5
$tan (angle B)=dfrac{12}{5}$
$$
angle B=tan^{-1}left(dfrac{12}{5}right)approx 67.38^circ
$$
adjacent side = 8
hypotenuse = 11
$cos (angle F)=dfrac{8}{11}$
$$
angle F=cos^{-1}left(dfrac{8}{11}right)approx43.34^circ
$$
b) $43^circ$
a) $sin 31^circapprox 0.515$
b) $cos 70^circapprox 0.342$
b) 0.342
$$
begin{equation*}f(theta)=aiff theta =f^{-1}(a)end{equation*}
$$
Be sure to set your calculator to DEGREE mode.
b) $theta=sin^{-1}(0.7113)=45^circ$
c) $theta=tan^{-1}(1.1145)=48^circ$
b) $45^circ$
c) $48^circ$
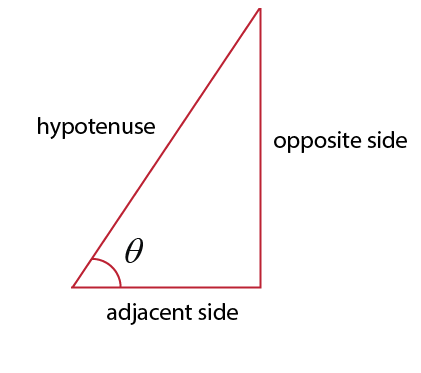
$sin theta = dfrac{text{opposite side}}{text{hypotenuse}}$
$cos theta = dfrac{text{adjacent side}}{text{hypotenuse}}$
$$
tan theta = dfrac{text{opposite side}}{text{adjacent side}}
$$
$$
color{white} ddd
$$
{text{The height of the tower is the sum of the }} hfill \
{text{opposite sides with respect to the angle of elevation}} hfill \
{text{and angle of depression}}{text{.}} hfill \
hfill \
tan {32^ circ } = frac{j}{{40}} hfill \
j = 40tan {32^ circ } approx 24.995 hfill \
hfill \
tan {42^ circ } = frac{k}{{40}} hfill \
k = 40tan {32^ circ } approx 36.016 hfill \
hfill \
x = j + k = 24.995 + 36.016 approx boxed{61{text{m}}} hfill \
hfill \
{text{The tower is 61 m high}} hfill \
end{gathered} ]
{text{Remember that}} hfill \
hfill \
tan theta = frac{{{text{opposite side}}}}{{{text{adjacent side}}}} hfill \
hfill \
{text{Notice that we can form two similar triangles}}{text{.}} hfill \
{text{We shall evaluate tan}}theta {text{ for both triangles}} hfill \
hfill \
{text{small triangle: }}tan theta = frac{{1.3}}{{1.8}} hfill \
{text{big triangle: }}tan theta = frac{x}{{35.2}} hfill \
hfill \
{text{Equate both }}tan theta hfill \
frac{{1.3}}{{1.8}} = frac{x}{{35.2}} hfill \
hfill \
x = 35.2left( {frac{{1.3}}{{1.8}}} right) approx boxed{25.42{text{ m}}} hfill \
hfill \
{text{The tower is 25}}{text{.42 m high}}{text{.}} hfill \
end{gathered} ]

