$bold{Concept:}$ For the quadratic function in vertex form $f(x)=a(x-h)^2+k$

direction of opening:

$a>0implies$ up
$a0implies { f(x)inbold{R};|;f(x)geq k}$

if $a<0implies { f(x)inbold{R};|;f(x)leq k}$

$bold{Solution:}$

a) Since $a=-3<0$, it opens downward. The vertex is $(2,5)$ and axis of symmetry is $x=2$

b) domain: ${ xin bold{R}}$

range: ${ f(x)inbold{R};|;f(x) leq 5}$

c) You can evaluate $f(x)$ for $x=0,1,2,3,4$ to obtain data points and then sketch the graph.

a) down, vertex $(2,5)$ , $x=2$

b) domain = ${ xin bold{R}}$ , range = ${ yin bold{R};|;yleq 5}$

c) see graph inside

$bold{Concept:}$ For the quadratic function in factored form $f(x)=a(x-r)(x-s)$

zeros: $r$ and $s$

direction of opening:

$a>0implies$ up
$a0implies { f(x)inbold{R};|;f(x)geq k}$

if $a<0implies { f(x)inbold{R};|;f(x)leq k}$

$bf{Solution:}$

a) Since $a=4>0$, it opens upwards and it has zeros at $x=2$ and $-6$.

The value of $x$ at the vertex corresponds to the average of two zeros.

$h=dfrac{2+(-6)}{2}=-2$

$k=f(-2)=4(-2-2)(-2+6)=-64$

and axis of symmetry is $x=-2$

b) domain: ${ xin bold{R}}$

range: ${ f(x)inbold{R};|;f(x) geq -64}$

c) You can plot the $x$-intercepts $(-6,0)$ and $(2,0)$ and the vertex$(-2,64)$ then draw a smooth curve.

a) up, zeros 2 and $-6$

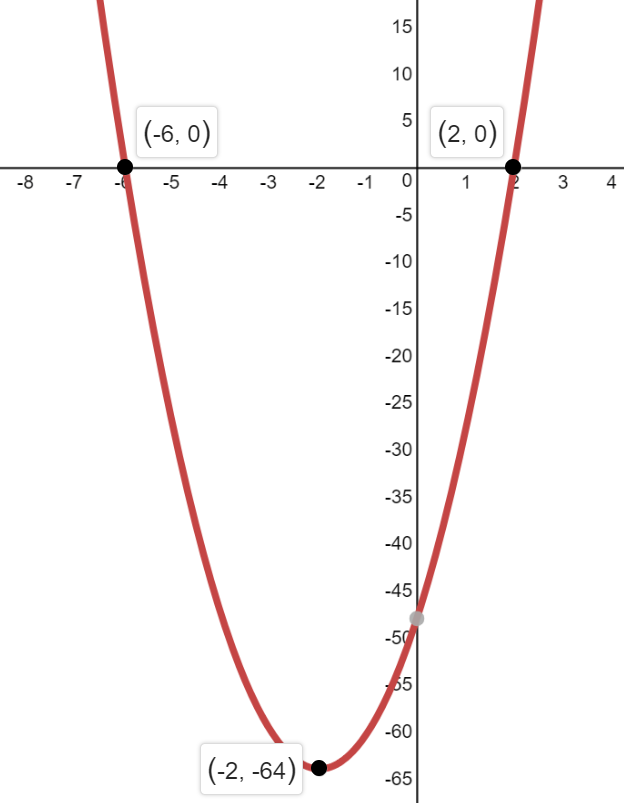
b) vertex $(-2,-64)$

c) domain: ${ xinbold{R}}$ ; range : ${ yin bold{R};|;ygeq -64}$

$bold{Concept:}$ If $(x_1,y)$ and $(x_2,y)$ are two points on a parabola with equal value of $y$, then the axis of symmetry is $x=dfrac{x_1+x_2}{2}$.

$bf{Solution:}$

The two given points $(-5,3)$ and $(3,3)$ has the same value of $y$-coordinate, thus, the average of the $x$-coordinates must correspond to the axis of symmetry.

axis of symmetry: $x=dfrac{-5+3}{2}=dfrac{-2}{2}=-1$

$$
x=-1
$$

$bold{Concept:}$ The maximum or minimum value will occur at the vertex. If $a>0$, the vertex corresponds to the minimum value while if $a<0$, the vertex corresponds to the maximum value.

$bold{Solution:}$

a) In vertex form $f(x)=a(x-h)^2+k$

The vertex is at $(h,k)$

In this case, $a=-3<0$,

so the maximum occurs at $(4,7)$

The maximum value is $7$ which occurs at $x=4$

b) In factored form $f(x)=a(x-r)(x-s)$

vertex$(h,k)$ where $h=dfrac{r+s}{2}$ and $k=f(h)$

In this case,

$h=dfrac{0+(-6)}{2}=-3$

$k=f(-3)=4(-3)(-3+6)=-36$

With $a=4>0$, the minimum occurs at $(-3,-36)$

The minimum value is $-36$ which occurs at $x=-3$

a) The maximum value is $7$ which occurs at $x=4$

b) The minimum value is $-36$ which occurs at $x=-3$

$bold{Concept:}$ The maximum or minimum value of a quadratic function occurs at its vertex. For the standard form

$f(x)=ax^2+bx+c$

the vertex is $(h,k)$ where

$h=-dfrac{b}{2a}$

$$
k=f(h)
$$

$bold{Solution:}$ Rewrite the function in standard form

$h(t)=-4.9t^2+28t+2$

$a=-4.9$ , $b=28$ , $c=2$

Since $a<0$, the vertex corresponds to the maximum.

We shall find the coordinates of the vertex to find the maximum height

$h=-dfrac{b}{2a}=-dfrac{28}{2(-4.9)}=2.86$

$k=f(2.86)=-4.9(2.86)^2+28(2.86)+2=42$ m

Therefore, the maximum height is $42$ m which occurs at about $2.9$ s

The maximum height is $42$ m which occurs at about $2.9$ s

To find the the inverse of $y=x^2$,

Replace $y$ with $x$ and replace $x$ with $y$ (swap the variables), then solve for $y$ in terms of $x$

$x=y^2implies y=pmsqrt{x}$

Therefore, $g(x)=sqrt{x}$ and $h(x)=-sqrt{x}$ are two branches of the inverse of $f(x)=x^2$

$g(x)=sqrt{x}$ and $h(x)=-sqrt{x}$ are two branches of the inverse of $f(x)=x^2$

For example, the inverse of the quadratic function $f(x)=x^2$ is $g(x)=pmsqrt{x}$. However, $g(x)$ fails the vertical line test.

a) From the graph, the vertex is $(2,4)$ so we can write the vertex form as

$f(x)=a(x-2)^2+4$

To find $a$, we can use any point on the parabola. We will choose $(1,2)$

$2=a(1-2)^2+4implies a=dfrac{2-4}{(1-2)^2}=-2$

$f(x)=y=-2(x-2)^2+4$

Now, we will find the inverse of this function by swapping $x$ and $y$

$x=-2(y-2)^2+4$

$(y-2)^2=dfrac{x-4}{-2}$

$y-2=pmsqrt{dfrac{4-x}{2}}$

$$
y=2pmsqrt{dfrac{4-x}{2}}
$$

From the graph, we see the following points $(0,-4)$ , $(1,2)$ , $(2,4)$ , $(3,2)$ , $(4,-4)$

We can sketch the inverse function by swapping the coordinates. Thus, the inverse shall contain the following points.

$(-4,0)$, $(2,1)$ , $(4,2)$, $(2,3)$ , $(-4,4)$

b) From the graph, the domain of the inverse relation is the set of $x$-values not more than $4$

domain = ${ xinbold{R};|;xleq 4}$

The range is the set of all real numbers.

range = ${ yinbold{R}}$

c) The inverse relation cannot pass the vertical line test. For example, the vertical line at $x=-4$ would touch the points $(-4,0)$ and $(-4,4)$, thus, it is not a function.

a) see graph inside

b) domain = ${ xinbold{R};|;xleq 4}$ ; range = ${ yinbold{R}}$

c) not a function ; does not pass vertical line test

In the following, remember that $sqrt{a^2b}=asqrt{b}$

a) $sqrt{98}$
$=sqrt{49times 2}$
$=sqrt{7^2times 2}$
$=7sqrt{2}$

b) $-5sqrt{32}$
$=-5sqrt{16times 2}$
$=-5sqrt{4^2times 2}$
$=(-5times 4)sqrt{2}$
$=-20sqrt{2}$

c) $4sqrt{12}-3sqrt{48}$
$=4sqrt{4times 3}-3sqrt{16times 3}$
$=4sqrt{2^2times 3}-3sqrt{4^2times 3}$
$=8sqrt{3}-12sqrt{3}$
$=-4sqrt{3}$

d) $(3-2sqrt{7})^2$
$=3^2-2(3)(-2sqrt{7})+(2sqrt{7})^2$
$=9-12sqrt{7}+4times 7$

$$
=37-12sqrt{7}
$$

a) $7sqrt{2}$

b) $-20sqrt{2}$

c) $-4sqrt{4}$

d) $37-12sqrt{7}$

Substitute the given values to the formula:

$a=5$, $b=7$ , $c=10$

$s=dfrac{1}{2}(a+b+c)=dfrac{1}{2}(5+7+10)=11$

$A=sqrt{s(s-a)(s-b)(s-c)}$

$=sqrt{11(11-5)(11-7)(11-10)}$

$=sqrt{11(6)(4)(1)}$

$=sqrt{264}$

$=sqrt{4times 66}$

$=sqrt{2^2times 66}$

$=2sqrt{66}$

The area of the triangle is $2sqrt{66}$ square units.

$2sqrt{66}$ square units

In this case,

$a=6$ , $b=3$

$c=sqrt{6^2+3^2}$

$c=sqrt{36+9}$

$c=sqrt{45}$

$c=sqrt{9times 5}$

$c=sqrt{3^2times 5}$

$c=3sqrt{5}$

The hypotenuse $c$ of a triangle with legs $a$ and $b$ can be calculated using Pythagorean formula:

$$
c^2=a^2+b^2
$$

$P=6+3+3sqrt{5}$

$P=9+3sqrt{5}$

Therefore, the perimeter of the triangle is

$P=9+3sqrt{5}$ cm

The perimeter of a triangle is the sum of all three sides.

$$
P=a+b+c
$$

$P=9+3sqrt{5}$ cm

$bold{Concept:}$ The $x$-intercepts of a quadratic function are the points at which the graph touches the $x$-axis or when $f(x)=0$

If $x_1$ and $x_2$ are the zeros of the quadratic function, then the $x$-intercepts are

$(x_1,0)$ and $(x_2,0)$

$bold{Solution:}$ We can solve this by factoring

$f(x)=2x^2+x-15=0$

$(2x-5)(x+3)=0$

$x=dfrac{5}{2}$ or $-3$

Therefore, the $x$-intercepts are

$left(dfrac{5}{2},0right)$ and $(-3,0)$

$left(dfrac{5}{2},0right)$ and $(-3,0)$

a) First find $t$ at year $2020$

$t=2020-2007=13$

Now substitute this value of $t$ to the population model

$P(t)=12t^2+800t+40;000$

$P(13)=12(13)^2+800(13)+40;000$

$P(13)=52;428$

b) We shall find the value of $t$ such that $P(t)=300;000$

$300;000=12t^2+800t+40;000$

$12t^2+800t-260;000=0$

We will use quadratic formula

$a=12$ , $b=800$ , $c=-260;000$

$t=dfrac{-bpmsqrt{b^2-4ac}}{2a}$

$t=dfrac{-800pmsqrt{800^2-4(12)(-260;000)}}{2(12)}$

$t=-184.25$ or $117.59$

We can confirm this by graphing.

Since $t=0$ at year 2007.

$t=-184.25implies text{ year }=2007-184.25=1823$

$t=117.59implies text{ year } = 2007+117.59=2125$

Thus, the population is predicted to be $300,000$ in 1823 and 2125.

$bold{Note:}$ The answer in your textbook is $1990$. This is obtained when the predicted population is 30,000 and not $300,000$. In this case,

$12t^2+800t+40;000=30;000$

$12t^2+800t+10;000=0$

$a=12$ , $b=800$ , $c=10;000$

$x=dfrac{-bpmsqrt{b^2-4ac}}{2a}$

$x=dfrac{-800pmsqrt{800^2-4(12)(10;000)}}{2(12)}$

$x=-50implies 2007-50=19567$

$-$16.67 $implies 2007-16.67=1990.33$

This occurs in year 1957 and 1990.

Let $x$ be the length of the rectangular garden and $w$ be the width.

We need to express the width in terms of the length $x$

Since the perimeter is $400$ m, we can write

$2x+2w=400$

$x+w=200implies w=200-x$

The area of the triangle is length $times$ width

$x(200-x)=8000$

$200x-x^2=8000$

$200x-x^2-8000=0$

$-x^2+200x-8000=0$

Solve by quadratic formula

$a=-1$ , $b=200$ , $c=-8000$

$x=dfrac{-bpmsqrt{b^2-4ac}}{2a}$

$x=dfrac{-200pmsqrt{(-200)^2-4(-1)(-8000)}}{2(-1)}$

$x=55.28$ or $144.72$

$w=200-55.28=144.72$

Therefore, both values of $x$ would lead to rectangle with dimensions

$55.28$ m by $144.72$ m

$55.28$ m by $144.72$ m

To determine whether $h(t)$ can have a value of $9$, we need to find range of the function.

Remember that for parabola opening downwards $a<0$, the range is $h(t)leq k$

$h(t)=14t-5t^2$

$a=-5$ , $b=14$, $c=0$

The value of $t$ that corresponds to the vertex is

$t=-dfrac{b}{2a}=-dfrac{14}{2(-5)}=-1.4$

Now we shall evaluate $h(t)$ at $t=-1.4$ to find $k$

$k=h(-1.4)=14(1.4)-5(1.4)^2=9.8$

Therefore, the maximum height is $9.8$, thus, it can reach a height of $9$ m.

To determine the number of zeros of a quadratic function in standard form, calculate $b^2-4ac$

$f(x)=ax^2+bx+c$

$b^2-4ac>0implies$ 2 zeros

$b^2-4ac=0implies$ 1 zero

$b^2-4ac0$

$(2k)^2+2(2k)(-3)+(-3)^2-16>0$

$4k^2-12k+9-16>0$

$4k^2-12k-7>0$

$(2k-7)(2k+1)>0$

$k=dfrac{7}{2}$ , $-dfrac{1}{2}$

This is a parabola that opens upward so the function would be greater than zero for values that are on the left of $-dfrac{1}{2}$ and to the right of $dfrac{7}{2}$

$kdfrac{7}{2}$

Example where $k<-dfrac{1}{2}$ is $k=-1$

$f(x)=4x^2-3x+2(-1)x+1$

$f(x)=4x^2-5x+1$

Example where $k>dfrac{7}{2}$ is $k=4$

$a=4$ , $b=2(4)-3=5$ , $c=1$

$$
y=4x^2+5x+1
$$

$x3.5$

$bold{Concept:}$ The break-even point of a profit function $P(x)$ are values of $x$ such that $P(x)=0$

$bold{Solution:}$ We need to solve the equation

$P(x)=-2x^2+7x+8=0$

We shall use quadratic formula

$a=-2$ , $b=7$ , $c=8$

$x=dfrac{-bpmsqrt{b^2-4ac}}{2a}$

$x=dfrac{-7pmsqrt{7^2-4(-2)(8)}}{2(-2)}$

$x=dfrac{-7pmsqrt{113}}{-4}$

$x=dfrac{7pmsqrt{113}}{4}$

$x=-0.9075$ or $4.408$

Since the number of bikes $x$ (in thousands) cannot be negative, choose only $x=4.408$
which corresponds to $4408$ bikes.

$4408$ bikes

$bold{Concept:}$ If a parabola has roots (zeros) $r$ and $s$, then the equation of parabola is

$y=a(x-r)(x-s)$

$y=a[x^2-(r+s)x+rs]$

To evaluate $a$, substitute any point on the parabola to the equation and solve for $a$

$bold{Solution:}$ In this case, $r=2+sqrt{3}$ , $s=2-sqrt{3}$

$r+s=(2+sqrt{3})+(2-sqrt{3})=4$

$rs=(2+sqrt{3})(2-sqrt{3})=2^2-(sqrt{3})^2=4-3=1$

Thus, the equation becomes

$y=a(x^2-4x+1)$

We are given that $(2,5)$ is a point on the parabola,

$5=a(2^2-4(2)+1)$

$a=dfrac{5}{2^2-4(2)+1}=-dfrac{5}{3}$

Therefore, the equation of the parabola is

$y=-dfrac{5}{3}(x^2-4x+1)$

$$
y=-dfrac{5}{3}+dfrac{20}{3}x-dfrac{5}{3}
$$

$$
y=-dfrac{5}{3}+dfrac{20}{3}x-dfrac{5}{3}
$$

begin{table}[]
defarraystretch{1.5}%
begin{tabular}{|l|l|}
hline
$bold{Form}$ & $bold{Family; of; Parabola}$ \ hline
begin{tabular}[c]{@{}l@{}}vertex form\ $f(x)=a(x-h)^2+k$end{tabular} & begin{tabular}[c]{@{}l@{}}if $a$ is varied\ $implies$ families with the same vertex and\ axis of symmetryend{tabular} \ hline
begin{tabular}[c]{@{}l@{}}factored form\ $f(x)=a(x-r)(x-s)$end{tabular} & begin{tabular}[c]{@{}l@{}}if $a$ is varied\ $implies$ families with the same $x$-intercepts\ and axis of symmetryend{tabular} \ hline
begin{tabular}[c]{@{}l@{}}standard form\ $f(x)=ax^2+bx+c$end{tabular} & begin{tabular}[c]{@{}l@{}}if $a$ and $b$ are varied\ $implies$ families with the same $y$-interceptend{tabular} \ hline
end{tabular}
end{table}

This is in vertex form with varying $a$, thus it will have the same vertex and axis of symmetry.

Now, we shall evaluate $a$ by substituting the coordinates of the point $(-2,6)$

$f(x)=a(x+3)^2-4$

$6=a(-2+3)^2-4$

$a=dfrac{6+4}{(-2+3)^2}=10$

The member that passes through $(-2,6)$ is

$$
f(x)=10(x+3)^2-4
$$

$$
f(x)=10(x+3)^2-4
$$

Interpret the given conditions:

parabolic arch $implies$ parabola that opens downward, we will arbitrarily choose the axis of symmetry of the parabola at $x=0$

$15$ m high $implies$ the vertex is $(0,15)$

$6$ m wide at a height of $8$ m $implies$ passes through $(-3,8)$ and $(3,8)$

a) With vertex at $(0,15)$, the parabola must belong to the family

$y=a(x-0)^2+15$

We will find $a$ by substituting the point $(3,8)$

$8=a(3-0)^2+15$

$a=dfrac{8-15}{3^2}=-dfrac{7}{9}$

Therefore, the equation of the parabola is

$$
y=-dfrac{7}{9}x^2+15
$$

b) The width of the base is distance between two zeros.

$-dfrac{7}{9}x^2+15=0$

$dfrac{7}{9}x^2=15$

$x=pmsqrt{dfrac{15}{7/9}}$

$x=pm 4.4$

Thus, the zeros are at $(-4.4,0)$ and $(4.4,0)$

The distance between these two points is $4.4-(-4.4)=8.8$

Therefore, the arch must be 8.8 m wide at the base.

a) $y=-dfrac{7}{9}x^2+15$

b) 8.8 m

$2x^2+4x-11=-3x+4$

$$
2x^2+7x-15=0
$$

Set the two equations equal to one another and put into standard form. Which is:

$$
ax^2+bx+c=0
$$

$$
(x+5)(2x-3)
$$

Solve for $x$. This can most easily be done by factoring. We know that $3(5)=15$ and that $2(5)-7=3$. Therefore

$x=-5$

$$
2x-3=0rightarrow x=frac{3}{2}=1.5
$$

Solve for $x$. This will be the x values for the points of intersection

$-3(1.5)+4=-.5$

$$
-3(-5)+4=19
$$

$(1.5,-0.5)$ and $(-5,19)$

$(1.5,-0.5)$ and $(-5,19)$

To find the intersection point of the baseball and the paintball, equate $h(t)=g(t)$

$h(t)=g(t)$

$-5t^2+20t+15=3t+3$

$-5t^2+17t+12=0$

$a=-5$, $b=17$, $c=12$

We shall first determine how many zeros are possible

$b^2-4ac=(17)^2-4(-5)(12)=529>0$

Since $b^2-4ac>0$, there will be two solutions.

We shall then use the quadratic formula

$t=dfrac{-bpmsqrt{b^2-4ac}}{2a}$

$t=dfrac{-17pmsqrt{529}}{2(-5)}$

$t=-0.6$ or 4

Time can’t be negative, so choose $t=4$

The height at $t=4$ can be solved using either $h(t)$ or $g(t)$

$g(t)=3(4)+3=15$ m

Therefore, the paintball will hit the baseball after 4 s at a height of 15 m.

$bold{Concept:}$ The intersection point of a parabola $f(x)$ and a line $g(x)$ are the solutions of $f(x)=g(x)$

If no values of $x$ satisfies the equation $(b^2-4ac<0)$, then $f(x)$ and $g(x)$ does not intersect.

$bold{Solution:}$ Equate $f(x)$ and $g(x)$

a) $f(x)=g(x)$

$x^2-6x+9=-3x-5$

$x^2-3x+14=0$

$a=1$ , $b=-3$ , $c=14$

$b^2-4ac=(-3)^2-4(1)(14)=-47<0$

Since $b^2-4ac<0$, the parabola and the line do not intersect.

a) No since $b^2-4ac$ of $f(x)-g(x)$ is negative.

b) $g(x)=3x-5$