
All Solutions
Page 2: Getting Started
Distributive property:
$a(b+c)=ab+ac$
$a-b(c-d)=a-bc+bd$
$(a+b)(c+d)=a(c+d)+b(c+d)$
Special products:
$(a+b)(a-b)=a^2-b^2$
$(a+b)^2=a^2+2ab+b^2$
$=3x+3y-5x+5y$
$=(3-5)x+(3+5)y$
$$
=-2x+8y
$$
$(4x-y)(4x+y)$
$=(4x)^2-(y)^2$
$$
=16x^2-y^2
$$
$=dfrac{1}{2}x^2+dfrac{1}{2}-dfrac{3}{2}x^2+dfrac{3}{2}$
$=left(dfrac{1}{2}-dfrac{3}{2}right)x^2+dfrac{1}{2}+dfrac{3}{2}$
$$
=-x^2+2
$$
$=4x^2+8x-2x^2+8x$
$=(4-2)x^2+(8+8)x$
$$
=2x^2+16x
$$
b) $16x^2-y^2$
c) $-x^2+2$
d) $2x^2+16x$
dfrac{1}{2}cdot x^{2}+dfrac{1}{2} cdot1-dfrac{3}{2}cdot x^{2}+dfrac{3}{2}cdot 1=\
\
-dfrac{2}{2}x^{2}+dfrac{4}{2}=-x^{2}+2$
4x(x+2)-2x(x-4)=4xcdot x+4xcdot2-2xcdot x+2xcdot4=\
4x^{2}+8x-2x^{2}+8x=2x^{2}+16x
$$
*How can we simplify the expressions?*
$$a(b+c)=ab+ac,$$
then collect *like terms* (terms with the same variable and exponent) to simplify it.
When collecting like terms, it is often a good idea to group them first before adding and/or subtracting.
Apply the Distributive Property for each multiplication, group like terms, then add/subtract them as follows:
$$begin{align*}
3(x+y)-5(x-y)&= 3x+3y-5x+5y\
&= (3x-5x )+(3y+5y)\
&= -2x+8y.
end{align*}$$
Apply the Distributive Property twice, group like terms, then add/subtract them as follows:
$$begin{align*}
(4x-y)(4x+y)&= 4x(4x-y)+y(4x-y)\
&= 16x^2-4xy+ 4xy-y^2\
&= 16x^2+(-4xy+ 4xy)-y^2\
&= 16x^2-y^2.
end{align*}$$
Apply the Distributive Property for each multiplication, group like terms, then add/subtract them as follows:
$$begin{align*}
dfrac{1}{2}(x^2+1)-dfrac{3}{2}(x^2-1)&=dfrac{1}{2}x^2+dfrac{1}{2}-dfrac{3}{2}x^2+dfrac{3}{2}\
&= left(dfrac{1}{2}x^2-dfrac{3}{2}x^2right)+left(dfrac{1}{2}+dfrac{3}{2}right)\
&=-x^2+2.
end{align*}$$
Apply the Distributive Property for each multiplication, group like terms, then add/subtract them as follows:
$$begin{align*}
4x(x+2)-2x(x-4)&= 4x^2+8x-2x^2+8x\
&= (4x^2-2x^2)+(8x+8x)\
&= 2x^2+16x.
end{align*}$$
We simplified the expressions by applying the Distributive Property and combining like terms.
(b) $16x^2-y^2$
(c) $-x^2+2$
(d) $2x^2+16x$
$-2x+8y$, if are $x=3$ and $y=-5$, we can evaluate this expression (substitute $x=3$ and $y=-5$)::
$$
-2x+8y=-2cdot3+8cdot(-5)=-6-40=-46
$$
$16x^{2}-y^{2}$, if are $x=3$ and $y=-5$, we can evaluate this expression (substitute $x=3$ and $y=-5$):
$$
16x^{2}-y^{2}=16cdot3^{2}-(-5)^{2}=16cdot9-25=144-25=119
$$
$-x^{2}+2$, if is $x=3$ , we can evaluate this expression (substitute $x=3$ ):
$$
-x^{2}+2=-3^{2}+2=-9+2=-7
$$
$2x^{2}+16x$, if is $x=3$, we can evaluate this expression (substitute $x=3$):
$$
2x^{2}+16x=2cdot3^{2}+16cdot3=2cdot9+48=18+48=66
$$
b) 119
c) -7
d) 66
a) $5x-8=7$
Add 8 to both sides
$5x=7+8$
$5x=15$
Divide both sides by 5
$dfrac{5x}{5}=dfrac{15}{5}$
$x=3$
Use distributive property: $a(b+c)=ab+ac$
$-2x+6=2-4x$
Transpose all terms with variables to the left
and all constants to the right.
$-2x+4x=2-6$
$2x=-4$
Divide both sides by $2$
$dfrac{2x}{2}=dfrac{-4}{2}$
$x=-2$
Multiply both sides by $12$
$12cdotleft(dfrac{5}{6}y-dfrac{3}{4}yright)=-3cdot (12)$
$10y-9y=-36$
$$
y=-36
$$
Multiply both sides by $12$
$12cdot dfrac{x-2}{4}=12cdot dfrac{2x+1}{3}$
$3(x-2)=4(2x+1)$
Apply distributive property $a(b+c)=ab+ac$
$3x-6=8x+4$
$3x-8x=4+6$
$-5x=10$
Divide both sides by $-5$
$dfrac{-5x}{-5}=dfrac{10}{-5}$
$$
x=-2
$$
b) $x=-2$
c) $y=-36$
d) $x=-2$
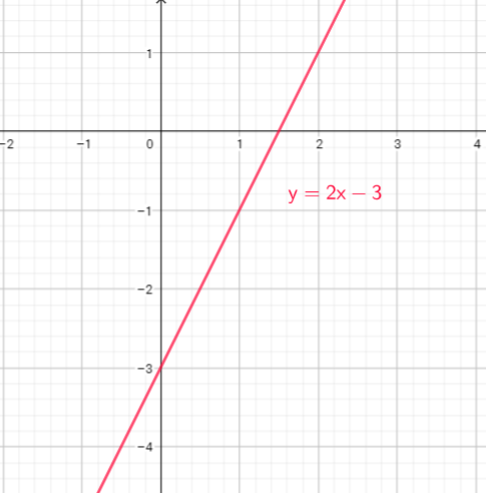
1. Locate the y-intercept on the graph and plot the point. The y-intercept is the solution to the equation $y=2x-3$ when $x = 0$:
If $x=0$, then, $y=2cdot0-3=0-3=-3$, so, the point is $(0,-3)$
1. Locate the x-intercept on the graph and plot the point. The x-intercept is the solution to the equation $y=2x-3$ when $y = 0$:
If $y=0$, then, $0=2x-3=$, $2x=3$ or $x=dfrac{3}{2}$ so, the point is $(dfrac{3}{2},0)$
3. Draw the line that connects the two points $(0,-3)$ and $(dfrac{3}{2},0)$
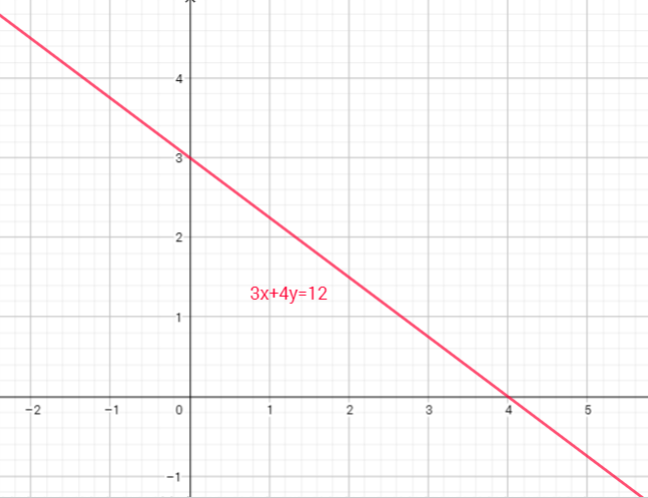
1. Locate the y-intercept on the graph and plot the point. The y-intercept is the solution to the equation $3x+4y=12$ when $x = 0$:
If $x=0$, then, $3cdot0+4y=12$, $0+4y=12$, $y=dfrac{12}{4}$, $y=3$ so, the point is $(0,3)$
1. Locate the x-intercept on the graph and plot the point. The x-intercept is the solution to the equation $3x+4y=12$ when $y = 0$:
If $y=0$, then, $3x+4cdot0=12$, $3x+0=12$, $x=dfrac{12}{3}$, $x=4$ , so, the point is $(4,0)$
3. Draw the line that connects the two points $(0,-3)$ and $(4,0)$
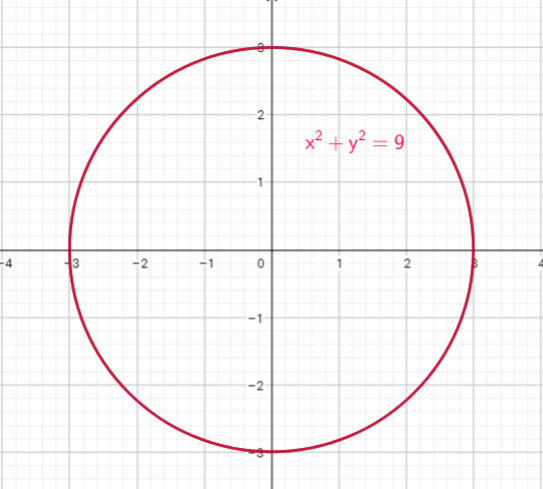
(0, 0) has equation $x^{2}+y^{2}=r^{2}$ where is $r$ its radius.
Now we can conclude, the circle $x^{2}+y^{2}=3^{2}$ is centered at the origin $(0,0)$,and its radius is equal $3$
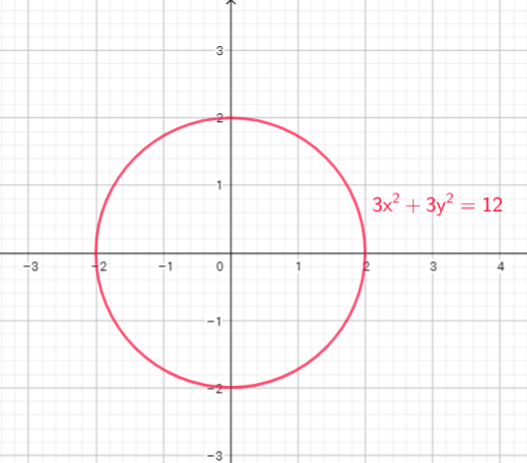
Now, equation of this circle is : $x^{2}+y^{2}=4$, or $x^{2}+y^{2}=2^{2}$
Use explanation on part a) we can conclude: This circle has center at the origin (0, 0) and its radius is $2$
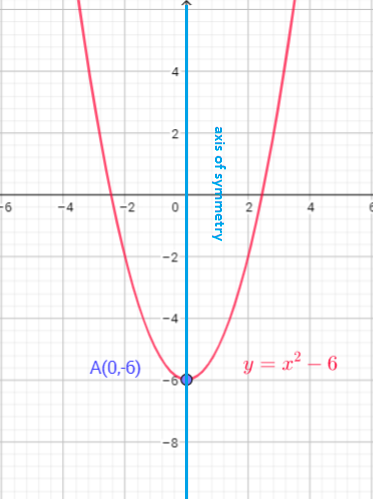
$y=a(x-h)^{2}+k$, then the vertex of the parabola is the point $(h,k)$.
The axis of symmetry of a parabola is a vertical line that divides the parabola into two congruent halves. The axis of symmetry always passes through the vertex of the parabola . The x-coordinate of the vertex is the equation of the axis of symmetry of the parabola.
In this case, vertex form of this equation is $y=1cdot(x-0)^{2}+(-6)$, so, the vertex of the parabola is $(0,-6)$, and axis of symmetry is a line $x=0$
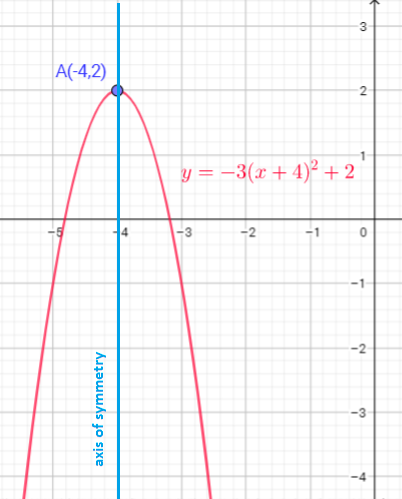
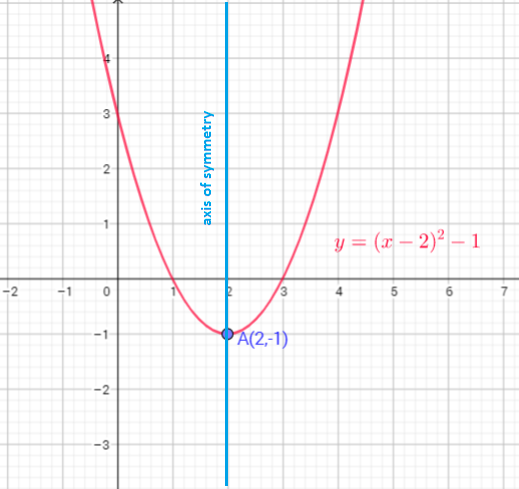
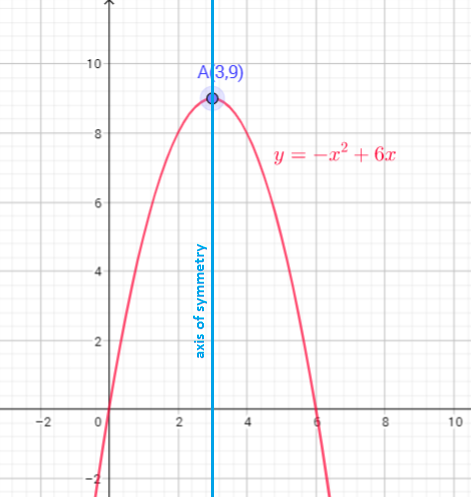
The graph of $y=x^{2}$ translate down 2 units
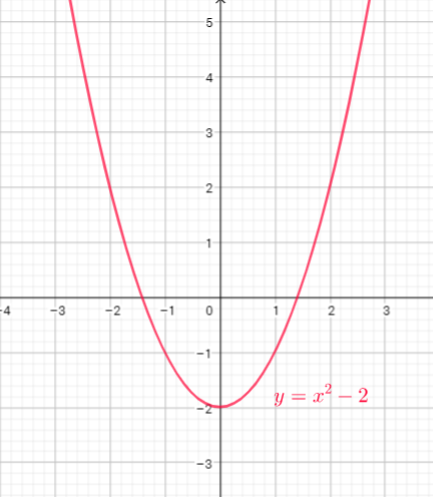
Function $y=x^{2}$ is reflect in x-axis then vertical stretch, multiply every y-coordinate by 4, then translate up 3 units
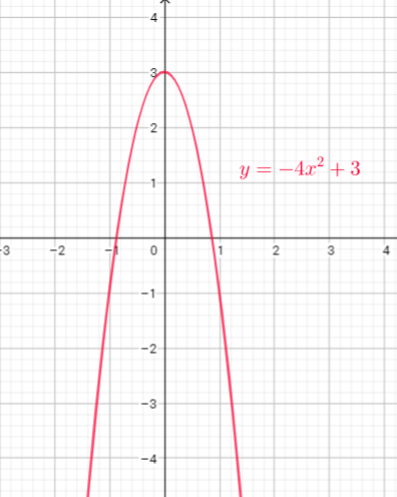
Function $y=x^{2}$ is shifted 1 units to the right, multiply every y-coordinate by $dfrac{1}{2}$, and move down 4 units
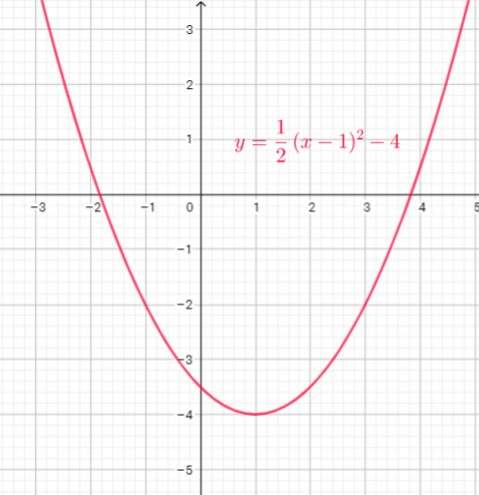
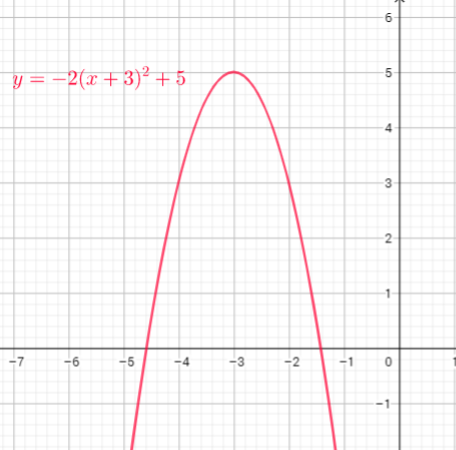
Function $y=x^{2}$ is shifted 3 units to the left, reflect in x-axis then vertical stretch, multiply every y-coordinate by 2, then translate up 5 units
b) Reflect in $x$-axis then vertical stretch by a factor of 4, translate 3 units upward
c) Vertical compression by a factor 2, translate 1 unit to the right, translate 4 units down
d) reflect in $x$-axis, vertical stretch by a factor of 2, horizontally translate 3 units to the left, vertically translate 5 units up
$x^{2}-5x+6=0$
This quadratic equation we can solve use the quadratic formula
$x_{1,2}=dfrac{-bpmsqrt{b^{2}-4ac}}{2a}$ where are
$a=1, b=-5$ and $c=6$
Substitute values $a=1, b=-5$ and $c=6$ in quadratic formula we get:
$x_{1,2}=dfrac{-(-5)pmsqrt{(-5)^{2}-4cdot1cdot6}}{2cdot1}$
$x_{1,2}=dfrac{5pmsqrt{25-24}}{2}$
$x_{1,2}=dfrac{5pm1}{2}$
$x_{1}=dfrac{5+1}{2}$ and $x_{2}=dfrac{5-1}{2}$
$x_{1}=dfrac{6}{2}$ and $x_{2}=dfrac{4}{2}$
$x_{1}=3$ and $x_{2}=2$
Solutions of quadratic equation are $x_{1}=3$ and $x_{2}=2$
$3x^{2}-5=70$
Add 5 on the both sides
$3x^{2}-5+5=70+5$
$3x^{2}=75$ divide both sides by 3
$x^{2}=25$
Take the square root of each side:
$x=pmsqrt{25}$
$x=pm5$
Solutions of quadratic equation are $x_{1}=-5$ and $x_{2}=5$
b) $x=pm 5$
bold{Property}
$$
bold{Linear;Relations}
$$
bold{Circles}
$$
bold{Quadratic;Relations}
$$
$y-y_1=m(x-x_1)$
$$
Ax+By=C
$$
(x-h)^2+(y-k)^2=r^2
$$
$$
y=a(x-h)^2+k
$$
crosses each axis not more than once
symmetric with respect to its center
crosses the $y$-axis only once
crosses the $x$-axis, 0, 1, or 2 times
partial variation
wheels and axles
area
force on a spring
kinetic energy
economic functions

