$bold{a);;;}$

$$
begin{align*}
x^2-6x-27&=x^2+(-9+3)x+(-9times 3)\
&=(x-9)(x+3)
end{align*}
$$

Remember that

$x^2+(a+b)x+(ab)=(x+a)(x+b)$

$bold{b);;;}$

$$
begin{align*} 25x^2-49 &=(5x)^2-(7)^2\
&=(5x+7)(5x-7)
end{align*}
$$

Remember that

$$
a^2-b^2=(a+b)(a-b)
$$

$$
bold{c);;;}
$$

$$
begin{align*} 4x^2+20x+25 &=(2x)^2+2(2x)(5)+5^2\
&=(2x+5)^2
end{align*}
$$

Remember that

$$
a^2+2ab+b^2=(a+b)^2
$$

$$
bold{d);;;}
$$

$$
begin{align*} 6x^2-x-2 &=6x^2-4x+3x-2\
&=2x(3x-2)+1(3x-2)\
&=(2x+1)(3x-2)\
end{align*}
$$

This is a quadratic trinomial with $aneq 1$ of the form

$ax^2+bx+c$

We must find numbers whose sum is $b$ and product is $ac$

In this case $ac=-12$ and $-1=-4+3$

Then decompose the middle term and find the common factor.

Remember that

$$
a(b+c)+d(b+c)=(a+d)(b+c)
$$

a) $(x-9)(x+3)$

b) $(5x+7)(5x-7)$

c) $(2x+5)^2$

d) $(2x+1)(3x-2)$

a) Given expression is: $ac+bc-ad-bd$.

$$
begin{align*}
ac+bc-ad-bd&=\
&=(ac+bc)-(ad+bd) tag{text{separate into two groups}}\
&=c(a+b)-d(a+b) tag{text{ factor out the GCF from each of the two groups}}\
&=(a+b)(c-d) tag{text{factor out (a+b)}}\
end{align*}
$$

b) Given expression is: $x^{2}+2x+1-y^{2}$

$$
begin{align*}
x^{2}+2x+1-y^{2}&=\
&=(x^{2}+2x+1)-y^{2} tag{text{group the first three terms together}}\
&=(x+1)^{2}-y^{2} tag{text{use square the binomials}}\
&=(x+1-y)(x+1+y) tag{text{use diference of two squares}}\
end{align*}
$$

a) Given expression is: $x^{2}-y^{2}-10y-25$.

$$
begin{align*}
x^{2}-y^{2}-10y-25&=\
&=x^{2}-(y^{2}+10y+25)tag{text{separate into two groups}}\
&=x^{2}-(y+5)^{2}\
&=(x-(y+5))(x+(y+5))\
&=(x-y-5)(x+y+5)
end{align*}
$$

a) $(a+b)(c-d)$

b) $(x+1-y)(x+1+y)$

c) $(x-y-5)(x+y+5)$

a) This is a given expression: $x^{2}-3x-28$

This is a trinomial, there we need use decomposition by finding two
numbers whose sum is -3 and whose product is -28.These numbers are -7, and then group the first two terms together and the last two terms together and factor out the common factor from each of the two groups. Two groups have a common $(x +4)$, so we can factor out $(x +4)$ :

$$
begin{align*}
x^{2}-3x-28&=\
&=x^{2}+4x-7x-28\
&=x(x+4)-7(x+4)\
&=(x+4)(x-7)\
end{align*}
$$

b) This is a given expression: $36x^{2}-25$

This is a binomial,use difference of squares we get :

$$
begin{align*}
36x^{2}-25&=\
&=(6x)^{2}-5^{2} \
&=(6x-5)(6x+5)\
end{align*}
$$

c) This is a given expression: $9x^{2}-42x+49$

This is a trinomial, use square of the binomial we get :

$$
begin{align*}
9x^{2}-42x+49&=\
&=(3x)^{2}-2cdot3xcdot7+7^{2}\
&=(3x-7)^{2}\
end{align*}
$$

d) This is a given expression: $2x^{2}-7x-15$

This is a trinomial, there we need use decomposition :

$$
begin{align*}
2x^{2}-7x-15&=\
&=2x^{2}-10x+3x-15tag{text{separate -7x as -10x+3x}}\
&=2x(x-5)+3(x-5) tag{text{factor out $x-5$}}\
&=(x-5)(2x+3)\
end{align*}
$$

a) $(x+4)(x-7)$

b) $(6x-5)(6x+5)$

c) $(3x-7)^{2}$

d) $(x-5)(2x+3)$

a) Given expression is: $4x^{3}-6x^{2}+2x$
$$
begin{align*}
4x^{3}-6x^{2}+2x&=\
&=2x(2x^{2}-3x+1) ~~text{text{divided each term by the
common factor 2x, factor out 2x}}\
&=2x(2x^{2}-2x-x+1) ~~text{text{use decomposition}}\
&=2x(2x(x-1)-(x-1))\
&=2x(x-1)(2x-1) ~~text{factor out (x-1)}
end{align*}
$$

b) Given expression is: $3x^{3}y^{2}-9x^{2}y^{4}+3xy^{3}$
$$
begin{align*}
&3x^{3}y^{2}-9x^{2}y^{4}+3xy^{3}=3xy^{2}(x^{2}-3xy^{2}+y)\ &text{divided each term by the
common factor $3xy^{2}$, factor out $3xy^{2}$}\
end{align*}
$$

c) Given expression is: $4a(a+1)-3(a+1)$

The two groups have the same common factor $(a+1)$, so we can factor out $(a+1)$ leaving the following:
$$
begin{align*}
4a(a+1)-3(a+1)&=(a+1)(4a-3)\
end{align*}
$$

d) Given expression is: $7x^{2}(x+1)-x(x+1)+6(x+1)$.

The three groups have the same common factor $(x+1)$, so we can factor out $(x+1)$ leaving the following:
$$
begin{align*}
7x^{2}(x+1)-x(x+1)+6(x+1)&=\
&=(x+1)(7x^{2}-x+6)\
end{align*}
$$

e) Given expression is: $5x(2-x)+4x(2x-5)-(3x-4)$

First, we need simplify this expression, and then group like terms.
$$
begin{align*}
5x(2-x)+4x(2x-5)-(3x-4)&=\
&=10x-5x^{2}+8x^{2}-20x-3x+4\
&=3x^{2}-13x+4\
&=3x^{2}-12-x+4\
&=3x(x-4)-(x-4)\
&=(x-4)(3x-1)\
end{align*}
$$

f) Given expression is:
$4t(t^{2}+4t+2)-2t(3t^{2}-6t+17)$

First, we use the distributive property, then simplify this expression, and then group like terms.
$$
begin{align*}
4t(t^{2}+4t+2)-2t(3t^{2}-6t+17)&=\
&=4t^{3}+16t^{2}+8t-6t^{3}+12t^{2}-34t\
&=-2t^{3}+28t^{2}-26t\
&=-2t(t^{2}-14t+13)\
&=-2t(t^{2}-t-13t+13)\
&=-2t(t(t-1)-13(t-1))\
&=-2t(t-1)(t-13)\
end{align*}
$$

a) $2x(x-1)(2x-1)$

b) $3xy^{2}(x^{2}-3xy^{2}+y)$

c) $(a+1)(4a-3)$

d) $(x+1)(7x^{2}-x+6)$

e) $(x-4)(3x-1)$

f) $-2t(t-1)(t-13)$

a) Here is the given polynomial: $x^{2}-5x-14$

$$
begin{align*}
x^{2}-5x-14&=x^{2}+2x-7x-14\
&=(x^{2}+2x)-(7x+14)\
&=x(x+2)-7(x+2)\
&=(x+2)(x-7)\
end{align*}
$$

In this part the first, we used decomposition by finding two numbers whose sum is -5 and whose product is -14, these numbers are 2 and -7

Then, we group the first two terms and the final two terms

Now, factor an $x$ out of the first grouping and a $7$ out of the second grouping.

We can factor out a common factor of $(x+2)$, so we get the final factored form.

b) Given expression is: $x^{2}+4xy-5y^{2}$

$$
begin{align*}
x^{2}+4xy-5y^{2}&=x^{2}+4xy+4y^{2}-9y^{2}\
&=(x^{2}+4xy+(2y)^{2})-(3y)^{2}\
&=(x+2y)^{2}-(3y)^{2}\
&=(x+2y-3y)(x+2y+3y)\
&=(x-y)(x+5y)\
end{align*}
$$

c) Given expression is: $6m^{2}-90m+324$.

$$
begin{align*}
6m^{2}-90m+324&=6(m^{2}-15m+54)\
&=6[m^{2}-6m-9m+54]\
&=6[(m-6m)-(9m-54)]\
&=6[m(m-6)-9(m-6)]\
&=6(m-6)(m-9)\
end{align*}
$$

In this part the first, factor out 6, then we used decomposition by finding two numbers whose sum is -15 and whose product is 54, these numbers are -6 and -9

Then, we group the first two terms and the final two terms

Now, factor an $m$ out of the first grouping and a $9$ out of the second grouping.

We can factor out a common factor of $(m-6)$, so we get the final factored form.

d) Given polynomial is: $2y^{2}+5y-7$

$$
begin{align*}
2y^{2}+5y-7&=2y^{2}-2y+7y-7\
&=(2y^{2}-2y)+(7y-7)\
&=2y(y-1)+7(y-1)\
&=(y-1)(2y+7)\
end{align*}
$$

There is used decomposition by finding two numbers whose sum is 5, these numbers are 2 and -7

Then, we group the first two terms and the final two terms

Now, factor an $2y$ out of the first grouping and a $7$ out of the second grouping.

We can factor out a common factor of $(y+1)$, so we get the final factored form.

e) Given polynomial is: $8a^{2}-2ab-21b^{2}$

$$
begin{align*}
8a^{2}-2ab+21b^{2}&=8a^{2}+12ab-14ab-21b^{2}\
&=(8a^{2}+12ab)-(14ab+21b^{2})\
&=4a(2a+3b)-7b(2a+3b)\
&=(2a+3b)(4a-7b)\
end{align*}
$$

In this part the first, we used decomposition by finding two terms whose sum is $-2ab$, these numbers are $12ab$ and $-14ab$

Then, we group the first two terms and the final two terms

Now, factor an $4a$ out of the first grouping and a $7b$ out of the second grouping.

We can factor out a common factor of $(2a+3b)$, so we get the final factored form.

f) Given expression is: $16x^{2}+76x+90$

$$
begin{align*}
16x^{2}+76x+90&=2(8x^{2}+38x+45)\
&=2(8x^{2}+18x+20x+45)\
&=2[(8x^{2}+18x)+(20x+45)]\
&=2[2x(4x+9)+5(4x+9)]\
&=2(4x+9)(2x+5)\
end{align*}
$$

The first, factor out 2, then used decomposition of the middle term by finding two numbers whose sum is 38, these numbers are 18 and 20

Then, we group the first two terms and the final two terms

Now, factor an $2x$ out of the first grouping and a $5$ out of the second grouping.

We can factor out a common factor of $(4x+9)$, so we get the final factored form.

a) $(x+2)(x-7)$

b) $(x-y)(x+5y)$

c) $6(m-6)(m-9)$

d) $(y-1)(2y+7)$

e) $(2a+3b)(4a-7b)$

f) $2(4x+9)(2x+5)$

In this exercise we need to notice is that we have got a difference of perfect squares.

$textbf{Difference of squares}$ can be factored as follows:

$$
color{#4257b2}{a^{2}-b^{2}=(a-b)(a+b)}
$$

a) Polynomial is: $x^{2}-9$

$$
begin{align*}
x^{2}-9&=x^{2}-3^{2}\
&=(x-3)(x+3)\
end{align*}
$$

b) Polynomial is: $4n^{2}-49$

$$
begin{align*}
4n^{2}-49&=(2n)^{2}-7^{2}\
&=(2n-7)(2n+7)\
end{align*}
$$

c) Polynomial is: $x^{8}-1$

$$
begin{align*}
x^{8}-1&=(x^{4})^{2}-1^{2}\
&=(x^{4}-1)(x^{4}+1)\
&=((x^{2})^{2}-1)(x^{4}+1)\
&=(x^{2}-1)(x^{2}+1)(x^{4}+1)\
&=(x-1)(x+1)(x^{2}+1)(x^{4}+1)\
end{align*}
$$

d) Polynomial is: $9(y-1)^{2}-25$

$$
begin{align*}
9(y-1)^{2}-25&=3^{2}(y-1)^{2}-5^{2}\
&=(3(y-1))^{2}-5^{2}\
&=(3y-3)^{2}-5^{2}\
&=(3y-3-5)(3y-3+5)\
&=(3y-8)(3y+2)\
end{align*}
$$

e) Polynomial is: $3x^{2}-27(2-x)^{2}$

$$
begin{align*}
3x^{2}-27(2-x)^{2}&=3[x^{2}-9(2-x)^{2}\
&=3[x^{2}-(3(2-x))^{2}]\
&=3[x^{2}-(6-3x)^{2}]\
&=3[(x-(6-3x))(x+(6-3x))]\
&=3(x-6+3x)(x+6-3x)\
&=3(4x-6)(-2x+6)\
&=3cdot2(2x-3)cdot(-2)(x-3)\
&=-12(2x-3)(x-3)\
end{align*}
$$

f) Polynomial is: $-p^{2}q^{2}+81$

$$
begin{align*}
-p^{2}q^{2}+81&=81-p^{2}q^{2}\
&=9^{2}-(pq)^{2}\
&=(9-pq)(9+pq)
end{align*}
$$

a) $(x-3)(x+3)$

b) $(2n-7)(2n+7)$

c) $(x+1)(x-1)(x^{2}+1)(x^{4}+1)$

d) $(3y-8)(3y+2)$

e) $-12(2x-3)(x-3)$

f) $(9-pq)(9+pq)$

a) Polynomial is: $ax+ay+bx+by$

$$
begin{align*}
ax+ay+bx+by&=(ax+ay)+(bx+by) tag{text{separate into two groups}}\
&=a(x+y)+b(x+y) tag{text{ factor out the GCF from each of the two groups}}\
&=(x+y)(a+b) tag{text{factor out (a+b)}}\
end{align*}
$$

b) Polynomial is: $2ab+2a-3b-3$

$$
begin{align*}
2ab+2a-3b-3&=(2ab+2a)-(3b+3) tag{text{separate into two groups}}\
&=2a(b+1)-3(b+1) tag{text{ factor out the GCF from each of the two groups}}\
&=(b+1)(2a-3) tag{text{factor out (b+1)}}\
end{align*}
$$

c) Polynomial is: $x^{3}+x^{2}-x-1$

$$
begin{align*}
x^{3}+x^{2}-x-1&=(x^{3}+x^{2})-(x+1) tag{text{separate into two groups}}\
&=x^{2}(x+1)-(x+1) tag{text{ factor out the GCF from each of the two groups}}\
&=(x+1)(x^{2}-1) tag{text{factor out (x+1)}}\
&=(x+1)(x-1)(x+1) tag{text{use difference of the squares}}\
&=(x+1)^{2}(x-1)\
end{align*}
$$

d) Polynomial is: $1-x^{2}+6x-9$

$$
begin{align*}
1-x^{2}+6x-9&=1-(x^{2}-6x+9) tag{text{group last three terms}}\
&=1-(x-3)^{2} tag{text{ use square of the binomial}}\
&=((1-(x-3))(1+(x-3)) tag{text{use difference of the square}}\
&=(1-x+3)(1+x-3) \
&=(4-x)(x-2)\
end{align*}
$$

e) Polynomial is: $a^{2}-b^{2}+25+10a$

$$
begin{align*}
a^{2}-b^{2}+25+10a&=a^{2}+10a+25-b^{2} tag{text{ change places of the terms}}\
&=(a^{2}+10a+25)-b^{2} tag{text{ group first three terms}}\
&=(a+5)^{2}-b^{2} tag{text{use square of the binomial}}\
&=(a+5-b)(a+5+b) tag{text{use difference of the squares}}
end{align*}
$$

f) Polynomial is: $2m^{2}+10m+10n-2n^{2}$

$$
begin{align*}
2m^{2}+10m+10n-2n^{2}&=2[m^{2}-n^{2}+10m+10n] tag{text{factor out 2, and change places of the terms}}\
&=2[(m^{2}-n^{2})+(10m+10n)] tag{text{group first two and last two terms separately}}\
&=2[(m-n)(m+n)+5(m+n)] tag{text{ use difference of the squares}}\
&=2(m+n)(m-n+5) tag{text{factor out (m+n)}}\
end{align*}
$$

a) $(x+y)(a+b)$

b) $(b+1)(2a-3)$

c) $(x+1)^{2}(x-1)$

d) $(4-x)(x-2)$

e) $(a+5-b)(a+5+b)$

f) $2(m+n)(m-n+5)$

If we simplify the right side of the equation and it becomes identical with the left side, then the statement is always true; otherwise, it is false. Apply distributive property to simplify the left side and compare it with the right side.

$$
begin{align*} (x-y)(x^2+y^2) &=x^2(x-y)+y^2(x-y)\
&=x^3-x^2y+xy^2-y^3\
&neq x^3-y^3
end{align*}
$$

Therefore, Andrij’s statement is NOT correct.

Andrij’s statement is NOT correct.

$$
(x-y)(x^2+y^2)=x^3-x^2y+xy^2-y^3neq x^3-y^3
$$

a) Given polynomial is: $2x(x-3)+7(3-x)$
$$
begin{align*}
2x(x-3)+7(3-x)&=2x(x-3)-7(x-3)\ &text{text{we get -1 in front of the second parenthese and change the places in parenthese }}\
&=(x-3)(2x-7)\ &text{text{factor out $ (x-3)$}}\
end{align*}
$$

b) Polynomial is: $xy+6x+5y+30$
$$
begin{align*}
xy+6x+5y+30&=(xy+6x)+(5y+30)\ &text{text{separate into two groups}}\
&=x(y+6)+5(y+6)\ &text{text{ factor out the GCF from each of the two groups}}\
&=(y+6)(x+5)\ &text{text{factor out (y+6)}}\
end{align*}
$$

c) Polynomial is : $x^{3}-x^{2}-4x+4$
$$
begin{align*}
x^{3}-x^{2}-4x+4&=
&=(x^{3}-x^{2})-(4x-4) text{text{group first two terms and last two terms separately}}\
&=x^{2}(x-1) -4(x-1)\ &text{text{ factor out the GCF from each of the two groups}}\
&=(x-1)(x^{2}-4)\ &text{text{factor out (x-1)}}\
&=(x-1)(x^{2}-2^{2})\
&=(x-1)(x-2)(x+2)\ &text{text{use difference od the squares}}
end{align*}
$$

d) Polynomial is: $y^{2}-49+14x-x^{2}$
$$
begin{align*}
y^{2}-49+14x-x^{2}&=y^{2}-(49-14x+x^{2})\ &text{text{group last three terms}}\
&=y^{2}-(7-x)^{2}\ &text{text{use square of the binomial}}\
&=(y-(7-x))(y+(7-x))\ &text{text{use difference of the squares}}\
&=(y-7+x)(y+7-x)\
end{align*}
$$

e) Polynomial is: $6x^{2}-21x-12x+42$
$$
begin{align*}
6x^{2}-21x-12x+42&=6x^{2}-12x-21x+42\ &text{text{change places of the middle terms}}\
&=(6x^{2}-12x)-(21x-42)\ &text{text{group first two and last two terms separately}}\
&=6x(x-2)-21(x-2)\ &text{text{ factor out the GCF from each of the two groups}}\
&=(x-2)(6x-21)\ &text{text{factor out (x-2)}}\
&=3(x-2)(2x-7)\
end{align*}
$$

f) Polynomial is: $12m^{3}-14m^{2}-30m+35$
$$
begin{align*}
12m^{3}-14m^{2}-30m+35&=(12m^{3}-14m^{2})-(30m-35)\ &text{text{group first two and last two terms separately}}\
&=2m^{2}(6m-7)-5(6m-7)\ &text{text{ factor out the GCF from each of the two groups}}\
&=(6m-7)(2m^{2}-5)\ &text{text{factor out (6m-7)}}\
end{align*}
$$

a) $(x-3)(2x-7)$

b) $(y+6)(x+5)$

c) $(x-1)(x-2)(x+2)$

d) $(y-7+x)(y+7-x)$

e) $3(x-2)(2x-7)$

f) $(6m-7)(2m^{2}-5)$

The factored form of the given function, $f(n)=2n^3+n^2+6n+3
,$ is

$$
begin{align*}
f(n)&=(2n^3+n^2)+(6n+3)
\&=
n^2(2n+1)+3(2n+1)
\&=
(2n+1)(n^2+3)
.end{align*}
$$

In the expression above, $(2n+1)$ is always an odd number greater than $1$ for any natural number, $n.$ Hence, $f(n)$ contains an odd factor greater than $1.$ That is, $f(n)$ is divisible by an odd number greater than $1.$

a)
$$
begin{align*}
c^{2}&=a^{2}+b^{2}\
a^{2}&=c^{2}-b^{2}\
&=(c-b)(c+b)tag{text{use difference of the square}}\
end{align*}
$$
.

So, answer is: $color{#c34632}{a^{2}=(c-b)(c+b)}$.

Use the $text{textcolor{#4257b2}{Pythagorean Theorem: $c^{2}=a^{2}+b^{2}$}}$.

b)

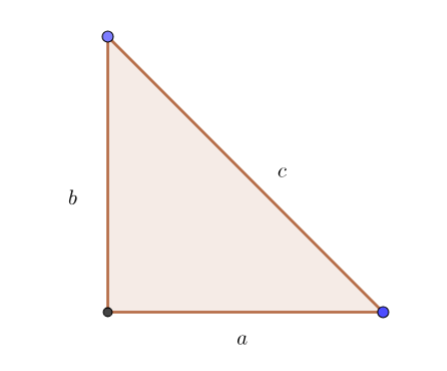
If hypotenuse 3 m longer than $b$, then $c=b+3$

Sum of the $b$ and hypotenuse is 11 m, then $b+c=11$.

Solving this system, we can determine $c$ and $b$:

$$
left.
begin{array}{rcl}
c&=&b+3 \
c+b&=&11
end{array}
right}\
\
left.
begin{array}{rcl}
c&=&b+3 \
b+3+b&=&11
end{array}
right}\
\
left.
begin{array}{rcl}
c&=&b+3 \
2b+3&=&11
end{array}
right}\
\
left.
begin{array}{rcl}
c&=&b+3 \
2b&=&8
end{array}
right}\
\
left.
begin{array}{rcl}
c&=&b+3 \
b&=&4
end{array}
right}\
\
left.
begin{array}{rcl}
c&=&4+3 \
b&=&4
end{array}
right}\
\
left.
begin{array}{rcl}
c&=&7 \
b&=&4
end{array}
right}
$$

Now, use part a) we can calculate $a$:

$$
begin{align*}
a^{2}&=(c-b)(c+b)\
a^{2}&=(7-4)(7+4)\
a^{2}&=3cdot11\
a^{2}&=33\
a&=sqrt{33}\
end{align*}
$$

Answer is: $a=sqrt{33}, b=4, c=7$

$$
a=sqrt{33}, b=4, c=7
$$

a.i) The area of the region between the planet and the inner ring can be derived by subtracting the area of the bigger circle by the area of the smaller circle. Using $A=pi r^2$ or the formula for the area of a circle, then

$$
begin{align*}
A&=A_{bigger}-A_{smaller}
\\
A&=pi (r_2)^2-pi (r_1)^2
\\
A&=pi r_2^2-pi r_1^2
\\
A&=pi(r_2^2-r_1^2)
\\
A&=pi(r_2+r_1)(r_2-r_1)
.end{align*}
$$

a.ii) The area of the region between the planet and the inner ring can be derived by subtracting the area of the bigger circle by the area of the smaller circle. Using $A=pi r^2$ or the formula for the area of a circle, then

$$
begin{align*}
A&=A_{bigger}-A_{smaller}
\\
A&=pi (r_3)^2-pi (r_1)^2
\\
A&=pi r_3^2-pi r_1^2
\\
A&=pi(r_3^2-r_1^2)
\\
A&=pi(r_3+r_1)(r_3-r_1)
.end{align*}
$$

a.iii) The difference in the areas of items (i) and (ii) is

$$
begin{align*}
&
pi(r_2^2-r_1^2)-pi(r_3^2-r_1^2)
\&=
pi[(r_2^2-r_1^2)-(r_3^2-r_1^2)]
\&=
pi[r_2^2-r_1^2-r_3^2+r_1^2]
\&=
pi[r_2^2-r_3^2]
\&=
pi[(r_2+r_3)(r_2-r_3)]
\&=
pi(r_2+r_3)(r_2-r_3)
.end{align*}
$$

a.i) $A=pi(r_2+r_1)(r_2-r_1)$

a.ii) $A=pi(r_3+r_1)(r_3-r_1)$

a.iii) $pi(r_2+r_3)(r_2-r_3)$

b) difference of the areas of the inner ring and the outer ring

begin{table}[]
defarraystretch{1.5}%
begin{tabular}{|l|l|}
hline
multicolumn{1}{|c|}{$bold{Strategy}$} & multicolumn{1}{c|}{$bold{Example}$} \ hline
(1) Find common factors. & $4x+12=4(x+3)$ \ hline
begin{tabular}[c]{@{}l@{}}(2) If it contains two terms that are perfect squares\ separated by minus sign, use $a^2-b^2=(a+b)(a-b)$end{tabular} & begin{tabular}[c]{@{}l@{}}$9x^2-16y^4$\ $=(3x)^2+(4y)^2$\ $=(3x+4y)(3x-4y)$end{tabular} \ hline
(3) For $ax^2+bx+c$ where $a=1$, do simple trinomials & $x^2+x-12=(x+4)(x-3)$ \ hline
(4) For $ax^2+bx+c$ where $aneq1$, do complex trinomials & $2x^2-5x-3=(2x+1)(x-3)$ \ hline
begin{tabular}[c]{@{}l@{}}(5) If it contains 4 or 6 terms with 3 or 4 squares, \ do grouping for difference of squaresend{tabular} & begin{tabular}[c]{@{}l@{}}$x^2+2x+1-y^2$\ $=(x+1)^2-y^2$\ $=(x+1+y)(x+1-y)$end{tabular} \ hline
(6) If it contains 3 terms and 2 perfect squares, do incomplete squares. & begin{tabular}[c]{@{}l@{}}$x^4+3x^2+4$\ $=x^4+(4x^2-x^2)+4$\ $=(x^4+4x^2+4)-x^2$\ $=(x^2+2)^2-x^2$\ $=(x^2+2+x)(x^2+2-x)$end{tabular} \ hline
end{tabular}
end{table}

a) $x^{4}+3x^{2}+36$ This is a given polynomial

$$
begin{align*}
x^{4}+3x^{2}+36&=x^{4} +12x^{2}+36-12x^{2}+3x^{2}\
&=(x^{4} +12x^{2}+36)-9x^{2}\
&=(x^{2}+6)^{2}-(3x)^{2} tag{text{use square of binomial}}\
&=(x^{2}+6-3x)(x^{2}+6+3x) tag{text{use difference of the square}}\
&=(x^{2}-3x+6)(x^{2}+3x+6)\
end{align*}
$$

b) $x^{4}-23x^{2}+49$ This is a given polynomial

$$
begin{align*}
x^{4}-23x^{2}+49&=x^{4} -14x^{2}+49+14x^{2}-23x^{2}\
&=(x^{4} -14x^{2}+49)-9x^{2}\
&=(x^{2}-7)^{2}-(3x)^{2} tag{text{use square of binomial}}\
&=(x^{2}-7-3x)(x^{2}-7+3x) tag{text{use difference of the square}}\
&=(x^{2}-3x-7)(x^{2}+3x-7)\
end{align*}
$$

a) $(x^{2}-3x+6)(x^{2}+3x+6)$

b) $(x^{2}-3x-7)(x^{2}+3x-7)$

a) $x^{4}-1$ This is a given binomial

$$
begin{align*}
x^{4}-1&=(x^{2})^{2}-1^{2}\
&=(x^{2}-1)(x^{2}+1) tag{text{use difference of squares}}\
&=(x-1)(x+1)(x^{2}+1) tag{text{use difference of squares}}\
end{align*}
$$

b) $x^{5}-1$ This is a given binomial

We know, $x^{3}-1=(x-1)(x^{2}+x+1)$, in general, applies

$$
begin{align*}
x^{n}-1&=(x-1)(x^{n-1}+x^{n-2}+…+x+1)
end{align*}
$$
for any $n in N$.

Use that, we can determine:

$$
begin{align*}
x^{5}-1&=(x-1)(x^{5-1}+x^{5-2}+x^{5-3}+x^{5-4}+1^{5-5})\
&=(x-1)(x^{4}+x^{3}+x^{2}+x+1)
end{align*}
$$

c)
$$
begin{align*}
x^{n}-1&=(x-1)(x^{n-1}1^{1}+x^{n-2}1^{2}+…+x^{1}1^{n-1}+x^{0}1^{n})\
&=(x-1)(x^{n-1}+x^{n-2}+…+x+1)
end{align*}
$$
for any $n in N$.

d)
$$
begin{align*}
x^{n}-y^{n}&=(x-y)(x^{n-1}y^{0}+x^{n-2}y^{1}+…+x^{1}y^{n-2}+x^{0}y^{n-1})\
&=(x-y)(x^{n-1}+x^{n-2}y+…+xy^{n-2}+y^{n-1})
end{align*}
$$
for any $n in N$.

a) $x^4-1=(x-1)(x^3+x^2+x+1)$

b) $x^5-1=(x-1)(x^4+x^3+x^2+x+1)$

c) $x^n-1=(x-1)(x^{n-1}y^0+x^{n-2}+…+x^0)$

d) $x^n-y^n=(x-y)(x^{n-1}y^0+x^{n-2}+x^{n-3}y^2+…+x^0y^{n-1}$

a) If $63=3(21)$ is expressed as:

$$
begin{align*}
(2^{2}-1)(2^{4}+2^{2}+2^{0})&=2^{2}cdot2^{4}+2^{2}cdot2^{2}+2^{2}cdot2^{0}-2^{4}-2^{2}-2^{0}\
&=2^6+2^{4}+2^{2}-2^{4}-2^{2}-2^{0}=2^{6}-2^{0}=2^{6}-1\
end{align*}
$$

If 63=7(9) is expressed as:

$$
begin{align*}
(2^{3}-1)(2^{3}+2^{0})&=2^{3}cdot2^{3}+2^{3}cdot2^{0}-1cdot2^{3}-1cdot2^{0}\
&=2^6+2^{3}-2^{3}-1=2^{6}-1\
end{align*}
$$

In both cases we get $63=2^{6}-1$.

b) We know: $35=5(7)$, so, if $m=35$, then:

$$
begin{align*}
n&=2^{m}-1 \
&=2^{35}-1\
&=(2^{5}-1)(2^{30}+2^{25}+2^{20}+2^{15}+2^{10}+2^{5}+2^{0})\
end{align*}
$$
.

Composite number is a whole number that can be divided exactly by numbers other than 1 or itself

So, we can conclude that: $text{textcolor{#4257b2}{$2^{35}-1$ is a composite number}}$.

c) Let $m$ be composite number. This means, exist real numbers $a, bne1$ such that $m=acdot b$. Use that, we get:

$$
begin{align*}
n&=2^{m}-1\
&=2^{ab}-1\
&=(2^{a})^{b}-1\
&=(2^{a}-1)(2^{b}+…+2^{0})\
end{align*}
$$

This result will always have two factors, so, if $m$ composite number, then, number $2^{m}-1=(2^{a}-1)(2^{b}+…+2^{0})$ must be composite number.

$$
begin{align*}
text{a)} ;;; &2^6+2^4+2^2-2^4-2^2-2^0=2^6-1\
&2^6+2^3-2^3-2^0=2^6-1\
text{b)} ;;; &35=5times 7\
&2^{35}-1=(2^5-1)(2^{30}+2^{25}+2^{20}+2^{15}+2^{10}+2^5+2^0);text{or}\
&2^{35}-1=(2^7-1)(2^{28}+2^{21}+2^{14}+2^7+2^0)\
text{c)} ;;;&text{Yes}
end{align*}
$$