$bold{Concept:}$ Given a function $f(x)$, the value of $f(x)$ at $x=a$ is $f(a)$

$bold{Solution:}$ $f(x)=2-3x$

Simplify substitute the given value of $x$

a) $f(2)=2-3(2)=2-6=-4$

b) $f(0)=2-3(0)=2-0=2$

c) $f(-4)=2-3(-4)=14$

d) $fleft(dfrac{1}{2}right)=2-3left(dfrac{1}{2}right)=dfrac{1}{2}$

e) $f(a)=2-3a$

f) $f(3b)=2-3(3b)=2-9b$

a) $-4$

b) $2$

c) $14$

d) $dfrac{1}{2}$

e) $2-3a$

f) $2-9b$

$bold{Concept:}$ Given a function $f(x)$, the value of $f(x)$ at $x=a$ is $f(a)$

$bold{Solution:}$ Examine the graph and look for the value of $y$ with the given value of $x$

a) when $x=1$, $y=2$ so $f(1)=2$

b) when $x=-2$, $y=-2$ so $g(-2)=-2$

c) $f(4)-g(-2)=-1-4=-5$

d) when $f(x)=-3$, $x=-3$ or $-4$

a) 2

b) 4

c) $-5$

d) $-3$ or $-4$

Let $x$ be the number of minutes after 11:00 a.m. and $f(x)$ be the amount milk in the carton.

a) We set $x=0$ as the time at 11:00 am where the volume is 1.2 L=1200 mL. Since the volume of milk is decreasing by $3$ mL/min.

$f(x)=1200-3x$

b) At 1:00 pm, 2 hours have passed since 11: am, thus $x=2times 60=120$

$f(120)=1200-3(120)=840$ mL

c) We shall find $x$ such that $f(x)=450$

$450=1200-3x$

$3x=1200-450$

$x=dfrac{1200-450}{3}$

$x=250$

Thus, there will be 450 mL left in the carton 250 minutes (4 hours and 10 minutes) after 11:00 which corresponds to 3:10 pm.

a) $f(x)=1200-3x$

b) $840$ mL

c) $3:10$ pm

a) $f(x)=(x-2)^{2}-1$

i) $f(-1)$ represents the value of the function when the input is $x=-1$.

Substitute $x=-1$ in $f(x)=(x-2)^{2}-1$

$f(-1)=(-1-2)^{2}-1$

$f(-1)=(-3)^{2}-1$

$f(-1)=9-1$

$f(-1)=8$

ii) $f(3)$ represents the value of the function when the input is $x=3$.

Substitute $x=3$ in $f(x)=(x-2)^{2}-1$

$f(3)=(3-2)^{2}-1$

$f(3)=(1)^{2}-1$

$f(3)=1-1$

$f(3)=0$

iii) $f(1.5)$ represents the value of the function when the input is $x=1.5$.

Substitute $x=1.5$ in $f(x)=(x-2)^{2}-1$

$f(1.5)=(1.5-2)^{2}-1$

$f(1.5)=(-0.5)^{2}-1$

$f(1.5)=0.25-1$

$f(1.5)=0.75$

b) $f(x)=2+3x-4x^{2}$

i) $f(-1)$ represents the value of the function when the input is $x=-1$.

Substitute $x=-1$ in $f(x)=2+3x-4x^{2}$

$f(-1)=2+3(-1)-4(-1)^{2}$

$$
f(-1)=2-3-4
$$

$$
f(-1)=-5
$$

ii) $f(3)$ represents the value of the function when the input is $x=3$.

Substitute $x=3$ in $f(x)=2+3x-4x^{2}$

$f(3)=2+3cdot3-4cdot3^{2}$

$f(3)=2+9-4cdot9$

$f(3)=2+9-36$

$$
f(3)=-25
$$

iii) $f(1.5)$ represents the value of the function when the input is $x=1.5$.

Substitute $x=1.5$ in $f(x)=2+3x-4x^{2}$

$f(1.5)=2+3cdot1.5-4(1.5)^{2}$

$f(1.5)=2+4.5-4cdot2.25$

$f(1.5)=-2+4.5-9$

$$
f(1.5)=-2.5
$$

a) 8, 0, $-0.75$

b) $-5$, $-25$, $-2.5$

a) $f(-3)$ represents the value of the function when the input is $x=-3$.

Substitute $x=-3$ in $f(x)=dfrac{1}{2x}$:

$$
f(-3)=dfrac{1}{2cdot(-3)}=dfrac{1}{-6}=-dfrac{1}{6}
$$

b) $f(0)$ represents the value of the function when the input is $x=0$.

Substitute $x=0$ in $f(x)=dfrac{1}{2x}$:

$f(0)=dfrac{1}{2cdot0}=dfrac{1}{0}$

We know dividing by zero is undefined, so , function $f(x)$ is not defined for $x=0$.

c)$f(1)$ represents the value of the function when the input is $x=1$ and $f(3)$ represents the value of the function when the input is $x=3$.

Substitute $x=1$ and $x=3$ in $f(x)=dfrac{1}{2x}$ and calculate:

$$
f(1)-f(3)=dfrac{1}{2cdot1}-dfrac{1}{2cdot3}=dfrac{1}{2}-dfrac{1}{6}=dfrac{1cdot3-1}{6}=dfrac{3-1}{6}=dfrac{2}{6}=dfrac{1}{3}
$$

d) $f(dfrac{1}{4})$ represents the value of the function when the input is $x=dfrac{1}{4}$ and $f(dfrac{3}{4})$ represents the value of the function when the input is $x=dfrac{3}{4}$.

Substitute $x=dfrac{1}{4}$ and $x=dfrac{3}{4}$ in $f(x)=dfrac{1}{2x}$ and calculate:

$$
f(dfrac{1}{4})+f(dfrac{3}{4})=dfrac{1}{2cdotdfrac{1}{4}}+dfrac{1}{2cdotdfrac{3}{4}}=dfrac{4}{2}+dfrac{2}{3}=dfrac{4cdot3+2cdot2}{6}=dfrac{12+4}{6}=dfrac{16}{6}=dfrac{8}{3}=2dfrac{2}{3}
$$

a) $-dfrac{1}{6}$

b) undefined

c) $dfrac{1}{3}$

d) $2dfrac{2}{3}$

a)

Domain of the function is $D_{f}=left{-2,0,2,3,5,7 right}$

Range of the function is $R=left{ 1,2,3,4,5right}$

b)

i) $f(3)=4$

ii) $f(5)=2$

iii) $f(5-3)=f(2)=5$

iv) $f(5)-f(3)=2-4=-2$

see graph:

If $x=3$, then $y=f(3)=4$

If $x=5$, then $y=f(5)=2$

If $x=2$, then $y=f(2)=5$

a) domain = $(-2, 0, 2, 3, 5, 7)$ ; range = $(1, 2, 3, 4, 5 )$

b) i) 4 ii) 2 iii) 5 iv) $-2$

a: $2a-5$

b: $2(b+1)-5=2b+2-5=2b-3$

c: $2(3c-1)-5=6c-2-5=6c-7$

d: $2(2-5x)-5=4-10x-5=-10x-1$

Substitute the value of $x$ into each respective equation

a) $2a-5$

b) $2b-3$

c) $6c-7$

d) $-10x-1$

Function is $g(y)=3t+5$

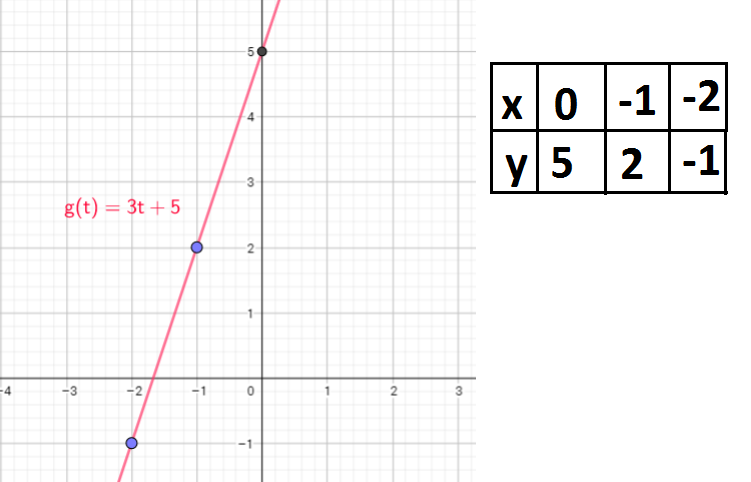
If $x=-2$, then $g(-2)=3(-2)+5=-6+5=-1$

If $x=-1$, then $g(-1)=3(-1)+5=-3+5=2$

If $x=0$, then $g(0)=3cdot0+5=0+5=5$

That means function passes through points $(-2,-1), (-1,2)$ and $(0,5)$

Function is $g(t)=3t+5$

i) $g(0)=3cdot0+5=0+5=5$

ii) $g(3)=3cdot3+5=9+5=14$

iii) $g(1)-g(0)=3cdot1+5-(3cdot0+5)=3+5-(0+5)=8-5=3$

iv) $g(2)-g(1)=3cdot2+5-(3cdot1+5)=6+5-(3+5)=11-8=3$

v) $g(1001)-g(1000)=3cdot1001+5-(3cdot1000+5)=3003+5-(3000+5)=3008-3005=3$

vi) $g(a+1)-g(a)=3(a+1)+5-(3a+5)=3a+3+5-3a-5=3$

Function is $g(t)=3t+5$. To find g(a) plug in $a$ wherever $t$ occurs in the equation of $g(t)$ and simplify

Function is $f(s)=s^{2}-6s+9$

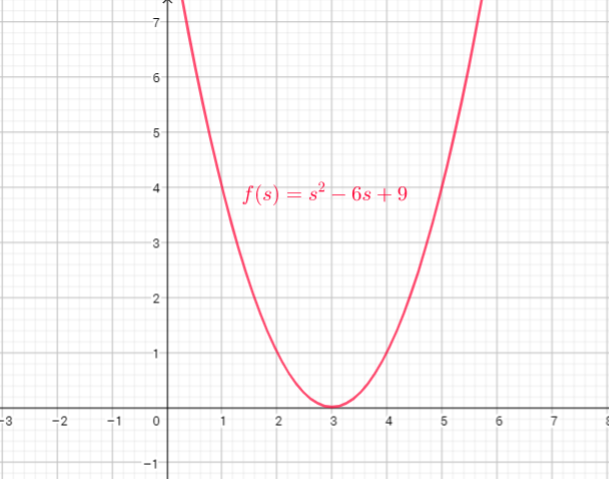
If $x=-2$, then $f(-2)=(-2)^{2}-6(-2)+9=4+12+9=25$

If $x=-1$, then $f(-1)=(-1)^{2}-6(-1)+9=1+6+9=16$

If $x=0$, then $f(0)=(0)^{2}-6cdot0+9=0+0+9=9$

If $x=2$, then $f(2)=(2)^{2}-6cdot2+9=4-12+9=1$

If $x=1$, then $f(1)=(1)^{2}-6cdot1+9=1-6+9=4$

Now, we can create table:

b)

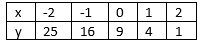
i) To find $f(0)$ , plug in 0 wherever $s$ occures in the equation of $f(s)$ and simplify to get $f(0)$

$f(0)=0^{2}-6cdot0+9=0-0+9=9$

ii) To find $f(1)$ , plug in 1 wherever $s$ occures in the equation of $f(s)$ and simplify to get $f(1)$

$f(1)=1^{2}-6cdot1+9=1-6+9=4$

iii) To find $f(2)$ , plug in 2 wherever $s$ occures in the equation of $f(s)$ and simplify to get $f(2)$

$f(2)=2^{2}-6cdot2+9=4-12+9=1$

iv) To find $f(3)$ , plug in 3 wherever $s$ occures in the equation of $f(s)$ and simplify to get $f(3)$

$f(3)=3^{2}-6cdot3+9=9-18+9=0$

v) $left(f(2)-f(1)right)-left(f(1)-f(0) right)=left(1-4 right)-left( 4-9right)=-3-(-5)=-3+5=2$

vi) $left(f(3)-f(2)right)-left(f(2)-f(1) right)=left(0-1 right)-left( 1-4right)=-1-(-3)=-1+3=2$

a) begin{tabular}{|l|l|l|l|l|}
hline
$s$ & 0 & 1 & 2 & 3 \ hline
$f(s)$ & 9 & 4 & 1 & 0 \ hline
end{tabular}\\
b) i) 9 $text{ }$ ii) 4 $text{ }$ iii) 1 $text{ }$ iv) 0 $text{ }$ v) 2 $text{ }$ vi) 2\
c) They are the same as they represent second differences, which are constant for a quadratic function.\\

a) Function is $f(x)=2(x-3)^{2}-1$

To find $f(-2)$ , plug in -2 wherever $x$ occures in the equation of $f(x)$ and simplify to get $f(-2)$

$$
f(-2)=2(-2-3)^{2}-1=2(-5)^{2}-1=2cdot25-1=50-1=49
$$

b) In part a) we are calculate $f(-2)=49$, so, if $x=-2$, then $y=f(-2)=49$. That means function $f$ passes through a point $(-2, f(-2))$, or $(-2,49)$.

Now we can conclude $f(-2)$ is the y-coordinate of the point on the graph with x-coordinate -2

c) Use graph of function $f$, we can see domain is $D_{f}=(-infty,+infty)=R$ and range is $R=[-1,+infty)$

d) I used the vertical-line test to see how
many points on the graph there were
for each value of $x$. Any vertical line drawn on the
graph intersects the graph at only
one point. This is the graph of a
function

a) 49

b) The $y$-coordinate of the point on the graph with $x$-coordinate $-2$

c) domain = ${ xin bold{R}}$ , range = ${ yinbold{R};|;ygeq -1}$

d) It passes the vertical-line test.

Given that $g(x)=4-5x$, we need to find the value of $x$ that satisfies the given $g(x)$

a) $g(x)=-6$

$-6=4-5x$

$5x=4+6$

$5x=10$

$dfrac{5x}{5}=dfrac{10}{5}$

$x=2$

b) $g(x)=2$

$2=4-5x$

$5x=4-2$

$5x=2$

$dfrac{5x}{5}=dfrac{2}{5}$

$$
x=dfrac{2}{5}
$$

c) $g(x)=0$

$0=4-5x$

$5x=4$

$dfrac{5x}{5}=dfrac{4}{5}$

$$
x=dfrac{4}{5}
$$

d) $g(x)=dfrac{3}{5}$

$dfrac{3}{5}=4-5x$

$5cdot dfrac{3}{5}=5cdot(4-5x)$

$3=20-25x$

$25x=20-3$

$25x=17$

$x=dfrac{17}{25}$

$$
text{a) 2};;;; ;; text{b)} dfrac{2}{5};;;;;; text{c)} dfrac{4}{5};;;;;;text{d)} dfrac{17}{25}
$$

a) Let $x$ be numbers of kilometers. Company need pay 50 dollars per day plus 0.15 for each kilometers $x$.
The daily rental cost as a function of the number of kilometres travelled is $f(x)=0.15x+50$ .

b) If we drive 472 km in one day, to find $f(472)$ , plug in 472 wherever $x$ occures in the equation of $f(x)$ and simplify to get $f(472)$
The rental cost :

$f(472)=50+0.15cdot472=50+70.8=120.8$ dollars

If we wont determine how far you can drive in a day for 80 dollars, we need substitute 80 dollars in equation $f(x)$, and calculate numbers of kilometers $x$ in this equation:

$f(x)=0.15x+50$

$80=0.15x+50$

$0.15x=80-50$

$0.15x=30$ divide both side by 0.15

$x=200$.

Solutin is : We can drive 200 km in a day for 80 dollars.

a) $f(x)=0.15x+50$

b) $$120.80$

c) 200 km

a) Think of a number $x$, multiply by 3 and subtract from 24, and the finaly, multiply by the number $x$

Function is $f(x)=(24-3x)x$

b)To find $f(3)$ , plug in 3 wherever $x$ occures in the equation of $f(x)$ and simplify to get $f(3)$

$f(3)=(24-3cdot3)cdot3=(24-9)cdot3=15cdot3=45$

To find $f(-5)$ , plug in -5 wherever $x$ occures in the equation of $f(x)$ and simplify to get $f(-5)$

$f(-5)=(24-3cdot(-5))cdot(-5)=(24+15)cdot(-5)=39cdot(-5)=-195$

To find $f(10)$ , plug in 10 wherever $x$ occures in the equation of $f(x)$ and simplify to get $f(10)$

$f(10)=(24-3cdot10)cdot10=(24-30)cdot10=-6cdot10=-60$

Quadratic function has maximum value in the point $(dfrac{-b}{2a}, f(dfrac{-b}{2a}))$

Our quadratic function is $f(x)=(24-3x)x$ or $f(x)=-3x^{2}+24x$

There is $a=-3,$ and $b=24$. Now can calculate:

$dfrac{-b}{2a}=dfrac{-24}{2(-3)}=dfrac{-24}{-6}=4$

Now we need calculate $f(-dfrac{b}{2a})$:

$f(dfrac{-b}{2a})=f(4)=(24-3cdot4)cdot4=(24-12)cdot4=12cdot4=48$

Now can conclude: Quadratic function
$f(x)=(24-3x)x$ has maximum in the point $(4,48)$. That means, the maximum result possible is 48.

a) $f(x)=x(24-3x)$

b) 45, $-195$, $-60$

c) 48

We can choose a suitable coordinate system. Since a parabola is symmetric, we can $bold{arbitrarily}$ choose its axis of symmetry at $x=0$.

Since the arch is 281 meters wide, the distance from its center to either of its x-intercept is $dfrac{281}{2}=140.5$. Also, the maximum height of 71 m shall occur at $x=0$ (at the axis of symmetry). Therefore, the equation can be written as

$f(x)=71-ax^2$

We must find the value of $a$ such that $f(x)=0$ when $x=140.5$

$0=71-acdot(140.5^2)implies a=dfrac{71}{140.5^2}=0.003596$

Therefore, the equation of the parabola is

$f(x)=71-0.0036x^2$

Note that other forms can be obtained if the axis of symmetry is set differently.

$bold{Alternative; Solution}$ We can arbitrarily place the left base of the arch at the origin $(0,0)$. In this case, the other $x$-intercept is at $(281,0)$

Thus, we can express the function is factored form

$y=a(x-0)(x-281)$

$y=ax(x-281)$

Now, we shall find the value of $a$

Since this is a symmetric parabolic arch, the maximum point must occur halfway between $x=0$ and $281$ which is at $x=140.5$ where $y=71$ m

Substituting this point to the equation to find $a$, we can get

$y=ax(x-281)$

$71=a(140.5)(140.5-281)$

$a=dfrac{71}{(140.5)(140.5-281)}=-0.0036$

Therefore, the equation of the parabola is

$f(x)=-0.0036x(x-281)$ or

$$
f(x)=0.0036x(281-x)
$$

$$
f(x)=0.0036x(281-x)
$$

b) If $x=-1$ we can calculate $y=f(-1)$. That means $f(-1)$ is $y$-coordinate of the point on the graph with x-coordinate -1.

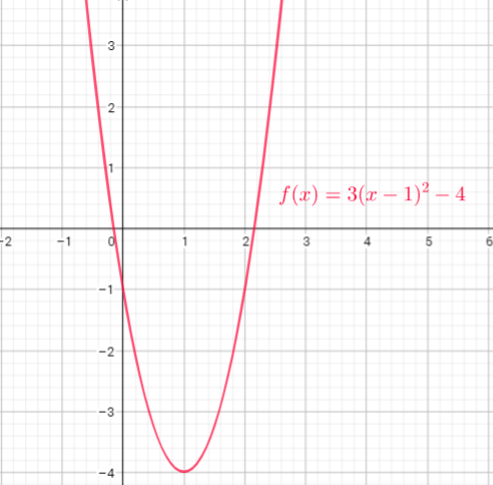
We need start from on x-axis where $x=-1$, move up to curve, then across to y-axis

c) Function is $f(x)=3(x-1)^{2}-4$

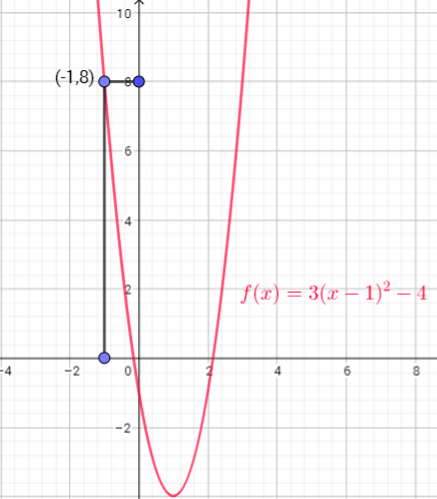
i) To find $f(2)-f(1)$ , plug in 2 and 1 wherever $x$ occures in the equation of $f(x)$ and simplify to get $f(2)-f(1)$

$f(2)-f(1)=[3(2-1)^{2}-4]-[3(1-1)^{2}-4]=[3cdot1^{2}-4]-[3cdot0^{2}-4]=[3-4]-[0-4]=-1+4=3$

ii) To find $2f(3)-7$ , plug in wherever $x$ occures in the equation of $f(x)$ and simplify to get $2f(3)-7$

$2f(3)-7=2cdot(3(3-1)^{2}-4)-7=2cdot(3cdot2^2-4)-7=2cdot(12-4)-7=2cdot8-7=16-7=9$

iii) To find $f(1-x)$ , plug in $1-x$ wherever $x$ occures in the equation of $f(x)$ and simplify to get $f(1-x)$

$$
f(1-x)=3(1-x-1)^{2}-4=3(-x)^{2}-4=3x^{2}-4
$$

a) $f(x)=3(x-1)^2-4$

b) The expression $f(-1)$ represents the distance of the graph from the $x$-axis when $x=-1$.
We can find it by creating a vertical line at $x=-1$ and the $y$-coordinate of the point that intersects with the graph is $f(-1)$

Our function is $f(x)=x^{2}+2x-15$.

a) If we wont determine the values of $x$ for $f(x)=0$ we need solve equation $f(x)=0$:

$f(x)=0$

$x^{2}+2x-15=0$

$(x+5)(x-3)=0$

$x+5=0$ or $x-3=0$

$x=-5$ or $x=3$

b) If we wont determine the values of $x$ for $f(x)=-12$ we need solve equation $f(x)=-12$:

$f(x)=-12$

$x^{2}+2x-15=-12$

$x^{2}+2x-15+12=0$

$x^{2}+2x-3=0$

$(x+3)(x-1)=0$

$x+3=0$ or $x-1=0$

$x=-3$ or $x=1$

b) If we wont determine the values of $x$ for $f(x)=-16$ we need solve equation $f(x)=-16$:

$f(x)=-16$

$x^{2}+2x-15=-16$

$x^{2}+2x-15+16=0$

$x^{2}+2x+1=0$

$(x+1)^{2}=0$

$x+1=0$

$$
x=-1
$$

a) $3,-5$

b) $1,-3$

c) $-1$

$f(x)=3x+1$

$g(x)=2-x$

We need to solve for $a$ that
satisfies the given condition.

a.) $f(a)=g(a)$

$3a+1=2-a$

$3a+a=2-1$

$4a=1$

$dfrac{4a}{4}=dfrac{1}{4}$

$$
a=dfrac{1}{4}
$$

b.) $f(a^2)=g(2a)$

$3(a^2)+1=2-(2a)$

$3a^2+2a-1=0$

$(3a-1)(a+1)=0$

$3a-1=0$ or $a+1=0$

$a=dfrac{1}{3}$ or $-1$

a.) $a=dfrac{1}{4}$

b.) $a=dfrac{1}{3}$ or $-1$

a) Linear function is $y=mx+n$

Linear function passes through points $(200,285)$ and $(60,75)$.

Now we can calculate slope

$m=dfrac{200-60}{285-75}=dfrac{140}{210}=dfrac{14}{21}=dfrac{2}{3}$

Use coordinate of one point and slope we can determine $n$:

$200=dfrac{2}{3}cdot285+n$

$n=200-190$

$n=10$

Linear function that will convert 285 to 200 and 75 to 60 is $y=dfrac{2}{3}x+10$

b) If $x=95$, then $y=dfrac{2}{3}cdot95+10$
, now we can determine $y$:

$y=dfrac{2}{3}cdot95+10=dfrac{190}{3}+dfrac{30}{3}=dfrac{210}{3}=73dfrac{1}{3}$

If $x=175$, then $y=dfrac{2}{3}cdot175+10$
, now we can determine $y$:

$y=dfrac{2}{3}cdot175+10=dfrac{350}{3}+dfrac{30}{3}=dfrac{380}{3}=126dfrac{2}{3}$

If $x=215$, then $y=dfrac{2}{3}cdot215+10$
, now we can determine $y$:

$y=dfrac{2}{3}cdot215+10=dfrac{430}{3}+dfrac{30}{3}=dfrac{460}{3}=153dfrac{1}{3}$

If $x=255$, then $y=dfrac{2}{3}cdot255+10$
, now we can determine $y$:

$$
y=dfrac{2}{3}cdot255+10=dfrac{510}{3}+dfrac{30}{3}=dfrac{540}{3}=180
$$

a) To convert the marks, we need to find the linear equation that passes through $(285,200)$ and $(75,60)$

Remember that the slope of a line is

$m=dfrac{y_2-y_1}{x_2-x_1}$

$m=dfrac{60-200}{75-285}=dfrac{2}{3}$

Now, we can use the point slope form

$y-y_1=m(x-x_1)$

$y-200=dfrac{2}{3}(x-285)$

$y=dfrac{2}{3}(x-285)+200$

$y=dfrac{2}{3}x-190+200$

$$
y=dfrac{2}{3}x+10
$$

b) Substitute the given values of $x$ and solve for $y$

$x=95$ , $y=dfrac{2}{3}(95)+10=73dfrac{1}{3}$

$x=175$ , $y=dfrac{2}{3}(175)+10=126dfrac{2}{3}$

$x=215$ , $y=dfrac{2}{3}(215)+10=153dfrac{1}{3}$

$x=255$, $y=dfrac{2}{3}(255)+10=180$

a) $f(x)=dfrac{2}{3}x+10$

b) $73dfrac{1}{3}$ , $126dfrac{2}{3}$ , $153dfrac{1}{3}$ , $180$

a) We are given that

$f(1)=1$

$f(x+1)=f(x)+3x(x+1)+1$

To evaluate the function at different values of $x$, simply substitute the $x$-values to the function.

$f(x+1)=f(x)+3x(x+1)+1$

$f(2)=f(1+1)=f(1)+3(1)(1+1)+1=1+3(1)(2)+1=8$

$f(3)=f(2+1)=f(2)+3(2)(2+1)+1=8+3(2)(3)+1=27$

$f(4)=f(3+1)=f(3)+3(3)(3+1)+1=27+3(3)(4)+1=64$

$f(5)=f(4+1)=f(4)+3(4)(4+1)+1=64+3(4)(5)+1=125$

$f(6)=f(5+1)=f(5)+3(5)(5+1)+1=126+3(5)(6)+1=216$

b) Observe that the range of $f(x)$ are all perfect cubes of its domain. Thus, we can write

$f(x)=x^3$

We can also verify this by

$f(x+1)=(x+1)^3$

$=x^3+3x^2+3x+1$

$=x^3+3x(x+1)+1$

Substitute $x^3=f(x)$

$$
f(x+1)=f(x)+3x(x+1)+1
$$

a) 8, 27, 64, 125, 216

b) $f(x)=x^3$