$g(0)=1-0^2=1$

$f(g(0))=f(1)=2(1)-3=2-3=-1$

#### (b)

$f(4)=2(4)-3=8-3=5$

$g(f(4))=g(5)=1-5^2=1-25=-24$

#### (c)

$g(-8)=1-(-8)^2=1-64=-63$

$(fcirc g)(-8)=f(-63)=2(-63)-3=-126-3=-129$

#### (d)

$gleft( dfrac{1}{2}right)=1-left(dfrac{1}{2} right)^2=1-dfrac{1}{4}=dfrac{3}{4}$

$(g circ g)left(dfrac{1}{2} right)=gleft(dfrac{3}{4} right)=1-left( dfrac{3}{4}right)^2=1-dfrac{9}{16}=dfrac{7}{16}$

#### (e)

$(f circ f^{-1})(1)=1$

#### (f)

$g(2)=1-2^2=1-4=-3$

$(g circ g)(2)=g(-3)=1-(-3)^2=1-9=-8$

$(g circ f)(2)=g(5)=3$

#### (b)

$(f circ f)(1)=f(2)=5$

#### (c)

$(f circ g)(5)=f(3)=10$

#### (d)

$(f circ g)(0)$ is undefined because there is no $g(0)$.

#### (e)

$(f circ f^{-1})(2)=2$

#### (f)

$$
(g^{-1} circ f)(1)=g^{-1}(2)=4
$$

$f(g(2))=f(5)=5$

#### (b)

$g(f(4))=g(3)=5$

#### (c)

$(g circ g)(-2)=g(1)=4$

#### (d)

$(f circ f)(2)=f(-1)$

$f(-1)$ does not exist, so $(f circ f)(2)$ is undefined.

$d(5)=80(5)=400$

$C(d(5))=C(400)=0.09(400)=36$

$textbf{It costs $ $36$ to travel for $5$ hours.}$

#### (b)

$C(d(t))$ represents the relationship between the time driven and the cost of gasoline.

$f(g(x))=f(x-1)=3(x-1)^2=3(x^2-2x+1)=3x^2-6x+3$

The domain is $left{xinBbb{R} right}$.

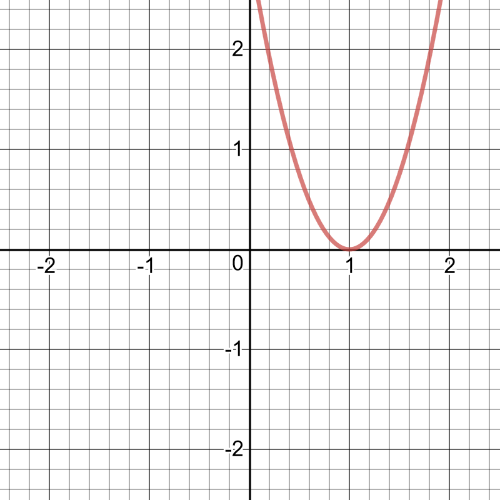
The domain is $left{xinBbb{R} right}$.

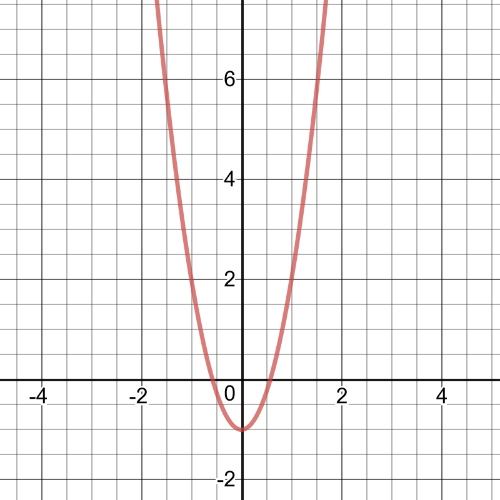
$f(g(x))=f(x^2+1)=2(x^2+1)^2+(x^2+1)=2(x^4+2x^2+1)+x^2+1$

$=2x^4+4x^2+2+x^2+1=2x^4+5x^2+3$

The domain is $left{xinBbb{R} right}$

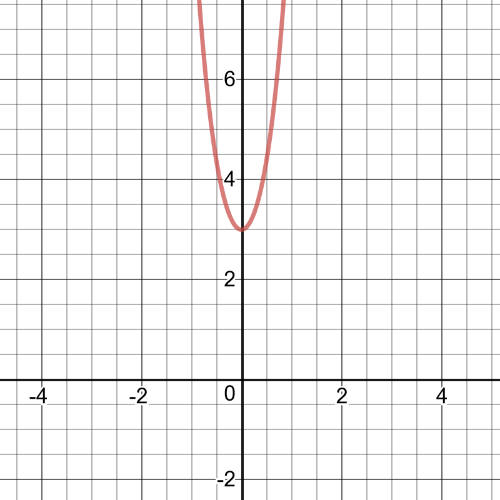
The domain is $left{ xinBbb{R}right}$.

$f(g(x))=f(2x-1)=2(2x-1)^3-3(2x-1)^2+(2x-1)-1$

$=2(8x^3-12x^2+6x-1)-3(4x^2-4x+1)+2x-1-1$

$=16x^3-24x^2+12x-2-12x^2+12x-3+2x-2$

$=16x^3-36x^2+26x-7$

The domain is $left{ xinBbb{R}right}$.

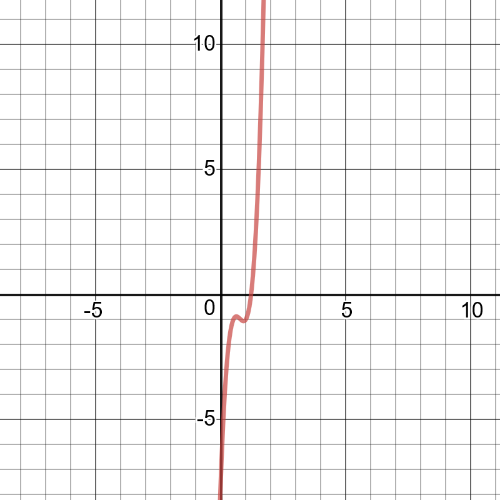
$=2(2x^3-3x^2+x-1)-1$

$=4x^3-6x^2+2x-2-1$

$=4x^3-6x^2+2x-3$

The domain is $left{xinBbb{R}right}$.

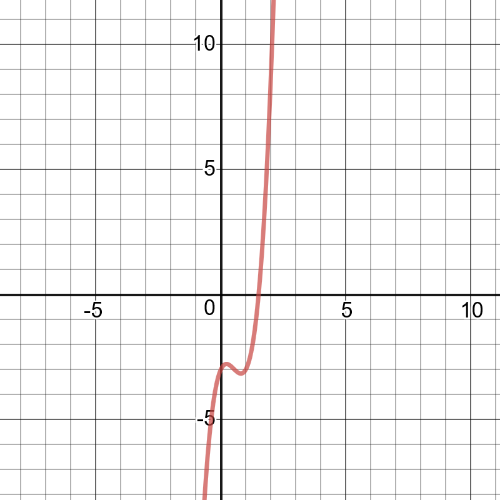
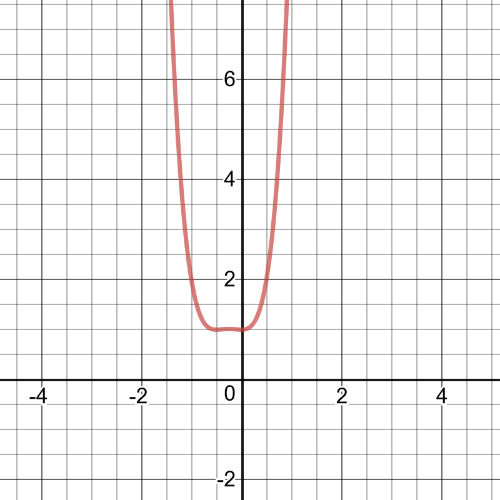
$f(g(x))=f(x+1)=(x+1)^4-(x+1)^2=(x+1)^2((x+1)^2-1)$

$=(x^2+2x+1)(x^2+2x+1-1)=(x^2+2x+1)(x^2+2x)$

$=x^4+2x^3+2x^3+4x^2+x^2+2x$

$=x^4+4x^3+5x^2+2x$

The domain is $left{xinBbb{R} right}$

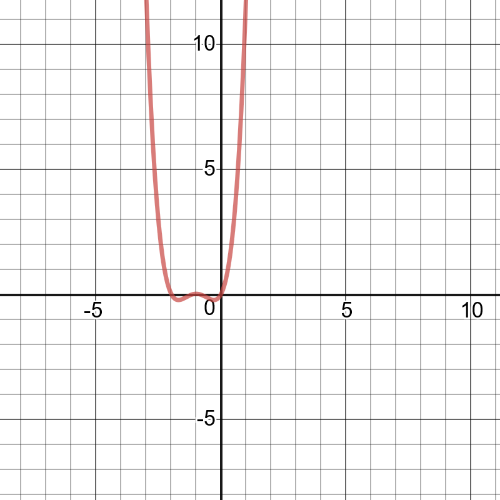
The domain is $left{xinBbb{R} right}$.

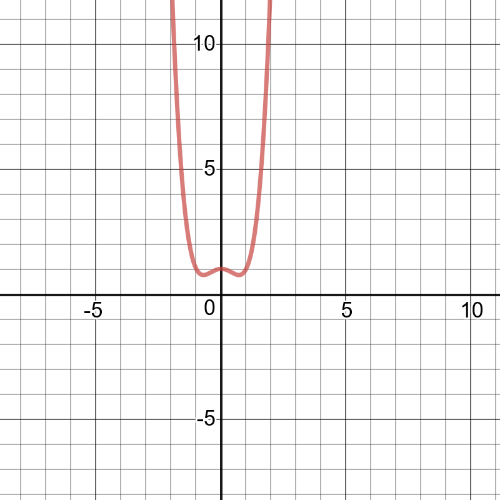
$f(f(x))=f()4x=sin 4x$

The domain is $left{xinBbb{R} right}$.

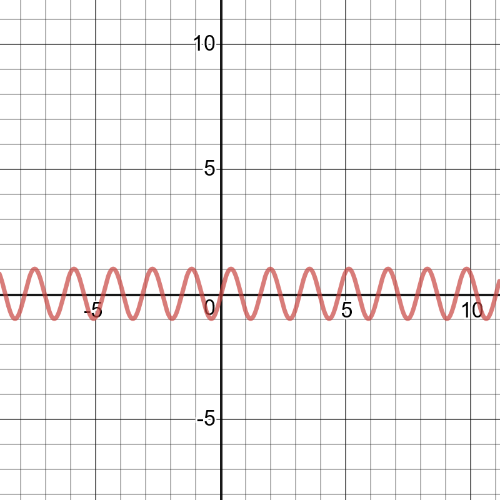
The domain is $left{xinBbb{R} right}$.

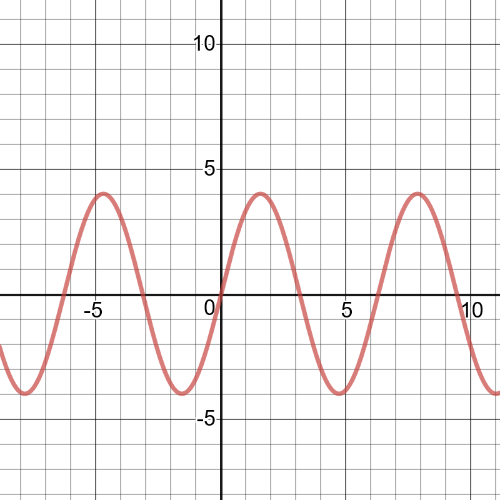
$f(g(x))=f(x+5)=|x+5|-2$

The domain is $left{xinBbb{R} right}$.

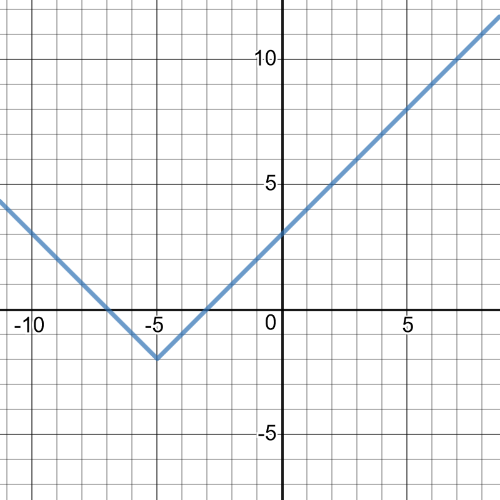
The domain is $left{xinBbb{R} right}$.

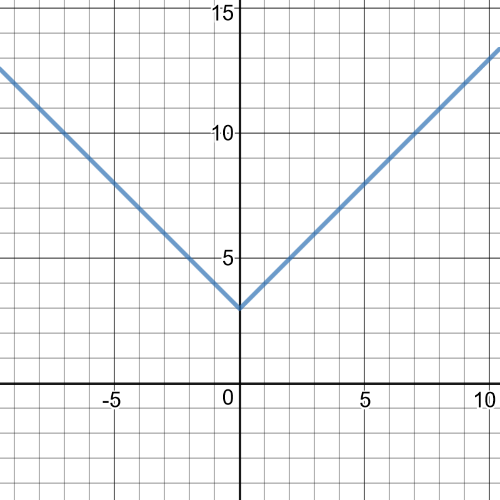
$f circ g=f(sqrt{x-4})=3sqrt{x-4}$

The domain is $left{xinBbb{R}|xgeq4 right}$ and the range is $left{ yinBbb{R}|ygeq0right}$.

$g circ f=g(3x)=sqrt{3x-4}$

The domain is $left{xinBbb{R}|xgeqdfrac{4}{3} right}$ and the range is $left{yinBbb{R}|ygeq 0 right}$.

#### (b)

$f circ g=f(3x+1)=sqrt{3x+1}$

The domain is $left{xinBbb{R}|xgeq -dfrac{1}{3} right}$ and the range is $left{yinBbb{R}|ygeq 0right}$.

$g circ f =g(sqrt{x})=3sqrt{x}+1$

The domain is $left{xinBbb{R}|xgeq 0 right}$ and the range is $left{yinBbb{R}|ygeq 1 right}$.

#### (c)

$f circ g=f(x^2)=sqrt{4-(x^2)^2}=sqrt{4-x^4}$

The domain is $left{xinBbb{R}|-sqrt{2}leq xleqsqrt{2} right}$ and the range is $left{yinBbb{R}|ygeq 0 right}$.

$g circ f=g(sqrt{4-x^2})=(sqrt{4-x^2})^2=4-x^2$

The domain is $left{xinBbb{R}|-2leq x leq2 right}$ and range is
$left{yinBbb{R}| 0 < y <2 right}$.

$f circ g=f(sqrt{x-1})=2sqrt{x-1}$

The domain is $left{x inBbb{R}| x geq 1 right}$ and the range is $left{yinBbb{R}|ygeq1 right}$.

$g circ f=g(2^x)=sqrt{2x-1}$

The domain is $left{xinBbb{R}|xgeq 0 right}$ and the range is $left{ yinBbb{R}| ygeq 0right}$.

#### (e)

$f circ g=f(log x)=10^{log x}=x$

The domain is $left{xinBbb{R} right}$ and the range is $left{yinBbb{R} right}$

#### (f)

$f circ g =f(5^{2x}+1)=sin(5^{2x}+1)$

The domain is $left{xinBbb{R} right}$ and the range is $left{ yinBbb{R}| -1 leq y leq 1right}$.

$g circ f=g(sin x)=5^{2sin x}+1$

The domain is $left{xinBbb{R} right}$ and the range is $left{yinBbb{R}|dfrac{26}{25}leq y leq 26 right}$.

Answers may vary. For example, $f(x)=sqrt{x}$ and $g(x)=x^2+6$

#### (b)

Answers may vary. For example, $f(x)=x^6$ and $g(x)=5x-8$

#### (c)

Answers may vary. For example, $f(x)=2^x$ and $g(x)=6x+7$

#### (d)

Answers may vary. For example,$f(x)=dfrac{1}{x}$ and $g(x)=x^3-7x+2$

#### (e)

Answers may vary. For example, $f(x)=sin^2 x$ and $g(x)=10x+5$

#### (f)

Answers may vary. For example, $f(x)=sqrt[3]{x}$ and $g(x)=(x+4)^2$

$(fcirc g)(x)=f(x^2)=2x^2-1$

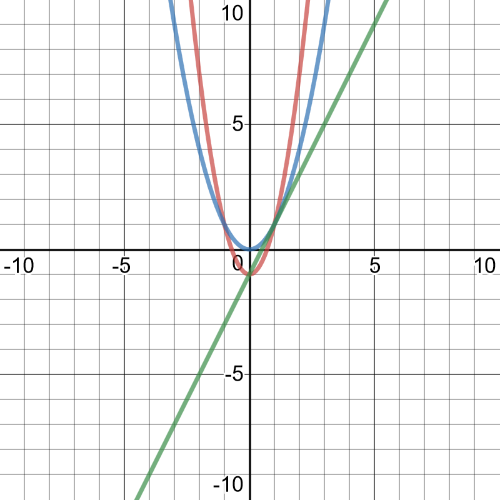
It is compressed by a factor of $2$ and translated down $1$ unit.

$f(g(x))=f(3x+2)=2(3x+2)-1=6x+4-1=6x+3$

The slope of $g(x)$ has been multiplied by $2$, and the $y$-intercept of $g(x)$ has been vertically translated $1$ unit up.

#### (b)

$$
g(f(x)=g(2x-1)=3(2x-1)+2=6x-3+2=6x-1
$$

The slope of $f(x)$ has been multiplied by $3$.

$d(s)=sqrt{16+s^2}; s(t)=560t$

#### (b)

$d(s(t))=sqrt{16+313600t^2}$, where $t$ is the time in hours and $d(s(t)$ is the distance in kilometers.

$textbf{The car is running most economically $2$ hours into the trip}$.

Graph $B(b)$; $f(x)$ is translated $3$ units to the right.

Graph $C(d)$; $f(x)$ is horizontally compressed by a factor of $dfrac{1}{2}$.

Graph $D(1)$; $f(x)$ is translated $4$ units down.

Graph $E(g)$; $f(x)$ is translated $3$ units up.

Graph $F(c)$; $f(x)$ is reflected in the $y$-axis.

$f(x)=dfrac{4}{x-3}$; $g(x)=1$

$textbf{Product:}$ $y=ftimes g$

$f(x)=x-3$;

$g(x)=dfrac{x+1}{(x-3)^2}$

$textbf{Quotient:}$ $y=fdiv g$

$f(x)=1+x; g(x)=x-3$

$textbf{Composition:}$ $y=f circ g$

$f(x)=dfrac{4}{x}+1$; $g(x)=x-3$

$f(k)=f(x(t(k)))$

$=f(x(3k-2))$

$=f(3(3k-2)+2)$

$=f(9k-6+2)$

$=f(9k-4)$

$=3(9k-4)-2$

$=27k-12-2$

$=27k-14$

#### (b)

$f(k)=f(x(t(k)))$

$=f(x(3k-5))$

$=fleft(sqrt{3(3k-5)-1} right)$

$=fleft(sqrt{9k-15-1} right)$

$=fleft(sqrt{9k-16} right)$

$$
=2sqrt{9k-16}-5
$$