(a) We need to solve the equation $color{#4257b2}3x-7=5-9x$. First, to solve this equation we need to make the variable $color{#4257b2}x$ in side alone, so the first step is to add $color{#4257b2}9x+7$ to each side as follows:

$$
because 3x-7=5-9x
$$

$therefore 3x-7+9x+7=5-9x+9x+7$ $text{add $color{#4257b2}9x+7$ to each side}$

$$
therefore 12x=12
$$

Now to find the value of $x$ we can divide the two sides by $12$

$$
therefore dfrac{12x}{12}=dfrac{12}{12}
$$

$$
therefore boxed{ x=1 }
$$

(b) We need to solve the equation $color{#4257b2}2left(x+3right)-dfrac{x}{4}=dfrac{1}{2}$. First, to solve this equation we need to make the variable $color{#4257b2}x$ in side alone, so the first step is to distribute $color{#4257b2}2$ which is multiplied by the bracket $color{#4257b2}left(x+3right)$ as follows:

$$
because 2left(x+3right)-dfrac{x}{4}=dfrac{1}{2}
$$

$$
therefore 2x+6-dfrac{x}{4}=dfrac{1}{2}
$$

Now we can multiply the two sides by $4$ to simplify as follows:

$$
therefore 8x+24-x=2
$$

$$
therefore 7x+24=2
$$

$therefore 7x=2-24=-22$ $text{move $24$ to the other side with the opposite sign}$

$therefore dfrac{7x}{7}=-dfrac{22}{7}=-3.14$ $text{divide the two sides by $7$}$

$$
therefore boxed{ x=-3.14 }
$$

(c) We need to solve the equation $color{#4257b2}x^{2}-5x-24=0$. First, we note that it is a quadratic equation, so we can factor to find the values of $color{#4257b2}x$ as follows:

$$
because x^{2}-5x-24=0
$$

$therefore left(x-8right)left(x+3right)=0$ factor

$therefore x-8=0$ or $x+3=0$ using the zero-factor property

$therefore x=8$ or $x=-3$

$therefore boxed{ x=-3 }$ or $boxed{ x=8 }$

(d) We need to solve the equation $color{#4257b2}6x^{2}+11x=0$. First, we note that it is a quadratic equation, so we can take $color{#4257b2}x$ as a common factor as follows:

$$
because 6x^{2}+11x=0
$$

$therefore xleft(6x+11right)=0$ $text{take $color{#4257b2}x$ as a common factor}$

$therefore x=0$ or $6x+11=0$ using the zero-factor property

Now we have two cases, so we have two solutions for $x$ the first solution is $color{#4257b2}x=0$ and we can get the second solution as follows:

$$
because 6x+11=0
$$

$therefore 6x=-11$ $text{move $11$ to the other side with the opposite sign}$

$therefore x=-dfrac{11}{6}=-1.83$ $text{divide the two sides by $6$}$

$therefore boxed{ x=0 }$ or $boxed{ x=-1.83 }$

(e) We need to solve the equation $color{#4257b2}x^{2}+2x-1=0$. First, we note that it is a quadratic equation on the standard form $color{#4257b2}a x^{2}+bx +c=0$, so we can use the quadratic formula to get the values of $color{#4257b2}x$ as follows:

$because x=dfrac{-bpm sqrt{b^{2}-4ac}}{2a}$ the quadratic formula

$therefore x=dfrac{-2pm sqrt{2^{2}-4cdot 1cdot (-1)}}{2cdot 1}$ $text{substitute $color{#4257b2}a=1, b=2$ and $color{#4257b2}c=-1$}$

$$
therefore x=dfrac{-2pm sqrt{4+4}}{2}
$$

$$
therefore x=dfrac{-2pm sqrt{8}}{2}
$$

$$
therefore x=dfrac{-2pm 2sqrt{2}}{2}
$$

$$
therefore x=-1pm sqrt{2}
$$

$therefore x=-1+sqrt{2}$ or $x=-1-sqrt{2}$

$therefore boxed{ x=0.41 }$ or $boxed{ x=-2.41 }$

(f) We need to solve the equation $color{#4257b2}3x^{2}=3x+1$. First, we note that it is a quadratic equation but is not on the standard form $color{#4257b2}a x^{2}+bx +c=0$, so the first step is subtract $color{#4257b2}3x+1$ from each side to make the equation on the standard from as follows:

$$
because 3x^{2}=3x+1
$$

$$
therefore 3x^{2}-3x-1=0
$$

Now our equation is on the standard form $color{#4257b2}a x^{2}+bx+c=0$, so we can use the quadratic formula to find the values of $x$ as follows:

$because x=dfrac{-bpm sqrt{b^{2}-4ac}}{2a}$ the quadratic formula

$therefore x=dfrac{-(-3)pm sqrt{(-3)^{2}-4cdot 3cdot (-1)}}{2cdot 3}$ $text{substitute $color{#4257b2}a=3, b=-3$ and $color{#4257b2}c=-1$}$

$$
therefore x=dfrac{3pm sqrt{9+12}}{6}
$$

$$
therefore x=dfrac{3pm sqrt{21}}{6}
$$

$$
therefore x=dfrac{3}{6}pm dfrac{sqrt{21}}{6}
$$

$therefore x=dfrac{3}{6}+dfrac{sqrt{21}}{6}$ or $x=dfrac{3}{6}-dfrac{sqrt{21}}{6}$

$therefore boxed{ x=1.26 }$ or $boxed{ x=-0.26 }$

$$
text{color{#c34632}$(a) x=1$ $(b) x=-3.14$
\
\
Large$color{#c34632}(c) x=-3 {color{Black$text{or}} $x=8$ $(d) x=0$ {color{Black}text{or}} $x=-1.83$}
\
\
Large$color{#c34632}(e) x=0.41 {color{Black$text{or}} $x=-2.41$ $(f) x=1.26$ {color{Black}text{or}} $x=-0.26$}}
$$

We need to show that the length of the line segment from $color{#4257b2}A(1, 0)$ to $color{#4257b2}Bleft(2, dfrac{1}{2}right)$ is the same length as the line segment from $color{#4257b2}C=left(-dfrac{1}{2}, 5right)$ to $color{#4257b2}D(0, 6)$.

First, we can use the Distance Formula to find the length between two points where the formula is $color{#4257b2}d=sqrt{left(x_{2}-x_{1}right)^{2}+left(y_{2}-y_{1}right)^{2}}$, where $color{#4257b2}d$ equals the distance of the line, $color{#4257b2}(x_{1}, y_{1})$ equal the coordinates of the first point of the line segment, and $color{#4257b2}(x_{2},y_{2})$ equal the coordinates of the second point of the line segment.

For the first line segment from $color{#4257b2}A(1, 0)$ to $color{#4257b2}Bleft(2, dfrac{1}{2}right)$

$$
therefore d_{1}=sqrt{left(2-1right)^{2}+left(dfrac{1}{2}-0right)^{2}}
$$

$$
therefore d_{1}=sqrt{1^{2}+left(dfrac{1}{2}right)^{2}}
$$

$$
therefore d_{1}=sqrt{1+dfrac{1}{4}}=sqrt{dfrac{5}{4}}
$$

$$
therefore boxed{ d_{1}=dfrac{sqrt{5}}{2}}
$$

Now we will find the length of the second segment to show if the two lengths are equal or not.

For the second line segment from $color{#4257b2}Cleft(-dfrac{1}{2}, 5right)$ to $color{#4257b2}Dleft(0, 6right)$

$$
therefore d_{2}=sqrt{left[0-left(-dfrac{1}{2}right)right]^{2}+left(6-5right)^{2}}
$$

$$
therefore d_{2}=sqrt{left(dfrac{1}{2}+1^{2}right)^{2}}
$$

$$
therefore d_{2}=sqrt{dfrac{1}{4}+1}=sqrt{dfrac{5}{4}}
$$

$$
therefore boxed{ d_{2}=dfrac{sqrt{5}}{2}}
$$

We note that $color{#4257b2}d_{1}=d_{2}$, so the length of the first line segment from $color{#4257b2}A$ to $color{#4257b2}B$ equals the length of the second line segment from $color{#4257b2}C$ to $color{#4257b2}D$

$$
text{color{#c34632}The length of the line segment from $A$ to $B$ is the same length as the line segment from $C$ to $D$}
$$

(a) We would like to find the six trigonometric ratios for $color{#4257b2}angle A$.

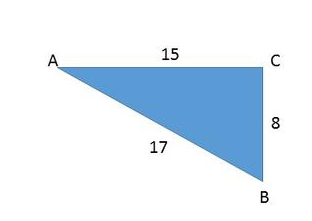
First, we note that it is a right triangle, so we can use the formulas of the trigonometric functions for the right triangle where

$$
boxed{ color{#4257b2}sin theta=dfrac{text{opposite}}{text{hypotenuse}}, cos theta=dfrac{text{adjacent}}{text{Hypotenuse}}, tan theta=dfrac{text{opposite}}{text{adjacent}} }
$$

Now we can get the values of the opposite, the adjacent and the hypotenuse for the angle $color{#4257b2}A$ from the triangle

$$
color{#4257b2}text{the opposite}=8, text{the adjacent}=15, text{the hypotenuse}=17
$$

Now we can substitute these values in the formulas of the trigonometric function as follows:

$$
sin A=dfrac{text{opposite}}{text{hypotenuse}}=boxed{ dfrac{8}{17} }
$$

$$
cos A=dfrac{text{adjacent}}{text{hypotenuse}}=boxed{ dfrac{15}{17} }
$$

$$
tan A=dfrac{text{opposie}}{text{adjacent}}=boxed{ dfrac{8}{15} }
$$

Now we can find the remaining trigonometric functions using the identities $color{#4257b2}csc theta=dfrac{1}{sin theta}, sec theta=dfrac{1}{cos theta}$ and $color{#4257b2}cot theta=dfrac{1}{tan theta}$

$$
csc A=dfrac{1}{sin theta}=dfrac{1}{dfrac{8}{17}}=boxed{ dfrac{17}{8} }
$$

$$
sec A=dfrac{1}{cos theta}=dfrac{1}{dfrac{15}{17}}=boxed{ dfrac{17}{15} }
$$

$$
cot A=dfrac{1}{tan theta}=dfrac{1}{dfrac{8}{15}}=boxed{ dfrac{15}{8} }
$$

(b) We would like to determine the measure of $color{#4257b2}angle A$ in radians, to one decimal place.

We have the values of the six trigonometric functions, so to find the angle $A$ we can find it through one of these values like $color{#4257b2}sin A=dfrac{8}{17}$. To get the angle $A$ we can take $color{#4257b2}sin^{-1}$ for each side

$$
sin A=dfrac{8}{17}
$$

$$
sin^{-1}left(sin Aright)=sin^{-1}left(dfrac{8}{17}right)
$$

$$
A=sin^{-1}left(dfrac{8}{17}right)
$$

Note that $color{#4257b2}sin^{-1}left(sin thetaright)=theta$. Now we can use the calculator to find the value of $color{#4257b2}sin^{-1}left(dfrac{8}{17}right)$

$$
boxed{ A=0.5 text{radians} }
$$

(c) We would like to determine the measure of $color{#4257b2}angle B$ in degrees, to one decimal place.

First, to determine the measure of $color{#4257b2}angle B$ we need to know at least one of its trigonometric functions, so we can use the formula $color{#4257b2}sin theta=dfrac{text{opposite}}{text{hypotenuse}}$ to get $color{#4257b2}sin B$. Note that the opposite for the angle $B$ equals $15$.

$$
sin B=dfrac{text{opposite}}{text{hypotenuse}}=dfrac{15}{17}
$$

Now we have the value of $color{#4257b2}sin B=dfrac{15}{17}$, so to get the angle $B$ we can take $color{#4257b2}sin^{-1}$ for each side

$$
sin B=dfrac{15}{17}
$$

$$
sin^{-1}left(sin Bright)=sin^{-1}left(dfrac{15}{17}right)
$$

$$
B=sin^{-1}left(dfrac{15}{17}right)
$$

Note that $color{#4257b2}sin^{-1}left(sin thetaright)=theta$. Now we can use the calculator to find the value of $color{#4257b2}sin^{-1}left(dfrac{15}{17}right)$

$$
boxed{ B=61.9text{textdegree} }
$$

$$
color{#c34632}(a) sin A=dfrac{8}{17}, cos A=dfrac{15}{17}, tan A=dfrac{8}{15}
$$

$$
color{#c34632} csc A=dfrac{17}{8}, sec A=dfrac{17}{15}, cot A=dfrac{15}{8}
$$

$$
text{color{#c34632}(b) $angle A=0.5 text{radians}$
\
\
Large{color{#c34632}(c) $angle B=61.9text{textdegree}$}}
$$

*(a)* The counter-clockwise angle between the initial arm and the terminal arm of an angle in standard position is the principal angle $theta$.

We can set a point $(-2,2)$ in the coordinate system and connect it to the origin of that system as depicted in *Figure 1*.

Figure 1.

If this line is a terminal arm of an angle in the standard position, the initial arm is the positive $x$-axis. Hence, the principal angle $theta$ is between these arms, as depicted in the figure above.

*(b)* The acute angle measures less than $90^{circ}$. One such angle we can notice between the negative $x$-axis and terminal arm of the angle $theta$. Let’s denote this angle $alpha$, as depicted in *Figure 2*.

Figure 2.

Note that this angle is an angle between the diagonal and the side of a square with a side of $2$. Diagonal divides the right angle of a square on half, so that we have
$$alpha=dfrac{90^{circ}}{2}=45^{circ}=dfrac{pi}{4}$$

*(c)* Note from the picture in the previous step that these two angles $alpha$ and $theta$ together make an angle of $180^{circ}=pi$, so that we can write
$$
alpha+theta=pi.$$
Subtracting $alpha$ throughout this equation, we can write
$$
theta=pi-alpha=pi-dfrac{pi}{4}=dfrac{3pi}{4}.$$

a) See the explanation.

b)$frac{pi}{4}$

c) $frac{3pi}{4}$

The unit circle is a circle with a radius $r=1$. The center of this circle is the origin of the coordinate system, as depicted in *Figure 1*.

Figure 1.

Every point on this circle we can connect to the circle center with its radius. Radius and positive $x$-axis are making a principle angle $theta$. Then, the $x$ coordinate of such a point will be equal to the cosine function of that angle, while the $y$ coordinate will correspond to the sine function of the same angle, as depicted in the figure above.

This property of a unit circle we will use to compute the coordinates of each given point on a unit circle

*(a)* If we start counterclockwise from the positive $x$ axis, the first point whose coordinates we need to determine is the point $A$. Note that this point is in the first quadrant, both $x$ and $y$ coordinates should be positive. We can compare it with the point with coordinates $left(-frac{sqrt{2}}{2},frac{sqrt{2}}{2}right)$, as depicted in *Figure 2*.

Figurea 2.

We can conclude that this point is point $A$ reflected about in $y$ axis. Hence, the $x$ coordinate of point $A$ will have the sign opposite to the one in $x$ coordinate of the point $left(-frac{sqrt{2}}{2},frac{sqrt{2}}{2}right)$, while $y$ coordinate will remain the same. Hence, for the coordinates of point $A$ we can write
$$
begin{align*}
x_A&=cos dfrac{pi}{4}=dfrac{sqrt{2}}{2}\
y_A&=sin dfrac{pi}{4}=dfrac{sqrt{2}}{2}end{align*}$$
or
$$A:left(dfrac{sqrt{2}}{2},dfrac{sqrt{2}}{2}right)$$

The next point we encounter is the point $B$. Note that this point is in the first quadrant, both $x$ and $y$ coordinates should be positive. We can compare it with the point with coordinates $left(frac{sqrt{3}}{2},frac{1}{2}right)$, as depicted in *Figure 3*.

Figure 3.

We can conclude that this point is $B$ reflected about the line that passes through the point $A$. Since $x_A=y_A$, this line is $y=x$. Hence, the $x$ and $y$ coordinate of the point $B$ and this point will be switched. Hence, for the coordinates of point $B$, we can write
$$
begin{align*}
x_B&=cos dfrac{pi}{3}=dfrac{1}{2}\
y_B&=sin dfrac{pi}{3}=dfrac{sqrt{3}}{2}end{align*}$$
or
$$B:left(dfrac{1}{2},dfrac{sqrt{3}}{2}right)$$

The next point we encounter is the point $C$. Note that this point is in the second quadrant, so the $x$ coordinate will be negative and the $y$ coordinate should be positive. We can compare it with the point $B$, as depicted in *Figure 4*.

Figure 4.

We can conclude that this point is point $B$ reflected about in $y$ axis. Hence, the $x$ coordinate of point $C$ will have the sign opposite to the one in $x$ coordinate of the point $B$, while $y$ coordinate will remain the same. Hence, for the coordinates of point $C$ we can write
$$
begin{align*}
x_C&=cos dfrac{2pi}{3}=-dfrac{1}{2}\
y_C&=sin dfrac{2pi}{3}=dfrac{sqrt{3}}{2}end{align*}$$
or
$$C:left(-dfrac{1}{2},dfrac{sqrt{3}}{2}right)$$

The next point we encounter is the point $D$. Note that this point is in the second quadrant, so the $x$ coordinate will be negative and the $y$ coordinate should be positive. We can compare it with the point with coordinates $left(frac{sqrt{3}}{2},frac{1}{2}right)$, as depicted in *Figure 5*.

Figure 5.

We can conclude that point $D$ is the point with coordinates $left(frac{sqrt{3}}{2},frac{1}{2}right)$ reflected about in $y$ axis. Hence, the $x$ coordinate of point $D$ will have the sign opposite to the one in $x$ coordinate of the point $left(frac{sqrt{3}}{2},frac{1}{2}right)$ r, while $y$ coordinate will remain the same. Hence, for the coordinates of point $D$ we can write
$$
begin{align*}
x_D&=cos dfrac{5pi}{6}=-dfrac{sqrt{3}}{2}\
y_D&=sin dfrac{5pi}{6}=dfrac{1}{2}end{align*}$$
or
$$D:left(-dfrac{sqrt{3}}{2},dfrac{1}{2}right)$$

The same method of conclusion we can apply to all other points. For the point $E$ we can conclude that it is a point $D$ reflected about the $x$ axis. Hence, the coordinates of these points will be the same, but the $y$ coordinate of point $E$ will have the opposite sign than the $y$ coordinate of point $D$. Hence, for the coordinates of point $E$ we can write
$$
begin{align*}
x_E&=cos dfrac{7pi}{6}=-dfrac{sqrt{3}}{2}\
y_E&=sin dfrac{7pi}{6}=-dfrac{1}{2}end{align*}$$
or
$$E:left(-dfrac{sqrt{3}}{2},-dfrac{1}{2}right).$$

For the point $F$ we can conclude that it is a point $left(-frac{sqrt{2}}{2},frac{sqrt{2}}{2}right)$ reflected about the $x$ axis. Hence, the coordinates of these points will be the same, but the $y$ coordinate of point $F$ will have the opposite sign than the $y$ coordinate of point $left(-frac{sqrt{2}}{2},frac{sqrt{2}}{2}right)$. Hence, for the coordinates of point $F$, we can write
$$
begin{align*}
x_F&=cos dfrac{5pi}{4}=-dfrac{sqrt{2}}{2}\
y_F&=sin dfrac{5pi}{4}=-dfrac{sqrt{2}}{2}end{align*}$$
or
$$F:left(-dfrac{sqrt{2}}{2},-dfrac{sqrt{2}}{2}right).$$

For the point $G$ we can conclude that it is a point $C$ reflected about the $x$ axis. Hence, the coordinates of these points will be the same, but the $y$ coordinate of point $G$ will have the opposite sign than the $y$ coordinate of point $C$. Hence, for the coordinates of point $G$, we can write
$$
begin{align*}
x_G&=cos dfrac{4pi}{3}=-dfrac{1}{2}\
y_G&=sin dfrac{4pi}{3}=-dfrac{sqrt{3}}{2}end{align*}$$
or
$$G:left(-dfrac{1}{2},-dfrac{sqrt{3}}{2}right).$$

For the point $H$ we can conclude that it is a point $B$ reflected about the $x$ axis. Hence, the coordinates of these points will be the same, but the $y$ coordinate of point $H$ will have the opposite sign than the $y$ coordinate of point $B$. Hence, for the coordinates of point $H$, we can write
$$
begin{align*}
x_H&=cos dfrac{5pi}{3}=dfrac{1}{2}\
y_H&=sin dfrac{5pi}{3}=dfrac{-sqrt{3}}{2}end{align*}$$
or
$$H:left(dfrac{1}{2},-dfrac{sqrt{3}}{2}right).$$

For the point $I$ we can conclude that it is a point $A$ reflected about the $x$ axis. Hence, the coordinates of these points will be the same, but the $y$ coordinate of point $I$ will have the opposite sign than the $y$ coordinate of point $A$. Hence, for the coordinates of point $I$, we can write
$$
begin{align*}
x_I&=cos dfrac{7pi}{4}=dfrac{sqrt{2}}{2}\
y_I&=sin dfrac{7pi}{4}=-dfrac{sqrt{2}}{2}end{align*}$$
or
$$I:left(dfrac{sqrt{2}}{2},-dfrac{sqrt{2}}{2}right).$$

For the point $J$ we can conclude that it is a point with coordinates $left(frac{sqrt{3}}{2},frac{1}{2}right)$ reflected about the $x$ axis. Hence, the coordinates of these points will be the same, but the $y$ coordinate of point $J$ will have the opposite sign than the $y$ coordinate of point with coordinates $left(frac{sqrt{3}}{2},frac{1}{2}right)$. Hence, for the coordinates of point $J$, we can write
$$
begin{align*}
x_J&=cos dfrac{11pi}{6}=dfrac{sqrt{3}}{2}\
y_J&=sin dfrac{11pi}{6}=-dfrac{1}{2}end{align*}$$
or
$$J:left(dfrac{sqrt{3}}{2},-dfrac{1}{2}right).$$

*(b)* As we said before, the cosine function we can read out from the $x$ coordinate of the corresponding point on the unit circle. The sine function we can read out from the $y$ coordinate. For the cosecant function we can use identity
$$
csc theta=dfrac{1}{sin theta}.
$$

*(i)* The point corresponding to the angle $frac{3pi}{4}$ is the point with coordinates $left(-frac{sqrt{2}}{2},frac{sqrt{2}}{2}right)$. Since the cosine function we can read out from the $x$ coordinate of this point, we can write
$$
cos dfrac{3pi}{4}=-dfrac{sqrt{2}}{2}.$$

*(ii)* The point corresponding to the angle $frac{11pi}{6}$ is the point $J:left(frac{sqrt{3}}{2},-frac{1}{2}right)$. Since the sine function we can read out from the $y$ coordinate of this point, we can write
$$
sin dfrac{11pi}{6}=-dfrac{1}{2}.$$

*(iii)* The point corresponding to the angle $pi$ is the point with coordinates $left(-1,0right)$. Since the cosine function we can read out from the $x$ coordinate of this point, we can write
$$
cos pi=-1.$$

*(iv)* The point corresponding to the angle $frac{pi}{6}$ is the point $left(frac{sqrt{3}}{2},frac{1}{2}right)$. Since the sine function we can read out from the $y$ coordinate of this point, we can write
$$
sin dfrac{pi}{6}=dfrac{1}{2}.$$

Furthermore, the cosecant function is the reciprocal of a sine and we have
$$
csc dfrac{pi}{6}=cfrac{1}{sin cfrac{pi}{6}}=cfrac{1}{cfrac{1}{2}}=2.

a) $A:left(frac{sqrt{2}}{2},frac{sqrt{2}}{2}right)$, $B:left(frac{1}{2},frac{sqrt{3}}{2}right)$, $C:left(-frac{1}{2},frac{sqrt{3}}{2}right)$, $D:left(-frac{sqrt{3}}{2},frac{1}{2}right)$, $E:left(-frac{sqrt{3}}{2},-frac{1}{2}right)$, $F:left(-frac{sqrt{2}}{2},-frac{sqrt{2}}{2}right)$, $G:left(-frac{1}{2},-frac{sqrt{3}}{2}right)$, $H:left(frac{1}{2},-frac{sqrt{3}}{2}right)$, $I:left(frac{sqrt{2}}{2},-frac{sqrt{2}}{2}right)$, $J:left(frac{sqrt{3}}{2},-frac{1}{2}right)$

b) *(i)* $-frac{sqrt{2}}{2}$, *(ii)*$-frac{1}{2}$, *(iii)* $-1$, *(iv)* 2

(a) We would like to find the five trigonometric ratios as fractions where
$color{#4257b2}tan x=-dfrac{3}{4}$. First, we can use the identity $color{#4257b2}cot theta=dfrac{1}{tan theta}$ to get the value of $color{#4257b2}cot x$.

$$
cot x=dfrac{1}{tan x}
$$

$$
cot x=dfrac{1}{-dfrac{3}{4}}=boxed{ -dfrac{4}{3} }
$$

Now we can use the Pythagorean identity $color{#4257b2}1+tan^{2}theta=sec^{2}theta$ to find $color{#4257b2}sec x$.

$1+tan^{2}x=sec^{2}x$

$$
1+left(-dfrac{3}{4}right)^{2}=sec^{2}x text{substitute $color{#4257b2}tan x=-dfrac{3}{4}$}
$$

$$
1+dfrac{9}{16}=sec^{2}x
$$

$$
sec^{2}x=dfrac{25}{16}
$$

Now we can take the square root for each side to get $color{#4257b2}sec x$

$$
therefore sec x=pm sqrt{dfrac{25}{16}}
$$

$$
therefore boxed{ sec x=pm dfrac{5}{4} }
$$

Note that there are two values for $color{#4257b2}sec x$ because $color{#4257b2}tan x$ is negative which means that $color{#4257b2}x$ may be in quadrant $2$ or quadrant $4$ where $color{#4257b2}sec x$ is positive in quadrant $4$ and negative in quadrant $2$.

Now we have the value of $color{#4257b2}sec B$, so we can use the identity $color{#4257b2}cos theta=dfrac{1}{sec theta}$ to find $color{#4257b2}cos B$

$$
cos B=dfrac{1}{sec B}
$$

$$
cos B=dfrac{1}{pm dfrac{5}{4}}=boxed{ pm dfrac{4}{5} }
$$

Now we can use the Pythagorean identity $color{#4257b2}1+cot^{2}theta=csc^{2}theta$ to find $color{#4257b2}csc x$.

$1+cot^{2}x=csc^{2}x$

$$
1+left(-dfrac{4}{3}right)^{2}=csc^{2}x text{substitute $color{#4257b2}cot x=-dfrac{4}{3}$}
$$

$$
1+dfrac{16}{9}=csc^{2}x
$$

$$
csc^{2}x=dfrac{25}{9}
$$

Now we can take the square root for each side to get $color{#4257b2}csc x$

$$
therefore csc x=pm sqrt{dfrac{25}{9}}
$$

$$
therefore boxed{ csc x=pm dfrac{5}{3} }
$$

Note that there are two values for $color{#4257b2}csc x$ because $color{#4257b2}tan x$ is negative which means that $color{#4257b2}x$ may be in quadrant $2$ or quadrant $4$ where $color{#4257b2}csc x$ is positive in quadrant $2$ and negative in quadrant $4$.

Now we have the value of $color{#4257b2}csc B$, so we can use the identity $color{#4257b2}sin theta=dfrac{1}{csc theta}$ to find $color{#4257b2}sin B$

$$
sin B=dfrac{1}{csc B}
$$

$$
sin B=dfrac{1}{pm dfrac{5}{3}}=boxed{ pm dfrac{3}{5} }
$$

(b) We would like to find the values of $x$, to one decimal place. Since we have the value of $color{#4257b2}tan x=-dfrac{3}{4}$, we can take $color{#4257b2}tan^{-1}$ for each side to get the values of $x$.

$$
tan x=-dfrac{3}{4}
$$

$$
tan^{-1}left(tan xright)=tan^{-1}left(-dfrac{3}{4}right)
$$

$$
x=tan^{-1}left(-dfrac{3}{4}right)
$$

Note that $color{#4257b2}tan^{-1}left(tan thetaright)=theta$.

But we know that $color{#4257b2}tan x$ is negative in quadrant $2$ and quadrant $4$, so we can find the values of $x$ where the reference angle by using the calculator is $color{#4257b2}0.6 text{radians}$

$$
x=pi-0.6 text{or} x=2pi-0.6
$$

$$
boxed{ x=2.5 text{radians} } text{or} boxed{ x=5.6 text{radians} }
$$

$$
text{color{#c34632}$(a) sin x=pm dfrac{3}{5}, cos x=pm dfrac{4}{5}, csc x=pm dfrac{5}{3}, sec x=pm dfrac{5}{4}, cot x=-dfrac{4}{3}$
\
\
color{#c34632}$(b) x=2.5 text{radians} {color{Black}text{or}} x=5.6 text{radians}$}
$$

(a) We would like to know if the relationship $color{#4257b2}tan theta=dfrac{sin theta}{cos theta}, cos theta ne 0$ is true or false.

We know that the identity $color{#4257b2}tan theta=dfrac{sin theta}{cos theta}$ is true and $color{#4257b2}cos theta$ shouldn’t equal zero because in this case $color{#4257b2}tan theta$ will be undefined.

So the relationship $color{#4257b2}tan theta=dfrac{sin theta}{cos theta}, cos ne 0$ is true.

(b) We would like to know if the relationship $color{#4257b2}sin^{2}theta+cos^{2}theta=1$ is true or false.

We know from the Pythagorean identity that $color{#4257b2}sin^{2}theta+cos^{2}theta=1$ is true.

So the relationship $color{#4257b2}sin^{2}theta+cos^{2}theta=1$ is true

(c) We would like to know if the relationship $color{#4257b2}\sec theta=dfrac{1}{sin theta}, sin theta ne 0$ is true or false.

We know that the identity $color{#4257b2}sec theta=dfrac{1}{cos theta}$ is true and the identity $color{#4257b2}csc theta=dfrac{1}{sin theta}$ is also true, so the relationship $color{#4257b2}sectheta=dfrac{1}{sin theta}, sin theta ne 0$ is not true.

So the relationship $color{#4257b2}sectheta=dfrac{1}{sin theta}, sin theta ne 0$ is false.

(d) We would like to know if the relationship $color{#4257b2}cos^{2}theta=sin^{2}theta-1$ is true or false.

We know from the Pythagorean identity that $color{#4257b2}sin^{2}theta+cos^{2}theta=1$, so if we transferred $color{#4257b2}sin^{2}theta$ to the other side with the opposite sign it will be $color{#4257b2}cos^{2}theta=1-sin^{2}theta$ not $color{#4257b2}cos^{2}theta=sin^{2}theta-1$.

So the relationship $color{#4257b2}cos^{2}theta=sin^{2}theta-1$ is false.

(e) We would like to know if the relationship $color{#4257b2}1+tan^{2}theta=sec^{2}theta$ is true or false.

We know from the Pythagorean identity that $color{#4257b2}1+tan^{2}theta=sec^{2}theta$ is true.

So the relationship $color{#4257b2}1+tan^{2}theta=sec^{2}theta$ is true.

(f) We would like to know if the relationship $color{#4257b2}cot theta=dfrac{cos theta}{sin theta}, sin theta ne 0$ is true or false.

We know that the identity $color{#4257b2}cot theta=dfrac{cos theta}{sin theta}$ is true and $color{#4257b2}sin theta$ shouldn’t equal zero because in this case $color{#4257b2}cot theta$ will be undefined.

So the relationship $color{#4257b2}cot theta=dfrac{cos theta}{sin theta}, sin ne 0$ is true.

$$
text{color{#c34632}(a) True (b) True (c) False (d) False (e) True (f) True}
$$