(a) We would like to write the expression $color{#4257b2}log left(45*68right)$ as a sum or difference of logarithms. First, we note that our expression is a logarithm of product, so we can use the product law of logarithms where $color{#4257b2}log_{a} xy=log_{a}x+log_{a}y$.

$$
log left(45*68right)=log 45+log 68
$$

So the expression $color{#4257b2}log left(45*68right)$ can be written as $boxed{ log 45+log 68 }$

(b) We would like to write the expression $color{#4257b2}log_{m} pq$ as a sum or difference of logarithms. First, we note that our expression is a logarithm of product, so we can use the product law of logarithms where $color{#4257b2}log_{a} xy=log_{a}x+log_{a}y$.

$$
log_{m} pq=log_{m} p+log_{m} q
$$

So the expression $color{#4257b2}log_{m} pq$ can be written as $boxed{ log_{m} p+log_{m} q }$

(c) We would like to write the expression $color{#4257b2}log left(dfrac{123}{31}right)$ as a sum or difference of logarithms. First, we note that our expression is a logarithm of quotient, so we can use the quotient law of logarithms where $color{#4257b2}log_{a}left(dfrac{x}{y}right)=log_{a}x-log_{a}y$.

$$
log left(dfrac{123}{31}right)=log 123-log 31
$$

So the expression $color{#4257b2}log left(dfrac{123}{31}right)$ can be written as $boxed{ log 123-log 31 }$

(d) We would like to write the expression $color{#4257b2}log_{m}left(dfrac{p}{q}right)$ as a sum or difference of logarithms. First, we note that our expression is a logarithm of quotient, so we can use the quotient law of logarithms where $color{#4257b2}log_{a}left(dfrac{x}{y}right)=log_{a}x-log_{a}y$.

$$
log_{m}left(dfrac{p}{q}right)=log_{m} p-log_{m} q
$$

So the expression $color{#4257b2}log_{m} left(dfrac{p}{q}right)$ can be written as $boxed{ log_{m} p-log_{m} q }$

(e) We would like to write the expression $color{#4257b2}log_{2}left(14*9right)$ as a sum or difference of logarithms. First, we note that our expression is a logarithm of product, so we can use the product law of logarithms where $color{#4257b2}log_{a} xy=log_{a}x+log_{a}y$.

$$
log_{2}left(14*9right)=log_{2} 14+log_{2} 9
$$

So the expression $color{#4257b2}log_{2} left(14*9right)$ can be written as $boxed{ log_{2} 14+log_{2} 9 }$

(f) We would like to write the expression $color{#4257b2}log_{4} left(dfrac{81}{30}right)$ as a sum or difference of logarithms. First, we note that our expression is a logarithm of quotient, so we can use the quotient law of logarithms where $color{#4257b2}log_{a}left(dfrac{x}{y}right)=log_{a}x-log_{a}y$.

$$
log_{4} left(dfrac{81}{30}right)=log_{4} 81-log_{4} 30
$$

So the expression $color{#4257b2}log_{4} left(dfrac{81}{30}right)$ can be written as $boxed{ log_{4} 81-log_{4} 30 }$

Large{$text{$text{color{#c34632}(a) $log 45+log 68$ (c) $log 123-log 31$ (e) $log_{2} 14+log_{2} 9$
\
\
\
Large{color{#c34632}(b) $log_{m} p+log_{m} q$ (d) $log_{m} p-log_{m} q$ (f) $log_{4} 81-log_{4} 30$}$}$

(a) We would like to express $color{#4257b2}log 5 + log 7$ as a logarithm of product or quotient. First, we note that our expression is a sum of logarithms, so we can use the product law of logarithms where $color{#4257b2}log_{a} xy=log_{a}x+log_{a}y$.

$$
log 5 + log 7=log (5*7)
$$

So the expression $color{#4257b2}log 5 + log 7$ can be written as $boxed{ log (5*7) }$

(b) We would like to express $color{#4257b2}log_{3} 4 – log_{3} 2$ as a logarithm of product or quotient. First, we note that our expression is a difference of logarithms, so we can use the quotient law of logarithms where $color{#4257b2}log_{a} left(dfrac{x}{y}right)=log_{a}x-log_{a}y$.

$$
log_{3} 4 + log_{3} 2=log_{3} left(dfrac{4}{2}right)
$$

So the expression $color{#4257b2}log_{3} 4 – log_{3} 2$ can be written as $boxed{ log_{3} left(dfrac{4}{2}right) }$

(c) We would like to express $color{#4257b2}log_{m} a + log_{m} b$ as a logarithm of product or quotient. First, we note that our expression is a sum of logarithms, so we can use the product law of logarithms where $color{#4257b2}log_{a} xy=log_{a}x+log_{a}y$.

$$
log_{m} a + log_{m} b=log_{m} (a b)
$$

So the expression $color{#4257b2}log_{m} a + log_{m} b$ can be written as $boxed{ log_{m} (a b) }$

(d) We would like to express $color{#4257b2}log x – log y$ as a logarithm of product or quotient. First, we note that our expression is a difference of logarithms, so we can use the quotient law of logarithms where $color{#4257b2}log_{a} left(dfrac{x}{y}right)=log_{a}x-log_{a}y$.

$$
log x – log y=log left(dfrac{x}{y}right)
$$

So the expression $color{#4257b2}log x – log y$ can be written as $boxed{ log left(dfrac{x}{y}right) }$

(e) We would like to express $color{#4257b2}log_{6} 7 + log_{6} 8 + log_{6} 9$ as a logarithm of product or quotient. First, we note that our expression is a sum of logarithms, so we can use the product law of logarithms where $color{#4257b2}log_{a} xyz=log_{a}x+log_{a}y+log_{a}z$.

$$
log_{6} 7 + log_{6} 8 + log_{6} 9=log_{6} (7*8*9)
$$

So the expression $color{#4257b2}log_{6} 7 + log_{6} 8 + log_{6} 9$ can be written as $boxed{ log_{6} (7*8*9) }$

(f) We would like to express $color{#4257b2}log_{4} 10 + log_{4} 12 – log_{4} 20$ as a logarithm of product or quotient. First, we note that the first two terms in our expression is a sum of logarithms, so we can use the product law of logarithms where $color{#4257b2}log_{a} xyz=log_{a}x+log_{a}y+log_{a}z$.

$$
begin{align*}
log_{4} 10 + log_{4} 12 – log_{4} 20&=left(log_{4} 10 + log_{4} 12right) – log_{4}20
\ \
&=log_{4} (10*12)-log_{4} 20
end{align*}
$$

Now we note that our expression is a difference of logarithms, so we can use the quotient law of logarithms where $color{#4257b2}log_{a} left(dfrac{x}{y}right)=log_{a}x-log_{a}y$.

$$
begin{align*}
log_{4} 10 + log_{4} 12 – log_{4} 20&=log_{4} (10*12)-log_{4} 20
\ \
&=log_{4} left(dfrac{10*12}{20}right)
end{align*}
$$

So the expression $color{#4257b2}log_{4} 10 + log_{4} 12 – log_{4} 20$ can be written as $boxed{ log_{4} left(dfrac{10*12}{20}right) }$

Large{$text{color{#c34632}(a) $log (5*7)$ (d) $log left(dfrac{x}{y}right)$
\
\
\
(b) $log_{3} left(dfrac{4}{2}right)$ (e) $log_{6} (7*8*9)$
\
\
\
(c) $log_{m} a b$ (f) $log_{4} left(dfrac{10*12}{20}right)$}$

(a) We would like to express $color{#4257b2}log 5^{2}$ in the form $color{#4257b2}r log_{a} x$. First, we note that our expression is a power of logarithm, so we can use the power law of logarithms where $color{#4257b2}log_{a} x^{r}=r log_{a} x$.

$$
log 5^{2}=2 log 5
$$

So the expression $color{#4257b2}log 5^{2}$ can be written as $boxed{ 2 log 5 }$

(b) We would like to express $color{#4257b2}log_{3} 7^{-1}$ in the form $color{#4257b2}r log_{a} x$. First, we note that our expression is a power of logarithm, so we can use the power law of logarithms where $color{#4257b2}log_{a} x^{r}=r log_{a} x$.

$$
log_{3} 7^{-1}=(-1) log_{3} 7=-log_{3} 7
$$

So the expression $color{#4257b2}log_{3} 7^{-1}$ can be written as $boxed{ -log_{3} 7 }$

(c) We would like to express $color{#4257b2}log_{m} p^{q}$ in the form $color{#4257b2}r log_{a} x$. First, we note that our expression is a power of logarithm, so we can use the power law of logarithms where $color{#4257b2}log_{a} x^{r}=r log_{a} x$.

$$
log_{m} p^{q}=q log_{m} p
$$

So the expression $color{#4257b2}log_{m} p^{q}$ can be written as $boxed{ q log_{m} p }$

(d) We would like to express $color{#4257b2}log sqrt[3]{45}$ in the form $color{#4257b2}r log_{a} x$. First, we have a cubic root, so we can rewrite it as power where $color{#4257b2}sqrt[3]{x}=x^{frac{1}{3}}$.

$$
log sqrt[3]{45}=log 45^{frac{1}{3}}
$$

Now we note that our expression is a power of logarithm, so we can use the power law of logarithms where $color{#4257b2}log_{a} x^{r}=r log_{a} x$.

$$
log sqrt[3]{45}=log 45^{frac{1}{3}}=dfrac{1}{3} log 45
$$

So the expression $color{#4257b2}log sqrt[3]{45}$ can be written as $boxed{ dfrac{1}{3} log 45 }$

(e) We would like to express $color{#4257b2}log_{7} 36^{0.5}$ in the form $color{#4257b2}r log_{a} x$. First, we note that our expression is a power of logarithm, so we can use the power law of logarithms where $color{#4257b2}log_{a} x^{r}=r log_{a} x$.

$$
log_{7} 36^{0.5}=0.5 log_{7} 36
$$

But we know that $color{#4257b2}36=6^{2}$, so we can replace $color{#4257b2}36$ in our expression by $color{#4257b2}6^{2}$ and use the power law of logarithms again.

$$
begin{align*}
log_{7} 36^{0.5}&=0.5 log_{7} 36
\ \
&=0.5 log_{7} 6^{2}
\ \
&=(0.5)cdot (2) log_{7} 6
\ \
&=log_{7} 6
end{align*}
$$

So the expression $color{#4257b2}log_{7} 36^{0.5}$ can be written as $boxed{ log_{7} 6 }$

(f) We would like to express $color{#4257b2}log_{5} sqrt[5]{125}$ in the form $color{#4257b2}r log_{a} x$. First, we have a fifth root, so we can rewrite it as power where $color{#4257b2}sqrt[5]{x}=x^{frac{1}{5}}$.

$$
log_{5} sqrt[5]{125}=log_{5} 125^{frac{1}{5}}
$$

Now we note that our expression is a power of logarithm, so we can use the power law of logarithms where $color{#4257b2}log_{a} x^{r}=r log_{a} x$.

$$
log_{5} sqrt[5]{125}=log_{5} 125^{frac{1}{5}}=dfrac{1}{5} log_{5} 125
$$

But we know that $color{#4257b2}125=5^{3}$, so we can replace $color{#4257b2}125$ in our expression by $color{#4257b2}5^{3}$ and use the power law of logarithms again.

$$
begin{align*}
log_{5} sqrt[5]{125}&=dfrac{1}{5} log_{5} 125
\ \
&=dfrac{1}{5} log_{5} 5^{3}
\ \
&=left(dfrac{1}{5}right)cdot (3) log_{5} 5
\ \
&=dfrac{3}{5} log_{5} 5
end{align*}
$$

So the expression $color{#4257b2}log_{5} sqrt[5]{125}$ can be written as $boxed{ dfrac{3}{5} log_{5} 5 }$

Large{$text{color{#c34632}(a) $2log 5$ (d) $dfrac{1}{3} log 45$
\
\
\
(b) $-log_{3} 7$ (e) $log_{7} 6$
\
\
\
(c) $q log_{m} p$ (f) $dfrac{3}{5} log_{5} 5$}$

(a) We would like to simplify and evaluate the expression $color{#4257b2}log_{3} 135-log_{3} 5$. First, we note that our expression is a difference of logarithms, so we can use the quotient law of logarithms where $color{#4257b2}log_{a} left(dfrac{x}{y}right)=log_{a} x-log_{a} y$.

$$
begin{align*}
log_{3} 135-log_{3} 5&=log_{3}left(dfrac{135}{5}right)
\ \
&=log_{3}27
\ \
&=log_{3} 3^{3}
end{align*}
$$

Now we note that our expression is simplified to the expression $color{#4257b2}log_{3} 3^{3}$ which is on the form of power logarithm, so we can use the power law of logarithms where $color{#4257b2}log_{a} m^{r}=r log_{a} m$.

$$
begin{align*}
log_{3} 135-log_{3} 5&=log_{3} 3^{3}
\ \
&=3 log_{3} 3
\ \
&=3cdot (1)=3
end{align*}
$$

Note that in the final step we used the property of logarithm where
$color{#4257b2}log_{a} a=1$.

So the expression $color{#4257b2}log_{3} 135-log_{3} 5$ equals $boxed{ 3 }$

(b) We would like to simplify and evaluate the expression $color{#4257b2}log_{5} 10+log_{5} 2.5$. First, we note that our expression is a sum of logarithms, so we can use the product law of logarithms where $color{#4257b2}log_{a} xy=log_{a} x+log_{a} y$.

$$
begin{align*}
log_{5} 10+log_{5} 2.5&=log_{5}left[(10)cdot (2.5)right]
\ \
&=log_{5} 25
\ \
&=log_{5} 5^{2}
end{align*}
$$

Now we note that our expression is simplified to the expression $color{#4257b2}log_{5} 5^{2}$ which is on the form of power logarithm, so we can use the power law of logarithms where $color{#4257b2}log_{a} m^{r}=r log_{a} m$.

$$
begin{align*}
log_{5} 10+log_{5} 2.5&=log_{5} 5^{2}
\ \
&=2 log_{5} 5
\ \
&=2cdot (1)=2
end{align*}
$$

Note that in the final step we used the property of logarithm where
$color{#4257b2}log_{a} a=1$.

So the expression $color{#4257b2}log_{5} 10+log_{5} 2.5$ equals $boxed{ 2 }$

(c) We would like to simplify and evaluate the expression $color{#4257b2}log 50+log 2$. First, we note that our expression is a sum of logarithms, so we can use the product law of logarithms where $color{#4257b2}log_{a} xy=log_{a} x+log_{a} y$.

$$
begin{align*}
log 50+log 2&=log left[(50)cdot (2)right]
\ \
&=log 100
\ \
&=log 10^{2}
end{align*}
$$

Now we note that our expression is simplified to the expression $color{#4257b2}log 10^{2}$ which is on the form of power logarithm, so we can use the power law of logarithms where $color{#4257b2}log_{a} m^{r}=r log_{a} m$.

$$
begin{align*}
log 50+log 2&=log 10^{2}
\ \
&=2 log 10
\ \
&=2cdot (1)=2
end{align*}
$$

Note that in the final step we used the property of logarithm where
$color{#4257b2}log 10=1$.

So the expression $color{#4257b2}log 50+log 2$ equals $boxed{ 2 }$

(d) We would like to simplify and evaluate the expression $color{#4257b2}log_{4} 4^{7}$. First, we note that our expression is on the form of power logarithm, so we can use the power law of logarithms where $color{#4257b2}log_{a} m^{r}=r log_{a} m$.

$$
begin{align*}
log_{4} 4^{7}&=7 log_{4} 4
\ \
&=7cdot (1)=7
end{align*}
$$

Note that in the final step we used the property of logarithm where
$color{#4257b2}log_{a} a=1$.

So the expression $color{#4257b2}log_{4} 4^{7}$ equals $boxed{ 7 }$

(e) We would like to simplify and evaluate the expression $color{#4257b2}log_{2} 224-log_{2} 7$. First, we note that our expression is a difference of logarithms, so we can use the quotient law of logarithms where $color{#4257b2}log_{a} left(dfrac{x}{y}right)=log_{a} x-log_{a} y$.

$$
begin{align*}
log_{2} 224-log_{2} 7&=log_{2}left(dfrac{224}{7}right)
\ \
&=log_{2} 32
\ \
&=log_{2} 2^{5}
end{align*}
$$

Now we note that our expression is simplified to the expression $color{#4257b2}log_{2} 2^{5}$ which is on the form of power logarithm, so we can use the power law of logarithms where $color{#4257b2}log_{a} m^{r}=r log_{a} m$.

$$
begin{align*}
log_{2} 224-log_{2} 7&=log_{2} 2^{5}
\ \
&=5 log_{2} 2
\ \
&=5cdot (1)=5
end{align*}
$$

Note that in the final step we used the property of logarithm where
$color{#4257b2}log_{a} a=1$.

So the expression $color{#4257b2}log_{2} 224-log_{2} 7$ equals $boxed{ 5 }$

(f) We would like to simplify and evaluate the expression $color{#4257b2}log sqrt{10}$. First, we know that $color{#4257b2}sqrt{x}=x^{frac{1}{2}}$, so we can replace $color{#4257b2}sqrt{10}$ in our expression by $color{#4257b2}10^{frac{1}{2}}$

$$
log sqrt{10}=log left(10right)^{frac{1}{2}}
$$

Now we note that our expression is on the form of power logarithm, so we can use the power law of logarithms where $color{#4257b2}log_{a} m^{r}=r log_{a} m$.

$$
begin{align*}
log sqrt{10}&=log left(10right)^{frac{1}{2}}
\ \
&=dfrac{1}{2} log 10
\ \
&=dfrac{1}{2} cdot (1)=dfrac{1}{2}
end{align*}
$$

Note that in the final step we used the property of logarithm where
$color{#4257b2}log 10=1$.

So the expression $color{#4257b2}log sqrt{10}$ equals $boxed{ dfrac{1}{2} }$

Large{$text{$text{color{#c34632}(a) $3$ (c) $2$ (e) $5$
\
\
Large{color{#c34632}(b) $2$ (d) $7$ (f) $dfrac{1}{2}$}$}$

We would like to describe how the graphs of $color{#4257b2}y=log_{2} (4x), y=log_{2} (8x)$ and $color{#4257b2}y=log_{2} left(dfrac{x}{2}right)$ are related to the graph of $color{#4257b2}log_{2} x$. First, we will try to find a relation between the functions $color{#4257b2}y=log_{2} (4x), y=log_{2} (8x)$ and $color{#4257b2}y=log_{2} left(dfrac{x}{2}right)$ which we can reach to the function $color{#4257b2}log_{2} x$.

We note that the $color{#4257b2}(8x)cdot left(dfrac{x}{2}right)=4 x^{2}$, so if we added the function to $color{#4257b2}log_{2}(8x)$ to the function $color{#4257b2}log_{2}left(dfrac{x}{2}right)$ the result can be calculated as follows:

$$
begin{align*}
log_{2}(8x)+log_{2}left(dfrac{x}{2}right)&=log_{2}left[(8x)cdot left(dfrac{x}{2}right)right]
\ \
&=log_{2} (4x^{2})
end{align*}
$$

Note that we used the product law of logarithms because we had a sum of logarithms where $color{#4257b2}log_{a} x+log_{a} y=log_{a} xy$.

Now we found that the result of the sum between the two functions $color{#4257b2}log_{2}(8x)$ and $color{#4257b2}log_{2}left(dfrac{x}{2}right)$ is $color{#4257b2}log_{2} (4x^{2})$, so now we will try to find relation between this result and the function $color{#4257b2}log_{2}(4x)$. We note that $color{#4257b2}dfrac{4x^{2}}{4x}=x$, so we can subtract the function $color{#4257b2}log_{2}(4x)$ from the function $color{#4257b2}log_{2} (4x^{2})$.

$$
begin{align*}
log_{2} (4x^{2})-log_{2} (4x)&=log_{2}left(dfrac{4x^{2}}{4x}right)
\ \
&=log_{2}x
end{align*}
$$

Note that we used the quotient law of logarithms because we had a difference of logarithms where $color{#4257b2}log_{a} x-log_{a} y=log_{a} left(dfrac{x}{y}right)$.

Now we prove that $color{#4257b2}log_{2}(8x)+log_{2}left(dfrac{x}{2}right)-log_{2} (4x)=log_{2}x$, so the graph of $color{#4257b2}log_{2}(8x)+log_{2}left(dfrac{x}{2}right)-log_{2} (4x)$ is the same graph of $color{#4257b2}log_{2}x$.

Now we will graph the two functions to prove graphically that the two functions have the same graph.

For $color{#4257b2}log_{2}(8x)+log_{2}left(dfrac{x}{2}right)-log_{2}(4x)$

For $color{#4257b2}log_{2}x$

We note that the two graphs are the same, so the relation is

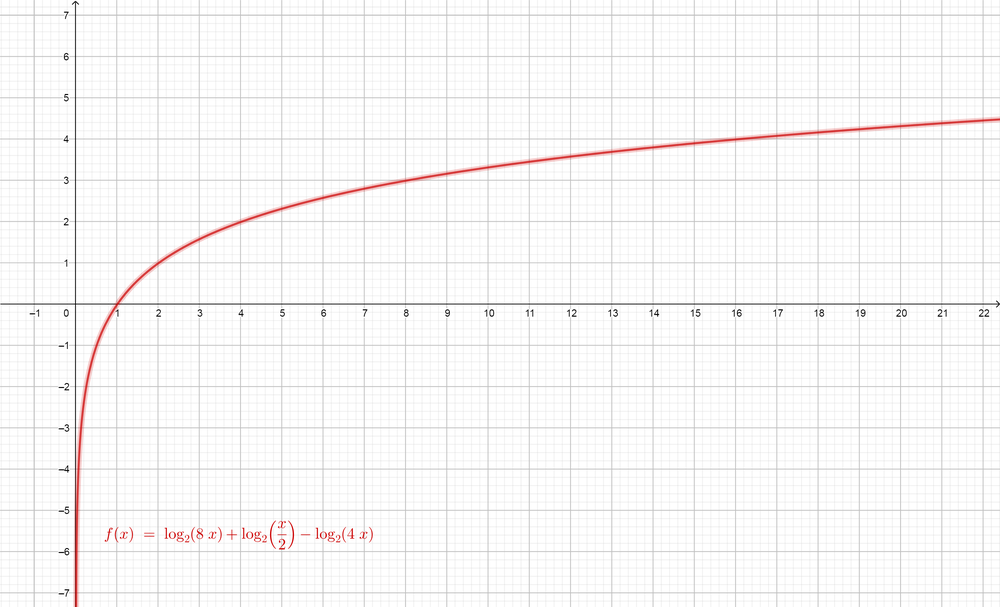
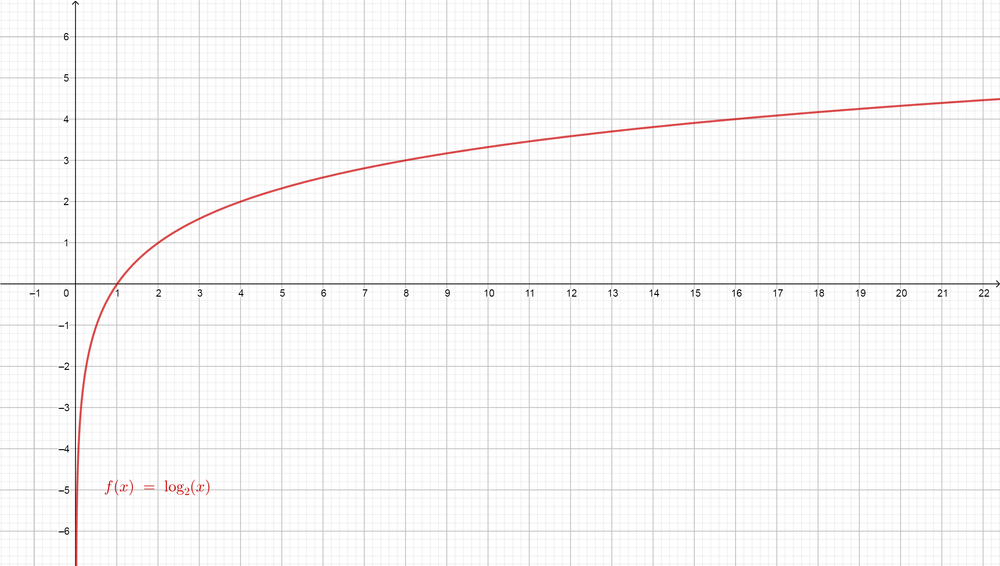
$$
color{#4257b2}log_{2}(8x)+log_{2}left(dfrac{x}{2}right)-log_{2}(4x)=log_{2}x
$$

$$
color{#c34632}log_{2}(8x)+log_{2}left(dfrac{x}{2}right)-log_{2}(4x)=log_{2}x
$$

(a) We would like to evaluate the logarithm $color{#4257b2}log_{25} 5^{3}$. First, we note that our expression is on the form of power logarithm, so we can use the power law of logarithms where $color{#4257b2}log_{a} m^{r}=r log_{a} m$.

$$
log_{25} 5^{3}=3 log_{25} 5
$$

But we know that $color{#4257b2}5=left(25right)^{frac{1}{2}}$, so we can replace $color{#4257b2}5$ from our logarithm by $color{#4257b2}(25)^{frac{1}{2}}$.

$$
log_{25} 5^{3}=3 log_{25} 5=3 log_{25} (25)^{frac{1}{2}}
$$

Note that we used this fact $color{#4257b2}5=(25)^{frac{1}{2}}$ to make the base of the logarithm equals the number inside the logarithm. Now we can use the power law of logarithms again to simplify our logarithm.

$$
begin{align*}
log_{25} 5^{3}&=3 log_{25} 5
\ \
&=3 log_{25} (25)^{frac{1}{2}}
\ \
&=3cdot left(dfrac{1}{2}right)log_{25} 25
\ \
&=dfrac{3}{2}cdot (1)=dfrac{3}{2}
end{align*}
$$

Note that in the final step we used the property of logarithm where
$color{#4257b2}log_{a} a=1$.

So the expression $color{#4257b2}log_{25} 5^{3}$ equals $boxed{ dfrac{3}{2} }$

(b) We would like to evaluate the logarithm $color{#4257b2}log_{6} 54+log_{6} 2 – log_{6} 3$. First, we note that the first two terms in our expression is a sum of logarithms, so we can use the product law of logarithms where $color{#4257b2}log_{a} x+log_{a} y=log_{a} xy$.

$$
begin{align*}
log_{6} 54+log_{6} 2 – log_{6} 3&=left(log_{6} 54+log_{6} 2right) – log_{6} 3
\ \
&=log_{6}left[(54)cdot (2)right]-log_{6} 3
\ \
&=log_{6} 108-log_{6} 3
end{align*}
$$

Now we note that our expression is simplified to a difference of logarithms, so we can use the quotient law of logarithms where $color{#4257b2}log_{a} x-log_{a} y=log_{a} left(dfrac{x}{y}right)$.

$$
begin{align*}
log_{6} 54+log_{6} 2 – log_{6} 3&=log_{6} 108-log_{6} 3
\ \
&=log_{6}left(dfrac{108}{3}right)
\ \
&=log_{6} 36
\ \
&=log_{6} 6^{2}
end{align*}
$$

Now we note that our expression is simplified to the expression $color{#4257b2}log_{6} 6^{2}$ which is on the form of power logarithm, so we can use the power law of logarithms where $color{#4257b2}log_{a} m^{r}=r log_{a} m$.

$$
begin{align*}
log_{6} 54+log_{6} 2 – log_{6} 3&=log_{6} 6^{2}
\ \
&=2 log_{6} 6
\ \
&=2cdot (1)=2
end{align*}
$$

Note that in the final step we used the property of logarithm where
$color{#4257b2}log_{a} a=1$.

So the expression $color{#4257b2}log_{6} 54+log_{6} 2 – log_{6} 3$ equals $boxed{ 2 }$

(c) We would like to evaluate the logarithm $color{#4257b2}log_{6} 6sqrt{6}$. First, we know that $color{#4257b2}sqrt{6}=left(6right)^{frac{1}{2}}$, so we can replace $color{#4257b2}sqrt{6}$ from our logarithm by $color{#4257b2}(6)^{frac{1}{2}}$.

$$
log_{6} 6sqrt{6}=log_{6}(6)cdot (6)^{frac{1}{2}}
$$

Now we can use the law of exponents where $color{#4257b2}x^{a}cdot x^{b}=x^{a+b}$.

$$
begin{align*}
log_{6} 6sqrt{6}&=log_{6}(6)cdot (6)^{frac{1}{2}}
\ \
&=log_{6} (6)^{1+frac{1}{2}}
\ \
&=log_{6} (6)^{frac{3}{2}}
end{align*}
$$

Now we note that our expression is on the form of power logarithm, so we can use the power law of logarithms where $color{#4257b2}log_{a} m^{r}=r log_{a} m$.

$$
begin{align*}
log_{6} 6sqrt{6}&=log_{6} (6)^{frac{3}{2}}
\ \
&=dfrac{3}{2} log_{6} 6
\ \
&=dfrac{3}{2}cdot (1)=dfrac{3}{2}
end{align*}
$$

Note that in the final step we used the property of logarithm where
$color{#4257b2}log_{a} a=1$.

So the expression $color{#4257b2}log_{6} 6sqrt{6}$ equals $boxed{ dfrac{3}{2} }$

(d) We would like to evaluate the logarithm $color{#4257b2}log_{2} sqrt{36} – log_{2} sqrt{72}$. First, we note that our expression is a difference of logarithms, so we can use the quotient law of logarithms where $color{#4257b2}log_{a} x-log_{a} y=log_{a} left(dfrac{x}{y}right)$.

$$
begin{align*}
log_{2} sqrt{36} – log_{2} sqrt{72}&=log_{2}left(dfrac{sqrt{36}}{sqrt{72}}right)
\ \
&=log_{2} left(sqrt{dfrac{36}{72}}right)
\ \
&=log_{2} left(sqrt{dfrac{1}{2}}right)
\ \
&=log_{2} left(dfrac{1}{sqrt{2}}right)
end{align*}
$$

But we know that $color{#4257b2}sqrt{2}=(2)^{frac{1}{2}}$, so we can replace $color{#4257b2}sqrt{2}$ from our logarithm by $color{#4257b2}(2)^{frac{1}{2}}$

$$
begin{align*}
log_{2} sqrt{36} – log_{2} sqrt{72}&=log_{2} left(dfrac{1}{sqrt{2}}right)
\ \
&=log_{2} left(dfrac{1}{(2)^{frac{1}{2}}}right)
\ \
&=log_{2} (2)^{-frac{1}{2}}
end{align*}
$$

Note that we used the property of exponents where $color{#4257b2}dfrac{1}{x^{a}}=x^{-a}$. Now we note that our expression is simplified to the expression $color{#4257b2}log_{2} 2^{-frac{1}{2}}$ which is on the form of power logarithm, so we can use the power law of logarithms where $color{#4257b2}log_{a} m^{r}=r log_{a} m$.

$$
begin{align*}
log_{2} sqrt{36} – log_{2} sqrt{72}&=log_{2} (2)^{-frac{1}{2}}
\ \
&=left(-dfrac{1}{2}right) log_{2} 2
\ \
&=left(-dfrac{1}{2}right)cdot (1)=-dfrac{1}{2}
end{align*}
$$

Note that in the final step we used the property of logarithm where
$color{#4257b2}log_{a} a=1$.

So the expression $color{#4257b2}log_{2} sqrt{36} – log_{2} sqrt{72}$ equals $boxed{ -dfrac{1}{2} }$

(e) We would like to evaluate the logarithm $color{#4257b2}log_{3} 54+log_{3} left(dfrac{3}{2}right)$. First, we note that our expression is a sum of logarithms, so we can use the product law of logarithms where $color{#4257b2}log_{a} x+log_{a} y=log_{a} xy$.

$$
begin{align*}
log_{3} 54+log_{3} left(dfrac{3}{2}right)&=log_{3}left[(54)cdot left(dfrac{3}{2}right)right]
\ \
&=log_{3} 81
\ \
&=log_{3} 3^{4}
end{align*}
$$

Now we note that our expression is simplified to the expression $color{#4257b2}log_{3} 3^{4}$ which is on the form of power logarithm, so we can use the power law of logarithms where $color{#4257b2}log_{a} m^{r}=r log_{a} m$.

$$
begin{align*}
log_{3} 54+log_{3} left(dfrac{3}{2}right)&=log_{3} 3^{4}
\ \
&=4 log_{3} 3
\ \
&=4cdot (1)=4
end{align*}
$$

Note that in the final step we used the property of logarithm where
$color{#4257b2}log_{a} a=1$.

So the expression $color{#4257b2}log_{3} 54+log_{3} left(dfrac{3}{2}right)$ equals $boxed{ 4 }$

(f) We would like to evaluate the logarithm $color{#4257b2}log_{8} 2+3log_{8} 2+dfrac{1}{2} log_{8} 16$. First, we know that $color{#4257b2}16=2^{4}$, so we can replace $color{#4257b2}16$ from our logarithm by $color{#4257b2}2^{4}$.

$$
log_{8} 2+3log_{8} 2+dfrac{1}{2} log_{8} 16=log_{8} 2+3log_{8} 2+dfrac{1}{2} log_{8} 2^{4}
$$

Now we note that the third term in our expression is on the form of power logarithm, so we can use the power law of logarithms where
$color{#4257b2}log_{a} m^{r}=r log_{a} m$.

$$
begin{align*}
log_{8} 2+3log_{8} 2+dfrac{1}{2} log_{8} 16&=log_{8} 2+3log_{8} 2+dfrac{1}{2} log_{8} 2^{4}
\ \
&=log_{8} 2+3log_{8} 2+left(dfrac{1}{2}right)cdot (4) log_{8} 2
\ \
&=log_{8} 2+3log_{8} 2+2 log_{8} 2
\ \
&=6log_{8} 2
end{align*}
$$

But we know that $color{#4257b2}2=(8)^{frac{1}{3}}$, so we can replace $color{#4257b2}2$ from our logarithm by $color{#4257b2}(8)^{frac{1}{3}}$.

$$
begin{align*}
log_{8} 2+3log_{8} 2+dfrac{1}{2} log_{8} 16&=6log_{8} 2
\ \
&=6 log_{8} (8)^{frac{1}{3}}
end{align*}
$$

Now we can use the power law of logarithms again to simplify our logarithm.

$$
begin{align*}
log_{8} 2+3log_{8} 2+dfrac{1}{2} log_{8} 16&=6 log_{8} (8)^{frac{1}{3}}
\ \
&=(6)cdot left(dfrac{1}{3}right) log_{8} 8=2log_{8} 8
\ \
&=2cdot(1)=2
end{align*}
$$

So the expression $color{#4257b2}log_{8} 2+3log_{8} 2+dfrac{1}{2} log_{8} 16$ equals $boxed{ 2 }$

Large{$text{$text{color{#c34632}(a) $dfrac{3}{2}$ (c) $dfrac{3}{2}$ (e) $4$
\
\
Large{color{#c34632}(b) $2$ (d) $-dfrac{1}{2}$ (f) $2$}$}$

(a) We would like to express $color{#4257b2}log_{b} xyz$ in terms of $color{#4257b2}log_{a}x, log_{b}y$ and $color{#4257b2}log_{b}z$. First, we note that our expression is a logarithm of product, so we can use the product law of logarithms where $color{#4257b2}log_{a} xyz=log_{a}x+log_{a}y+log_{a}z$.

$$
log_{b} xyz=log_{b}x+log_{b}y+log_{b}z
$$

So the expression $color{#4257b2}log_{b} xyz$ can be written as $boxed{ log_{b}x+log_{b}y+log_{b}z }$

(b) We would like to write the expression $color{#4257b2}log_{b} left(dfrac{z}{xy}right)$ as a sum or difference of logarithms. First, we note that our expression is a logarithm of quotient, so we can use the quotient law of logarithms where $color{#4257b2}log_{a}left(dfrac{x}{y}right)=log_{a}x-log_{a}y$.

$$
log_{b} left(dfrac{z}{xy}right)=log_{b} z-log_{b} xy
$$

Now we note that the second term in our expression is a logarithm of product, so we can use the product law of logarithms where
$color{#4257b2}log_{a} xy=log_{a}x+log_{a}y$.

$$
begin{align*}
log_{b} left(dfrac{z}{xy}right)&=log_{b} z-log_{b} xy
\ \
&=log_{b}z-left(log_{b}x+log_{b}yright)
\ \
&=log_{b}z-log_{b}x-log_{b}y
end{align*}
$$

So the expression $color{#4257b2}log_{b} left(dfrac{z}{xy}right)$ can be written as $boxed{ log_{b}z-log_{b}x-log_{b}y }$

(c) We would like to express $color{#4257b2}log_{b} x^{2}y^{3}$ in terms of $color{#4257b2}log_{a}x, log_{b}y$ and $color{#4257b2}log_{b}z$. First, we note that our expression is a logarithm of product, so we can use the product law of logarithms where $color{#4257b2}log_{a} xy=log_{a}x+log_{a}y$.

$$
log_{b} x^{2}y^{3}=log_{b}x^{2}+log_{b}y^{3}
$$

Now we note that the two terms in our expression is in the form of the power logarithm, so we can use the power law of logarithms where
$color{#4257b2}log_{a}m^{r}=r log_{a}m$.

$$
begin{align*}
log_{b} x^{2}y^{3}&=log_{b}x^{2}+log_{b}y^{3}
\ \
&=2log_{b} x+3log_{b}y
end{align*}
$$

So the expression $color{#4257b2}log_{b} x^{2}y^{3}$ can be written as $boxed{ 2log_{b} x+3log_{b}y }$

(d) We would like to express $color{#4257b2}log_{b} sqrt{x^{5} y z^{3}}$ in terms of $color{#4257b2}log_{a}x, log_{b}y$ and $color{#4257b2}log_{b}z$. First, we know that $color{#4257b2}sqrt{x}=(x)^{frac{1}{2}}$, so we can use this fact to replace $color{#4257b2}sqrt{x^{5} y z^{3}}$ in oue expression by $color{#4257b2}left(x^{5} y z^{3}right)^{frac{1}{2}}$.

$$
log_{b} sqrt{x^{5} y z^{3}}=log_{b} left(x^{5} y z^{3}right)^{frac{1}{2}}
$$

Now we note that our expression is in the form of the power logarithm, so we can use the power law of logarithms where $color{#4257b2}log_{a}m^{r}=r log_{a}m$.

$$
begin{align*}
log_{b} sqrt{x^{5} y z^{3}}&=log_{b} left(x^{5} y z^{3}right)^{frac{1}{2}}
\ \
&=dfrac{1}{2}log_{b} x^{5} y z^{3}
end{align*}
$$

Now we note that our expression is a logarithm of product, so we can use the product law of logarithms where $color{#4257b2}log_{a} xyz=log_{a}x+log_{a}y+log_{a}z$.

$$
begin{align*}
log_{b} sqrt{x^{5} y z^{3}}&=dfrac{1}{2}log_{b} x^{5} y z^{3}
\ \
&=dfrac{1}{2}left(log_{b} x^{5}+log_{b} y+log_{b} z^{3}right)
end{align*}
$$

Now we note that the first and third terms in our expression is in the form of the power logarithm, so we can use the power law of logarithms again where $color{#4257b2}log_{a}m^{r}=r log_{a}m$.

$$
begin{align*}
log_{b} sqrt{x^{5} y z^{3}}&=dfrac{1}{2}left(log_{b} x^{5}+log_{b} y+log_{b} z^{3}right)
\ \
&=dfrac{1}{2}left(5log_{b} x+log_{b} y+3log_{b} zright)
\ \
&=dfrac{5}{2} log_{b} x+dfrac{1}{2} log_{b} y+dfrac{3}{2} log_{b} z
end{align*}
$$

So the expression $color{#4257b2}log_{b} sqrt{x^{5} y z^{3}}$ can be written as $boxed{ dfrac{5}{2} log_{b} x+dfrac{1}{2} log_{b} y+dfrac{3}{2} log_{b} z }$

$$
text{color{#c34632}(a) $log_{b}x+log_{b}y+log_{b}z$ (c) $2log_{b} x+3log_{b}y$
\
\
\
color{#c34632}(b) $log_{b}z-log_{b}x-log_{b}y$ (d) $dfrac{5}{2} log_{b} x+dfrac{1}{2} log_{b} y+dfrac{3}{2} log_{b} z$}
$$

We would like to explain why $color{#4257b2}log_{5} 3+log_{5} left(dfrac{1}{3}right)=0$. First, we will simplify the left side and evaluate it to see if it is equals zero or not.

We note that the left side $color{#4257b2}log_{5} 3+log_{5} left(dfrac{1}{3}right)$ is a sum of logarithms, so we can use the product law of logarithms where $color{#4257b2}log_{a} x+log_{a} y=log_{a} xy$.

$$
begin{align*}
log_{5} 3+log_{5} left(dfrac{1}{3}right)&=log_{5}left[(3)cdot left(dfrac{1}{3}right)right]
\ \
&=log_{5}left[(cancel{3})cdot left(dfrac{1}{cancel{3}}right)right]
\ \
&=log_{5} 1
end{align*}
$$

But we know that $color{#4257b2}5^{0}=1$, so we can replace $color{#4257b2}1$ from the our expression by $color{#4257b2}5^{0}$ to simplify.

$$
begin{align*}
log_{5} 3+log_{5} left(dfrac{1}{3}right)&=log_{5} 1
\ \
&=log_{5} 5^{0}
end{align*}
$$

Now we note that the left side is simplified to the expression $color{#4257b2}log_{5} 5^{0}$ which is on the form of power logarithm, so we can use the power law of logarithms where $color{#4257b2}log_{a} m^{r}=r log_{a} m$.

$$
begin{align*}
log_{5} 3+log_{5} left(dfrac{1}{3}right)&=log_{5} 5^{0}
\ \
&=(0)cdot log_{5} 5
\ \
&=0cdot (1)=0
end{align*}
$$

Note that in the final step we used the property of logarithm where
$color{#4257b2}log_{a} a=1$.

So we proved that the left side equals zero and this is the explanation why $color{#4257b2}log_{5} 3+log_{5} left(dfrac{1}{3}right)=0$.

Large{$text{color{#c34632}$log_{5} 3+log_{5}left(dfrac{1}{3}right)=0$}$

(a) We would like to write the expression $color{#4257b2}3log_{5} 2+log_{5} 7$ as a single logarithm. First, we note that the first term in our expression is a single logarithm which multiplied by a number, so we can use the power law of logarithms where $color{#4257b2}r log_{a} m=log_{a} m^{r}$.

$$
begin{align*}
3log_{5} 2+log_{5} 7&=log_{5} 2^{3}+log_{5} 7
\ \
&=log_{5} 8+log_{5} 7
end{align*}
$$

Now we note that our expression is a sum of logarithms, so we can use the product law of logarithms where $color{#4257b2}log_{a} x+log_{a} y=log_{a} xy$.

$$
begin{align*}
3log_{5} 2+log_{5} 7&=log_{5} 2^{3}+log_{5} 7
\ \
&=log_{5} 8+log_{5} 7
\ \
&=log_{5} left[left(8right)cdot left(7right)right]
\ \
&=log_{5} 56
end{align*}
$$

So the expression $color{#4257b2}3log_{5} 2+log_{5} 7$ can be simplified to the single logarithm $boxed{ log_{5} 56 }$

(b) We would like to write the expression $color{#4257b2}2log_{3} 8-5log_{3} 2$ as a single logarithm. First, we know that $color{#4257b2}8=2^{3}$, so we can replace $color{#4257b2}8$ from our expression by $color{#4257b2}2^{3}$.

$$
2log_{3} 8-5log_{3} 2=2log_{3} 2^{3}-5log_{3} 2
$$

Now we note that the first term in our expression is on the form of the power logarithm, so we can use the power law of logarithms where
$color{#4257b2}log_{a} m^{r}=r log_{a} m$.

$$
begin{align*}
2log_{3} 8-5log_{3} 2&=2log_{3} 2^{3}-5log_{3} 2
\ \
&=(2)cdot (3)log_{3} 2-5log_{3} 2
\ \
&=6log_{3} 2-5log_{3} 2
\ \
&=log_{3} 2
end{align*}
$$

So the expression $color{#4257b2}2log_{3} 8-5log_{3} 2$ can be simplified to the single logarithm $boxed{ log_{3} 2 }$

(c) We would like to write the expression $color{#4257b2}2log_{2} 3+log_{2} 5$ as a single logarithm. First, we note that the first term in our expression is a single logarithm which multiplied by a number, so we can use the power law of logarithms where $color{#4257b2}r log_{a} m=log_{a} m^{r}$.

$$
begin{align*}
2log_{2} 3+log_{2} 5&=log_{2} 3^{2}+log_{2} 5
\ \
&=log_{2} 9+log_{2} 5
end{align*}
$$

Now we note that our expression is a sum of logarithms, so we can use the product law of logarithms where $color{#4257b2}log_{a} x+log_{a} y=log_{a} xy$.

$$
begin{align*}
2log_{2} 3+log_{2} 5&=log_{2} 3^{2}+log_{2} 5
\ \
&=log_{2} 9+log_{2} 5
\ \
&=log_{2} left[(9)cdot (5)right]
\ \
&=log_{2} 45
end{align*}
$$

So the expression $color{#4257b2}2log_{2} 3+log_{2} 5$ can be simplified to the single logarithm $boxed{ log_{2} 45 }$

(d) We would like to write the expression $color{#4257b2}log_{3} 12+log_{3} 2 – log_{3} 6$ as a single logarithm. First, we note that the first two terms in our expression is a sum of logarithms, so we can use the product law of logarithms where
$color{#4257b2}log_{a} x+log_{a} y=log_{a} xy$.

$$
begin{align*}
log_{3} 12+log_{3} 2 – log_{3} 6&=left(log_{3} 12+log_{3} 2right) – log_{3} 6
\ \
&=log_{3}left[(12)cdot (2)right]-log_{3} 6
\ \
&=log_{3} 24-log_{3} 6
end{align*}
$$

Now we note that our expression is simplified to a difference of logarithms, so we can use the quotient law of logarithms where $color{#4257b2}log_{a} x-log_{a} y=log_{a} left(dfrac{x}{y}right)$.

$$
begin{align*}
log_{3} 12+log_{3} 2 – log_{3} 6&=log_{3} 24-log_{3} 6
\ \
&=log_{3}left(dfrac{24}{6}right)
\ \
&=log_{3} 4
end{align*}
$$

So the expression $color{#4257b2}log_{3} 12+log_{3} 2 – log_{3} 6$ can be simplified to the single logarithm $boxed{ log_{3} 4 }$

(e) We would like to write the expression $color{#4257b2}log_{4} 3+dfrac{1}{2} log_{4} 8 – log_{4} 2$ as a single logarithm. First, we know that $color{#4257b2}8=2^{3}$, so we can replace $color{#4257b2}8$ from our expression by $color{#4257b2}2^{3}$.

$$
log_{4} 3+dfrac{1}{2} log_{4} 8 – log_{4} 2=log_{4} 3+dfrac{1}{2} log_{4} 2^{3} – log_{4} 2
$$

Now we note that the second term in our expression is on the form of the power logarithm, so we can use the power law of logarithms where
$color{#4257b2}r log_{a} m=log_{a} m^{r}$.

$$
begin{align*}
log_{4} 3+dfrac{1}{2} log_{4} 8 – log_{4} 2&=log_{4} 3+dfrac{1}{2} log_{4} 2^{3} – log_{4} 2
\ \
&=log_{4} 3+left(dfrac{1}{2}right)cdot (3) log_{4} 2 – log_{4} 2
\ \
&=log_{4} 3+dfrac{3}{2} log_{4} 2 – log_{4} 2
\ \
&=log_{4} 3+dfrac{1}{2} log_{4} 2
end{align*}
$$

Now we note that the second term in our expression is a single logarithm which is multiplied by a number, so we can use the power law of logarithms where
$color{#4257b2}r log_{a} m=log_{a} m^{r}$.

$$
begin{align*}
log_{4} 3+dfrac{1}{2} log_{4} 8 – log_{4} 2&=log_{4} 3+dfrac{1}{2} log_{4} 2
\ \
&=log_{4} 3+log_{4} (2)^{frac{1}{2}}
\ \
&=log_{4} 3+log_{4} sqrt{2}
end{align*}
$$

Now we note that our expression is a sum of logarithms, so we can use the product law of logarithms where
$color{#4257b2}log_{a} x+log_{a} y=log_{a} xy$.

$$
begin{align*}
log_{4} 3+dfrac{1}{2} log_{4} 8 – log_{4} 2&=log_{4} 3+log_{4} sqrt{2}
\ \
&=log_{4}left[(3)cdot left(sqrt{2}right)right]
\ \
&=log_{4} 3sqrt{2}
end{align*}
$$

So the expression $color{#4257b2}log_{4} 3+dfrac{1}{2} log_{4} 8 – log_{4} 2$ can be simplified to the single logarithm $boxed{ log_{4} 3sqrt{2} }$

(f) We would like to write the expression $color{#4257b2}2log 8+log 9-log 36$ as a single logarithm. First, we note that the first term in our expression is a single logarithm which multiplied by a number, so we can use the power law of logarithms where $color{#4257b2}r log_{a} m=log_{a} m^{r}$.

$$
begin{align*}
2log 8+log 9-log 36&=log 8^{2}+log 9-log 36
\ \
&=log 64+log 9-log 36
end{align*}
$$

Now we note that the first two terms in our expression is a sum of logarithms, so we can use the product law of logarithms where $color{#4257b2}log_{a} x+log_{a} y=log_{a} xy$.

$$
begin{align*}
2log 8+log 9-log 36&=log 64+log 9-log 36
\ \
&=left(log 64+log 9right)-log 36
\ \
&=log left[left(64right)cdot left(9right)right]-log 36
\ \
&=log 576-log 36
end{align*}
$$

Now we note that our expression is a difference of logarithms, so we can use the quotient law of logarithms where $color{#4257b2}log_{a} x-log_{a} y=log_{a} left(dfrac{x}{y}right)$.

$$
begin{align*}
2log 8+log 9-log 36&=log 576-log 36
\ \
&=log left(dfrac{576}{36}right)
\ \
&=log 16
end{align*}
$$

So the expression $color{#4257b2}2log 8+log 9-log 36$ can be simplified to the single logarithm $boxed{ log 16 }$

Large{$text{$text{color{#c34632}(a) $log_{5} 56$ (c) $log_{2} 45$ (e) $log_{4} 3sqrt{2}$
\
\
Large{color{#c34632}(b) $log_{3} 2$ (d) $log_{3} 4$ (f) $log 16$}$}$

(a) We would like to express each side of the equation $color{#4257b2}log_{2} x=2log_{2} 7+log_{2} 5$ as a single logarithm and then compare the two sides to solve the equation. First, we note that the left side is a single logarithm, so we will simplify the right side to make to a single logarithm. We note that the first term in the right side of our equation is a single logarithm which multiplied by a number, so we can use the power law of logarithms where $color{#4257b2}r log_{a} m=log_{a} m^{r}$.

$$
begin{align*}
text{The right side}&=2log_{2} 7+log_{2} 5
\ \
&=log_{2} 7^{2}+log_{2} 5
\ \
&=log_{2} 49+log_{2} 5
end{align*}
$$

Now we note that the right side is a sum of logarithms, so we can use the product law of logarithms where $color{#4257b2}log_{a} x+log_{a} y=log_{a} xy$.

$$
begin{align*}
text{The right side}&=log_{2} 49+log_{2} 5
\ \
&=log_{2}left[(49)cdot (5)right]
\ \
&=log_{2} 245
end{align*}
$$

So the right side can be simplified to the single logarithm $boxed{ log_{2} 245 }$

Now we can compare the two sides of our equation to solve.

$$
log_{2} x=2log_{2} 7+log_{2} 5
$$

$$
log_{2} x=log_{2} 245
$$

We note that each side of our equation is a single logarithm with base $color{#4257b2}2$, so the value of $color{#4257b2}x$ must equals $color{#4257b2}245$ to make the equation true.

So the solution of the equation $color{#4257b2}log_{2} x=2log_{2} 7+log_{2} 5$ is $boxed{ x=245 }$

(b) We would like to express each side of the equation $color{#4257b2}log x=2log 4+3log 3$ as a single logarithm and then compare the two sides to solve the equation. First, we note that the left side is a single logarithm, so we will simplify the right side to make to a single logarithm. We note that each of terms in the right side of our equation is a single logarithm which multiplied by a number, so we can use the power law of logarithms where $color{#4257b2}r log_{a} m=log_{a} m^{r}$.

$$
begin{align*}
text{The right side}&=2log 4+3log 3
\ \
&=log 4^{2}+log 3^{3}
\ \
&=log 16+log 27
end{align*}
$$

Now we note that the right side is a sum of logarithms, so we can use the product law of logarithms where $color{#4257b2}log_{a} x+log_{a} y=log_{a} xy$.

$$
begin{align*}
text{The right side}&=log 16+log 27
\ \
&=log left[(16)cdot (27)right]
\ \
&=log 432
end{align*}
$$

So the right side can be simplified to the single logarithm $boxed{ log 432 }$

Now we can compare the two sides of our equation to solve.

$$
log x=2log 4+3log 3
$$

$$
log x=log 432
$$

We note that each side of our equation is a single logarithm with base $color{#4257b2}10$, so the value of $color{#4257b2}x$ must equals $color{#4257b2}432$ to make the equation true.

So the solution of the equation $color{#4257b2}log x=2log 4+3log 3$ is $boxed{ x=432 }$

(c) We would like to express each side of the equation
$color{#4257b2}log_{4} x+log_{4} 12=log_{4} 48$ as a single logarithm and then compare the two sides to solve the equation. First, we note that the the left side is a sum of logarithms, so we can use the product law of logarithms where
$color{#4257b2}log_{a} x+log_{a} y=log_{a} xy$.

$$
begin{align*}
text{The left side}&=log_{4} x+log_{4} 12
\ \
&=log_{4} left[(x)cdot (12)right]
\ \
&=log_{4} (12x)
end{align*}
$$

So the left side can be simplified to the single logarithm $boxed{ log_{4} (12x) }$

Now we can compare the two sides of our equation to solve.

$$
log_{4} x+log_{4} 12=log_{4} 48
$$

$$
log_{4} (12x)=log_{4} 48
$$

We note that each side of our equation is a single logarithm with base $color{#4257b2}4$, so the value of $color{#4257b2}12x$ must equals $color{#4257b2}48$ to make the equation true.

$$
12x=48
$$

Now we can divide the two sides by $12$

$$
dfrac{12x}{12}=dfrac{48}{12}
$$

$$
x=4
$$

So the solution of the equation $color{#4257b2}log_{4} x+log_{4} 12=log_{4} 48$ is $boxed{ x=4 }$

(d) We would like to express each side of the equation
$color{#4257b2}log_{7} x=2log_{7} 25-3log_{7} 5$ as a single logarithm and then compare the two sides to solve the equation. First, we note that the left side is a single logarithm, so we will simplify the right side to make to a single logarithm. We note that each of terms in the right side of our equation is a single logarithm which multiplied by a number, so we can use the power law of logarithms where $color{#4257b2}r log_{a} m=log_{a} m^{r}$.

$$
begin{align*}
text{The right side}&=2log_{7} 25-3log_{7} 5
\ \
&=log_{7} 25^{2}-log_{7} 5^{3}
\ \
&=log_{7} 625-log_{7} 125
end{align*}
$$

Now we note that the right side is a difference of logarithms, so we can use the quotient law of logarithms where $color{#4257b2}log_{a} x-log_{a} y=log_{a} left(dfrac{x}{y}right)$.

$$
begin{align*}
text{The right side}&=log_{7} 625-log_{7} 125
\ \
&=log_{7} left(dfrac{625}{125}right)
\ \
&=log_{7} 5
end{align*}
$$

So the right side can be simplified to the single logarithm $boxed{ log_{7} 5 }$

Now we can compare the two sides of our equation to solve.

$$
log_{7} x=2log_{7} 25-3log_{7} 5
$$

$$
log_{7} x=log_{7} 5
$$

We note that each side of our equation is a single logarithm with base $color{#4257b2}7$, so the value of $color{#4257b2}x$ must equals $color{#4257b2}5$ to make the equation true.

So the solution of the equation $color{#4257b2}log_{7} x=2log_{7} 25-3log_{7} 5$ is $boxed{ x=5 }$

(e) We would like to express each side of the equation
$color{#4257b2}log_{3} x=2log_{3} 10-log_{3} 25$ as a single logarithm and then compare the two sides to solve the equation. First, we note that the left side is a single logarithm, so we will simplify the right side to make to a single logarithm. We note that the first term in the right side of our equation is a single logarithm which multiplied by a number, so we can use the power law of logarithms where $color{#4257b2}r log_{a} m=log_{a} m^{r}$.

$$
begin{align*}
text{The right side}&=log_{3} x=2log_{3} 10-log_{3} 25
\ \
&=log_{3} 10^{2}-log_{3} 25
\ \
&=log_{3} 100-log_{3} 25
end{align*}
$$

Now we note that the right side is a difference of logarithms, so we can use the quotient law of logarithms where $color{#4257b2}log_{a} x-log_{a} y=log_{a} left(dfrac{x}{y}right)$.

$$
begin{align*}
text{The right side}&=log_{3} 100-log_{3} 25
\ \
&=log_{3}left(dfrac{100}{25}right)
\ \
&=log_{3} 4
end{align*}
$$

So the right side can be simplified to the single logarithm $boxed{ log_{3} 4 }$

Now we can compare the two sides of our equation to solve.

$$
log_{3} x=2log_{3} 10-log_{3} 25
$$

$$
log_{3} x=log_{3} 4
$$

We note that each side of our equation is a single logarithm with base $color{#4257b2}3$, so the value of $color{#4257b2}x$ must equals $color{#4257b2}4$ to make the equation true.

So the solution of the equation $color{#4257b2}log_{3} x=2log_{3} 10-log_{3} 25$ is $boxed{ x=4 }$

(f) We would like to express each side of the equation
$color{#4257b2}log_{5} x-log_{5} 8=log_{5} 6+3log_{5} 2$ as a single logarithm and then compare the two sides to solve the equation. First, we will simplify the left side and then simplify the right side to make them as a single logarithm. We note that the left side of our equation is $color{#4257b2}log_{5}x-log_{5}8$ which is a difference of logarithms, so we can use the quotient law of logarithms where $color{#4257b2}log_{a} x-log_{a} y=log_{a} left(dfrac{x}{y}right)$.

$$
begin{align*}
text{The left side}&=log_{5} x-log_{5} 8
\ \
&=log_{5}left(dfrac{x}{8}right)
end{align*}
$$

So the left side can be simplified to the single logarithm $boxed{ log_{5}left(dfrac{x}{8}right) }$

Now we will simplify the right side. We note that the right side
$color{#4257b2}log_{5} 6+3log_{5} 2$ where the second term in the right side is a single logarithm which multiplied by a number, so we can use the power law of logarithms where $color{#4257b2}r log_{a} m=log_{a} m^{r}$.

$$
begin{align*}
text{The right side}&=log_{5} 6+3log_{5} 2
\ \
&=log_{5} 6+log_{5} 2^{3}
\ \
&=log_{5} 6+log_{5} 8
end{align*}
$$

Now we note that the right side is a sum of logarithms, so we can use the product law of logarithms where $color{#4257b2}log_{a} x+log_{a} y=log_{a} xy$.

$$
begin{align*}
text{The right side}&=log_{5} 6+log_{5} 8
\ \
&=log_{5}left[(6)cdot (8)right]
\ \
&=log_{5} 48
end{align*}
$$

So the right side can be simplified to the single logarithm $boxed{ log_{5} 48 }$

Now we can compare the two sides of our equation to solve.

$$
log_{5} x-log_{5} 8=log_{5} 6+3log_{5} 2
$$

$$
log_{5}left(dfrac{x}{8}right)=log_{5} 48
$$

We note that each side of our equation is a single logarithm with base $color{#4257b2}5$, so the value of $color{#4257b2}dfrac{x}{8}$ must equals $color{#4257b2}48$ to make the equation true.

$$
dfrac{x}{8}=48
$$

Now we can multiply the two sides by $color{#4257b2}8$ to find the value of $color{#4257b2}x$.

$$
(8)cdot left(dfrac{x}{8}right)=(48)cdot (8)
$$

$$
cancel{(8)}cdot left(dfrac{x}{cancel{8}}right)=384
$$

$$
x=384
$$

So the solution of the equation $color{#4257b2}log_{5} x-log_{5} 8=log_{5} 6+3log_{5} 2$ is $boxed{ x=384 }$

Large{$text{$text{color{#c34632}(a) $x=245$ (c) $x=4$ (e) $x=4$
\
\
Large{color{#c34632}(b) $x=432$ (d) $x=5$ (f) $x=384$}$}$

(a) We would like to write the expression $color{#4257b2}log_{2} x+log_{2} y+log_{2} z$ as a single logarithm. First, we note that our expression is a sum of logarithms, so we can use the product law of logarithms where
$color{#4257b2}log_{a} x+log_{a} y+log_{a} z=log_{a} xyz$.

$$
log_{2} x+log_{2} y+log_{2} z=log_{2} xyz
$$

So the expression $color{#4257b2}log_{2} x+log_{2} y+log_{2} z$ can be simplified to the single logarithm $boxed{ log_{2} xyz }$

(b) We would like to write the expression $color{#4257b2}log_{5} u-log_{5} v + log_{5} w$ as a single logarithm. First, we note that the first two terms in our expression is a difference of logarithms, so we can use the quotient law of logarithms where
$color{#4257b2}log_{a} x-log_{a} y=log_{a} left(dfrac{x}{y}right)$.

$$
begin{align*}
log_{5} u-log_{5} v + log_{5} w&=left(log_{5} u-log_{5} vright) + log_{5} w
\ \
&=log_{5}left(dfrac{u}{v}right)+log_{5} w
end{align*}
$$

Now we note that our expression is simplified to a sum of logarithms, so we can use the product law of logarithms where $color{#4257b2}log_{a} x+log_{a} y=log_{a} xy$.

$$
begin{align*}
log_{5} u-log_{5} v + log_{5} w&=log_{5}left(dfrac{u}{v}right)+log_{5} w
\ \
&=log_{5}left[left(dfrac{u}{v}right)cdot (w)right]
\ \
&=log_{5} left(dfrac{uw}{v}right)
end{align*}
$$

So the expression $color{#4257b2}log_{5} u-log_{5} v + log_{5} w$ can be simplified to the single logarithm $boxed{ log_{5} left(dfrac{uw}{v}right) }$

(c) We would like to write the expression $color{#4257b2}log_{6} a-left(log_{6} b + log_{6} cright)$ as a single logarithm. First, we note that the second and third terms in our expression each of them is a sum of logarithms, so we can use the product law of logarithms where
$color{#4257b2}log_{a} x+log_{a} y=log_{a} xy$.

$$
begin{align*}
log_{6} a-left(log_{6} b + log_{6} cright)&=log_{6} a-log_{6}left[(b)cdot (c)right]
\ \
&=log_{6} a-log_{6} bc
end{align*}
$$

Now we note that our expression is simplified to a difference of logarithms, so we can use the quotient law of logarithms where $color{#4257b2}log_{a} x-log_{a} y=log_{a} left(dfrac{x}{y}right)$.

$$
begin{align*}
log_{6} a-left(log_{6} b + log_{6} cright)&=log_{6} a-log_{6} bc
\ \
&=log_{6}left(dfrac{a}{bc}right)
end{align*}
$$

So the expression $color{#4257b2}log_{6} a-left(log_{6} b + log_{6} cright)$ can be simplified to the single logarithm $boxed{ log_{6}left(dfrac{a}{bc}right) }$

(d) We would like to write the expression $color{#4257b2}log_{2} x^{2}-log_{2} xy + log_{2} y^{2}$ as a single logarithm. First, we note that the first two terms in our expression is a difference of logarithms, so we can use the quotient law of logarithms where $color{#4257b2}log_{a} x-log_{a} y=log_{a} left(dfrac{x}{y}right)$.

$$
begin{align*}
log_{2} x^{2}-log_{2} xy + log_{2} y^{2}&=left(log_{2} x^{2}-log_{2} xyright) + log_{2} y^{2}
\ \
&=log_{2}left(dfrac{x^{2}}{xy}right)+log_{2} y^{2}
\ \
&=log_{2}left(dfrac{x}{y}right)+log_{2} y^{2}
end{align*}
$$

Now we note that our expression is simplified to a sum of logarithms, so we can use the product law of logarithms where $color{#4257b2}log_{a} x+log_{a} y=log_{a} xy$.

$$
begin{align*}
log_{2} x^{2}-log_{2} xy + log_{2} y^{2}&=log_{2}left(dfrac{x}{y}right)+log_{2} y^{2}
\ \
&=log_{2}left[left(dfrac{x}{y}right)cdot left(y^{2}right)right]
\ \
&=log_{2}left[left(dfrac{x}{cancel{y}}right)cdot left(y^{cancel{2}}right)right]
\ \
&=log_{2} xy
end{align*}
$$

So the expression $color{#4257b2}log_{2} x^{2}-log_{2} xy + log_{2} y^{2}$ can be simplified to the single logarithm $boxed{ log_{2} xy }$

(e) We would like to write the expression $color{#4257b2}1+log_{3} x^{2}$ as a single logarithm. First, we know from the properties of logarithms that $color{#4257b2}log_{a} a=1$, so we can say that $color{#4257b2}log_{3} 3=1$ and we can use this fact to replace $color{#4257b2}1$ from our expression by $color{#4257b2}log_{3} 3$.

$$
1+log_{3} x^{2}=log_{3} 3+log_{3} x^{2}
$$

Note that we used this fact to make the two terms in our expression have the same base. Now we note that our expression is a sum of logarithms, so we can use the product law of logarithms where
$color{#4257b2}log_{a} x+log_{a} y+log_{a} z=log_{a} xyz$.

$$
begin{align*}
1+log_{3} x^{2}&=log_{3} 3+log_{3} x^{2}
\ \
&=log_{3}left[(3)cdot left(x^{2}right)right]
\ \
&=log_{3} 3x^{2}
end{align*}
$$

So the expression $color{#4257b2}1+log_{3} x^{2}$ can be simplified to the single logarithm $boxed{ log_{3} 3x^{2} }$

(f) We would like to write the expression $color{#4257b2}3log_{4} x+2log_{4} x-log_{4} y$ as a single logarithm. First, we note that the first two terms in our expression each of them is a single logarithm which multiplied by a number, so we can use the power law of logarithms where $color{#4257b2}r log_{a} m=log_{a} m^{r}$.

$$
3log_{4} x+2log_{4} x-log_{4} y=log_{4} x^{3}+log_{4} x^{2}-log_{4} y
$$

Now we note that the first two terms in our expression is a sum of logarithms, so we can use the product law of logarithms where $color{#4257b2}log_{a} x+log_{a} y=log_{a} xy$.

$$
begin{align*}
3log_{4} x+2log_{4} x-log_{4} y&=log_{4} x^{3}+log_{4} x^{2}-log_{4} y
\ \
&=left(log_{4} x^{3}+log_{4} x^{2}right)-log_{4} y
\ \
&=log_{4} left[left(x^{3}right)cdot left(x^{2}right)right]-log_{4} y
\ \
&=log_{4} x^{5}-log_{4} y
end{align*}
$$

Now we note that our expression is a difference of logarithms, so we can use the quotient law of logarithms where $color{#4257b2}log_{a} x-log_{a} y=log_{a} left(dfrac{x}{y}right)$.

$$
begin{align*}
3log_{4} x+2log_{4} x-log_{4} y&=log_{4} x^{5}-log_{4} y
\ \
&=log_{4} left(dfrac{x^{5}}{y}right)
end{align*}
$$

So the expression $color{#4257b2}3log_{4} x+2log_{4} x-log_{4} y$ can be simplified to the single logarithm $boxed{ log_{4} left(dfrac{x^{5}}{y}right) }$

Large{$text{$text{color{#c34632}(a) $log_{2} xyz$ (c) $log_{6} left(dfrac{a}{bc}right)$ (e) $log_{3} 3x^{2}$
\
\
Large{color{#c34632}(b) $log_{5} left(dfrac{uw}{v}right)$ (d) $log_{2} xy$ (f) $log_{4} left(dfrac{x^{5}}{y}right)$}$}$

We would like to write the expression $color{#4257b2}dfrac{1}{2} log_{a} x+dfrac{1}{2} log_{a} y-dfrac{3}{4} log_{a} z$ as a single logarithm. First, we note that all terms in our expression each of them is a single logarithm which multiplied by a number, so we can use the power law of logarithms where $color{#4257b2}r log_{a} m=log_{a} m^{r}$.

$$
begin{align*}
dfrac{1}{2} log_{a} x+dfrac{1}{2} log_{a} y-dfrac{3}{4} log_{a} z&=log_{a} left(xright)^{frac{1}{2}}+log_{a} left(yright)^{frac{1}{2}}-log_{a} left(zright)^{frac{3}{4}}
\ \
&=log_{a} sqrt{x}+log_{a} sqrt{y}-log_{a} sqrt[4]{z^{3}}
end{align*}
$$

Note that $color{#4257b2}(m)^{frac{a}{b}}=sqrt[b]{m^{a}}$, so we replace $color{#4257b2}left(xright)^{frac{1}{2}}, left(yright)^{frac{1}{2}}$ and $color{#4257b2}left(zright)^{frac{3}{4}}$ in oue expression by $color{#4257b2}sqrt{x}, sqrt{y}$ and $color{#4257b2}sqrt[4]{z^{3}}$ respectively. Now we note that the first two terms in our expression is a sum of logarithms, so we can use the product law of logarithms where $color{#4257b2}log_{a} x+log_{a} y=log_{a} xy$.

$$
begin{align*}
dfrac{1}{2} log_{a} x+dfrac{1}{2} log_{a} y-dfrac{3}{4} log_{a} z&=log_{a} sqrt{x}+log_{a} sqrt{y}-log_{a} sqrt[4]{z^{3}}
\ \
&=left(log_{a} sqrt{x}+log_{a} sqrt{y}right)-log_{a} sqrt[4]{z^{3}}
\ \
&=log_{a} left[left(sqrt{x}right)cdot left(sqrt{y}right)right]-log_{a} sqrt[4]{z^{3}}
\ \
&=log_{a} sqrt{xy}-log_{a} sqrt[4]{z^{3}}
end{align*}
$$

Now we note that our expression is a difference of logarithms, so we can use the quotient law of logarithms where $color{#4257b2}log_{a} x-log_{a} y=log_{a} left(dfrac{x}{y}right)$.

$$
begin{align*}
dfrac{1}{2} log_{a} x+dfrac{1}{2} log_{a} y-dfrac{3}{4} log_{a} z&=log_{a} sqrt{xy}-log_{a} sqrt[4]{z^{3}}
\ \
&=log_{a} left(dfrac{sqrt{xy}}{sqrt[4]{z^{3}}}right)
end{align*}
$$

So the expression $color{#4257b2}dfrac{1}{2} log_{a} x+dfrac{1}{2} log_{a} y-dfrac{3}{4} log_{a} z$ can be simplified to the single logarithm $boxed{ log_{a} left(dfrac{sqrt{xy}}{sqrt[4]{z^{3}}}right) }$

Large{$text{color{#c34632}$log_{a} left(dfrac{sqrt{xy}}{sqrt[4]{z^{3}}}right)$}$

We would like to describe the transformations that take the graph
$color{#4257b2}f(x)=log_{2}x$ to the graph $color{#4257b2}g(x)=log_{2}8x^{3}$. First, we note that the graph $color{#4257b2}g(x)=log_{2}8x^{3}$ contains $color{#4257b2}x^{3}$, so the first step is to multiply the function $color{#4257b2}f(x)=log_{2}x$ by $color{#4257b2}3$ and then use the property of power law of logarithms where $color{#4257b2}r log_{a} m=log_{a} m^{r}$

$$
f(x)=log_{2}x
$$

$$
3 f(x)=3log_{2}x
$$

$$
3f(x)=log_{2} x^{3}
$$

Now we note that the function $color{#4257b2}3 f(x)$ is the same of the function $color{#4257b2}g(x)$ but the only difference that in the function $color{#4257b2}g(x)$ there is $color{#4257b2}8$ which is multiplied by $color{#4257b2}x^{3}$, so we can add $color{#4257b2}log_{2} 8$ to the function $color{#4257b2}3 f(x)$ and then use the property of the product law of logarithms where $color{#4257b2}log_{a} x+log_{a} y=log_{a} xy$ to make the two functions equals each others.

$$
3 f(x)=log_{2} x^{3}
$$

$$
3 f(x)+log_{2} 8=log_{2} x^{3}+log_{2} 8
$$

$$
3 f(x)=log_{2}left[(x^{3})cdot (8)right]
$$

$$
3 f(x)+log_{2} 8=log_{2} left(8x^{3}right)
$$

But we know that $color{#4257b2}8=2^{3}$, so we can replace $color{#4257b2}8$ from our function by $color{#4257b2}2^{3}$.

$$
3 f(x)+log_{2} 2^{3}=log_{2}left(8x^{3}right)
$$

Now we note that the left side in our function is on the form of the power logarithms, so we can use the power law of logarithms where
$color{#4257b2}log_{a} m^{r}=r log_{a} m$.

$$
3 f(x)+log_{2} 2^{3}=log_{2}left(8x^{3}right)
$$

$$
3 f(x)+3 log_{2} 2=log_{2}left(8x^{3}right)
$$

$$
3 f(x)+3=log_{2}left(8x^{3}right)
$$

Note that in the final step we used the property of logarithms $color{#4257b2}log_{a} a=1$. Now we note that the function $color{#4257b2}3 f(x)+3=log_{2}left(8x^{3}right)$ which equals the function $color{#4257b2}g(x)$, so the transformation that takes the function $color{#4257b2}f(x)$ to the function $color{#4257b2}g(x)$ is $boxed{ 3 f(x)+3 }$

$$
color{#c34632}3 f(x)+3=g(x)
$$

The laws of logarithms are as follows, where $a>0$, $x>0$ and $y>0$

**Product law**
$$log_a xy=log_ax+log_aytag{1}$$
**Quotient law**
$$log_a dfrac{x}{y}=log_ax-log_aytag{2}$$
**Power law**
$$log_a x^r=rlog_axtag{3}$$

We can use all of these laws or just some of them to compute two equivalent logarithm functions, which have the same graph. Answers may vary. But we can choose to make a function that is a composite function of a product, power, and quotient function such as
$$
y=log_2dfrac{5x^3}{7}$$
The equivalent function will be
$$
y=log_25+3log_2x-log_27tag{4}$$

To prove that these two functions are equivalent and have the same graph, we will start from the function
$$y=log_2dfrac{5x^3}{7}$$

and decompose it using three laws of logarithms. It yields:
$$
begin{align*}
y&=log_2dfrac{5x^3}{7}\
&overset{(2)}{=}log_25x^3-log_27\
&overset{(1)}{=}log_25+log_2x^3-log_27\
&overset{(3)}{=}log_25+3log_2x-log_27\
end{align*}$$
The end result is the same as given in Eq. $(4)$ and hence, these two functions really are equivalent and therefore, have the same graph.

Answers may vary. One possible solution $
y=log_2dfrac{5x^3}{7}$
and
$
y=log_25+3log_2x-log_27$

We would like to evaluate $color{#4257b2}log_{3} left(dfrac{sqrt[5]{27}}{2187}right)$ as a single logarithm. First, we know that $color{#4257b2}27=3^{3}$ and $color{#4257b2}2187=3^{7}$, so we can replace $color{#4257b2}27$ and $color{#4257b2}2187$ by $color{#4257b2}3^{3}$ and $color{#4257b2}3^{7}$ to simpliy.

$$
log_{3} left(dfrac{sqrt[5]{27}}{2187}right)=log_{3} left(dfrac{sqrt[5]{3^{3}}}{3^{7}}right)
$$

But we know that $color{#4257b2}sqrt[a]{x^{b}}=(x)^{frac{b}{a}}$, so we can replace $color{#4257b2}sqrt[5]{3^{3}}$ by $color{#4257b2}(3)^{frac{3}{5}}$.

$$
begin{align*}
log_{3} left(dfrac{sqrt[5]{27}}{2187}right)&=log_{3} left(dfrac{sqrt[5]{3^{3}}}{3^{7}}right)
\ \
&=log_{3} left(dfrac{(3)^{frac{3}{5}}}{3^{7}}right)
end{align*}
$$

Now we can use the property of exponents where $color{#4257b2}dfrac{x^{a}}{x^{b}}=(x)^{a-b}$.

$$
begin{align*}
log_{3} left(dfrac{sqrt[5]{27}}{2187}right)&=log_{3} left(dfrac{sqrt[5]{3^{3}}}{3^{7}}right)
\ \
&=log_{3} left(dfrac{(3)^{frac{3}{5}}}{3^{7}}right)
\ \
&=log_{3} (3)^{frac{3}{5}-7}
\ \
&=log_{3} (3)^{-frac{32}{5}}
end{align*}
$$

Now we note that our expression is on the form of the power of logarithms, so we can use the power law of logarithms where $color{#4257b2}log_{a} m^{r}=r log_{a} m$.

$$
begin{align*}
log_{3} left(dfrac{sqrt[5]{27}}{2187}right)&=log_{3} (3)^{-frac{32}{5}}
\ \
&=-dfrac{32}{5} log_{3} 3
\ \
&=-dfrac{32}{5}
end{align*}
$$

Note that in the final step we used the property $color{#4257b2}log_{a} a=1$ to replace $color{#4257b2}log_{3} 3$ by $color{#4257b2}1$. So the expression $color{#4257b2}log_{3} left(dfrac{sqrt[5]{27}}{2187}right)$ equals $boxed{ -dfrac{32}{5} }$

Large{$text{color{#c34632}$-dfrac{32}{5}$}$

We would like to explain why $color{#4257b2}log_{x} x^{m-1}+1=m$. First, we will simplify the left side and evaluate it to see if it equals $color{#4257b2}m$ or not.

We note that the left side $color{#4257b2}log_{x} x^{m-1}+1$ is is on the form of power logarithm, so we can use the power law of logarithms where $color{#4257b2}log_{a} m^{r}=r log_{a} m$.

$$
log_{x} x^{m-1}+1=left(m-1right)log_{x} x+1
$$

Now we can use the property of logarithm where $color{#4257b2}log_{a} a=1$ to replace $color{#4257b2}log_{x} x$ by $color{#4257b2}1$.

$$
begin{align*}
log_{x} x^{m-1}+1&=left(m-1right)log_{x} x+1
\ \
&=left(m-1right)cdot (1)+1
\ \
&=m-1+1
\ \
&=m
end{align*}
$$

So we proved that the left side equals $color{#4257b2}m$ which means that it equals the right side. So we explained why $color{#4257b2}log_{x} x^{m-1}+1=m$.

Large{$text{color{#c34632}$log_{x} x^{m-1}+1=m$}$

We would like to find the value of $color{#4257b2}log_{b} xsqrt{x}$ if we know that $color{#4257b2}log_{b} x=0.3$. First, we know that $color{#4257b2}sqrt{x}=left(xright)^{frac{1}{2}}$, so we can replace $color{#4257b2}sqrt{x}$ from our logarithm by $color{#4257b2}(x)^{frac{1}{2}}$.

$$
log_{b} xsqrt{x}=log_{b} (x)cdot (x)^{frac{1}{2}}
$$

Now we can use the law of exponents where $color{#4257b2}x^{a}cdot x^{b}=x^{a+b}$.

$$
begin{align*}
log_{b} xsqrt{x}&=log_{b} (x)cdot (x)^{frac{1}{2}}
\ \
&=log_{b} (x)^{1+frac{1}{2}}
\ \
&=log_{b} (x)^{frac{3}{2}}
end{align*}
$$

Now we note that our expression is on the form of power logarithm, so we can use the power law of logarithms where $color{#4257b2}log_{a} m^{r}=r log_{a} m$.

$$
begin{align*}
log_{b} xsqrt{x}&=log_{b} (x)^{frac{3}{2}}
\ \
&=dfrac{3}{2} log_{b} x
end{align*}
$$

But we know that $color{#4257b2}log_{b} x=0.3$, so we can substitute this value in our logarithm.

$$
begin{align*}
log_{b} xsqrt{x}&=dfrac{3}{2} log_{b} x
\ \
&=left(dfrac{3}{2}right)cdot 0.3
\ \
&=0.45
end{align*}
$$

So the expression $color{#4257b2}log_{b} xsqrt{x}$ equals $boxed{ 0.45 }$

Large{$text{color{#c34632}$0.45$}$

We would like to use graphing technology to draw the graphs
$color{#4257b2}y=log x+log 2x$ and $color{#4257b2}y=log 2x^{2}$. First we will graph the first function and then graph the second function in a different plane.

For $color{#4257b2}y=log x+log 2x$

For $color{#4257b2}y=log 2x^{2}$

Although the graphs are different, we can simplify the first expression using the law of logarithms produces the second expression. First, we note that the first expression $color{#4257b2}y=log x+log 2x$ is a sum of logarithms, so we can use the product law of logarithms where $color{#4257b2}log_{a} x+log_{b} y=log_{a} xy$.

$$
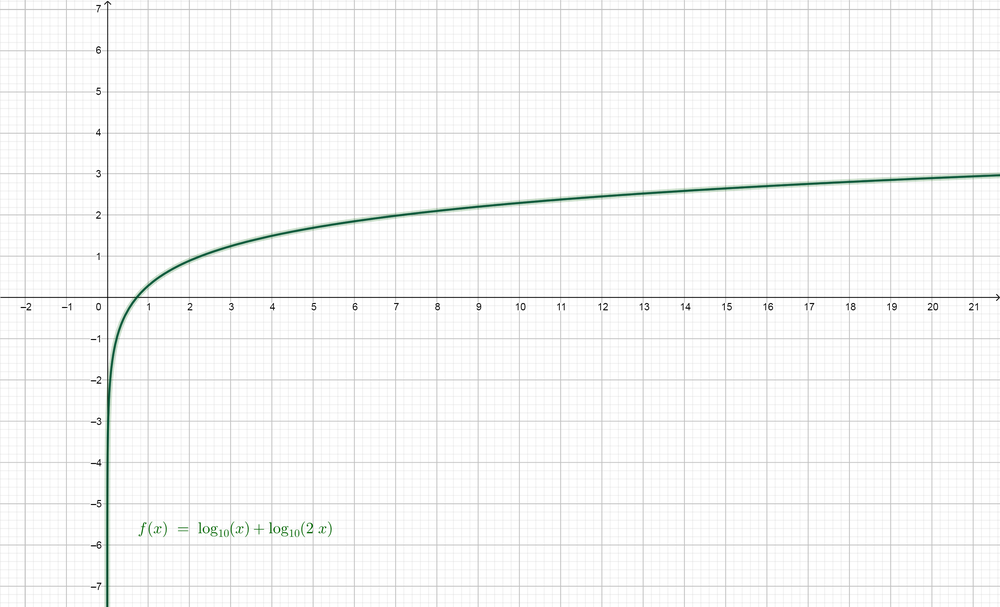
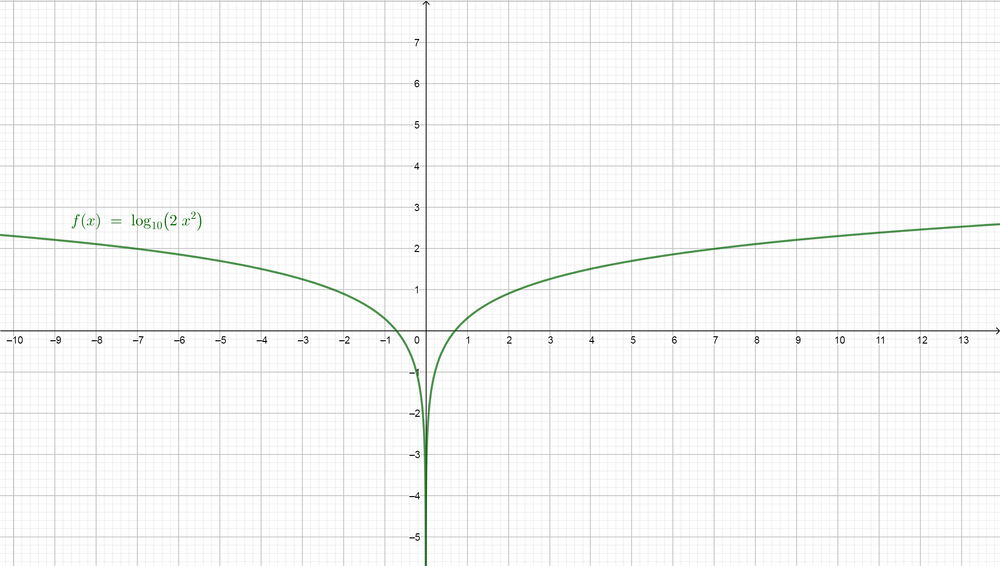
begin{align*}
y&=log x+log 2x
\ \
&=log left[(x)cdot (2x)right]
\ \
&=log 2x^{2}
end{align*}
$$

So the expression $color{#4257b2}y=log x+log 2x$ can be simplified to $color{#4257b2}log 2x^{2}$ which means that it equals the second expression $color{#4257b2}y=log 2x^{2}$.

The reason why the two graphs are different is that the domain of the first expression $color{#4257b2}y=log x+log 2x$ is $color{#4257b2}x > 0$ because we know that if $color{#4257b2}log_{a} x=b$, so $color{#4257b2}x$ must be positive because the exponent form of it is $color{#4257b2}a^{b}=x$ and we know that any exponent give positive number, but in the second expression $color{#4257b2}y=log 2x^{2}$ the domain is $color{#4257b2}R$ because if we substituted $color{#4257b2}x$ with a negative number, then the expression $color{#4257b2}2 x^{2}$ will be positive because of the square on $color{#4257b2}x$. So this is the reason why the two graphs are different.

$$
text{color{#c34632}The two graphs are different}
$$

The laws of logarithms are as follows, where $a>0$, $x>0$ and $y>0$

**Product law**
$$log_a xy=log_ax+log_aytag{1}$$
**Quotient law**
$$log_a dfrac{x}{y}=log_ax-log_aytag{2}$$
**Power law**
$$log_a x^r=rlog_axtag{3}$$

Answers may vary. But to simplify the proof, let’s choose any logarithm of $a$ to base $a$, since $log_aa=1$. Let’s choose $log_55$.

The product law we can prove by starting from the right hand side of the Eq. $(1)$ and transform the expression until we obtain the left hand side of the Eq. $(1)$. Hence, it yields:
$$begin{align*}
log_55+log_55&=1+1\
&=2\
&=log_525\
&=log_5 (5cdot5)
end{align*}$$

The Quotient law we can prove by starting from the right hand side of the Eq. $(2)$ and transform the expression until we obtain the left hand side of the Eq. $(2)$. Hence, it yields:
$$begin{align*}
log_55-log_55&=1-1\
&=0&&[log_a1=0]\
&=log_51\
&=log_5 dfrac{5}{5}end{align*}$$

The Power law we can prove by starting from the left hand side of the Eq. $(3)$ and transform the expression until we obtain the right hand side of the Eq. $(3)$. Hence, it yields:
$$begin{align*}
log_55^2
&=log_525\
&=2\
&= 2cdot1\
&=2cdotlog_5 5
end{align*}$$