Write the inverse form for the following expressions.

$$
color{#4257b2}text{(a)} y=4^x
$$

$y=a^x$ has an inverse form of $y=log_a(x)$

$$
y=4^x y=log_4(x)
$$

$$
color{#4257b2}text{(b)} y=a^x
$$

$y=a^x$ has an inverse form of $y=log_a(x)$

$$
y=a^x y=log_a(x)
$$

$$
color{#4257b2}text{(c)} y=left(dfrac{3}{4}right)^x
$$

$y=a^x$ has an inverse form of $y=log_a(x)$

$$
y=left(dfrac{3}{4}right)^x y=log_{tfrac{3}{4}}(x)
$$

$$
color{#4257b2}text{(d)} m=p^q
$$

$y=a^x$ has an inverse form of $y=log_a(x)$

$$
m=p^q m=log_p(q)
$$

$$
text{color{#c34632}(a) $y=log_4(x)$ (b) $y=log_a(x)$
\ \
(c) $y=log_{tfrac{3}{4}}(x)$ (d) $m=log_p(q)$}
$$

Describe the transformation that made for the following terms.

$$
color{#4257b2}text{(a)} f(x)=-3log(2x)
$$

$$
a=-3 k=2
$$

$$
color{#4257b2}text{(b)} f(x)=log(x-5)+2
$$

$$
d=5 c=2
$$

$$
color{#4257b2}text{(c)} f(x)=dfrac{1}{2} log(5x)
$$

$$
a=dfrac{1}{2} k=5
$$

$$
color{#4257b2}text{(d)} f(x)=logleft(-dfrac{1}{3} xright)-3
$$

$$
k=-dfrac{1}{3} c=-3
$$

$$
text{color{#c34632}(a) $a=-3, k=2$ (b) $d=5, c=2$
\ \
(c) $a=dfrac{1}{2}, k=5$ (d) $k=-dfrac{1}{30}, c=-3$}
$$

Write the equation of the function that resulted from the each of the following transformation.

$$
color{Brown}text{Note that: parent function is} y=log(x)
$$

$$
color{#4257b2}text{(a)} a=dfrac{2}{5} c=-3
$$

$$
y=dfrac{2}{5} log(x)-3
$$

$$
color{#4257b2}text{(b)} a=-1 k=2 d=3
$$

$$
y=-log(2x-3)
$$

$$
color{#4257b2}text{(c)} a=5 k=-dfrac{1}{2}
$$

$$
y=5 logleft(-dfrac{1}{2}xright)
$$

$$
color{#4257b2}text{(d)} k=-1 d=-4 c=-2
$$

$$
y=log(-x+4)-2
$$

$$
text{color{#c34632}(a) $y=dfrac{2}{5} log(x)-3$ (b) $y=-log(2x-3)$
\ \
(c) $y=5 logleft(-dfrac{1}{2}xright)$ (d) $y=log(-x+4)-2$}
$$

Describe how the graph of $f(x)=log(x)$ and $g(x)=3log(x-1)+2$ are similar yet different.

(a) For the function of $f(x)=log(x)$

Domain $=(0, infty)$, Range $=(-infty, infty)$, Symptote equation $(x=0)$

(b) For the function of $f(x)=log(x)$

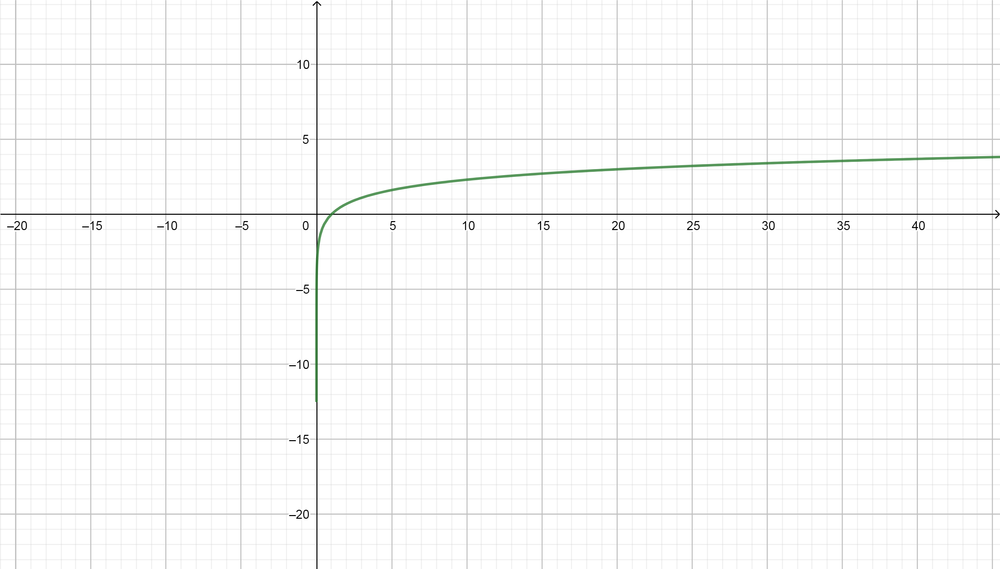
Domain $=(1, infty)$, Range $=(-infty, infty)$, Symptote equation $(x=1)$

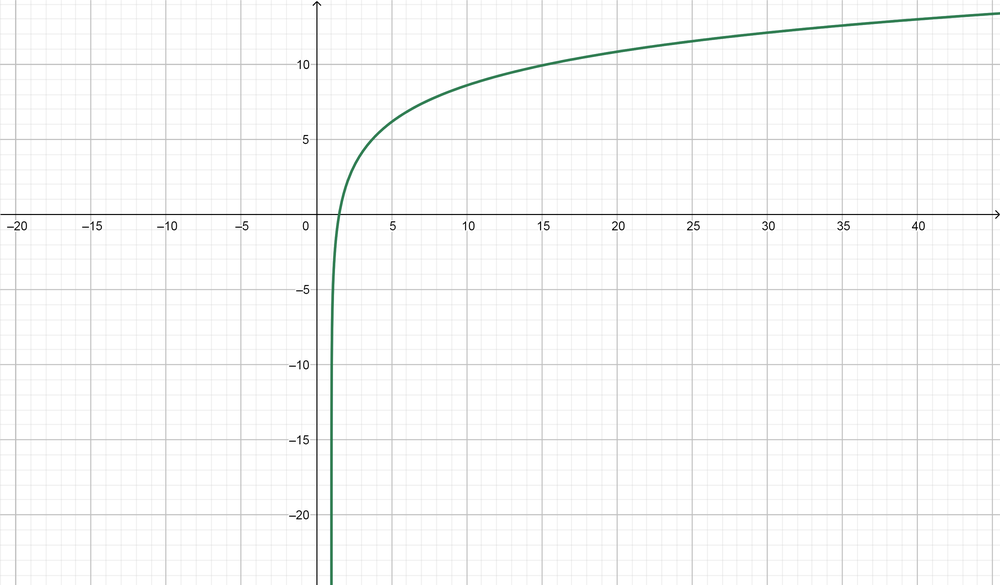
$$
text{color{#c34632}(a) Domain $=(0, infty)$, Range $=(-infty, infty)$, Symptote equation $(x=0)$
\ \
(b) Domain $=(1, infty)$, Range $=(-infty, infty)$, Symptote equation $(x=1)$}
$$

(a) We would like to evaluate $color{#4257b2}log_{7} 343$. First, we can let the solution of this expression equals $color{#4257b2}x$ and then try to solve it.

$$
log_{7} 343=x
$$

Now we note that we have an equation on the logarithmic form, so we can convert it to the exponential form where we know that if $color{#4257b2}log_{a} x=b$, then $color{#4257b2}a^{b}=x$.

$$
log_{7} 343=x
$$

$$
7^{x}=343
$$

But we know that $color{#4257b2}343=7^{3}$, so we can replace $color{#4257b2}343$ from the right side by $color{#4257b2}7^{3}$.

$$
7^{x}=7^{3}
$$

Now we note that the two sides have the same base $color{#4257b2}7$, so the exponent of the left side must equal the exponent of the right side where we know that if $color{#4257b2}x^{a}=x^{b}$, then $color{#4257b2}a=b$

$$
7^{x}=7^{3}
$$

$$
x=3
$$

So we find that $color{#4257b2}x=3$, so the value of $color{#4257b2}log_{7} 343$ is $boxed{ 3 }$

(b) We would like to evaluate $color{#4257b2}log_{frac{1}{5}} 25$. First, we can let the solution of this expression equals $color{#4257b2}x$ and then try to solve it.

$$
log_{frac{1}{5}} 25=x
$$

Now we note that we have an equation on the logarithmic form, so we can convert it to the exponential form where we know that if $color{#4257b2}log_{a} x=b$, then $color{#4257b2}a^{b}=x$.

$$
left(dfrac{1}{5}right)^{x}=25
$$

Now we can use the property of exponents $color{#4257b2}dfrac{1}{x^{a}}=x^{-a}$ to replace $color{#4257b2}dfrac{1}{5}$ from the left side by $color{#4257b2}5^{-1}$.

$$
left(5^{-1}right)^{x}=25
$$

Now we can use the property of exponents $color{#4257b2}left(x^{a}right)^{b}=x^{ab}$ to simplify the left side.

$$
5^{(-1)cdot (x)}=25
$$

$$
5^{-x}=25
$$

But we know that $color{#4257b2}25=5^{2}$, so we can replace $color{#4257b2}25$ from the right side by $color{#4257b2}5^{2}$.

$$
5^{-x}=5^{2}
$$

Now we note that the two sides have the same base $color{#4257b2}5$, so the exponent of the left side must equal the exponent of the right side where we know that if $color{#4257b2}x^{a}=x^{b}$, then $color{#4257b2}a=b$.

$$
5^{-x}=5^{2}
$$

$$
-x=2
$$

Now we can divide the two sides by $color{#4257b2}-1$ to find the value of $color{#4257b2}x$.

$$
dfrac{-x}{-1}=dfrac{2}{-1}
$$

$$
x=-2
$$

So we find that $color{#4257b2}x=-2$, so the value of $color{#4257b2}log_{frac{1}{5}} 25$ is $boxed{ -2 }$

(c) We would like to evaluate $color{#4257b2}log_{19} 1$. First, we can let the solution of this expression equals $color{#4257b2}x$ and then try to solve it.

$$
log_{19} 1=x
$$

Now we note that we have an equation on the logarithmic form, so we can convert it to the exponential form where we know that if $color{#4257b2}log_{a} x=b$, then $color{#4257b2}a^{b}=x$.

$$
log_{19} 1=x
$$

$$
19^{x}=1
$$

But we know that $color{#4257b2}1=a^{0}$ where $color{#4257b2}a$ is any integer number, so we can replace $color{#4257b2}1$ from the right side by $color{#4257b2}19^{0}$.

$$
19^{x}=19^{0}
$$

Now we note that the two sides have the same base $color{#4257b2}19$, so the exponent of the left side must equal the exponent of the right side where we know that if $color{#4257b2}x^{a}=x^{b}$, then $color{#4257b2}a=b$

$$
19^{x}=19^{0}
$$

$$
x=0
$$

So we find that $color{#4257b2}x=0$, so the value of $color{#4257b2}log_{19} 1$ is $boxed{ 0 }$

(d) We would like to evaluate $color{#4257b2}log_{4} dfrac{1}{256}$. First, we can let the solution of this expression equals $color{#4257b2}x$ and then try to solve it.

$$
log_{4} dfrac{1}{256}=x
$$

Now we note that we have an equation on the logarithmic form, so we can convert it to the exponential form where we know that if $color{#4257b2}log_{a} x=b$, then $color{#4257b2}a^{b}=x$.

$$
4^{x}=dfrac{1}{256}
$$

But we know that $color{#4257b2}256=4^{4}$, so we can replace $color{#4257b2}256$ from the right side by $color{#4257b2}4^{4}$.

$$
4^{x}=dfrac{1}{4^{4}}
$$

Now we can use the property of exponents $color{#4257b2}dfrac{1}{x^{a}}=x^{-a}$ to replace $color{#4257b2}dfrac{1}{4^{4}}$ from the right side by $color{#4257b2}4^{-4}$.

$$
4^{x}=4^{-4}
$$

Now we note that the two sides have the same base $color{#4257b2}4$, so the exponent of the left side must equal the exponent of the right side where we know that if $color{#4257b2}x^{a}=x^{b}$, then $color{#4257b2}a=b$.

$$
4^{x}=4^{-4}
$$

$$
x=-4
$$

So we find that $color{#4257b2}x=-4$, so the value of $color{#4257b2}log_{4} dfrac{1}{256}$ is $boxed{ -4 }$

Large{$text{color{#c34632}(a) $log_{7} 343=3$ (c) $log_{19} 1=0$
\
\
(b) $log_{frac{1}{5}} 25=-2$ (d) $log_{4} dfrac{1}{256}=-4$}$

(a) We would like to evaluate $color{#4257b2}log_{3} 53$. First, we can let the solution of this expression equals $color{#4257b2}x$ and then try to solve it.

$$
log_{3} 53=x
$$

Now we note that we have an equation on the logarithmic form, so we can convert it to the exponential form where we know that if $color{#4257b2}log_{a} x=b$, then $color{#4257b2}a^{b}=x$.

$$
log_{3} 53=x
$$

$$
3^{x}=53
$$

Now we note the two sides have different bases, so we can use the graph calculator to find the value of $color{#4257b2}x$. First, we will graph the function of the left side $color{#4257b2}3^{x}$ and then graph the line of the right side $color{#4257b2}y=53$ on the same plane and then find the point where the two graph will intersect and find the value of $color{#4257b2}x$ at this point.

We note from the two graphs that they intersect at the point $color{#4257b2}A$ where the value of $color{#4257b2}x$ at this point is $color{#4257b2}3.614$.

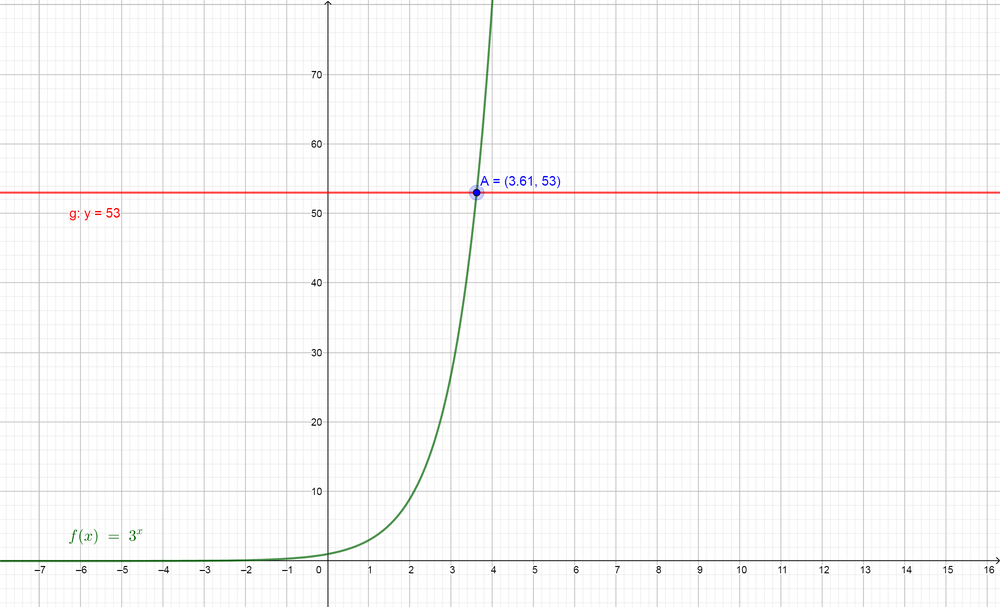
So we find that $color{#4257b2}x=3.614$, so the value of $color{#4257b2}log_{3} 53$ is $boxed{ 3.614 }$

(b) We would like to evaluate $color{#4257b2}log_{4} dfrac{1}{10}$. First, we can let the solution of this expression equals $color{#4257b2}x$ and then try to solve it.

$$
log_{4} dfrac{1}{10}=x
$$

Now we note that we have an equation on the logarithmic form, so we can convert it to the exponential form where we know that if $color{#4257b2}log_{a} x=b$, then $color{#4257b2}a^{b}=x$.

$$
log_{4} dfrac{1}{10}=x
$$

$$
4^{x}=dfrac{1}{10}
$$

Now we note the two sides have different bases, so we can use the graph calculator to find the value of $color{#4257b2}x$. First, we will graph the function of the left side $color{#4257b2}4^{x}$ and then graph the line of the right side $color{#4257b2}y=dfrac{1}{10}$ on the same plane and then find the point where the two graph will intersect and find the value of $color{#4257b2}x$ at this point.

We note from the two graphs that they intersect at the point $color{#4257b2}A$ where the value of $color{#4257b2}x$ at this point is $color{#4257b2}-1.661$.

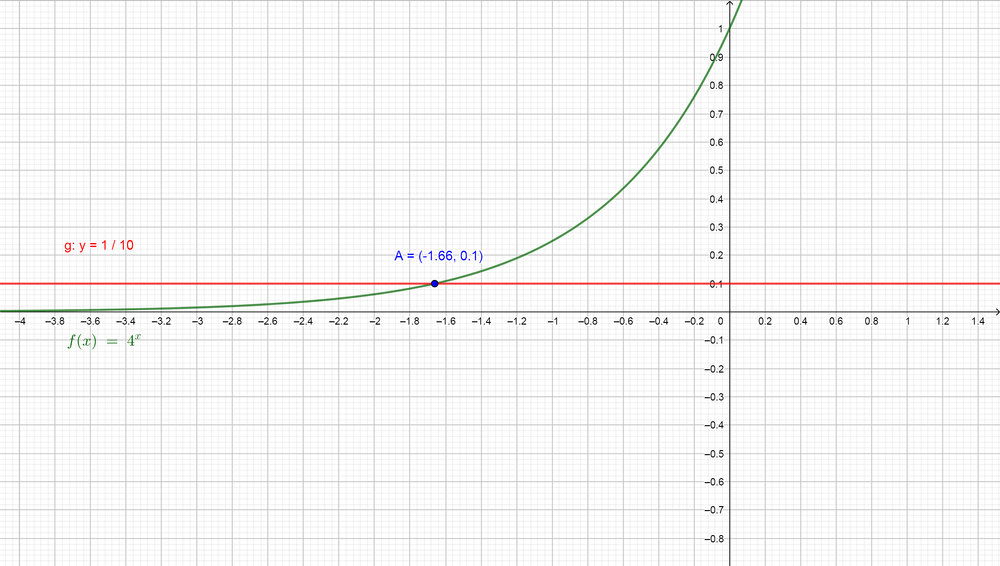
So we find that $color{#4257b2}x=-1.661$, so the value of $color{#4257b2}log_{4} dfrac{1}{10}$ is $boxed{ -1.661 }$

(c) We would like to evaluate $color{#4257b2}log_{6} 159$. First, we can let the solution of this expression equals $color{#4257b2}x$ and then try to solve it.

$$
log_{6} 159=x
$$

Now we note that we have an equation on the logarithmic form, so we can convert it to the exponential form where we know that if $color{#4257b2}log_{a} x=b$, then $color{#4257b2}a^{b}=x$.

$$
log_{6} 159=x
$$

$$
6^{x}=159
$$

Now we note the two sides have different bases, so we can use the graph calculator to find the value of $color{#4257b2}x$. First, we will graph the function of the left side $color{#4257b2}6^{x}$ and then graph the line of the right side $color{#4257b2}y=159$ on the same plane and then find the point where the two graph will intersect and find the value of $color{#4257b2}x$ at this point.

We note from the two graphs that they intersect at the point $color{#4257b2}A$ where the value of $color{#4257b2}x$ at this point is $color{#4257b2}2.829$.

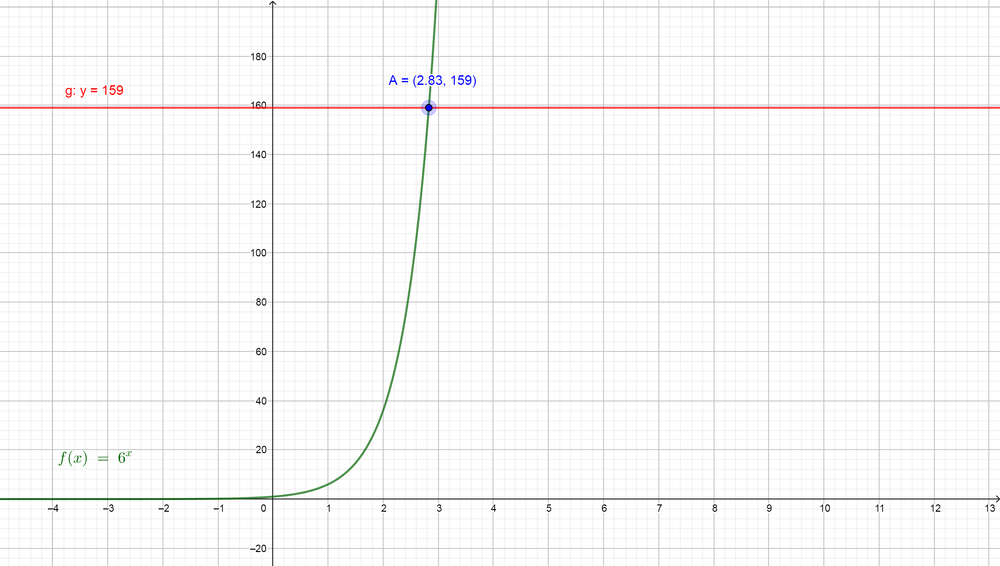
So we find that $color{#4257b2}x=2.829$, so the value of $color{#4257b2}log_{6} 159$ is $boxed{ 2.829 }$

(d) We would like to evaluate $color{#4257b2}log_{15} 1456$. First, we can let the solution of this expression equals $color{#4257b2}x$ and then try to solve it.

$$
log_{15} 1456=x
$$

Now we note that we have an equation on the logarithmic form, so we can convert it to the exponential form where we know that if $color{#4257b2}log_{a} x=b$, then $color{#4257b2}a^{b}=x$.

$$
log_{15} 1456=x
$$

$$
15^{x}=1456
$$

Now we note the two sides have different bases, so we can use the graph calculator to find the value of $color{#4257b2}x$. First, we will graph the function of the left side $color{#4257b2}15^{x}$ and then graph the line of the right side $color{#4257b2}y=1456$ on the same plane and then find the point where the two graph will intersect and find the value of $color{#4257b2}x$ at this point.

We note from the two graphs that they intersect at the point $color{#4257b2}A$ where the value of $color{#4257b2}x$ at this point is $color{#4257b2}2.69$.

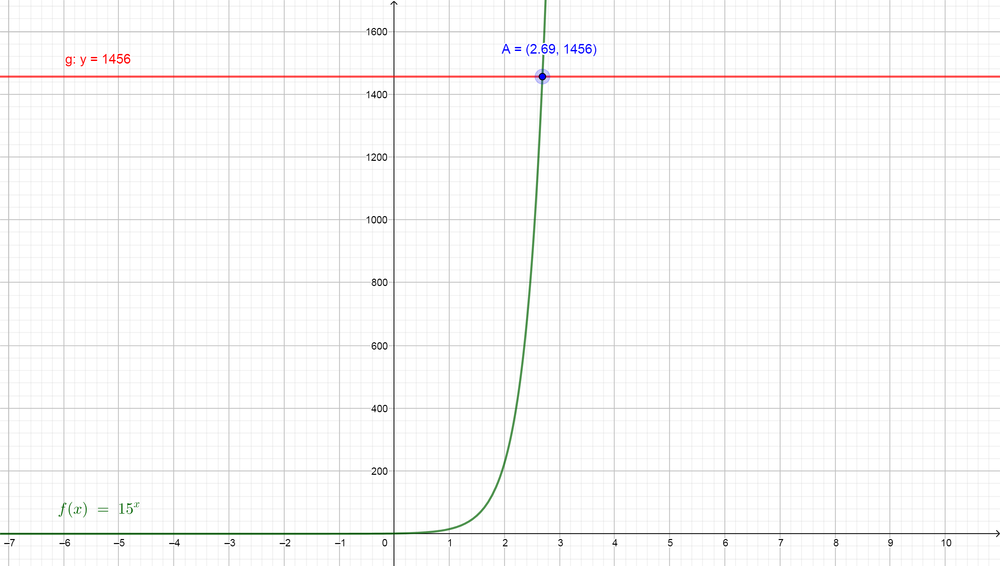
So we find that $color{#4257b2}x=2.69$, so the value of $color{#4257b2}log_{15} 1456$ is $boxed{ 2.69 }$

Large{$text{color{#c34632}(a) $log_{3} 53=3.614$ (c) $log_{6} 159=2.829$
\
\
(b) $log_{4} dfrac{1}{10}=-1.661$ (d) $log_{15} 1456=2.69$}$

(a) We would like to express $color{#4257b2}log 5+log 11$ as a single logarithm. First, we note that our expression is a sum of logarithms, so we can use the product law of logarithms where $color{#4257b2}log_{a} x+log_{a} y=log_{a} xy$.

$$
begin{align*}
log 5+log 11&=log (5)cdot (11)
\ \
&=log 55
end{align*}
$$

So the expression $color{#4257b2}log 5+log 11$ can be written as $boxed{ log 55 }$

(b) We would like to express $color{#4257b2}log 20-log 4$ as a single logarithm. First, we note that our expression is a difference of logarithms, so we can use the quotient law of logarithms where $color{#4257b2}log_{a} x-log_{a} y=log_{a} left(dfrac{x}{y}right)$.

$$
begin{align*}
log 20-log 4&=log left(dfrac{20}{4}right)
\ \
&=log 5
end{align*}
$$

So the expression $color{#4257b2}log 20-log 4$ can be written as $boxed{ log 5 }$

(c) We would like to express $color{#4257b2}log_{5} 6+log_{5} 8-log_{5} 12$ as a single logarithm. First, we note that the first two terms of our expression is a sum of logarithms, so we can use the product law of logarithms where $color{#4257b2}log_{a} x+log_{a} y=log_{a} xy$.

$$
begin{align*}
log_{5} 6+log_{5} 8-log_{5} 12&=log_{5} [(6)cdot (8)]-log_{5} 12
\ \
&=log_{5} 48-log_{5} 12
end{align*}
$$

Now we note that our expression is simplified to $color{#4257b2}log_{5} 48-log_{5} 12$ which is a difference of logarithms, so we can use the quotient law of logarithms where $color{#4257b2}log_{a} x-log_{a} y=log_{a} left(dfrac{x}{y}right)$.

$$
begin{align*}
log_{5} 6+log_{5} 8-log_{5} 12&=log_{5} 48-log_{5} 12
\ \
&=log_{5} left(dfrac{48}{12}right)
\ \
&=log_{5} 4
end{align*}
$$

So the expression $color{#4257b2}log_{5} 6+log_{5} 8-log_{5} 12$ can be written as $boxed{ log_{5} 4 }$

(d) We would like to express $color{#4257b2}2log 3+4log 2$ as a single logarithm. First, we note that the two terms of our expression each of them is a single logarithm which is multiplied by a number, so we can use the power law of logarithms where $color{#4257b2}r log_{m} x=log_{m} x^{r}$.

$$
begin{align*}
2log 3+4log 2&=log 3^{2}+log 2^{4}
\ \
&=log 9+log 16
end{align*}
$$

Now we note that our expression is simplified to $color{#4257b2}log 9+log 16$ which is a sum of logarithms, so we can use the product law of logarithms where $color{#4257b2}log_{a} x+log_{a} y=log_{a} xy$.

$$
begin{align*}
2log 3+4log 2&=log 9+log 16
\ \
&=log [(9)cdot (16)]
\ \
&=log 144
end{align*}
$$

So the expression $color{#4257b2}2log 3+4log 2$ can be written as $boxed{ log 144 }$

Large{$text{color{#c34632}(a) $log 55$ (c) $log_{5} 4$
\
\
(b) $log 5$ (d) $log 144$}$

(a) We would like to use the laws of logarithms to evaluate $color{#4257b2}log_{6} 42-log_{6} 7$. First, we note that our expression is a difference of logarithms, so we can use the quotient law of logarithms where $color{#4257b2}log_{a} x-log_{a} y=log_{a} left(dfrac{x}{y}right)$.

$$
begin{align*}
log_{6} 42-log_{6} 7&=log_{6} left(dfrac{42}{7}right)
\ \
&=log_{6} 6
end{align*}
$$

But we from the properties of logarithms that $color{#4257b2}log_{a} a=1$, so we can replace $color{#4257b2}log_{6} 6=1$.

$$
begin{align*}
log_{6} 42-log_{6} 7&=log_{6} 6
\ \
&=1
end{align*}
$$

So the expression $color{#4257b2}log_{6} 42-log_{6} 7$ equals $boxed{ 1 }$

(b) We would like to use the laws of logarithms to evaluate
$color{#4257b2}log_{3} 5+log_{3} 18-log_{3} 10$. First, we note that the first two terms of our expression is a sum of logarithms, so we can use the product law of logarithms where $color{#4257b2}log_{a} x+log_{a} y=log_{a} xy$.

$$
begin{align*}
log_{3} 5+log_{3} 18-log_{3} 10&=log_{3} [(5)cdot (18)]-log_{3} 10
\ \
&=log_{3} 90-log_{3} 10
end{align*}
$$

Now we note that our expression is simplified to $color{#4257b2}log_{3} 90-log_{3} 10$ which is a difference of logarithms, so we can use the quotient law of logarithms where $color{#4257b2}log_{a} x-log_{a} y=log_{a} left(dfrac{x}{y}right)$.

$$
begin{align*}
log_{3} 5+log_{3} 18-log_{3} 10&=log_{3} 90-log_{3} 10
\ \
&=log_{3} left(dfrac{90}{10}right)
\ \
&=log_{3} 9
\ \
&=log_{3} 3^{2}
end{align*}
$$

Now we note that our expression is simplified to $color{#4257b2}log_{3} 3^{2}$ which is a power of logarithms, so we can use the power law of logarithms where
$color{#4257b2}log_{m} x^{r}=r log_{m} x$.

$$
begin{align*}
log_{3} 5+log_{3} 18-log_{3} 10&=log_{3} 3^{2}
\ \
&=2log_{3} 3
\ \
&=2cdot (1)=2
end{align*}
$$

Note that in the final step we used the property of logarithms $color{#4257b2}log_{a} a=1$. So the expression $color{#4257b2}log_{3} 5+log_{3} 18-log_{3} 10$ equals $boxed{ 2 }$

(c) We would like to use the laws of logarithms to evaluate $color{#4257b2}log_{7} sqrt[3]{49}$. First, we know that $color{#4257b2}49=7^{2}$, so we can replace $color{#4257b2}49$ from our expression by $color{#4257b2}7^{2}$.

$$
log_{7} sqrt[3]{49}=log_{7} sqrt[3]{7^{2}}
$$

But we know that $color{#4257b2}sqrt[a]{x^{b}}=x^{frac{b}{a}}$, so we can replace $color{#4257b2}log_{7} sqrt[3]{7^{2}}$ from our expression by $color{#4257b2}7^{frac{2}{3}}$.

$$
begin{align*}
log_{7} sqrt[3]{49}&=log_{7} sqrt[3]{7^{2}}
\ \
&=log_{7} (7)^{frac{2}{3}}
end{align*}
$$

Now we note that our expression is simplified to $color{#4257b2}log_{7} 7^{frac{2}{3}}$ which is a power of logarithms, so we can use the power law of logarithms where
$color{#4257b2}log_{m} x^{r}=r log_{m} x$.

$$
begin{align*}
log_{7} sqrt[3]{49}&=log_{7} (7)^{frac{2}{3}}
\ \
&=dfrac{2}{3} log_{7} 7
\ \
&=left(dfrac{2}{3}right)cdot (1)
\ \
&=dfrac{2}{3}
end{align*}
$$

Note that in the final step we used the property of logarithms $color{#4257b2}log_{a} a=1$. So the expression $color{#4257b2}log_{7} sqrt[3]{49}$ equals $boxed{ dfrac{2}{3} }$

(d) We would like to use the laws of logarithms to evaluate $color{#4257b2}2log_{4} 8$. First, we note that our expression each of them is a single logarithm which is multiplied by a number, so we can use the power law of logarithms where $color{#4257b2}r log_{m} x=log_{m} x^{r}$.

$$
begin{align*}
2log_{4} 8&=log_{4} 8^{2}
\ \
&=log_{4} 64
end{align*}
$$

But we know that $color{#4257b2}64=4^{3}$, so we can replace $color{#4257b2}64$ from our expression by $color{#4257b2}4^{3}$.

$$
begin{align*}
2log_{4} 8&=log_{4} 64
\ \
&=log_{4} 4^{3}
end{align*}
$$

Now we note that our expression is simplified to $color{#4257b2}log_{4} 4^{3}$ which is a power of logarithms, so we can use the power law of logarithms where
$color{#4257b2}log_{m} x^{r}=r log_{m} x$.

$$
begin{align*}
2log_{4} 8&=log_{4} 4^{3}
\ \
&=3log_{4} 4
\ \
&=3cdot (1)
\ \
&=3
end{align*}
$$

Note that in the final step we used the property of logarithms $color{#4257b2}log_{a} a=1$. So the expression $color{#4257b2}2log_{4} 8$ equals $boxed{ 3 }$

Large{$text{color{#c34632}(a) $log_{6} 42-log_{6} 7=1$ (c) $log_{7} sqrt[3]{49}=dfrac{2}{3}$
\
\
(b) $log_{3} 5+log_{3} 18-log_{3} 10=2$ (d) $2log_{4} 8=3$}$

We would like to describe how the graph of $color{#4257b2}y=log (10000x)$ is related to the graph of $color{#4257b2}log x$. First, we note that the function $color{#4257b2}y=log (10000x)$ is a product of logarithms, so we can use the product law of logarithms where $color{#4257b2}log_{a} xy=log_{a} x+log_{a} y$.

$$
y=log (10000x)
$$

$$
y=log 10000+log x
$$

But we know that $color{#4257b2}10000=10^{4}$, so we can replace $color{#4257b2}10000$ from our function by $color{#4257b2}10^{4}$.

$$
y=log 10^{4}+log x
$$

Now we note that the first term of the right side is a power of logarithm, so we can use the power law of logarithms where $color{#4257b2}log_{m} x^{r}=r log_{m} x$.

$$
y=log 10^{4}+log x
$$

$$
y=4 log 10+log x
$$

But we know that $color{#4257b2}log 10=1$, so we can simplify our function using this fact.

$$
y=4cdot (1)+log x
$$

$$
y=4+log x
$$

So the function of the first graph is simplified to $color{#4257b2}4+log x$ which is the same of the second graph but the only difference that it is shifted by $color{#4257b2}4$, so the relation between the two graphs that $boxed{ y_{1}=4+y_{2}}$ where $color{#4257b2}y_{1}$ and $color{#4257b2}y_{2}$ are the graphs of the two functions respectively.

Now we can graph the functions on the same plane to show the relation between them on the graph and to verify that the first function is the same of the second but shifted by $color{#4257b2}4$ in the positive y-axis.

Large{$text{color{#c34632}$y_{1}=4+y_{2}$}$

(a) We would like to solve $color{#4257b2}5^{x}=3125$. First, we need to make the two sides have the same base because in this case the two exponents will equal each others. We know that $color{#4257b2}3125=5^{5}$, so we can replace $color{#4257b2}3125$ from the right side by $color{#4257b2}5^{5}$.

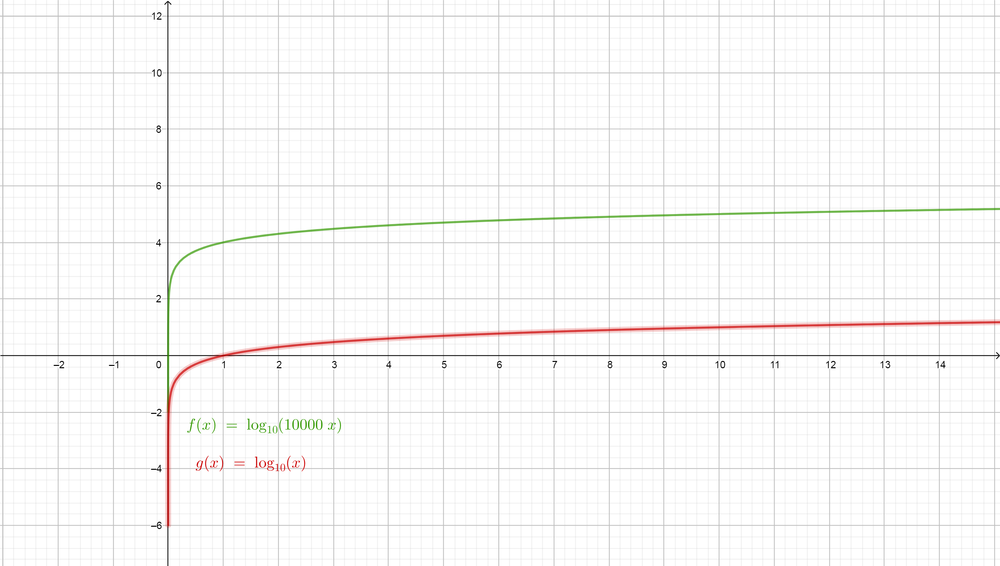
$$
5^{x}=3125
$$

$$
5^{x}=5^{5}
$$

Now the two sides have the same base $color{#4257b2}5$, so the exponent of the left side will equal the exponent of the right side.

$$
5^{x}=5^{5}
$$

$$
x=5
$$

So the solution of the equation is $boxed{ x=5 }$

(b) We would like to solve $color{#4257b2}4^{x}=16 sqrt{128}$. First, we need to make the two sides have the same base because in this case the two exponents will equal each others. We know that $color{#4257b2}4=2^{2}, 16=2^{4}$ and $color{#4257b2}128=2^{7}$, so we can substitute these values in our equations to simplify.

$$
4^{x}=16 sqrt{128}
$$

$$
(2^{2})^{x}=2^{4} sqrt{2^{7}}
$$

But we know that $color{#4257b2}sqrt{x^{a}}=x^{frac{a}{2}}$, so we can use this fact to replace $color{#4257b2}sqrt{2^{7}}$ from the right side by $color{#4257b2}2^{frac{7}{2}}$ to simplify our equation.

$$
(2^{2})^{x}=2^{4} sqrt{2^{7}}
$$

$$
(2^{2})^{x}=(2)^{4}cdot (2)^{frac{7}{2}}
$$

But we know from the exponent property that $color{#4257b2}(x^{a})^{b}=x^{a b}$, so we can use this property to simplify the left side.

$$
2^{(2)cdot (x)}=(2)^{4}cdot (2)^{frac{7}{2}}
$$

$$
2^{2x}=(2)^{4}cdot (2)^{frac{7}{2}}
$$

Now we can use the property of exponents $color{#4257b2}x^{a}cdot x^{b}=x^{a+b}$ to simplify the right side.

$$
2^{2x}=2^{4+frac{7}{2}}
$$

$$
2^{2x}=2^{frac{15}{2}}
$$

Now the two sides have the same base $color{#4257b2}2$, so the exponent of the left side will equal the exponent of the right side.

$$
2^{2x}=2^{frac{15}{2}}
$$

$$
2x=dfrac{15}{2}
$$

Now we can divide the two sides by $color{#4257b2}2$

$$
dfrac{2x}{2}=dfrac{dfrac{15}{2}}{2}
$$

$$
x=dfrac{15}{4}
$$

So the solution of the equation is $boxed{ x=dfrac{15}{4} }$

(c) We would like to solve $color{#4257b2}4^{5x}=16^{2x-1}$. First, we need to make the two sides have the same base because in this case the two exponents will equal each others. We know that $color{#4257b2}16=4^{2}$, so we can replace $color{#4257b2}16$ from our equation by $color{#4257b2}4^{2}$.

$$
4^{5x}=16^{2x-1}
$$

$$
4^{5x}=(4^{2})^{2x-1}
$$

But we know from the exponent property that $color{#4257b2}(x^{a})^{b}=x^{a b}$, so we can use this property to simplify our equation.

$$
4^{5x}=4^{(2)cdot (2x-1)}
$$

$$
4^{5x}=4^{4x-2}
$$

Now the two sides have the same base $color{#4257b2}4$, so the exponent of the left side will equal the exponent of the right side.

$$
5x=4x-2
$$

Now we can subtract $color{#4257b2}4x$ from each side to make the variable $color{#4257b2}x$ in the left side alone.

$$
5x-4x=4x-2-4x
$$

$$
x=-2
$$

So the solution of the equation is $boxed{ x=-2 }$

(d) We would like to solve $color{#4257b2}3^{5x} 9^{x^{2}}=27$. First, we need to make the two sides have the same base because in this case the two exponents will equal each others. We know that $color{#4257b2}9=3^{2}$ and $color{#4257b2}27=3^{3}$, so we can substitute these values in our equations to simplify.

$$
3^{5x} 9^{x^{2}}=27
$$

$$
(3^{5x})cdot (3^{2})^{x^{2}}=3^{3}
$$

But we know from the exponent property that $color{#4257b2}(x^{a})^{b}=x^{a b}$, so we can use this property to simplify the left side.

$$
(3^{5x})cdot (3)^{(2)cdot (x^{2})}=3^{3}
$$

$$
(3)^{5x}cdot (3)^{2x^{2}}=3^{3}
$$

Now we can use the property of exponents $color{#4257b2}x^{a}cdot x^{b}=x^{a+b}$ to simplify the right side.

$$
3^{5x+2x^{2}}=3^{3}
$$

Now the two sides have the same base $color{#4257b2}3$, so the exponent of the left side will equal the exponent of the right side.

$$
3^{5x+2x^{2}}=3^{3}
$$

$$
5x+2x^{2}=3
$$

Now we can subtract $color{#4257b2}3$ from each side to make the right side equals zero.

$$
5x+2x^{2}-3=3-3
$$

$$
2x^{2}+5x-3=0
$$

Now we have a quadratic equation, so we can factor to find the values of $color{#4257b2}x$.

$$
2x^{2}+5x-3=0
$$

$$
(2x-1)(x+3)=0
$$

Now we can use the zero-factor property.

$$
2x-1=0 text{or} x+3=0
$$

$$
x=dfrac{1}{2} text{or} x=-3
$$

So the solutions of the equation are $boxed{ x=dfrac{1}{2} } text{or} boxed{ x=-3 }$

Large{$text{$text{color{#c34632}(a) $x=5$ (c) $-2$
\
\
\
Large{color{#c34632}(b) $x=dfrac{15}{4}$ (d) $x=dfrac{1}{2} {color{Black}text{or}} x=-3$}$}$

(a) We would like to solve $color{#4257b2}6^{x}=78$. First, we note that the two sides have different bases, so we can take $color{#4257b2}log_{6}$ for each side to simplify the left side.

$$
6^{x}=78
$$

$$
log_{6} 6^{x}=log_{6} 78
$$

Now we note that the left side is a power of logarithm, so we can use the power law of logarithms where $color{#4257b2}log_{m} x^{r}=r log_{m} x$.

$$
log_{6} 6^{x}=log_{6} 78
$$

$$
x log_{6} 6=log_{6} 78
$$

Now we can use the property of logarithm $color{#4257b2}log_{a} a=1$, to replace $color{#4257b2}log_{6} 6$ by $color{#4257b2}1$.

$$
xcdot (1)=log_{6} 78
$$

$$
x=log_{6} 78
$$

Now we can use the calculator to determine $color{#4257b2}log_{6} 78$ to find the value of $color{#4257b2}x$.

$$
x=2.432
$$

So the solution of the equation is $boxed{ x=2.432 }$

(b) We would like to solve $color{#4257b2}(5.4)^{x}=234$. First, we note that the two sides have different bases, so we can take $color{#4257b2}log$ for each side to simplify the left side.

$$
(5.4)^{x}=234
$$

$$
log (5.4)^{x}=log 234
$$

Now we note that the left side is a power of logarithm, so we can use the power law of logarithms where $color{#4257b2}log_{m} x^{r}=r log_{m} x$.

$$
log (5.4)^{x}=log 234
$$

$$
x log 5.4=log 234
$$

Now we can divide the two sides by $color{#4257b2}log 5.4$ to make $color{#4257b2}x$ in the left side alone.

$$
dfrac{x log 5.4}{log 5.4}=dfrac{log 234}{log 5.4}
$$

$$
x=dfrac{log 234}{log 5.4}
$$

Now we can use the calculator to determine $color{#4257b2}log 234$ and $color{#4257b2}log 5.4$ to find the value of $color{#4257b2}x$.

$$
x=dfrac{2.369}{0.732}
$$

$$
x=3.235
$$

So the solution of the equation is $boxed{ x=3.235 }$

(c) We would like to solve $color{#4257b2}8(3^{x})=132$. First, we can divide the two sides by $color{#4257b2}8$ to simplify.

$$
8(3^{x})=132
$$

$$
dfrac{8(3^{x})}{8}=dfrac{132}{8}
$$

$$
3^{x}=16.5
$$

Now we note that the two sides have different bases, so we can take $color{#4257b2}log_{3}$ for each side to simplify the left side.

$$
log_{3} 3^{x}=log_{3} 16.5
$$

Now we note that the left side is a power of logarithm, so we can use the power law of logarithms where $color{#4257b2}log_{m} x^{r}=r log_{m} x$.

$$
x log_{3} 3=log_{3} 16.5
$$

Now we can use the property of logarithm $color{#4257b2}log_{a} a=1$, to replace $color{#4257b2}log_{3} 3$ by $color{#4257b2}1$.

$$
xcdot (1)=log_{3} 16.5
$$

$$
x=log_{3} 16.5
$$

Now we can use the calculator to determine $color{#4257b2}log_{3} 16.5$ to find the value of $color{#4257b2}x$.

$$
x=2.552
$$

So the solution of the equation is $boxed{ x=2.552 }$

(d) We would like to solve $color{#4257b2}200 (1.23)^{x}=540$. First, we can divide the two sides by $color{#4257b2}200$ to simplify.

$$
200 (1.23)^{x}=540
$$

$$
dfrac{200 (1.23)^{x}}{200}=dfrac{540}{200}
$$

$$
(1.23)^{x}=2.7
$$

Now we note that the two sides have different bases, so we can take $color{#4257b2}log$ for each side to simplify the right side.

$$
log (1.23)^{x}=log 2.7
$$

Now we note that the right side is a power of logarithm, so we can use the power law of logarithms where $color{#4257b2}log_{m} x^{r}=r log_{m} x$.

$$
x log 1.23=log 2.7
$$

Now we can divide the two sides by $color{#4257b2}log 1.23$ to make $color{#4257b2}x$ in the left side alone.

$$
dfrac{x log 1.23}{log 1.23}=dfrac{log 2.7}{log 1.23}
$$

$$
x=dfrac{log 2.7}{log 1.23}
$$

Now we can use the calculator to determine $color{#4257b2}log 2.7$ and $color{#4257b2}log 1.23$ to find the value of $color{#4257b2}x$.

$$
x=dfrac{0.431}{0.09}=4.798
$$

So the solution of the equation is $boxed{ x=4.798 }$

Large{$text{$text{color{#c34632}(a) $x=2.432$ (c) $x=2.552$
\
\
Large{color{#c34632}(b) $x=3.235$ (d) $x=4.798$}$}$

(a) We would like to solve the equation $color{#4257b2}4^{x}+6 left(4^{-x}right)=5$. First, we can multiply the two sides by $color{#4257b2}4^{x}$ to eliminate $color{#4257b2}4^{-x}$.

$$
4^{x}+6 left(4^{-x}right)=5
$$

$$
left(4^{x}right)cdot left(4^{x}right)+6 left(4^{-x}right)cdot left(4^{x}right)=5left(4^{x}right)
$$

Now we can use the property of exponents $color{#4257b2}x^{a}cdot x^{b}=x^{a+b}$ to simplify the left side.

$$
4^{x+x}+6 left(4^{-x+x}right)=5left(4^{x}right)
$$

$$
4^{2x}+6 left(4^{0}right)=5left(4^{x}right)
$$

$$
4^{2x}+6 (1)=5left(4^{x}right)
$$

$$
4^{2x}+6=5left(4^{x}right)
$$

Note that $color{#4257b2}a^{0}=1$ where $color{#4257b2}a$ is any real number, so we replaced $color{#4257b2}4^{0}$ by $color{#4257b2}1$. Now we can subtract $color{#4257b2}5left(4^{x}right)$ from each side to make the right side equals zero.

$$
4^{2x}+6-5left(4^{x}right)=0
$$

$$
4^{2x}-5left(4^{x}right)+6=0
$$

Now we can let $color{#4257b2}y=4^{x}$, then $color{#4257b2}y^{2}=left(4^{x}right)^{2}=4^{2x}$ and we can substitute these suppositions in our equation.

$$
4^{2x}-5left(4^{x}right)+6=0
$$

$$
y^{2}-5 y+6=0
$$

Now we have a quadratic equation, so we can factor to find the values of $color{#4257b2}y$.

$$
(y-2)(y-3)=0
$$

Now we can use the zero-factor property.

$$
y-2=0 text{or} y-3=0
$$

$$
y=2 text{or} y=3
$$

Now we can do back substitution where we know that $color{#4257b2}y=4^{x}$.

$$
4^{x}=2 text{or} 4^{x}=3
$$

Now we have two cases, so we can solve each case to find the values of $color{#4257b2}x$.

For $color{#4257b2}4^{x}=2$

We know that $color{#4257b2}4=2^{2}$, so we can replace $color{#4257b2}4$ from the left side by $color{#4257b2}2^{2}$.

$$
left(2^{2}right)^{x}=2
$$

$$
2^{(2)cdot (x)}=2
$$

$$
2^{2x}=2
$$

$$
2^{2x}=2^{1}
$$

Now we note that the two sides have the same base $color{#4257b2}2$, so the exponent of the left side must equal the exponent of the right side.

$$
2x=1
$$

Now we can divide the two sides by $color{#4257b2}2$ to find the values of $color{#4257b2}x$.

$$
dfrac{2x}{2}=dfrac{1}{2}
$$

$$
x=dfrac{1}{2}=0.5
$$

So the solution of the first case is $color{#4257b2}x=0.5$.

For $color{#4257b2}4^{x}=3$

Now we note that the two sides have different bases, so can take $color{#4257b2}log_{4}$ fro each side to simplify the left side.

$$
log_{4} 4^{x}=log_{4} 3
$$

Now we note that the left side is a power of logarithms, so we can use the power law of logarithms where $color{#4257b2}log_{m} x^{r}=r log_{m} x$.

$$
x log_{4} 4=log_{4} 3
$$

But we know that $color{#4257b2}log_{a} a=1$, so we can replace $color{#4257b2}log_{4} 4$ from the left side by $color{#4257b2}1$.

$$
xcdot (1)=log_{4} 3
$$

$$
x=log_{4} 3
$$

Now we can use the calculator to determine $color{#4257b2}log_{4} 3$ to find the value of $color{#4257b2}x$.

$$
x=0.792
$$

So the solution of the second case is $color{#4257b2}x=0.792$.

Now we found the solution of each case, so the solutions of the equation are $boxed{ x=0.5 } text{or} boxed{ x=0.792 }$

(b) We would like to solve the equation $color{#4257b2}8 left(5^{2x}right)+8 left(5^{x}right)=6$. First, we can divide the two sides by $color{#4257b2}2$ to simplify.

$$
8 left(5^{2x}right)+8 left(5^{x}right)=6
$$

$$
dfrac{8 left(5^{2x}right)}{2}+dfrac{8 left(5^{x}right)}{2}=dfrac{6}{2}
$$

$$
4 left(5^{2x}right)+4 left(5^{x}right)=3
$$

Now we can subtract $color{#4257b2}3$ from each side to make the right side equals zero.

$$
4 left(5^{2x}right)+4 left(5^{x}right)-3=0
$$

Now we can let $color{#4257b2}y=5^{x}$, then $color{#4257b2}y^{2}=left(5^{x}right)^{2}=5^{2x}$ and we can substitute these suppositions in our equation.

$$
4 left(5^{2x}right)+4 left(5^{x}right)-3=0
$$

$$
4y^{2}+4 y-3=0
$$

Now we have a quadratic equation, so we can factor to find the values of $color{#4257b2}y$.

$$
(2y-1)(2y+3)=0
$$

Now we can use the zero-factor property.

$$
2y-1=0 text{or} 2y+3=0
$$

$$
y=dfrac{1}{2}=0.5 text{or} y=-dfrac{3}{2}=-1.5
$$

Now we can do back substitution where we know that $color{#4257b2}y=5^{x}$.

$$
y=0.5 text{or} y=-1.5
$$

$$
5^{x}=0.5 text{or} 5^{x}=-1.5
$$

But we know that if $color{#4257b2}a$ and $color{#4257b2}x$ are any real numbers, so $color{#4257b2}a^{x} > 1$ because we know that the result of any exponent must be positive, so the solution of $color{#4257b2}5^{x}=-1.5$ is refused.

$$
5^{x}=0.5
$$

Now we note that the two sides have different bases, so can take $color{#4257b2}log_{5}$ fro each side to simplify the left side.

$$
log_{5} 5^{x}=log_{5} 0.5
$$

Now we note that the left side is a power of logarithms, so we can use the power law of logarithms where $color{#4257b2}log_{m} x^{r}=r log_{m} x$.

$$
x log_{5} 5=log_{5} 0.5
$$

But we know that $color{#4257b2}log_{a} a=1$, so we can replace $color{#4257b2}log_{5} 5$ from the left side by $color{#4257b2}1$.

$$
xcdot (1)=log_{5} 0.5
$$

$$
x=log_{5} 0.5
$$

Now we can use the calculator to determine $color{#4257b2}log_{5} 0.5$ to find the value of $color{#4257b2}x$.

$$
x=-0.431
$$

So the solution of the equation is $boxed{ x=-0.431 }$

Large{$text{color{#c34632}(a) $x=0.5 {color{Black}text{or}} x=0.792$ (b) $x=-0.431$}$

We would like to know the time which a certain substance with mass $color{#4257b2}20 text{g}$ will take to decay to $color{#4257b2}7 text{g}$. First, we can use the formula $color{#4257b2}M(t)=Pleft(dfrac{1}{2}right)^{frac{t}{h}}$ where $color{#4257b2}M(t)$ is the mass after decay, $color{#4257b2}P$ is the mass of the substance before decay, $color{#4257b2}t$ is the time it will take to decay and $color{#4257b2}h$ is the half life time. Now we know that the half life time of the substance $color{#4257b2}h=3.6 text{days}$, the mass of the substance before the decay $color{#4257b2}P=20 text{g}$ and the mass of the substance after the decay $color{#4257b2}M=7 text{g}$, so we can substitute these values in the formula of the mass to calculate the time.

$$
M(t)=Pleft(dfrac{1}{2}right)^frac{t}{h}
$$

$$
7=20left(dfrac{1}{2}right)^{frac{t}{3.5}}
$$

Now we can divide the two sides by $color{#4257b2}20$.

$$
dfrac{7}{20}=dfrac{20left(0.5right)^{frac{t}{3.6}}}{20}
$$

$$
0.35=left(0.5right)^{frac{t}{3.6}}
$$

Now we note the two sides have different bases, so we can take $color{#4257b2}log$ for each side to simplify the right side.

$$
log 0.35=log left(0.5right)^{frac{t}{3.6}}
$$

Now we note that the right is a power of logarithm, so we can use the power law of logarithms where $color{#4257b2}log_{m} x^{r}=r log_{m} x$.

$$
log 0.35=dfrac{t}{3.6} log 0.5
$$

$$
log 0.35=dfrac{t log 0.5}{3.6}
$$

Now we can multiply the two sides by $color{#4257b2}dfrac{3.6}{log 0.5}$ to make $color{#4257b2}t$ in the right side alone.

$$
left(log 0.35right)cdot left(dfrac{3.6}{log 0.5}right)=left(dfrac{t log 0.5}{3.6}right)cdot left(dfrac{3.6}{log 0.5}right)
$$

$$
dfrac{3.6 log 0.35}{log 0.5}=left(dfrac{t cancel{log 0.5}}{cancel{3.6}}right)cdot cancel{left(dfrac{3.6}{log 0.5}right)}
$$

$$
dfrac{3.6 log 0.35}{log 0.5}=t
$$

Now we can use the calculator to determine $color{#4257b2}log 0.35$ and $color{#4257b2}log 0.5$ to find the value of $color{#4257b2}t$.

$$
dfrac{3.6 (-0.456)}{-0.301}=t
$$

$$
5.45=t
$$

So the time which the substance will take to decay to mass $color{#4257b2}7 text{g}$ is $boxed{ t=5.45 text{days} }$

Large{$text{color{#c34632}$t=5.45 text{days}$}$

(a) We would like to solve the equation $color{#4257b2}log_{5} (2x-1)=3$. First, we have an equation on the logarithmic form, so we can convert it to the exponential form where we know that if $color{#4257b2}log_{a} x=b$, then $color{#4257b2}x=a^{b}$.

$$
log_{5} (2x-1)=3
$$

$$
2x-1=5^{3}
$$

$$
2x-1=125
$$

Now we can add $color{#4257b2}1$ to each side to make $color{#4257b2}x$ in the left side alone.

$$
2x-1+1=125+1
$$

$$
2x=126
$$

Now we can divide the two sides by $color{#4257b2}2$ to find the value of $color{#4257b2}x$.

$$
dfrac{2x}{2}=dfrac{126}{2}
$$

$$
x=63
$$

So the solution of the equation is $boxed{ x=63 }$

(b) We would like to solve the equation $color{#4257b2}log 3x=4$. First, we have an equation on the logarithmic form, so we can convert it to the exponential form where we know that if $color{#4257b2}log x=b$, then $color{#4257b2}x=10^{b}$.

$$
log 3x=4
$$

$$
3x=10^{4}
$$

$$
3x=10000
$$

Now we can divide the two sides by $color{#4257b2}3$ to find the value of $color{#4257b2}x$.

$$
dfrac{3x}{3}=dfrac{10000}{3}
$$

$$
x=dfrac{10000}{3}
$$

So the solution of the equation is $boxed{ x=dfrac{10000}{3} }$

(c) We would like to solve the equation $color{#4257b2}log_{4} (3x-5)=log_{4} 11+log_{4} 2$. First, we note that the right side is a sum of logarithms, so we can use the product law of logarithms where $color{#4257b2}log_{a} x+log_{a} y=log_{a} xy$.

$$
log_{4} (3x-5)=log_{4} 11+log_{4} 2
$$

$$
log_{4} (3x-5)=log_{4} (11)(2)
$$

$$
log_{4} (3x-5)=log_{4} 22
$$

Now we note that the two sides each of them is a logarithm with the same base, so the two expressions must equal each other because we know that if $color{#4257b2}log_{a} M=log_{a} N$, then $color{#4257b2}M=N$.

$$
log_{4} (3x-5)=log_{4} 22
$$

$$
3x-5=22
$$

Now we can add $color{#4257b2}5$ to each side to make $color{#4257b2}3x$ in the left side alone.

$$
3x-5+5=22+5
$$

$$
3x=27
$$

Now we can divide the two sides by $color{#4257b2}3$ to find the value of $color{#4257b2}x$.

$$
dfrac{3x}{3}=dfrac{27}{3}
$$

$$
x=9
$$

So the solution of the equation is $boxed{ x=9 }$

(d) We would like to solve the equation $color{#4257b2}log (4x-1)=log (x+1)+log 2$. First, we note that the right side is a sum of logarithms, so we can use the product law of logarithms where $color{#4257b2}log_{a} x+log_{a} y=log_{a} xy$.

$$
log (4x-1)=log (x+1)+log 2
$$

$$
log (4x-1)=log (x+1)cdot (2)
$$

$$
log (4x-1)=log (2x+2)
$$

Now we note that the two sides each of them is a logarithm with the same base, so the two expressions must equal each other because we know that if $color{#4257b2}log_{a} M=log_{a} N$, then $color{#4257b2}M=N$.

$$
4x-1=2x+2
$$

Now we can add $color{#4257b2}-2x+1$ to each side to make $color{#4257b2}x$ in the left side alone.

$$
4x-1-2x+1=2x+2-2x+1
$$

$$
4xcancel{-1}-2xcancel{+1}=cancel{2x}+2cancel{-2x}+1
$$

$$
2x=3
$$

Now we can divide the two sides by $color{#4257b2}2$ to find the value of $color{#4257b2}x$.

$$
dfrac{2x}{2}=dfrac{3}{2}
$$

$$
x=dfrac{3}{2}
$$

So the solution of the equation is $boxed{ x=dfrac{3}{2} }$

Large{$text{color{#c34632}(a) $x=63$ (c) $x=9$
\
\
(b) $x=dfrac{10000}{3}$ (d) $x=dfrac{3}{2}$}$

(a) We would like to solve the equation $color{#4257b2}log (x+9)-log x=1$. First, we note that the left side is a difference of logarithms, so we can use the quotient law of logarithms where $color{#4257b2}log_{a} x-log_{a} y=log_{a} left(dfrac{x}{y}right)$.

$$
log (x+9)-log x=1
$$

$$
log left(dfrac{x+9}{x}right)=1
$$

Now we have an equation on the logarithmic form, so we can convert it to the exponential form where we know that if $color{#4257b2}log x=b$, then $color{#4257b2}x=10^{b}$.

$$
log left(dfrac{x+9}{x}right)=1
$$

$$
dfrac{x+9}{x}=10^{1}
$$

$$
dfrac{x+9}{x}=10
$$

Now we can multiply the two sides by $color{#4257b2}x$ eliminate the denominator in the left side.

$$
(x)cdot left(dfrac{x+9}{x}right)=10 x
$$

$$
cancel{(x)}cdot left(dfrac{x+9}{cancel{x}}right)=10x
$$

$$
x+9=10x
$$

Now we can subtract $color{#4257b2}x$ from each side to make the variable $color{#4257b2}x$ in the right side alone.

$$
x+9-x=10x-x
$$

$$
9=9x
$$

Now we can divide the two sides by $color{#4257b2}9$.

$$
dfrac{9}{9}=dfrac{9x}{9}
$$

$$
1=x
$$

Now we found one solution for $color{#4257b2}x$, so the next step is to check this value in the original equation to know if they verify it or not.

For $color{#4257b2}x=1$

$$
log (x+9)-log x=1
$$

$$
log (1+9)-log 1=1
$$

$$
log 10-log 1=1
$$

$$
1-0=1
$$

$$
1=1
$$

So the solution $color{#4257b2}x=1$ is true because it verifies the original equation.

So the solution of the equation is $boxed{ x=1 }$

(b) We would like to solve the equation $color{#4257b2}log x+log (x-3)=1$. First, we note that the left side is a sum of logarithms, so we can use the product law of logarithms where $color{#4257b2}log_{a} x+log_{a} y=log_{a} xy$.

$$
log x+log (x-3)=1
$$

$$
log x(x-3)=1
$$

$$
log (x^{2}-3x)=1
$$

Now we have an equation on the logarithmic form, so we can convert it to the exponential form where we know that if $color{#4257b2}log x=b$, then $color{#4257b2}x=10^{b}$.

$$
log (x^{2}-3x)=1
$$

$$
x^{2}-3x=10^{1}
$$

$$
x^{2}-3x=10
$$

Now we can subtract $color{#4257b2}10$ from each side to make the right side equals zero.

$$
x^{2}-3x-10=0
$$

Now we have a quadratic equation, so we can factor it to find the values of $color{#4257b2}x$.

$$
(x-5)(x+2)=0
$$

Now we can use the zero-factor property.

$$
x-5=0 text{or} x+2=0
$$

$$
x=5 text{or} x=-2
$$

Now we found two solutions for $color{#4257b2}x$, so the next step is to check these values in the original equation to know if they verify it or not.

For $color{#4257b2}x=5$

$$
log x+log (x-3)=1
$$

$$
log 5+log (5-3)=1
$$

$$
log 5+log 2=1
$$

$$
0.7+0.3=1
$$

$$
1=1
$$

So the solution $color{#4257b2}x=5$ is true because it verifies the original equation.

For $color{#4257b2}x=-2$

$$
log x+log (x-3)=1
$$

$$
log (-2)+log (-2-3)=1
$$

$$
log (-2)+log (-5)=1
$$

But we know that $color{#4257b2}log -2$ and $color{#4257b2}log -5$ are undefined because the number inside the logarithm must be positive, so the solution $color{#4257b2}x=-2$ is false because it doesn’t verify the original equation.

So the solution of the equation is $boxed{ x=5 }$

(c) We would like to solve the equation $color{#4257b2}log (x-1)+log (x+2)=1$. First, we note that the left side is a sum of logarithms, so we can use the product law of logarithms where $color{#4257b2}log_{a} x+log_{a} y=log_{a} xy$.

$$
log (x-1)+log (x+2)=1
$$

$$
log (x-1)(x+2)=1
$$

$$
log (x^{2}+x-2)=1
$$

Now we have an equation on the logarithmic form, so we can convert it to the exponential form where we know that if $color{#4257b2}log x=b$, then $color{#4257b2}x=10^{b}$.

$$
x^{2}+x-2=10^{1}
$$

$$
x^{2}+x-2=10
$$

Now we can subtract $color{#4257b2}10$ from each side to make the right side equals zero.

$$
x^{2}+x-2-10=0
$$

$$
x^{2}+x-12=0
$$

Now we have a quadratic equation, so we can factor it to find the values of $color{#4257b2}x$.

$$
(x-3)(x+4)=0
$$

Now we can use the zero-factor property.

$$
x-3=0 text{or} x+4=0
$$

$$
x=3 text{or} x=-4
$$

Now we found two solutions for $color{#4257b2}x$, so the next step is to check these values in the original equation to know if they verify it or not.

For $color{#4257b2}x=3$

$$
log (x-1)+log (x+2)=1
$$

$$
log (3-1)+log (3+2)=1
$$

$$
log 2+log 5=1
$$

$$
0.3+0.7=1
$$

$$
1=1
$$

So the solution $color{#4257b2}x=3$ is true because it verifies the original equation.

For $color{#4257b2}x=-4$

$$
log (x-1)+log (x+2)=1
$$

$$
log (-4-1)+log (-4+2)=1
$$

$$
log (-5)+log (-2)=1
$$

But we know that $color{#4257b2}log -5$ and $color{#4257b2}log -2$ are undefined because the number inside the logarithm must be positive, so the solution $color{#4257b2}x=-4$ is false because it doesn’t verify the original equation.

So the solution of the equation is $boxed{ x=3 }$

(d) We would like to solve the equation $color{#4257b2}log sqrt{x^{2}-1}=2$. First, we have an equation on the logarithmic form, so we can convert it to the exponential form where we know that if $color{#4257b2}log x=b$, then $color{#4257b2}x=10^{b}$.

$$
log sqrt{x^{2}-1}=2
$$

$$
sqrt{x^{2}-1}=10^{2}
$$

$$
sqrt{x^{2}-1}=100
$$

Now we square the two sides to eliminate the square root in the left side.

$$
left(sqrt{x^{2}-1}right)^{2}=100^{2}
$$

$$
x^{2}-1=10000
$$

Now we can add $color{#4257b2}1$ to each side to make $color{#4257b2}x^{2}$ in the left side alone.

$$
x^{2}=10000+1
$$

$$
x^{2}=10001
$$

Now we can take the square root for each side to find the value of $color{#4257b2}x$.

$$
x=pm sqrt{10001}
$$

$$
x=pm 100.005
$$

Now we found two solutions for $color{#4257b2}x$, so the next step is to check these values in the original equation to know if they verify it or not.

For $color{#4257b2}x=100.005$

$$
log sqrt{x^{2}-1}=2
$$

$$
log sqrt{(100.005)^{2}-1}=2
$$

$$
log sqrt{10001-1}=2
$$

$$
log sqrt{10000}=2
$$

$$
log 100=2
$$

$$
2=2
$$

So the solution $color{#4257b2}x=100.005$ is true because it verifies the original equation.

For $color{#4257b2}x=-100.005$

$$
log sqrt{x^{2}-1}=2
$$

$$
log sqrt{(-100.005)^{2}-1}=2
$$

$$
log sqrt{10001-1}=2
$$

$$
log sqrt{10000}=2
$$

$$
log 100=2
$$

$$
2=2
$$

So the solution $color{#4257b2}x=-100.005$ is true because it verifies the original equation.

So the solutions of the equation are $boxed{ x=100.005 } text{or} boxed{ x=-100.005 }$

Large{$text{color{#c34632}(a) $x=1$ (c) $x=3$
\
\
(b) $x=5$ (d) $x=100.005 {color{Black}text{or}} x=-100.005$}$

We would like to determine the intensity of a baby screaming $color{#4257b2}I$ where the relation is $color{#4257b2}L=10log left(dfrac{I}{I_{0}}right)$ if the noise level is $color{#4257b2}100 text{dB}$ and $color{#4257b2}I_{0}=10^{-12}$. First, sine we know the relation between the noise level $color{#4257b2}L$ and the intensity $color{#4257b2}I$, we can substitute the values of the noise level and $color{#4257b2}I_{0}$ to determine the intensity of a baby screaming.

$$
L=10log left(dfrac{I}{I_{0}}right)
$$

$$
100=10log left(dfrac{I}{10^{-12}}right)
$$

Now we can divide the two sides by $color{#4257b2}10$.

$$
dfrac{100}{10}=dfrac{10log left(dfrac{I}{10^{-12}}right)}{10}
$$

$$
10=log left(dfrac{I}{10^{-12}}right)
$$

Now we note that our equation is on the logarithmic form, so we can convert it to the exponential form where we know that if $color{#4257b2}log x=b$, then $color{#4257b2}x=10^{b}$.

$$
10=log left(dfrac{I}{10^{-12}}right)
$$

$$
dfrac{I}{10^{-12}}=10^{10}
$$

Now we can multiply the two sides by $color{#4257b2}10^{-12}$.

$$
left(10^{-12}right)cdot left(dfrac{I}{10^{-12}}right)=(10)^{10}cdot (10)^{-12}
$$

$$
cancel{left(10^{-12}right)}cdot left(dfrac{I}{cancel{10^{-12}}}right)=(10)^{10}cdot (10)^{-12}
$$

$$
I=(10)^{10}cdot (10)^{-12}
$$

Now we can use the property of exponents $color{#4257b2}x^{a}cdot x^{b}=x^{a+b}$.

$$
I=(10)^{10-12}
$$

$$
I=10^{-2}
$$

$$
I=.01
$$

So the intensity of a baby screaming is $boxed{ I=.01 text{W/$m^{2}$} }$

$$text{$text{color{#c34632}I=.01 text{W/m^{2$$}$}$}$

$$
text{color{#4257b2}(a) Determine the intensity of an engine that is rated of $82$ dB}
$$

$$
L=10logleft(dfrac{I}{I_{o}}right) 82=10logleft(dfrac{I}{10^{-12}}right)
$$

Divide both of sides by $(10)$ as follows:

$$
8.2=logleft(dfrac{I}{10^{-12}}right)
$$

Use the exponential standard form as follows:

$$
because log_{10}(x)=b x=10^b
$$

$$
therefore left(dfrac{I}{10^{-12}}right)=10^{8.2}
$$

Isolate the $(I)$ in the left side as follows:

$$
I=10^{8.2}cdot10^{-12} I=10^{8.2-12}
$$

$$
I=10^{-3.8} text{W/m}^2
$$

$$
text{color{#c34632}$I=10^{-3.8} text{W/m}^2$}
$$

If one earthquake has a magnitude of $(6.2)$ on the Richter scale and second earthquake has a magnitude of $(5.5)$ on the Richter scale. Compare the intensities of two earthquakes.

$$
L=10logleft(dfrac{I}{I_{o}}right) 6.2=10logleft(dfrac{I}{I_{o}}right)
$$

$$
L=10logleft(dfrac{I}{I_{o}}right) 5.5=10logleft(dfrac{I}{I_{o}}right)
$$

Divide both of sides by $(10)$ as follows:

$$
0.62=logleft(dfrac{I}{I_{o}}right)
$$

$$
0.55=logleft(dfrac{I}{I_{o}}right)
$$

Use the exponential standard form as follows:

$$
because log_{10}(x)=b x=10^b
$$

$$
therefore left(dfrac{I_{6.2}}{I_{o}}right)=10^{0.62}
$$

$$
therefore left(dfrac{I_{5.5}}{I_{o}}right)=10^{0.55}
$$

Isolate the $(I)$ in the left side as follows:

$$
I_{6.2}=10^{0.62}cdot I_{o}
$$

$$
I_{5.5}=10^{0.55}cdot I_{o}
$$

$$
dfrac{I_{6.2}}{I_{5.5}}=dfrac{10^{0.62}cdot I_{o}}{10^{0.55}cdot I_{o}} dfrac{I_{6.2}}{I_{5.5}}=dfrac{1}{10^{0.07}}=1.175
$$

$$
text{color{#4257b2}$therefore $The sound of the first earthquake is $(1.175)$ times less intense than the second earthquake.}
$$

$$
text{color{#c34632}The sound of the first earthquake is $(1.175)$ times less intense than the second earthquake.}
$$

$$
text{color{#4257b2}Pure water has a $(PH=7)$.How many times more acidic is milk with a $(PH=6.4)$}
$$

According to the standard form of the concentration equation $PH=-log(H^+)$

$$
7=-log(H^+)
$$

$$
6.4=-log(H^+)
$$

Multiply the entire equation by $(-1)$ as follows:

$$
-7=log(H^+)
$$

$$
-6.4=log(H^+)
$$

Use exponential standard form as follows:

$$
10^{-7}=H_{text{water}}^{+}
$$

$$
10^{-6.4}=H_{text{milk}}^{+}
$$

$$
dfrac{H_{text{water}}^{+}}{H_{text{milk}}^{+}}=dfrac{10^{-7}}{10^{-6.4}}
$$

$$
dfrac{H_{text{water}}^{+}}{H_{text{milk}}^{+}}=10^{-7+6.4}=10^{-0.6}
$$

$$
dfrac{H_{text{water}}^{+}}{H_{text{milk}}^{+}}=dfrac{1}{10^{0.6}}=0.25119
$$

$$
text{color{#4257b2}$therefore$ The milk is more acidic by $(0.25119)$ times more than the pure water.}
$$

$$
text{color{#c34632}The milk is more acidic by $(0.25119)$ times more than the pure water.}
$$

$$
text{color{#4257b2}Does in an increase the acidity from $(PH=4.7)$ to $(PH=2.3)$ results in the same change in the ion hydrogen concentration as a decrease in alkalinity from $(PH=12.5)$ to $(PH=10.1)$. Explain}
$$

In standard condition, if the $(PH7)$ that indication is more alkalinity.

In this case, the acidity increases when it away from $(7)$ and decrease when it approaches from $(7)$

Alkalinity increases when it away from $(7)$ and decrease when it approaches from $(7)$

$$
text{color{#c34632}Acidity increases when it away from $(7)$ and decrease \ when it approaches from $(7)$
\ \
Alkalinity increases when it away from $(7)$ and decrease \ when it approaches from $(7)$}
$$

$$
text{color{#4257b2}How long will it take for the population to decline to $(15000)$, if the population town decreasing a rate by $(1.6)$ hundred percent per year and the population today is $(20000)$ }
$$

Interest rate per year is $(0.016) cdot (20000)=320$ population per year

$a_{0}=20000$ dollar

$$
a_{1}=20000-320=19680=a_{0}-320
$$

$$
a_{2}=19680-320=19360=a_{1}-320=a_{0}-320-320=a_{0}-2(320)
$$

$$
color{#4257b2}a_{n}=20000-320n
$$

$$
15000=20000-320n
$$

Isolate the variables on the left side as follows:

$$
20000-15000=320n 320n=5000
$$

Divide both of sides by $(320)$ as follows:

$$
n=dfrac{5000}{320} n=15.625
$$

$$
text{color{#4257b2}$therefore$ The time needed to population decline to $(15000)$ is $(15.625)$ year.}
$$

$$
text{color{#c34632}The time needed to population decline to $(15000)$ is $(15.625)$ year.}
$$

Note that the exponential growth function we can write as
$$
f(x)=a(1+r)^x,tag{1}
$$
where $a$ is the initial population, $r$ is the rate of growth, and $x$ is the number of growth periods.

The average rate of change over a time period $[t_1,t_2]$ is
$$
r_a=dfrac{f(t_2)-f(t_1)}{t_2-t_1}.tag{2}$$

*(a)* Using Eq, $(2)$ over the entire time period by setting $t_1=1950$, $t_2=1994$, $f(t_1)=132,459$ and $f(t_2)=514,013$ we obtain
$$
r_i=dfrac{514,013-132,459}{1994-1950}=8,671 mathrm{people/year}.$$

*(b)* Using Eq, $(2)$ over the first $30$ years by setting $t_1=1950$, $t_2=1980$, $f(t_1)=132,459$ and $f(t_2)=345,890$ we obtain
$$
r_i=dfrac{345,890-132,459}{1980-1950}=7,114 mathrm{people/year}.$$

Since the rate of change in population over the first $30$ years is smaller than the rate of change over the whole time period, we can conclude that the population growth over the first $30$ years was slower than over than whole time period.

*(c)* The initial population is $a=132,459$. Note that the rate of growth $r$ we can obtain by using the date from the table and Eq.$(1)$ over any time period. If we choose this time period to be first $20$ years, substituting the values in Eq.$(1)$ we obtain
$$
253,539=132,458(1+r)^{20}.$$
Dividing by $132,458$ throughout and reversing the direction of equation, we obtain:
$$
begin{align*}
(1+r)^{20}&=dfrac{253,539}{132,458}\
(1+r)^{20}&=1.9&&text{[Rise both sides to the power $frac{1}{20}$]}\
1+r&=1.9^{tfrac{1}{20}}\
1+r&=1.03.
end{align*}$$
Using $1+r=1.03$ and $a=132,459$ we can rewrite Eq.$(1)$ for the population growth in this city
$$
f(x)=132,459(1.03)^x.$$

The exponential function we can also obtain using the graphing calculator. Press STAT ENTER . Move the cursor over to the first position in L1,
and enter the values for time, setting $1950=0$, $1970=20$ nad so on. Press ENTER after each value. Repeat this for the column in L2 entering the population. To determine the equation of the line or curve of best fit, press STAT and move right over to CALC. Press 0 ExpReg. If under Xlist and Ylist is not L1 and L2, press 2ND 1 , 2ND 2. Scroll down to Calculate and press ENTER. You will obtain values $a=134321.86$ and $b=1.0314…$. Note that $aapprox134322$ ans $bapprox1.03$. Hence, our exponential function is
$$f(x)=134,322(1.03)^x.$$

*(d)* To find an instantaneous rate, graph the function $f(x)=134,322(1.03)^x$ on a graphing calculator. Use TRACE and left and right arrows to find values on either side of the given year, reading out two $x$ values $x_1$, $x_2$ and two $y$ values $y_1$,$y_2$. The instantaneous rate is
$$
r_i=dfrac{y_2-y_1}{x_2-x_1}.tag{2}$$

*(i)* Note that the year $1970$ is $20$ years from the initial year. Hence, trace the $x$ value as closest to the value $20$ and read out the values of $x$. Answers may vary, but we can choose $x_1=19.8$ and $y_1=241080$. Moving cursor to pass the value $20$, we can read out $x_2=20.2$ and $y_2=244131$. Now using the Eq. $(2)$, we obtain
$$r_i=dfrac{244131-241080}{20.2-19.8}=7,627$$

*(ii)* Note that the year $1990$ is $40$ years from the initial year. Hence, trace the $x$ value as closest to the value $40$ and read out the values of $x$. Answers may vary, but we can choose $x_1=39.8$ and $y_1=435416$. Moving cursor to pass the value $20$, we can read out $x_2=40.2$ and $y_2=440928$. Now using the Eq. $(2)$, we obtain
$$r_i=dfrac{440928-435416}{40.2-39.8}=13,780$$

a)$r_i=8,671 mathrm{people/year}$
b)$r_i=7,114 mathrm{people/year}$
c) $f(x)=134,322(1.03)^x$
d) i)$r_i=7,627$
ii)$r_i=13,780$