
All Solutions
Page 111: Check Your Understanding
$dfrac{f(a+h)-f(a)}{h}$ where $h$ is a very small value.
$C(1.5)= 0.3(1.5)^2-0.9(1.5)+1.675=1$
$C(1.501)=0.3(1.501)^2-0.9(1.501)+1.675=1.000 000 3$
$dfrac{1.000 000 3 – 1}{0.01}= 0.000 03$
When $1500$ items are produced, the instantaneous rate of change is zero. Therefore, the most economcal production level occurs when $1500$ items are produced.
$dfrac{Delta{P}}{Delta{t}}=dfrac{P(3.01)-P(2.99)}{3.01-2.99}=dfrac{0}{0.02}=0$
So, $textbf{the average rate of change in blood pressure at $t=3$ is }0$.
$textbf{Tangent line must have a positive slope on the left side of point}$ $(a, f(a))$.
#### (b)
$textbf{Tangent line must have a negative slope on the right side of point}$ $(a, f(a))$.
$textbf{Tangent line must have a negative slope on the left side of point $(a, f(a))$}$.
#### (b)
$textbf{Tangent line must have a positive slope on the right side of point $(a, f(a))$}$.
Let’s take point $(-7,-10)$ which is on the left side of given point $(-6,-10.5)$ and calculate slope of the tangent line before given point:
$textbf{slope}$ = $dfrac{-10.5+10}{-6+7}=dfrac{-0.5}{1}=-0.5$
So, we can see that this $textbf{slope on the left side is negative}$.
Now, let’s calculate slope on the right side of given point $(-6.-10.5)$, for this, we will use point $(-5,-10)$:
$textbf{slope}$ = $dfrac{-10.5+10}{-6+5}=dfrac{-0.5}{-1}=0.5$.
So, we can see that this $textbf{slope on the right side is postive}$.
Using two of previous tasks, we can conclude that point $(-6,-10.5)$ is $textbf{minumum}$.
#### (b)
Let’s take point $(0,9)$ which is on the left side of given point $(0.5,10.5)$ and calculate slope of the tangent line before given point:
$textbf{slope}$ = $dfrac{10.5-9}{0.5-0}=dfrac{0.5}{0.5}=1$
So, we can see that this $textbf{slope on the left side is positive}$.
Now, let’s calculate slope on the right side of given point $(0.5,10.5)$, for this, we will use point $(1,9)$:
$textbf{slope}$ = $dfrac{9-10.5}{1-0.5}=dfrac{-0.5}{0.5}=-1$.
So, we can see that this $textbf{slope on the right side is negative}$.
Using two of previous tasks, we can conclude that point $(0.5,10.5)$ is $textbf{maximum}$.
Let’s take point $(0,0)$ which is on the left side of given point $(dfrac{pi}{2},5)$ and calculate slope of the tangent line before given point:
$textbf{slope}$ = $dfrac{5-0}{dfrac{pi}{2}-0}=dfrac{5}{dfrac{pi}{2}}=dfrac{10}{pi}$
So, we can see that this $textbf{slope on the left side is positive}$.
Now, let’s calculate slope on the right side of given point $(dfrac{pi}{2},5)$, for this, we will use point $(pi,0)$:
$textbf{slope}$ = $dfrac{0-5}{pi-dfrac{pi}{2}}=-dfrac{5}{dfrac{pi}{2}}=-dfrac{10}{pi}$.
So, we can see that this $textbf{slope on the right side is negative}$.
Using two of previous tasks, we can conclude that point $(dfrac{pi}{2},5)$ is $textbf{maximum}$.
#### (d)
Let’s take point $(-dfrac{pi}{2},4.5)$ which is on the left side of given point $(0,4.5)$ and calculate slope of the tangent line before given point:
$textbf{slope}$ = $dfrac{-4.5-4.5}{0+dfrac{pi}{2}}=dfrac{-9}{dfrac{pi}{2}}=-dfrac{18}{pi}$
So, we can see that this $textbf{slope on the left side is negative}$.
Now, let’s calculate slope on the right side of given point $(0,4.5)$, for this, we will use point $(dfrac{pi}{2},4.5)$:
$textbf{slope}$ = $dfrac{4.5+4.5}{dfrac{pi}{2}-0}=dfrac{9}{dfrac{pi}{2}}=dfrac{18}{pi}$.
So, we can see that this $textbf{slope on the right side is positive}$.
Using two of previous tasks, we can conclude that point $(0,4.5)$ is $textbf{minimum}$.
#### (a)
Here we have that:
$f'(x)=2x-4$ $Rightarrow$ $f'(2)=0$
$textbf{So, we can conclude that point $(2,1)$ is maximum or minimum of given function.}$
#### (b)
Here we have that:
$f'(x)=-2x-12$ $Rightarrow$ $f'(-6)=0$
$textbf{So, we can conclude that point $(-6,41.75)$ is maximum or minimum of given function.}$
#### (c)
Here we have that:
$f'(x)=2x-9$ $Rightarrow$ $f'(4.5)=0$
$textbf{So, we can conclude that point $(4.5,-20.25)$ is maximum or minimum of given function.}$
Here we have that:
$f'(x)=-3sin{x}$ $Rightarrow$ $f'(0)=0$
$textbf{So, we can conclude that point $(0,3)$ is maximum or minimum of given function.}$
#### (e)
Here we have that:
$f'(x)=3x^2-3$ $Rightarrow$ $f'(-1)=0$
$textbf{So, we can conclude that point $(-1,2)$ is maximum or minimum of given function.}$
#### (f)
Here we have that:
$f'(x)=-3x^2+12$ $Rightarrow$ $f'(2)=0$
$textbf{So, we can conclude that point $(2,15)$ is maximum or minimum of given function.}$
$h'(t)=-32t+90=0$ $Rightarrow$ $t=2.81$ s
So, at $t=2.81$ s, pilot will be at maximum altitude.$textbf{We have that slope of tangent line at certain points before that maximum alitude is positive, and slope of tangent line after maximum point is negtive}$, as we explained in earlier tasks.
(i)
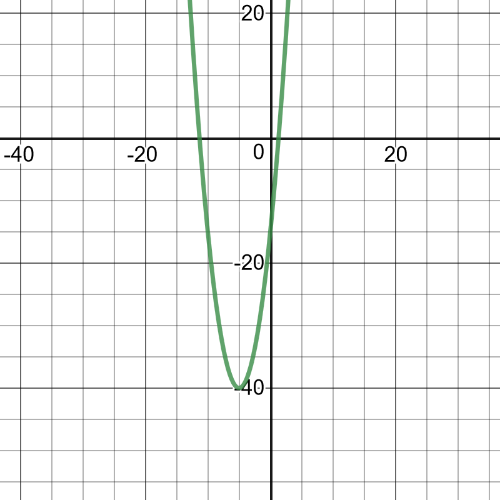
From the graph we can see that $textbf{minimum point is}$ $(-5,-40)$.
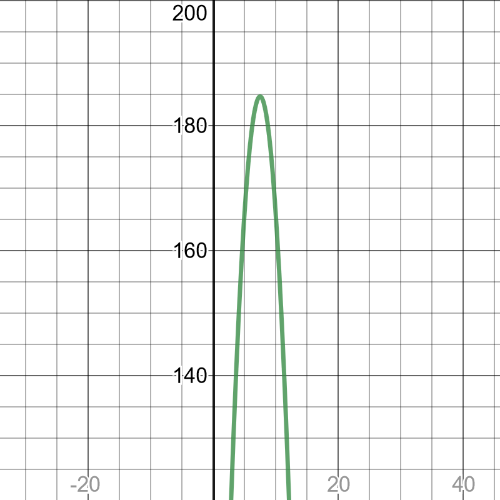
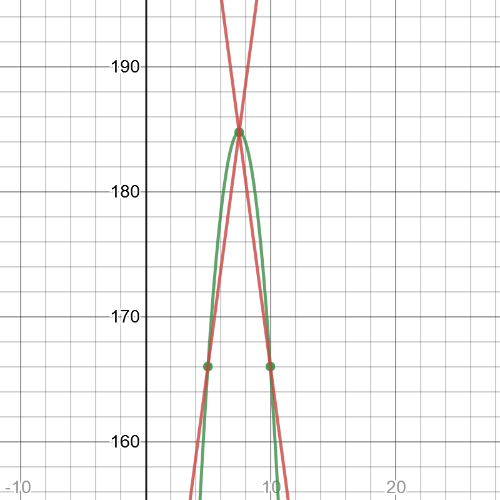
We can see that $textbf{maximum point}$ is $(7.5,184.75)$.
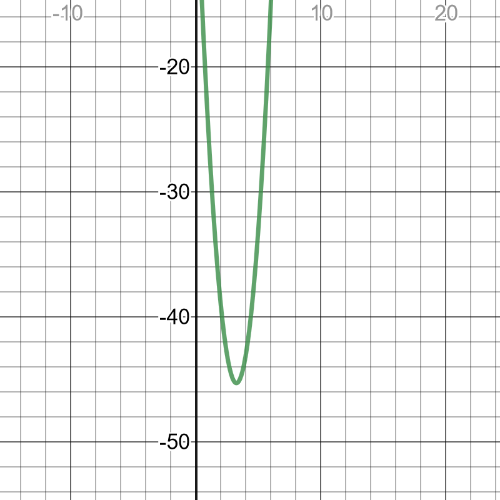
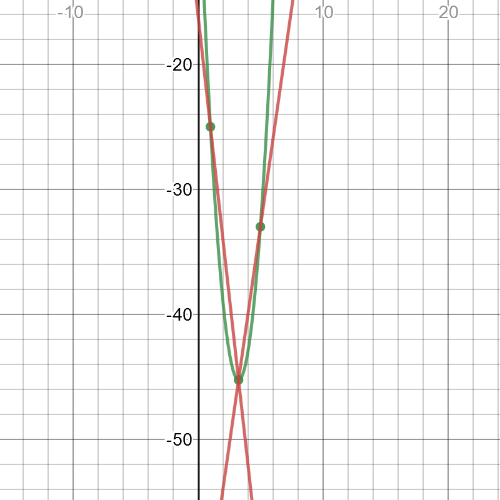
We can from the garph that $textbf{minimum point}$ is $(3.25,-45.25)$.
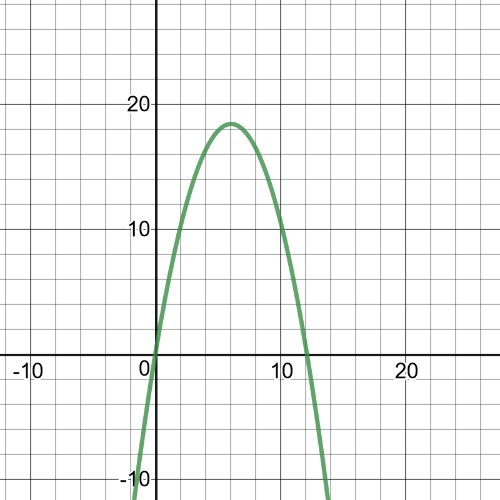
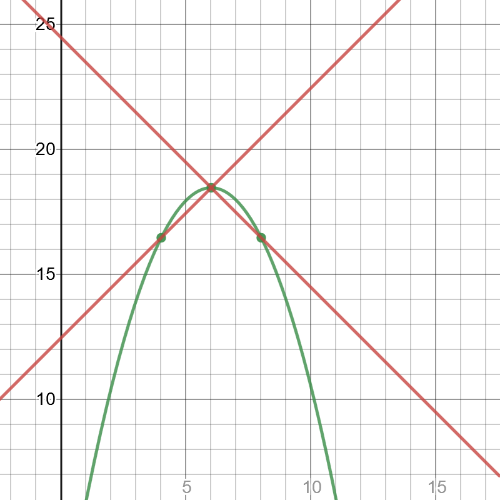
We can see from the graph that $textbf{maximum point}$ is $(6,18.45)$.
(i)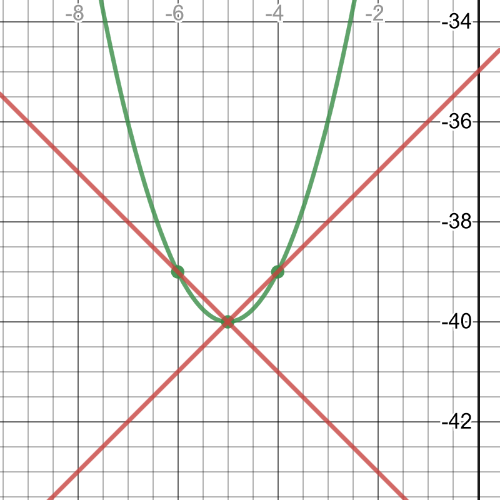
According to previous tasks, we can see that when we have $textbf{maximum point}$, slope of the tangent line before that point has $textbf{positive slope}$, and slope of the tangent line after that point has $textbf{negative slope}$.
And when we have $textbf{minimum point}$, slope of the tangent line before that point has $textbf{negative slope}$, and slope of the tangent line after that point has $textbf{positive slope}$.
(i)
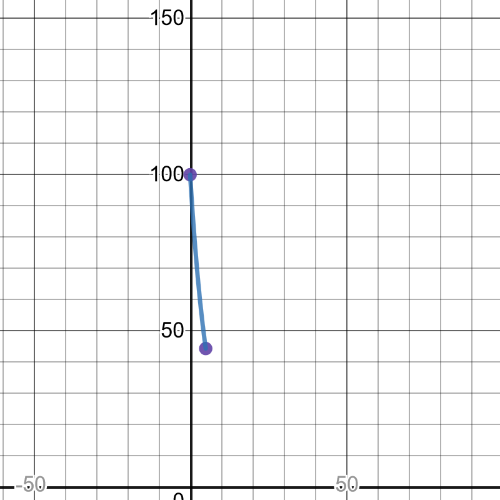
From the following graph we can see that $textbf{minimum point}$ is $(5,44.38)$ and $textbf{maximum point}$ is $(0,100)$ on given interval in the task.
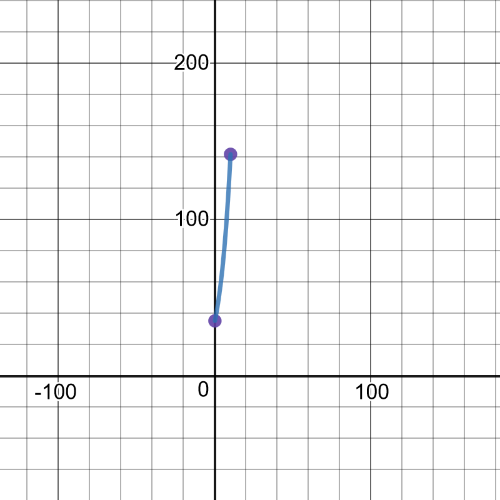
We can see from the following graph that $textbf{minimum point}$ is $(0,35)$ and $textbf{maximum point}$ is $(10,141.59)$ on given interval in this task:
$textbf{The maximum value}$ on given interval for value $x$, $aleq{x}leq{b}$ will occure for $x=a$ if given function is decreasing, like we had in part (i).And opposite, if the function is increasing, $textbf{maximum value}$ on given interval will occure for $x=b$, like we had at part (ii).
an equation for the slope of any secant line on the graph of $h(t)$:
$m=dfrac{h(0.5+h)-h(0.5)}{h}=dfrac{-5(0.5+h)^2+5(0.5+h)+10-11.25}{h}=dfrac{-5(0.25+h+h^2)+2.5+5h-1.25}{h}=dfrac{-1.25-5h-5h^2+1.25+5h}{h}=-dfrac{5h^2}{h}=-5h$
Now, replace $h$ with small numbers, we have next:
$h=-0.01$ $Rightarrow$ $m=0.05$
$h=0.01$ $Rightarrow$ $m=-0.05$
So, we have that:
$textbf{instaneous rate of change}$ = $dfrac{0.05+(-0.05)}{2}=0$
We also have that:
$h(0.5)=11.25$
$h(0.4)=11.2$
$h(0.6)=11.2$
Since the slope of the tangent is equal to zero when $t=0.5$ and since
the values of the function when $t=0.6$ and $t=0.4$ $textbf{are smaller}$ than the value when $t=0.5$, a maximum value occurs at that point.
Now, we will estimate instaneous rate of change in $t=1.5$ s, it suppouse to be $0$ in this moment:
$textbf{instaneous rate of cnage}$ = $dfrac{h(1.6)-h(1.4)}{1.6-1.4}=dfrac{0}{0.2}=0$
an equation for the slope of any secant line on the graph of $R(x)$:
$m=dfrac{R(5)-R(5-h)}{h}=dfrac{30025-(-(5-h)^2+10(5-h)+30000)}{h}=dfrac{25+(5-h)^2-10(5-h)}{h}=dfrac{25+25-10h+h^2-50+10h}{h}=-dfrac{h^2}{h}=h$
Now, replace $h$ with small numbers, we have next:
$h=-0.01$ $Rightarrow$ $m=-0.01$
$h=0.01$ $Rightarrow$ $m=0.01$
So, we have that:
$textbf{instaneous rate of change}$ = $dfrac{0.01+(-0.01)}{2}=0$
We also have that:
$R(5)=30025$
$R(4)=30024$
$R(6)=30024$
Since the slope of the tangent is equal to zero when $x=5$ and since
the values of the function when $x=6$ and $x=4$ $textbf{are smaller}$ than the value when $x=5$, a maximum value occurs at that point.
$dfrac{pi}{2}$ $rightarrow$ $dfrac{1}{k}dfrac{pi}{2}$
$dfrac{1}{k}dfrac{pi}{2}$ $rightarrow$ $dfrac{1}{k}dfrac{pi}{2}+d$
$textbf{So, in this case, maximum value for the transformed function we will get when}$ $x=dfrac{1}{k}dfrac{pi}{2}+d$.
For $x=-2$, we will use interval $-2.01leq{-2}leq-1.99$:
$textbf{instaneous rate of change}$ = $dfrac{f(-1.99)-f(-2.01)}{-1.99+2.01}=-dfrac{0.08}{0.02}=-4$
For $x=-1$, we will use interval $-1.01leq{-1}leq-0.99$:
$textbf{instaneous rate of change}$ = $dfrac{f(-0.99)-f(-1.01)}{-0.99+1.01}=-dfrac{0.04}{0.02}=-2$
For $x=2$, we will use interval $1.99leq{2}leq2.01$:
$textbf{instaneous rate of change}$ = $dfrac{f(2.01)-f(1.99)}{2.01-1.99}=dfrac{0.08}{0.02}=4$
For $x=3$, we will use interval $2.99leq{3}leq3.01$:
$textbf{instaneous rate of change}$ = $dfrac{f(3.01)-f(2.99)}{3.01-2.99}=dfrac{0.12}{0.02}=6$
$textbf{We can conclude that instaneous rate of change for value $x$ is $2x$}$.
Now, we will do the same for function $f(x)=x^3$:
For $x=-2$, we will use interval $-2.01leq{-2}leq-1.99$:
$textbf{instaneous rate of change}$ = $dfrac{f(-1.99)-f(-2.01)}{-1.99+2.01}=dfrac{0.24}{0.02}=12$
For $x=-1$, we will use interval $-1.01leq{-2}leq-0.99$:
$textbf{instaneous rate of change}$ = $dfrac{f(-0.99)-f(-1.01)}{-0.99+1.01}=dfrac{0.06}{0.02}=3$
For $x=2$, we will use interval $1.99leq{2}leq2.01$:
$textbf{instaneous rate of change}$ = $dfrac{f(2.01)-f(1.99)}{2.01-1.99}=dfrac{0.24}{0.02}=12$
$textbf{instaneous rate of change}$ = $dfrac{f(3.01)-f(2.99)}{3.01-2.99}=dfrac{0.54}{0.02}=27$
So, in this case $textbf{we can conclude that instaneous rate of change for given value $x$ is $3x^2$}$.
$f(x)=x^3: 12, 3, 12, 27$; inst.rate of ch=$3x^2$

